Aprendizaje automático y Data Science (Parte 16): Una nueva mirada a los árboles de decisión

Breve panorámica

En un artículo anterior de esta serie, hablamos de los árboles de decisión. Aprendimos qué son y creamos un algoritmo para clasificar datos meteorológicos. Sin embargo, el código y las explicaciones presentadas en ese artículo aparentemente no eran lo suficientemente claras, pues aún recibo mensajes pidiendo un enfoque mejor para construir árboles de decisión. Por eso me ha parecido que merece la pena escribir un segundo artículo y ofrecer un código mejor. Además, una buena comprensión de los árboles de decisión resulta esencial para dar el siguiente paso: los algoritmos de bosque aleatorio, de los que hablaremos en los siguientes artículos.

¿Qué es un árbol de decisión?

Un árbol de decisión es una estructura de árbol similar a un diagrama de flujo en la que cada nodo interno representa la verificación de un atributo (o característica), cada rama representa el resultado de la verificación y cada nodo hoja representa una etiqueta de clase o un valor continuo. El nodo superior de un árbol de decisión se denomina "raíz", mientras que las hojas son los resultados o predicciones.

¿Qué es un nodo?

En un árbol de decisión, un nodo es un componente fundamental que representa un punto de decisión basado en una característica o atributos concretos. Existen dos tipos principales de nodos en el árbol de decisión: los nodos internos y los nodos hoja.

Nodo interno

• Un nodo interno es un punto de decisión en el árbol en el que se verifica una característica concreta. La verificación se basa en una determinada condición, por ejemplo, si el valor de una característica supera un umbral o pertenece a una determinada categoría.
• Los nodos internos tienen ramas (aristas) que conducen a nodos hijos. El resultado de la verificación determinará qué rama seguir.
• Los nodos internos, que son los dos nodos hijos izquierdo y derecho, son nodos dentro del nodo central del árbol.

Nodo hoja (o nodo terminal)

• Un nodo hoja es el punto final del árbol donde se toma la decisión o predicción final, y denota la etiqueta de clase en una tarea de clasificación, o el valor predicho en una tarea de regresión.
• Los nodos hoja no tienen ramas que surjan de ellos, son los puntos finales del proceso de toma de decisiones.
• En el código, los representaremos usando una variable de tipo double.

class Node
{
  public:
    // for decision node
       
    uint feature_index;
    double threshold;
    double info_gain;
     
    // for leaf node
     
    double leaf_value;   
      
    Node *left_child;  //left child Node
    Node *right_child; //right child Node

    Node() : left_child(NULL), right_child(NULL) {} // default constructor

    Node(uint feature_index_, double threshold_=NULL, Node *left_=NULL, Node *right_=NULL, double info_gain_=NULL, double value_=NULL)
        : left_child(left_), right_child(right_)
    {
        this.feature_index = feature_index_;
        this.threshold = threshold_;
        this.info_gain = info_gain_;
        this.value = value_;
    }
    
   void Print()
    {
      printf("feature_index: %d \nthreshold: %f \ninfo_gain: %f \nleaf_value: %f",feature_index,threshold, info_gain, value);
    }    
};

A diferencia de algunos de los algoritmos de aprendizaje automático que hemos escrito desde cero como parte de esta serie, los árboles de decisión pueden ser difíciles de representar usando código y resultan a veces confusos porque requieren el uso de clases y funciones recursivas. En mi experiencia, esto puede ser muy difícil de representar en cualquier lenguaje, excepto Python.

Componentes del nodo:

Un nodo de un árbol de decisión suele contener la siguiente información:

01. Condiciones de verificación

Los nodos internos tienen condiciones de verificación basadas en un atributo y un umbral o categoría específicos. Esta condición determina cómo se dividirán los datos en nodos hijos.

Usted no ve una condición de verificación en esta clase Node. La implementaremos dentro de la función build_tree, que se integra con la clase node porque devuelve un ejemplar de la clase node.

Node *build_tree(matrix &data, uint curr_depth=0);

02. Característica y valor umbral

Indica qué atributo se está comprobando en el nodo y el valor umbral o la categoría usada para la separación.

uint feature_index;
double threshold;

03. Etiqueta o valor de la clase

Un nodo hoja almacena la etiqueta de la clase (para la clasificación) o el valor (para la regresión) predichos.

double leaf_value;   

04. Nodos hijos

Los nodos internos tienen nodos hijos que se corresponden con los diferentes resultados de la condición de verificación. Cada nodo hijo representa un subconjunto de datos que cumple la condición.

Node *left_child;  //left child Node
Node *right_child; //right child Node

Ejemplo

Vamos a analizar un árbol de decisión simple para clasificar si una fruta es una manzana o una naranja, basándonos en su color.

[Nodo]

Característica: color

Condición de la prueba: ¿el color es rojo?

Si es igual a True, se desplazará al hijo izquierdo, y si es false, se desplazará al hijo derecho

[Nudo hoja - manzana]

-Etiqueta de clase: manzana

[Nudo hoja - naranja]

-Etiqueta de clase: naranja

Tipos de árboles de decisión:

Árboles de clasificación y regresión CART (Classification and Regression Trees): se utiliza tanto para tareas de clasificación como de regresión. Separa los datos según el criterio de Gini en caso de clasificación y del error estándar de la media en caso de regresión.

ID3 (Dicotomizador iterativo 3): se utiliza principalmente para tareas de clasificación. Usa el concepto de entropía e información incremental para tomar decisiones.

C4.5 es la versión mejorada de ID3 utilizada para la categorización. Usa un factor de ganancia para eliminar el desplazamiento hacia los atributos con más niveles.

Como utilizaremos un árbol de decisión con fines clasificatorios, construiremos un algoritmo ID3 que funcione basándose en la ganancia de información, el cálculo de criterios y las características categóricas:

ID3 (dicotomizador iterativo 3)

El ID3 utiliza el criterio de ganancia de información para seleccionar la mejor división de datos en cada nodo interno del árbol. El criterio de ganancia de información mide la reducción de entropía o incertidumbre tras dividir un conjunto de datos.

double CDecisionTree::information_gain(vector &parent, vector &left_child, vector &right_child)
 {  
    double weight_left = left_child.Size() / (double)parent.Size(),
           weight_right = right_child.Size() / (double)parent.Size();
    
    double gain =0;    
    switch(m_mode)
      {
       case  MODE_GINI:
         gain = gini_index(parent) - ( (weight_left*gini_index(left_child)) + (weight_right*gini_index(right_child)) );
         break;
       case MODE_ENTROPY:
         gain = entropy(parent) - ( (weight_left*entropy(left_child)) + (weight_right*entropy(right_child)) );
         break;
      }
    
   return gain;
 }

La entropía es la medida de la incertidumbre o el desorden en un conjunto de datos. El algoritmo ID3 trata de reducir la entropía seleccionando una división de características que dé lugar a subconjuntos con etiquetas de clase más homogéneas.

double CDecisionTree::entropy(vector &y)
 {    
   vector class_labels = matrix_utils.Unique_count(y);
     
   vector p_cls = class_labels / double(y.Size());
  
   vector entropy = (-1 * p_cls) * log2(p_cls);
  
  return entropy.Sum();
 }

Para obtener más flexibilidad, podemos elegir entre la entropía y el criterio de Gini, que también se utiliza a menudo en los árboles de decisión y realiza la misma función que la entropía. Ambos estiman la impureza o el desorden en el conjunto de datos.

double CDecisionTree::gini_index(vector &y)
 {
   vector unique = matrix_utils.Unique_count(y);
   
   vector probabilities = unique / (double)y.Size();
   
   return 1.0 - MathPow(probabilities, 2).Sum();
 }

Aquí tenemos las fórmulas para calcular estos valores:

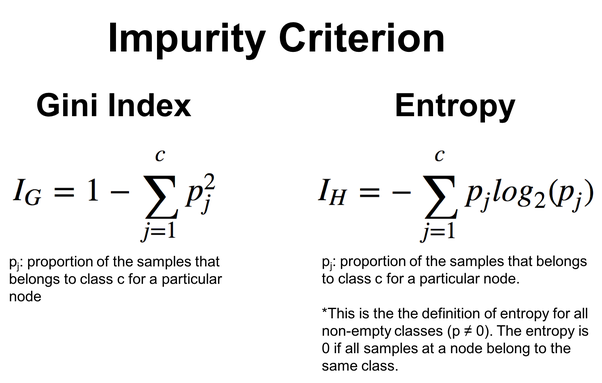
El algoritmo ID3 resulta especialmente adecuado para características categóricas, mientras que la selección de características y umbrales se basa en la reducción de entropía para la categorización. Más abajo veremos este principio en acción con el ejemplo del algoritmo del árbol de decisión.

Algoritmo del árbol de decisión

01. Criterios de separación

Los criterios estándar para separar datos en la clasificación son el coeficiente de Gini y la entropía, mientra que para los problemas de regresión será el error cuadrático medio. Nos centraremos en las funciones de división del algoritmo del árbol de decisión, que comienza con una estructura para almacenar la información de los datos que se van a dividir.

//A struct containing splitted data information
struct split_info
  {
   uint feature_index;
   double threshold;
   matrix dataset_left,
          dataset_right;
   double info_gain;
  };

Usando el valor umbral, dividiremos los datos y pondremos los objetos con valores inferiores a este umbral en la matriz dataset_left y el resto en dataset_right. Después, devuelve un ejemplar de la estructura Split_info. 

split_info CDecisionTree::split_data(const matrix &data, uint feature_index, double threshold=0.5)
 {
   int left_size=0, right_size =0;
   vector row = {};
   
   split_info split;
   
   ulong cols = data.Cols();
   
   split.dataset_left.Resize(0, cols);
   split.dataset_right.Resize(0, cols);
      
    for (ulong i=0; i<data.Rows(); i++)
     {       
       row = data.Row(i);
       
       if (row[feature_index] <= threshold)
        {
          left_size++;
          split.dataset_left.Resize(left_size, cols);
          split.dataset_left.Row(row, left_size-1); 
        }
       else
        {
         right_size++;
         split.dataset_right.Resize(right_size, cols);
         split.dataset_right.Row(row, right_size-1);         
        }
     }
   return split;
 }

A partir del conjunto de divisiones, el algoritmo deberá determinar cuál es la mejor, es decir, la que proporciona la máxima ganancia de información.

split_info CDecisionTree::get_best_split(matrix &data, uint num_features)
  {
  
   double max_info_gain = -DBL_MAX;
   vector feature_values = {};
   vector left_v={}, right_v={}, y_v={};
   
//---
   
   split_info best_split;
   split_info split;
   
   for (uint i=0; i<num_features; i++)
     {
       feature_values = data.Col(i);
       vector possible_thresholds = matrix_utils.Unique(feature_values); //Find unique values in the feature, representing possible thresholds for splitting.
                  
         for (uint j=0; j<possible_thresholds.Size(); j++)
            {              
              split = this.split_data(data, i, possible_thresholds[j]);
              
              if (split.dataset_left.Rows()>0 && split.dataset_right.Rows() > 0)
                {
                  y_v = data.Col(data.Cols()-1);
                  right_v = split.dataset_right.Col(split.dataset_right.Cols()-1);
                  left_v = split.dataset_left.Col(split.dataset_left.Cols()-1);
                  
                  double curr_info_gain = this.information_gain(y_v, left_v, right_v);
                                    
                  if (curr_info_gain > max_info_gain) // Check if the current information gain is greater than the maximum observed so far.
                    {             
                      #ifdef DEBUG_MODE
                        printf("split left: [%dx%d] split right: [%dx%d] curr_info_gain: %f max_info_gain: %f",split.dataset_left.Rows(),split.dataset_left.Cols(),split.dataset_right.Rows(),split.dataset_right.Cols(),curr_info_gain,max_info_gain);
                      #endif 
                      
                      best_split.feature_index = i;
                      best_split.threshold = possible_thresholds[j];
                      best_split.dataset_left = split.dataset_left;
                      best_split.dataset_right = split.dataset_right;
                      best_split.info_gain = curr_info_gain;
                      
                      max_info_gain = curr_info_gain;
                    }
                }
            }    
     }
     
    return best_split;
  }

La función busca características comunes y posibles umbrales para hallar la mejor división que maximice la ganancia de información. El resultado es una estructura split_info que contiene información sobre el objeto, el valor umbral y los subconjuntos asociados a la mejor división.

02. Construcción del árbol

Los árboles de decisión se construyen dividiendo recursivamente el conjunto de datos según las características hasta que se cumple una condición de parada (por ejemplo, alcanzar una determinada profundidad o un número mínimo de muestras).

Node *CDecisionTree::build_tree(matrix &data, uint curr_depth=0)
 {
    matrix X;
    vector Y;
      
    matrix_utils.XandYSplitMatrices(data,X,Y); //Split the input matrix into feature matrix X and target vector Y.
    
    ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset.
        
    Node *node= NULL; // Initialize node pointer
            
    if (samples >= m_min_samples_split && curr_depth<=m_max_depth)
      {
         split_info best_split = this.get_best_split(data, (uint)features);
         
         #ifdef DEBUG_MODE
          Print("best_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold);
         #endif 
                  
         if (best_split.info_gain > 0)
           {
             Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1);
             Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1);
                          
             node = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain);
             return node;
           }
      }      
     
     node = new Node();
     node.leaf_value = this.calculate_leaf_value(Y);
          
     return node;
 }

if (best_split.info_gain > 0):

La línea de código anterior verifica si se ha recibido la información.

Dentro de esta unidad, sucede lo siguiente:

Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1);

Creamos recursivamente el nodo hijo izquierdo.

Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1);

Creamos recursivamente el nodo hijo correcto.

node = new Node(best_split.feature_index, best_split.threshold, left_child, right_child, best_split.info_gain);

Creamos un nodo de decisión con la información de la mejor división.

node = new Node();      

Si no se requieren más divisiones, crearemos un nuevo nodo hoja.

node.value = this.calculate_leaf_value(Y);

Luego estableceremos el valor del nodo hoja utilizando la función calculate_leaf_value.

return node;

Y retornaremos el nodo que represente la división u hoja actual.

Para facilitar el trabajo con las funciones, la función build_tree puede dejarse dentro de la función de aptitud, que se utiliza habitualmente en los módulos de aprendizaje automático en Python.

void CDecisionTree::fit(matrix &x, vector &y)
 {
   matrix data = matrix_utils.concatenate(x, y, 1);
   
   this.root = this.build_tree(data);
 }

Luego haremos predicciones al entrenar y probar el modelo

vector CDecisionTree::predict(matrix &x)
 {
    vector ret(x.Rows());
    
    for (ulong i=0; i<x.Rows(); i++)
       ret[i] = this.predict(x.Row(i));
       
   return ret;
 }

Haremos las predicciones en tiempo real

double CDecisionTree::predict(vector &x)
 {     
   return this.make_predictions(x, this.root);
 }

Todo el trabajo sucio relacionado se realizará en la función make_predictions:

double CDecisionTree::make_predictions(vector &x, const Node &tree)
 {
    if (tree.leaf_value != NULL) // This is a leaf leaf_value
      return tree.leaf_value;
      
    double feature_value = x[tree.feature_index];
    double pred = 0;
    
    #ifdef DEBUG_MODE
      printf("Tree.threshold %f tree.feature_index %d leaf_value %f",tree.threshold,tree.feature_index,tree.leaf_value);
    #endif 
    
    if (feature_value <= tree.threshold)
      {
       pred = this.make_predictions(x, tree.left_child);  
      }
    else
     {
       pred = this.make_predictions(x, tree.right_child);
     }
     
   return pred;
 }

Más información:

Ahora comprobaremos si el valor de la característica es menor o igual que el valor umbral del nodo actual.

if (feature_value <= tree.threshold): 

Dentro de esta unidad, sucede lo siguiente:

Después llamaremos recursivamente a la función make_predictions para el nodo hijo izquierdo.

pred = this.make_predictions(x, *tree.left_child);

En caso contrario, si (Else, If) el valor de la característica superará el valor umbral:

Luego llamaremos recursivamente a la función make_predictions para el nodo hijo derecho.

pred = this.make_predictions(x, *tree.right_child);

return pred;

 Retornamos la previsión.

Cálculo de los valores de las hojas

La siguiente función calcula el valor de la hoja:

double CDecisionTree::calculate_leaf_value(vector &Y)
 {   
   vector uniques = matrix_utils.Unique_count(Y);
   vector classes = matrix_utils.Unique(Y);
   
   return classes[uniques.ArgMax()];
 }

La función retornará el elemento de Y con el número más alto, es decir, encontrará el elemento más común de la lista.

Todo esto se reduce a la clase CDecisionTree

enum mode {MODE_ENTROPY, MODE_GINI};

class CDecisionTree
  {
CMatrixutils   matrix_utils;

protected:
      
   Node *build_tree(matrix &data, uint curr_depth=0);
   double  calculate_leaf_value(vector &Y);
   
//---
   
   uint m_max_depth;
   uint m_min_samples_split;
   
   mode m_mode;
   
   double  gini_index(vector &y);
   double  entropy(vector &y);
   double  information_gain(vector &parent, vector &left_child, vector &right_child);
   
   
   split_info  get_best_split(matrix &data, uint num_features);
   split_info  split_data(const matrix &data, uint feature_index, double threshold=0.5);
   
   double make_predictions(vector &x, const Node &tree);
   void delete_tree(Node* node);
   
public:
                     Node *root;
                     
                     CDecisionTree(uint min_samples_split=2, uint max_depth=2, mode mode_=MODE_GINI);
                    ~CDecisionTree(void);
                    
                     void fit(matrix &x, vector &y);
                     void print_tree(Node *tree, string indent=" ",string padl="");
                     double predict(vector &x);
                     vector predict(matrix &x);
  };

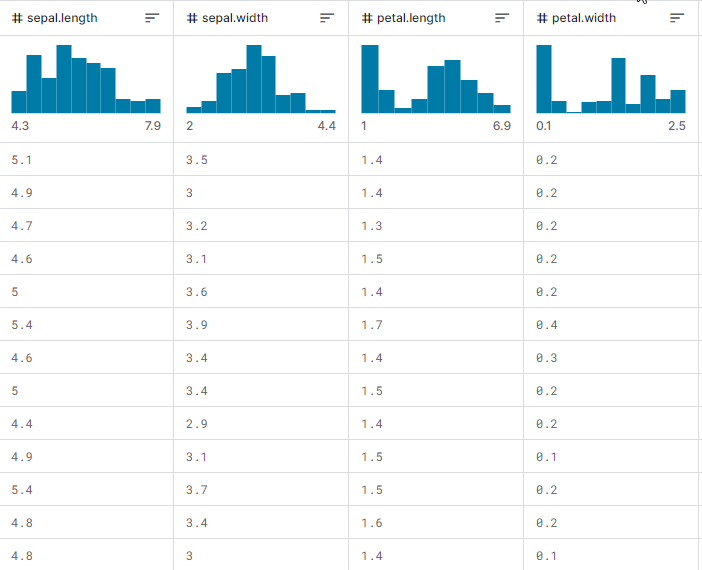
Ahora veremos cómo funciona todo en acción, cómo construir un árbol y cómo utilizarlo para la previsión en el entrenamiento y las pruebas, así como en el comercio en tiempo real. Trabajaremos con la muestra de datos iris-CSV y comprobaremos el funcionamiento en la clase.

Entrenaremos el modelo de árbol de decisión en cada inicialización del asesor experto, comenzando con la carga de los datos de entrenamiento desde el archivo CSV:

int OnInit()
  {
  matrix dataset = matrix_utils.ReadCsv("iris.csv"); //loading iris-data
  
  decision_tree = new CDecisionTree(3,3, MODE_GINI); //Initializing the decision tree
  
  matrix x; vector y;
  matrix_utils.XandYSplitMatrices(dataset,x,y); //split the data into x and y matrix and vector respectively
  
  
  decision_tree.fit(x, y);  //Building the tree
  decision_tree.print_tree(decision_tree.root); //Printing the tree
  
  vector preds = decision_tree.predict(x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(y, preds)); //Measuring the accuracy
  
   return(INIT_SUCCEEDED);
  }

Este será el aspecto de la matriz de conjuntos de datos al mostrarse. La última columna ha pasado por el codificador. Uno (1) significa Setosa, dos (2) Versicolor y tres (3) Virginica.

Print("iris-csv\n",dataset);

MS      0       08:54:40.958    DecisionTree Test (EURUSD,H1)   iris-csv
PH      0       08:54:40.958    DecisionTree Test (EURUSD,H1)   [[5.1,3.5,1.4,0.2,1]
CO      0       08:54:40.958    DecisionTree Test (EURUSD,H1)    [4.9,3,1.4,0.2,1]
...
...

NS      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [5.6,2.7,4.2,1.3,2]
JK      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [5.7,3,4.2,1.2,2]
...
...

NQ      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [6.2,3.4,5.4,2.3,3]
PD      0       08:54:40.959    DecisionTree Test (EURUSD,H1)    [5.9,3,5.1,1.8,3]]

Muestra del árbol

Si observamos detenidamente el código, veremos que la función print_tree toma la raíz del árbol como uno de sus argumentos. Esta función intenta registrar una vista general del árbol. Veamos su trabajo más de cerca.

void CDecisionTree::print_tree(Node *tree, string indent=" ",string padl="")
  {
     if (tree.leaf_value != NULL)
        Print((padl+indent+": "),tree.leaf_value); 
     else //if we havent' reached the leaf node keep printing child trees
       {
         padl += " ";
         
         Print((padl+indent)+": X_",tree.feature_index, "<=", tree.threshold, "?", tree.info_gain);
         
         print_tree(tree.left_child, "left","--->"+padl);
         
         print_tree(tree.right_child, "right","--->"+padl);
       }
  }  

Más información:

Estructura del nodo:

La función asume que la clase Node representa un árbol de decisión. Cada nodo puede ser un nodo de decisión o un nodo finito. Los nodos de decisión tienen el índice de característica feature_index, el umbral threshold, la información info_gain y el valor de hoja leaf_value.

Muestra del nodo de solución:

Si el nodo actual no es un nodo final (es decir, tree.leaf_value es igual a NULL), la función ofrecerá información sobre el nodo de decisión. Se mostrará una condición para la separación, por ejemplo, "X_2 <= 1,9 ? 0,33" y el nivel de separación.

Muestra del nodo hoja:

Si el nodo actual es un nodo hoja (es decir, tree.leaf_value no es NULL), mostrará el valor final junto con el nivel de separación. Por ejemplo, "left: 0.33".

Recursión:

A continuación, la función se llamará a sí misma recursivamente para los hijos izquierdo y derecho del nodo Node actual. El argumento padl añadirá una separación al mensaje, haciendo que la estructura de árbol sea más legible.

Muestra de print_tree para el árbol de decisión construido dentro de la función OnInit:

CR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)     : X_2<=1.9?0.3333333333333334
HO      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   ---> left: 1.0
RH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->  right: X_3<=1.7?0.38969404186795487
HP      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->   left: X_2<=4.9?0.08239026063100136
KO      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_3<=1.6?0.04079861111111116
DH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 2.0
HM      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 3.0
HS      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_3<=1.5?0.2222222222222222
IH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 3.0
QM      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 2.0
KP      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->   right: X_2<=4.8?0.013547574039067499
PH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_0<=5.9?0.4444444444444444
PE      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 2.0
DP      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 3.0
EE      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   --->--->--->   right: 3.0

Impresionante.

A continuación mostraremos la precisión de nuestro modelo entrenado:

  vector preds = decision_tree.predict(x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(y, preds)); //Measuring the accuracy

Resultados

PM      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Confusion Matrix
CE      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   [[50,0,0]
HR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)    [0,50,0]
ND      0       09:26:39.990    DecisionTree Test (EURUSD,H1)    [0,1,49]]
GS      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   
KF      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Classification Report
IR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   
MD      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
EQ      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   1.0    50.00     50.00     100.00       50.00     50.0
HR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   2.0    51.00     50.00     100.00       50.50     50.0
PO      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   3.0    49.00     50.00     100.00       49.49     50.0
EH      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   
PR      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.99
HQ      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Average   50.00    50.00    100.00      50.00    150.0
DJ      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   W Avg     50.00    50.00    100.00      50.00    150.0
LG      0       09:26:39.990    DecisionTree Test (EURUSD,H1)   Train Acc = 0.993

Hemos alcanzado una precisión del 99,3%, lo cual indica que nuestro árbol de decisión se ha aplicado con éxito. Esta precisión resulta coherente con lo que cabría esperar del modelo Scikit-Learn al resolver un problema de conjunto de datos simple.

Vamos a continuar el entrenamiento y a probar el modelo con datos fuera de muestra.

  matrix train_x, test_x;
  vector train_y, test_y;
  
  matrix_utils.TrainTestSplitMatrices(dataset, train_x, train_y, test_x, test_y, 0.8, 42); //split the data into training and testing samples

  
  decision_tree.fit(train_x, train_y);  //Building the tree
  decision_tree.print_tree(decision_tree.root); //Printing the tree
  
  vector preds = decision_tree.predict(train_x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(train_y, preds)); //Measuring the accuracy
  
//---

  preds = decision_tree.predict(test_x); //making the predictions on a test data
  
  Print("Test Acc = ",metrics.confusion_matrix(test_y, preds)); //Measuring the accuracy

Resultados

QD      0       14:56:03.860    DecisionTree Test (EURUSD,H1)     : X_2<=1.7?0.34125
LL      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   ---> left: 1.0
QK      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->  right: X_3<=1.6?0.42857142857142855
GS      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->   left: X_2<=4.9?0.09693877551020412
IL      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->   left: 2.0
MD      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_3<=1.5?0.375
IS      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: 3.0
QR      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: 2.0
RH      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   --->--->  right: 3.0
HP      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Confusion Matrix
FG      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   [[42,0,0]
EO      0       14:56:03.860    DecisionTree Test (EURUSD,H1)    [0,39,0]
HK      0       14:56:03.860    DecisionTree Test (EURUSD,H1)    [0,0,39]]
OL      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   
KE      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Classification Report
QO      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   
MQ      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
OQ      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   1.0    42.00     42.00     78.00       42.00     42.0
ML      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   3.0    39.00     39.00     81.00       39.00     39.0
HK      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   2.0    39.00     39.00     81.00       39.00     39.0
OE      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   
EO      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Accuracy                                   1.00
CG      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Average   40.00    40.00    80.00      40.00    120.0
LF      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   W Avg     40.05    40.05    79.95      40.05    120.0
PR      0       14:56:03.860    DecisionTree Test (EURUSD,H1)   Train Acc = 1.0
CD      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Confusion Matrix
FO      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   [[9,2,0]
RK      0       14:56:03.861    DecisionTree Test (EURUSD,H1)    [1,10,0]
CL      0       14:56:03.861    DecisionTree Test (EURUSD,H1)    [2,0,6]]
HK      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   
DQ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Classification Report
JJ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   
FM      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
QM      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   2.0    12.00     11.00     19.00       11.48     11.0
PH      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   3.0    12.00     11.00     19.00       11.48     11.0
KD      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   1.0    6.00     8.00     22.00       6.86     8.0
PP      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   
LJ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.83
NJ      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Average   10.00    10.00    20.00      9.94    30.0
JR      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   W Avg     10.40    10.20    19.80      10.25    30.0
HP      0       14:56:03.861    DecisionTree Test (EURUSD,H1)   Test Acc = 0.833

El modelo tiene una precisión del 100% en los datos de entrenamiento y del 83% en los datos fuera de muestra.

El árbol de decisión y la IA en el comercio 

No obstante lo dicho, a nosotros nos interesa un ámbito específico de aplicación de los modelos basados en árboles de decisión: el comercio. Para usar este modelo en el comercio, deberemos formular el problema a resolver.

El problema:

Usaremos un modelo de árbol de decisión de IA para hacer predicciones sobre la barra actual en cuanto a si el mercado está subiendo o bajando.

Como con cualquier modelo, ofreceremos a nuestro modelo un conjunto de datos de entrenamiento. Para ello, usaremos dos indicadores de tipo oscilador: el indicador RSI y el oscilador estocástico. En esencia, necesitaremos que el modelo comprenda los patrones entre estos dos indicadores y cómo determinan el movimiento del precio en la barra actual.

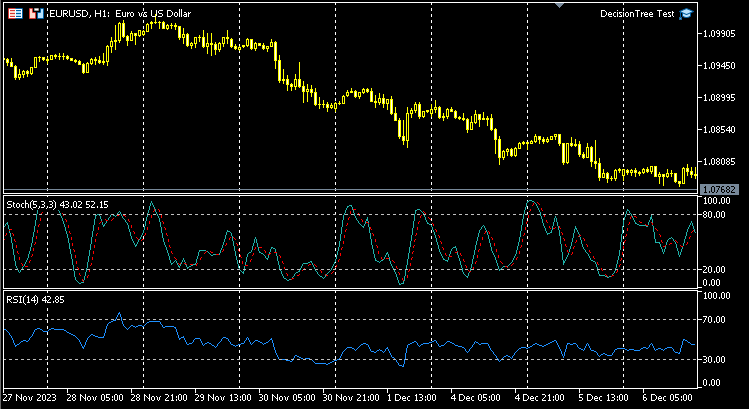
Estructura de datos:

A continuación le mostraremos la estructura en la que se almacenan los datos recogidos para el entrenamiento y las pruebas. Lo mismo ocurrirá con los datos utilizados para las previsiones en tiempo real.

struct data{
   vector stoch_buff, 
          signal_buff, 
          rsi_buff, 
          target;
} data_struct;

Recogida de datos, entrenamiento y prueba del árbol de decisión

void TrainTree()
 {
  matrix dataset(train_bars, 4);
  vector v;

//--- Collecting indicator buffers

  data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 1, train_bars);
  data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 1, train_bars);
  data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 1, train_bars);
  
//--- Preparing the target variable
   
  MqlRates rates[];
  ArraySetAsSeries(rates, true); 
  int size = CopyRates(Symbol(), PERIOD_CURRENT, 1,train_bars, rates);
  
  data_struct.target.Resize(size); //Resize the target vector
  
  for (int i=0; i<size; i++)
    {
      if (rates[i].close > rates[i].open)
        data_struct.target[i] = 1;
      else 
        data_struct.target[i] = -1;
    }
  
  dataset.Col(data_struct.rsi_buff, 0);
  dataset.Col(data_struct.stoch_buff, 1);
  dataset.Col(data_struct.signal_buff, 2);
  dataset.Col(data_struct.target, 3);
   
  decision_tree = new CDecisionTree(min_sample,max_depth_, tree_mode); //Initializing the decision tree
  

  matrix train_x, test_x;
  vector train_y, test_y;
  
  matrix_utils.TrainTestSplitMatrices(dataset, train_x, train_y, test_x, test_y, 0.8, 42); //split the data into training and testing samples

  
  decision_tree.fit(train_x, train_y);  //Building the tree
  decision_tree.print_tree(decision_tree.root); //Printing the tree
  
  vector preds = decision_tree.predict(train_x); //making the predictions on a training data
  
  Print("Train Acc = ",metrics.confusion_matrix(train_y, preds)); //Measuring the accuracy
  
//---

  preds = decision_tree.predict(test_x); //making the predictions on a test data
  
  Print("Test Acc = ",metrics.confusion_matrix(test_y, preds)); //Measuring the accuracy
 }

Hemos fijado la muestra mínima (parámetro min-sample) en 3 y la profundidad máxima (max-depth) = 5.

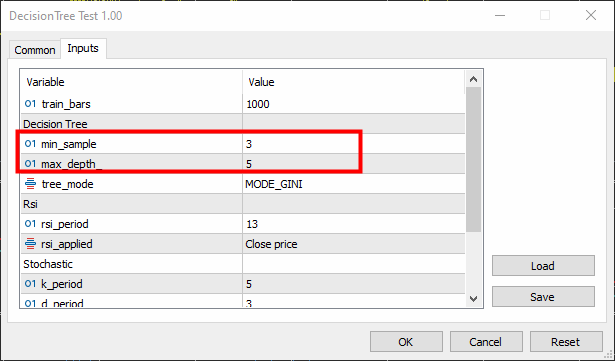
Resultados

KR      0       16:26:53.028    DecisionTree Test (EURUSD,H1)     : X_0<=65.88930872549261?0.0058610536710859695
CN      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->  left: X_0<=29.19882857713344?0.003187469522387243
FK      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->   left: X_1<=26.851851851853503?0.030198175526895188
RI      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_2<=7.319205739522295?0.040050858232676456
KG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=23.08345903222593?0.04347468770545693
JF      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_0<=21.6795921184317?0.09375
PF      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
ER      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: -1.0
QF      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_2<=3.223853479489069?0.09876543209876543
LH      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
FJ      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
MM      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
MG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->   right: 1.0
HH      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->   right: X_0<=65.4606831930956?0.0030639039663222234
JR      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_0<=31.628407983040333?0.00271101025966336
PS      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=31.20436037455599?0.0944903581267218
DO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_2<=14.629981942657205?0.11111111111111116
EO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: 1.0
IG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: -1.0
EI      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     right: 1.0
LO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->     right: X_0<=32.4469112469684?0.003164795835173595
RO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_1<=76.9736842105244?0.21875
RO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
PG      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
MO      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_0<=61.82001028403415?0.0024932856070305487
LQ      0       16:26:53.028    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
EQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
LE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_2<=84.68660541575225?0.09375
ED      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    left: -1.0
LM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
NE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->  right: X_0<=85.28191275702572?0.024468404842877933
DK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->   left: X_1<=25.913621262458935?0.01603292204455742
LE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    left: X_0<=72.18709160232456?0.2222222222222222
ED      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_1<=15.458937198072245?0.4444444444444444
QQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     left: 1.0
CS      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     right: -1.0
JE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
QM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_0<=69.83504428897093?0.012164425148527835
HP      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=68.39798826749553?0.07844460227272732
DL      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      left: X_1<=90.68322981366397?0.06611570247933873
DO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: 1.0
OE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
LI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_1<=88.05704099821516?0.11523809523809525
DE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: 1.0
DM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: -1.0
LG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     right: X_0<=70.41747488780877?0.015360959832756427
OI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     left: 1.0
PI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_0<=70.56490391752676?0.02275277028755862
CF      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
MO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
EG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->   right: X_1<=97.0643939393936?0.10888888888888892
CJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->   left: 1.0
GN      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->    right: X_0<=90.20261550045987?0.07901234567901233
CP      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->     left: X_0<=85.94461490761033?0.21333333333333332
HN      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->     left: -1.0
GE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->      right: X_1<=99.66856060606052?0.4444444444444444
GK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      left: -1.0
IK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->--->--->      right: 1.0
JM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   --->--->--->--->    right: -1.0
KE      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Confusion Matrix
DO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   [[122,271]
QF      0       16:26:53.029    DecisionTree Test (EURUSD,H1)    [51,356]]
HS      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
LF      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Classification Report
JR      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
ND      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
GQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   1.0    173.00     393.00     407.00       240.24     393.0
HQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   -1.0    627.00     407.00     393.00       493.60     407.0
PM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
OG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.60
EO      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Average   400.00    400.00    400.00      366.92    800.0
GN      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   W Avg     403.97    400.12    399.88      369.14    800.0
LM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Train Acc = 0.598
GK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Confusion Matrix
CQ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   [[75,13]
CK      0       16:26:53.029    DecisionTree Test (EURUSD,H1)    [86,26]]
NI      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
RP      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Classification Report
HH      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
LR      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   _    Precision  Recall  Specificity  F1 score  Support
EM      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   -1.0    161.00     88.00     112.00       113.80     88.0
NJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   1.0    39.00     112.00     88.00       57.85     112.0
LJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   
EL      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Accuracy                                   0.51
RG      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Average   100.00    100.00    100.00      85.83    200.0
ID      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   W Avg     92.68    101.44    98.56      82.47    200.0
JJ      0       16:26:53.029    DecisionTree Test (EURUSD,H1)   Test Acc = 0.505

El modelo ha mostrado una precisión del 60% durante el entrenamiento y del 50,5% durante las pruebas. El resultado, por decirlo suavemente, no ha sido bueno. Puede haber muchas razones, como la calidad de los datos usados para construir el modelo o la presencia de malos predictores. La causa más común puede ser que los parámetros del modelo no se hayan ajustado correctamente.

Para solucionar esto, deberemos personalizar los parámetros para encontrar los más adecuados para nuestros fines específicos. 

Ahora vamos a escribir una función que realice predicciones en tiempo real. 

int desisionTreeSignal()
 {
//--- Copy the current bar information only

   data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 0, 1);
   data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 0, 1);
   data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 0, 1);
   
   x_vars[0] = data_struct.rsi_buff[0];
   x_vars[1] = data_struct.stoch_buff[0];
   x_vars[2] = data_struct.signal_buff[0];
   
   return int(decision_tree.predict(x_vars));
 }

Utilizaremos una lógica simple para negociar:

Si el árbol de decisión pronostica -1 (lo cual significa que la vela cerrará a la baja), abriremos una transacción de venta. Si pronostica una clase 1 (que indica que la vela cerrará más alto de lo que se ha abierto), colocaremos una transacción de compra.

void OnTick()
  {
//---
    if (!train_once)              // You want to train once during EA lifetime 
      TrainTree();
    train_once = true;
    
    if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening 
      {
        int signal = desisionTreeSignal();
        double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
        SymbolInfoTick(Symbol(), ticks);
        
         if (signal == -1)
           {
              if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist
                m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point());
           }
         else
           {
             if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY))  // If a buy trade doesnt exist
               m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point());
           }
      }
  }

Hemos hecho la prueba en un periodo de un mes de 01/01/2023 a 01/02/2023 a los precios de apertura, solo para ver si funcionaría.

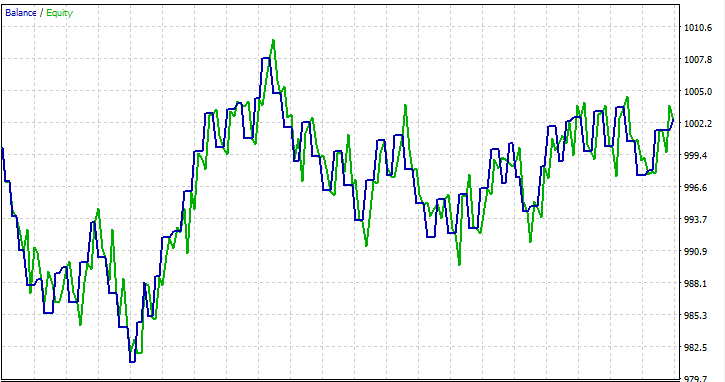
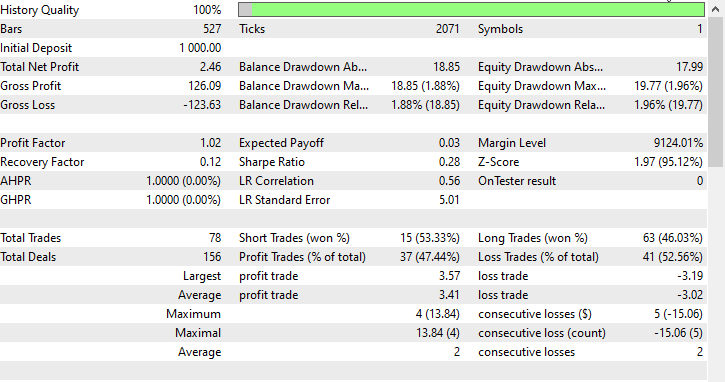
Preguntas frecuentes sobre árboles de decisión en el trading:

Pregunta	Respuesta
¿Es importante la normalización de las entradas en los árboles de decisión?	No, la normalización en general no resulta crucial para los árboles de decisión. Los árboles de decisión se dividen según los umbrales de las funciones, y la escala de las funciones no afecta a la estructura del árbol. No obstante, recomendamos comprobar el efecto de la normalización en el rendimiento del modelo.
¿Cómo procesan los árboles de decisión las variables categóricas en los datos comerciales?	Los árboles de decisión pueden procesar de forma natural variables categóricas. Realizan divisiones binarias en función de si se cumple una condición, incluidas las condiciones para variables categóricas. El árbol identificará los puntos de división óptimos para las características categóricas.
¿Pueden usarse los árboles de decisión para predecir series temporales en el comercio?	Aunque los árboles de decisión pueden utilizarse para la previsión de series temporales en el comercio, no resultan tan eficaces para captar patrones temporales complejos como, por ejemplo, las redes neuronales recurrentes (RNN) y otros modelos similares. Dicho esto, los métodos de conjunto, como los bosques aleatorios, pueden ofrecer una mayor fiabilidad.
¿Son susceptibles los árboles de decisión al problema del sobreentrenamiento?	Los árboles de decisión, especialmente los árboles de decisión profundos, pueden resultar propensos al sobreentrenamiento debido al ruido en los datos de entrenamiento. Técnicas como la poda y la limitación de la profundidad de los árboles pueden utilizarse para evitar el sobreentrenamiento en los programas comerciales.
¿Son adecuados los árboles de decisión para analizar la importancia de las características en los modelos comerciales?	Sí, los árboles de decisión son un método natural de evaluar la importancia de las características. Las características que más contribuyen a dividir las decisiones en la parte superior del árbol tienden a ser más importantes. Este análisis puede ofrecer información sobre los factores que influyen en las decisiones comerciales.
¿Son sensibles los árboles de decisión a los valores atípicos de los datos?	Los árboles de decisión pueden ser sensibles a estos, sobre todo si el árbol es profundo. Los valores atípicos pueden provocar divisiones debido al ruido. Para reducir esta sensibilidad, podemos aplicar pasos de preprocesamiento durante los cuales se detectan y eliminan dichos valores atípicos.
¿Existen hiperparámetros concretos personalizables para los árboles de decisión en los modelos de negociación?	Sí, los hiperparámetros clave personalizables incluyen la profundidad del árbol la muestra mínima por hoja el criterio de división (por ejemplo, el criterio de Gini o la entropía). Podemos utilizar la validación cruzada para encontrar los valores óptimos de los hiperparámetros para determinados conjuntos de datos.
¿Pueden los árboles de decisión formar parte de un enfoque de conjunto?	Sí, los árboles de decisión pueden formar parte de métodos de conjunto, como los bosques aleatorios, que combinan varios árboles para mejorar el rendimiento general del pronóstico. Los métodos de conjunto suelen ser sólidos y eficaces en las aplicaciones comerciales.

Ventajas de los árboles de decisión:

Interpretabilidad:

• Los árboles de decisión son fáciles de entender e interpretar. La representación gráfica de la estructura de árbol nos permite visualizar claramente los procesos de toma de decisiones.

Trabajo con la no linealidad:

• Los árboles de decisión pueden capturar relaciones no lineales en los datos, lo cual los hace adecuados para resolver problemas en los que los límites de decisión no son lineales.

Trabajo con tipos de datos mixtos:

• Los árboles de decisión pueden admitir tanto datos numéricos como categóricos sin necesidad de un preprocesamiento significativo.

Importancia de las características:

• Los árboles de decisión ofrecen una forma natural de evaluar la importancia de las características, ayudando a identificar los factores críticos que afectan a la variable objetivo.

No hacen suposiciones sobre la distribución de los datos:

• Esto las hace bastante versátiles y aplicables a diferentes conjuntos de datos.

Resistencia a los valores atípicos:

• Los árboles de decisión son relativamente resistentes a los valores atípicos porque las divisiones se basan en comparaciones relativas y no se ven afectadas por los valores absolutos.

Selección automática de variables:

• El proceso de construcción del árbol incluye la selección automática de variables, lo cual reduce la necesidad de seleccionar características manualmente.

Puede procesar valores ausentes:

• Los árboles de decisión pueden tratar los valores que faltan en los objetos sin necesidad de imputación, pues la división se realiza en función de los datos disponibles.

Desventajas de los árboles de decisión:

Sobreentrenamiento:

• Los árboles de decisión son propensos al sobreentrenamiento, especialmente si son profundos y captan ruido en los datos de entrenamiento. Para resolver este problema se recurre, por ejemplo, a la poda.

Inestabilidad:

• Pequeños cambios en los datos pueden provocar cambios significativos en la estructura del árbol, haciendo que los árboles de decisión resulten inestables.

Tendencia a las clases dominantes:

• En conjuntos de datos con clases desequilibradas, los árboles de decisión pueden verse desplazados hacia la clase dominante, lo cual provoca un rendimiento subóptimo para las clases menos representadas.

Solución global y localizada:

• El objetivo de los árboles de decisión es encontrar divisiones óptimas locales en cada nodo, lo cual puede no conducir necesariamente a una solución óptima global.

Expresividad limitada:

• Los árboles de decisión no siempre son capaces de expresar relaciones complejas en los datos, en comparación con modelos más sofisticados, como las redes neuronales.

No apto para muestra continua:

• Mientras que los árboles de decisión resultan adecuados para tareas de clasificación, no lo son para tareas que requieren una muestra continua.

Sensible a los datos ruidosos:

• Los árboles de decisión pueden ser sensibles a los datos ruidosos, y los valores atípicos pueden dar lugar a ciertas divisiones basadas en el ruido y no en patrones significativos.

Tendencia a las características dominantes:

• Las características con más niveles o categorías pueden parecer más importantes debido a la forma en que se produce la división, lo cual puede dar lugar a desplazamientos. Este problema puede resolverse usando técnicas como el escalado de características.

Eso es todo, gracias por su atención.

Puede seguir el proceso de desarrollo del proyecto y contribuir al algoritmo del árbol de decisión y muchos otros modelos de IA en mi repositorio en GitHub: https://github.com/MegaJoctan/MALE5/tree/master

Contenidos del anexo:

tree.mqh	Archivo principal que debe incluirse. Código de árbol de decisión del que hablamos principalmente en el documento.
metrics.mqh	Funciones y código para medir el rendimiento de los modelos de aprendizaje automático.
matrix_utils.mqh	Funciones adicionales para trabajar con matrices.
preprocessing.mqh	Biblioteca para preprocesar datos de entrada sin procesar con el fin de adecuarlos para su uso en los modelos de aprendizaje automático.
DecisionTree Test.mq5(EA)	Archivo principal. Asesor para ejecutar el árbol de decisión.