Neural networks made easy (Part 26): Reinforcement Learning

MetaTrader 5 — Trading | 7 November 2022, 16:09

6 474

Dmitriy Gizlyk

3.1. Implementation using MQL5

Introduction

In the previous articles of this series, we have already seen supervised and unsupervised learning algorithms. This article opens another machine learning chapter: Reinforcement Learning. These algorithms are based on the implementation of learning by trial and error, which can be compared with the learning system of living organisms. This property enables the use of such algorithms for solving problems that require the development of certain strategies. Obviously, trading can be attributed to such problems since all traders follow certain strategies for successful trading. Therefore, the use of such technology can be useful for our specific area.

1. Fundamentals of reinforcement learning

Before we start learning about specific algorithms, let's study the basic concepts and philosophy behind the reinforcement learning. First of all, pay attention that in reinforcement learning, the model is not treated as something separate. It deals with the interaction between the process subjects. For a better understanding of the overall process, it would be useful to introduce a person as one of the process participants. We are well aware of our actions. In this case, it will be easier for us to understand the model behavior.

So, we live in a constantly changing world. The changes depend on us and our actions, to some extent. But, to a greater extent, the changes do not depend on us. This is because millions of other people live in the world and perform certain actions. Furthermore, there are many factors that do not depend on the people.

Similarly, in reinforcement learning, there is the Environment, which is the personification of our world.Some Agent interacts with the Environment. The Agent can be compared to a person living in this Environment. The Environment is constantly changing.

We always look around, evaluate objects by touch, and listen to sounds. So, we evaluate our world every moment through our senses. In our minds, we fix its state.

Similarly, the Environment generates its State which is evaluated by the Agent.

Similarly to us acting in accordance with our world view, the Agent performs an Action according to its Policy(strategy).

The impact causes the Environment to change with a certain degree of probability. For each action, the Agent receives from the Environment some Rewards. The Rewards can be either positive or negative. Based on the rewards, the Agent can evaluate the usefulness of the actions taken.

Reinforcement learning

Note that the rewards policy may be different. There may be one-step options when the Environment) returns the Rewards after each action. But there are many other tasks, when it is difficult or impossible to evaluate each action. Rewards can only be granted at the end of the session. For example, if we consider a game of chess, we can try to give an expert assessment of each move based on whether the position has improved or worsened. But the main goal is to win the game. This is the reward that covers all possible previous reports. Otherwise, the model will be "playing just to play" and will find a way to loop being obsessed with getting the maximum reward, rather than advancing to the final.

Similarly, position opened in the market can at some moment be positive and at some negative. But the result of a trading operation can only be assessed after it is closed.

Cases like these show that quite often Rewards do not depend on one individual Actions). But they depend on a number of successive Actions.

This determines the model training goal. Just as we strive to obtain the maximum profit in trading, the model is trained to obtain the maximum Rewards for a certain finite interval. It can be a game or a session. Or just a time period.

Please note here two related requirements for the use of reinforcement learning methods.

First, the process under study must satisfy the requirement of the so-called Markov Decision Process. Simply put, every Action taken by the Agent depends only on the current State. None of the previously performed Actions or observed States no longer affects the Agent's Actions and Environments changes. All their influence has already been taken into account in the current State.

Of course, in real conditions it is difficult to find a process that satisfies such a requirement. And it's definitely not trading. Before making a trading operation, traders carefully analyze data for a certain time interval with various details. However, the influence of all events gradually decreases and is compensated by new events. Therefore, we can always say that the current state includes events for a certain time interval. We can also add timestamps to indicate how long ago an event occurred.

The second requirement is the finiteness of the process. As mentioned earlier, the goal of training the model is to maximize Rewards. And we can evaluate the profitability of the strategy only for equal time periods. If a strategy operates persistently well, it will generate more profit over more time. This means that for infinite processes the total Rewards may tend to infinity.

Therefore, for the infinite processes (to which trading also refers), to satisfy this requirement, we must limit the size of the training sample to some time frame. On the other hand, the training sample must be representative. Because we need a strategy that can work at least for some time after the end of the training period. The longer the period of the adequate model operation, the better.

Remember, we talked about the same when we started studying supervised learning algorithms. We will talk about the differences in different teaching methods a little later.

Now I would like to mention the importance of creating the right model reward policy for the actions performed. You have probably heard about the importance of a proper organization of the reward system in personnel management. The appropriate reward system stimulates the company personnel to increase productivity and the quality of the work performed. Similarly, the right reward system can be the key to training the model and achieving the desired result. This is especially important for tasks with delayed rewards.

It can be difficult to correctly distribute the final reward among all the actions taken on the way to achieving the final goal. For example, how to divide the profit or loss from the transaction between the position opening and closing operations. The first thing that comes to mind is to divide equally between both operations. But, unfortunately, this is not always true. You can open a position at the right moment, so that the price moves in your direction. How to determine the moment of exit? We can close the position earlier and miss out on some of the potential profit. Or you can hold the position too long and close when the price starts to roll back against you. Thus, part of the possible profit will be missed. In a worse case, you can even close with a loss. In this case, a seemingly good position opening operation will receive a negative reward due to a bad position closing operation. Don't you think this is unfair? Moreover, due to this negative reward, next time the model will consider this entry not suitable. So, you will miss even more profit.

Of course, the reverse situation is also possible: You open an unsuccessful position. We are not discussing the reason for this. But luckily, the price reverses after some time and starts moving in your direction. So, you manage to close the position with a profit. The model receives a positive reward, considers such an entry successful and, if such a pattern occurs, opens a deal again. But this time you are not lucky and the price does not reverse.

True, the model learns from multiple deals. It collects and averages trading statistics. But an incorrect reward system can spoil everything and direct the model training in a wrong direction.

Therefore, when building supervised learning models, you should be very careful in developing a reward system.

2. Difference from previously considered methods

Let's look at the difference between reinforcement learning methods and the previously discussed supervised and unsupervised learning algorithms. All methods have some model and a training sample on which they learn. When using supervised learning methods, the training sample includes pairs of initial states and correct answers provided by the "supervisor". In unsupervised learning, we only have a training sample — the algorithms look for internal similarities and structure of individual states to separate them. The training sample is static in both cases. The model operation never changes the sample.

In the case of reinforcement learning, we do not have a training sample in the usual sense. We have some Environment which generates the current State. Well, we can sample different environment states for the training sample. But there is another relationship between the Environment and the Agent. After evaluating the state of the system, the agent performs some action. This action affects the environment and may change it. Also, the environment must return a response to the action in the form of Rewards.

The Reward received from the Environment can be compared with the "reference supervisor response" in supervised learning methods. But there is a fundamental difference here. In supervised learning, we have the only correct answer for each situation and learn from it. In the reinforcement learning, we only get a reaction to the Agent's action. We don't know how the reward is formed. Moreover, we don't know whether it is maximum or minimum, or how far it is from extreme values. In other words, we know the Agent's action and its estimate. But we don't know what the "reference" should have been. To find this out, we need to perform all possible actions from a particular state. And in this case, we will get the evaluation of all actions in one state.

Now let's remember that in the next time period we get into a new Environment State, which depends on the Action taken by the Agent at the previous step.

And we also strive to obtain the maximum total remuneration for the entire analyzed period. Thus, in order to obtain a reference Action for each State, we need a large number of full passes for all possible states of the Environment for all possible Actions performed by the Agent.

Such an approach would be extremely long and labor-intensive. Therefore, to find optimal strategies, we will use some heuristics, which we will talk about a little later.

Let's summarize.

Supervised Learning	Unsupervised learning	Reinforcement learning
Trained to approximate reference values	Learns the data structure	Trained by trial and error until the maximum reward is obtained
Reference values required	No reference values required	Environment response to agent actions required
The model does not affect the original data	The model does not affect the original data	The Agent can influence the Environment

3. Cross entropy method

I suggest that we start our acquaintance with the reinforcement learning algorithms with the cross-entropy method. Please note that the use of this method has some limitations. To use it correctly, the Environment must have a finite number of States. Also, the Agent is limited to a finite number of possible Actions. Of course, we must comply with the above requirements of the Markov process and the limited training period.

This method is fully consistent with the trial and error ideology. Remember how you, getting into an unfamiliar environment, begin to perform various actions in order to explore the new environment. These actions can be either random or based on your experience gained in similar conditions.

Similarly, the Agent makes several passes from start to finish in the Environment being studied. In each State, it performs a certain Action. The action can be either completely random or dictated by a certain Policy that is included in the Agent during initialization. The number of such passes can be different; it is a hyperparameter determined by the model architect.

During each pass through the environment being explored, we save each state, the action taken, and the total rewards of each pass.

Of all the passes, we select from 20% to 50% of the best passes by the total rewards and update the Agent's policy based on the results. The policy update formula is shown below.

Policy update

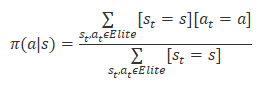
After updating the policy, we repeat the passes through the Environment. Select the best passages. Update the agent policy.

Repeat until the desired result is obtained or the growth of the model profitability stops.

3.1. Implementation using MQL5

The algorithm of the cross-entropy method may sound simple but its implementation using MQL5 tools is not so simple. This method assumes a finite number of possible Environment States and Agent Actions. The Agent's Actions are clear, but there is a big question with the finiteness of the number of possible States of the Environment.

Let's get back to the unsupervised learning problems. In particular, clustering problems. When studying k-means method, we divided all possible states into 500 clusters. I think this is an acceptable solution to the problem of the finiteness of the number of possible states.

This is enough to demonstrate the algorithm. Now, we will not go into detail on the influence of the agent's actions on the system state.

The MQL5 code for the implementation of the cross-entropy method algorithm is attached in the EA file "crossenteopy.mq5". At the beginning, include the necessary libraries. In this case, we will implement a tabular version of the cross-entropy method, so we do not use the neural network library. We will study their use in reinforcement learning algorithms in the next articles within this series.

#include "..\Unsupervised\K-means\kmeans.mqh"
#include <Trade\SymbolInfo.mqh>
#include <Indicators\Oscilators.mqh>

Next, declare external variables, which are almost identical to those used in the EA demonstrating the k-means method. This is natural, as we are going to use the method to cluster the graphical patterns of the market situation.

input int                  StudyPeriod =  15;            //Study period, years
input uint                 HistoryBars =  20;            //Depth of history
input int                  Clusters    =  500;           //Clusters
ENUM_TIMEFRAMES            TimeFrame   =  PERIOD_CURRENT;
//---
input int                  Samples     =  100;
input int                  Percentile  =  70;
      int                  Actions     =  3;
//---
input group                "---- RSI ----"
input int                  RSIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   RSIPrice    =  PRICE_CLOSE;   //Applied price
//---
input group                "---- CCI ----"
input int                  CCIPeriod   =  14;            //Period
input ENUM_APPLIED_PRICE   CCIPrice    =  PRICE_TYPICAL; //Applied price
//---
input group                "---- ATR ----"
input int                  ATRPeriod   =  14;            //Period
//---
input group                "---- MACD ----"
input int                  FastPeriod  =  12;            //Fast
input int                  SlowPeriod  =  26;            //Slow
input int                  SignalPeriod =  9;            //Signal
input ENUM_APPLIED_PRICE   MACDPrice   =  PRICE_CLOSE;   //Applied price

Three variables have been added to implement the cross-entropy method:

Samples — the number of passes for each policy update iteration
Percentile — the percentile to select reference passes for policy update
Actions — the number of possible actions of the Agent

The number of possible states of the system is determined by the number of clusters created by the k-means method.

In the EA initialization method, initialize the objects for working with indicators and the object for clustering graphical patterns.

int OnInit()
  {
//---
   Symb = new CSymbolInfo();
   if(CheckPointer(Symb) == POINTER_INVALID || !Symb.Name(_Symbol))
      return INIT_FAILED;
   Symb.Refresh();
//---
   RSI = new CiRSI();
   if(CheckPointer(RSI) == POINTER_INVALID || !RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice))
      return INIT_FAILED;
//---
   CCI = new CiCCI();
   if(CheckPointer(CCI) == POINTER_INVALID || !CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice))
      return INIT_FAILED;
//---
   ATR = new CiATR();
   if(CheckPointer(ATR) == POINTER_INVALID || !ATR.Create(Symb.Name(), TimeFrame, ATRPeriod))
      return INIT_FAILED;
//---
   MACD = new CiMACD();
   if(CheckPointer(MACD) == POINTER_INVALID || !MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice))
      return INIT_FAILED;
//---
   Kmeans = new CKmeans();
   if(CheckPointer(Kmeans) == POINTER_INVALID)
      return INIT_FAILED;
//---
   bool    bEventStudy = EventChartCustom(ChartID(), 1, 0, 0, "Init");
//---
   return(INIT_SUCCEEDED);
  }

In the EA deinitialization method, delete all the above created objects. As you know, the deinitialization method is called when the program is closed. So, it is a good practice to implement memory cleanup in it.

void OnDeinit(const int reason)
  {
//---
   if(CheckPointer(Symb) != POINTER_INVALID)
      delete Symb;
//---
   if(CheckPointer(RSI) != POINTER_INVALID)
      delete RSI;
//---
   if(CheckPointer(CCI) != POINTER_INVALID)
      delete CCI;
//---
   if(CheckPointer(ATR) != POINTER_INVALID)
      delete ATR;
//---
   if(CheckPointer(MACD) != POINTER_INVALID)
      delete MACD;
//---
   if(CheckPointer(Kmeans) != POINTER_INVALID)
      delete Kmeans;
//---
  }

The algorithm implementation and the model training are provided in the Train function. Implement preparatory work at the function beginning. It starts with the creation of an object for working with an OpenCL device. This technology will be used to implement the k-means algorithm. For details about how to implement it please see the article "Neural networks made easy (Part 15): Data clustering using MQL5".

void Train(void)
  {
   COpenCLMy *opencl = OpenCLCreate(cl_unsupervised);
   if(CheckPointer(opencl) == POINTER_INVALID)
     {
      ExpertRemove();
      return;
     }
   if(!Kmeans.SetOpenCL(opencl))
     {
      delete opencl;
      ExpertRemove();
      return;
     }

Next, update historical data.

   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);
//---
   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

Next, load the pretrained k-means model. Do not forget to control the process at each step.

   int handl = FileOpen(StringFormat("kmeans_%d.net", Clusters), FILE_READ | FILE_BIN);
   if(handl == INVALID_HANDLE)
     {
      ExpertRemove();
      return;
     }
   if(FileReadInteger(handl) != Kmeans.Type())
     {
      ExpertRemove();
      return;
     }
   bool result = Kmeans.Load(handl);
   FileClose(handl);
   if(!result)
     {
      ExpertRemove();
      return;
     }

After successful completion of the above operations, check if there is enough historical data.

   int total = bars - (int)HistoryBars - 480;
   double data[], fractals[];
   if(ArrayResize(data, total * 8 * HistoryBars) <= 0 ||
      ArrayResize(fractals, total * 3) <= 0)
     {
      ExpertRemove();
      return;
     }

Next, create a history sample to be clustered.

   for(int i = 0; (i < total && !IsStopped()); i++)
     {
      Comment(StringFormat("Create data: %d of %d", i, total));
      for(int b = 0; b < (int)HistoryBars; b++)
        {
         int bar = i + b + 480;
         int shift = (i * (int)HistoryBars + b) * 8;
         double open = Rates[bar]
                       .open;
         data[shift] = open - Rates[bar].low;
         data[shift + 1] = Rates[bar].high - open;
         data[shift + 2] = Rates[bar].close - open;
         data[shift + 3] = RSI.GetData(MAIN_LINE, bar);
         data[shift + 4] = CCI.GetData(MAIN_LINE, bar);
         data[shift + 5] = ATR.GetData(MAIN_LINE, bar);
         data[shift + 6] = MACD.GetData(MAIN_LINE, bar);
         data[shift + 7] = MACD.GetData(SIGNAL_LINE, bar);
        }
      int shift = i * 3;
      int bar = i + 480;
      fractals[shift] = (int)(Rates[bar - 1].high <= Rates[bar].high && Rates[bar + 1].high < Rates[bar].high);
      fractals[shift + 1] = (int)(Rates[bar - 1].low >= Rates[bar].low && Rates[bar + 1].low > Rates[bar].low);
      fractals[shift + 2] = (int)((fractals[shift] + fractals[shift]) == 0);
     }
   if(IsStopped())
     {
      ExpertRemove();
      return;
     }
   CBufferFloat *Data = new CBufferFloat();
   if(CheckPointer(Data) == POINTER_INVALID ||
      !Data.AssignArray(data))
      return;
   CBufferFloat *Fractals = new CBufferFloat();
   if(CheckPointer(Fractals) == POINTER_INVALID ||
      !Fractals.AssignArray(fractals))
      return;

And perform the clustering.

//---
   ResetLastError();
   Data = Kmeans.SoftMax(Data);

Next, we can proceed to working with the cross-entropy method. First, prepare the necessary variables. Here we will fill in the zero values in the system states matrix states and in the performed actions matrix actions. The matrix data rows will correspond to the passes. Their columns represent each step of the corresponding pass. Thus, states will store the state at each step of the appropriate pass. The actions matrix will store the action performed at the relevant step.

The CumRewards vector will be used to accumulate the reward of each pass.

The Agent's policy will be initialized with equal probabilities for each action.

   vector   env = vector::Zeros(Data.Total() / Clusters);
   vector   target = vector::Zeros(env.Size());
   matrix   states = matrix::Zeros(Samples, env.Size());
   matrix   actions = matrix::Zeros(Samples, env.Size());
   vector   CumRewards = vector::Zeros(Samples);
   double   average = 1.0 / Actions;
   matrix   policy = matrix::Full(Clusters, Actions, average);

Please note that the above example is a quite "unrealistic", while it is made only to demonstrate the technology. Therefore, in order to avoid an increase in the number of possible system states, I excluded the influence of the Agent's actions on changing the subsequent state. This enabled the preparation of a sequence of all system states for the analyzed period in the env vector. The use of the target data from the supervised learning problem enables us to create a vector of target values target. There will be no such opportunity when solving practical problems. Therefore, to obtain this data, we will need to refer to the Environment every time.

   for(ulong state = 0; state < env.Size(); state++)
     {
      ulong shift = state * Clusters;
      env[state] = (double)(Data.Maximum((int)shift, Clusters) - shift);
      shift = state * Actions;
      target[state] = Fractals.Maximum((int)shift, Actions) - shift;
     }

This completes the preparatory work. Let's proceeds to the direct implementation of the cross-entropy method algorithm. As described above, the algorithm will be implemented in a loop system.

The outer loop will count the number of iterations related to the update the Agent's Policy. In this loop, first reset the cumulative reward vectors.

   for(int iter = 0; iter < 200; iter++)
     {
      CumRewards.Fill(0);

Then, create a nested loop of passes through the analyzed process.

      for(int sampl = 0; sampl < Samples; sampl++)
        {

Each pass also contains a nested loop that goes through all the steps of the process. At each step, we select the most likely action for the current state. If this state is new, select a new action randomly. After that, pass the selected Action to Environment and receive a reward.

In this implementation, I assigned a reward of 1 for the correct action (corresponds to the reference) and -1 for other cases.

Save the current state and action and move on to the next step (a new iteration of the loop).

         for(ulong state = 0; state < env.Size(); state++)
           {
            ulong a = policy.Row((int)env[state]).ArgMax();
            if(policy[(int)env[state], a] <= average)
               a = (int)(MathRand() / 32768.0 * Actions);
            if(a == target[state])
               CumRewards[sampl] += 1;
            else
               CumRewards[sampl] -= 1;
            actions[sampl, state] = (double)a;
            states[sampl,state]=env[state];
           }

After completing all the passes, determine the pass reward level for the reference passes.

      double percentile = CumRewards.Percentile(Percentile);

Then, update the Agent's Policy. To do this, implement a system of loops through all performed passes and select only the reference ones from them.

For reference passes, loop through all completed steps and for each visited state increase the counter of the corresponding completed action by 1. Since we check only the reference passes, we consider the actions taken to be correct. Because they provided the highest rewards.

      policy.Fill(0);
      for(int sampl = 0; sampl < Samples; sampl++)
        {
         if(CumRewards[sampl] < percentile)
            continue;
         for(int state = 0; state < env.Size(); state++)
            policy[(int)states[sampl, state], (int)actions[sampl, state]] += 1;
        }

After counting the actions of the reference strategies, normalize the policy so that the total probability of taking actions for each state is 1. To do this, loop through all the rows of the Policy matrix policy. Each row of this matrix corresponds to a certain state of the system, and the column corresponds to the action performed. If no actions have been saved for any state, consider all actions to be equally possible for such a state.

      for(int row = 0; row < Clusters; row++)
        {
         vector temp = policy.Row(row);
         double sum = temp.Sum();
         if(sum > 0)
            temp = temp / sum;
         else
            temp.Fill(average);
         if(!policy.Row(temp, row))
            break;
        }

After completing the loop iterations, we obtain the updated Policy of our Agent.

For information, output the maximum reward received and proceed to a new iteration through the Environment being analyzed.

      PrintFormat("Iteration %d, Max reward %.0f", iter, CumRewards.Max());
     }

After the model training is completed, delete the objects of the training sample and call the procedure to close the EA work.

   if(CheckPointer(Data) == POINTER_DYNAMIC)
      delete Data;
   if(CheckPointer(Fractals) == POINTER_DYNAMIC)
      delete Fractals;
   if(CheckPointer(opencl) == POINTER_DYNAMIC)
      delete opencl;
   Comment("");
//---
   ExpertRemove();
  }

Find the entire EA code and all libraries in the attachment.

Conclusion

This article has opened a new chapter in our Machine Learning study: Reinforcement Learning. This approach is closest in spirit to how living organisms learn. It is organized on the principles of trial and error. The approach is rather promising, as it allows you to build logically sound strategies for the model behavior based on unlabeled data. However, this requires thorough preparation of the model reward system.

In the article, we considered one of the reinforcement learning algorithms, the Cross-Entropy method. This method is simple to understand, but it has a number of limitations. However, a rather simplified implementation example shows the rather large potential of this approach.

In the next articles, we will continue to study reinforcement learning and will get acquainted with other algorithms. Some of them will use neural networks to train the Agent.

List of references

Programs used in the article

#	Name	Type	Description
1	crossenteopy.mq5	EA	Expert Advisor to train the model
2	kmeans.mqh	Class library	Library for implementing the k-means method
3	unsupervised.cl	Code Base	OpenCL program code library to implement the k-means method

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/11344

Attached files |

Download ZIP

MQL5.zip (85.7 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.