Neural networks made easy (Part 27): Deep Q-Learning (DQN)

MetaTrader 5 — Trading systems | 8 November 2022, 15:48

6 535

Dmitriy Gizlyk

Introduction

In the previous article, we started exploring reinforcement learning methods and built our first cross-entropy trainable model. In this article, we continue to study reinforcement learning methods. We will proceed to the Deep Q-Learning method. By using Deep Q-Learning, in 2013 the DeepMind team managed to create a model that can successfully play seven Atari computer games. It is noteworthy that for all 7 games, they trained the same model without changing the architecture or hyperparameters. According to the training results, the model was able to improve the previously achieved results in 6 of the analyzed games. In addition, in three games the model outperformed a human. The publication of this work initiated a new stage in the development of reinforcement learning methods. Let's study this method and try to use it to solve trading related problems.

1. The concept of a Q-function

First, let's get back to the material studied in the last article. In reinforcement learning, we build the process of interaction between an Agent and its Environment. The agent analyzes the current state of the environment and performs an action that changes the state of the environment. In response to the action, the environment returns rewards to the agent. The agent does not know how the rewards are formed. The agent's goal is to receive the maximum possible total rewards for the session under analysis.

Pay attention that the agent does not receive the reward for the action. It receives the reward for transition from one state to another. At the same time, performing a certain action in a similar situation does not guarantee a transition to the same state. Performing an action gives only some probability of transition to the expected state. The probabilities and dependencies of states, actions and transitions are unknown to the agent. The agent must learn them from the process of interaction with the environment.

In fact, reinforcement learning is based on the assumption that there is some relationship between the current state, the action taken, and the reward. In mathematical terms, there is a function Q which, depending on the state s and actions a, returns the reward r. It is denoted as Q(s|a). This function is referred to as the action utility function.

The agent does not know this function. But if it exists, then in the process of interaction with the environment, by repeating the actions an infinite number of times, we can approximate this function.

In real conditions, it is not possible to repeat states and actions an infinite number of times. But with enough repetitions, we can approximate the function with an acceptable error. The form of the Q-function expression can be different. In the previous article, while determining the utility of each action, we built a table of dependencies of the state, action, and average reward. There are other forms of expressing the Q-function which are quite acceptable or can generate even better results. These can be decision trees, neural networks, etc.

Please note that the Q-function approximated by the agent does not predict the rewards. It only returns the expected returns based on the agent's past experience of interacting with the environment.

2. Deep Q-learning

You have probably already guessed that deep Q-learning involves using a neural network to approximate a Q-function. What is the advantage of such an approach? Remember the implementation of the cross-entropy tabular method in the last article. I emphasized that the implementation of a tabular method assumes a finite number of possible states and actions. So, we have limited the number of possible states by clustering the initial data. But is it so good? Will clustering always produce better results? The use of a neural network does not limit the number of possible states. I think this is a great advantage when solving trading related problems.

The very first obvious approach is to replace the table from the previous article with a neural network. But, unfortunately, it's not that easy. In practice, the approach turned out to be not as good as it seemed. To implement the approach, we need to add a few heuristics.

First, let's look at the agent training goal. In general, its goal is to maximize the total rewards. Look at the figure below. The agent has to move from the cell start to the cell Finish. The agent will receive the reward once, when it gets to the Finish cell. In all other states, the reward is zero.

Discount factor

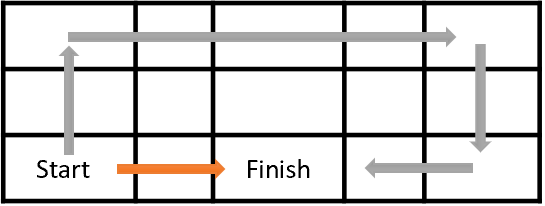
The figure shows two paths. For us it is obvious that the orange path is shorter and more preferable. But in terms of reward maximization, they are equivalent.

Similarly, in trading, it is more preferable to receive income immediately than to invest funds now and to receive income in the distant future. This considers the value of the money: the interest rate, inflation and a number of other variables. We do the same here. To solve the problem, we introduce a discount factor ɣ, which will reduce the value of future rewards.

Cumulative rewards

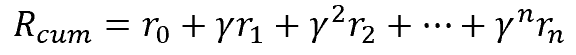
The discount factor ɣ can be in the range from 0 to 1. If the discount factor is 1, then no discounting occurs. And with a discount factor of 0, future rewards will be ignored. In practice, the discount factor is set close to 1.

But there is another problem here. What looks good in theory may not always work in practice. We can easily calculate future rewards when we have a complete transition and reward map. Among them, we can choose the best path with the maximum rewards at the end. But when solving practical problems, we do not know what the next state will be after a certain action is performed. Neither do we know the rewards. All this is already applicable to the immediate next step. It is even more serious when we talk about the entire path to the end of the session. We cannot see into the future. To receive the next reward, the agent needs to perform an action. Only after the transition to a new state, the environment will return the rewards. Furthermore, we have no way back. We cannot go back to the previous state and take another action in order to choose the best one later.

Therefore, we will apply dynamic programming methods. In particular, the Bellman optimization method. It says that in order to select the optimal strategy, it is necessary to select the optimal action at each step. That is, by selecting the action with the maximum reward at each step, we will get the maximum cumulative rewards for the session. The mathematical formula for updating the action utility function is shown below.

Bellman optimization

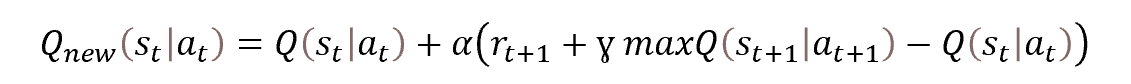
Look at the formula. Doesn't it remind you of the stochastic gradient descent weight update formula? Indeed, in order to update the value of the action utility function, we need the previous value of the function plus some deviation multiplied by the learning factor.

It can also be noticed in the presented function, that to determine the value of the function at the time point t, we need the value of the action utility function at the next time step at the point t+1. In other words, being in the state st, we take the action at and after we transit to state st+1, we get the reward rt+1. To update the value of the action's utility function, we need to add the maximum of the action's utility function to the rewards in the next step. That is, we add the maximum expected rewards that we can get in the next step. Of course, our agent cannot look into the future and determine the future reward. But it can use its approximation function: being in the state st+1, it can calculate the value of the function for all possible actions from the given state and take the highest of the obtained values. In the process of learning, its values will at first be far from true. But it's better than nothing. As the agent learns, the forecasting error will decrease.

2.1. Experience replay

Stochastic gradient descent is good because it allows the updating of the function values based on the values of a small sample from the population. Actually, it allows our agent to update the action utility function values at each step of the session. But in supervised learning, we used a training sample in which the states are independent of each other. To strengthen this property, we shuffled the population each time before selecting a new training data set.

However now, in supervised learning, our agent moves in time through our environment, performs an action and each time enters a new state which is closely related to the previous one. Look around you. Whether you are walking or sitting and performing some action, the environment around you does not change dramatically. You action changes only a small part of it, where this action is directed. Similarly, the states of the environment under study will not change much when the agent performs actions. This means that successive states will be greatly interrelated. Our agent will observe the autocorrelation of such states.

The difficulty relates to the fact that even the use of a small training coefficient does not prevent the agent from adjusting the action utility function to the current state, sacrificing the memory of past experience.

In supervised learning, the use of independent states after a large number of iterations makes it possible to average the model's weight values. In the case of reinforcement learning, when we train the model using connected and practically unchanged states, the model is retrained to the current state.

As in any time series, the relationship of states decreases as time between them increases. Therefore, to solve this problem, we need to use states scattered along the timeline when training our agent model. This can be easily done if we have historical data. But when moving along the environment, our agent does not have such a memory. It only sees the current state and cannot jump from one state to another.

So, why don't we organize memory for the agent? Look, to update the value of the action utility function, we need the following data set:

State -> Action -> Reward -> State

Let's make it so that, while moving along the environment, the agent will save the necessary data set into a buffer. The buffer size is a hyperparameter and is determined by the model architecture. When the buffer is full, newly arriving data will oust older ones. To train the model, we will not use the current state, but we will use data randomly selected from the agent's memory. This way we minimize the relationship between individual states and increase the model's ability to generalize analyzed data.

2.2. Using Target Net

Another point that you should pay attention to when learning the action utility function is the maximum value of this function at the next step maxQ(st+1|at+1). Please note that this is a "value from the future". So, we take a predicted value based on the approximated action utility function. But being at the time t, we cannot change the value from the time t+1 state. Each time we update the function value, we update the weights of the model and thereby change the next predicted value.

Moreover, we train our agent to get the maximum reward. So, at each model update iteration, we maximize the expected value. The use of the predicted value recursively maximizes the updated value. In this way, we maximize the values of our action utility function in a progression. This leads to an overestimation of our function values and to an error increase in predicting the action utility. This is not very good. Therefore, we need a stationary mechanism for assessing the utility of a future action.

We could address this issue by creating an additional model to predict the utility of a future action. But this approach would require additional costs to train the second model. This is something we would like to avoid. On the other hand, we are already training a model that performs this functionality. But after the weights are changed, the model should return the values of the function as before the update. This controversial problem can be solved by copying the model. We simply create two instances of the same action utility function model. One instance is trained, and the other one is used to predict the utility of the future action.

Once the model of the action utility function is fixed, it soon becomes irrelevant in the learning process. This can make further training inefficient. To eliminate the influence of this factor, we will need to update the model of predictive values in the learning process. The second instance will not be trained in parallel. Instead, we will copy the weights from the trained instance of the action utility function model into the second one with a certain periodicity. Thus, by training only one model, we get quite up-to-date 2 instances of the action utility function model and avoid the recursive overestimation of predictive values.

Let us summarize the above:

To train the agent, we use a neural network.
The neural network is trained to predict the expected value of the action utility Q-function.
To minimize the correlation between neighboring states, the learning process uses a memory buffer, from which states are extracted randomly.
To predict the future value of the Q-function, there is the second Target Net model, which is a "frozen" copy of the trained model.
The Target Net is actualized by periodically copying weight matrices from the trained model.

Now, let us loot at the implementation of the described approach using MQL5.

3. Implementation using MQL5

To implement the deep Q-learning algorithm using MQL5, we will use the "Q-learning.mq5" EA file. The full Expert Advisor code can be found in the attachment. Here we will focus only on the implementation of the deep Q-learning method.

Before proceeding with the implementation, let us decide what the initial data and the reward system will be. The initial data is the same we used for previous experiments. So, what about the reward system? The fractals forecasting problem we considered earlier is rather artificial. Of course, we could create a model to determine the maximum possible number of fractals. But our main goal is to obtain the maximum profit from trading operations.

In this context, it makes perfect sense to use the size of the next candle as the reward size. Of course, the sign of the reward must correspond to the operation performed. In a simplified model, we have two trading operations: buy and sell. We can also be out of position.

Here we will not complicate the model by determining the position volume, position increase or partial closing. Let us assume that the agent can be in a position with a fixed lot. Also, the agent can close all positions and stay out of the market.

In addition, when it comes to the reward policy, we must understand that the training result largely depends on a properly prepared reward system. The reinforcement learning practice offers a plethora of examples where an incorrectly chosen reward policy led to unexpected results. The model can learn to draw wrong conclusions. It can also get stuck in trying to get the maximum reward without achieving the desired result. For example, we can reward the model for opening and closing positions. But if this reward exceeds that for the profit accumulated from the trade, the model can learn to simply open and close positions. SO, the model will maximize rewards while we will maximize losses.

On the other hand, if we penalize the model for opening and closing a position, similar to the commission for an operation, the model can simply learn to stay outside the market. No profit, but no loss either.

Considering all of the above, I decided to create a model with three possible actions: Buy, Sell, Out of the market.

The agent will predict the direction of the expected movement on each new candlestick and will choose an action without taking into account the previous ones. So, to simplify the model, we will not input into the agent information about whether it is in a position or about the position direction. Accordingly, the agent does not track position opening and closing. No reward is given for position opening and closing.

To minimize the "out of the market" time, we will penalize the absence of a position. But this penalty is lower than the penalty for a losing position.

So, here is the agent reward policy:

A profitable position receives a reward equal to the candlestick body size (analyze the system state at each candlestick; we are in a position from the candlestick opening to its closing).
The "out of the market" state is penalized in the size of the candlestick body (the candlestick body size with a negative sign to indicate lost profits).
A losing position is penalized by the double candlestick body size (loss + lost profit).

Now that we have defined the reward system, we can move on directly to method implementation.

As mentioned above, our model will use two neural networks. For this purpose, we need to create two objects for working with neural networks. We will train StudyNet, while TargetNet will be used to predict future values of the Q-function.

CNet                StudyNet;
CNet                TargetNet;

To organize the work of the deep Q-learning method, we also need new external variables that will determine the hyperparameters for building and training the model.

Batch — weight update batch size
UpdateTarget — the number of updates of the weights matrix of the trained model before copying to the "frozen" model that predicts future Q-function values
Iterations — the total number of iterations of trained model updates during training
DiscountFactor — future reward discount factor

input int                  Batch =  100;
input int                  UpdateTarget = 20;
input int                  Iterations = 1000;
input double               DiscountFactor =   0.9;

The creation of the neural network model will be implemented outside this EA. To create it, we will use a tool from the articles related to Transfer Learning. This approach will allow us to conduct experiments using various architectures without modifying the EA. Therefore, in the EA initialization method, only implement the loading of a previously created model.

//---
   float temp1, temp2;
   if(!StudyNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false) ||
      !TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
      return INIT_FAILED;

Please note that since we are using two instances of the same model, both models are loaded from the same file.

The possibility to use different architectural solutions implies not only the use of different architectures of hidden layers and their sizes, but also the possibility of adjusting the depth of the analyzed history. Previously, we created the model in the EA code, and the history depth was determined by an external parameter. Now we can determine the analyzed history depth by the size of the source data layer. The EA will determine it analytically, based on the source data layer size. Only the number of neurons per candlestick of the analyzed history and the size of the results layer remain unchanged. Because these parameters are structurally related to the indicators used and the number of predictable actions.

   if(!StudyNet.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   StudyNet.getResults(TempData);
   if(TempData.Total() != Actions)
      return INIT_PARAMETERS_INCORRECT;

We have not previously discussed the size of the original layer in the deep Q-learning model. As mentioned above, the Q-function returns the expected reward depending on the state and the action taken. To determine the most useful action, we need to calculate the function value for all possible actions in the current state. The use of a neural network enables the creation of the results layer in which the number of neurons is equal to the number of all possible actions. In this case, each neuron of the results layer will be responsible for predicting the utility of a particular action. That will provide the utility values of all actions in one pass of the neural network. Then we just have to choose the maximum value.

The rest of the EA initialization function remains unchanged. Its full code is provided in the attachment.

The model training process will be created in the Train function. At the beginning of the function body, determine the size of the training session and load the historical data. This is similar to the earlier considered procedures in supervised and unsupervised learning algorithms.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);
//---
   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

Since we are using historical data to train model, there is no need to create a memory buffer. We can simply use all historical data as a single memory buffer. But if a model is trained in real time, we need to add a memory buffer and manage it.

Next, prepare the auxiliary variables:

total — the size of the training sample
use_target — Target Net use flag to predict future rewards

   int total = bars - (int)HistoryBars - 240;
   bool use_target = false;

We use the use_target flag because we need to disable future rewards prediction until the first update of the Target Net model. It's actually quite a subtle point. At the initial step, the model is initialized with random weights. Therefore, all predicted values will be random. Most likely, they will be very far from the true values. The use of such random values can distort the model learning process. In this case, the model will approximate not the true values of the rewards, but random values embedded in the model itself. Therefore, before the first iteration of the Target Net model update, we should eliminate this noise.

Next, implement a system of agent training loop. The outer loop will count the total number of iterations of updating the weight matrix of our agent.

   for(int iter = 0; (iter < Iterations && !IsStopped()); iter += UpdateTarget)
     {
      int i = 0;

In a nested loop, we will count the weight update batch size and the number of updates before the actualization of Target Net. It should be noted here that weights in our model are updated at each iteration of the backpropagation pass. Therefore, the use of the update batch does not look quite correct, because for our model it is always set to 1. However, in order to balance the number of processed states between Target Net actualizations, their frequency will be equal to the product of the package size and the number of updates between actualizations.

In the loop body, we randomly determine the state of the system for the current model training iteration. We also clear the buffers to write two subsequent states. The first state will be used for the feed-forward pass of the trained model. The second one will be used for predictive Q-function values in Target Net.

      for(int batch = 0; batch < Batch * UpdateTarget; batch++)
        {
         i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (total));
         State1.Clear();
         State2.Clear();
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;

Then, in a nested loop, fill the prepared buffers with historical data. To avoid unnecessary operations, before filling the second state buffer, check the use of the Target Net flag. The buffer is filled only when necessary.

         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) ||
               !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
               !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
               break;
            if(!use_target)
               continue;
            //---
            bar_t --;
            open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            rsi = (float)RSI.Main(bar_t);
            cci = (float)CCI.Main(bar_t);
            atr = (float)ATR.Main(bar_t);
            macd = (float)MACD.Main(bar_t);
            sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State2.Add((float)Rates[bar_t].close - open) || !State2.Add((float)Rates[bar_t].high - open) ||
               !State2.Add((float)Rates[bar_t].low - open) || !State2.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State2.Add(sTime.hour) || !State2.Add(sTime.day_of_week) || !State2.Add(sTime.mon) ||
               !State2.Add(rsi) || !State2.Add(cci) || !State2.Add(atr) || !State2.Add(macd) || !State2.Add(sign))
               break;
           }

After successfully filling the buffers with historical data, check their size and perform a feed-forward pass of both models. Do not forget to check the operation results.

         if(IsStopped())
           {
            ExpertRemove();
            return;
           }
         if(State1.Total() < (int)HistoryBars * 12 ||
            (use_target && State2.Total() < (int)HistoryBars * 12))
            continue;
         if(!StudyNet.feedForward(GetPointer(State1), 12, true))
            return;
         if(use_target)
           {
            if(!TargetNet.feedForward(GetPointer(State2), 12, true))
               return;
            TargetNet.getResults(TempData);
           }

After a successful feed-forward pass, we receive a reward from the environment and prepare a buffer of targets for the backpropagation pass according to the reward policy defined above.

Please pay attention to the following two moments. First, we check the use of the Target Net flag. Add a predictive value only in case of a positive result. If the flus if set to false, the predictive values of the Q-function should be set to 0.

The second thins is the diversion from the Bellman equation. As you remember, the Bellman equation uses the maximum value of the future reward. This way the model is trained to earn the maximum profit. This approach, of course, leads to maximum profitability. But in the case of trading, when price charts are filled with a lot of noise, this leads to an increase in the number of trades. Furthermore, the noise reduces the quality of forecasts. This can be compared to trying to predict each new candle. This potentially leads to opening and closing of positions on almost every new candle, instead of determining the trend and opening a position in the trend direction.

In order to eliminate the influence of the above factor, I decided to divert from the Bellman equation. To update the Q-function model, I will use unidirectional values. The maximum will only be used for the "out of the market" action.

         Rewards.Clear();
         double reward = Rates[i - 1 + 240].close - Rates[i - 1 + 240].open;
         if(reward >= 0)
           {
            if(!Rewards.Add((float)(reward + (use_target ? DiscountFactor * TempData.At(0) : 0))) ||
               !Rewards.Add((float)(-2 * (use_target ? reward + DiscountFactor * TempData.At(1) : 0)))
               ||
               !Rewards.Add((float)(-reward + (use_target ? DiscountFactor * TempData.At(TempData.Maximum(0, 3)) : 0))))
               return;
           }
         else
            if(!Rewards.Add((float)(2 * reward + (use_target ? DiscountFactor * TempData.At(0) : 0))) ||
               !Rewards.Add((float)(-reward + (use_target ? DiscountFactor * TempData.At(1) : 0))) ||
               !Rewards.Add((float)(reward + (use_target ? DiscountFactor * TempData.At(TempData.Maximum(0, 3)) : 0))))
               return;

After preparing the reward buffer, run the backpropagation pass in the trained model. Again, check the operation execution result.

         if(!StudyNet.backProp(GetPointer(Rewards)))
            return;
        }

This completes the operations of the nested loop which counts agent training iterations. After its completion, update the Target Net model. Our models do not have weight exchange methods. I decided not to invent anything new. Instead, we will use the existing mechanism for saving and loading the model. In this case, we get the exact copy of the model with all its contents.

So, save the trained model to a file, and load the saved model from the file to TargetNet. Do not forget to check the operation result.

      if(!StudyNet.Save(FileName + ".nnw", StudyNet.getRecentAverageError(), 0, 0, Rates[i].time, false))
         return;
      float temp1, temp2;
      if(!TargetNet.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false))
         return;
      use_target = true;
      PrintFormat("Iteration %d, loss %.5f", iter, StudyNet.getRecentAverageError());
     }

After the TargetNet model is successfully updated, change its use flag, print an informational message to the log, and move on to the next iteration of the outer loop.

Once the training process completes, clear the comments and initiate the closing of the model training EA.

   Comment("");
//---
   ExpertRemove();
  }

The full Expert Advisor code can be found in the attachment.

4. Testing

The method was tested on the EURUSD data with the H1 timeframe for the last 2 years. The same data was used in all previous experiments. Indicators were used with default parameters.

A convolutional model of the following architecture was created for testing purposes:

Initial data layer, 240 elements (20 candles, 12 neurons per description of one candle).
Convolutional layer, input data window 24 (2 candles), step 12 (1 candle), 6 filters output.
Convolutional layer, input data window 2, step 1, 2 filters.
Convolutional layer, input data window 3, step 1, 2 filters.
Convolutional layer, input data window 3, step 1, 2 filters.
Fully connected neural layer with 1000 elements.
Fully connected neural layer with 1000 elements.
Fully connected layer of 3 elements (results layer for 3 actions).

Layers from 2 to 7 were activated by the sigmoid. For the result layer, the hyperbolic tangent was used as the activation function.

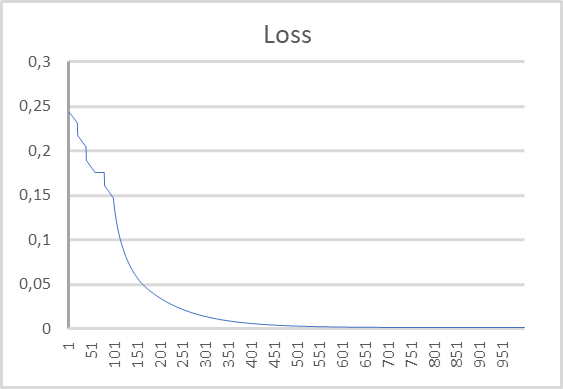
The figure below shows the error dynamics graph. As you can see from the graph, during the learning process, the error in predicting the expected reward was reducing quickly. After 500 iterations it became close to 0. The model training process of 1000 iterations ended with an error of 0.00105.

DQN Model testing graph

Conclusion

In this article, we continued studying reinforcement learning methods. We looked at the deep Q-learning method that was introduced by the DeepMind team in 2013. The publication of this work initiated a new stage in the development of reinforcement learning methods. This method showed the possibility prospects of training models to build strategies. Furthermore, the use of one model allows training it to solve various problems without making structural changes to its architecture or hyperparameters. These were the first experiments when the trained algorithm outperformed the EA results.

We have seen the method implementation using MQL5. The model testing results demonstrate the possibility of using the method to build working trading models.

List of references

Programs used in the article

#	Name	Type	Description
1	Q-learning.mq5	EA	Expert Advisor to train the model
2	NeuroNet.mqh	Class library	Library for creating neural network models
3	NeuroNet.cl	Code Base	OpenCL program code library to create neural network models

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/11369

Attached files |

Download ZIP

MQL5.zip (66.7 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.