
MQL5 Wizard Techniques you should know (Part 61): Using Patterns of ADX and CCI with Supervised Learning
Introduction
We continue our look at how indicator pairings that track different aspects of the markets can be paired with machine learning to build a trading system. For these next articles, we are looking at the pairing of the Average Directional Index (ADX) oscillator with the Commodity Channel Index (CCI). The ADX is a predominantly a trend confirmation indicator, while the CCI is a momentum indicator. We touched on these two properties when we were looking at the patterns for individual indicators in past articles like this one. To recap, though, trend confirmation measures how strong a given price trend is; with a strength pointing to suitability for entry. Momentum indicators on the other hand measure the rate of price change. The more rapidly price is changing in a given direction, the less likely one is to suffer adverse excursions.

Commodity Channel Index (CCI)
We are testing our networks, that take indicator signals as input, in Python. This is because Python presently offers significant performance advantage when compared to MQL5. However, as I have mentioned in recent articles, MQL5 can match or come close to these performances by using OpenCL. This however requires one to have a GPU in order to benefit from OpenCL’s speed. For now though, when both languages are used on similar CPUs, Python clearly comes out on top and so that is what we will test and develop our models with.
MetaTrader has built a Python Module that not only allows the loading of broker price data into Python, but also allows the placing of trades from Python. More on this can be found here and here. We therefore use part of these modules to log onto our broker and pull price data to python for our supervised-learning MLP. Once we have this price data, we then need to define our indicator functions. If we start with the CCI, our implementation can be as follows:
def CCI(df, period=14): """ Calculate Commodity Channel Index (CCI) :param df: pandas DataFrame with columns ['high', 'low', 'close'] :param period: lookback period (default 20) :return: Series with CCI values """ # Calculate Typical Price typical_price = (df['high'] + df['low'] + df['close']) / 3 # Calculate Simple Moving Average of Typical Price sma = typical_price.rolling(window=period).mean() # Calculate Mean Deviation mean_deviation = typical_price.rolling(window=period).apply( lambda x: np.mean(np.abs(x - np.mean(x))), raw=True) # Calculate CCI df['cci'] = (typical_price - sma) / (0.015 * mean_deviation) return df[['cci']]
The CCI is an oscillator that puts a metric on how much an asset’s price deviates from its statistical average. Prima-face, this can be helpful to traders in identifying overbought or oversold conditions. Our implemented function above takes a pandas-data-frame with 'high', 'low', and 'close' price columns and a look back period (with a default of 14) to compute CCI values. The ‘Typical Price’ calculation sets the average of high, low, and close prices to represent/cover most of the price-action over the averaged period. It is the arithmetic mean of these three major prices, for each timeframe, and it helps simplify price data into a single representative value. This aids in reducing noise from intraday fluctuations. This step is foundational since CCI is based on deviations from this typical price and using all three (high, low, and close) helps ensure a balanced view of price action. One therefore needs to ensure that the Pandas Data frame that retrieves broker price data via the MetaTrader 5 module has all these columns, since missing values will lead to errors.
A simple moving average (SMA) smooths the typical price over the specified period, to establish a baseline. This is done by computing the SMA over the specified input period (default 14) so it can act like a reference. This is important because short term price fluctuations do get smoothed out, thus providing a representative ‘normal’ price level. The rolling function requires enough data points, at least the input period squared) in order to compute a valid SMA. If the dataset is too short, then initial NaN values may require special handling (via functions like dropna()… etc.)
The mean deviation then measures the average absolute deviation of these representative typical prices from their SMA, thus capturing price volatility. For each window, a computation of the absolute differences between each typical price and the window’s mean, is performed, and then they are averaged. This is essential because the mean deviation sizes up price volatility, which is indispensable for scaling CCI, which in turn is vital in reflecting an asset’s typical price swings. This also ensures a comparison across different assets. The application of the lambda function is computationally intense for large datasets, which is why it would be a good idea to use vectorized alternatives or libraries such as ta-lib. In doing this, one still needs to import NumPy.
The CCI formula, then, combines all the above components to compute a value, which is then scaled by a constant of 0.015, for normalization. The constant of 0.015 is a standard scaling factor that seeks to keep CCI values in the ±100 range. This is not always achieved though, however that is the goal. This is core to the CCI formula, since it translates raw price deviations into a standardized oscillator. Values above +100 would then indicate over bought conditions, while values below -100 would suggest oversold conditions. With this formula, one should watch for division-by-zero errors if the mean deviation is zero. Though rare, this scenario is possible with flat prices. A small epsilon value (e.g., 1e-10) can then be added to the denominator as needed to mitigate this.
The return statement returns a data frame containing only the ‘cci’ column. If additional columns are required for debugging or additional analysis (e.g., 'typical_price') then this statement can be modified to include them.
Average Directional Index (ADX)
The ADX, as mentioned above, measures trend strength, regardless of direction. This is done by using the Directional Movement Index that primarily constitutes 2 buffers (+DI and -DI). This function, just like the CCI above, takes a pandas-data-frame with 'high', 'low', and 'close' columns and a look back period (default 14) to compute ADX, +DI, and -DI values. Its implementation in Python is as follows:
def ADX(df, period=14): """ Calculate Average Directional Index (ADX) :param df: pandas DataFrame with columns ['high', 'low', 'close'] :param period: lookback period (default 14) :return: DataFrame with ADX, +DI, -DI columns """ # Calculate +DM, -DM, and True Range df['up_move'] = df['high'] - df['high'].shift(1) df['down_move'] = df['low'].shift(1) - df['low'] df['+dm'] = np.where( (df['up_move'] > df['down_move']) & (df['up_move'] > 0), df['up_move'], 0.0 ) df['-dm'] = np.where( (df['down_move'] > df['up_move']) & (df['down_move'] > 0), df['down_move'], 0.0 ) # Calculate True Range df['tr'] = np.maximum( df['high'] - df['low'], np.maximum( abs(df['high'] - df['close'].shift(1)), abs(df['low'] - df['close'].shift(1)) )) # Smooth the values using Wilder's smoothing method (EMA with alpha=1/period) df['+dm_smoothed'] = df['+dm'].ewm(alpha=1/period, adjust=False).mean() df['-dm_smoothed'] = df['-dm'].ewm(alpha=1/period, adjust=False).mean() df['tr_smoothed'] = df['tr'].ewm(alpha=1/period, adjust=False).mean() # Calculate +DI and -DI df['+di'] = 100 * (df['+dm_smoothed'] / df['tr_smoothed']) df['-di'] = 100 * (df['-dm_smoothed'] / df['tr_smoothed']) # Calculate DX df['dx'] = 100 * (abs(df['+di'] - df['-di']) / (df['+di'] + df['-di'])) # Calculate ADX df['adx'] = df['dx'].ewm(alpha=1/period, adjust=False).mean() # Return the relevant columns return df[['adx', '+di', '-di']]
The two computed buffers for directional movement (+DM, -DM), put a size to upward and downward price movements to assess directional strength. They are derived from the difference between consecutive high moves (up-move) and the opposite, which is the difference between consecutive lows (down-move). This is important because these are the building blocks for +DM and -DM, which in turn set directional momentum. By using shifted values, we ensure comparison across different periods. An assignment to the +DM as the up-move is done when it exceeds the down-move and is positive; otherwise, +DM is 0. Similarly, -DM is given a down-move value when it exceeds up-move to make it positive. This helps filter out non-dominant or negative movements.
The NumPy where() function is efficient for vectorized operations, therefore you should ensure NumPy is imported. Verification that up-move and down-move calculations are correct is also important to avoid misclassifying movements. The use of shift(1) introduces NaN for the first row that requires handling in downstream calculations or when returning results. It is always essential to ensure ‘high’, and ‘low’ columns are numeric.
The true range, TR, measures price volatility and this helps account for gaps and intraday ranges. The computation is performed by taking the highest of three values; the high-low range, the absolute high to prior close range, and the absolute low to prior close range. This helps in taking into account price gaps and volatility. This measurement to asset volatility is important since it acts as a denominator for normalizing +DI and -DI. This means ADX is representative of trend strength relative to price movement. NumPy’s maximum function ensures largest range gets picked. Handling of NaN’s from shift(1) should also be watched.
Wilder’s smoothing applies an exponential moving average with a particular alpha to smooth +DM, -DM, and TR. Alpha is 1/period and the use of False for the adjust parameter means more weight is given to recent data, which mimics Wilder’s original method. Smoothing helps reduce noise, making the indicator data sets more reliable for trend analysis. The ewm function is efficient but sensitive to the alpha parameter.
The directional indicators normalize the smoothed movements by true range in order to compare bullish vs. bearish strength. The scaling by 100 helps express them as percentages. This is important since +DI and -DI put a number on how bullish and bearish a trend is, relative to volatility. Crossovers between +DI and -DI therefore signal potential trend changes. Zero-divide-protection can be introduced by adding a small epsilon value. The scaling factor of 100 is standard for ease in interpretation.
The DX buffer determines the scaled absolute difference between +DI and -DI, divided by their sum. This is essential in sizing the relative strength of directional movement. DX is an important intermediate step to ADX, tasked with capturing the ‘intensity’ of a trend (whether bullish or bearish). Care should be taken to handle cases where +di + -di are zero to avoid division errors. Zero can be returned, or the calculation can be skipped.
Finally, ADX averages the directional Index to gauge overall trend strength. Smoothing of the DX values, when using Wilder’s EMA to compute ADX, tends to reflect trend strength over the long run. This is the final indicator output, with values above 25 marking a strong trend, while those below 20 are taken to suggest a weak or ranging market. It is important to ensure consistent alpha values across all smoothing steps for coherence.
The return statement yields a data-frame with columns for 'adx', '+di', and '-di' which are the complete set of indicator buffers for the ADX indicator. This provides the relevant metrics for trend analysis to traders with the addition of intermediate columns of 'dx' or 'tr' possible for debugging or customizing the indicator.
The Features
We bring readings from these two functions together to create a multidimensional signal array that essentially combines ADX (for trend strength) and CCI (for momentum) to identify specific market conditions, such as trend initiation, reversals, or overbought/oversold states. The signals generated from combining these two indicators are what we refer to as features in the broader scheme of things. Recall in the last 4 articles we had 5 principal data sets when we considered the indicator pairing of MA and the stochastic oscillator. These were Features, States, Actions, Rewards, and Encodings. These Features here then are the equivalent to what we had then.
The pairing of these 2 indicators is used with the premise that 10 feature patterns can be generated from their pairing. They could be more, of course, but for our purposes this number will suffice. We are assigning a function to each pattern. Each function will return a NumPy array with each column representing a condition (dimension), where 1 indicates the condition was met and 0 means otherwise. The functions will take as inputs pandas-data-frames. These inputs are labelled adx_df (with 'adx', '+di', '-di' columns); cci_df (with 'cci' column); and optionally price_df (with 'high', 'low', 'close' columns).
We implement these functions in Python to expedite the testing process but also need to have a similar implementation in MQL5 for deployment/ use of our final Expert Advisor. MQL5’s inbuilt handling of the indicator points raised above in the CCI & ADX means they would not be an issue when the Expert Advisor is being used. To recap, for Python though, adx_df and cci_df should be validated to ensure required columns are present, with also NaN values being handled by drop or fill to avoid errors in comparisons. Shift operations such as shift(1) inherently introduce NaNs for the first row. Setting the first row to 0 therefore is a standard way of managing this. Vectorized operations should ideally be introduced for large datasets, since the used NumPy where() function and astype(int) may be insufficient.
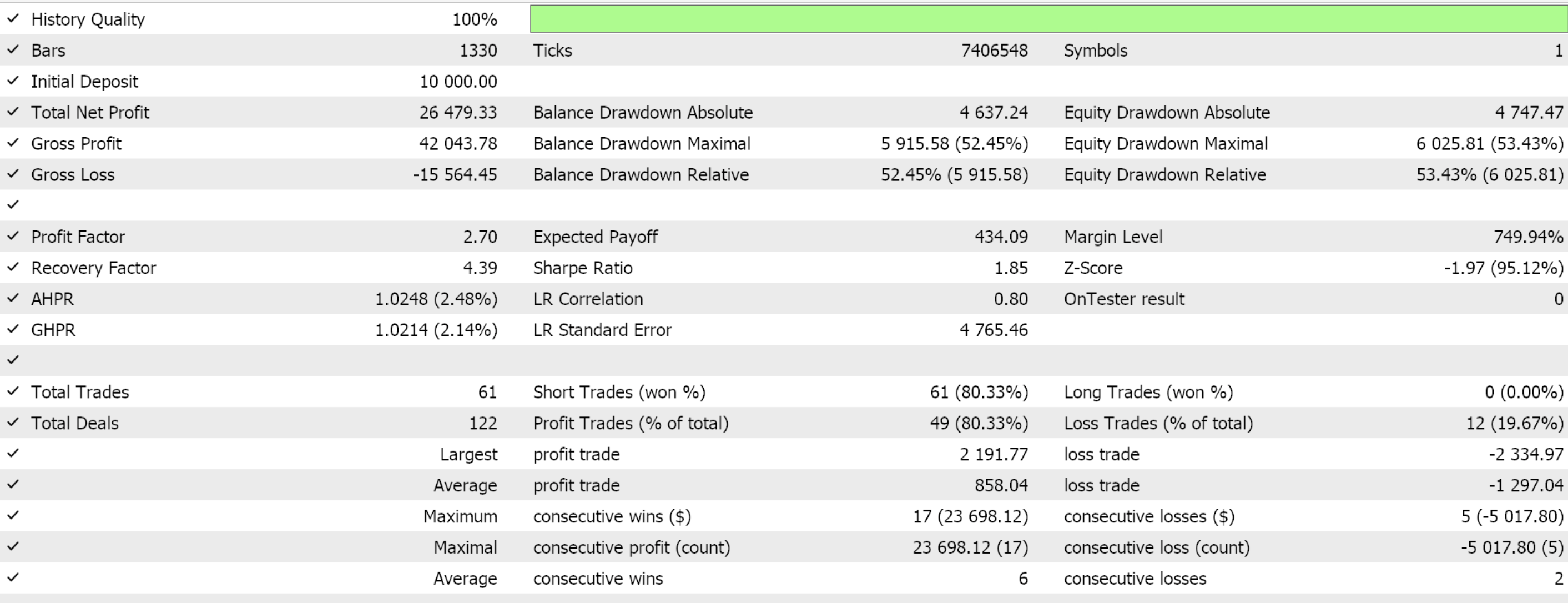
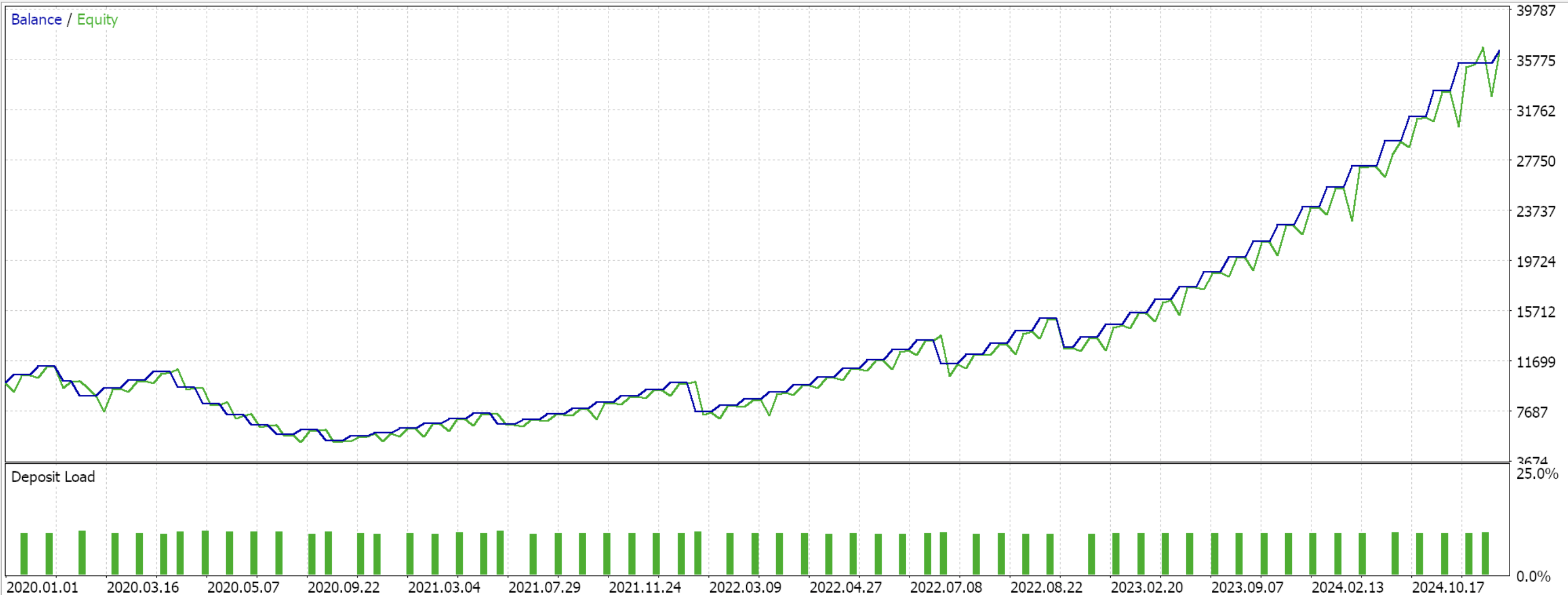
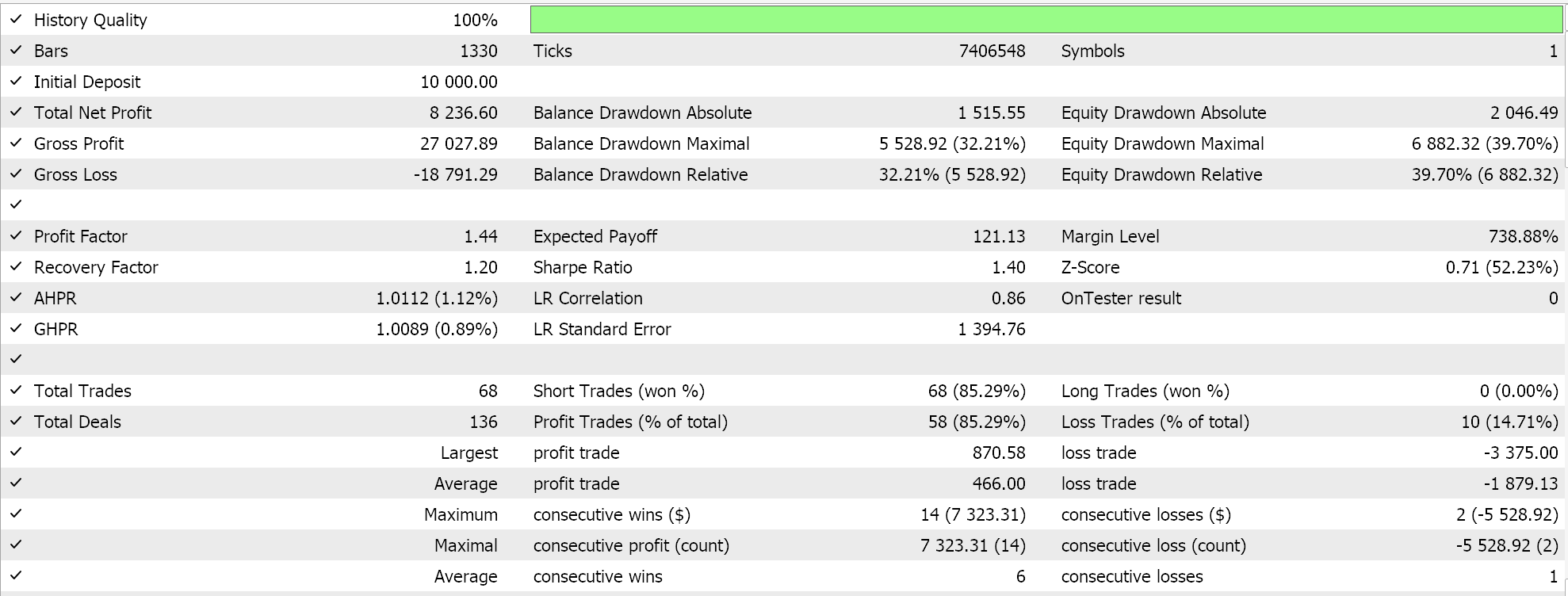
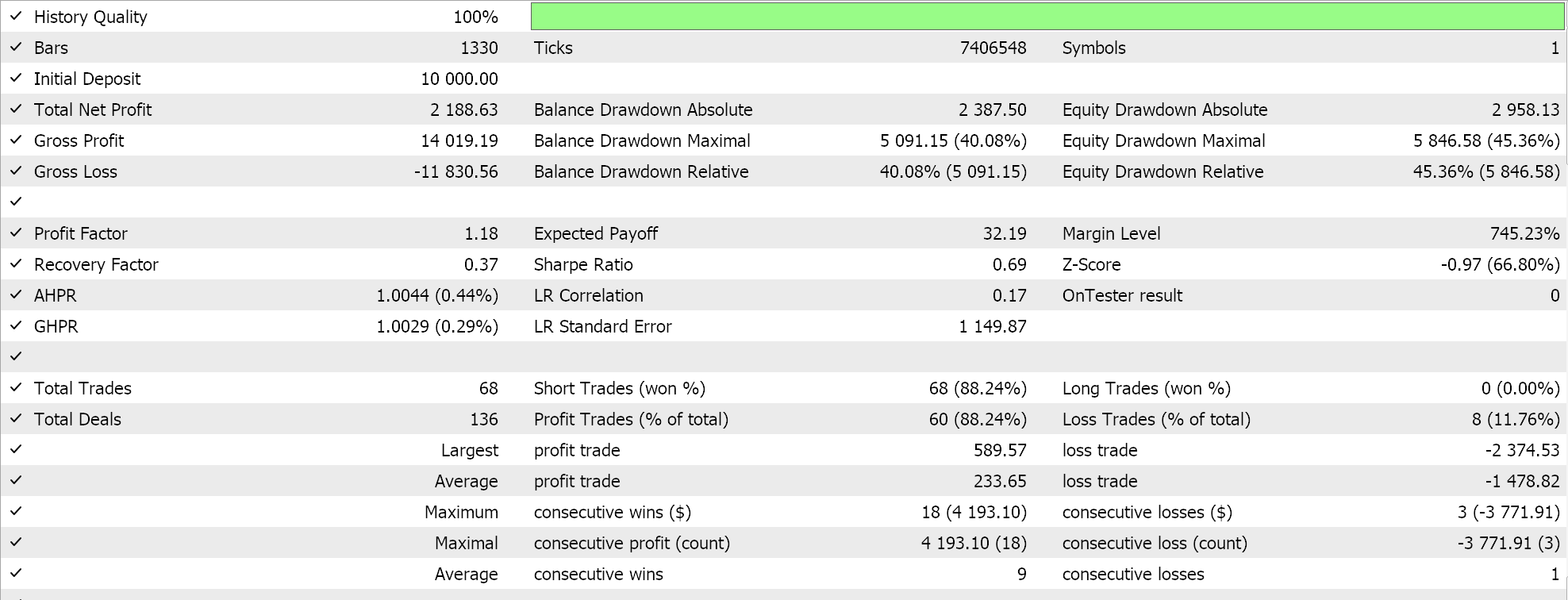
All features were tested/ trained on the pair EURUSD on the daily time frame from 2020.01.01 to 2024.01.01. The forward walk period was 2024.01.01 to 2025.01.01. Only features 2, 3, and 4 were able to forward walk and so their results are shared along their respective descriptions.
Feature-0
This is a pattern based on ADX > 25 and CCI Crossovers at ±100. It provides breakout momentum confirmation or the start of a trend. The 25 level is significant for the ADX, therefore whenever it is crossed together with CCI key level of 100 a new trend is a high probability. The use of these 2 indicators helps filter noise. It is always important when seeking trend starts to wait for ADX to test the 25 level. Anything below 20 should be avoided. It's a high probability setup in assets known for trending, like some Equity Indices, etc.
The generated feature vector from these signals is a 6-dim vector. Our Python and MQL5 implementation are as follows:
def feature_0(adx_df, cci_df): """ Creates a 3D signal array with the following dimensions: 1. ADX > 25 crossover (1 when crosses above 25, else 0) 2. CCI > +100 crossover (1 when crosses above +100, else 0) 3. CCI < -100 crossover (1 when crosses below -100, else 0) """ # Initialize empty array with 3 dimensions and same length as input feature = np.zeros((len(adx_df), 6)) # Dimension 1: ADX > 25 crossover feature[:, 0] = (adx_df['adx'] > 25).astype(int) feature[:, 1] = (adx_df['adx'].shift(1) <= 25).astype(int) # Dimension 2: CCI > +100 crossover feature[:, 2] = (cci_df['cci'] > 100).astype(int) feature[:, 3] = (cci_df['cci'].shift(1) <= 100).astype(int) # Dimension 3: CCI < -100 crossover feature[:, 4] = (cci_df['cci'] < -100).astype(int) feature[:, 5] = (cci_df['cci'].shift(1) >= -100).astype(int) # Set first row to 0 (no previous values to compare) feature[0, :] = 0 return feature
if(Index == 0) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] > 25 ? 1.0f : 0.0f); _features[1] = (_adx[1] <= 25 ? 1.0f : 0.0f); _features[2] = (_cci[0] > 100 ? 1.0f : 0.0f); _features[3] = (_cci[1] <= 100 ? 1.0f : 0.0f); _features[4] = (_cci[0] < -100 ? 1.0f : 0.0f); _features[5] = (_cci[1] >= -100 ? 1.0f : 0.0f); } }
We have broken down our MLP input vector for this pattern to its key constituent signals. These are: ADX being previously below 25, then ADX being above 25, CCI being previously below +100, CCI now being above +100, CCI being previously above -100, CCI being currently below -100. With this setup, obviously not all situations can be true at the same time. What it allows us though it to customize all our price data points instead of grouping them around the typical pattern logic.
Traditionally though a bullish setup would be when the ADX crosses from below 25 to close above it followed by the CCI also crossing from below +100 to close above +100. Likewise, the bearish pattern would be if again the ADX crosses the 25 level to close above it, but the CCI crosses the -100 level from above to close below it. If we were to generate strict vectors that only test for these ‘true’ bullish or bearish setups, then our input vector would be sized 3 with less variability across the vast test data. Our chosen option of 6-dim input data captures these traditional metrics, but also ‘continuous’ data that would otherwise be ignored by the more ‘discrete’/ ‘traditional’ setup.
Feature-1
This pattern evolves around ADX > 25 and CCI Crosses of the ±50 levels from Opposite Sides. It is a momentum re-entry in an established trend. It is ideal for pullback continuation trades given that the ADX confirms trend integrity and the CCI detects recovery after a short counter trend. This is a pattern suited for trend followers aiming to enter a trend after retracement. The CCI’s cross at the zero bound is also an important cue that should not be rushed over. Trailing stops can also be placed on this signal for traders already in the trend who are looking to protect gains. Our Python and MQL5 implementation are as follows:
def feature_1(adx_df, cci_df): """ Creates a modified 3D signal array with: 1. ADX > 25 (1 when above 25, else 0) 2. CCI crosses from below 0 to above +50 (1 when condition met, else 0) 3. CCI crosses from above 0 to below -50 (1 when condition met, else 0) """ # Initialize empty array with 3 dimensions feature = np.zeros((len(adx_df), 5)) # Dimension 1: ADX above 25 (continuous, not just crossover) feature[:, 0] = (adx_df['adx'] > 25).astype(int) # Dimension 2: CCI crosses from <0 to >+50 feature[:, 1] = (cci_df['cci'] > 50).astype(int) feature[:, 2] = (cci_df['cci'].shift(1) < 0).astype(int) # Dimension 3: CCI crosses from >0 to <-50 feature[:, 3] = (cci_df['cci'] < -50).astype(int) feature[:, 4] = (cci_df['cci'].shift(1) > 0).astype(int) # Set first row to 0 (no previous values to compare) feature[0, :] = 0 return feature
else if(Index == 1) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] > 25 ? 1.0f : 0.0f); _features[1] = (_cci[0] > 50 ? 1.0f : 0.0f); _features[2] = (_cci[1] < 0 ? 1.0f : 0.0f); _features[3] = (_cci[0] < -50 ? 1.0f : 0.0f); _features[4] = (_cci[1] > 0 ? 1.0f : 0.0f); } }
Our function generates a 5-dim output vector of binary values, where the constituents are: whether ADX is above the 25 level, whether previous CCI was above 0; whether current CCI is below or equal to -50; whether previous CCI was below 0; whether current CCI as above or equal to 50. Traditionally, a bullish setup would be if the ADX is above 25 and CCI was below zero previously but is now above 50. A bearish setup would be if again ADX is above 25 and CCI was above 0 previously but is now below or equal to -50. Points mentioned above in moving towards a more continuous/ regressive mapping than a discrete one do also apply here.
Feature-2
This pattern is based on ADX > 25 with Price and CCI providing Divergences. This is also a divergence setup or a reversal within a trend. It uses classic momentum divergence pattern with ADX as a trend filter. It indicates potential reversal, even while the trend remains active. This pattern would be suited to situations where it is combined with price action or support/resistance for better confirmation. It is also ideal in situations where the divergence forms after an extended move. Caution is however encouraged as divergence is often only an early signal since a lot of them fail if they are coming off a very strong trend. Our Python and MQL5 implementation are as follows:
def feature_2(adx_df, cci_df, price_df): """ Creates a 5D signal array with: 1. ADX > 25 (1 when above 25, else 0) 2. Lower low (1 when current low < previous low, else 0) 3. Higher CCI (1 when current CCI > previous CCI, else 0) 4. Higher high (1 when current high > previous high, else 0) 5. Lower CCI (1 when current CCI < previous CCI, else 0) """ # Initialize empty array with 5 dimensions feature = np.zeros((len(price_df), 5)) # Dimension 1: ADX above 25 feature[:, 0] = (adx_df['adx'] > 25).astype(int) # Dimension 2: Lower low feature[:, 1] = (price_df['low'] < price_df['low'].shift(1)).astype(int) # Dimension 3: Higher CCI feature[:, 2] = (cci_df['cci'] > cci_df['cci'].shift(1)).astype(int) # Dimension 4: Higher high feature[:, 3] = (price_df['high'] > price_df['high'].shift(1)).astype(int) # Dimension 5: Lower CCI feature[:, 4] = (cci_df['cci'] < cci_df['cci'].shift(1)).astype(int) # Set first row to 0 (no previous values to compare) feature[0, :] = 0 return feature
else if(Index == 2) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2 && CopyRates(Symbol(),Period(),T, 2, _r) >= 2) { _features[0] = (_adx[0] > 25 ? 1.0f : 0.0f); _features[1] = (_r[0].low <= _r[1].low ? 1.0f : 0.0f); _features[2] = (_cci[0] > _cci[1] ? 1.0f : 0.0f); _features[3] = (_r[0].high > _r[1].high ? 1.0f : 0.0f); _features[4] = (_cci[0] < _cci[1] ? 1.0f : 0.0f); } }
The output for our function is a 6-dim vector consisting of: whether ADX is above 25; the price lows have moved lower; the CCI has moved higher; the price highs have moved higher; and finally if CCI has moved lower. Ordinarily, a bullish setup would consist of ADX being above 25, with price registering lower lows on rising momentum as marked by the CCI. Similarly, the bearish setup the ADX would still be above 25 but with price marking higher highs yet the CCI is registering a decline.
Feature-3
This pattern combines rising ADX with CCI in Neutral Zones. It acts as a trend confirmation with a neutral zone CCI. It focuses on sustained momentum in a rising or falling trend. When the CCI is in a neutral zone (0 to +/-100) it often means price is making a steady but not extreme moves. It tends to be safer than overbought/oversold signals, with less false entry risk. Could be taken as a ‘trend-is your-friend’ in less volatile markets. When combined, with moving average alignment or price structure, it can provide more safety. Our Python and MQL5 implementation are as follows:
def feature_3(adx_df, cci_df): """ Creates a 3D signal array with: 1. ADX rising (1 when current ADX > previous ADX, else 0) 2. CCI between 0 and +100 (1 when in range, else 0) 3. CCI between 0 and -100 (1 when in range, else 0) """ # Initialize empty array with 3 dimensions feature = np.zeros((len(adx_df), 5)) # Dimension 1: ADX rising feature[:, 0] = (adx_df['adx'] > adx_df['adx'].shift(1)).astype(int) # Dimension 2: CCI between 0 and +100 feature[:, 1] = (cci_df['cci'] > 0).astype(int) feature[:, 2] = (cci_df['cci'] < 100).astype(int) # Dimension 3: CCI between 0 and -100 feature[:, 3] = (cci_df['cci'] < 0).astype(int) feature[:, 4] = (cci_df['cci'] > -100).astype(int) # Set first row to 0 (no previous ADX value to compare) feature[0, :] = 0 return feature
else if(Index == 3) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] > _adx[1] ? 1.0f : 0.0f); _features[1] = (_cci[0] > 0 ? 1.0f : 0.0f); _features[2] = (_cci[1] < 100 ? 1.0f : 0.0f); _features[3] = (_cci[0] < 0 ? 1.0f : 0.0f); _features[4] = (_cci[1] > -100 ? 1.0f : 0.0f); } }
Our function generates a 5-dim vector that is made up of: whether ADX has increased; whether CCI is above 0; whether CCI is below +100; whether CCI is below 0; and whether CCI is above -100. The traditional bullish setup for this is rising ADX with CCI being above 0 but below +100. The flip bearish pattern is also ADX rising but CCI being below 0 but above -100. This pattern emphasizes a rising ADX (not just > 25). Additionally, neutral CCI ranges tend to target early trend development phases, unlike Feature 0’s extreme crossover, for example.

Feature-4
This pattern uses setups where ADX > 25 with CCI Recovery from Extremes. It is a failure swing setup. It captures momentum traps where CCI breaks an extreme level but then fails to continue. The addition of ADX ensures this is not a whipsaw situation within a consolidation. This pattern is often seen before reversals or sharp snap backs. It is best used in volatile trading sessions (or news driven events like Non-Farm-Payrolls announcements). The key here though is to watch for wick candles (pin bars) on failed swing days for stronger confirmation. Our Python and MQL5 implementation are as follows:
def feature_4(adx_df, cci_df): """ Creates a 3D signal array with: 1. ADX > 25 (1 when above 25, else 0) 2. CCI dips below -100 then closes above it (1 when condition met, else 0) 3. CCI breaks above +100 then closes below it (1 when condition met, else 0) """ feature = np.zeros((len(cci_df), 5)) # Dimension 1: ADX above 25 feature[:, 0] = (adx_df['adx'] > 25).astype(int) # Dimension 2: CCI dips below -100 then closes above it feature[:, 1] = (cci_df['cci'].shift(1) < -100).astype(int) feature[:, 2] = (cci_df['cci'] > -100).astype(int) # Dimension 3: CCI breaks above +100 then closes below it feature[:, 3] = (cci_df['cci'].shift(1) > 100).astype(int) feature[:, 4] = (cci_df['cci'] < 100).astype(int) return feature
else if(Index == 4) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] > 25 ? 1.0f : 0.0f); _features[1] = (_cci[0] < -100 ? 1.0f : 0.0f); _features[2] = (_cci[1] > -100 ? 1.0f : 0.0f); _features[3] = (_cci[0] > 100 ? 1.0f : 0.0f); _features[4] = (_cci[1] < 100 ? 1.0f : 0.0f); } }
Our feature-4 function gives us a 5-dim vector that outputs binary values of 1s and 0s on whether: ADX is below 20; CCI was below -100; CCI is now above -100; CCI was above +100; and if CCI is now below +100; A typical bullish signal that seeks momentum shift would therefore be if the ADX is below 20 and the CCI moves from below -100 to above -100. A flip bearish pattern would also therefore be if again the ADX is below 20 signalling a weak prevalent-trend and the CCI signals a decline in positive momentum by moving from above +100 to close below the +100 level.

Feature-5
This pattern simply uses ADX < 20 with Extreme CCI Spikes. It serves as a low volatility precursor to a momentum spike. It helps spot early-stage breakouts by watching for CCI bursts during a low-ADX phase. Not only that, but it aims to help traders set up a position before a trend begins. When implementing this pattern, it is often a good idea to use tight stops, since a lot of spikes can fake out. This pattern could provide an extra edge when combined with other indicators, such as the Bollinger-Band-Squeezes or volume-breakouts. It is, however, better suited for smaller time frames (e.g., M15 to H1) since these better facilitate quick momentum trades. Our Python and MQL5 implementation are as follows:
def feature_5(adx_df, cci_df): """ Creates a 3D signal array with: 1. ADX < 20 (1 when below 20, else 0) - indicates weak trend 2. CCI spikes above 150 (1 when condition met, else 0) - extreme overbought 3. CCI drops below -150 (1 when condition met, else 0) - extreme oversold """ # Initialize array feature = np.zeros((len(cci_df), 5)) # Dimension 1: ADX below 20 (weak trend) feature[:, 0] = (adx_df['adx'] < 20).astype(int) # Dimension 2: CCI spikes above 150 (sudden extreme overbought) # Using 2-bar momentum to detect "sudden" spikes feature[:, 1] = (cci_df['cci'] > 150).astype(int) feature[:, 2] = (cci_df['cci'].shift(1) < 130).astype(int) # Dimension 3: CCI drops below -150 (sudden extreme oversold) # Using 2-bar momentum to detect "sudden" drops feature[:, 3] = (cci_df['cci'] < -150).astype(int) feature[:, 4] = (cci_df['cci'].shift(1) > -130).astype(int) return feature
else if(Index == 5) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] < 20? 1.0f : 0.0f); _features[1] = (_cci[0] > 150 ? 1.0f : 0.0f); _features[2] = (_cci[1] < 130 ? 1.0f : 0.0f); _features[3] = (_cci[0] < -150 ? 1.0f : 0.0f); _features[4] = (_cci[1] > -130 ? 1.0f : 0.0f); } }
Our feature function 5 generates a 5-dim vector to feed to our MLP. Captured signals are: whether ADX is below 20; whether CCI is above +150; whether CCI had prior been below +130; whether CCI is below -150; and finally whether CCI had been above -130. It uses the ADX marker of being above 25 to ensure a strong trend is in play, aims to detect CCI recovery from extreme levels and in general focuses on reversals or momentum shifts.
A typical bullish setup would be when ADX is above 25, CCI had been below +130 and is now at +150. Similarly, a bearish setup would also require ADX to be above 25 with CCI now at -150, having previously tested -130.
Feature-6
This feature is about ADX crossing below 40 with CCI crossovers. An exit signal for trend exhaustion, this pattern is marked by a falling ADX that signals a weakening trend. Once CCI also crosses back to neutral or the opposite side, this also portends fading momentum. It can be taken as a risk-reduction signal that serves as a marker for trailing stop adjustment or profit taking. It can also be combined with candle stick patterns for cleaner exits, however, entrance of new trades with this setup in play is often ill-advised. Our Python and MQL5 implementation are as follows:
def feature_6(adx_df, cci_df): """ Creates a 3D signal array with: 1. ADX crosses below 40 (1 when crosses down, else 0) 2. CCI crosses below +100 (1 when crosses down, else 0) 3. CCI crosses above -100 (1 when crosses up, else 0) """ # Initialize array with zeros feature = np.zeros((len(cci_df), 6)) # Dimension 1: ADX crosses below 40 feature[:, 0] = (adx_df['adx'] < 40).astype(int) feature[:, 1] = (adx_df['adx'].shift(1) >= 40).astype(int) # Dimension 2: CCI crosses below +100 feature[:, 2] = (cci_df['cci'] < 100).astype(int) feature[:, 3] = (cci_df['cci'].shift(1) >= 100).astype(int) # Dimension 3: CCI crosses above -100 feature[:, 4] = (cci_df['cci'] > -100).astype(int) feature[:, 5] = (cci_df['cci'].shift(1) <= -100).astype(int) return feature
else if(Index == 6) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] < 40? 1.0f : 0.0f); _features[1] = (_adx[1] < 40? 1.0f : 0.0f); _features[2] = (_cci[0] < 100 ? 1.0f : 0.0f); _features[3] = (_cci[1] >= 100 ? 1.0f : 0.0f); _features[4] = (_cci[0] > -100 ? 1.0f : 0.0f); _features[5] = (_cci[1] <= -100 ? 1.0f : 0.0f); } }
Our feature 6 function outputs a 6-dim vector comprising: whether ADX is now below 40; whether ADX had previously been above 40; whether CCI is below 100; whether CCI had previously been above 100; whether CCI is above -100; and finally whether CCI had previously been below -100. A bearish termination pattern (the equivalent of a bullish) is when ADX drops from 40 to below 40 and the CCI had been below -100 but is now above it. Conversely, the bullish termination pattern (equivalent to bearish) is when again the ADX drops from 40 and the CCI also declines from +100 to fall below that level. Best suited as an exit or exit warning pattern, however it is included here as an entry signal solely for testing purposes.
Feature-7
This one involves ADX > 25 with CCI Zero-Line Crossovers. It is a trend catcher once the CCI crosses the zero-line. This is because the CCI’s crossing of the zero-line acts as a momentum pivot point. Since the ADX is also confirming strength, this setup offers clean mid-trend entries. This pattern tends to be more dependable when price is making higher highs or lower lows. Entering at multiple points with this pattern as signal could be worth considering. Back testing should be done for time alignment or session volatility window. Our Python and MQL5 implementation are as follows:
def feature_7(adx_df, cci_df): """ Creates Feature-7 3D signal array with: 1. ADX > 25 (1 when above 25, else 0) - trend strength 2. CCI crosses above 0 (1 when bullish crossover, else 0) 3. CCI crosses below 0 (1 when bearish crossover, else 0) """ # Initialize array with zeros feature = np.zeros((len(cci_df), 5)) # Dimension 1: ADX above 25 (continuous signal) feature[:, 0] = (adx_df['adx'] > 25).astype(int) # Dimension 2: CCI crosses above 0 (bullish) feature[:, 1] = (cci_df['cci'] > 0).astype(int) feature[:, 2] = (cci_df['cci'].shift(1) <= 0).astype(int) # Dimension 3: CCI crosses below 0 (bearish) feature[:, 3] = (cci_df['cci'] < 0).astype(int) feature[:, 4] = (cci_df['cci'].shift(1) >= 0).astype(int) return feature
else if(Index == 7) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] > 25? 1.0f : 0.0f); _features[1] = (_cci[0] > 0? 1.0f : 0.0f); _features[2] = (_cci[1] <= 0 ? 1.0f : 0.0f); _features[3] = (_cci[0] < 0 ? 1.0f : 0.0f); _features[4] = (_cci[1] >= 0 ? 1.0f : 0.0f); } }
Our feature-7 function also returns a 5-dim output vector. This vector logs: whether ADX is above 25; whether CCI is above 0; whether CCI had previously been below or equal to 0; whether CCI is below 0; and finally whether CCI had previously been above or equal to 0. The typical patterns from which it is derived have the bullish signal being indicated if the ADX is above 25 and CCI had been below 0 but is now above 0. Similarly, the bearish pattern is if the ADX again is above 25 and the CCI is now below 0 having previously been above 0.
Feature-8
Our 9th feature signal relies on ADX < 20 with CCI Extreme Pullbacks. It amounts to an ADX strength filter plus a CCI overbought/ oversold reversal indicator. A classic range-reversal that gets filtered by the ADX. In weak-trending or whipsawed markets, CCI reversals tend to perform better. It should ideally only be used when ADX is truly low (below 20) and should not be applied in trending markets. Pairing with Bollinger-Bands or the RSI can be suitable for multi-indicator confirmation. This reversal pattern could be ideal for mean reversion assets like commodities or currency-pairs. Our Python and MQL5 implementation are as follows:
def feature_8(adx_df, cci_df): """ Creates a 3D signal array with: 1. ADX < 20 (1 when below 20, else 0) - weak trend 2. CCI rises from -200 to -100 (1 when condition met, else 0) - extreme oversold bounce 3. CCI falls from +200 to +100 (1 when condition met, else 0) - extreme overbought pullback """ # Initialize array with zeros feature = np.zeros((len(cci_df), 5)) # Dimension 1: ADX below 20 (weak trend) feature[:, 0] = (adx_df['adx'] < 20).astype(int) # Dimension 2: CCI rises from -200 to -100 # Using 2-bar lookback to detect the move feature[:, 1] = (cci_df['cci'] > -100).astype(int) feature[:, 2] = (cci_df['cci'].shift(1) <= -200).astype(int) # Dimension 3: CCI falls from +200 to +100 # Using 2-bar lookback to detect the move feature[:, 3] = (cci_df['cci'] < 100).astype(int) feature[:, 4] = (cci_df['cci'].shift(1) >= 200).astype(int) return feature
else if(Index == 8) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 2) { _features[0] = (_adx[0] < 20? 1.0f : 0.0f); _features[1] = (_cci[0] > -100? 1.0f : 0.0f); _features[2] = (_cci[1] <= -200 ? 1.0f : 0.0f); _features[3] = (_cci[0] < 100 ? 1.0f : 0.0f); _features[4] = (_cci[1] >= 200 ? 1.0f : 0.0f); } }
Feature-8’s function output is also a 5-dim vector of binary values. These, mark: whether ADX is below 20; CCI is above -100; CCI was below -200; CCI is below +100; was above +200. The bullish signal from which these patterns are derived is therefore when ADX is below 20 and the CCI crosses to above -100 having previously tested -200. Conversely, the bearish pattern is when again ADX is below 20 and the CCI crosses to below +100 having been above +200 previously.
Feature-9
Our final feature uses, again, the ADX > 25 with CCI Delayed Crossings. This pattern represents opposing signal rejection or a trap filter. It is adept at spotting false breaks or fake outs against the dominant trend. In these setups, often price suggests reversal, however the CCI rejects this proposition by reaffirming prevalent trend. It is suitable for trend-trap protection. It is combinable with candlestick confirmation or volume dropoff after fake out. Good for traders that ‘were burnt’ from false prior signals and need a confidence filter. Our Python and MQL5 implementation are as follows:
def feature_9(adx_df, cci_df): feature = np.zeros((len(cci_df), 7)) cci = cci_df['cci'].values # Dimension 1 feature[:, 0] = (adx_df['adx'] > 25).astype(int) # Dimension 2: Below 0 then above +50 within 20 periods feature[:, 1] = (cci < 0).astype(int) feature[:, 2] = (np.roll(cci, 1) >= 0).astype(int) below_zero = (feature[:, 1]==1) & (feature[:, 2]==1) feature[:, 3] = 0 for i in np.where(below_zero)[0]: if i+20 < len(cci) and np.max(cci[i+1:i+21]) > 50: feature[:, 3] = 1 break # Dimension 3: Above 0 then below -50 within 20 periods feature[:, 4] = (cci > 0).astype(int) feature[:, 5] = (np.roll(cci, 1) <= 0).astype(int) feature[:, 6] = 0 above_zero = (feature[:, 4]==1) & (feature[:, 5]==1) for i in np.where(above_zero)[0]: if i+20 < len(cci) and np.min(cci[i+1:i+21]) < -50: feature[:, 6] = 1 break return feature
else if(Index == 9) { if(CopyBuffer(A.Handle(), 0, T, 2, _adx) >= 2 && CopyBuffer(C.Handle(), 0, T, 1, _cci) >= 21) { _features[0] = (_adx[0] > 25? 1.0f : 0.0f); _features[1] = (_cci[0] < 0? 1.0f : 0.0f); _features[2] = (_cci[1] >= 0 ? 1.0f : 0.0f); _features[3] = (_cci[ArrayMaximum(_cci,1,20)] > 50 ? 1.0f : 0.0f); _features[4] = (_cci[0] > 0? 1.0f : 0.0f); _features[5] = (_cci[1] <= 0 ? 1.0f : 0.0f); _features[6] = (_cci[ArrayMinimum(_cci,1,20)] < -50 ? 1.0f : 0.0f); } }
This pattern generates a 7-dim vector that maps: ADX is above 25; whether CCI is below 0; whether previous CCI was above 0; whether in a period of 20 bars prior to the last, the CCI was above the 50 level; whether CCI is above 0; whether previous CCI was below 0; and finally whether in a period of 20 bars prior to the last the CCI dropped below -50.
The indicated signal patterns from which these signals are generated are as follows. For a bullish signal the ADX needs to be above 25, and the CCI needs to have retested a positive above 0 level having dipped below it with a maximum of up to 50 in 20 bars prior to the dip. Likewise, a bearish pattern is when the CCI has just dipped below 0 having been above it previously with another low of at least -50 in the 20 bars prior to the spike above 0. Test results for this pattern did not forward walk, and so they are not shared, but all source is attached at bottom for further independent testing.
Conclusion
We have looked at the joint patterns of the ADX and CCI in a supervised learning MLP, with mixed to poor results in the forward walk. This was an attempt at having the input vector more continuous and less discrete, as we had in article 57 for the moving average and stochastic oscillator article. Even though this may be to blame, we will stick with this approach in the next pieces as we also see how the other methods of machine learning can be used with these indicators.
| Name | Description |
|---|---|
| 61_0.onnx | MLP for pattern 0 |
| 61_1.onnx | MLP for pattern 1 |
| 61_2.onnx | MLP for pattern 2 |
| 61_3.onnx | MLP for pattern 3 |
| 61_4.onnx | MLP for pattern 4 |
| 61_5.onnx | MLP for pattern 5 |
| 61_6.onnx | MLP for pattern 6 |
| 61_7.0nnx | MLP for pattern 7 |
| 61_8.onnx | MLP for pattern 8 |
| 61_9.onnx | MLP for pattern 9 |
| 61_x.mqh | Pattern processing file |
| SignalWZ_61.mqh | Signal class file |
| wz_61.mq5 | Wizard Assembled Expert Advisor to show included files |
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Price Action Analysis Toolkit Development (Part 21): Market Structure Flip Detector Tool
Price Action Analysis Toolkit Development (Part 21): Market Structure Flip Detector Tool
 From Basic to Intermediate: FOR Statement
From Basic to Intermediate: FOR Statement
 Data Science and ML (Part 37): Using Candlestick patterns and AI to beat the market
Data Science and ML (Part 37): Using Candlestick patterns and AI to beat the market
 Building a Custom Market Regime Detection System in MQL5 (Part 2): Expert Advisor
Building a Custom Market Regime Detection System in MQL5 (Part 2): Expert Advisor
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use