Statistische Arbitrage durch kointegrierte Aktien (Teil 1): Engle-Granger- und Johansen-Kointegrationstests
Einführung
Dies ist der erste von zwei Artikeln, die zeigen, wie man Kointegration in statistischen Arbitrage-Handelsstrategien nutzen kann. Statistische Arbitragestrategien werden von vielen fälschlicherweise als magische Null-Risiko-Strategien angesehen, während sie für den durchschnittlichen Kleinhändler praktisch unmöglich sind. Dieses Missverständnis ist auf Legenden zurückzuführen, die sich um die erstaunlichen Ergebnisse einiger großer Akteure ranken, auf die ewige Suche nach dem Heiligen Gral des Handels durch unerfahrene Menschen und schließlich auf das mangelnde Wissen darüber, was statistische Arbitrage ist.
Wenn sie richtig entwickelt und durch die richtige Infrastruktur für die Auftragsausführung unterstützt werden, können sie langfristig ein geringes Risiko und eine beständige Rentabilität aufweisen. Aber im Allgemeinen erfordern sie wie jede andere Handelsaktivität auch ein angemessenes Risikomanagement. Noch einmal: Statistische Arbitrage-Strategien sind keine magischen Null-Risiko-Strategien.
In einem früheren Artikel haben wir einen einfachen korrelationsbasierten Paarhandel durchgeführt, der im Backtest gut abschnitt, aber kläglich scheiterte, als wir ihn zwei Wochen lang auf einem Echtzeit-Demokonto laufen ließen. Dies ist wahrscheinlich der deutlichste Beweis dafür, dass Backtests nützlich sind, um die Durchführbarkeit einer Strategie zu beurteilen, aber gleichzeitig fast nichts über die reale Welt aussagen können. Und mehr noch, es ist ein klarer Beweis dafür, dass statistische Arbitrage nicht risikofrei ist. Selbst eine vielversprechende Strategie erfordert ein sorgfältiges Risikomanagement, das wir in unserem Beispielprototyp nicht implementiert haben, und eine angemessene Auftragsausführungsumgebung, um die es in diesem Artikel geht.
Warum waren die Ergebnisse im Demokonto im Vergleich zum Backtest so schlecht? Wie könnten wir unsere Instrumente über den Korrelationskoeffizienten hinaus, der die Bewegung zwischen zwei Vermögenswerten erfasst, verbessern, um einen robusteren Rahmen zur Erkennung langfristiger Dynamiken bei mehr als zwei Vermögenswerten zu haben? Wie können wir über den einfachen Paarhandel hinausgehen und das Portfolio auf eine Gruppe von Aktien aus demselben Sektor erweitern?
Erfolg im Backtest, Misserfolg in Echtzeit
Kürzlich hatten mein Partner und ich ein informelles Treffen mit einer Händlerin, die mit Dollarkontrakten an der brasilianischen Börse B3 arbeitet. Sie sagte, sie hätte gerne die Mittel, um „eine Art statistische Arbitrage bei Agrarrohstoffen“ auszuprobieren, aber da sie eine traditionelle diskretionäre Händlerin ist, die in technischer Analyse und Preisaktionen ausgebildet ist und keinen ausgeprägten Hintergrund in Mathematik oder Statistik hat, sagte sie positiv, dass statistische Arbitrage für sie „unerreichbar“ wäre. Sie wiederholte die altbekannte Überzeugung, über die wir zu Beginn sprachen, nämlich die, dass statistische Arbitrage für den Einzelhändler nicht erreichbar ist.
Um es kurz zu machen und direkt auf das zu kommen, wonach Sie hier suchen, machen wir daraus eine Herausforderung unter Freunden: Was wäre, wenn wir unsere Freizeit nutzen würden, um ein automatisiertes statistisches Arbitrageverfahren für Lernzwecke zu entwickeln? Aber wie soll das gehen, wenn keiner von uns ein großer Statistiker oder Mathematiker ist oder über die nötige Rechenleistung verfügt, um die großen Spieler zu schlagen? Wir taten, was Lernende normalerweise tun: Wir begannen mit akademischer Forschung, um das Problem und die bereits auf dem Markt befindlichen Alternativen zu verstehen, und studierten die Erfolge, aber auch die Misserfolge.
Unsere ersten kleinen Schritte führten zu einem Artikel, den ich kürzlich hier über den Mathematiker und Hedgefondsmanager Jim Simons und seinen legendären Medallion-Fonds veröffentlichte. In diesem Artikel haben wir einen einfachen EA verwendet, um die statistische Arbitrage zwischen XAUEUR und XAUUSD zu veranschaulichen.
Die untenstehende Grafik zeigt unsere Backtest-Ergebnisse, die wir hier veröffentlicht haben.
Abb. 1 - Backtest-Ergebnisse des Pairs-Trading EA (früherer Artikel)
Um die Funktionsfähigkeit in der realen Welt zu testen, haben wir diesen einfachen EA zwei Wochen lang auf einem provisionsbasierten Demokonto ohne Streuung laufen lassen. Die Ergebnisse waren katastrophal.
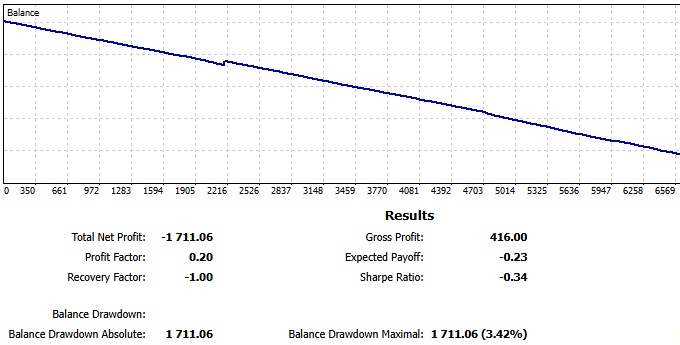
Abb. 2 - ReportHistory von zwei Wochen auf dem Demokonto für den Pairs-Trading EA
Wahrscheinliche Ursachen
Wenn wir nach den Gründen für das Scheitern einer Handelsstrategie suchen, sind wir versucht, zunächst die Parameter zu verändern. Versuchen wir es jedoch mit einer systematischeren Vorgehensweise, indem wir die Ursachen untersuchen.
Zwei aufeinanderfolgende schlechte Wochen?
Vielleicht waren es einfach zwei aufeinander folgende schlechte Wochen auf dem Markt? Selbst beim Backtest gab es einige ausgeglichene Perioden und sogar einige Perioden mit minimalem Drawdown, nicht wahr?
Ja, aber selbst in unseren schlechtesten Wochen hatten wir nie so viele Niederlagen hintereinander. Während wir in diesem Echtzeittest maximal vier Mal in Folge gewonnen haben, haben wir maximal zweiundvierzig Mal in Folge verloren! Während wir im Durchschnitt nur einen Sieg in Folge erzielt haben, haben wir im Durchschnitt fünf Niederlagen in Folge erlitten. Zusammenfassend lässt sich sagen, dass fast alle unsere Handelsgeschäfte verloren haben!
Abb. 3 - Abfolge der Verluste von Paartrading EA auf dem Demokonto
Offensichtlich war irgendetwas nicht in Ordnung, etwas ganz anderes als unsere Backtest-Umgebung. Außerdem ist der Paarhandel per Definition marktneutral, d. h. er ist nicht an die Rendite von Wertpapieren gebunden.(Der Paarhandel, als einfachste Form der statistischen Arbitrage, ist im Allgemeinen marktneutral. Unsere akademische Forschung zeigt jedoch, dass dies nicht immer im weitesten Sinne der Fall ist. Es gibt Situationen, in denen statistische Arbitrage je nach gewählter Absicherungsmethode Markt- oder Branchenrisiken mit sich bringen kann. Wir werden uns damit befassen, wenn wir an dem Modul für das Risiko-/Geldmanagement unseres Rahmens arbeiten. Für den Moment können wir unseren einfachen Paarhandel als marktneutral betrachten).
Jim Simons verdiente eine Menge Geld, als die Märkte während der Subprime-Krise 2008 implodierten. Der Medallion-Fonds war nicht der einzige Hedge-Fonds, der auf statistische Arbitrage setzte. Warum also verdienten sie Millionen, während ihre Kollegen durch den Absturz in Stücke gerissen wurden? Es scheint, als ob sie etwas besser machen als die Konkurrenz. Trotz der äußerst geheimen Natur ihrer Operationen hinterließen sie einige wertvolle Hinweise, die heute sogar offensichtlich sind, aber auch häufig von Kleinhändlern übersehen werden. Das Medallion-Team wurde und wird von riesigen Mengen an hochwertigen Daten angetrieben. Außerdem investierten sie in die beste Rechenleistung und die schnellste Weiterleitung von Aufträgen.
Eine schlechte Woche ist also wahrscheinlich nicht die Ursache. Es zeigt sich, dass statistische Arbitrage zwar marktneutral ist, aber gleichzeitig sehr empfindlich auf Daten und Timing reagiert.
Neue Umgebung?
Vielleicht war es der Wechsel des Brokers, mit einem anderen Spread? Bei Paaren, die sehr kurzfristig mit Tausenden von Einträgen pro Woche gehandelt werden, kann die Geld-Brief-Spanne leicht zu einem Problem werden. Wie Sie wissen, werden die von Forex-Brokern angebotenen Dienstleistungen in der Regel über die Geld-/Briefspanne und/oder prozentuale Provisionen bezahlt, die über das gehandelte Volumen abgerechnet werden.
Aber wir können die Verteilung verwerfen. Für den Backtest habe ich absichtlich ein Konto mit hohem Spread verwendet, mit durchschnittlich 170 Pips für Gold und ~50 Pips für XAUEUR. Für das Demokonto wechselte ich zu einem kommissionsbasierten Konto mit einem durchschnittlichen Spread von ~20 Pips für XAUUSD und ~10 Pips für XAUEUR.
Da wir im Demokonto eine geringere Geld-/Briefspanne hatten, ist die Spanne hier wahrscheinlich nicht der Schuldige.
Slippage?
Arbitrage ist in der Regel zeitabhängig, und unsere Paarhandelsstrategie ist sehr zeitabhängig. Sehen wir uns also an, was unsere CFD-Broker-Vereinbarung zur Ausführungspolitik über das Timing der Aufträge zu sagen hat.
Der letzte, der mir in den Sinn kommt, ist der übliche Verdächtige: Slippage. Wir schickten Sofortaufträge zum Marktpreis, und jemand anders schloss die Lücke zuerst. Wenn dies der Fall ist, ist hier nichts falsch. Diese Art von „Frontrunning“ ist legitim. Das ist in der Tat der Name des Spiels in der Arbitrage. Es bedeutet nur, dass jemand mehr und/oder bessere Ressourcen hat: bessere Hardware, kollokierte Server in der Nähe des Brokers oder einfach eine bessere Software, die für hohe Leistung optimiert ist, während wir einen Prototyp verwenden. Wahrscheinlich haben wir das Rennen mit mehreren Spieler verloren, jeder mit einigen dieser Vorteile, und schließlich einige Spieler mit allen Vorteilen. Das heißt, einige große Spieler haben unseren bescheidenen Prototyp gedemütigt.
Im Benutzerhandbuch des Metatrader 5 sehen wir, dass Verzögerungen bei Backtests simulieren kann.
„Der Strategietester ermöglichte die Emulation von Netzwerkverzögerungen während eines Expert Advisor-Betriebs, um realitätsnahe Bedingungen für die Tests zu schaffen. Zwischen dem Platzieren einer Handelsanfrage und deren Ausführung im Strategietester wird eine gewisse Zeitverzögerung eingefügt. Vom Zeitpunkt der Absendung der Anfrage bis zu ihrer Ausführung kann sich der Preis ändern. So können die Nutzer beurteilen, wie sich die Geschwindigkeit der Handelsabwicklung auf die Handelsergebnisse auswirkt.
Im Modus „Sofortige Ausführung“ können die Nutzer zusätzlich die Antwort des EA auf einen Requote vom Handelsserver überprüfen. Übersteigt die Differenz zwischen Anforderungs- und Ausführungskurs den in der Order angegebenen Abweichungswert, erhält der EA einen Requote.“
Wir haben das gemacht, indem wir eine zufällige Verzögerung eingestellt haben...
Abb. 4 - Einstellungen des Metatrader 5-Testers mit simulierter Verzögerung
... und BINGO! Auch wenn der Slippage nicht der einzige Schuldige ist, scheint unser üblicher Verdächtiger hier der Hauptverdächtige zu sein.
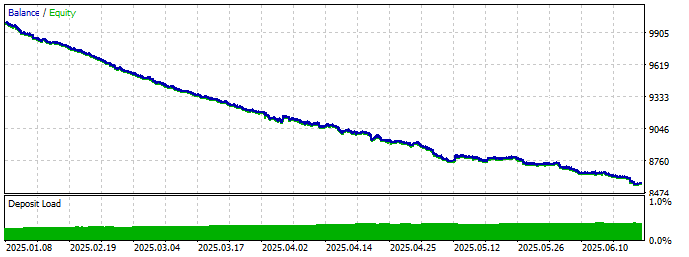
Abb. 5 - Ergebnisdiagramm nach Ausführung mit simulierter Verzögerung
Wir könnten versuchen, die maximal zulässige Abweichung in unserem Code festzulegen, aber diese Einschränkung würde unsere gesamte Strategie untergraben. Damit es rentabel ist, müssen wir fast sofort den richtigen Preis erwischen. Außerdem ist die Einstellung der maximalen Abweichung normalerweise nur bei professionellen Konten möglich, was uns von unserem Hauptziel, der Entwicklung eines statistischen Arbitrage-Rahmens für den durchschnittlichen Einzelhändler, abbringen würde.
Das Hauptproblem: die Ausführung
Mit Arbitrage kann man Geld verdienen, indem man alles kauft und verkauft, vom Toaster bis zu Token, von Rohstoffen bis zu Währungen und alles dazwischen. Wir können uns vorstellen, dass es begann, als die Menschen anfingen, Waren zu tauschen, noch bevor es Geld in dem Sinne gab, wie wir es heute verstehen. Das Konzept ist einfach: Wenn der hypothetische Toaster auf Marktplatz A zu billig ist, können wir ihn vielleicht dort kaufen und auf Marktplatz B verkaufen, wo er zum „richtigen Preis“ angeboten wird. Wenn die Preisdifferenz ausreicht, um die Transaktionskosten zu decken, können wir bei minimalem Risiko einen Gewinn erzielen.
Der Haken an der Sache ist, dass der Gewinn bei minimalem Risiko die Menschen anzieht. Je höher das Risiko-Ertrags-Verhältnis ist, desto größer ist das Publikum. Wenn es um Arbitrage auf den Finanzmärkten für Rohstoffe und Währungen geht, können die Gewinne riesig sein, und die Zahl derer, die versuchen, den unterbewerteten Vermögenswert zu kaufen, wird ebenfalls riesig sein, wobei jeder Spieler darum kämpft, vor seinen Konkurrenten zu bieten. Das Bedürfnis, als Erster ein Gebot abzugeben - und den Auftrag ausgeführt zu bekommen - führte schließlich zur Entwicklung der Infrastruktur, der Methoden und der Praxis des Hochfrequenzhandels (HFT). Wie Sie wahrscheinlich wissen, ist HFT nicht so einfach, und es ist nicht billig.
Das Hauptproblem besteht darin, dass der durchschnittliche Kleinhändler nicht über die erforderlichen Ressourcen verfügt, um die großen Akteure in Sachen Geschwindigkeit zu schlagen. Selbst wenn wir das Fehlen eines hochqualifizierten Teams von Statistikern und Mathematikern ignorieren, das von einer hohen Rechenleistung unterstützt wird, um die Modelle zu entwickeln, brauchen wir heute immer noch mindestens eine Kollokation, einen Hochleistungscode, einen Makler, der in der Lage ist, den Auftrag innerhalb weniger Millisekunden zu versenden/zu leiten...
Die Backtest-Ergebnisse zeigten die theoretische Tragfähigkeit der Strategie im Kontext einer idealen Auftragsausführung. Das heißt, dass unsere Befehle sofort ausgeführt wurden, wenn es um praktische Maßnahmen ging. Keine Netzwerkverzögerungen, keine Broker-Server-Fehler.
Es ist leicht einzusehen, dass dies nichts für den durchschnittlichen Kleinhändler ist. Wenn wir als bescheidene Kleinhändler von der Arbitrage auf den Finanzmärkten profitieren wollen, müssen wir Alternativen zu unserem naiven Prototyp des Paarhandels finden. Wir müssen Muster und Anomalien erforschen und finden, die nicht so sehr an die Geschwindigkeit gebunden sind.
Von der Korrelation zur Kointegration
Zuvor haben wir den Finanzmarkt so vorgestellt, wie Jim Simons ihn beschrieben hat, nämlich als ein Rätsel, das sich ständig verändert. Ein Rätsel, das von den Betreibern eine ständige Anpassung erfordert, um die Gewinne zu maximieren und die Verluste zu minimieren. Wir haben ein minimales „Portfolio“ aus zwei Vermögenswerten, XAUUSD und XAUEUR, zusammengestellt und die Abweichung vom Mittelwert ihrer Notierungen gegenüber dem amerikanischen Dollar als statistische Beziehung gewählt. Die Ausweitung des Spreads und die anschließende Rückkehr zum Mittelwert waren unsere Einstiegs- bzw. Ausstiegssignale.
An diesem Punkt ist unser statistisches „Arbitrage-Portfolio“ sehr begrenzt, ebenso wie unsere statistischen Beziehungen. Da sich die Geschwindigkeit unserer Kontrolle entzieht, können wir sie vorerst als verfrühte Optimierung betrachten. Zunächst müssen wir unsere Fähigkeiten verbessern, bevor wir unsere Zeit mit Dingen verbringen, auf die wir keinen Einfluss haben. Wir müssen unser Portfolio erweitern. Wir brauchen mehr statistische Beziehungen in unserem Screening-Arsenal und mehr statistische Messgrößen, die als Handelsauslöser dienen.
Die Kriterien, nach denen wir diese Paare ausgewählt haben, waren Korrelationen. Wir haben unsere Suche auf die wichtigsten Devisenmärkte beschränkt und das am stärksten korrelierende Paar in einem bestimmten Zeitintervall ausgewählt. Jetzt werden wir die Kointegration in unsere Portfolioauswahl einbeziehen.
Nach Angaben der Statistiker,
„Die Korrelation erfasst nur die kurzfristigen Beziehungen, während die Kointegration die langfristigen Gleichgewichtsbeziehungen erfasst. Zwei Variablen können hoch korreliert, aber nicht kointegriert sein, und umgekehrt“ [Alexander, 2001].
Der Korrelationskoeffizient gibt an, inwieweit sich die Kurse von XAUUSD und XAUEUR gleichzeitig in dieselbe Richtung bewegen. Durch einen Kointegrationstest wird eine langfristig gültige Äquivalenz zwischen den Vermögenswerten festgestellt. Außerdem sind wir bei der Verwendung des Korrelationskoeffizienten auf zwei Vermögenswerte beschränkt, aber bei der Prüfung auf Kointegration entfällt diese Beschränkung, sodass wir mehrere Portfoliokandidaten gleichzeitig prüfen können. Dies macht einen Kointegrationstest ideal für unsere Zwecke.
Als Händler oder EA-Entwickler brauchen wir die Mathematik hinter den Kointegrationstests nicht zu kennen. Da wir die Python-Integration für Metatrader 5 für unsere Datenanalyse und Portfolioauswahl verwenden werden, können wir die vorgefertigten Python-Funktionen aus spezialisierten Bibliotheken nutzen. Auch die KI-Assistenten, die ich beim Schreiben dieses Artikels geprüft habe - einschließlich der in Metatrader 5 eingebetteten GPTs - können Ihnen bei der Entwicklung einfacher Skripte für diesen Zweck helfen und Zeit sparen.
Als Händler müssen wir wissen, was Kointegration bedeutet und wie wir sie nutzen können, um Chancen zu erkennen, insbesondere auf dem Aktienmarkt, wo die Kointegration bekanntermaßen nützlicher und effektiver ist als bei Währungen. Als EA-Entwickler müssen wir wissen, wie wir die besten verfügbaren Bibliotheken verwenden und wie wir die Ergebnisse interpretieren können, damit wir iterieren und verbessern können. Durch die Verwendung hochwertiger Bibliotheken - und das Python-Ökosystem zeichnet sich durch hochwertige Bibliotheken für Mathematik, Statistik und maschinelles Lernen aus - sparen wir Zeit, vermeiden Fehler und haben möglicherweise eine bessere Leistung.
Wenn Sie sich eingehender mit dem Thema befassen wollen, empfehle ich Ihnen das oben zitierte Buch der Autorin Carol Alexander, genauer gesagt das Kapitel 12, das ganz der Kointegration gewidmet ist. In diesem Buch spannt Frau Alexander einen Bogen von der Geschichte des Einsatzes der Kointegration in der Finanzwelt bis hin zu ihrer Anwendbarkeit auf verschiedenen Märkten, einschließlich des Devisenmarktes. Ihr Lehrbuch ist ein sehr bekanntes Nachschlagewerk auf diesem Gebiet.
Sehen wir uns an, wie wir zwei der am meisten empfohlenen Kointegrationstests, den Engle-Granger-Test und den Johansen-Test, in verschiedenen Anlageklassen anwenden können und wie ihre Ergebnisse zu lesen sind.
Der Engle-Granger-Kointegrationstest
Der Engle-Granger-Kointegrationstest kann verwendet werden, um den Grad der Kointegration zwischen zwei Vermögenswerten zu bewerten. Ihr Zweck ist die Beantwortung der Frage: Besteht zwischen diesen beiden Vermögenswerten eine langfristige Gleichgewichtsbeziehung? Was uns als Händler und EA-Entwickler betrifft, so wird uns dieser Test zeigen, ob der Spread der beiden Vermögenswerte eine Rückkehr zum Mittelwert aufweist. Die Antwort ist jedoch nicht binär: ja oder nein. Ähnlich wie der Pearson-Korrelationstest, den wir zuvor gesehen haben, liefert er uns einen relativen Wert (p-Wert), der den Ergebnissen anderer Paare gegenübergestellt werden sollte, um uns zu sagen, welches von ihnen am stärksten integriert ist.
Der p-Wert ist die Wahrscheinlichkeit, dass die Daten beobachtet werden, wenn es KEINE Kointegration gäbe. Das heißt, je kleiner der p-Wert ist, desto besser. Es gibt bekannte Schwellenwerte. Ein p-Wert < 0,05 wird in der Regel als moderates Signal für Kointegration angesehen. Ein p-Wert < 0,01 ist ein starkes Signal, und ein p-Wert > 0,05 ist ein Signal für keine Kointegration. Wie immer beim Handel sollten Sie diese Schwellenwerte für Ihren speziellen Anwendungsfall fein abstimmen.
Der Python-Code zur Durchführung beider Kointegrationstests verwendet die bekannte Bibliothek statsmodels.
„Ein Python-Modul, das Klassen und Funktionen für die Schätzung vieler verschiedener statistischer Modelle sowie für die Durchführung statistischer Tests und die statistische Datenexploration bereitstellt.“
from datetime import datetime, timedelta import MetaTrader5 as mt5 import pandas as pd import numpy as np from statsmodels.tsa.stattools import coint import matplotlib.pyplot as plt # connect to MetaTrader 5 terminal if not mt5.initialize(login=********, server="MetaQuotes-Demo",password="********"): print("initialize() failed, error code =",mt5.last_error()) quit() # Forex majors - check your Market Watch names symbols = ['EURUSD', 'GBPUSD', 'USDJPY', 'AUDUSD', 'USDCAD', 'NZDUSD', 'USDCHF']
Wir suchen nach dem am stärksten kointegrierten Paar unter den großen Devisenmärkten. Wir erwarten nicht, dass wir eine hohe Kointegrationsrate finden. Sie soll lediglich veranschaulichen, wie der Engle-Granger-Test funktioniert.
# define the timeframe and the number of days timeframe = mt5.TIMEFRAME_D1 # Daily n_days = 600 utc_to = datetime.now() utc_from = utc_to - timedelta(days=n_days)
Wir werden die Variablen utc_from und utc_to verwenden, um mit mt5.copy_rates_range Symbolkurse für 600 Handelstage abzufragen. Ein Jahr hat etwa 250 Handelstage.
# download historical data for each symbol data = {} for symbol in symbols: # Make sure the symbol is available in Market Watch mt5.symbol_select(symbol, True) # Get historical rates rates = mt5.copy_rates_range(symbol, timeframe, utc_from, utc_to) if rates is None or len(rates) == 0: print(f"No data for {symbol}.") continue df = pd.DataFrame(rates) df['time'] = pd.to_datetime(df['time'], unit='s') df.set_index('time', inplace=True) data[symbol] = df['close']
In dieser for-Schleife fragen wir die Schlusskurse für jedes Symbol ab, konvertieren sie in einen Pandas DataFrame und setzen das Array „time“ als unseren tabellarischen Datenindex.
Nach der Verkettung der Datenrahmen und der Entfernung von Zeilen mit fehlenden Werten, die unsere Ergebnisse verzerren könnten, führen wir den Kointegrationstest durch.
# Store cointegration test results results = [] # Test all unique pairwise combinations for cointegration pairs = [(a, b) for i, a in enumerate(data.columns) for j, b in enumerate(data.columns) if i < j] print("Cointegration test results (Engle-Granger):") for a, b in pairs: score, pvalue, _ = coint(data[a], data[b]) results.append((a, b, pvalue)) print(f"{a} vs {b} | p-value: {pvalue:.4f}")
Index(['EURUSD', 'GBPUSD', 'USDJPY', 'AUDUSD', 'USDCAD', 'NZDUSD', 'USDCHF'], dtype='object')
Ergebnisse des Kointegrationstests (Engle-Granger):
EURUSD gegenüber GBPUSD | p-Wert: 0.3183
EURUSD vs USDJPY | p-value: 0.6990
EURUSD vs AUDUSD | p-value: 0.9308
EURUSD vs USDCAD | p-value: 0.9206
EURUSD vs NZDUSD | p-value: 0.9741
EURUSD vs USDCHF | p-value: 0.4342
GBPUSD vs USDJPY | p-value: 0.3273
GBPUSD vs AUDUSD | p-value: 0.7995
GBPUSD vs USDCAD | p-value: 0.6264
GBPUSD vs NZDUSD | p-value: 0.7810
GBPUSD vs USDCHF | p-value: 0.0238
USDJPY vs AUDUSD | p-value: 0.6299
USDJPY vs USDCAD | p-value: 0.5620
USDJPY vs NZDUSD | p-value: 0.6398
USDJPY vs USDCHF | p-value: 0.2377
AUDUSD vs USDCAD | p-value: 0.1260
AUDUSD vs NZDUSD | p-value: 0.2920
AUDUSD vs USDCHF | p-value: 0.5980
USDCAD vs NZDUSD | p-value: 0.0052
USDCAD vs USDCHF | p-value: 0.8574
NZDUSD vs USDCHF | p-value: 0.6384
Am meisten kointegriertes Paar: USDCAD und NZDUSD (p = 0,0052)
Sobald wir die beiden am stärksten kointegrierten Paare haben, können wir entscheiden, ob wir sie in unser Paarhandelsportfolio aufnehmen. In der nachstehenden Grafik ist deutlich zu erkennen, dass sich der Spread wieder dem Mittelwert annähert, aber die Frage ist: Lohnt sich der Handel?
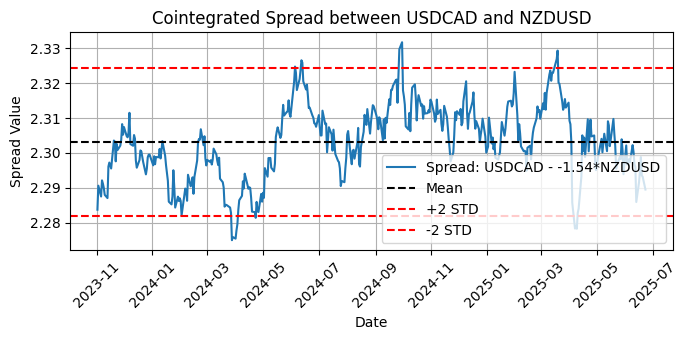
Abb. 6 - Darstellung des kointegrierten Spreads zwischen USDCAD und NZDUSD mit Mittelwert und zwei Standardabweichungen
Die gestrichelte schwarze Linie gibt den Mittelwert der Streuung an. Dies ist das langfristige Gleichgewichtsniveau. Die beiden gestrichelten roten Linien zeigen die beiden Standardabweichungsbereiche (STD) an. Diese definieren Schwellenwerte für die Identifizierung möglicher Handelssignale, wenn die Spanne ungewöhnlich hoch oder niedrig ist, sodass die Anzahl der Standardabweichungen ein ernsthafter Kandidat für Ihre Optimierung ist.
Das Absicherungsverhältnis
Beachten Sie den Wert von -1,54, der bei der Berechnung des langfristigen Spreads verwendet wurde.
Spanne = USDCAD - (-1,54) * NZDUSD
oder
USDCAD + 1,54 * NZDUSD
Dieser Wert ist das Absicherungsverhältnis. Dies ist das optimale Verhältnis, das statistisch über eine lineare Regression geschätzt wird und USDCAD und NZDUSD so aneinander angleicht, dass ihr Spread stationär ist, d.h. um den konstanten Mittelwert oszilliert, was für Mean-Reversion-Strategien entscheidend ist. Durch die Verwendung dieses Absicherungsverhältnisses wissen wir, dass wir die Preise auf der gleichen Skala vergleichen, wobei ihre Volatilität und Richtungsbeziehung korrigiert werden.
Der Spread gibt die relativen Fehlbewertungen wieder. In der Terminologie des Paarhandels würde man sagen, dass der Spread bei einem Wert von über +2 STD historisch hoch ist und wir in Erwägung ziehen können, den Spread zu verkaufen; umgekehrt ist der Spread bei einem Wert von unter -2 STD historisch niedrig und wir können in Erwägung ziehen, den Spread zu kaufen.
Um auf der Grundlage dieser Daten ein marktneutrales Paar für den Handel zu konstruieren, würden wir für jede Einheit USDCAD, die wir kaufen würden, gleichzeitig 1,54 Einheiten NZDUSD verkaufen (oder umgekehrt, je nach Signalrichtung). Wenn sich der Spread dann wieder dem Mittelwert annähert, beenden wir den Handel und schließen beide Positionen.
Sie können denselben Code für Symbole aus allen Märkten und Anlageklassen verwenden. Um es so zu verwenden, wie es ist, ersetzen Sie einfach die Symbolnamen ganz oben.
Der Johansen-Kointegrationstest
Der Johansen-Kointegrationstest soll dieselbe Frage beantworten wie der Engle-Granger-Test: Besteht zwischen diesen Vermögenswerten eine langfristige Gleichgewichtsbeziehung? In der Praxis und für unsere Zwecke hier besteht der Hauptunterschied darin, dass der Johansen-Test mehr als zwei Aktiva gleichzeitig bewerten kann und uns sagt, ob diese N Aktiva eine gemeinsame Spanne für eine Rückkehr zum Mittelwert aufweisen. Wir können sie als ein leistungsfähiges Instrument zur Bewertung der möglichen Kointegration in einer Gruppe von Aktien desselben Sektors betrachten, wie z. B. Ölaktien, Technologiewerte usw. Sie ermöglicht es uns, drei, vier oder mehr Aktien (oder andere Vermögenswerte) zu finden, die eine gemeinsame langfristige Gleichgewichtsbeziehung aufweisen.
Sie prüft, ob es Kombinationen von Variablen gibt, die zum Mittelwert zurückkehren (stationär sind), auch wenn die ursprünglichen Reihen dies nicht sind, und schätzt, wie viele kointegrierende Beziehungen zwischen den Variablen bestehen. Diese Zahl wird als Kointegrationsrang bezeichnet.
Der Test liefert zwei Hauptstatistiken: die Trace-Statistik und den kritischen Wert.
Sie erhalten eine Trace-Statistik für jeden möglichen Rang (0, 1, 2, ..., N-1, wobei N die Anzahl der Reihen ist). Eine größere Trace-Statistik deutet auf einen stärkeren Nachweis der Kointegration hin. Der kritische Wert ist der Schwellenwert, mit dem die Trace-Statistik verglichen wird. Es hängt ab von:
- der Anzahl der zu bewertenden Variablen,
- der Länge der Probe,
- dem Konfidenzniveau (90%, 95% oder 99%).
In diesem speziellen Fall kann man sich die Anzahl der Variablen als die Anzahl der getesteten Symbole vorstellen.
# Johansen Test from datetime import datetime, timedelta import MetaTrader5 as mt5 import pandas as pd import numpy as np from statsmodels.tsa.stattools import coint from statsmodels.tsa.vector_ar.vecm import coint_johansen import matplotlib.pyplot as plt # Create a matrix for the test log_prices = data.apply(np.log) johansen_result = coint_johansen(log_prices, det_order=0, k_ar_diff=1) # Trace statistics and critical values print("\nJohansen Test Results (Trace Statistic):") for i, stat in enumerate(johansen_result.lr1): cv = johansen_result.cvt[i, 1] # 5% critical value print(f"Rank {i}: Trace Stat = {stat:.2f} | 5% CV = {cv:.2f} | {'Significant' if stat > cv else 'Not significant'}")
Wir können die Ergebnisse für die anderen Konfidenzniveaus sehen, indem wir sie einstellen:
johansen_result.cvt[i, 0] für 90%
johansen_result.cvt[i, 2] für 99%
Bei einem Konfidenzniveau von 95 % (kritischer Wert von 5 %) sind dies unsere Ergebnisse für die Forex-Majors im gleichen Zeitraum und D1-Zeitrahmen, die wir mit Engle-Granger getestet haben.
Index(['EURUSD', 'GBPUSD', 'USDJPY', 'AUDUSD', 'USDCAD', 'NZDUSD', 'USDCHF'], dtype='object')
Ergebnisse des Johansen-Tests (Trace-Statistik):
Rang 0: Trace Stat = 105,25 | 5% CV = 125,62 | Nicht signifikant
Rang 1: Trace Stat = 68.10 | 5% CV = 95.75 | Nicht signifikant
Rang 2: Trace Stat = 42.01 | 5% CV = 69.82 | Nicht signifikant
Rang 3: Trace Stat = 25,83 | 5% CV = 47,85 | Nicht signifikant
Rang 4: Trace Stat = 11,73 | 5% CV = 29,80 | Nicht signifikant
Rang 5: Trace Stat = 5,74 | 5% CV = 15,49 | Nicht signifikant
Rang 6: Trace Stat = 0,58 | 5% CV = 3,84 | Nicht signifikant
Wie zu erwarten war, gibt es keine signifikante Kointegration zwischen den sieben großen Devisenmärkten.
Wenn wir jedoch die beiden bekannten Google- und Nvidia-Aktien im H1-Zeitrahmen testen (siehe unten), erhalten wir ein signifikantes Kointegrationsergebnis für denselben Zeitraum und dasselbe Konfidenzintervall.
Index(['NVDA', 'GOOGL'], dtype='object')
Anzahl der Beobachtungen: 5769
Anzahl der Variablen: 2
Ergebnisse des Johansen-Tests (Trace-Statistik):
Rang 0: Trace Stat = 18,71 | 5% CV = 15,49 | Signifikant
Rang 1: Trace Stat = 0,29 | 5% CV = 3,84 | Nicht signifikant
Am meisten kointegriertes Paar (Engle-Granger): NVDA und GOOGL | p-value: 0.0824
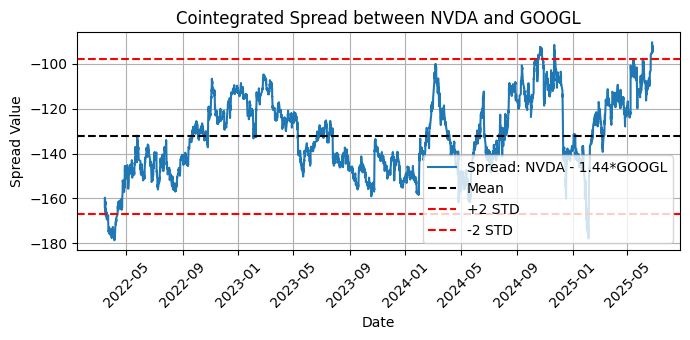
Abb. 7 - Darstellung des kointegrierten Spreads zwischen NVDA und GOOGL mit Mittelwert und zwei Standardabweichungen
Ok, wir haben eine signifikante Kointegration für GOOGL und NVDA nach Johansen, aber einen Engle-Granger p-value über 0,05, was ein Signal für keine Kointegration ist. Warum diese widersprüchlichen Ergebnisse? Was bedeutet das?
Führen wir dasselbe Skript aus, nur mit umgekehrter Reihenfolge der Symbole, so sehen Sie einen interessanten Unterschied zwischen dem Engle-Granger- und dem Johansen-Test.
Index(['GOOGL', 'NVDA'], dtype='object')
Anzahl der Beobachtungen: 5769
Anzahl der Variablen: 2
Ergebnisse des Johansen-Tests (Trace-Statistik):
Rang 0: Trace Stat = 18,71 | 5% CV = 15,49 | Signifikant
Rang 1: Trace Stat = 0,29 | 5% CV = 3,84 | Nicht signifikant
Am meisten kointegriertes Paar (Engle-Granger): GOOGL und NVDA | p-value: 0.0403
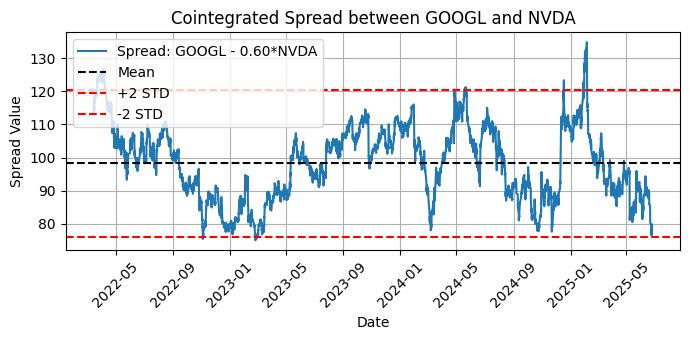
Abb. 8 - Darstellung des kointegrierten Spreads zwischen GOOGL und NVDA mit Mittelwert und zwei Standardabweichungen
Wie Sie sehen können, reagiert Engle-Granger empfindlich auf die Reihenfolge, während Johansen von der Änderung nicht betroffen ist. Wenn Sie sich eingehend mit den Feinheiten des Johansen-Tests befassen, werden Sie feststellen, dass er in einigen Fällen eine gewisse Empfindlichkeit gegenüber der Reihenfolge aufweisen kann, insbesondere bei kurzen Stichproben oder wenn wir uns am Rande der statistischen Signifikanz befinden. In der Regel ist sie jedoch theoretisch unempfindlich gegenüber der Reihenfolge. Wenn Sie nach einer Änderung der Reihenfolge inkonsistente Ergebnisse erhalten, fügen Sie als erste Maßnahme mehr Daten zu Ihrer Stichprobe hinzu. Aus diesem Grund haben wir den D1-Zeitrahmen (täglich) durch einen H1-Zeitrahmen (stündlich) ersetzt, um eine größere Stichprobe für den Test zu erhalten.
Die Tatsache, dass Engle-Granger empfindlich auf die Reihenfolge der Variablen reagiert, legt nahe, dass Sie immer beide Richtungen testen und die Ergebnisse durch visuelle Inspektion der Diagramme bewerten sollten, um zu sehen, ob die Streuung zum Mittelwert zurückkehrt
Prüfung der Stationarität der Spanne
Die Streuung ist eine Zeitreihe, und um sicher zu sein, dass sie zum Mittelwert zurückkehrt, müssen wir ihre Stationarität prüfen, d. h. wir müssen prüfen, ob sich ihr Mittelwert, ihre Varianz und ihre Kovarianz im Laufe der Zeit nicht verändern. Die Modellierung und Vorhersage mit Techniken wie ARIMA-Modellen ist einfacher, wenn die Zeitreihe stationär ist.
Die gleiche Python-Bibliothek, die wir zum Testen auf Kointegration verwendet haben, verfügt über vorgefertigte Funktionen zum Testen auf Stationarität, den Augmented Dickey Fuller (ADF“-Test) und den Kwiatkowski-Phillips-Schmidt-Shin (KPSS“-Test).
from statsmodels.tsa.stattools import adfuller (...) adf_result = adfuller(spread)
ADF-Test auf Streuung:
ADF-Statistik: -3,0946
p-value : 0.0270
Kritische Werte:
1%: -3.4315
5%: -2.8620
10%: -2.5670
✅ Die Spanne ist stationär (Ablehnung der Nullhypothese).
from statsmodels.tsa.stattools import kpss (...) def run_kpss(series, regression='c'): statistic, p_value, lags, crit_values = kpss(series, regression=regression, nlags='auto') (...) # Run KPSS test on the residuals run_kpss(spread, regression='c') # 'c' = test for level stationarity (use 'ct' for trend)
KPSS-Test zur Streuung:
KPSS-Statistik : 2.2702
p-value : 0.0100
Verwendete Verzögerungen : 44
Kritische Werte: 10% : 0.347
5% : 0.463
2.5% : 0.574
1% : 0.739
❌ Die Spanne ist NICHT stationär (Ablehnung der Stationarität).
Es scheint, als hätten wir wieder widersprüchliche Ergebnisse. ADF sagt, dass unser Spread stationär ist, aber KPSS stimmt dem nicht zu. Kein Grund zur Panik. Die Betreuer von statsmodels waren sorgfältig genug, um uns eine klare Erklärung zu geben, wie beide Tests in jeder möglichen Kombination von Ergebnissen zu interpretieren sind. Hier zitiere ich das Dokument von statsmodels, weil ich denke, dass es kaum noch präziser und klarer sein kann.
„Fall 1: Beide Tests kommen zu dem Ergebnis, dass die Reihe nicht stationär ist - Die Reihe ist nicht stationär
Fall 2: Beide Tests kommen zu dem Ergebnis, dass die Reihe stationär ist - Die Reihe ist stationär
Fall 3: KPSS weist auf Stationarität und ADF auf Nicht-Stationarität hin - Die Reihe ist trendstabil. Der Trend muss entfernt werden, um die Reihe streng stationär zu machen. Die verzerrte Reihe wird auf Stationarität geprüft.
Fall 4: KPSS weist auf Nicht-Stationarität und ADF auf Stationarität hin - Die Reihe ist differenzstationär. Die Differenzierung ist zu verwenden, um Reihen stationär zu machen. Die differenzierte Reihe wird auf Stationarität geprüft.“
Wir sind also darüber informiert, dass unser Spread nicht streng stationär, sondern differenziell stationär ist. Was bedeutet das? Das bedeutet, dass diese Zeitreihe zwar driften kann, die Veränderungen aber stabil sind. Sie kann in eine streng stationäre Zeitreihe umgewandelt werden, indem einfach die Differenzen zwischen aufeinanderfolgenden Werten genommen werden. Es überrascht nicht, dass diese Technik als Differenzierung bezeichnet wird. Sie beseitigt Trends und saisonale Schwankungen und macht unsere Zeitreihen für eine effektivere Analyse und Prognose bereit.
Müssen wir unseren Spanne streng stationär machen? Viele Zeitreihenmodelle setzen voraus, dass die Daten stationär sind, aber das ist nicht der Fall. Wir werden uns in unserer Kointegrationsimplementierung nicht mit Prognosemodellen befassen.
Wir werden überhaupt keine Prognosen erstellen, aber vielleicht schadet es nicht, zu wissen, dass die Kointegrationsanalyse nicht mit den Kointegrationstests endet.
Schlussfolgerung
In diesem Artikel sind wir beim Aufbau unseres statistischen Arbitrage-Rahmens für den einfachen Händler einen Schritt weiter gegangen. Wir haben unser statistisches Instrumentarium für die Portfoliobildung um zwei weitere Instrumente erweitert: den Engle-Granger- und den Johansen-Kointegrationstest. Wir erfuhren, was wir von den einzelnen Tests zu erwarten haben und wie man die Ergebnisse am einfachsten auswertet. Außerdem haben wir gesehen, wie man die Stationarität der Spanne mit Hilfe des Augmented Dickey Fuller („ADF“) Tests und des Kwiatkowski-Phillips-Schmidt-Shin („KPSS“) Tests überprüft.
Dies war der erste von zwei Artikeln, in denen die grundlegenden Werkzeuge vorgestellt wurden. Der folgende Artikel ergänzt diese Fibel mit einer Implementierung, Backtests und Optimierungen für ein Paar kointegrierter Devisensymbole und für eine Gruppe kointegrierter Aktiensymbole aus demselben Sektor.
Ich wage zu behaupten, dass der wichtigste Inhalt hier nicht die Präsentation der Werkzeuge, der Funktionen oder sogar des Beispielcodes ist. Die wichtigste Erkenntnis hierbei ist, dass die wertvollste Fähigkeit, die Sie bei der Entwicklung Ihrer statistischen Arbitragestrategie haben, das Verständnis des Vermögenswerts oder der Gruppe von Vermögenswerten ist, mit denen Sie arbeiten, wenn Sie ein Einzelhändler sind, der keine mathematischen oder statistischen Kenntnisse hat, ein Nicht-Entwickler-Händler.
Ihr Wissen über die Märkte ist unbezahlbar, denn die harte Arbeit in Mathematik und Statistik wurde bereits von hochqualifizierten Fachleuten für Sie geleistet, und diese Arbeit ist in vielen Open-Source-Bibliotheken kostenlos verfügbar, einschließlich der MQL5-Bibliotheken, die auf der Metatrader 5-Plattform zusammen mit dem unschätzbaren KI-Assistenten verfügbar sind, um Ihnen bei der richtigen Implementierung zu helfen.
Erlernte Lektion: Wenn Sie nur über begrenzte Ressourcen verfügen, sollten Sie sich von geschwindigkeitsabhängigen Strategien fernhalten und versuchen, die Daten auf kreative Weise zu untersuchen, indem Sie Ihre Marktkenntnisse nutzen.
Referenzen
- Alexander, C. (2001). Market Models: A Guide to Financial Data Analysis, Wiley.
- Engle, R. F., & Granger, C. W. J. (1987). Co-integration and error correction: representation, estimation, and testing. Econometrica.
- Gatev, E., Goetzmann, W. N., & Rouwenhorst, K. G. (2006). "Pairs Trading: Performance of a Relative-Value Arbitrage Rule." Review of Financial Studies.
- Johansen, S. (1988). Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control.
| Angehängte Datei | Beschreibung |
|---|---|
| coint.ipynb | Diese Datei ist ein vereinfachtes Jupyter-Notebook, das Python-Code enthält, um einen einzelnen Engle-Granger-Kointegrationstest für ein Paar von Handelsinstrumenten durchzuführen. |
| coint_googl_nvda.ipynb | Bei dieser Datei handelt es sich um ein erweitertes Jupyter-Notebook, das Python-Code enthält, um sowohl den Engle-Granger- als auch den Johansen-Kointegrationstest über eine (theoretisch) unbegrenzte Anzahl von Handelsinstrumenten sowie den Test auf Spread-Stationarität durchzuführen. |
| helper_quotes_to_db.ipynb | Diese Datei ist ein Hilfsmittel, um heruntergeladene Symbolzitate in einer sqlite3-Datenbank zu speichern. Es handelt sich auch um ein Jupyter-Notebook mit Python-Code. Damit sollen redundante Downloads vermieden und die Offline-Arbeit ermöglicht werden. |
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18702
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 MQL5-Assistenz-Techniken, die Sie kennen sollten (Teil 74): Verwendung von Ichimoku-Mustern und ADX-Wilder mit überwachtem Lernen
MQL5-Assistenz-Techniken, die Sie kennen sollten (Teil 74): Verwendung von Ichimoku-Mustern und ADX-Wilder mit überwachtem Lernen
 Einführung in MQL5 (Teil 18): Einführung in das Muster der Wolfe-Wellen
Einführung in MQL5 (Teil 18): Einführung in das Muster der Wolfe-Wellen
 Entwicklung des Price Action Analysis Toolkit (Teil 32): Python-Engine für Kerzenmuster (II) – Erkennung mit Ta-Lib
Entwicklung des Price Action Analysis Toolkit (Teil 32): Python-Engine für Kerzenmuster (II) – Erkennung mit Ta-Lib
 Singuläre Spektralanalyse in MQL5
Singuläre Spektralanalyse in MQL5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Interessanter Artikel! Ich habe bereits an ähnlichen Projekten gearbeitet und hatte auch Probleme bei der Live-Ausführung :)
Aber der Artikel ist gut geschrieben. Neulinge auf diesem Gebiet werden ihm leicht folgen können.