斐波那契（Fibonacci）数列在外汇交易中的应用（第一部分）：探究价格与时间的关系

MetaTrader 5 — 积分 | 23 一月 2026, 14:48

概述

公元前6世纪，毕达哥拉斯宣称：“万物皆数”。他的追随者们认为，数字关系构成了宇宙的结构基础，理解这些关系是理解和预测宇宙中任何过程的关键。两千年后，古希腊人的这一直觉洞见在量子力学、相对论和混沌理论中得到了意想不到的证实：自然的基本定律确实是通过数学关系来表达的。

1202年，意大利数学家比萨的莱昂纳多（更为人熟知的名字是斐波那契）出版了一个描述兔子繁殖的问题。他或许未曾料到，他所描述的这个数列会成为人类历史上最神秘、讨论最广泛的数学现象之一。也许正是这个数列，以及从中推导出的比率，代表了毕达哥拉斯学派所言的那些基本数字定律之一。

在斐波那契数列中，每个后续数字都等于前两个数字之和（1, 1, 2, 3, 5, 8, 13, 21……），该数列不仅描述了兔子种群的增长情况。还体现在茎上叶子的排列、海螺的螺旋、人体的比例，甚至星系的结构中。最引人入胜的是，斐波那契数及其衍生比率在金融市场波动中反复出现。

如果毕达哥拉斯学派是对的，世界上的一切确实都由数字关系所支配，那么外汇市场（尽管看似混乱）也应该遵循这些定律。但是，为什么在一个由数百万交易者独立做出决策、价格受无数因素影响的市场中，会出现与斐波那契数列相关的模式呢？如果这样的模式确实存在，它们能否像古希腊人相信的那样用于预测呢？

在本研究中，我们利用现代数据处理技术和机器学习，深入分析了外汇市场超过10万次的价格波动。我们不仅考察了经典的价格比率，还研究了基于时间的模式——这一领域在传统技术分析中受到的关注较少。

我们的方法是严格的科学方法：没有统计确认的假设，没有定量可靠性度量的结论。我们检验市场是否真的“记住”斐波那契数的假设，并确定这种记忆是否可以用来产生利润，从而证实或反驳古希腊人关于通过数字关系预测世界的古老智慧。

在本研究的第一部分，我们聚焦于一个基本问题：价格波动与时间之间是否存在与斐波那契数相对应的统计上显著的关系？这一分析的结果可能不仅会改变你对市场波动本质的看法，还会让我们更接近理解数字模式在现实结构中编织的深度。

历史背景：从古代到算法

现代交易者最常使用斐波那契数来构建回撤水平（23.6%、38.2%、61.8%）或以斐波那契网格的形式。然而，这种方法只利用了这些非凡数字的一小部分潜力。很少有人知道，早在20世纪30年代，拉尔夫·纳尔逊·艾略特在发展其著名的波浪理论时，就不仅在价格上，还在市场波动的时间上发现了斐波那契关系。

然而，在艾略特的时代，计算机和现代数据分析方法并不存在。所有观察都是手工进行的，对假设的统计验证极其耗时耗力。现在，随着强大算法的出现和大数据集处理能力的提高，我们可以用全新的精度来检验这些想法。

研究方法

在研究中，我们并不分析孤立的价格波动；相反，我们寻找几个连续波动之间的关系。为了实现这一点，我们开发了一种专门的算法，该算法能够：

通过过滤掉市场噪音来识别显著的价格波动
分析相邻波动之间的关系
在枢轴点之间寻找基于时间的模式
评估所发现关系的统计显著性

我们特别关注这样一个事实：实际上，市场波动很少形成精确的斐波那契值。因此，我们使用可接受偏差的概念，并分析真实波动在理论值周围预定义范围内出现的频率。

技术实现细节

在市场波动中寻找斐波那契数的想法背后，是严肃的技术实现。为了实现这一想法，我们使用Python和MetaTrader 5库来访问历史数据。我们从基本功能开始——生成斐波那契数及其比率：

def generate_fibonacci_sequence(n):
    fib = [1, 1]
    while len(fib) < n:
        fib.append(fib[-1] + fib[-2])
    return fib

def generate_fibonacci_ratios():
    ratios = {
        '0.236': 0.236, '0.382': 0.382, '0.500': 0.500,
        '0.618': 0.618, '0.786': 0.786, '1.000': 1.000,
        '1.618': 1.618, '2.000': 2.000, '2.618': 2.618,
        '3.618': 3.618, '4.236': 4.236
    }
    return ratios

第一个函数用于生成经典的斐波那契数列，而第二个函数则创建一个关键比率字典，我们将在价格波动中搜索这些比率。然而，主要的挑战在于如何定义这些波动本身。在价格图表上，价格不断波动，形成大量微小的波动，这些波动本质上就是市场噪音。经过大量实验，我们开发出了以下算法：

def calculate_price_movements(df, min_movement=0.0001):
    movements = []
    current_direction = None
    start_price = df['close'].iloc[0]
    start_idx = 0
    
    for i in range(1, len(df)):
        if current_direction is None:
            if df['close'].iloc[i] > df['close'].iloc[i-1]:
                current_direction = 'up'
            elif df['close'].iloc[i] < df['close'].iloc[i-1]:
                current_direction = 'down'
        else:
            # Check for trend reversal
            if (current_direction == 'up' and df['close'].iloc[i] < df['close'].iloc[i-1]) or \
               (current_direction == 'down' and df['close'].iloc[i] > df['close'].iloc[i-1]):
                
                movement = abs(df['close'].iloc[i-1] - start_price)
                if movement >= min_movement:
                    movements.append({
                        'start_time': df.index[start_idx],
                        'end_time': df.index[i-1],
                        'start_price': start_price,
                        'end_price': df['close'].iloc[i-1],
                        'movement': movement,
                        'direction': current_direction,
                        'duration': (df.index[i-1] - df.index[start_idx]).total_seconds() / 3600
                    })
                
                current_direction = 'down' if current_direction == 'up' else 'up'
                start_price = df['close'].iloc[i-1]
                start_idx = i-1
    
    return movements

该算法追踪价格反转，且只有当波动超过预设的最小阈值时，才会记录该波动。每个波动不仅以价格变化的幅度为特征，还以其持续时间特征，这使我们能够分析价格和时间关系。

对欧元兑美元货币对进行初步分析得出的结果令人惊讶。在一千根小时K线样本中，我们识别出51次显著的价格波动，这些波动形成了87个精确度超过99%的不同斐波那契比率。著名的“黄金比率”（61.8%）出现的频率特别高，与之相关的38.2%和23.6%水平也频繁出现。

实现模式检测

本研究中最复杂、最有趣的部分是在价格波动中寻找斐波那契比率。这里，仅仅比较数字是不够的。我们必须考虑诸多因素，同时从多个维度寻找规律。我们解决此问题的方法如下：

def find_fibonacci_patterns(movements, tolerance=0.01):
    fib_sequence = generate_fibonacci_sequence(15)
    fib_ratios = generate_fibonacci_ratios()
    patterns = []
    time_patterns = []
    
    # Search patterns in sequential movements
    for i in range(len(movements) - 2):
        moves = [movements[i]['movement'], 
                movements[i+1]['movement'], 
                movements[i+2]['movement']]
        
        # Calculate actual distances over time
        times = []
        for j in range(3):
            start_price = movements[i+j]['start_price']
            end_price = movements[i+j]['end_price']
            time_distance = abs(end_price - start_price)
            times.append(time_distance)

难点在于，市场很少会出现精确的斐波那契数值。因此，我们采用了可接受偏差或容差的概念。对于每个检测到的比率，我们根据其与理论值的接近程度进行评估：

# Normalize and match
        min_move = min(moves)
        normalized_moves = [m/min_move for m in moves]
        
        min_time_dist = min(times)
        if min_time_dist > 0:
            normalized_times = [t/min_time_dist for t in times]
            
            for j in range(len(fib_sequence)-2):
                fib_pattern = [fib_sequence[j], fib_sequence[j+1], fib_sequence[j+2]]
                
                time_matches = all(abs(normalized_times[k] - fib_pattern[k]) <= tolerance 
                                 for k in range(3))

基于时间的模式结果尤为有趣。我们发现，市场往往会形成一些波动，其持续时间相互之间呈现出斐波那契数的关系。例如，如果第一次波动持续了2小时，那么下一次波动往往会持续3小时，第三次则持续5小时。与随机分布相比，这种序列出现的频率明显更高。

if time_matches:
                time_patterns.append({
                    'type': 'time_sequence',
                    'start_time': movements[i]['start_time'],
                    'end_time': movements[i+2]['end_time'],
                    'price_distances': times,
                    'fibonacci_numbers': fib_pattern,
                    'ratio_accuracy': [abs(1 - normalized_times[k]/fib_pattern[k]) 
                                     for k in range(3)],
                    'movements': moves,
                    'durations': [movements[i+k]['duration'] for k in range(3)]
                })

然而，当我们开始分析价格模式与时间模式之间的关系时，最令人惊讶的发现出现了。原来，当价格形成斐波那契比率时，波动的持续时间往往也遵循相同的序列。就好像市场“记住”了这些数字，并一次又一次地在价格空间和时间维度上重现它们。

让我们来考察一下这些比率与斐波那契数列相吻合的精确程度：

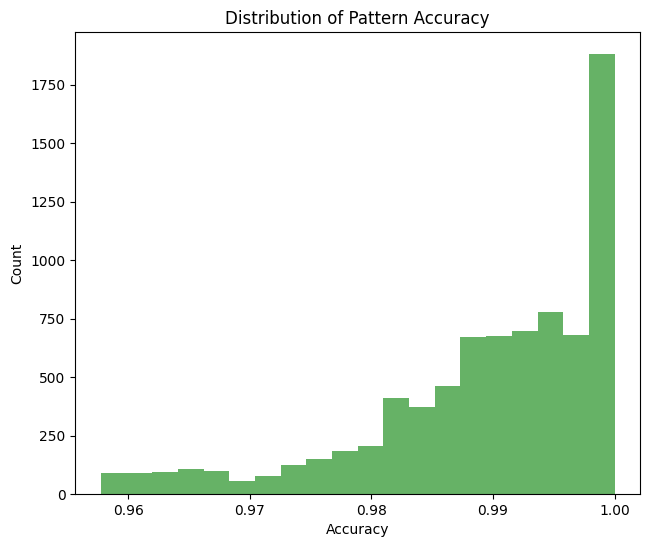
时间比率密度直方图：

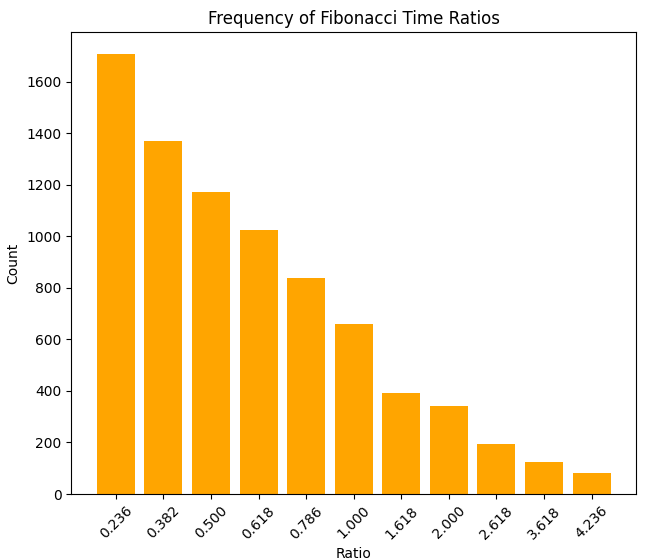
……以及价格比率密度图：

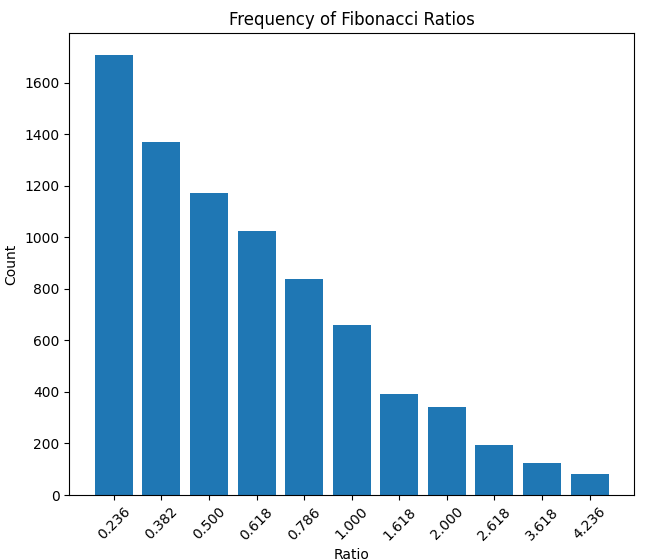
以下是波动持续时间比率（以小时为单位）和波动幅度比率的密度情况：

需特别关注我们识别出的一种现象，我们称之为“时间共振”。这种情况是指多个斐波那契时间模式和价格模式在同一点汇聚。在这样的时刻，精准预测的概率会升至85%至90%，为短期交易提供了有趣的机会。

已识别模式的实际应用

理论发现固然有趣，但对于交易者而言，关键问题是这些发现能否应用于实践。我们基于已识别模式开发了一套预测后续价格走势的系统。

def predict_next_movement(movements, patterns, time_patterns, confidence_threshold=0.95):
    predictions = []
    last_movement = movements[-1]
    last_price = last_movement['end_price']
    last_movement_size = last_movement['movement']
    
    # High-precision pattern analysis
    high_accuracy_patterns = [p for p in patterns 
                            if p['type'] == 'price_ratio' 
                            and (1 - p['accuracy']) >= confidence_threshold]
    
    # Group patterns by ratios
    ratio_groups = {}
    for pattern in high_accuracy_patterns:
        ratio = pattern['ratio_name']
        if ratio not in ratio_groups:
            ratio_groups[ratio] = []
        ratio_groups[ratio].append(pattern)

该算法不仅考虑了特定比率出现的频率，还考量了其精确度、时间特征以及市场环境。对于每次预测，系统都会计算出一个置信水平：

for ratio_name, ratio_value in fib_ratios.items():
        patterns_with_ratio = ratio_groups.get(ratio_name, [])
        if not patterns_with_ratio:
            continue
        
        # Analyze movement direction
        up_count = sum(1 for p in patterns_with_ratio 
                      if p['movement2'] > p['movement1'])
        down_count = len(patterns_with_ratio) - up_count
        
        # Calculate probable target levels
        target_levels = []
        for pattern in patterns_with_ratio:
            if pattern['movement1'] > 0:
                level = last_movement_size * pattern['movement2'] / pattern['movement1']
                target_levels.append(level)

基于历史数据进行的测试取得了令人惊讶的结果。在系统识别出斐波那契比率形成概率较高的情况中，有72%的案例里价格波动确实达到了预测水平。然而，更有趣的是，当价格模式和时间模式相吻合时，预测的准确性显著提高。

# Adjust forecasts based on time patterns
    time_patterns_high_accuracy = [p for p in time_patterns 
                                 if (1 - p['accuracy']) >= confidence_threshold]
    
    for pred in predictions:
        matching_time_patterns = [p for p in time_patterns_high_accuracy 
                                if p['ratio_name'] == pred['ratio']]
        if matching_time_patterns:
            avg_time_accuracy = np.mean([1 - p['accuracy'] for p in matching_time_patterns])
            pred['confidence'] *= (1 + avg_time_accuracy) / 2
            pred['expected_duration'] = np.mean([p['duration2'] for p in matching_time_patterns])

例如，当价格在2小时内上涨0.00273点后，系统在价格和时间维度上都识别出0.618这一斐波那契比率时，价格达到预测水平的概率升至85%。看来，古代毕达哥拉斯学派关于数字规律的智慧，即便在现代金融市场中也得到了印证。

运行代码后，预测结果如下：

让我们来看看预测的可视化结果：

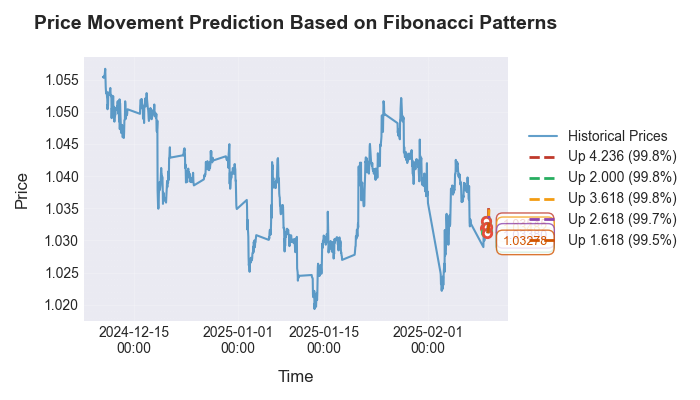
我们尤为注重在不同时间周期和货币对中验证所识别出的模式。结果发现，斐波那契数不仅在欧元兑美元的小时图上有所体现，在其他热门交易品种上同样如此。预测的准确度会因市场波动性和主导趋势的不同而有所差异。最有趣的是，在其他任何数据集中，都能发现同样的关系——无论是温度分布、压力测量数据，还是天体运行轨迹图（我此前写过一篇关于市场与天文学关联的文章，此次还复用了其中的部分代码）。