Portfolio Trading in MetaTrader 4
Magnus
ab integro saeclorum nascitur ordo
Publius
Vergilius Maro, Eclogues
Einleitung
Das Portfolio Prinzip ist schon seit langer Zeit bekannt. Durch die Diversifizierung der Einlagen in verschiedene Richtungen, können die Investoren die Verlustrisiken in ihren Portfolios minimieren und die Einnahmen glätten. Die Portfoliotheorie hat 1950 an Fahrt gewonnen, als das erste mathematische Modell von Harry Markowitz vorgeschlagen wurde In den 1980er Jahren hat ein Forscherteam von Morgan Stanley die ersten Spread Trading-Strategien entwickelt und damit den Weg in die Gruppe der neutralen Marktstrategien geebnet. Die heutigen Portfoliotheorien sind sehr vielfältig und komplex, so dass es fast unmöglich ist, alle Portfoliostrategien in einem einzigen Artikel zu beschreiben. Daher betrachten wir hier nur eine kleine Auswahl an spekulativen Strategien, sowie deren Umsetzung in dem MetaTrader 4.
Einige Definitionen aus diesem Artikel lauten wie folgt:
- Portfolio (Korb, Synthetisches Finanzinstrument) — Eine Gruppe von Positionen von verschiedenen Handelns-Instrumenten, mit einer optimal berechneten Größe. Die Positionen bleiben für einige Zeit offen, werden als eine Gesamtposition verfolgt und geschlossen, wenn Sie ein gemeinsames positives Ergebnis liefern.
- Portfolio (Korb, Synthetisches Finanzinstrument) Anpassung — Ändern der Zusammenstellung von Handelns-Instrumenten und oder deren Volumen, um Verluste zu minimieren oder Zwischenergebnisse zu verbessern.
- Synthetisches Volumen — Anzahl der synthetischen Positionen (Wie oft das Portfolio gekauft oder verkauft wurde).
- Virtueller Gewinn/Verlust - Finanzergebnis, das gewonnen werden kann, wenn Sie eine Position innerhalb eines bestimmten Zeitintervalls halten.
Die Klassischen Investment-Portfolios werden in der Regel an Börsen angewendet Aber ein solches Vorgehen passt nicht sehr gut zu dem Forex-Markt, da hier die meisten Portfolios spekulativ sind. Hier werden sie etwas anders erzeugt und gehandelt. Was Forex angeht, sind die Portfolio-Strategien eigentlich mehrfach Währungshandel-Strategien, allerdings sind nicht alle mehrfach Währungs-Strategieen auch Portfolio Strategien Wenn Symbole unabhängig gehandelt werden und keine Dynamik des Gesamtergebnisses verfolgt wird, ist dies ein Multi-Symbol Handel. Wenn mehrere unabhängige Systeme auf einem einzigen Handelskonto handeln, ist dies ein Strategie-Portfolio. Hier betrachten wir ein Portfolio-Trading im engeren Sinne – Es wird eine synthetische Position aus mehreren Symbolen gebildet und anschließend verwaltet.
Prinzipien
Die Weiterentwicklung des Portfolios besteht aus zwei Phasen: Auswählen der Symbole, Berechnung der Lotgröße und der Richtungen. Hier besprechen wir nur ein paar einfache Portfolio-Entwicklungsmethoden zusammen mit Algorithmus -Beispielen. Insbesondere verwenden wir die Methode der normalen-kleinsten-Quadrate (OLS) und die Hauptkomponentenanalyse (PCA) als Grundlage. Weitere Informationen finden Sie hier:
Wenn wir ein Portfolio entwickeln, dann ist es normalerweise notwendig, das gewünschte Portfolio Diagramm-Verhalten zu definieren. Das Portfolio-Diagramm zeigt die Änderungen des Gesamtgewinns aller Positionen innerhalb eines bestimmten Zeitintervalls, die in das Portfolio aufgenommen wurden. Portfolio-Optimierung ist eine Suche nach einer Kombination der Lotgrößen und der Richtungen, die am besten zu dem gewünschten Portfolio-Verhalten passt. Beispielsweise, in Abhängigkeit von unserer Aufgabe, könnte es eventuell für ein Portfolio notwendig sein, eine Wiederholung des Durchschnittswert zu bekommen oder die Attribute eines genau definierten Trends zu verfolgen oder der Chart soll einem Diagramm einer Funktion ähnlich sein.
Drei Portfolio-Typen(Trend, Flach, Funktion):
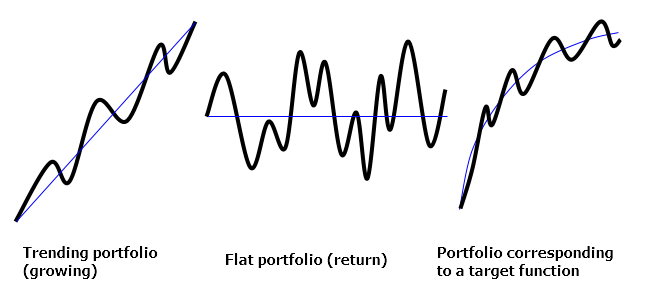
Ein Portfolio kann durch die folgende Gleichung dargestellt werden:
A*k1 + B*k2 + C*k3 + ... = F,
wobei
A, B, C... sind Zeitreihen, die den Portfolio-Symbolen entsprechen
k1, k2, k3 ... sind die Lotgrößen der Symbole (positiv — Kauf, negativ — Verkauf)
F — Zielfunktion (Wird über Punkte in einer Zeitreihe festgelegt)
Dies ist eine multivariate lineare Regressionsgleichung mit einem Null-Konstanten Ausdruck. Seine Wurzeln finden Sie leicht mit OLS. Zu aller erst sollten vergleichbare Zeitreihen erzeugt werden. Die Preispunkte sollten auf die hinterlegte Währung gebracht werden. In diesem Fall sollte jedes Element von jeder Zeitserie einem virtuellen Profitwert eines Lots des entsprechenden Symbols zu einem bestimmten Zeitpunkt darstellen. In der Regel werden in statistischen Anwendungsaufgaben vorläufige Preis-Algorithmen oder die Verwendung von Preisunterschieden empfohlen. Jedoch könnte dieses in unserem Falle möglicherweise unnötig oder sogar schädlich sein, da kritische Gesamtdaten der Symbol-Dynamik auf diesem Weg zerstört werden.
Die Zielfunktion definiert den Portfolio-Diagramm-Typ. Die Zielwerte-Funktion sollte vorläufig für jeden Punkt entsprechend berechnet werden. Zum Beispiel bei der Entwicklung eines einfachen wachsenden Portfolios (Trend Portfolio) hat das Zielportfolio die Werte 0, 1 * S, 2 * S, 3 * S, etc., wobei S ein Inkrement ist - der Geldwert, zu dem das Portfolio an jeder Bar in einem vorgegebenen Intervall erhöht werden sollte. Der OLS-Algorithmus fügt A, B, C,... Zeitreihen hinzu, so dass ihre Summe mit Blick auf das Ziel des Funktionsplans wiederholt wird. Um dies zu erreichen, minimiert der OLS-Algorithmus die Summe der quadrierten Abweichungen zwischen der Summe der Serie und der Zielfunktion. Dies ist eine statistische Standardaufgabe. Es ist kein detailliertes Verständnis der Algorithmus-Operation erforderlich, da Sie eine vorgefertigte Bibliothek verwenden können.
Es kann auch vorkommen, dass die Zielfunktion nur Null-Werte enthält (Flache Portfolios (Seitwätstrends)). In diesem Fall sollte ein zusätzliches Verhältnis zur Summen-Grenze hinzugefügt werden (z. B.: k1 + K2 + k3 +... = 1) um die Lösung einer Regressionsgleichung mit Null Wurzeln zu umgehen. Die Alternative wäre ein verschieben eines Gleichungs-Ausdrucks auf die rechte Seite, so dass aus ihr eine Zielfunktion wird, die das Verhältnis von -1 hat, während die übrigen Bedingungen wie gewohnt optimiert werden. In diesem Fall setzen wir den Korb der Instrumente einem ausgewählten Instrument gleich, wodurch wir ein Spread-Portfolio erzeugen. Abschließend kann der weiter fortgeschrittene PCA-Algorithmus verwendet werden, um solche Portfolios zu entwickeln. Sie wendet die Instrument-Kovarianzmatrix zur Berechnung des Koeffizienten Vektors, entsprechend der Punktwolken-Kreuzabschnitt-Hyperfläche mit minimalen Rest-Varianz des Portfolios an. Auch hier müssen Sie nicht die Algorithmen im Detail verstehen, da Sie eine vorgefertigte Bibliothek verwenden können.
Algorithms
Jetzt ist es Zeit, alle beschriebenen Ideen in die MQL Sprache umzusetzen. Wir verwenden eine bekannte ALGLIB Mathe-Bibliothek, die für MT4 angepasst wurde. Manchmal können während der Installation Probleme auftreten. Daher gehe ich näher darauf ein. Wenn mehrere Terminals auf einem PC installiert sind, ist es sehr wichtig, die richtigen Daten-Ordner zu finden, da der Compiler die Bibliothek nicht sieht, wenn sie sich in einem anderen Terminal-Data-Ordner befindet.
ALGLIB Bibliothek installieren:
- Laden Sie die Bibliothek herunter (https://www.mql5.com/de/code/11077), und entpacken Sie die Zip-Datei;
- Öffnen Sie den 'include' Ordner und suchen Sie das Mathe -Verzeichnis;
- Starten Sie die МetaТrader 4-Plattform, zu der die Bibliothek hinzugefügt werden soll;
- Wählen Sie den Menübefehl: Datei – Open Data-Ordner;
- Öffnen Sie MQL4 und beziehen Sie den Unterordner mit ein;
- Kopieren Sie den Mathe Ordner in den Include-Ordner des Terminals;
- Überprüfen Sie die Ergebnisse: Die *.mhq Dateien sollten in dem Ordner MQL4\Include\Math\Alglib sein.
Die Beispielfunktion für die Berechnung des Kontraktkurses ist nachfolgend dargestellt:
double ContractValue(string symbol,datetime time,int period) { double value=MarketInfo(symbol,MODE_LOTSIZE); // receive lot size string quote=SymbolInfoString(symbol,SYMBOL_CURRENCY_PROFIT); // receive calculation currency if(quote!="USD") // Falls die berechnete Währung nicht USD ist, wird eine Konvertierung durchgeführt { string direct=FX_prefix+quote+"USD"+FX_postfix; // form a direct quote for calculation currency if(MarketInfo(direct,MODE_POINT)!=0) // Überprüfen, ob sie vorhanden ist { int shift=iBarShift(direct,period,time); // auffinden der Bar über die Zeit double price=iClose(direct,period,shift); // erhalten des Kurses der Bar if(price>0) value*=price; // Berechnung des Kurses } else { string indirect=FX_prefix+"USD"+quote+FX_postfix; // bilden eines umgekehrten Quotes für die berechnete Währung int shift=iBarShift(indirect,period,time); // Auffinden der Bar über die Zeit double price=iClose(indirect,period,shift); // Erhalt des Kurses der Bar if(price>0) value/=price; // Berechnung des Kurses } } if(Chart_Currency!="USD") // Falls die Zielwährung nicht USD ist, führe eine Konvertierung durch { string direct=FX_prefix+Chart_Currency+"USD"+FX_postfix; // Bilden eines direkten Kurses für die Zielwährung if(MarketInfo(direct,MODE_POINT)!=0) // Überprüfen, ob sie vorhanden ist { int shift=iBarShift(direct,period,time); // auffinden der Bar über die Zeit double price=iClose(direct,period,shift); // erhalten des Kurses der Bar if(price>0) value/=price; // Berechnung des Kurses } else { string indirect=FX_prefix+"USD"+Chart_Currency+FX_postfix; // Bilden eines umgekehrten Kurses für die Zielwährung int shift=iBarShift(indirect,period,time); // Auffinden der Bar über die Zeit double price=iClose(indirect,period,shift); // Erhalt des Kurses der Bar if(price>0) value*=price; // Berechnung des Kurses } } return(value); }
Diese Funktion werden wir in der Zukunft immer verwenden. Sie arbeitet mit Währungspaaren, Indizes, Futures und CFDs. Außerdem berücksichtigt sie auch Symbol Präfixe und Postfixe (FX_prefix, FX_postfix) von einigen Brokern. Das Ergebnis wird in eine Zielwährung (Chart_Currency) umgewandelt. Wenn wir zum Tagespreis des Symbols den zurückgegebenen Funktionswert multiplizieren, erhalten wir den Preis eines Lots des Symbols. Nach der Aufsummierung aller Vertragspreise in das Portfolio unter Berücksichtigung der Lots, erhalten wir den Preis für das gesamte Portfolio. Wenn wir nach einer Zeit einen Preisunterschied mit dem Funktionswert multiplizieren, erhalten wir den Gewinn oder den Verlust, der während dieser Preisänderung erzeugt wurde.
Der nächste Schritt ist die Berechnung des virtuellen Gewinns für alle einzelnen Lot-Kontrakte. Die Berechnung erfolgt als ein zweidimensionales Array, wo die erste Dimension ein Punkt-Index in der berechneten Zeit ist, und die zweite Dimension ein Symbol Index ist (die zweite Dimensionsgröße kann auf eine bestimmte Anzahl Begrenzt werden, da man weiß, dass die Anzahl der Symbole eine bestimmte Menge nicht überschreiten wird):
double EQUITY[][100]; // erste Dimension ist für Bars, während die zweite für Symbole ist
Zunächst sollten wir die erste Preise für alle Symbole (die linke Begrenzung des berechneten Intervalls) hinterlegen. Dann wird die Differenz zwischen dem Anfangs- und Endwert an jedem Punkt des Calculatied Intervalls berechnet und mit den Vertragspreis multipliziert. In einer Schleife verschieben wir uns im Zeitintervall jedes Mal um eine nach rechts.
for(int i=0; i<variables+constants; i++) // Portfolio Symbol-Schleife (Variablen und Modell-Konstanten) { int shift=iBarShift(SYMBOLS[i],Timeframe,zero_time); // erhalt eines Bar-Index über die Zeit für einen Nullpunkt opening[i]=iClose(SYMBOLS[i],Timeframe,shift); // Bar Preis erhalten und speichern im Array } points=0; // Punkte in der Variablen berechnen datetime current_time=zero_time; // Starten der Schleife vom Nullpunkt while(current_time<=limit_time) // die Zeit-Label im optimierten Intervall weitergeben { bool skip_bar=false; for(int i=0; i<variables+constants; i++) // Symbol-Schleife des Portfolios(Variablen und Modell-Konstanten) if(iBarShift(SYMBOLS[i],Timeframe,current_time,true)==-1) // Überprüfen ob die Bar für das Symbol existiert skip_bar=true; // Wenn die Bar nicht vorhanden ist, überspringen der anderen Symbole if(!skip_bar) // fortsetzen des Vorgangs, wenn die Bar zwischen allen Symbolen synchronisiert wird { points++; // erhöhen Sie die Anzahl der Punkte um einen TIMES[points-1]=current_time; // Zeit-Label im Speicher speichern for(int i=0; i<variables+constants; i++) // Die Profit-Berechnung-Schleife für alle Symbole innerhalb dieses Punktes { int shift=iBarShift(SYMBOLS[i],Timeframe,current_time); // erhalten des Bar-Index über die Zeit closing[i]=iClose(SYMBOLS[i],Timeframe,shift); // Erhalten des Preises der Bar double CV=ContractValue(SYMBOLS[i],current_time,Timeframe); // Berechnung des Preises des Kontraktes profit[i]=(closing[i]-opening[i])*CV; // Berechnung des Profites über die Preisdifferenz und die Kosten EQUITY[points-1,i]=profit[i]; // Abspeichern des Profit-Wertes } } current_time+=Timeframe*60; // Zum nächsten Zeitintervall springen }
In den oben genannten Code-Fragment, Zero_time – Zeit des berechneten Intervalls der linken Grenze, Limit_time — von dem berechneten Abstand der rechten Begrenzung, Zeitrahmen – Anzahl der Minuten in einer Bar des Zeitrahmens, Punkte — ermittelte Gesamtpunktzahl in der berechneten Zeit. Die strikte Zeit-Label Compliance-Regel wird im obigen Beispiel verwendet. Wenn eine Bar eines Symbols für ein bestimmtes Zeit-Label fehlt, wird eine Position übersprungen und es erfolgt eine Verschiebung zum nächsten. Die Verwaltung der Zeit-Label ist sehr wichtig für die vorläufige Datenaufbereitung, da der Datenversatz bei verschiedenen Symbolen Verzerrungen im Portfolio verursachen kann.
Die Portfolio-Beispieldaten für drei Symbole und eine eigenständige Funktion (Quadratwurzel Parabel):
DATE/TIME AUDJPY GBPUSD EURCAD MODEL 03.08.16 14:00 0 0 0 0 03.08.16 15:00 -61,34 -155 -230,06 10,21 03.08.16 16:00 -82,04 -433 -219,12 14,43 03.08.16 17:00 -39,5 -335 -356,68 17,68 03.08.16 18:00 147,05 -230 -516,15 20,41 03.08.16 19:00 169,73 -278 -567,1 22,82 03.08.16 20:00 -14,81 -400 -703,02 25 03.08.16 21:00 -109,76 -405 -753,15 27 03.08.16 22:00 -21,74 -409 -796,49 28,87 03.08.16 23:00 51,37 -323 -812,04 30,62 04.08.16 00:00 45,43 -367 -753,36 32,27 04.08.16 01:00 86,88 -274 -807,34 33,85 04.08.16 02:00 130,26 -288 -761,16 35,36 04.08.16 03:00 321,92 -194 -1018,51 36,8 04.08.16 04:00 148,58 -205 -927,15 38,19 04.08.16 05:00 187 -133 -824,26 39,53 04.08.16 06:00 243,08 -249 -918,82 40,82 04.08.16 07:00 325,85 -270 -910,46 42,08 04.08.16 08:00 460,02 -476 -907,67 43,3 04.08.16 09:00 341,7 -671 -840,46 44,49
Nun, da wir die Daten erstellt haben, ist es Zeit, diese dem Optimierungsmodell zu schicken. Die Optimierung wird mit den LRBuildZ, LSFitLinearC und PCABuildBasis Funktionen aus der ALGLIB Bibliothek durchgeführt. Diese Funktionen werden in der Bibliothek selbst kurz beschrieben, als auch auf der offiziellen Projekt-Website: http://www.alglib.net/dataanalysis/linearregression.php und hier: http://www.alglib.net/dataanalysis/principalcomponentsanalysis.php.
Stellen Sie zunächst sicher, dass die Bibliothek enthalten ist.
#include <Math\Alglib\alglib.mqh>
Als nächstes sollte das Codefragment in Anbetracht der Modellelemente für jedes Optimierungsmodell festgelegt werden. Zunächst betrachten wir das Probe-Trend-Modell:
if(Model_Type==trend) { int info,i,j; // Definieren der Arbeits-Variablen CLinearModelShell LM; // definieren Sie ein spezielles Objekt-Modell CLRReportShell AR; // definieren Sie einen speziellen Objekt-Bericht CLSFitReportShell report; // weiteres Objekt definieren CMatrixDouble MATRIX(points,variables+1); // definieren Sie eine Matrix für die Speicherung aller Daten if(Model_Growth==0) { Alert("Zero model growth!"); error=true; return; } // Überprüfen Sie die Modellparameter for(j=0; j<points; j++) // Berechnung der Zielfunktion durch Optimierung der Intervall-Punkte { double x=(double)j/(points-1)-Model_Phase; // Berechnung der x-Koordinate if(Model_Absolute) x=MathAbs(x); // Falls notwendig, wird das Modell symmetrisch gemacht MODEL[j]=Model_Growth*x; // Berechnung der y-Koordinate } double zero_shift=-MODEL[0]; if(zero_shift!=0) for(j=0; j<points; j++) MODEL[j]+=zero_shift; // Verschieben des Modells vertikal zu den Nullpunkt for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // Laden der Symboldaten auf die matrix for(j=0; j<points; j++) MATRIX[j].Set(variables,MODEL[j]); // Laden der Modelldaten auf die matrix CAlglib::LRBuildZ(MATRIX,points,variables,info,LM,AR); // Start der Regressionsrechnung if(info<0) { Alert("Error in regression model!"); error=true; return; } // Überprüfen des Ergebisses CAlglib::LRUnpack(LM,ROOTS,variables); // Wurzeln der Gleichung erhalten }
Auf den ersten das mag kompliziert erscheinen, aber im Grunde ist alles einfach. Zu Beginn wird die lineare Trendfunktion errechnet und die Werte werden auf dem Modell Array platziert. Der Model_Growth-Parameter legt den Wachstums-Wert für den gesamten Berechnungs-Intervall fest (der Wert, mit denen das Portfolio in der Einzahlungswährung wachsen soll). Model_Absolute und Model_Phase Parameter sind optional und haben keine Bedeutung in der aktuellen Phase. Die Matrix wird für Berechnungen (MATRIX) erstellt. Die Daten der virtuellen Gewinne aller Kontrakte aus dem EQUITY-Array, als auch die Zielwerte für die Funktion des Modell-Arrays werden bis zur letzten Zeile aus der Matrix heruntergeladen. Die Anzahl der unabhängigen Regressionsgleichungsvariablen wird in 'Variablen' gespeichert. Danach wird die LRBuildZ Funktion aufgerufen, um die Berechnung durchzuführen. Danach werden die Wurzeln der Regressionsgleichung mit LRUnpack-Funktion in die Ursprungs-Arrays geschrieben. Die ganze komplexe Mathematik befindet sich in der Bibliothek, während Sie die vorgefertigten Funktionen verwenden können. Die größte Schwierigkeit ist hier technischer Natur, in Bezug auf die korrekten Aufrufe und Beibehaltung der Daten während der Vorbereitungen.
Das gleichen Code-Fragment kann für jede Funktion verwendet werden. Ersetzen Sie einfach die Inhalte des Modell Array mit Ihrer Zielfunktion. Eine Beispielrechnung für die parabolische Quadratwurzel Funktion wird unten gezeigt:
for(j=0; j<points; j++) // die Zielfunktion durch Optimierung Intervall Punkte berechnen { double x=(double)j/(points-1)-Model_Phase; // Berechnung des Wertes der x-Achse int sign=(int)MathSign(x); // definieren des Vorzeichens if(Model_Absolute) sign=1; // Falls notwendig, das Modell symmetrisch gestalten MODEL[j]=sign*Model_Growth*MathSqrt(MathAbs(x)); // Berechnung des Wertes der y-Achse }
Im folgenden ist ein Beispiel für eine komplexere Funktion, die die Summe aus einem linearen Trend und Oberschwingungen präsentiert:
for(j=0; j<points; j++) // Berechnung der Zielfunktion durch die Optimierung der Intervall-Punkte { double x=(double)j/(points-1)*Model_Cycles-Model_Phase; // calculate the X axis value if(Model_Absolute) x=MathAbs(x); // Falls notwendig, das Modell symmetrisch gestalten MODEL[j]=Model_Amplitude*MathSin(2*M_PI*x); // Berechnung des Wertes der y-Achse }
Im obigen Beispiel ist es möglich, eine Trend Größe (mit Model_Growth Parameter) und die Amplitude der Schwingung (mit Model_Amplitude Parameter) zu verwalten. Die Anzahl der Oszillation Zyklen wird durch Model_Cycles, festgelegt, während Oszillation Phasenverschiebung mit Model_Phase ausgeführt wird.
Darüber hinaus sollte die vertikale Verschiebung durchgeführt werden, damit die Funktion bei einem Nullpunkt gleich Null ist, um sicherzustellen, dass die Berechnungen korrekt sind:
double zero_shift=-MODEL[0]; // Lesen Sie den Modellwert am Nullpunkt if(zero_shift!=0) // Sicherstellen, dass er nicht Null ist for(j=0; j<points; j++) // Alle Intervall-Punkte übergeben MODEL[j]+=zero_shift; // Verschieben aller Modell-Punkte
Diese Beispiele machen es leicht, eine benutzerdefinierte Funktion zu entwickeln. Sie können beliebige Funktionen, je nach Aufgabe und Handels-Setup erstellen. Je komplexer die Funktion ist, desto schwieriger ist es, die beste Lösung zu wählen, da der Markt nicht verpflichtet ist, der Funktion zu folgen. Hier ist die Funktion nur ein Näherungswert.
Sie brauchen keine Zielfunktion für die Erstellung von Spreads und den Erhalt von flachen Portfolios. Wenn Sie beispielsweise eine Spanne zwischen zwei Symbol-Körben erstellen möchten, wird der optimierte Korb auf den Hauptteil der Matrix geladen, während der Referenz-Korb als eine Zielfunktion dient und auf die letzte Spalte der Matrix als Gesamtbetrag geladen wird:
for(i=0; i<variables; i++) // Schleife durch die optimierte Korb-Symbole for(j=0; j<points; j++) // Schleife über die berechneten Intervallpunkte MATRIX[j].Set(i,EQUITY[j,i]); // Laden der Symbol-Werte des optimierten Korbes auf die Spalte der Matrix for(i=variables; i<variables+constants; i++) // Schleife über die Referenz-Korb-Symbole for(j=0; j<points; j++) // Schleife über die berechneten Intervallpunkte MODEL[j]+=EQUITY[j,i]*LOTS[i]; // Laden der Symbol-Werte des Referenz-Korbes auf die letzte Spalte der Matrix
Unten ist eine Beispielrechnung für flache Portfolios, wo die LSFitLinearC Funktion das Portfolio möglichst symmetrisch um Null, innerhalb des berechneten Zeitraums, berechnet.
if(Model_Type==fitting) { int info,i,j; // Definieren von Variablen CLSFitReportShell report; // Das spezielle Objektmodell definieren CMatrixDouble CONSTRAIN(1,variables+1); // die Matrix des linearen Einschränkungen definieren CMatrixDouble MATRIX(points,variables); // definieren der Matrix für die Speicherung aller Daten ArrayInitialize(MODEL,0); // Auffüllen des Modells mit Nullwerten CONSTRAIN[0].Set(variables,1); // Die einzige Limitierung setzen for(i=0; i<variables; i++) CONSTRAIN[0].Set(i,1); // Summe der Wurzeln sollte gleich 1 sein. for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // Laden der Symboldaten auf die Matrix CAlglib::LSFitLinearC(MODEL,MATRIX,CONSTRAIN,points,variables,1,info,ROOTS,report); // berechnen des Optimierungsmodell mit OLS if(info<0) { Alert("Error in linear fitting model!"); error=true; return; } // Überprüfen des Ergebnisses }
Unten ist noch ein anderes wichtiges Beispiel für die Berechnung eines flachen Portfolios mit einer minimalen Varianz mit der PCA-Methode dargestellt. Hier berechnet die PCABuildBasis Funktion die Verhältnisse, so dass der Portfolio-Graph innerhalb des Berechnungs-Intervalls möglichst komprimiert bleibt:
if(Model_Type==principal) { int info,i,j; // Definieren von Variablen double VAR[]; // die Varianz Array definieren ArrayResize(VAR,variables); // konvertieren des Arrays in die notwendige Dimension CMatrixDouble VECTOR(variables,variables); // den Koeffizientenmatrix-Vektor definieren CMatrixDouble MATRIX(points,variables); // definieren der Matrix für die Speicherung aller Daten for(i=0; i<variables; i++) for(j=0; j<points; j++) MATRIX[j].Set(i,EQUITY[j,i]); // Die Symboldaten auf die Matrix laden CAlglib::PCABuildBasis(MATRIX,points,variables,info,VAR,VECTOR); // berechnen der orthogonalen Basis mit PCA if(info<0) { Alert("Error in principal component model!"); error=true; return; } // Überprüfung des Ergebnisses for(i=0; i<variables; i++) ROOTS[i]=VECTOR[i][variables-1]; // Laden der optimalen Verhältnisse }
Machen Sie sich keine Sorgen, wenn Sie durch diese mathematische Konzepte überfordert fühlen. Wie ich bereits gesagt habe, müssen Sie die mathematischen Details zur Entwicklung und Nutzung von Portfolios nicht verstehen. Im Allgemeinen sieht die Abfolge von Phasen wie folgt aus:
| 1 | Berechnung der virtuellen Gewinne für Portfolio-Symbole mit einzelnen Lots |
| 2 | Berechnung der Zielwerte für die Funktion |
| 3 | Der Optimierungsalgorithmus für die Lot-Größe |
| 4 | Portfolio-Volumen-Normalisierung |
| 5 | Graphen-Berechnung und Handel mit dem Portfolio |
Nun, da wir die Stamm-Arrays mit den optimalen Verhältnissen über eine Reihe von Prozeduren erhalten haben, ist es an der Zeit, die Verhältnisse in Lots umzuwandeln. Um dies zu tun, brauchen wir eine Normalisierung: Skalierung und Rundung. Das Einstelluen einer erforderlichen Skala macht das Handeln viel bequemer. Das Runden ist notwendig, um die Lots den Anforderungen des Maklers anzupassen. Manchmal wird auch empfohlen, eine Normalisierung der Portfolio-Gesamtmarge durchführen, aber diese Methode hat gravierende Nachteile (da die Marge der einzelnen Symbole unterschiedlich ist und sich ändern kann). Daher ist es viel vernünftiger, Normalisierung nach einem Portfolio-Preis oder der Volatilität durchzuführen.
Es folgt ein einfaches Beispiel für den Normalisierungsalgorithmus durch den Portfolio-Preis:
double total_value=0; // Definieren der Variablen für den Portfolio-Preis for(int i=0; i<variables+constants; i++) // Übergabe aller Portfolio-Symbole total_value+=closing[i]*ContractValue(SYMBOLS[i],limit_time,Timeframe)*MathAbs(LOTS[i]); // berechnen und summieren der Preisbestandteile if(total_value==0) { Alert("Zero portfolio value!"); error=true; return; } // Stellen Sie sicher, dass das Ergebnis nicht Null ist scale_volume=Portfolio_Value/total_value; // ein Skalierungsverhältnis finden for(int i=0; i<variables+constants; i++) // Erneut alle Portfolio-Symbole weitergeben LOTS[i]=NormalizeDouble(LOTS[i]*scale_volume,Lots_Digits); // konvertieren der Lots auf den gewünschten Gesamtpreis
Hier wird der Portfolio-Preis über die Proportionen den Anforderungen angepasst. Portfolio_Value — erforderlich Portfolio Preis, Total_value — Gesamtportfolio Preis mit den Standard-Verhältnissen, Scale_volume — Skalierungsverhältnis, Lots_Digits — Lots Kapazität, Lots — Array der Lot-Werte die für den Handel geeignet sind.
Die Lot-Werte bilden die endgültige Portfoliostruktur. Positive Lots entsprechen einer Long-Position, während negative Lots – Short-Positionen darstellen. Aufgrund der bekannten Portfoliostruktur, können wir den Chart plotten und Handelsgeschäfte mit dem Portfolio durchführen. Unten stehend finden Sie eine Beispiel-Portfolio-Struktur nach der Normalisierung:
| Symbol | AUDJPY | GBPUSD | EURCAD |
| Lot | -0,07 | -0,11 | -0,11 |
Das Portfolio-Diagramm wird nur mit Close-Preise geplottet und in einem separaten Indikator-Unterfenster angezeigt. Um das Portfolio Diagramm erstellen zu können, müssen wir jede Diagramm-Bar auf die gleiche Art und Weise berechnen, wie wir die virtuellen Gewinne für separate Symbole zuvor berechnet haben. Aber jetzt sind sie zusammengefasst, unter Berücksichtigung zugewiesenen Lots:
for(int j=draw_begin; j>=draw_end; j--) // Durchlauf durch die Diagramm-Balken innerhalb des Zeichnungs-Intervalls { double profit=0; // beginnen Sie mit dem Wert for(int i=0; i<variables; i++) // Übergabe aller Symbole { if(Fast_Period>0 && Slow_Period>0 && number!=N_TOTAL) // zusätzliche Prüfungen durchführen { int shift=iBarShift(SYMBOLS[i],Period(),Time[j]); // bar-Index über die Zeit erhalten double CV=ContractValue(SYMBOLS[i],Time[j],Period()); // Berechnung des Preises des Kontraktes double fast=iMA(SYMBOLS[i],Period(),Fast_Period,0,MODE_SMA,PRICE_CLOSE,shift); // Berechnung der langsamen Mittelung double slow=iMA(SYMBOLS[i],Period(),Slow_Period,0,MODE_SMA,PRICE_CLOSE,shift); // Berechnung der schnellen Mittelung profit+=(fast-slow)*CV*LOTS[i]; // Berechnung des Schwingungsmodells } else { int shift=iBarShift(SYMBOLS[i],Period(),Time[j]); // erhalten des Bar-Index über die Zeit double closing=iClose(SYMBOLS[i],Period(),shift); // Erhalten des Preises des Symbols an diesem Punkt double CV=ContractValue(SYMBOLS[i],Time[j],Period()); // Berechnung des Preises des Kontraktes profit+=(closing-OPENINGS[i])*CV*LOTS[i]; // Berechnung des Profites über die Preisdifferenz und die Kosten } } BUFFERS[number].buffer[j]=NormalizeDouble(profit,2); // den Gewinn-Wert in dem Indikator-Array speichern }
In diesem Codefragment können wir sehen, dass zwischen dem ersten und letzten Balken im Diagramm geplottet wird: Draw_begin und Draw_end. Der Portfoliowert ist gleich der Summe der Gewinne/Verluste auf alle Symbole, die über den Preisunterschied berechnet und mit einem Kontraktpreis und den zuvor berechneten Lots multipliziert werden. Die technischen Aspekte der Indikator Puffer, Formatierung und dergleichen habe ich übersprungen. Das fertige Beispiel Portfolio-Indicator, wird im folgenden Abschnitt beschrieben.
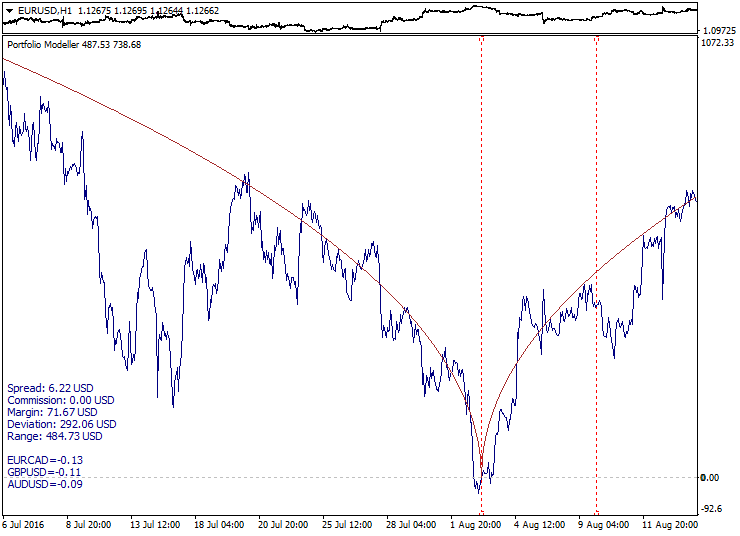
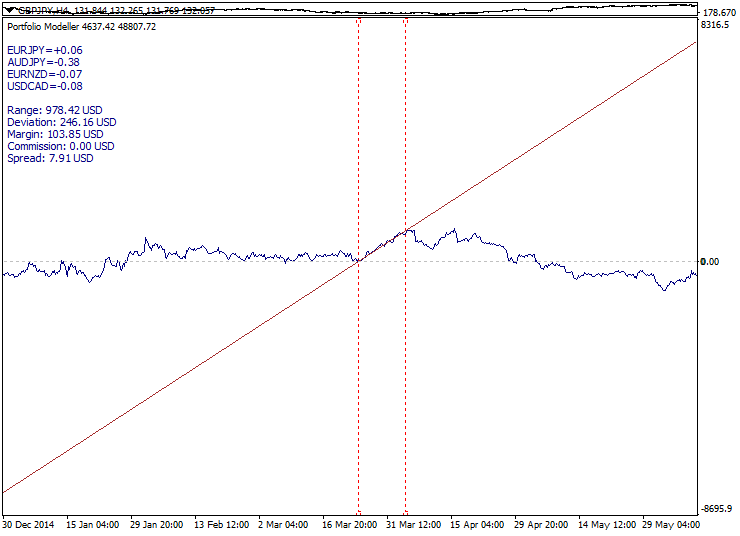
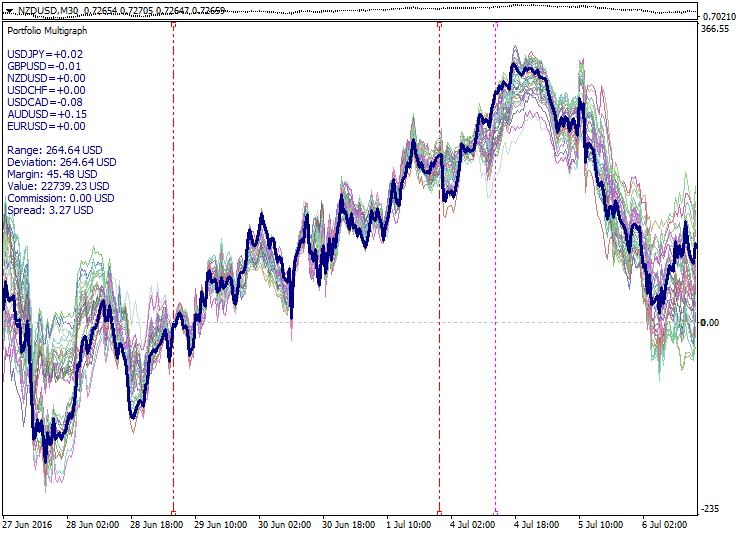
Hier können Sie ein Beispiel der Konstruktion eines Portfolio-Graphen (Indikator untere Teilfenster) mit dem angefügten Ziel-Funktionsgraphen überprüfen:
Hier dient die Quadratwurzel-Parabel symmetrische bezogen auf den Referenzpunkt (Model_Absolute = True) als die Zielfunktion. Berechnete Intervall-Grenzen werden als rote gepunktete Linien angezeigt, während sich das Portfolio-Diagramm tendenziell entlang der Funktions-Ziellinie, innerhalb und außerhalb der berechneten Abstände, bewegt.
Sie können technische Analysen von Portfolio-Graphen, ähnlich wie bei gewöhnlichen Symbol Preis-Charts, einschließlich der Anwendung von gleitenden Durchschnitten, Trendlinien und Ebenen, durchführen. Dies erweitert die Fähigkeit für das Analysieren und das Handeln, so dass Sie zur Auswahl der Portfoliostruktur für ein bestimmtes Handels-Setup auf ein Portfolio-Diagramm, z. B. Korrektur nach einem Trend-Impuls, Trend Schwächung, Beenden einer Seitwärtsbewegung, Überkauft/Überverkauft, Konvergenz/Divergenz, Breakout, Ebene Konsolidierung und andere Setups anwenden können. Die Qualität eines Handels-Setup wird beeinflusst durch die Zusammenstellung des Portfolios, die Optimierungsmethode, die Zielfunktion und das ausgewählte historische Segment.
Für die Auswahl des passenden Volumens, ist es notwendig, die Portfolio-Volatilität zu kennen. Da das Portfolio-Diagramm auf der Kontowährung basiert, können Sie die Reichweite der Portfolio-Fluktuation und das Potenzial eines Drawdowns direkt in dieser Währung mit dem Cursormodus "Fadenkreuz" und "ziehen" ermitteln.
Ein Trading-System sollte auf Portfolioverhalten und Setup-Statistiken beruhen. Bis jetzt haben wir nicht die Tatsache erwähnt, das sich das Portfolio-Verhalten außerhalb des Optimierung-Intervalls dramatisch ändern kann. Ein Seitwärtstrend kann sich in einen Trend ändern, während ein Trend zu einer Umkehr werden kann. Ein Trading-System sollte auch berücksichtigen, dass sich die Portfolio-Eigenschaften im Laufe der Zeit ändern können. Dieses Thema wird weiter unten diskutiert.
Handelsgeschäfte mit einem Portfolio bestehen aus einem einmaligen Kauf/Verkauf aller Portfolio-Symbole mit berechneten Mengen. Für mehr Komfort wäre es sinnvoll, einen speziellen Expert Advisor auszuführen, der alle Routinearbeiten, einschließlich der Abfrage der Portfolio-Struktur-Daten, das vorbereiten der synthetische Positionen, die Nachverfolgung der Einstiegslevel, das Sichern der Gewinne und das Begrenzen der Verluste, vornimmt. Wir werden die folgenden Bestimmungen für den EA-Betrieb festlegen: synthetisches Portfolio für Long- und Synthetisches Portfolio für Short-Position (wo Long-Positionen durch Short-Positionen ersetzt werden und umgekehrt). Der EA sollte die Möglichkeit besitzen, Positionen zu sammeln, synthetische Volumen zu verfolgen sowie Portfolio-Netting und Transformation durchführen zu können. Der EA wird im nächsten Abschnitt betrachtet, aber seine Struktur wird aufgrund der begrenzten Größe des Artikels nicht erklärt.
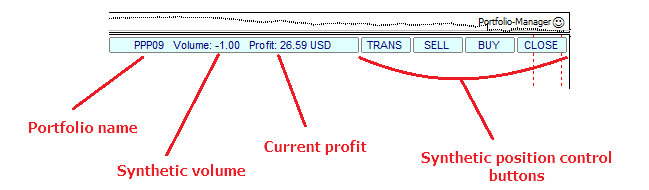
Unten ist das Beispiel des minimalistischen Interfaces für ein Portfolio-EA:
Manchmal ist es notwendig, nicht nur ein, sondern mehrere Portfolios zu bilden. Im einfachsten Fall wird es für den Vergleich von zwei Portfolios verwendet. Einige Aufgaben erfordern eine Gesamtportfolio-Serie auf einem einzigen Historien-Segment, welches zu einer Reihe von Portfolios mit bestimmten Mustern führt. Um solche Aufgaben zu realisieren, muss der Algorithmus für die Erzeugung eines Portfolios einer bestimmten Vorlage entsprechen. Ein Beispiel der Umsetzung eines solchen Indikators finden Sie im nächsten Abschnitt. Hier wollen wir nur seine kritischsten Funktionen beschreiben.
Wir müssen zum Beispiel ein Struktur-Array zum Speichern der Daten von mehreren Portfolios vereinbaren:
struct MASSIVE // definieren der Struktur mit mehreren Datentypen { string symbol[MAX_SYMBOLS]; // Text-Array für die Portfolio-Symbole double lot[MAX_SYMBOLS]; // numerischen Array für Lots string formula; // String mit der Portfolio-Gleichung double direction; // Portfolio-Direction-Attribut double filter; // Filter Attribute }; MASSIVE PORTFOLIOS[DIM_SIZE]; // Erstellen des Struktur-Arrays für die Gruppe von Portfolios
In diesem Codefragment legt DIM_SIZE die maximale Größe für die Speicherung von Portfolios fest. Die Struktur ist wie folgt organisiert: Symbol – Portfolio Symbol Array, lot – Lot-Array für Portfolio-Symbole, Formel — Text-String mit der Portfolio-Gleichung, Richtung — Portfolio Richtung (long oder short), Filtern – Filter-Attribut (enthalten/ausgeschlossen). Die Anwendung des Struktur-Arrays ist bequemer und vernünftiger als separate Arrays zu verwenden.
Das Struktur-Array kann auch für die Speicherung von Portfolio-Diagramm-Puffer-Arrays erstellt werden:
struct STREAM{double buffer[];}; // definieren der Struktur mit einem numerischen Array STREAM BUFFERS[DIM_SIZE]; // das Struktur-Array erstellen
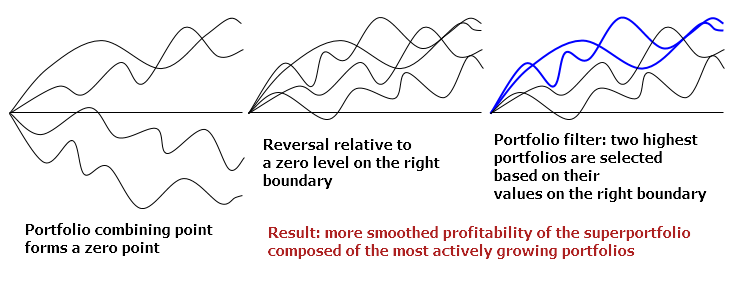
Portfolios innerhalb des Satzes variieren je nach deren Symbolkombinationen. Diese Kombinationen können im Voraus festgelegt oder nach bestimmten Regeln generiert werden. Das Arbeiten mit einer Reihe von Portfolios umfasst mehrere Stufen, je nach Aufgabe. Betrachten wir nun die folgende Abfolge von Phasen:
| 1 | Charts von separaten Portfolios berechnen |
| 2 | Kombinieren eine Reihe von Portfolios auf einen Nullpunkt |
| 3 | Portfolios im Verhältnis zu einem Nullpegel umkehren |
| 4 | Anwenden des Filters auf einen Satz von Portfolios |
| 5 | Summierung – bilden eines Superportfolios |
Das Bild unten zeigt diese Schritte:
Eine vertikale Verschiebung wird verwendet, um die Portfolios zu kombinieren. Ein Portfolio wird umgekehrt, wenn es mit -1 multipliziert wird. Schließlich wird ein Filter angewendet. Es folgt hier keine detaillierte Beschreibung dieser Algorithmen, um eine große Menge an Routine-Code zu vermeiden.
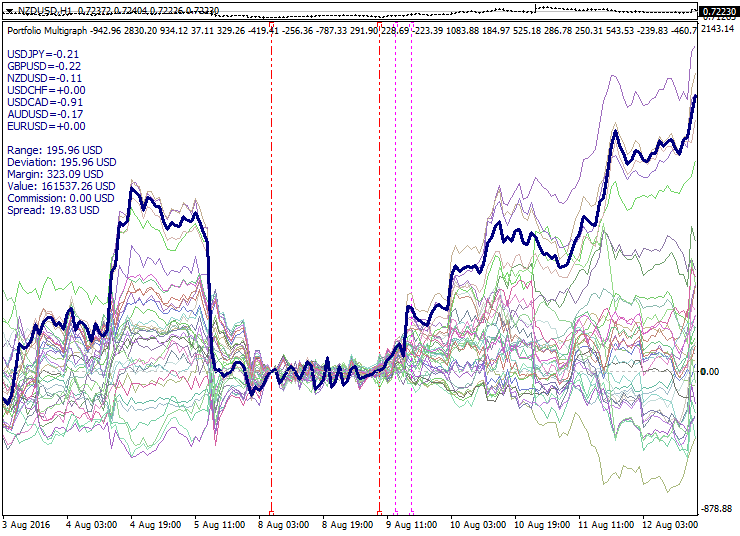
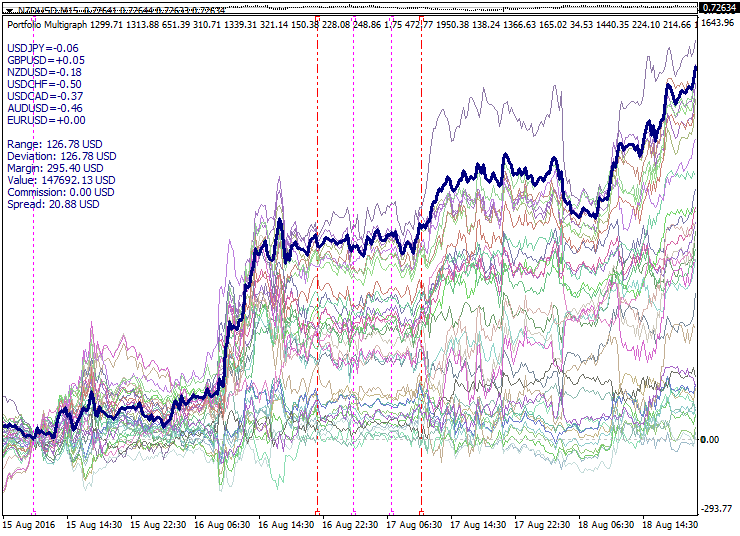
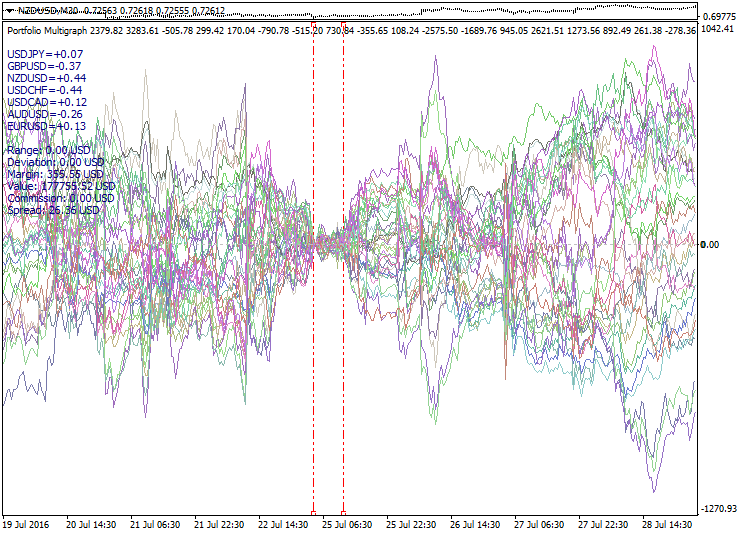
Es folgt ein Muster-Set von Portfolios, die nach den genannten Prinzipien konstruiert werden:
Die Grafik zeigt eine Reihe von Portfolios, berechnet vom PCA-Modell, mit einem kurzen Periode. Die berechneten Intervall-Grenzen werden als rote gestrichelte Linien angezeigt. Hier sehen wir den Ausdehnung des Portfolios-Sets auf beiden Seiten des Optimierungs-Intervalls. Der Nullpunkt ist an der linken Optimierungs-Intervallgrenze, während die Momente der Umkehrung relativ zu Null und die Filteranwendung sich durch die violett gepunkteten Linien auszeichnen. Die dicke Linie beschreibt das Superportfolio, bestehend aus den aktivsten Portfolios und den daraus resultierenden Lauf vom Nullpunkt aus.
Das kombinieren von Portfolios bietet zusätzliche Möglichkeiten für die Analyse und die Entwicklung von Trading-Strategien. Zum Beispiel Diversifikation zwischen Portfolios, Spreads zwischen Portfolios, Konvergenz-Divergenz der Reihe von Portfolios, warten auf das Drehen eines Portfolios, das Bewegen von einem Portfolio zu einem Anderen und andere Ansätze.
Implementationsbeispiele
Die in dem aktuellen Artikel beschriebenen Methoden wurden als ein Portfolio-Indikator und ein halbautomatischer EA umgesetzt. Hier finden Sie die Anweisungen, den Quellcode zum Herunterladen. Diesen können Sie noch an Ihre Bedürfnisse anpassen:
-
Portfolio Modeller - Portfolio Entwickler und Optimierer. Er beinhaltet mehrere Optimierungs-Modelltypen mit konfigurierbaren Parametern. Außerdem können Sie Ihre eigenen Modelle und Zielfunktionen hinzufügen. Es gibt auch grundlegende Werkzeuge für die technische Analyse von Portfolios, sowie verschiedene Chart-Formatierungsoptionen.
-
Portfolio Multigraph - Generator von Portfolio-Sätzen mit den gleichen Modellen und Parametern und Zusatzoptionen wie Portfolio-Transformation und Filterung, sowie das Erstellen eines Superportfolios.
-
Portfolio Manager - EA für die Arbeit mit Portfolios und Superportfolios. Er arbeitet in Verbindung mit dem Portfolio-Indikator und ermöglicht die Eröffnung und Verwaltung von synthetischen Positionen, sowie die Portfolio-Korrektur-Funktion und ein Auto-trading-Modus, basierend auf den grafischen Linien der virtuellen Aufträge.
Download link: https://www.mql5.com/ru/code/11859 (in Russian)
Trading-Strategien
Es gibt viele Trading-Strategien basieren auf der Anwendung von synthetischen Instrumenten. Betrachten wir ein paar grundlegende Ideen, die nützlich sein können, wenn Sie eine Portfolio Trading-Strategie erstellen. Lassen Sie uns aber auch gleichzeitig nicht die Risiken und Grenzen vergessen.
Der klassische Ansatz zur Erzeugung eines Portfolios ist das Auffinden unterbewerteter Assets mit einem Wachstumspotenzial und diese in das Portfolio einzubinden. Die Portfolio-Volatilität ist immer niedriger als die Summe der Volatilitäten der darin enthaltenen Instrumente. Dieser Ansatz eignet sich für die Börse, aber es ist von begrenztem Nutzen auf Forex, da Währungen im Gegensatz zu Aktien in der Regel kein nachhaltiges Wachstum aufweisen.
Unten stehend finden Sie Warren Buffetts langfristiges Portfolio:
Beim Arbeiten mit Standard Investment-Portfolios ist es notwendig, sorgfältig den aktuellen Anlagenstatus zu bewerten um es während der Abwärtsbewegung zu kaufen.
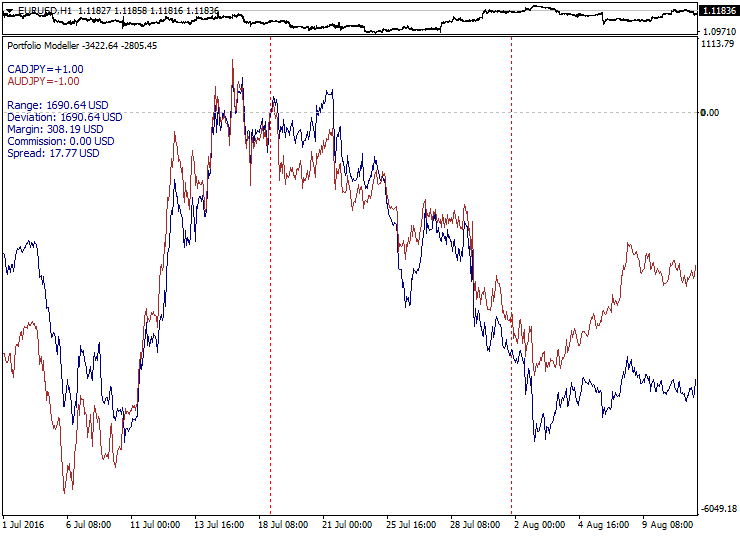
Die erste und einfachste Möglichkeit für den spekulativen Portfoliohandel ist ein Paar-Handel – Erstellen eines Spread von zwei korrelierenden Symbolen. Bei Forex ist dieser Ansatz begrenzt, da selbst hoch korrelierende Währungspaare keine Kointegration besitzen und daher im Laufe der Zeit erheblich voneinander abweichen können. In diesem Fall beschäftigen wir uns mit einem "broken spread". Übrigens, ein solches Pair-Trading verwandelt das Handeln in ein synthetisches Cross-Rate, da Paare mit einer gemeinsamen Währung in der Regel in einem Spread enthalten sind. Diese Art von Paar-Handel ist eine sehr schlechte Idee. Nach dem Öffnen entgegengesetzter Positionen durch Spread, müssen wir manchmal sehr lange warten, bis die Kurven wieder zusammenlaufen.
Unten ist ein Beispiel für hoch korrelieren Paare und ihre schrittweise und unvermeidliche Abweichung:
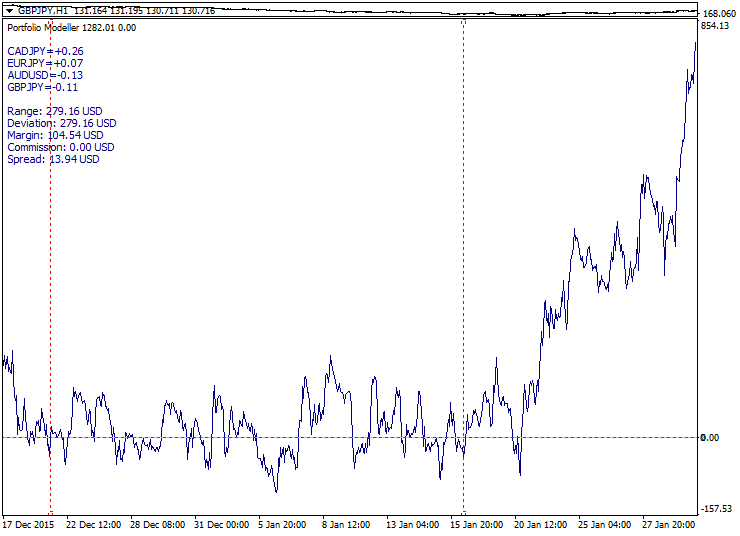
Die Entwicklung dieses Ansatzes ist ein multilaterales Spread-Trading, wenn drei oder mehr Währungspaare im Spread enthalten sind. Das ist schon besser als ein Paar-Handel, da es einfacher ist eine gleichmäßigere Verteilung mit einer größeren Anzahl an Kombinationsmöglichkeiten zu erhalten. Es bleiben jedoch die gleichen Risiken: Die Verteilung kann voneinander abweichen und nicht wieder zusammenlaufen. Es ist viel einfacher, in einem ruhigen Markt eine zurückkehrende Verteilung zu erreichen, aber starke fundamentalen Nachrichten können ein schnelle und unumkehrbare Divergenz erzeugen. Interessant ist, wenn wir die Zahl der Instrumente in der Verteilung erhöhen, die Wahrscheinlichkeit für eine stärkere Divergenz höher ist, da mehr Währungen beteiligt sind, die auf eine Pressemitteilung reagieren können. Das Warten auf das Zusammenlaufen wäre wieder eine äußerst negative Strategie, da dies nur auf einem ruhigen seitwärts tendierenden Markt funktioniert.
Unten ist ein Beispiel für ein Multi-Lateral-Verhalten einer Verteilung während einer Pressemitteilung:
Spread-trading hat mehr Möglichkeiten auf Aktien- oder Börsenmärkten, wenn es eine grundlegende Verbindung zwischen den Objekten gibt. Es gibt jedoch noch keine Garantie gegen die Entstehung von Gaps bei Dividenden-Tagen oder während des Ablaufes der Futures-Kontrakte. Spreads können auch aus Marktindizes und Futures betehen, aber dies erfordert die Berücksichtigung von Exchange-Trading-Funktionen.
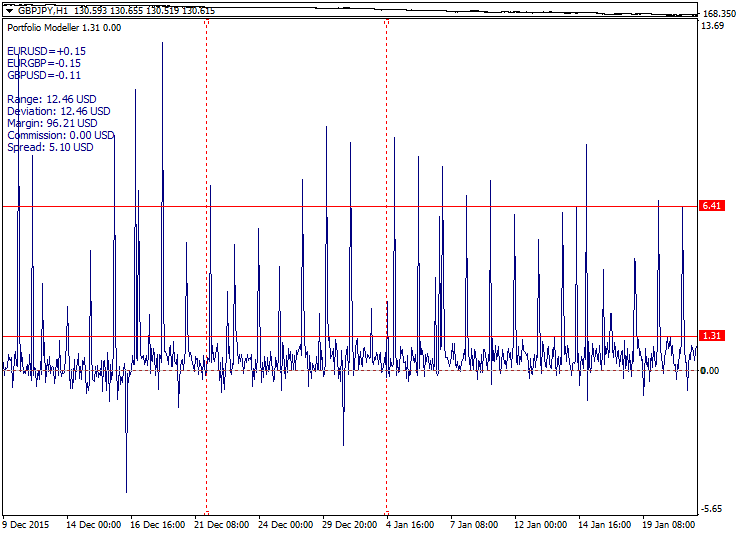
Eine Sackgasse des Spread-Trading wird durch ein Multi-Lock dargestellt, wenn zyklisch verwandte Währungspaare (zum Beispiel EUR/USD-GBPUSD-EURGBP) ausgewählt und verwendet werden, um eine ausgewogene Verteilung zu bilden. In diesem Fall haben wir eine perfekte Verbreitung die aber nicht handelbar ist, da der gesamte Spread und die Provisionen zu hoch sind. Wenn wir versuchen, die Lots ein wenig aus dem Gleichgewicht zu bringen, wird die Grafik mehr Trendähnlich, was dem Spread-Trading widerspricht, da die Kosten zu hoch bleiben, was somit diesen Ansatz bedeutungslos macht.
Im folgenden ist ein Beispiel für ein ausgewogenes Multi-Lock. Der Gesamtspread ist als zwei rote Linien dargestellt:
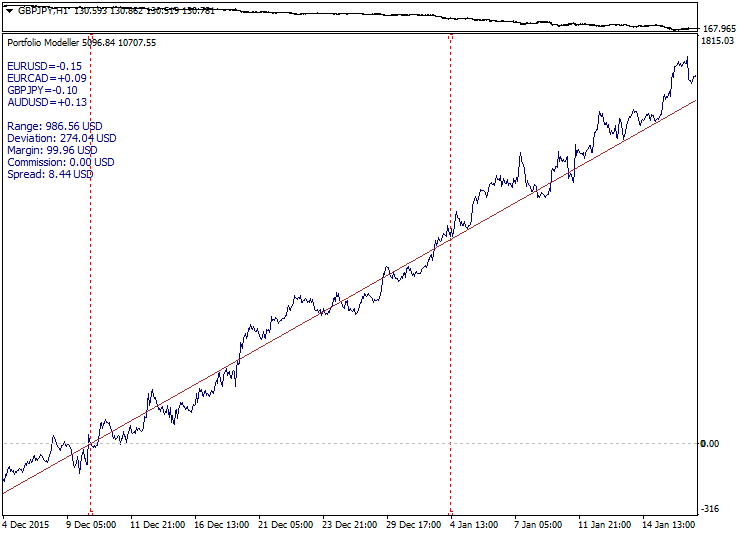
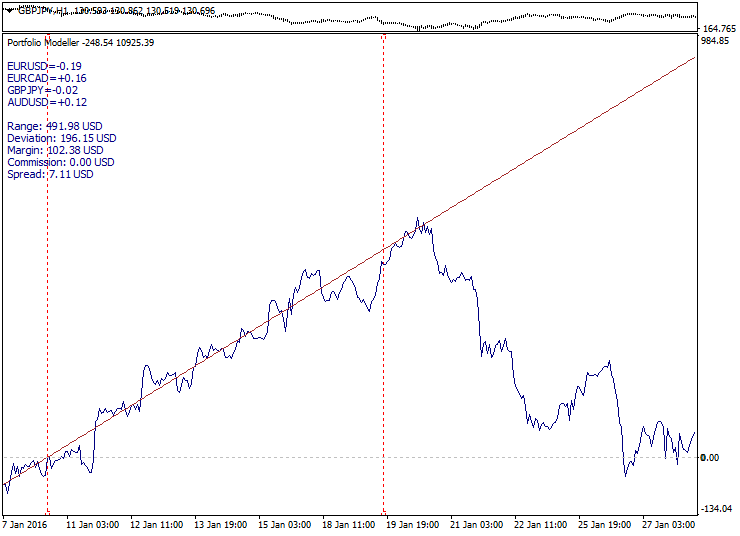
Spread-Trading Nachteile veranlassen uns zu Trend-Modellen zu wechseln. Auf den ersten Blick scheint hier alles harmonisch zu sein: Trend identifizieren, während einer Korrektur eintreten und auf höheren Ebenen mit Gewinn verlassen.
Unten ist ein Beispiel für eine gutes Trendmodell:
Aber es wird sich herausstellen dass Trendmodelle nicht immer so einfach zu handhaben sind. Manchmal wächst das Portfolio nicht weiter und manchmal dreht es scharf nach unten. In diesen Fällen haben wir einen gebrochenen Trend. Dieses passiert oft in kurzen und mittelfristigen Modellen. Die Handelseffizienz hängt stark von der Markt-Phase ab. Wenn der Markt trendy ist, funktioniert das System gut. Wenn der Markt seitwärts geht oder besonders volatil ist, treten zahlreiche Verluste auf.
Unten sehen Sie einen starken Trend-Abschluss:
Diese Nachteile fordern uns auf, die traditionellen Ansätze zu überdenken. Nun werfen wir einen Blick auf die Spread-Breakout und Trend-Umkehr Trading-Methoden. Die allgemeine Vermutung ist, dass, da wir Portfolio-Instabilität nicht vermeiden können, wir lernen sollten, wie man diese benutzt.
Um eine Spread-Breakout-Setup zu entwickeln, müssen wir eine sehr kompakte kurzperiodische Verteilung mit minimalen Schwankungen im Vorgriff auf eine starke Bewegung schaffen. Je mehr wir die Portfolio-Volatilität komprimieren, umso stärker bricht sie aus. Für den beschleunigten Spread-Ausbruch ist es möglich, ein Setup vor Beginn des Handels und vor den Nachrichten in bestimmten Intervallen von einem ruhigen Markt zu bilden. Die PCA-Optimierungsmethode eignet sich am besten für die Volatilität-Kompression. In diesem Setup wissen wir nicht im Voraus, in welche Richtung der Ausbruch stattfinden wird, daher ist der Einstieg bereits durch die Spread-Grenzen definiert.
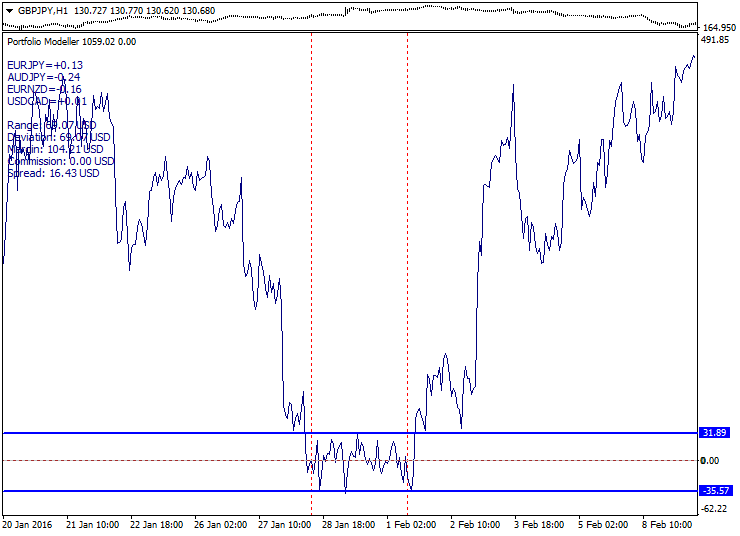
Unten stehend finden Sie ein Beispiel-Ausstieg aus dem kurzperiodischen Ausbreitungs-Kanal mit hervorgehobenen Spread-Kanal-Grenzen:
Die Vorteile der Methode: kurzperiodischen Spreads sind häufig und die Volatilität nach dem Ausbruch überschreitet oft die Bandbreite des Spread-Korridors. Die Nachteile: Spreads erweitern sich während Pressemitteilungen und es kann sich eine "Säge" bilden, wenn sich der Preis ein paar Mal hoch und runter bewegt. Es kann ein konservativer Einstieg als Alternative vorgeschlagen werden, wenn nach dem Ausbruch eine Korrektur an die Grenzen des Korridors stattfindet.
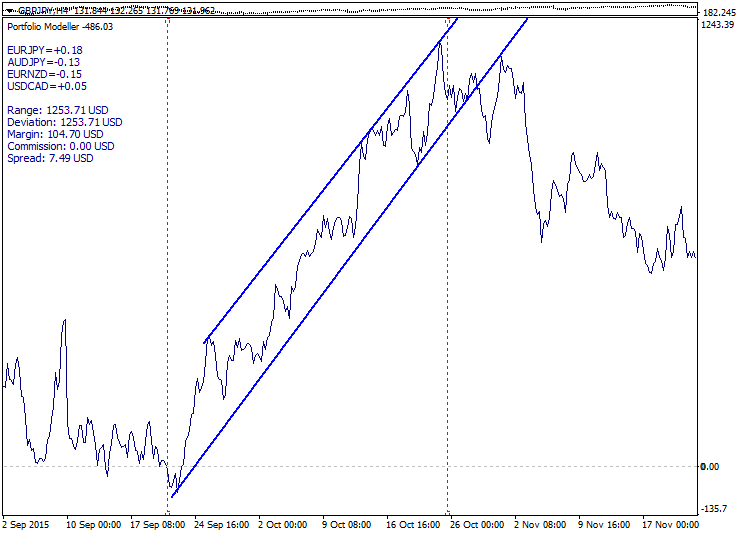
Um ein Trend-Umkehr-Setup zu erstellen, wird ein Trendmodell erstellt, und es werden umkehrende Bewegungen und Portfolio-Preisniveaus verfolgt. Die Bewegungsrichtung ist klar definiert, aber wir wissen im Voraus nicht, wann der Trend umkehrt. Für den konservativen Einstieg wird die Überquerung einer internen Trendlinie, die umgekehrte Korrektur und der Rollback nachverfolgt. Für einen aggressiven Einstieg werden das Berühren einer externen Trendlinie und das Rollback verfolgt.
Nachfolgend sehen Sie ein Beispiel eines Trend-Portfolios mit einer externen und einer internen Linie:
Die Vorteile der Methode: guter Einstiegspreis, Komfort, extreme Preisinstabilität arbeitet zu Gunsten des Setups. Nachteile: Der Portfolio-Preis kann den Trend aus fundamentalen Gründen folgen. Um die Situation zu verbessern, können wir in unterteilten Volumen auf mehreren Ebenen einsteigen.
Ein ähnliches Setup kann mit der parabolischen Quadratwurzel-Modell-Funktion implementiert werden. Das Setup basiert auf einer bekannten Eigenschaft: Wenn der Preis eine theoretische Grenze im Markt erreicht, wird die weitere Bewegung verhindert. Wie in anderen Fällen, wird die Zielfunktion für die Optimierung an die aktuellen Marktverhältnisse angepasst. Wenn sich die Märkte nach der normalen Gaußverteilung verhalten würden, dann würde das zeitbasierte Quadratwurzel-Gesetz immer perfekt funktionieren, aber da das Marktverhalten in seiner Natur Fraktal und nicht-stationär ist, ist die situative Anpassung erforderlich.
Mehr über Markt-Distributionen finden Sie in den folgenden Büchern von Edgar Peters:
- Chaos und Ordnung an den Kapitalmärkten
- Fraktal-Marktanalyse
Es folgt ein Beispiel für eine Abkehr von der parabolischen Portfolio-Funktion :
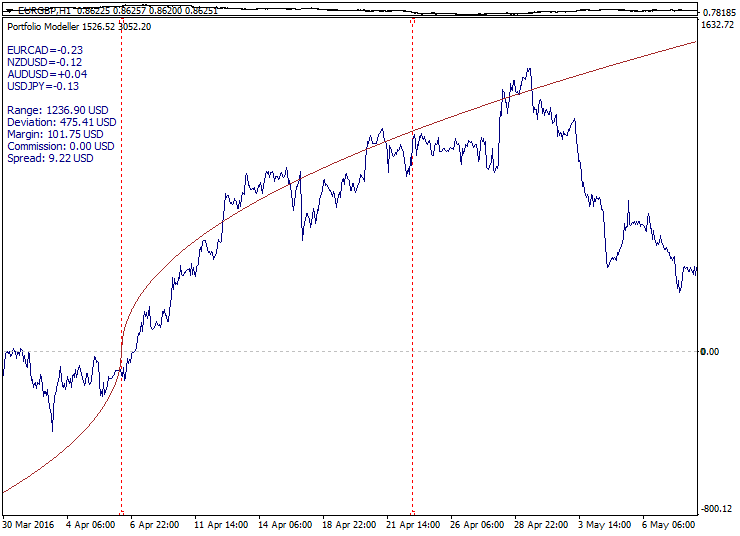
Diese Einstellung eignet sich zur Anpassung an mittelfristigen Schwankungen Jedoch kann sich genau wie bei einem Trend-Setup ein Portfolio-Preis nach oben durch Fundamentalfaktoren verschieben. Der Markt ist nicht verpflichtet, jeder Ziel-Funktion zu folgen, aber weder ist er verpflichtet, noch muss er davon abweichen. Es bleiben immer einige Freiheitsgrade und Dualität. Alle Tradingsetups sind nicht marktneutral im absoluten Sinne, jedoch basieren sie auf irgendeiner Form der technischen Analyse.
Die duale Natur des Trendes- und der Seitwärtsbewegung kann unten gesehen werden. Ein Trendmodell ähnelt auf einer größeren Skala einer ungleichmäßigen Seitwärtsbewegung:
Abgesehen von Symbol-Kombination und Modelltyp ist die Lokalisierung der Intervall Grenzen von großer Bedeutung bei der Entwicklung eines Portfolios. Bei der Konfiguration eines Portfolios kann es sinnvoll sein, die Grenzen zu verschieben und die Ergebnisse zu vergleichen. Eine gute Auswahl an Grenzen ermöglicht die Suche nach Portfolios, die im Hinblick auf eine Trading-Setup besser geeignet sind. Wenn eine Portfolio-Position ein Drawdown beginnt, ist es möglich, das Portfolio zu korrigieren, ohne bestehende Positionen zu schließen. Das Verschieben der Grenzen passt die Portfolio-Kurve an eine veränderte Situation an. Positionen sollten entsprechend nach der Neuordnung des Portfolios korrigiert werden. Dies bedeutet nicht, dass sich der Drawdown sofort verringert, aber das korrigierte Portfolio könnte effizienter geworden sein.
Als nächstes betrachten wir einige Eigenschaften von Portfolio-Sets und ihre Einsatzmöglichkeiten in Trading-Systemen.
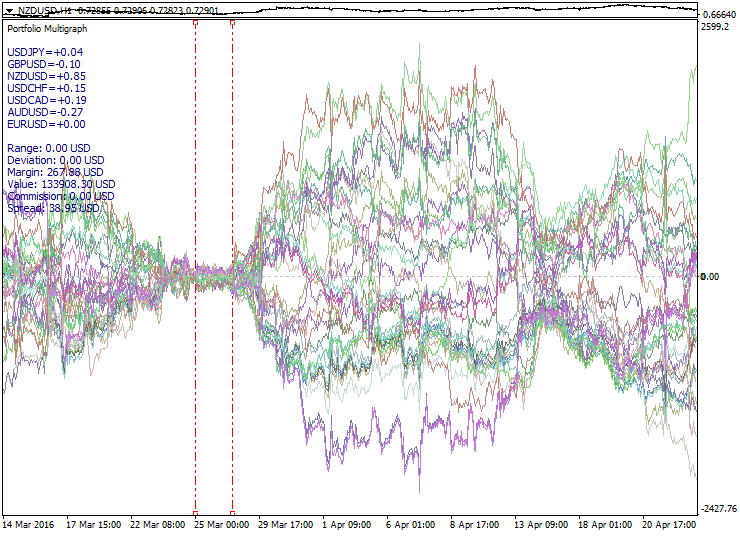
Die erste Eigenschaft der Portfolio-Sets, worauf ein Auge geworfen werden sollte, ist eine Erweiterung oder Divergenz des Portfolios mit einem Abstand vom Nullpunkt. Es wäre nur natürlich und sinnvoll, diese Eigenschaft für den Handel zu verwenden: Kauf von steigenden Portfolios und Verkauf bei Fallenden.
Nachfolgend ist ein Beispiel, wie Portfolios erweitert werden können:
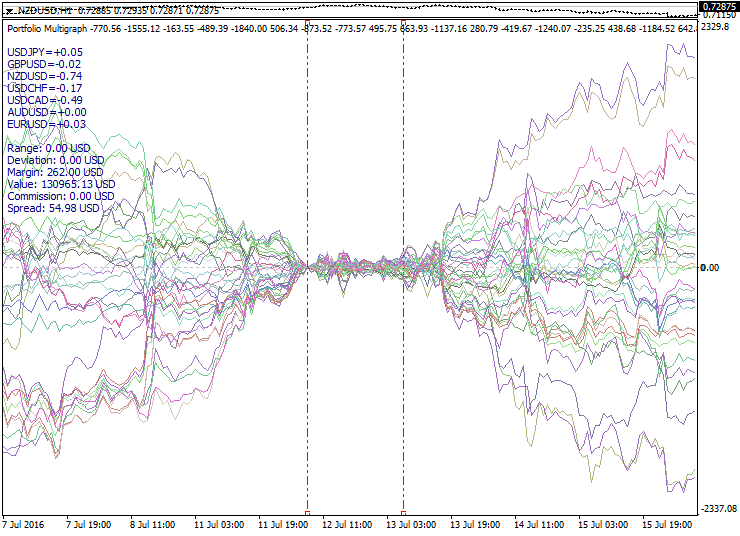
Die zweite Eigenschaft – Portfolio Kompressionseinstellungen (Konvergenz) – Dies ist das Gegenteil zu der vorherigen Eigenschaft. Es geschieht nach einer Erweiterung. Expansions und Kompressions-Zyklen deuten darauf hin, dass dieses Verhalten verwendet werden kann, um synthetische Positionen in Erwartung der Rückkehr in die Mitte des Sets nach Erreichen einem möglichen Höchstmaßes an Ausdehnung zu öffnen. Jedoch kann der höchste Grad an Ausdehnung immer variieren und es ist nicht möglich vorherzusagen, wo die endgültige Grenze der Ausdehnung liegt.
Nachfolgend ist ein Beispiel, mit einem komprimierten Portfolio-Set:
Die Anwendung von verschiedenen Zielfunktionen, Filtrationsparametern, Umkehrungen und Kombinationen bieten auf der Suche nach effizienten Trading-Setups eine gute Möglichkeiten zum Experimentieren. In der Regel können alle Setups in zwei Klassen unterteilt werden: Ausbrüche und Trading-Roll-Backs.
Unten ist ein Beispiel des ersten Trading-Typ-Setups mit einer Umkehr und Verschiebung eines Portfolio-Sets:
Nachfolgend finden Sie eine Beispiel-Rollback-Trading Setup, basierend auf dem Multi-Trend-Modell:
Eine weitere wiederkehrende Portfolio-Eigenschaft ist ein Twist-Satz (Selbst kreuzend) In der Regel entspricht dies einer Änderung eines Markt-Trends. Wenn wir im Hinblick auf eine Ausdehnung des Portfolios handeln, ist eine Wendung (Twist) negativ, was eine Neuordnung erfordert. Für andere Strategien kann das Kreuzen von Portfolio-Kurven dazu verwendet werden vielversprechende und zu Ende gespielte Portfolios zu erkennen. Außerdem ist es notwendig, die bereits zurückgelegte Strecke, die Level, die Position in einem Set und die Position relativ zu der Zielfunktion zu betrachten.
Es folgt ein Beispiel für ein Set, welches sich mehrfach dreht:
Wir haben uns bis jetzt nicht auf das Volume-Management-Problem konzentriert, obwohl dies ein wichtiger Bestandteil eines jeden Handelssystems ist. Im Allgemeinen können wir die folgenden Ansätze beschreiben:
- Handel mit einer einzelnen synthetischen Position (am einfachsten)
- Aufteilung der Volumen (erweiterter Einstieg auf Ebenen)
- Hinzufügen zu einem wachsenden Portfolio (pyramidisieren durch Trend)
- Hinzufügen eines Portfolios bei einem Drawdown (Position verbilligen)
- Hinzufügen eines Portfolios nach einer Korrektur (Beendende Methode)
- Hinzufügen eines Portfolios nach einer Umkehrung (expansive Strategie)
- Hinzufügen zu neuen Portfolios (Portfolio-Konsolidierung)
- Kombinierter Ansatz (eine Kombination aus mehreren Ansätzen)
Die Spezifische Volumen-Methode sollte je nach Trading-Systemfunktionen ausgewählt werden. Wenn Sie den Gewinn und den Drawdown planen, sollten Ihre Berechnungen auf einer Portfolio-Volatilität beruhen. Im einfachsten Fall kann die Portfolio-Volatilität als der Bewegungsbereich von ihren Graphen in einem bestimmten Segment ausgewertet werden. Es ist viel besser, Volatilität nicht nur innerhalb des Optimierungsintervalls, sondern auch mit der Historie zu bewerten. Mit der Kenntnis der Portfolio-Volatilität, ist es möglich, einen theoretischen Wert des insgesamt maximalen Drawdowns bei einer Reihe von Positionen zu berechnen. Traditionell warnen wir davor, allzu häufig aggressive Volumen hinzuzufügen. Die gesamten Mittel für eine Portfoliodeckung auf einem Trading-Konto sollten ungünstige Kursbewegung unter Berücksichtigung aller zusätzlichen Positionen aushalten können.
Multi-Portfoliohandel bedeutet systematische Portfolioauswahl und Konsolidierung. Wenn ein Portfolio gekauft wurde und ein weiteres hinzugefügt wird, kann dies einen positiven Diversifikationseffekt haben, wenn zwischen den Portfolios deutliche Unterschiede bestehen. Aber wenn die Portfolios korrelieren, kann dies einen negativen Effekt haben, da sie beide bei einem Drawdown in eine ungünstigen Bewegung geraten können. Im Normalfall sollten Sie es vermeiden, korrelierende Portfolios hinzuzufügen. Auf den ersten Blick sieht der Handel mit zwei korrelierenden Portfolios sehr vielversprechend aus, aber bei näherer Betrachtung zeigt sich, dass solche Spreads nicht anders als übliche Spreads sind, da sie nicht stationär sind.
Verschiedenen Exit-Strategien können in Multi-Portfoliohandel angewendet werden, einschließlich:
- Schließung bei einem Gesamtergebnis aller Portfolios
- schließen eine Gruppe von Portfolios bei dem Gesamtergebnis der Gruppe
- Schließen von bestimmten Portfolios bei Erreichen von Zielen und Grenzen.
Für eine Reihe von Strategien ist der Einstiegspunkt von entscheidender Bedeutung. Wenn zum Beispiel eine Strategie auf extreme Kurssprünge vor eine Trendwende oder bei einer Korrektur ausgelegt ist, dann ist der Zeitraum für einen Einstieg sehr kurz. Andere Strategien sind mehr auf die optimale Berechnung des Hinzufügens von Positionen und dem Portfolio-Auswahl-Prinzip angewiesen. In diesem Fall können individuelle Portfolios einen Drawdown starten, aber andere (effizientere) Portfolios innerhalb der konsolidierten Serie passen das Gesamtergebnis an.
Schlussfolgerung
Portfolio-Trading Vorteile: Die Optimierung erlaubt es Ihnen, eine Portfolio-Kurve nach ihren Vorstellungen zu erzeugen, so wie ein gewünschtes Trading-Setup zu bilden und es genauso zu handeln, wie normale Symbole auf einem Chart. Entgegen dem Handel mit Trading-Portfolios ist das Kaufen und Verkaufen von konventionellen Assets eine passive Art des Handelns, da einem Trader nur die Möglichkeit bleibt, den aktuellen Preis zu akzeptieren oder ihn nicht zu verwenden. Zudem können Händler ihre Portfolios an die neuen Marktbedingungen anpassen.
Portfolio-Trading Nachteile: Standard pending-Orders sind nicht anwendbar, strengere Anforderungen an Mindestvolumen, größere Spreads auf Diagrammen kleiner gleich М30, Intraday-Scalping kaum möglich, es gibt keine OHLC-Daten, es können nicht alle Indikatoren auf Portfolios angewendet werden.
Im Allgemeinen ist dies ein eher spezifischer Ansatz beim Handeln. Wir haben hier nur einen einführenden Überblick über die Portfolio-Eigenschaften und Arbeitsmethoden gegeben. Wenn Sie die Portfolio-Handelssysteme weiter studieren möchten, empfehle ich die MetaTrader 5-Plattform dafür, damit die Markt-Verteilungs-Eigenschaften mit spezialisierten Statistikpaketen untersucht werden können.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2646
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Lifehack für den Händler: "Stille" Optimierung oder die optische Auswertung des Handels
Lifehack für den Händler: "Stille" Optimierung oder die optische Auswertung des Handels
 Cross-Plattform Expert Advisor: Orders
Cross-Plattform Expert Advisor: Orders
 Arbeiten mit Körben von Währungspaaren am Devisenmarkt
Arbeiten mit Körben von Währungspaaren am Devisenmarkt
 Tiefes Neuronales Netzwerk mit geschichtetem RBM. Selbsttraining, Selbstkontrolle
Tiefes Neuronales Netzwerk mit geschichtetem RBM. Selbsttraining, Selbstkontrolle
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.