MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 66): Verwendung von FrAMA-Mustern und des Force Index mit dem Punktprodukt-Kernel

Einführung

In unserem letzten Artikel, in dem wir das Paar dieser Indikatoren als Quelle für Einstiegssignalmuster für einen Expert Advisor vorgestellt haben, waren die Ergebnisse des Forward Walk nicht so vielversprechend. Wir haben einige Gründe dafür genannt und auch darauf hingewiesen, dass das Training und die Optimierung, die wir durchführen, nur für ein Jahr gelten und dass es daher für jedes Muster unerlässlich ist, es so umfassend wie möglich auf einer riesigen Menge von Daten zu testen. Im Anschluss an diesen Teil untersuchen wir wie immer die Muster, die vorwärts gehen konnten. Dies geschieht durch maschinelles Lernen.

Bei der Anwendung von Algorithmen des maschinellen Lernens in MQL5 ist OpenCL immer eine Option, allerdings erfordert dies oft eine GPU-Hardware. Das ist zwar schön, aber die Code-Bibliothek von Python ist inzwischen recht umfangreich, und viele Effizienzgewinne lassen sich auch mit einer CPU erzielen. Das ist es, was wir in dieser Artikelserie erforschen, und deshalb kodieren wir in diesem Beitrag, wie schon in einigen früheren, unsere neuronalen Netze in Python, weil die Kodierung und das Training in Python sehr effizient sind. 

Von unseren zehn Mustern (Pattern), die wir im letzten Artikel optimiert oder trainiert haben, konnten nur 2 laufen. Pattern-6 und Pattern-9. Daher testen wir diese mit einem neuronalen Netzwerk weiter, wie wir es bei den vergangenen Partikeln getan haben, mit dem Unterschied, dass wir ein neuronales Faltungsnetzwerk, auch CNN genannt, verwenden. Dieser CNN wird den Punktprodukt-Kernel implementieren. Zunächst definieren wir jedoch, wie immer bei Python-Implementierungen, die Indikatorfunktionen, die wir benötigen, um Signale an unser Netzwerk zu liefern. 

Die Funktion Fractal Adaptive Moving Average (FrAMA)

Der FrAMA ist ein dynamischer gleitender Durchschnitt, der seine Glättung in Abhängigkeit von den fraktalen Dimensionen der Kursbewegungen anpasst. Dadurch reagiert er eher auf größere Preisänderungen und weniger auf Störungen. Wir implementieren diese Funktion in Python wie folgt;

def FrAMA(df, period=14, price_col='close'):
    """
    Calculate Fractal Adaptive Moving Average (FrAMA) for a DataFrame with price data.
    
    Args:
        df: Pandas DataFrame with a price column (default 'close').
        period: Lookback period for fractal dimension (default 20).
        price_col: Name of the price column (default 'close').
        
    Returns:
        Pandas DataFrame with a single column 'main' containing FrAMA values.
    """
    prices = df[price_col]
    frama = pd.Series(index=prices.index, dtype=float)
    
    for t in range(period, len(prices)):
        # 1. High-Low range (volatility proxy)
        high = prices.iloc[t-period:t].max()
        low = prices.iloc[t-period:t].min()
        range_hl = high - low
        
        # 2. Fractal Dimension (simplified)
        fd = 1.0 + (np.log(range_hl + 1e-9) / np.log(period))  # Avoid log(0)
        
        # 3. Adaptive EMA smoothing factor
        alpha = 2.0 / (period * fd + 1)
        
        # 4. Update FrAMA (recursive EMA)
        frama.iloc[t] = alpha * prices.iloc[t] + (1 - alpha) * frama.iloc[t-1]
    
    return pd.DataFrame({'main': frama})

Unsere obige Funktion bietet uns eine flexible Eingabe, da sie einen Pandas-Datenrahmen mit anpassbaren Preisspalten- und Periodenparametern akzeptiert. Es verwendet einen Volatilitätsproxy für die Hoch-Tief-Spanne, um die Marktvolatilität zu schätzen und berechnet eine vereinfachte fraktale Dimension, um die Preiskomplexität zu messen. Unsere Funktion aktualisiert den FrAMA über eine rekursive EMA.

Wenn wir unseren Code durchgehen, extrahieren wir als erstes die angegebene Preisspalte aus dem Eingabedatenrahmen. Diese Extraktion gewährleistet, dass die Funktion mit jeder vom Nutzer angegebenen Preisspalte funktioniert. Wir vermeiden Hardcoding und erhalten die Kompatibilität. Bei der Verwendung dieser Funktion kann es sinnvoll sein, sie zu verbessern, indem man überprüft, ob die Spalte für den Eingabepreis im Datenrahmen vorhanden ist, und indem man sicherstellt, dass die Preisdaten sauber sind, ohne NaNs oder fehlende Werte, da FrAMA empfindlich auf Preiseingaben reagiert.

Als Nächstes wird eine leere Pandas-Reihe mit demselben Index initialisiert, da dadurch Speicher für FrAMA-Werte reserviert wird, der mit dem Index des Eingabedatenrahmens übereinstimmt, was eine effiziente iterative Aktualisierung ermöglicht. Wenn dies verwendet wird, benötigt FrAMA ein Rückblicksfenster zur Berechnung, was bedeutet, dass die ersten Werte NaN sind und verwaltet oder zu Nullen gemacht werden müssen. Außerdem muss sichergestellt werden, dass der Preisindex konsistent ist, z. B. durch Preis-Zeit-Paarung, um eine Fehlanpassung zu vermeiden.

Damit gelangen wir in die for-Schleife, in der wir die Hoch-Tief-Spanne über den Rückblickszeitraum berechnen, um die Volatilität zu schätzen. Für jeden Zeitschritt t nehmen wir den Höchst- und den Tiefstpreis im t-Perioden-Fenster und berechnen deren Differenz. Die Hoch-Tief-Spanne dient als Proxy für die Marktvolatilität, die für die Bestimmung der fraktalen Dimension wichtig ist. Eine größere Spanne bedeutet eine höhere Volatilität, die die Anpassungsfähigkeit von FrAMA beeinflusst. Bei der Implementierung kann ein Fehlerbehandlungsmechanismus, der auf NaNs achtet, dazu beitragen, fehlende Daten zu beheben.

Anschließend berechnen wir die vereinfachte fraktale Dimension anhand des logarithmischen Verhältnisses des oberen und unteren Bereichs. Der Term von Epsilon mit 1e-9 verhindert die Division durch Null oder den Logarithmus von Null für den Fall, dass der Bereich-hl Null ist. Die fraktale Dimension, fd, misst die Komplexität oder die Tendenz der Preise. Ein höherer fd, der näher an 2 liegt, bedeutet, dass wir uns in einem unruhigen, lauten Markt befinden. Andererseits deutet ein niedrigerer fd-Wert, der näher bei 1 liegt, auf tendenzielle Märkte hin. Dieser Parameter bestimmt also die Anpassungsfähigkeit von FrAMA. Die 1e9 ist ein numerischer Stabilitätstrick, der sicherstellt, dass sie klein genug ist, um die Ergebnisse nicht zu verzerren. Außerdem ist die hier verwendete fraktale Dimension eine vereinfachte Version; für kompliziertere Formate können Box-Counting-Methoden verwendet werden. Danach wird der Glättungsfaktor Alpha berechnet.

Dies ist ein Glättungsfaktor für den exponentiellen gleitenden Durchschnitt auf der Grundlage der fraktalen Dimension und der Periode. Er ist wichtig, weil das adaptive Alpha bestimmt, wie stark FrAMA auf neue Preise reagiert. Ein höherer fd, der in einem lauteren Markt erzielt wird, reduziert Alpha und verlangsamt den EMA, um das Rauschen zu filtern. Ein niedrigerer fd, der in tendenziellen Märkten erzielt wird, erhöht das Alpha und macht den FrAMA reaktionsfähiger auf Preisänderungen.

Diese Formel schafft also ein Gleichgewicht zwischen Reaktionsfähigkeit und Geschmeidigkeit. Der Zeitraum kann zur Steuerung der Empfindlichkeit eingestellt werden. Es ist darauf zu achten, dass der Nenner Periode * fd + 1 positiv ist, um Divisionsprobleme zu vermeiden.

Unsere nächste Codezeile aktualisiert den FrAMA-Wert zum Zeitpunkt t unter Verwendung der EMA-Formel, die eine gewichtete Kombination aus dem aktuellen Preis und dem vorherigen FrAMA-Wert ist. Dies ist wichtig, denn die rekursive EMA-Berechnung ist das Herzstück von FrAMA und erzeugt einen geglätteten adaptiven gleitenden Durchschnitt, der sich über Alpha an die Marktbedingungen anpasst. Zu den Änderungen, die an dieser Implementierung vorgenommen werden können, gehört, dass die ersten FrAMA-Werte keine NaNs sind und dass diese Prüfungen auch die Randfälle des FrAMA-Puffers umfassen sollten.

Die letzte Codezeile der FrAMA-Funktion gibt die FrAMA-Werte als Pandas-Datenrahmen mit einer einzigen Spalte namens main zurück. Dadurch wird das Ausgabeformat für die Kompatibilität mit anderen technischen Analysetools oder Plotbibliotheken standardisiert. Die Verwendung des Spaltennamens „main“ ist bei Indikatoren mit einem einzigen Puffer üblich. Bei der Integration in verschiedene Umgebungen, in denen dieser Name ein Aufrufpunkt ist, kann er auf „FrAMA“ oder etwas Spezifischeres angepasst werden. Es muss auch sichergestellt werden, dass der zurückgegebene Datenrahmen mit dem Index des Eingabedatenrahmens übereinstimmt.

Force Index Oszillator Funktion

Dieser Oszillator misst die Stärke von Kursbewegungen, indem er Kursänderungen und Handelsvolumen zusammenführt. Dieser wird mit einem EMA geglättet, um Trends oder Umkehrungen hervorzuheben. Wir implementieren dies in Python wie folgt:

def ForceIndex(df, period=14, price_col='close', volume_col='tick_volume'):
    """
    Calculate Force Index for a DataFrame with price and volume data.
    
    Args:
        df: Pandas DataFrame with columns for price and volume (default 'close' and 'volume').
        period: Smoothing window for EMA (default 13).
        price_col: Name of the price column (default 'close').
        volume_col: Name of the volume column (default 'volume').
        
    Returns:
        Pandas DataFrame with a single column 'main' containing Force Index values.
    """
    closes = df[price_col]
    volumes = df[volume_col]
    
    # 1. Raw Force Index = Price Delta * Volume
    price_delta = closes.diff()
    raw_force = price_delta * volumes
    
    # 2. Smooth with EMA
    alpha = 2.0 / (period + 1)
    force_index = pd.Series(index=closes.index, dtype=float)
    
    for t in range(1, len(raw_force)):
        if pd.isna(raw_force.iloc[t]):
            force_index.iloc[t] = np.nan
        else:
            force_index.iloc[t] = alpha * raw_force.iloc[t] + (1 - alpha) * force_index.iloc[t-1]
    
    return pd.DataFrame({'main': force_index})

Unsere obige Funktion bietet ebenso wie die FrAMA Eingabeflexibilität, da sie anpassbare Preis- und Mengenspalten akzeptiert. Es verwendet die Berechnung der rohen Kraft, indem es Preisänderungen und Volumen kombiniert, um den Kauf- und Verkaufsdruck zu messen. Führt eine EMA-Glättung durch, um Rauschen zu reduzieren und anhaltende Bewegungen zu betonen. Umgang mit NaNs. Schließlich wird die Ausgabe standardisiert, indem ein Datenrahmen zur einfachen Integration zurückgegeben wird.

Wenn wir die Zeilen durchgehen, extrahieren wir zunächst den Schlusskurs und das Volumen aus dem Eingabedatenrahmen der Pandas-Serie. Dies ist wichtig, weil dadurch die relevanten Daten für Berechnungen isoliert werden, was Flexibilität bei den Spaltennamen und eine effiziente Verarbeitung ermöglicht. Mögliche Änderungen können darin bestehen, zu überprüfen, ob price_col und volume_col im Datenrahmen vorhanden sind, um Fehler zu vermeiden, und sicherzustellen, dass die Volumendaten nicht negativ und die Preisdaten sauber sind, da der Force Index auf beiden beruht.

Als Nächstes setzen wir das Preisdelta auf die Differenz der Schlusskurse. Die von uns in Python verwendete Methode liefert einen Puffer, der die Differenz zwischen aufeinander folgenden Schlusskursen berechnet, um die Preisbewegung zu messen. Dies ist von Bedeutung, da die Preisänderung die Richtung und das Ausmaß der volumengewichteten Drift des Marktes widerspiegelt, die eine Schlüsselkomponente des Force Index ist. Der NaN-Wert für den ersten Index muss durch Konvertierung in Null behandelt werden, und auch Fälle von fehlenden Werten müssen behandelt werden.

Anschließend bestimmen wir den Wert des RohForce Indexes, der sich aus dem Preisdelta und unserem Volumen ergibt. Python vereinfacht die Kodierung, indem es Puffer/Arrays so multipliziert, als wären sie skalare Werte. Dieses Produkt stellt die Stärke der Preisbewegung dar. Er kombiniert die Preisdynamik mit dem Volumen, um den Kauf- oder Verkaufsdruck zu quantifizieren. Eine große Preisänderung bei hohem Volumen deutet in der Regel auf eine stärkere Überzeugung des Marktes hin. Bei der Durchführung dieses Vektorprodukts ist es ratsam, zusätzlich zu unserem obigen Code sicherzustellen, dass die Volumen- und Preisdelta-Puffer nach Index ausgerichtet sind, um Fehlberechnungen zu vermeiden. Es ist auch zu beachten, dass dieser rohe Force Index verrauscht sein kann und daher in einem späteren Stadium geglättet werden kann.

Als Nächstes stellen wir den Alphawert ein. Dies ist die Berechnung des EMA-Glättungsfaktors auf der Grundlage des angegebenen Zeitraums unter Verwendung der Standard-EMA-Formel 2/(N + 1). Dies ist wichtig, weil es die Gewichtung der neuen Daten gegenüber den historischen Daten im geglätteten Force Index bestimmt. Ein kleineres Alpha, das aus einem größeren Zeitraum stammt, führt in der Regel zu gleichmäßigeren Ergebnissen. Wir verwenden standardmäßig einen Zeitraum von 14 Jahren, und das ist üblich. Je nach verwendetem Zeitrahmen sollten jedoch Anpassungen vorgenommen werden. Typischerweise eignen sich kürzere Zeiträume gut für den Intraday-Handel, während längere Zeiträume mit täglichen oder größeren Zeitrahmen funktionieren könnten. Es ist auch wichtig, dass der Periodenwert positiv ist, um Fehler bei der Nullteilung zu vermeiden.

Anschließend initialisieren wir den eigentlichen Puffer für den Force Index aus dem Pandas-Datenrahmen. Dabei wird einfach ein leerer Puffer mit demselben Index wie die Preisdaten gefüllt, um geglättete Werte des Force Index zu speichern. Es ist wichtig, weil es dazu dient, Speicher im Voraus zuzuweisen und auch die Indexausrichtung sicherzustellen, zwei Dinge, die iterative EMA-Berechnungen erleichtern. Anfängliche NaN-Werte werden erwartet, da der erste Force Index einen vorherigen Wert erfordert.

Wir überprüfen daher, ob der rohe Force Index zum Zeitpunkt t NaN ist. Dies gewährleistet Robustheit, indem fehlende Daten explizit behandelt werden, was ungültige UKORE-Berechnungen verhindert. Daten aus der realen Welt sind oft lückenhaft, daher sollte man sie nicht übersehen, auch wenn dies noch so abwegig erscheint. In der Tat ist das Protokollieren oder Markieren von NaN-Werten bei der Fehlersuche eine gute Praxis.

Anschließend wird der Force Indexpuffer zu jedem Zeitpunkt t unter Verwendung der EMA-Formel aktualisiert. Dabei wird der aktuelle rohe Force Index mit dem vorherigen geglätteten Wert kombiniert. Dies ist wichtig, da es sich um einen zentralen Glättungsschritt handelt, der das Rauschen im rohen Force Index reduziert und anhaltende Trends oder Umkehrungen hervorhebt. In diesem Schritt muss sichergestellt werden, dass force_index[t-1] richtig initialisiert wird, da NaN oft der Wert für frühe Indizes ist. Die Randfälle dieses Puffers müssen daher richtig behandelt werden.

Anschließend geben wir die geglätteten Force Indexwerte als Pandas-Datenrahmen mit einer einzigen Spalte namens main zurück. Das standardisierte Ausgabeformat ermöglicht, wie bereits oben bei FrAMA argumentiert, eine bessere Integration und Visualisierung in sekundären Formaten oder Tools, je nach den Anforderungen der Nutzer. Die Kennzeichnung „main“ entspricht in der Regel den „Konventionen“ der technischen Analyse. Es ist wichtig sicherzustellen, dass der Index des Datenrahmens mit der Eingabe übereinstimmt, um eine nahtlose Zusammenführung zu ermöglichen.

Nachdem wir unsere Indikatorfunktionen in Python definiert haben, ist es nun an der Zeit, die beiden Signalmuster zu betrachten, die wir im letzten Artikel vorwärts laufen lassen konnten. Diese waren Pattern-6 und Pattern-9. Wir implementieren diese als einfachen 2-Bit-Vektor, der als Eingabe für unser neuronales Netz dient. Diese „Bits“ stehen für Auf- und Abwärtstrends, wobei die Werte bei jedem Index entweder 0 oder 1 sind. Zur Erinnerung: Der Eingabevektor hat eine Größe von 2, und am ersten Index wird 0 protokolliert, wenn ALLE Aufwärtsbedingungen nicht erfüllt sind, oder 1, wenn sie alle erfüllt sind. In ähnlicher Weise protokollieren wir beim zweiten Index 0, wenn ALLE Abwärtsbedingungen nicht erfüllt sind, oder 1, wenn sie ALLE erfüllt sind.

Zuvor haben wir Szenarien betrachtet, in denen wir die einzelnen Bestandteile des Auf- und Abwärtssignals aufgeschlüsselt haben, um komplexere Eingangsvektoren für unsere neuronalen Netze zu erhalten. Die daraus resultierenden Vorwärtsbewegungen waren nicht so vielversprechend und schienen eher dem Ansatz zu ähneln, den wir in einem früheren Artikel mit der Kombination mehrerer Muster in einem einzigen Expert Advisor ausprobiert haben.

Diese Analyse könnte jedoch falsch sein, sodass die Leser den beigefügten Quellcode verwenden und ändern und unabhängige Tests durchführen können, um zu ihren eigenen Schlussfolgerungen zu gelangen. Der beigefügte Code soll im MQL5-Assistenten verwendet werden, und es gibt hier Anleitungen, wie man das macht.

Die Funktion Feature-6

Unsere Implementierung der Funktion Pattern-6 in Python erzeugt ein 2D-Array mit binären Signalen von 0 oder 1, wie oben beschrieben. Wir beginnen mit der Initialisierung unseres Feature-Output-Arrays mit Nullen. Diese Ausgabe ist ein NumPy 2D-Array, das einer zweispaltigen Matrix entspricht. Die Anzahl der Zeilen dieser „Matrix“ wird auf die Größe oder Länge eines der Eingabedatenrahmen „one_df“ festgelegt. Durch diese Initialisierung wird die Ausgabestruktur so eingerichtet, dass Auf- und Abwärtssignale getrennt gespeichert werden. Die Initialisierung mit Null bedeutet, dass keine Signale erzeugt werden, wenn die Musterbedingungen nicht erfüllt sind, was einen „Neustart“ bedeutet.

Bei der Implementierung ist darauf zu achten, dass die Länge des ersten Pandas-Eingabedatenrahmens mit der des zweiten „two_df“ und des Preisdatenrahmens „price_df“ übereinstimmt, um eine falsche Indexausrichtung zu vermeiden. Die 2D-Struktur ist der Schlüssel zur Unterscheidung von Auf- und Aufwärtssignalen, daher ist es wichtig zu prüfen, ob die Form den Erwartungen entspricht. So setzen wir es um:

def feature_6(one_df, two_df, price_df):
    """
    Generate binary signals based on sustained price-FrAMA alignment and Force Index momentum.
    
    Args:
        one_df: DataFrame with FrAMA values ('main' column).
        two_df: DataFrame with Force Index values ('main' column).
        price_df: DataFrame with price data ('close' column).
    
    Returns:
        2D NumPy array with bullish (column 0) and bearish (column 1) signals.
    """
    feature = np.zeros((len(one_df), 2))
    
    feature[:, 0] = ((price_df['close'] > one_df['main']) &
                     (price_df['close'].shift(1) > one_df['main'].shift(1)) &
                     (price_df['close'].shift(2) > one_df['main'].shift(2)) &
                     (two_df['main'] > 0.0) &
                     (two_df['main'].shift(1) < two_df['main'].shift(2))).astype(int)
    feature[:, 1] = ((price_df['close'] < one_df['main']) &
                     (price_df['close'].shift(1) < one_df['main'].shift(1)) &
                     (price_df['close'].shift(2) < one_df['main'].shift(2)) &
                     (two_df['main'] < 0.0) &
                     (two_df['main'].shift(1) < two_df['main'].shift(2))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Wir fahren dann fort, unsere Aufwärtserwartungen oder den ersten Indexwert in jeder Zeile zu definieren. Um den letzten Artikel noch einmal zu rekapitulieren: Wenn der aktuelle Kurs über dem FrAMA liegt, der vorherige Kurs ebenfalls über dem vorherigen FrAMA liegt, vor zwei Perioden die gleiche Situation herrschte, der aktuelle Force Index positiv ist und vor einer Periode der Force Index unter dem jetzigen Wert lag, dann haben wir ein Aufwärts-Setup.

Diese erste Säulenlinie umfasst den Aufwärtstrend und stellt sicher, dass das Signal nur dann ausgelöst wird, wenn der Preistrend dauerhaft über dem adaptiven FrAMA liegt, was auf einen Aufwärtstrend hindeutet. Der Force Index bestätigt den starken Kaufdruck. Der Drei-Perioden-Check sorgt für mehr Robustheit, während der Force Index-Check schwache Bewegungen ausschließt. Bei der Implementierung ist es wichtig zu prüfen, ob alle Eingabedatenrahmen indexmäßig ausgerichtet sind und gültige Daten enthalten. Die Operationen shift() erzeugen NaNs für frühe Zeilen, die behandelt werden müssen, bevor Indikatorwerte zurückgegeben werden können. 

Die zweite Spalte definiert das Abwärtssignal mit den folgenden analogen Bedingungen: der aktuelle Kurs liegt unter dem FrAMA; der vorherige Kurs liegt ebenfalls unter dem FrAMA; die gleiche Bedingung ist vor zwei Perioden eingetreten; der aktuelle Force Index ist negativ; und der Force Index vor einer Periode liegt über dem aktuellen Force Index und dem Force Index vor zwei Perioden. Die n-Form im Force Index, die auf eine Zunahme des negativen Volumens oder der Stimmung hinweist.

Dieses Muster spiegelt das Aufwärtsmuster für Verkaufsgelegenheiten wider. Er identifiziert anhaltende Abwärtstrends mit starkem Verkaufsdruck. Die Symmetrie gewährleistet eine einheitliche Logik in beiden Mustern. Ähnlich wie bei einem Aufwärtsmuster ist es von entscheidender Bedeutung, den Datenabgleich sicherzustellen. Es sollte auch geprüft werden, ob dieses Muster ausreichend häufig auftritt. Die Momentum-Prüfung des Force Index (`Shift(1) < Shift(2)`) kann sich in Auf- und Abwärtsmärkten unterschiedlich verhalten. Es ist daher wichtig, die historische Leistung zu analysieren, um ihre Zuverlässigkeit zu überprüfen.

Als Nächstes setzen wir die ersten beiden Zeilen des Merkmalsarrays auf Null, da die Operationen „.shift(1)“ und „.shift(2)“ für diese Zeilen NaNs erzeugen, was diese Bedingungen undefiniert macht. Dies verhindert ungültige Signale in den ersten Zeilen, wenn die historischen Daten unzureichend sind, und gewährleistet eine saubere und brauchbare Ausgabe ohne manuelle Nachbearbeitung. Diese Prüfung ist entscheidend für die Robustheit, und da dieses Muster durch mehr als zwei Schichten implementiert werden kann (z. B. wenn die verglichenen Perioden größer als 2 sind), ist es wichtig zu überprüfen, ob die Einstellung nur der ersten beiden Zeilen auf der Grundlage der verwendeten maximalen Anzahl von Schichten ausreichend ist. Wenn zusätzliche Schichten hinzukommen, sollte dies entsprechend angepasst werden.

Zusammenfassend lässt sich sagen, dass sich das Aufwärtsmuster auf einen anhaltenden Preis - FrAMA Aufwärtskreutz von mindestens 3 Perioden mit einem positiven und kürzlich U-förmigen Force Index konzentriert. Er bestätigt, ob Aufwärtstrends einen langen Atem haben. Das Abwärtsmuster ist eine Umkehrung davon, indem es auf einem anhaltenden Abwärts-Kreuz zwischen Preis und FrAMA für mindestens 3 Perioden und einem negativen Force Index mit einem aktuellen n-förmigen Muster beruht. Sie bestätigt auch, dass der Abwärtstrend intakt ist.

Ein Hauptunterschied zwischen den beiden ist, dass sie nicht nur symmetrisch und gegensätzlich sind, sondern dass der Stimmungs-Check für den Kraft-Index ausschließlich einen kürzlichen Anstieg in der Größenordnung erfordert, der sich aufgrund der Asymmetrie in Auf- und Abwärtsmärkten unterschiedlich verhalten kann. So neigen die Märkte beispielsweise dazu, schneller zu fallen als zu steigen.

Die Funktion Feature-9

Diese Python-Implementierung von signal-9 konzentriert sich auf den Abgleich der Stimmung in einer einzigen Periode über den Preis, den FrAMA und den Force Index, wodurch sie empfindlicher auf kurzfristige Änderungen reagiert als 'feature_6'. Wir beginnen wie bei Feature-9 mit der Initialisierung unserer Zielausgabe mit Nullen. Dies ist ein ähnlicher Aufbau wie bei Feature-6, wobei die anfängliche Größe des 2D-NumPy-Arrays so eingestellt wird, dass sie der Länge eines der Eingabedatenrahmen, one-df, entspricht.  Wir implementieren es in Python wie folgt:

def feature_9(one_df, two_df, price_df):
    """
    Generate binary signals based on single-period momentum alignment of price, FrAMA, and Force Index.
    
    Args:
        one_df: DataFrame with FrAMA values ('main' column).
        two_df: DataFrame with Force Index values ('main' column).
        price_df: DataFrame with price data ('close' column).
    
    Returns:
        2D NumPy array with bullish (column 0) and bearish (column 1) signals.
    """
    feature = np.zeros((len(one_df), 2))
    
    feature[:, 0] = ((price_df['close'] > price_df['close'].shift(1)) &
                     (one_df['main'] > one_df['main'].shift(1)) &
                     (two_df['main'] > two_df['main'].shift(1))).astype(int)
    feature[:, 1] = ((price_df['close'] < price_df['close'].shift(1)) &
                     (one_df['main'] < one_df['main'].shift(1)) &
                     (two_df['main'] < two_df['main'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Für beide Merkmalsfunktionen gilt, dass one-df der FrAMA-Datenrahmen ist, während two-df der Force Index-Datenrahmen ist. Daraus folgt, dass wir, wie in Feature-6 erwähnt, überprüfen müssen, ob der Ein-Daten-Frame, der Zwei-Daten-Frame und der Preis-Daten-Frame die gleiche Länge haben, um Formabweichungen zu vermeiden. Diese Matrix/2D-Matrix trennt Auf- und Abwärtsmuster, daher ist es wichtig, die Zeilengröße zu überprüfen.

Die Aufwärtsbedingung ist auch das, worauf wir bei diesem Muster zunächst achten. Die Bedingungen sind: der aktuelle Kurs ist höher als der vorherige Schlusskurs; der aktuelle FrAMA ist höher als der vorherige FrAMA und der aktuelle Force Index ist höher als der letzte Wert. Dies zeigt ein kurzfristiges Aufwärtsmomentum, bei dem der Preis, der FrAMA und der Force Index alle steigen, was ein Zeichen für einen gleichgerichteten Kaufdruck ist. Es ist auch etwas empfindlicher als Feature-6, da es nur eine einzige Periode prüft. Dies könnte ihn für Scalping oder kurzfristigen Handel besser geeignet machen.

Bei der Verwendung ist es wichtig, die Datenausrichtung über alle Eingänge hinweg sicherzustellen, um falsch ausgerichtete Vergleiche zu vermeiden. Da dieses Muster empfindlich auf einperiodige Veränderungen reagiert, müssen wir seine Signalhäufigkeit testen, um ein Überhandeln zu vermeiden, falls die Märkte auf verrauschte Daten treffen. Die Visualisierung von Signalen auf einem Preis-Chart, um sicherzustellen, dass sie mit der erwarteten Volumenstimmung übereinstimmen, kann ebenfalls konstruktiv sein.

Wir legen das Abwärtsmuster für Feature-9 fest, wenn die folgenden Bedingungen erfüllt sind: der aktuelle Kurs ist niedriger als der vorherige Kurs; der aktuelle FrAMA ist niedriger als der vorherige FrAMA; und der aktuelle Force Index ist niedriger als der vorherige Force Index. Dies ist ein Zeichen für eine kurzfristige Abwärtsstimmung, bei der alle drei Indikatoren rückläufig sind, was auf einen gleichgerichteten Verkaufsdruck hindeutet. Die Konzentration auf einen einzigen Zeitraum führt dazu, dass er auf unmittelbare Abschwünge reagiert.

Auch hier gilt, wie schon bei dem Aufwärtsmuster, dass die Validierung der Datenintegrität und die Prüfung der Signalfrequenz von entscheidender Bedeutung sind. In volatilen Märkten können Abwärtssignale häufiger ausgelöst werden, daher ist eine Analyse der historischen Performance wichtig für die Feinabstimmung dieser Strategie.

Dann setzen wir die ersten Zeilen des Ausgabe-Arrays auf Null, weil wir, wie bereits oben erwähnt, Shift verwenden, und geben das Array als Ausgabe der Funktion zurück.

CNN mit Punktprodukt-Kernel

Der von uns gewählte Algorithmus für maschinelles Lernen zur Erweiterung der Muster von FrAMA und des Force Indexes ist ein neuronales Faltungsnetzwerk, das den Punktprodukt-Kernel verwendet. Wir erreichen dies über die Klasse DotProductConv1D. Diese Klasse ist ein PyTorch-Modul für neuronale Netze, das 1D-Faltungen mit einem Punktprodukt-Attention-Mechanismus kombiniert, der von der Transformer-Architektur inspiriert ist.

Es verarbeitet Eingabedaten der Form [Charge, Kanäle, Breite] und gibt einen einzelnen Wert pro Probe im Bereich [0, 1] aus. Ein Wert von 0 wäre eine Abwärtsprognose, während ein Wert von 1 eine Aufwärtsprognose wäre. Der Punktprodukt-Aufmerksamkeitsmechanismus ermöglicht es dem Netz, sich auf relevante Teile der Eingabesequenz zu konzentrieren, während die Faltungsschichten die Daten in einen geeigneten Raum für die Aufmerksamkeitsberechnung projizieren.

Die Verwendung dieses Kerns in einem CNN ist aus einer Reihe von Gründen vorteilhaft. Erstens ermöglicht es eine selektive Fokussierung auf relevante Merkmale. Der Punktprodukt-Aufmerksamkeits-Mechanismus berechnet Ähnlichkeitswerte zwischen Abfrage- und Schlüsselvektoren, wodurch das Netz wichtige Schlüsselschritte oder Merkmale stärker gewichten kann. Dies kann bei einigen Zeitreihen von Vorteil sein, z. B. wenn bestimmte Zeiträume aussagekräftiger sind, z. B. volatile Zeiträume gegenüber nicht volatilen Zeiträumen. Zweitens wird ein globales kontextuelles Bewusstsein eingeführt.

Im Gegensatz zu herkömmlichen CNNs, die sich auf Kernel fester Größe und lokale rezeptive Felder stützen, ermöglicht die Punktprodukt-Aufmerksamkeit, dass jeder Zeitschritt alle anderen Zeitschritte berücksichtigt und somit weitreichende Abhängigkeiten erfasst werden, ohne dass die Kernelgröße zunimmt. Drittens wird das Modell durch die dynamische Gewichtung, bei der die Aufmerksamkeitswerte dynamisch auf der Grundlage der Eingaben berechnet werden, an unterschiedliche Muster in den Daten, wie z. B. unterschiedliche Marktbedingungen innerhalb der Zeitreihe, angepasst. 

Schließlich ergeben sich ergänzende Stärken aus der Kombination mit CNNs, die gut für die lokale Merkmalsextraktion geeignet sind, und dem Punktprodukt-Kernel, der gut für globale Beziehungen geeignet ist. Die Aufmerksamkeit des Punktprodukts ist auch bei moderaten Sequenzlängen rechnerisch effizient, während das 1D-CNN die Dimensionalität der Eingänge reduziert, wodurch das gesamte Modell im Vergleich zu vollständigen Transformatormodellen leicht ist. Unsere Auflistung für diese Netzklasse lautet wie folgt:

class DotProductConv1D(nn.Module):
    def __init__(self, in_channels=1, out_channels=1, kernel_size=3):
        super().__init__()
        self.kernel_size = kernel_size
        self.padding = kernel_size // 2
        
        # Projections for dot product attention (1D convolution)
        self.query = nn.Conv1d(in_channels, out_channels, kernel_size=1)
        self.key = nn.Conv1d(in_channels, out_channels, kernel_size=1)
        self.value = nn.Conv1d(in_channels, out_channels, kernel_size=1)
        
        # Output projection to produce a single value per sample
        self.proj = nn.Sequential(
            nn.Conv1d(out_channels, 1, kernel_size=1),
            nn.AdaptiveAvgPool1d(1),  # Reduce width to 1 (global average pooling)
            nn.Sigmoid()  # Ensures output in [0, 1]
        )

    def forward(self, x):
        B, C, W = x.shape  # [Batch, Channels, Width]
        
        # Compute Q/K/V (all [B, out_channels, W])
        q = self.query(x)
        k = self.key(x)
        v = self.value(x)
        
        # Dot product attention
        attn = torch.bmm(q.transpose(1, 2), k)  # [B, W, W]
        attn = F.softmax(attn / (W ** 0.5), dim=-1)  # Scaled softmax
        
        # Apply attention to values
        out = torch.bmm(v, attn.transpose(1, 2))  # [B, out_channels, W]
        
        # Project to [B, 1, 1] and squeeze to [B, 1]
        out = self.proj(out)  # [B, 1, 1]
        return out.squeeze(-1)  # [B, 1]

Als erstes definieren wir die Klasse als Unterklasse von PyTorchs „nn.module“. Dadurch kann es als neuronales Netzmodul mit automatischer Parameterverwaltung und GPU-Unterstützung verwendet werden. Dann initialisieren wir das Modul mit Parametern für Eingangskanäle, Ausgangskanäle für Aufmerksamkeitsprojektionen und eine Kernel-Größe für Padding-Berechnungen. Diese Parameter bestimmen die Kapazität des Netzes und die Kompatibilität mit den Eingangsdaten. Anschließend berechnen wir die Padding-Größe, um die Länge der Eingabesequenz nach der Faltung beizubehalten, indem wir eine ganzzahlige Division verwenden, um eine symmetrische Auffüllung zu gewährleisten.

Als Nächstes definieren wir drei 1D-Faltungsschichten, die wir verwenden, um die Eingabe in Abfrage-, Schlüssel- und Wertetensoren für den Aufmerksamkeitsmechanismus zu projizieren. Jeder hat einen Kernel der Größe 1 und wirkt als lineare Transformation pro Zeitschritt. Anschließend definieren wir die Pipeline für die Ausgabeprojektion. Sie reduziert den Kanal des Aufmerksamkeitsausgangs auf 1. Sie wendet ein globales Durchschnitts-Pooling an, um die zeitliche Dimension auf einen einzigen Wert zu reduzieren. Schließlich wird die Ausgabe in einen einzelnen Skalar im Bereich [0, 1] umgewandelt. 

Nach der Definition dieses „Klassenkopfes“ können wir nun die Vorwärtsfunktion beschreiben. Das erste, was wir im Forward tun, ist die Anwendung der Abfrage-, Schlüssel- und Wertfaltungsschichten auf den Eingabetensor „x“, der die Form „[B, C, W]“ hat, wodurch drei Tensoren der Form [B, out_channels, W] entstehen. Anschließend berechnen wir die Punktprodukt-Aufmerksamkeitsbewertungen, indem wir eine Batch-Matrix-Multiplikation („bmm“) zwischen dem transponierten Abfrage-Tensor (`[B, W, out_channels]`) und dem Schlüssel-Tensor (`[B, out_channels, W]`) durchführen, was eine Aufmerksamkeitsmatrix der Form [B, W, W] ergibt.

Anschließend wird ein skalierter Soft Max auf die Aufmerksamkeitswerte angewendet, indem die Quadratwurzel der Sequenzlänge geteilt wird, um die Gradienten zu stabilisieren. Schließlich normalisieren wir entlang der letzten Dimension, um Aufmerksamkeitsgewichte zu erhalten, die sich auf 1 summieren. Die Ausgabe der Vorwärtsfunktion definieren wir als Nächstes, indem wir eine Stapelmatrixmultiplikation zwischen „v“ („[B, out_channels, W]“) und der transponierten Aufmerksamkeitsmatrix („[B, W, W]“) durchführen, um eine Ausgabeform von „[B, out_channels, W]“ zu erzeugen.

Anschließend wird die Aufmerksamkeitsausgabe durch die Projektionspipeline ('self.proj') geleitet, um einen Tensor der Form '[B, 1, 1]' zu erzeugen. Anschließend wird die letzte Dimension einfach ausgeklammert, sodass die zurückgegebene Ausgabe die Form '[B, 1]' hat.

Tests

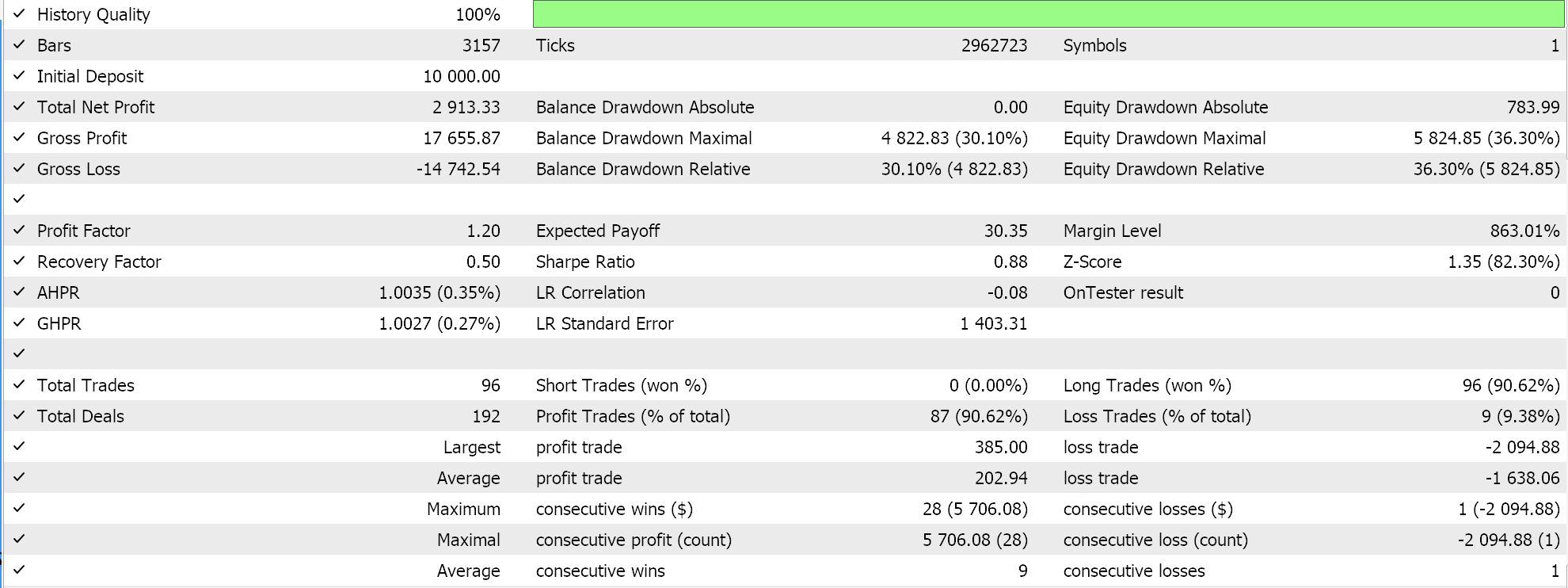
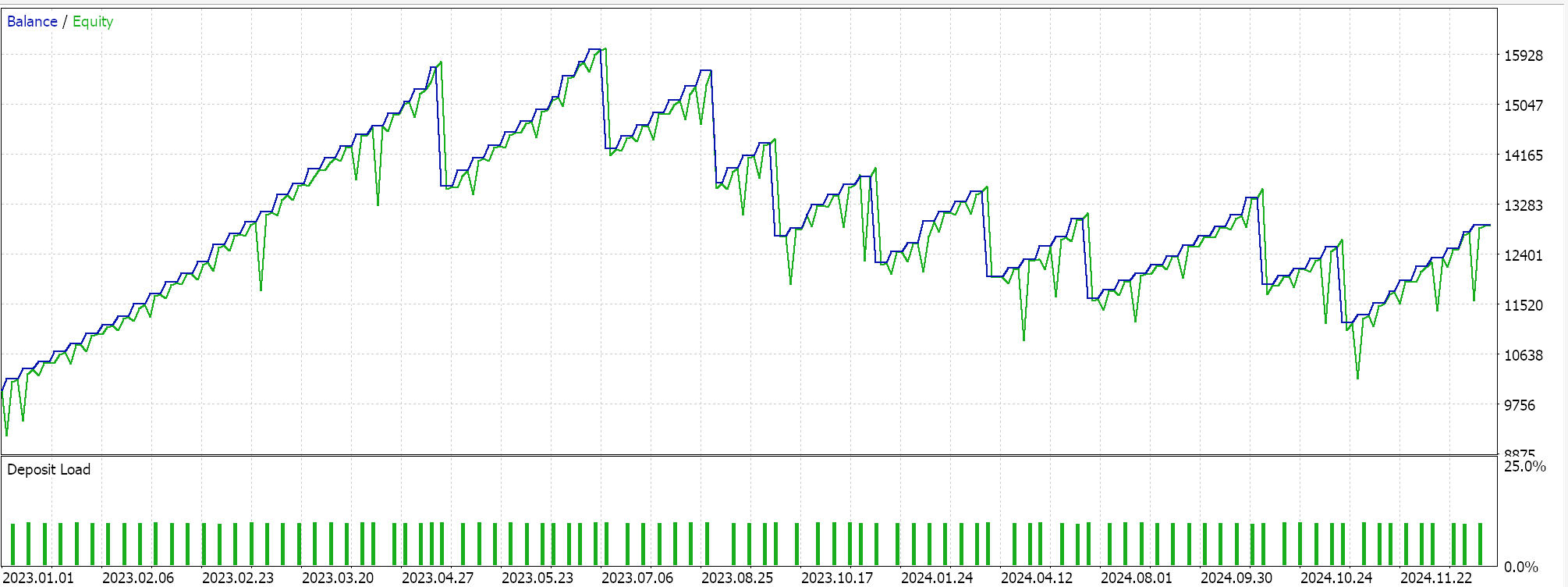
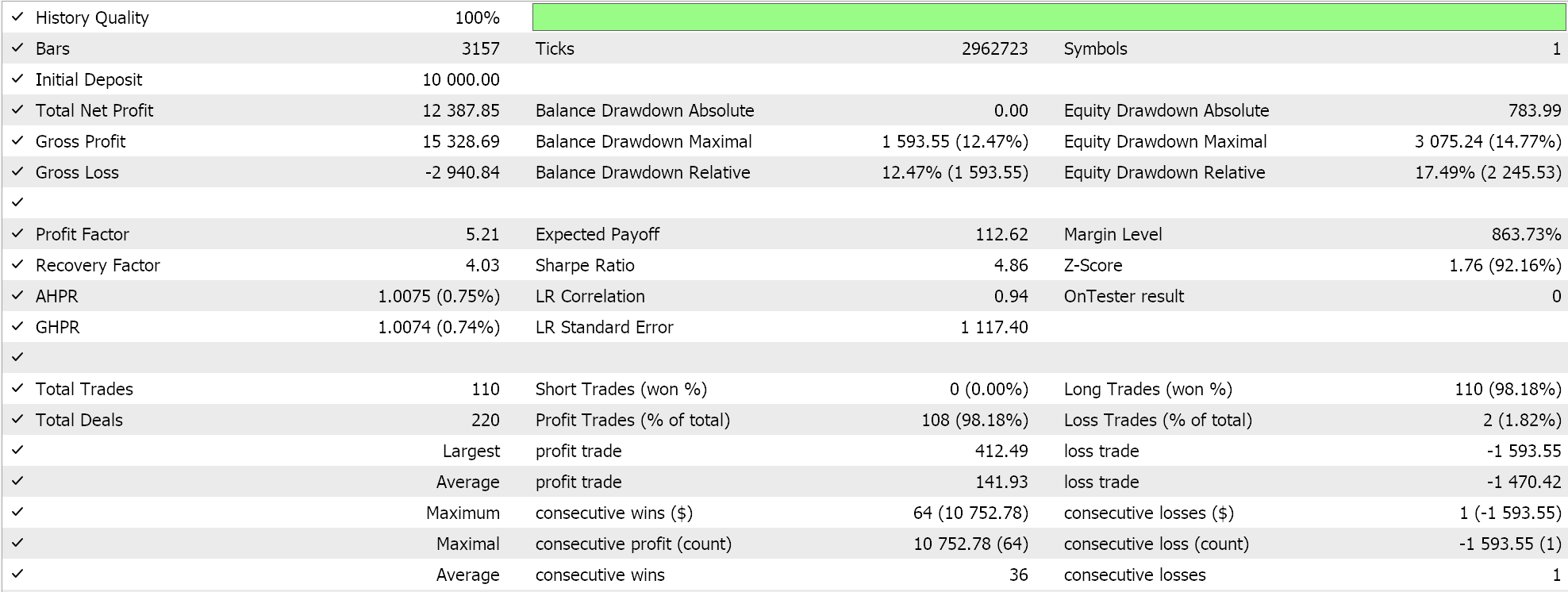
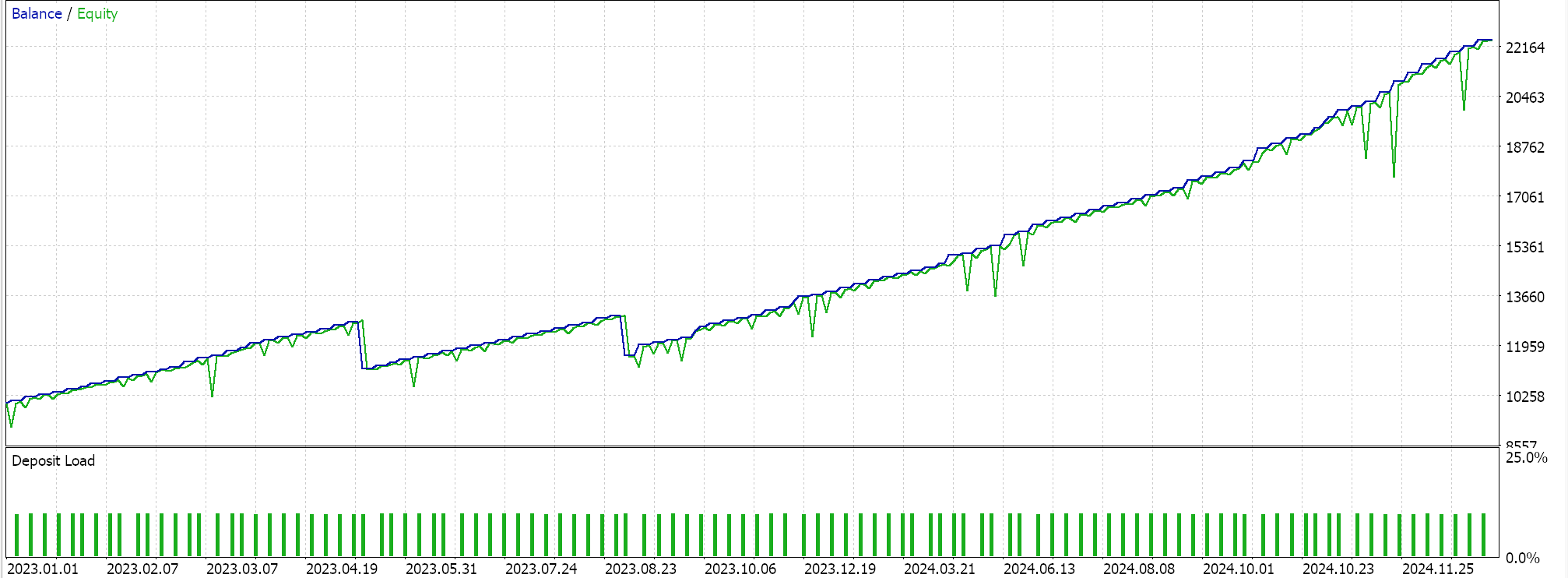
Im Folgenden werden die Ergebnisse der Testläufe für die beiden Merkmalsmuster 6 und 9 vorgestellt. Beide scheinen vorwärts zu gehen, aber wie immer basierte unser Training auf einem sehr begrenzten Datensatz, und daher ist immer ein ausführlicheres Testen seitens des Lesers erforderlich, bevor irgendwelche langfristigen Schlussfolgerungen aus den Testberichten gezogen werden können:

Für Pattern-6.

Für Pattern-9.

Schlussfolgerung

Wir haben gezeigt, wie maschinelles Lernen unter Verwendung eines Produktkerns eingesetzt werden kann, um das vorläufige Potenzial, das sich aus den Signalen des FrAMA-Indikators und des Force-Index-Oszillators ergibt, zu erweitern und möglicherweise zu nutzen. Wir haben nur die beiden Pattern-6 und -9 getestet, was sehr einschränkend ist, aber neben den anderen 8, die wir nicht berücksichtigt haben, gibt es mehrere andere Implementierungen der Paarung von nur diesen beiden Indikatoren, die erforscht werden können.

Name	Beschreibung
wz_66.mq5	Wizard assemblierter Expert Advisor, dessen Header die enthaltenen Dateien anzeigt
SignalWZ_66.mqh	Datei der nutzerdefinierte Signalklassen
66_6.0nnx	Pattern-6 ONNX-Datei
66_9.onnx	Pattern-9 ONNX-Datei