MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 64): Verwendung von Mustern von DeMarker und Envelope-Kanälen mit dem Kernel des weißen Rauschens

Einführung

Wir knüpfen an unseren letzten Artikel an, in dem wir den momentumbasierten DeMarker-Indikator mit den Unterstützungs-/Widerstandsbändern der Envelopes gepaart haben, indem wir untersuchen, wie ihre Signale für das maschinelle Lernen nutzbar gemacht werden können. Wir haben in den letzten Artikeln ähnliche Ansätze zu Indikatorpaaren vorgestellt, und Leser, die eine Einführung suchen, können diese nachlesen. Im Wesentlichen implementieren wir die MQL5-Indikatoren in der Sprache Python, wobei wir Kursdaten verwenden, die mit dem MetaTrader 5 Python-Modul importiert wurden. Mit diesem Modul können Sie sich beim Server Ihres Brokers anmelden und Kursdaten und Symbolinformationen abrufen.

Indikatoren in Python

Python verfügt über eine Vielzahl von Bibliotheken für die technische Analyse, die leicht importiert und zur Implementierung einer Vielzahl von Indikatoren verwendet werden können. Das derzeitige Problem besteht jedoch darin, dass sie nicht alle dem Standard entsprechen und dass bei einigen von ihnen einige Indikatoren fehlen. Zum Beispiel fehlt in der Pandas-Bibliothek für technische Analysen der DeMarker-Oszillator, während er im Modul „ta“ oder „Technische Analyse“ verfügbar ist. Andererseits sind die Envelopes zwar in der Pandas-Bibliothek für technische Analysen vorhanden, aber nicht in der „ta“-Bibliothek in ihrer Rohform. Der Grund dafür ist, dass „ta“ stattdessen die verwandten Indikatoren Bollinger Bands und Donchian Channel anbietet.

Und das Lustige ist, dass die Implementierung eines eigenen Indikators „von Grund auf“ heutzutage genauso wenig Mühe macht (wenn nicht sogar weniger) wie die Installation einer dieser Bibliotheken, um diese Standardfunktionen zu nutzen. Wir implementieren also unsere eigenen Funktionen für DeMarker und Envelopes, was auf dem Papier dazu führen sollte, dass unser Python etwas schneller läuft, da es weniger Modulverweise gibt.

Der DeMarker

Der DeMarker-Indikator ist ein Oszillator, der die Extrema der Kauf- und Verkaufsbedingungen eines Vermögenswerts über einen bestimmten Zeitraum hinweg verfolgt. Wie bereits im letzten Artikel vorgestellt, liegt er zwischen 0 und 1, wobei Werte über 0,7 auf überkaufte Bedingungen hindeuten, während Werte unter 0,3 überverkaufte Bedingungen bedeuten. Wir entscheiden uns dafür, sie als nutzerdefinierte Funktion in Python wie folgt zu implementieren:

def DeMarker(df, period=14):
    """
    Calculate DeMarker indicator for a DataFrame with OHLC prices
    
    Args:
        df: Pandas DataFrame with columns ['open', 'high', 'low', 'close']
        period: Lookback period (default 14)
        
    Returns:
        Pandas Series with DeMarker values
    """
    # Calculate DeMax and DeMin
    demax = df['high'].diff().clip(lower=0)
    demin = -df['low'].diff().clip(upper=0)
    
    # Smooth the values using SMA
    demax_sma = demax.rolling(window=period).mean()
    demin_sma = demin.rolling(window=period).mean()
    
    # Calculate DeMarker
    demarker = demax_sma / (demax_sma + demin_sma)
    return pd.DataFrame({'main': demarker})

Die Eingaben für unsere Funktion sind die Datenrahmen „df“ und „period“. Der Datenrahmen „df“ ist ein Pandas-Datenrahmen, der Eröffnungs-, Höchst-, Tiefst- und Schlusskursdaten enthält, während „period“ der Rückblickzeitraum für die DeMarker-Berechnungen ist. Diese Funktion kapselt die DeMarker-Logik und bietet gleichzeitig Modularität und Wiederverwendbarkeit.

Die Berechnung von DeMax liefert die Differenz der aufeinanderfolgenden Höchstpreise (df['high'].diff()). Wenn die Differenz in diesem Puffer positiv ist, was steigende Höchstwerte bedeuten würde, bleibt sie im Puffer, andernfalls wird der Wert auf Null gesetzt. Diese Einstellung auf Null wird durch die Clip-Funktion (clip(lower=0)) vorgenommen. Ähnlich verhält es sich mit den Differenzen bei den Tiefstpreisen: Wenn die Differenz negativ ist (d. h. der aktuelle Tiefstpreis ist niedriger als der vorherige Tiefstpreis), wird dieser Wert als absoluter Wert im Puffer gespeichert, andernfalls wird er durch Abschneiden (clip(upper=0)) ebenfalls auf Null gesetzt.

Die Verfolgung dieser absoluten Veränderungen ist wichtig, weil DeMax die Preisdynamik nach oben misst, indem es Anstiege bei hohen Preisen feststellt, während DeMin die Preisdynamik nach unten misst, indem es Rückgänge bei niedrigen Preisen festhält. Diese beiden Metriken sind für DeMarker von zentraler Bedeutung, da sie bestimmen, wie stark sich der Preis im Vergleich zu früheren Zeiträumen bewegt. In Python muss bei der Implementierung der Funktion diff() unbedingt sichergestellt werden, dass der Eingabedatenrahmen genügend Datenpunkte enthält und dass die erste Zeile immer einen NaN-Wert hat.

Danach werden die Werte in jedem Puffer geglättet. Durch die Glättung wird das Rauschen in den einzelnen Reihen reduziert und die Indikatorwerte reagieren weniger empfindlich auf kurzfristige Preisschwankungen. Die Methode rolling(window=period).mean() berechnet den Durchschnitt über den angegebenen Zeitraum, was zu einer Verzögerung führt, die oft mit dem Zweck des Indikators, Makrotrends zu identifizieren, übereinstimmt. Die ersten der period-1 Werte sind NaN, da die Daten für das rollierende Fenster nicht ausreichen, und sollten durch Weglassen oder Auffüllen mit normalisierten Werten behandelt werden. Die Wahl der Zeitspanne wirkt sich auch auf die Empfindlichkeit des DeMarkers aus, wobei eine kürzere Zeitspanne ihn empfindlicher macht.

Wir berechnen dann den DeMarker-Wert, indem wir den DeMax-Mittelwert durch seinen Wert plus den DeMin-Mittelwert teilen. Durch diesen Schritt wird DeMarker auf den Bereich 0 bis 1 normalisiert, was die Interpretation erleichtert. Das Verhältnis misst die relative Stärke der Aufwärtsbewegungen im Verhältnis zu den gesamten Kursbewegungen, d. h. sowohl Aufwärts- als auch Abwärtsbewegungen. Werte nahe bei 1 deuten auf ein starkes Aufwärtsmomentum hin, während Werte nahe bei 0 ein stärkeres Abwärtsmomentum bedeuten.

Bei der Umsetzung ist darauf zu achten, dass bei diesem Schritt keine Division durch Null erfolgt. Dies ist jedoch ein seltenes Ereignis, da sich die Preise ständig ändern, insbesondere bei den Höchst- und Tiefstständen. Die Funktion gibt dann die DeMarker-Werte als Pandas-Data-Frame mit einer einzigen Spalte zurück, die wir als „main“ bezeichnen wollen. Das Format des Datenrahmens gewährleistet die Kompatibilität mit anderen auf Pandas basierenden Analysetools und ermöglicht die einfache Integration in ein größeres Handelssystem.

Die Envelopes

Die Envelopes sind ein Unterstützungs-/Widerstandsindikator, der zwei Bänder, ein oberes und ein unteres Band, um einen gleitenden Durchschnitt des Preises darstellt. Die Bänder sind um einen festen Abweichungsbetrag in Prozent versetzt, was Händlern helfen kann, Näherungswerte für Bereiche der Unterstützung und des Widerstands zu erhalten, wenn der Preis diese Bänder berührt. Unsere Python-Implementierung sieht folgendermaßen aus:

def Envelopes(df, period=14, deviation=0.1):
    """
    Calculate Price Envelopes for a DataFrame with OHLC prices
    
    Args:
        df: Pandas DataFrame with columns ['open', 'high', 'low', 'close']
        period: MA period (default 20)
        deviation: Percentage deviation from MA (default 0.05 for 5%)
        
    Returns:
        DataFrame with columns ['upper', 'ma', 'lower']
    """
    # Calculate moving average (typically using close prices)
    ma = df['close'].rolling(window=period).mean()
    
    # Calculate upper and lower envelopes
    upper = ma * (1 + deviation)
    lower = ma * (1 - deviation)
    
    return pd.DataFrame({'upper': upper, 'ma': ma, 'lower': lower})

Unser obiger Code bietet eine flexible Möglichkeit zur Berechnung von Envelopes, mit anpassbaren Perioden und Abweichungs-Eingabeparametern für verschiedene Strategien. Der erste Schritt bei der Berechnung der Envelopes ist die Berechnung des gleitenden Durchschnitts. Wir verwenden einen einfachen gleitenden Durchschnitt der Schlusskurse über die eingegebene Periodenlänge. Der MA fungiert als Mittellinie der Envelopes und des mittleren Preises des Trends. Die Pufferberechnung rolling(window=period).mean() gibt einen Vektor/Puffer mit Mittelwerten zurück, wobei die ersten period-1 Werte erwartungsgemäß ein NaN sind. Diese sollten angemessen behandelt werden.

Anschließend berechnen wir die Pufferwerte des oberen und unteren Bandes. Die Berechnungen für des oberen Envelopes wird durch Multiplikation des MA mit (1 + Abweichung) durchgeführt. Beträgt unsere Abweichung beispielsweise 10 %, dann liegt die obere Bandbreite bei 110 % des MA. Da unser Standardwert für die Abweichung 0,1 beträgt, entspricht dies 10 %. Die Berechnungen für den unteren Envelope ergeben sich aus der Multiplikation des MA mit (1 - Abweichung), was in unserem Fall 90% entspricht.

Das obere und das untere Band legen die Preisspanne fest, innerhalb derer sich der Preis unter „normalen“ Bedingungen bewegen dürfte. Wenn die Kurse eines der beiden Bänder berühren, ergeben sich Szenarien für einen Ausbruch oder eine Umkehrung, da wir diese Bänder als unsere Unterstützungs- und Widerstandsniveaus betrachten. Diese beiden Situationen deuten auf Trendfortsetzungen oder überkaufte/überverkaufte Oszillationen des Marktes hin.

Der Parameter deviation (Abweichung) steuert die Breite der Envelopes. Eine höhere prozentuale Abweichung bedeutet breitere Bandbreiten, die für volatile Vermögenswerte geeignet sein können, während eine geringere Abweichung ein viel engeres Band für stabile Vermögenswerte schafft. Diese Abweichung sollte positiv sein, um ungültige Banden zu vermeiden. Diese Envelopes sind symmetrisch bezüglich des MA, wobei eine gleiche Volatilität oberhalb und unterhalb des Trends angenommen wird. Bei asymmetrischen Bändern kann stattdessen das Bollinger-Band verwendet werden.

Der zurückgegebene Pandas-Datenrahmen enthält 3 Spalten mit „upper“, „lower“ und „ma“. Dieses Datenrahmenformat ermöglicht einen einfachen Zugriff auf alle drei Komponenten und damit die Visualisierung, Signalerzeugung oder weitere Analyse.

Funktionen in Python

Was wir als Features bezeichnen, sind vektorisierte Darstellungen der Signale der beiden Indikatoren DeMarker und Envelopes. Diese Merkmale dienen dann als Eingaben für unser maschinelles Lernmodell, ein rekurrentes neuronales Netz, das einen Kernel mit weißem Rauschen verwendet (mehr dazu später). Diese Implementierung des maschinellen Lernens in Python baut auf den Funktionen auf, die wir uns im letzten Artikel angesehen haben und die insgesamt 10 sind. Von diesen 10 waren nur 6 in der Lage, den Vorwärtstest zu bestehen. 0,1,5,6,7 und 8. Dies sind also die Merkmale, die wir mit unserem rekurrenten, neuronalen Netz (RNN) testen werden. Wir müssen sie daher von Hand in Python codieren, bevor wir sie in das RNN einspeisen.

Feature-0

Wie wir im letzten Artikel gesehen haben, erzeugt Feature-0, auch bekannt als Pattern-0, Signale, die darauf basieren, dass der DeMarker die überkauften oder überverkauften Schwellenwerte überschreitet und der Kurs gleichzeitig die oberen oder unteren Bänder der Envelopes durchquert. Wir implementieren dies daher in Python wie folgt

def feature_0(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] <= 0.3) &
                     (price_df['close'] > env_df['lower']) &
                     (price_df['close'].shift(1) <= env_df['lower'].shift(1)) &
                     (price_df['close'].shift(2) >= env_df['lower'].shift(2))).astype(int)
    feature[:, 1] = ((dem_df['main'] >= 0.7) &
                     (price_df['close'] < env_df['upper']) &
                     (price_df['close'].shift(1) >= env_df['upper'].shift(1)) &
                     (price_df['close'].shift(2) <= env_df['upper'].shift(2))).astype(int)
    
    # Set first 2 rows to 0 (no previous values to compare)
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Unsere erste Codezeile in der Funktion erstellt ein mit Nullen gefülltes NumPy-Array mit der Form (len(dem_df), 2), das kategorisch Auf- und Abwärtssignale speichert. Er initialisiert das Array und stellt sicher, dass alle Zeilen standardmäßig auf Null stehen. Die Größe des Arrays muss mit der Länge des Datenrahmens übereinstimmen, um einen Indexversatz zu vermeiden.

Der Index für den Aufwärts-Check liegt bei 0 und wird zuerst geprüft. Wie im letzten Artikel dargelegt, ergibt sich aus unserer obigen Implementierung ein Aufwärtssignal, wenn sich der DeMarker im überverkauften Bereich befindet (typischerweise unter 0,3), der aktuelle Schlusskurs über der unteren Envelope liegt, der vorherige Schlusskurs bei oder unter dem unteren Envelope lag und der Schlusskurs vor zwei Perioden bei oder über der unteren Envelope lag.

Diese Prüfung der Aufwärtsbedingung kombiniert die überverkaufte DeMarker-Bedingung mit einem Kursausbruch über der untere Envelope, was auf eine mögliche Trendfortsetzung oder -umkehr hindeutet. Die Shift-1- und Shift-2-Bedingungen stellen sicher, dass der Preis mit dem unteren Envelope, dem Prior, wie im letzten Artikel definiert, interagiert hat. In der Praxis können einige zusätzliche Maßnahmen hinzugefügt werden. Diese können mehrere Perioden umfassen, um Fehlanzeigen zu reduzieren, indem ein bestimmtes Preismuster verlangt wird. Außerdem werden durch die Überprüfung von env_df['lower'] und price_df['close'] auf NaNs ungültige Vergleiche vermieden.

Die Abwärtsspalte kennzeichnet ein Signal als generiert, wenn sich der DeMarker im überkauften Bereich befindet, der aktuelle Schlusskurs unter der oberen Envelope liegt, der vorherige Schlusskurs bei oder über der oberen Envelope lag und der Schlusskurs vor zwei Perioden bei oder unter dem oberen Envelope lag. Dieses Muster erfasst potenzielle Umkehrungen oder Rückschläge nach einem überkauften Zustand. Bei der Nutzung sollte eine ausreichende Datenhistorie für den Schichtbetrieb gewährleistet sein.

Zu diesem Zweck setzen wir die anfänglichen Zeilenwerte für die ersten 2 Werte auf Null. Das liegt daran, dass wir die Werte von shift-1 und shift-2 verwenden.

Die return-Anweisung gibt das NumPy-Array zurück, das unsere Signalmuster enthält. So entsteht ein Format, das sich für die Eingabe in unser RNN eignet. Die Interaktion des mehrperiodigen Envelopes (Shift(1) und Shift(2)) fügt eine zeitliche Bestätigungsebene hinzu, de facto einen oder mehrere zusätzliche Filter, was sie im Vergleich zu anderen einfachen Signalen, die auf dem Kreuzen beruhen, einzigartiger macht.

Feature-1

Dieses Muster erzeugt Signale, wenn sich der DeMarker in den extremen Zonen des überkauften oder überverkauften Bereichs befindet und der Preis für mehrere aufeinander folgende Perioden außerhalb der oberen/unteren Bänder der Envelopes bleibt. Wir implementieren es in Python wie folgt:

def feature_1(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] > 0.7) &
                     (price_df['close'] > env_df['upper']) &
                     (price_df['close'].shift(1) > env_df['upper'].shift(1))).astype(int)
    feature[:, 1] = ((dem_df['main'] < 0.3) &
                     (price_df['close'] < env_df['lower']) &
                     (price_df['close'].shift(1) < env_df['lower'].shift(1))).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

Unser erster Schritt ist, wie bei Feature-0, die Größe des Arrays zu bestimmen und es mit Nullen zu initialisieren. Die Initialisierung impliziert standardmäßig keine Signale, was besser ist als ein NaN. Als Nächstes legen wir die Werte für jeden Index fest. Für den ersten Index bzw. die erste Spalte prüfen wir, ob eine Aufwärtstrend vorliegt. Unser Code prüft, ob sich DeMarker im überkauften Bereich (>0,7) befindet, der aktuelle Schlusskurs über dem oberen Envelope liegt und der vorherige Schlusskurs ebenfalls über dem oberen Envelope lag. 

Dies ist wichtig, weil es ein starkes Aufwärtsmomentum in Situationen identifiziert, in denen der Preis trotz eines überkauften DeMarkers über der oberen Envelope gehalten wird. Wie im letzten Artikel dargelegt, deutet dies eher auf eine Trendfortsetzung als auf eine Trendumkehr hin. Auf dieser Grundlage setzt unser Code dann den nächsten Indexwert fest, der auf Abwärtsbedingungen prüft. Die Auflistung prüft, ob sich der DeMarker im überverkauften Bereich (<0,3) befindet, der aktuelle Schlusskurs unter dem unteren Envelope liegt und der vorherige Schlusskurs ebenfalls unter dem unteren Envelope lag.

Als erwartetes Spiegelbild des Aufwärtssignals erfasst es ein starkes Abwärtsmomentum mit einer anhaltenden Kursbewegung unterhalb dem unteren Envelope. Dies bedeutet eine Fortsetzung des Abwärtstrends, wie auch im letzten Artikel dargelegt. Da wir Verschiebungsvergleiche verwenden, müssen wir die erste Zeile der Werte auf 0 setzen. Wir setzen in diesem Fall nur die erste Zeile, da unsere Vergleichsverschiebung nur für einen Index gilt. Die Return-Anweisung liefert das Signal-Array im NumPy-Format.

Diese Funktion erfasst nachhaltige Kursausbrüche jenseits der Envelopesbänder, die durch extreme DeMarker-Werte bestätigt werden, ein Zeichen für eine starke Trendfortsetzung. Er signalisiert vor allem eine Gelegenheit, sich einem bestehenden Trend anzuschließen, und nicht die Vorwegnahme von Umkehrungen. Es unterscheidet sich von Feature-0, da es sich auf aufeinanderfolgende Perioden außerhalb der Bänder konzentriert, ohne dass ein Crossover-Muster erforderlich ist.

Feature-5

Feature-5 ist das nächste der Muster, die im letzten Artikel weiterlaufen konnten. Ähnlich wie unsere beiden obigen Funktionen bezieht es seine Signale aus den DeMarker-Extremwerten, verwendet jedoch die Richtung der Envelopesbänder, anstatt sich auf die Preisinteraktion mit den Bändern zu konzentrieren. Wir implementieren es in Python wie folgt:

def feature_5(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] > 0.7) &
                     (env_df['upper'] > env_df['upper'].shift(1))).astype(int)
    feature[:, 1] = ((dem_df['main'] < 0.3) &
                     (env_df['lower'] < env_df['lower'].shift(1))).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

Wie bei den anderen beiden Funktionen muss zunächst das Ausgabe-Array mit Nullen initialisiert und seine Größe auf 2 gesetzt werden. Dies wird durch die erste Zeile des Codes in unserer obigen Funktion erfüllt. Anschließend wird der erste Indexwert festgelegt, der wie bei den anderen Merkmalen auf eine Aufwärtstrend hin überprüft wird.  Die Voraussetzung dafür ist relativ einfach: Wenn der DeMarker überkauft ist (>0,7) und der obere Envelope ansteigt, dann haben wir ein Aufwärtssignal. Als Nächstes legen wir den zweiten Indexwert fest, der auf einen Abwärtstrend hin überprüft. Wie nicht anders zu erwarten, deuten ein DeMarker unter 0,3 und ein rückläufiger unterer Bereich der Envelopes auf ein rückläufiges Signal hin. Dann setzen wir, wie erwartet, die Werte der ersten Zeile auf Null, um ungültige Vergleiche durch das NaN zu vermeiden, das aus dem Verschiebungsvergleich resultiert.

Feature-6

Feature-6 oder Pattern-6, wie im letzten Artikel vorgestellt, generiert Signale, die auf Veränderungen des DeMarker-Momentums und der Preiswellenformationen auf den Bändern des Envelopesindikators basieren. Wir implementieren dies in Python wie folgt:

def feature_6(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] > dem_df['main'].shift(1)) &
                     (price_df['low'].shift(1) <= env_df['lower'].shift(1)) &
                     (price_df['low'].shift(2) >= env_df['lower'].shift(2)) &
                     (price_df['low'].shift(3) <= env_df['lower'].shift(3)) &
                     (price_df['low'].shift(4) >= env_df['lower'].shift(4))).astype(int)
    feature[:, 1] = ((dem_df['main'] < dem_df['main'].shift(1)) &
                     (price_df['high'].shift(1) >= env_df['upper'].shift(1)) &
                     (price_df['high'].shift(2) <= env_df['upper'].shift(2)) &
                     (price_df['high'].shift(3) >= env_df['upper'].shift(3)) &
                     (price_df['high'].shift(4) <= env_df['upper'].shift(4))).astype(int)
    
    # Set first 4 rows to 0 (no previous values to compare)
    feature[0, :] = 0
    feature[1, :] = 0
    feature[2, :] = 0
    feature[3, :] = 0
    
    return feature

Das Initialisierungsprotokoll ähnelt dem, was wir bereits oben betrachtet haben, wobei die Unterschiede erwartungsgemäß in den eingestellten Array-Werten liegen. Für den ersten Index, der den Aufwärtstrend prüft, wird 1 (gleichbedeutend mit true) vergeben, wenn die Kaufbedingung erfüllt ist. Diese Bedingung ist ein steigender DeMarker in Verbindung mit einem engen Preismuster in Bezug zum unteren Envelope über vier vorhergehende abwechselnde Perioden von unten und oben. Der zweite Index prüft, ob ein Abwärtstrend vorliegt, indem er feststellt, ob der DeMarker abnimmt, und zwar genau wie die Aufwärtsbestätigung eines M-Schlusskursmusters am oberen Band.

Als Nächstes werden die Anfangszeilen auf Null gesetzt, um ungültige Indikatorvergleiche zu vermeiden. Ungültige Vergleiche würden durchgeführt, wenn keine Zuweisung von Nullen erfolgt, da diese Werte standardmäßig NaNs sind, wobei NaNs aus der Verwendung von Verschiebungsvergleichen resultieren. Unsere Nullzuweisung erstreckt sich also über 4 Zeilen von 0 bis 3, da wir für die Indizes 1 bis 4 Shift verwendet haben.

Feature-7

Diese Funktion generiert, wie im letzten Artikel dargelegt, Signale auf der Grundlage von DeMarker-Werten mit unterschiedlichen Zeitverzögerungen und Preisüberschneidungen der Envelopesbänder. Dies lenkt den Blick auf Schwungverschiebungen. Wir implementieren dies in Python wie folgt:

def feature_7(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:DEM(X()) >= 0.5 && DEM(X() + 2) <= 0.3 && Close(X()) > ENV_UP(X()) && Close(X() + 1) <= ENV_UP(X() + 1)
    feature[:, 0] = ((dem_df['main'] >= 0.5) &
                     (dem_df['main'].shift(2) <= 0.3) &
                     (price_df['close'] >= env_df['upper']) &
                     (price_df['close'].shift(1) <= env_df['upper'].shift(1))).astype(int)
    feature[:, 1] = ((dem_df['main'] <= 0.5) &
                     (dem_df['main'].shift(2) >= 0.8) &
                     (price_df['close'] <= env_df['lower']) &
                     (price_df['close'].shift(1) >= env_df['lower'].shift(1))).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

Bei der Initialisierung wird die Größe auf 2 gesetzt und mit Nullen aufgefüllt, wobei der erste Index dann zur Prüfung auf ein langes Signal verwendet wird. Unser Code kennzeichnet einen Aufwärtstrend als wahr, wenn der aktuelle DeMarker neutral ist oder steigt ist (>=0,5); und der DeMarker vor zwei Perioden überverkauft war (<=0,3); und der aktuelle Schlusskurs an oder unter dem oberen Envelope liegt. Diese langwierigen Anforderungen sind dazu gedacht, den Wechsel von überverkauften zu neutralen oder Aufwärtsbedingungen zu erfassen, der durch einen Ausbruch über den oberen Envelope bestätigt wird. Dies deutet in der Regel auf eine starke Umkehr oder eine Trendeinleitung hin. Die Shift(2)-Bedingung führt eine Verzögerung ein, die eine aktuelle überverkaufte Situation erfordert. 

Die Abwärtsbedingung bei Index 1 ist erfüllt, wenn der aktuelle DeMarker neutral bis fallend ist (<= 0,5); und der DeMarker vor zwei Perioden überkauft war (>=0,8); und der aktuelle Schlusskurs an oder unter dem unteren Envelope liegt; und schließlich der vorherige Schlusskurs an oder über der unteren Envelope lag. Abschließend weisen wir nur der ersten Zeile den Wert Null zu, da wir nur einen Verschiebungsindex verwenden.

Feature-8

Unsere letzte Funktion liefert Signale, wenn DeMarker sich in extremen Zonen befindet und der Tiefst- bzw. Höchststand des Preises deutlich außerhalb der Envelopesbänder liegt, was extreme Preisbewegungen bedeutet. Wir implementieren es in Python wie folgt:

def feature_8(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:DEM(X()) > 0.7 && Low(X()) > ENV_UP(X())
    feature[:, 0] = ((dem_df['main'] > 0.7) &
                     (price_df['low'] > env_df['upper'])).astype(int)
    feature[:, 1] = ((dem_df['main'] < 0.3) &
                     (price_df['high'] < env_df['lower'])).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    # feature[0, :] = 0
    
    return feature

Zunächst wird das NumPy-Ausgangsarray mit Nullen initialisiert und auf 2 verkleinert, dann wird der Wert für den Index 0 festgelegt. Dieser Index, wie auch alle anderen oben genannten Muster, zeigt an, ob er steigt. In diesem Fall liegt ein Aufwärtssignal vor, wenn der DeMarker überkauft ist (>0,7) und der aktuelle Tiefstkurs über dem oberen Envelope liegt. Dieses Muster deutet in der Regel auf eine starke Aufwärtsbewegung hin, da der niedrigste Kurs der Periode den oberen Envelope übersteigt. Dies deutet in der Regel auf eine erhebliche Aufwärtsdynamik hin.

Der Abwärts-Check, der dem Index 1 zugeordnet wird, wird bestätigt, wenn der DeMarker überverkauft ist (<0,3) und das aktuelle Hoch unter dem unteren Envelope liegt. Diese beiden Szenarien sind selten, aber bei unseren Tests im letzten Artikel konnten wir ein paar Handelsgeschäfte finden. In Live-Situationen kann jedoch aufgrund der Seltenheit ein zusätzlicher Bestätigungsfilter zur Sicherheit eingesetzt werden.

RNN in Python

Unser rekurrentes neuronales Netz (RNN), das die vektorisierten Indikatorausgaben von den Merkmalen 0, 1, 5, 6, 7 und 8 empfängt, ist ein neuronales Netzmodul von PyTorch, das ein Standard-RNN mit einem Mechanismus zur Rauschinjektion kombiniert, um die Robustheit zu erhöhen oder stochastische Prozesse zu modellieren. Sie ist auf Regressionsaufgaben zugeschnitten und erzeugt einen einzigen Ausgabewert pro Eingabesequenz. Diese Rauschinjektion wird auf die versteckten Zustände des RNN angewandt, moduliert durch eine Projektionsschicht und eine sigmoidale und eine sigmoidale Aktivierung, um die Auswirkungen zu kontrollieren.

Die Eingabe für dieses RNN ist ein Tensor der Form (batch_size, input_size). Das Design besteht aus einer RNN-Schicht, gefolgt von einer linearen Projektion für das Rauschen und einer abschließenden, vollständig verbundenen Schicht für die Ausgabe. Das Hinzufügen des Rauschens erfolgt mit Hilfe eines Kernels aus weißem Rauschen in die verborgenen Zustände des RNN. Dies kann on-the-fly geschehen oder als vorberechneter Tensor bereitgestellt werden. Die Ausgabe ist ein einzelner Regressionswert für jede Sequenz und seine Form ist (batch_size). Dies wird in Python wie folgt umgesetzt:

# Define the network as a class
class WhiteNoiseRNN(nn.Module):
    def __init__(self, input_size=5, hidden_size=64, num_layers=1):
        super().__init__()
        self.hidden_size = hidden_size
        self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True)
        self.noise_proj = nn.Linear(hidden_size, hidden_size)  # Projects noise to hidden space
        self.fc = nn.Linear(hidden_size, 1)  # Single output for regression
        
    def forward(self, x, noise_std=0.05):
        """
        Args:
            x: Input tensor of shape (batch_size, seq_len, input_size)
            noise_std: Either:
                - float: Standard deviation for generated noise
                - tensor: Pre-computed noise (must match rnn_out shape: batch_size × seq_len × hidden_size)
        """
        # Ensure proper input dimensions
        if x.dim() == 2:
            x = x.unsqueeze(1)  # (batch, features) → (batch, 1, features)
            
        # RNN processing
        rnn_out, _ = self.rnn(x)  # (batch_size, seq_len, hidden_size)
        
        # Noise injection
        if isinstance(noise_std, torch.Tensor):
            noise_std = noise_std.float()
            if noise_std.dim() == 1:
                noise_std = noise_std.view(-1, 1, 1)  # (batch,) → (batch, 1, 1)
            noise = noise_std.expand_as(rnn_out)
        elif noise_std > 0:
            noise = torch.randn_like(rnn_out) * noise_std
        else:
            noise = 0
            
        if isinstance(noise, torch.Tensor):
            projected_noise = self.noise_proj(noise)
            rnn_out = rnn_out + torch.sigmoid(rnn_out) * projected_noise
            
        return self.fc(rnn_out[:, -1, :])  # (batch_size,)

Aus der obigen Auflistung geht hervor, dass die Klasse WhiteNoiseRNN als Unterklasse von nn.Module definiert ist und mit den drei Eingabeparametern Eingabegröße, Größe der verborgenen Schicht und Anzahl der Schichten initialisiert wird. In diesem Schritt werden die Netzarchitektur und die Hyperparameter festgelegt.

Durch die Vererbung von nn.Module können die Autograd- und Modellverwaltungsfunktionen von PyTorch, z. B. für Training und Auswertung, einfach genutzt werden. Die Wahl der Eingabegröße wird durch die Merkmalsdimensionalität der Eingabedaten bestimmt. In unserem Fall haben alle Features 2 Dimensionen, also wird dieser Wert 2 sein.

Die verborgene Größe legt die Kapazität des Modells fest. Größere Werte erhöhen die Aussagekraft des Modells, bergen aber die Gefahr einer Überanpassung und eines erhöhten Rechenaufwands. Für die meisten einfachen Aufgaben oder Probleme reicht es aus, die Anzahl der Ebenen auf 1 zu setzen, eine Erhöhung dieses Wertes führt jedoch zu Problemen mit verschwindenden Gradienten.

Wir rufen die Initialisierung super() auf, um die übergeordnete Klasse, das nn.Module, aufzurufen und die ordnungsgemäße Einrichtung der PyTorch-Modulfunktionalität, wie z. B. die Parameterverfolgung und die Geräteverwaltung, sicherzustellen. Durch die Aufnahme dieses Aufrufs in die Regel lassen sich viele Initialisierungsfehler vermeiden. Der Parameter für die verborgene Größe wird als Instanzvariable für die mögliche Verwendung in anderen Methoden gespeichert.

Wir initialisieren die Klassenvariable rnn als eine RNN-Schicht mit der angegebenen Eingabegröße, versteckten Größe und Anzahl der Schichten. Wenn Sie den Parameter batch-first auf true setzen, wird sichergestellt, dass die Eingabe- und Ausgabetensoren Formen haben, die die Größe der verarbeiteten Charge als erste Dimension innerhalb der Form annehmen. Dann definieren wir eine Projektionsschicht für das Rauschen, um Rauschen in die gleiche Dimensionalität zu projizieren wie die versteckten Zustände des RNN. Dadurch kann das Rauschen transformiert werden, sei es durch Skalierung oder Drehung usw., bevor es den verborgenen Zuständen hinzugefügt wird, sodass die Rauschinjektion lernfähig ist. Dies verbessert die Fähigkeit des Modells, sich während des Trainings an die Lärmbelastung anzupassen. Die lineare Schicht fügt Parameter hinzu, die die Komplexität des Modells erhöhen, sodass ein ausreichendes Training erforderlich ist.

Dann definieren wir eine vollständig verbundene Schicht, um den endgültigen versteckten Zustand des RNN auf einen einzigen Ausgabewert abzubilden. Das Ergebnis ist die Regressionsausgabe, die die Dimensionalität des verborgenen Zustands auf einen einzigen Skalar reduziert. Dies ist für die Aufgabe des Modells von entscheidender Bedeutung, insbesondere dann, wenn es um die Vorhersage eines kontinuierlichen Wertes geht, wie es in unserem Fall der Fall ist.

Die Vorwärtsmethode definiert einen Vorwärtsdurchlauf des Netzes, bei dem die Eingabe x verarbeitet und Rauschen mit einer Standardabweichung noise_std angewendet wird. Diese Funktion implementiert die Kernberechnung, die Kombination, die RNN-Verarbeitung, die Rauschinjektion und die Ausgabevorhersage. Es ist immer wichtig, sicherzustellen, dass x vor der Eingabe richtig geformt und vorverarbeitet wird. Der Standardwert noise_std von 0,05 ist ein Hyperparameter, der auf der Grundlage des gewünschten Rauschpegels angepasst werden muss. Bei Verwendung von vorberechnetem Rauschen sollten dessen Form und Typ überprüft werden, um Laufzeitfehler zu vermeiden.

Die erste Aktion in der Vorwärtsfunktion besteht darin, x durch Hinzufügen einer Sequenzlänge der Dimension 1 umzuformen. Dies gewährleistet die Kompatibilität mit dem RNN, das auch bei Eingaben in Einzelschritten eine Sequenzdimension erwartet. Es macht das Modell auch flexibel für ein- und mehrstufige Eingaben.

Als Nächstes verarbeiten wir das RNN, indem wir x, die Eingabe, durch das RNN leiten, um versteckte Zustände für jeden Zeitschritt zu erzeugen. Die Ergebnisse sind zweifach. Erstens erhalten wir rnn_out, einen Tensor, der die verborgenen Zustände enthält; zweitens erhalten wir _, den verborgenen Zustand der letzten Schicht, den wir in diesem Fall ignorieren, weil wir ihn nicht verwenden. Diese Verarbeitung ist von entscheidender Bedeutung, da das RNN zeitliche Abhängigkeiten in der Eingabesequenz erfasst und damit das Rückgrat der sequentiellen Verarbeitung des Modells bildet. Diese verborgenen Zustände sind die primären Mechanismen für die Rauschinjektion und die Leistungsprognose.

Danach wird mit der vorberechneten Rauschbehandlung fortgefahren, die in der oberen if-Klausel überprüft wird. Wir konvertieren den Tensor in Float, um die Konsistenz zu gewährleisten, formen die 1D-Tensoren für die Übertragung um und erweitern das Rauschen, damit es der Form von rnn_out entspricht. Wenn das Rauschen erzeugt wird, können wir die verborgenen Zustände mit Zufälligkeit versehen und sie so robuster gegenüber dem stochastischen Modellierungsprozess machen. Das Rauschen wird durch noise_std skaliert, wodurch seine Stärke kontrolliert wird. Andernfalls, wenn es kein Rauschen gibt und noise_std gleich Null oder negativ ist, wird noise ebenfalls mit Null bewertet. Dies ermöglicht es dem Modell, ohne Rauschen zu arbeiten, was für deterministische Prognosen oder bei der Fehlersuche konstruktiv sein kann.

Nach der Zuweisung des Rauschwerts projizieren wir das Rauschen durch die lineare Schicht noise_proj, um es an den verborgenen Zustandsraum anzupassen. Dadurch wird die Auswirkung des Rauschens mit Hilfe des Sigmoid der RNN-Ausgabe moduliert und zu den versteckten Zuständen hinzugefügt. Wie bereits erwähnt, macht diese lineare Projektion die Rauschinjektion lernfähig, sodass das Modell die Wirkung des Rauschens während des Trainings anpassen kann. Der Term torch.sigmoid(rnn_out) skaliert das Rauschen zwischen 0 und 1, um sicherzustellen, dass es die verborgenen Zustände nicht überwältigt. Dieser Ansatz, so wird argumentiert, erhöht die Robustheit durch die Einführung kontrollierter Stochastik, die eine Überanpassung verhindern kann.

Dann wählen wir den versteckten Zustand des letzten Zeitschritts aus und leiten ihn durch die vollständig verknüpfte Schicht, um eine einzige Ausgabe pro Sequenz zu erzeugen. Der verborgene Zustand des letzten Zeitschritts fasst die Informationen aus der Sequenz zusammen, was sich für Regressionsaufgaben eignet. Die fc-Schicht bildet den verborgenen Zustand auf die gewünschte Ausgabe ab.

Tests

Nachdem wir unser Netzwerk definiert haben, führen wir Tests mit den sechs Mustern durch, die wir im letzten Artikel durchlaufen haben: 0, 1, 5, 6, 7 und 8. Vor dem letzten Artikel hatten wir uns mit Netzwerk-Inputs beschäftigt, die länger waren, weil sie die Indikatorsignale nicht um eine Auf- oder Abwärtsbedingung koppelten.

Wir haben das in diesem Artikel nicht getan, da alle Muster eindeutig einen Aufwärts- und einen Abwärtsprüfindex haben. Dies könnte erklären, warum wir im letzten Artikel auch einen höheren Prozentsatz an Vorwärtsbewegungen hatten als im vorherigen, wo wir dies nicht befolgten. Wir testen mit GBP USD. Die Trainingsläufe werden für das Jahr 2023 mit dem 4-Stunden-Zeitrahmen in Python durchgeführt. Die Python-Schulung gibt uns Hinweise darauf, ob wir kaufen oder verkaufen sollten.

Da das importierte ONNX-Modell in MetaTrader 5 dann in einem assistentengestützten Expert Advisor verwendet wird, der gewichtete Kauf- und Verkaufsbedingungen verwendet, müssen auch diese Werte optimiert werden, und zwar ebenfalls für das Jahr 2023.

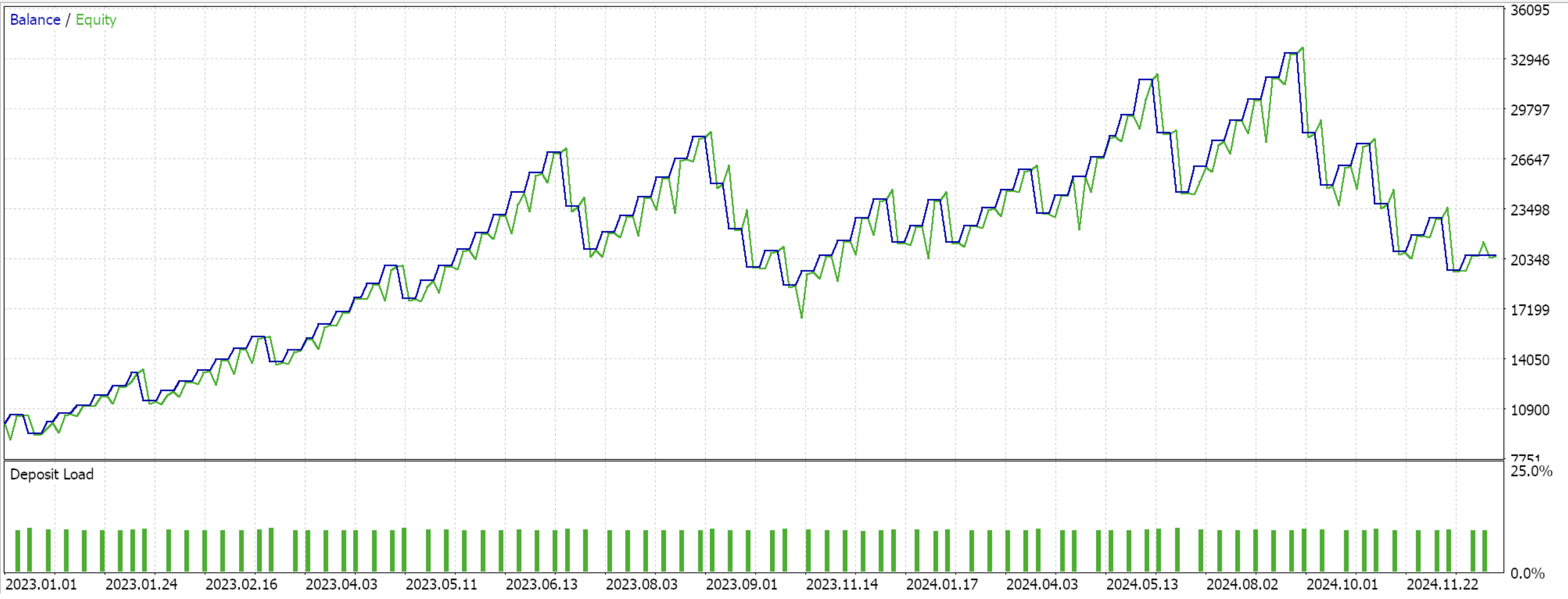
Nach dem Training und der Optimierung führen wir Testläufe vom 2023.01.01 bis 2025.01.01 durch und erhalten die folgenden Ergebnisse für alle 6 Muster/Merkmale:

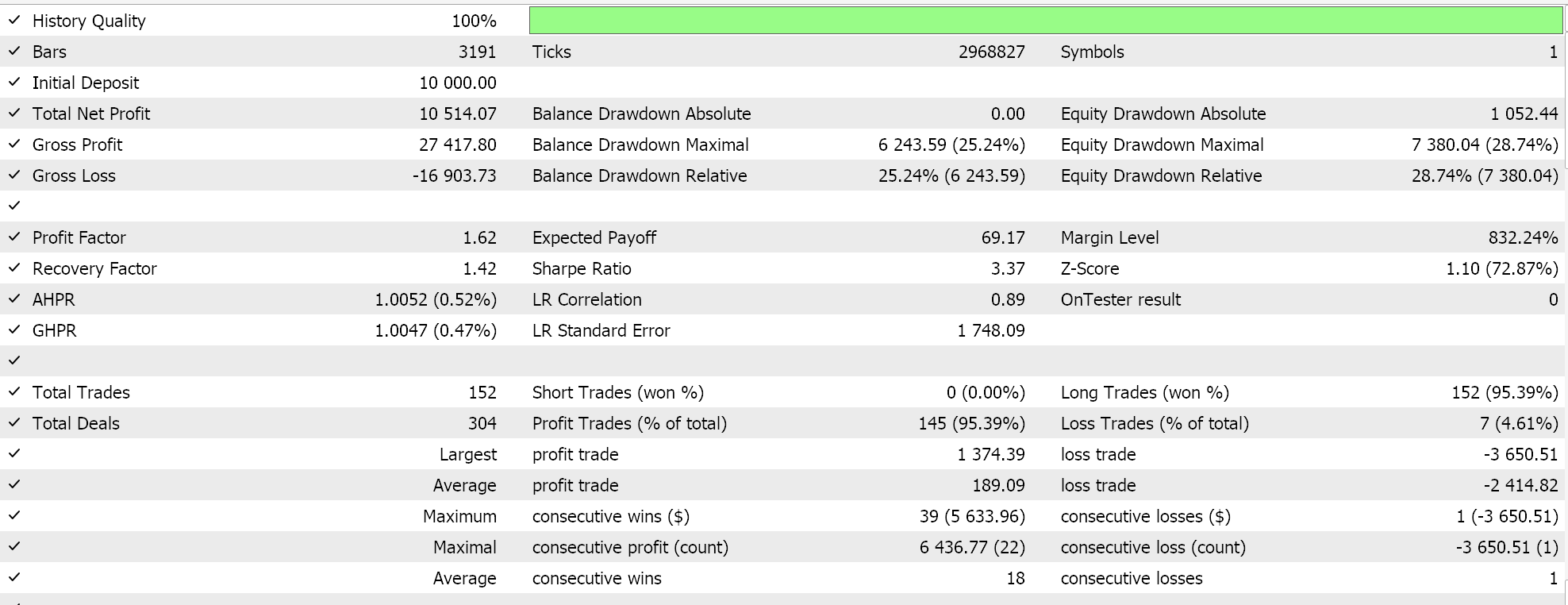
Feature-0 kein Vorwärtstest

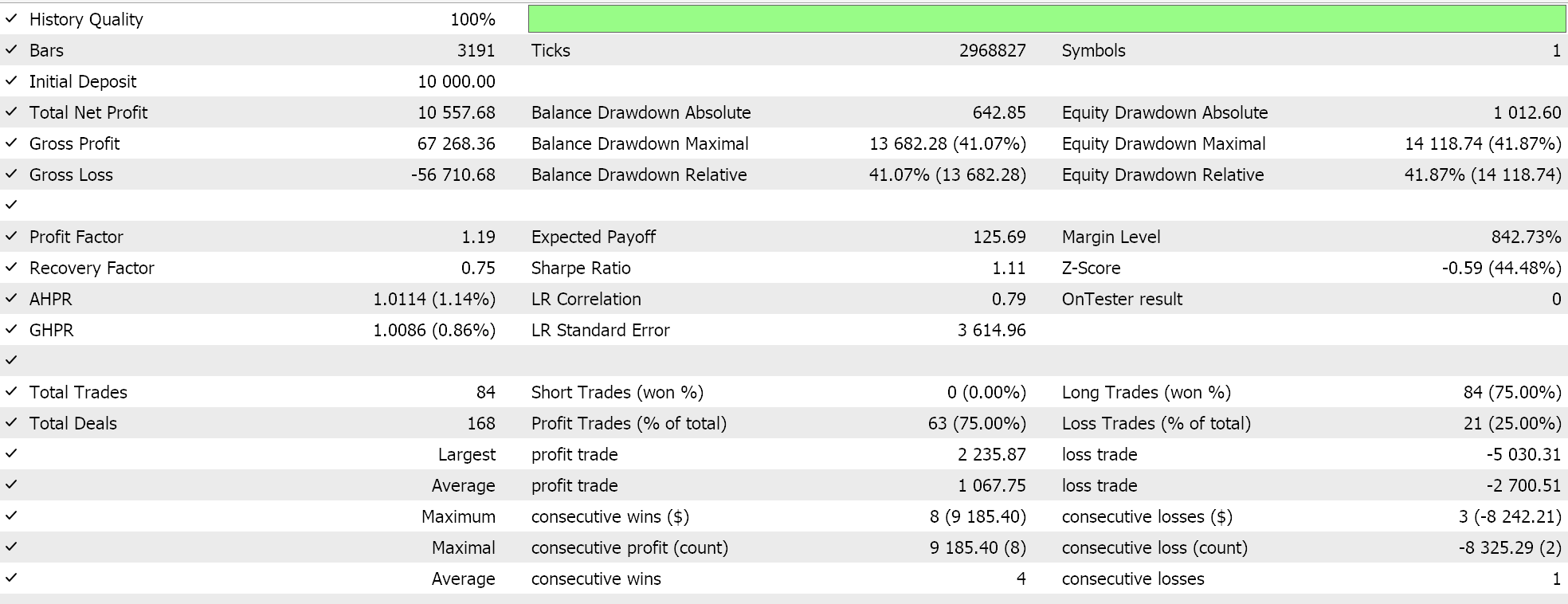
Feature-1 kein Vorwärtstest

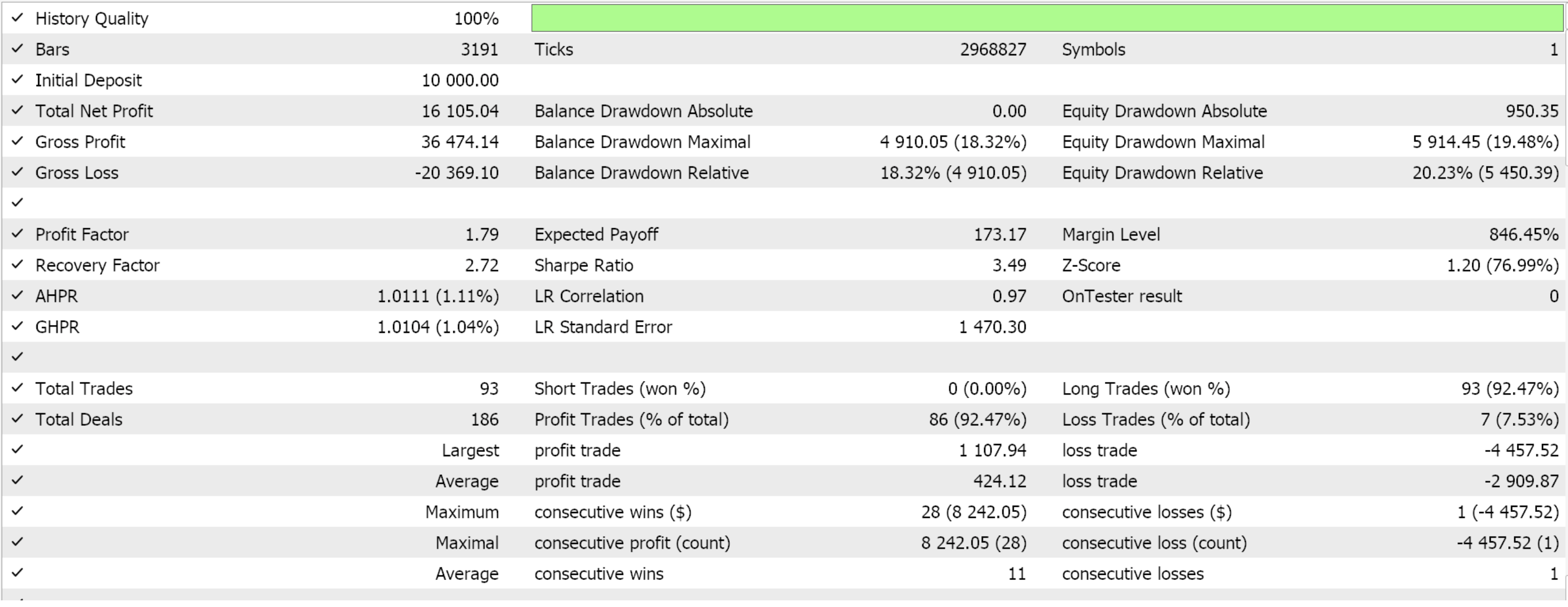
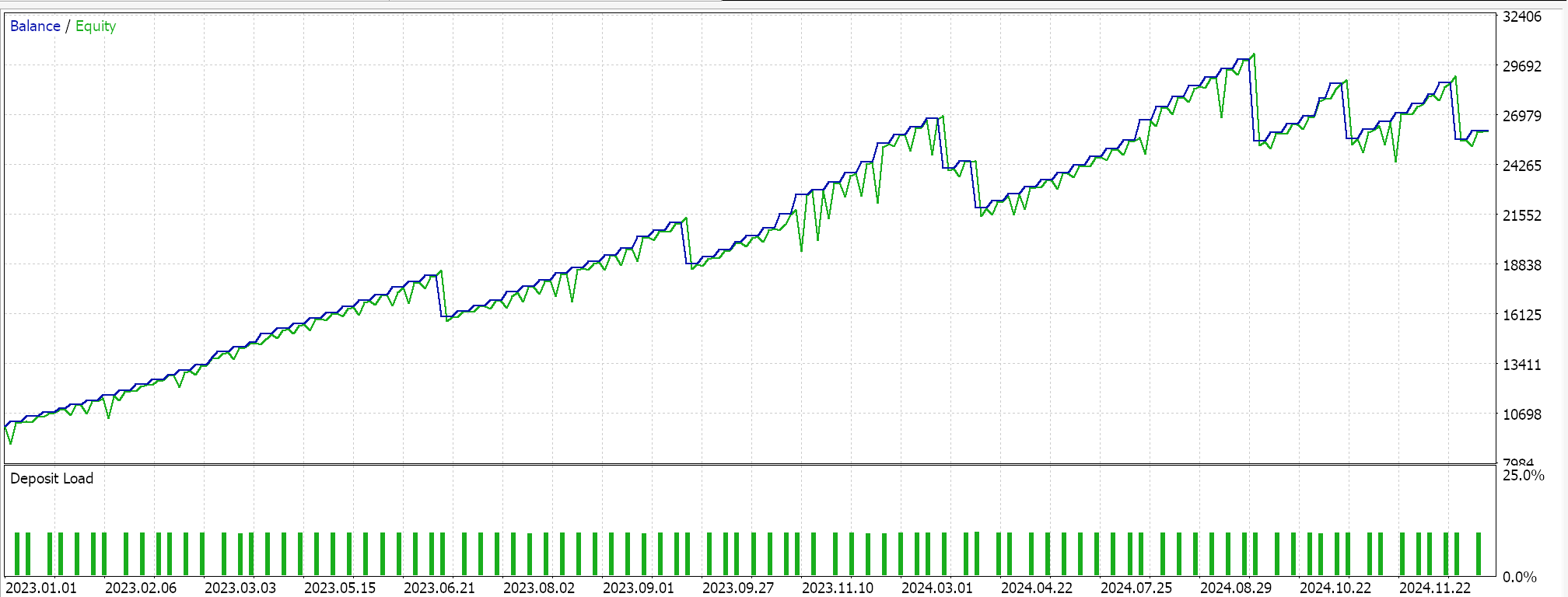
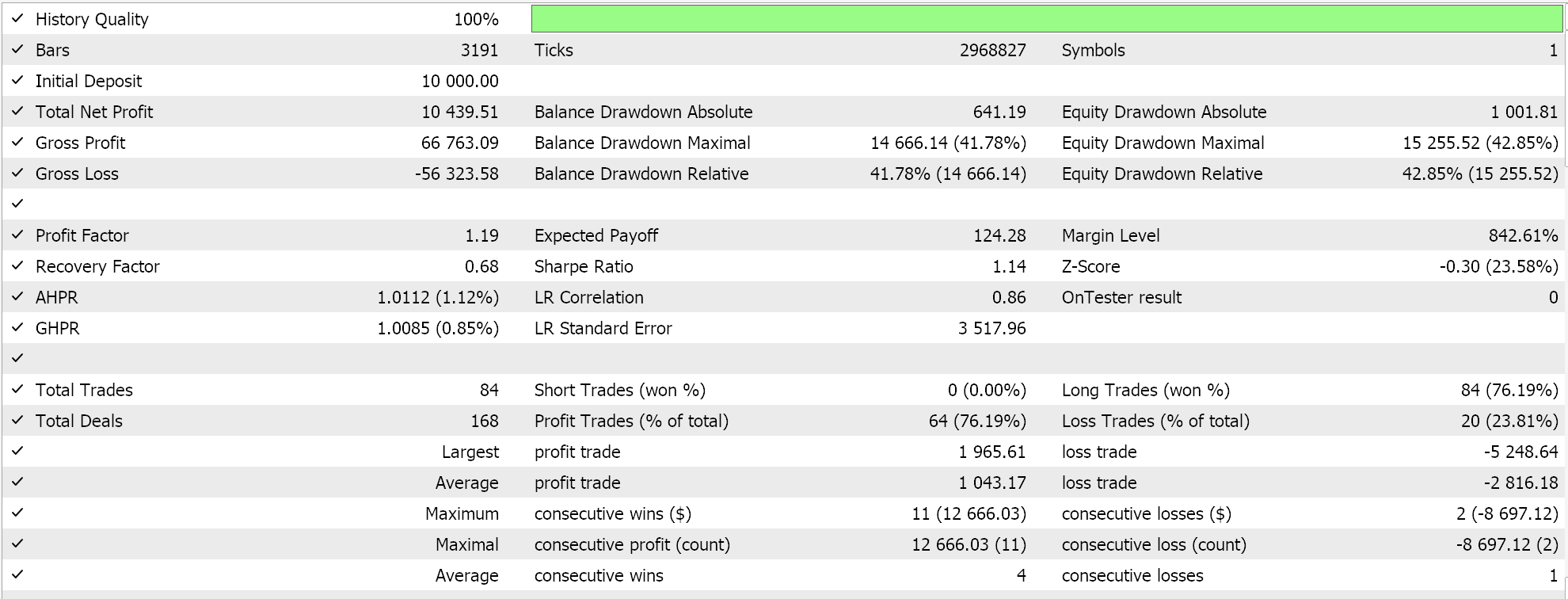
Feature-5 mit Vorwärtstest

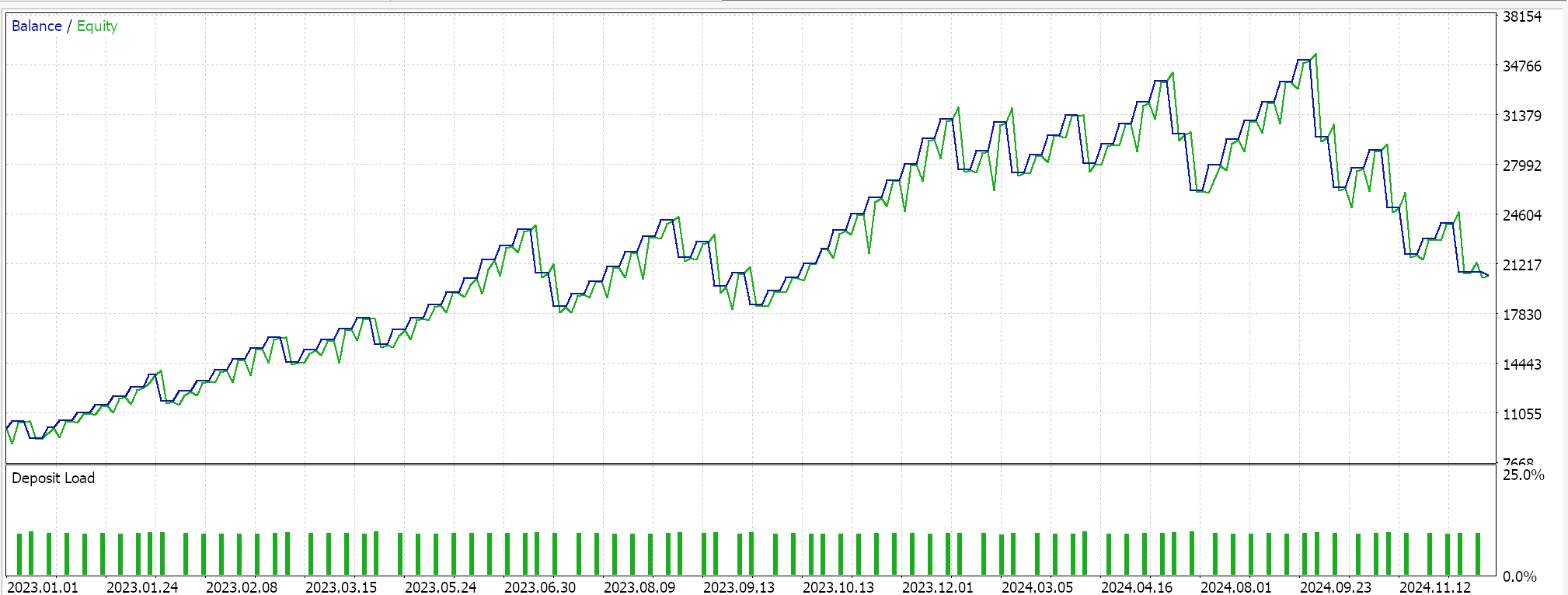
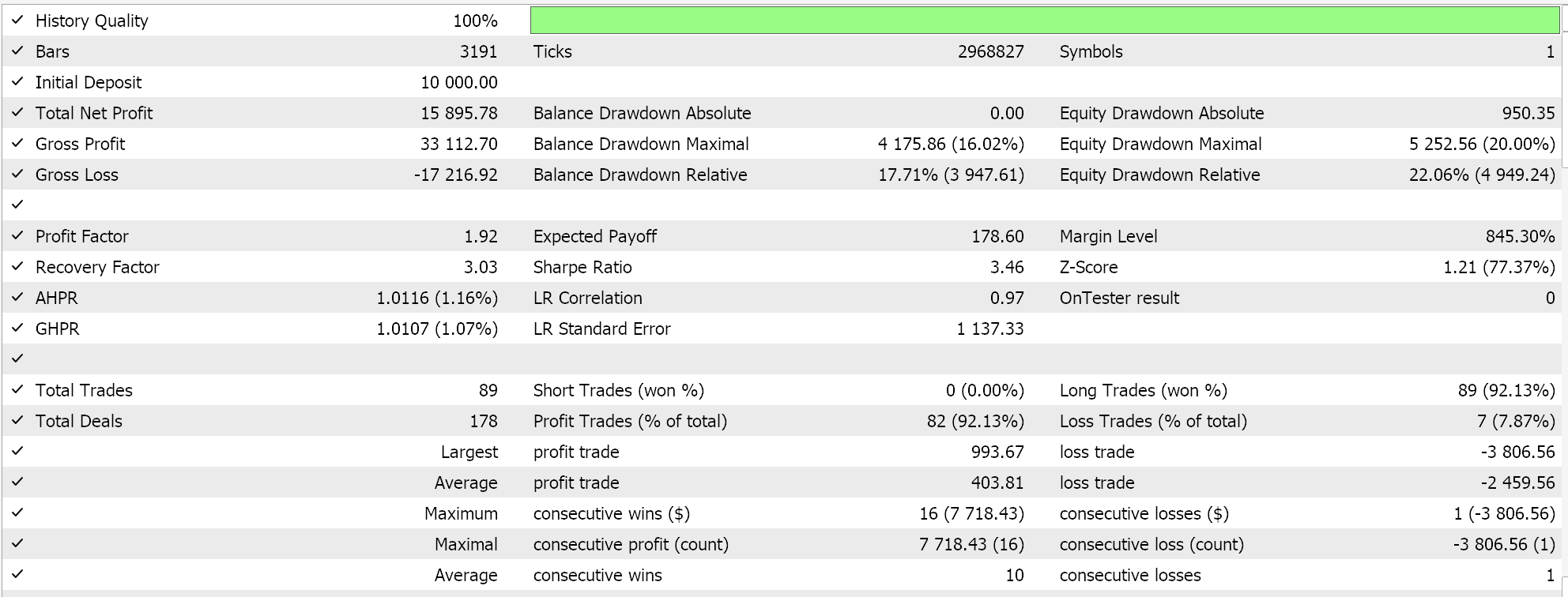
Feature-6 kein Vorwärtstest

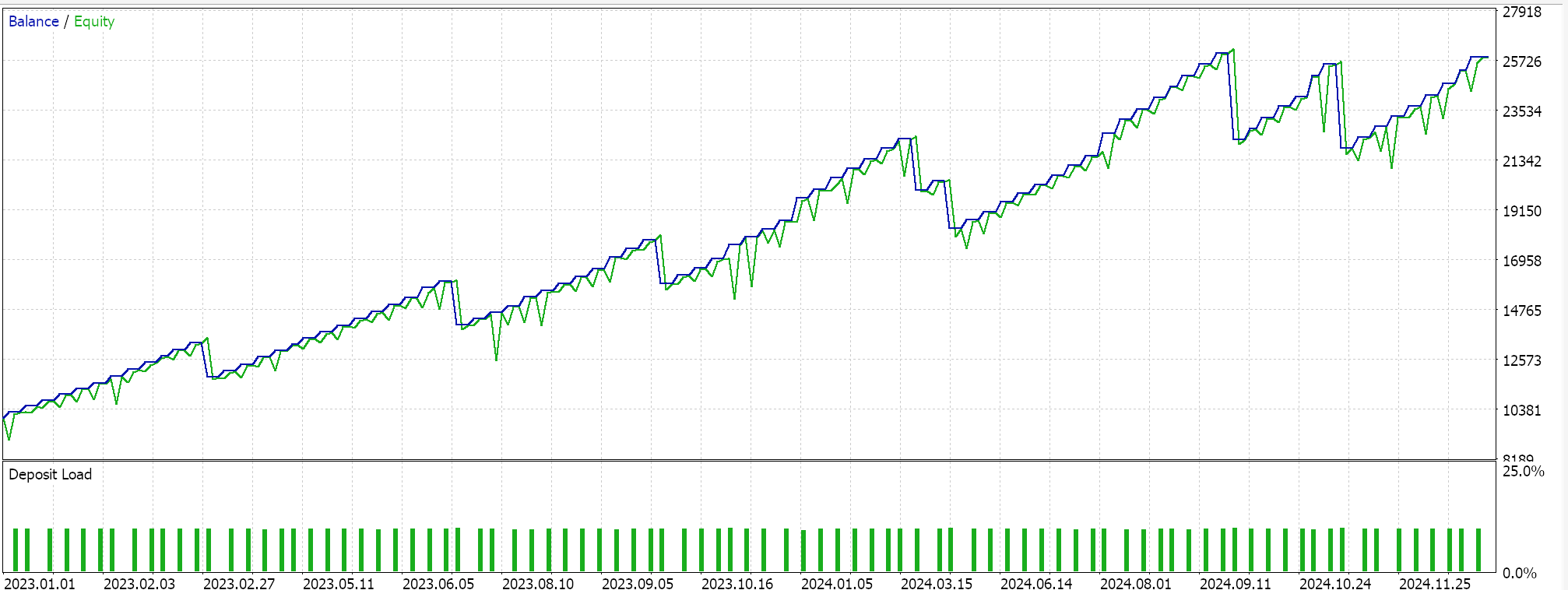
Feature-7 mit Vorwärtstest

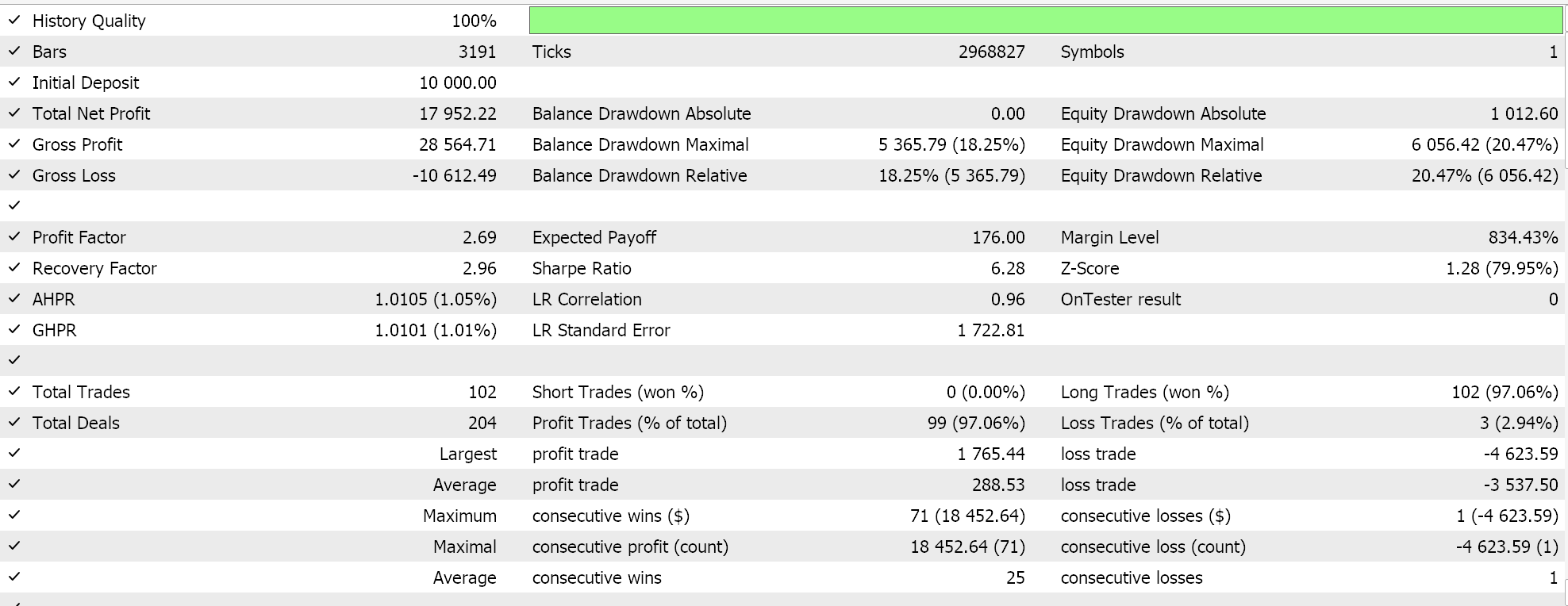
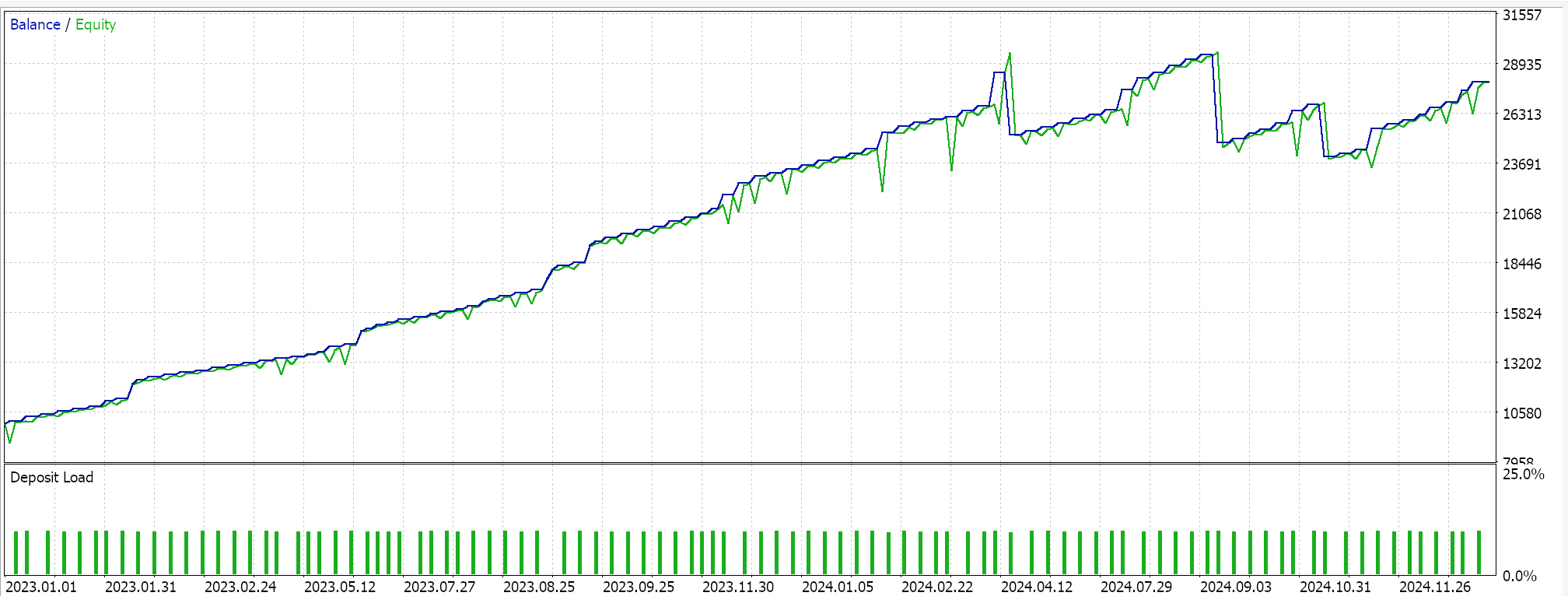
Feature-8 mit Vorwärtstest

Schlussfolgerung

Wir haben Muster untersucht, die sich aus der Kombination der Indikatoren von DeMarker und Envelopes ergeben. Ein Momentum-Oszillator und ein Unterstützungs-/Widerstandsindikator, deren komplementäres Zusammenspiel erstmals im letzten Artikel getestet wurde, wurden im Handel auf Basis von Rohmustern verwendet . In diesem Artikel haben wir diese Muster durch ein rekurrentes neuronales Netz verarbeitet, das beim Training den Kernel des weißen Rauschens verwendet, um die gleichen Indikatormuster zu verarbeiten. Wir müssen noch ein neuronales Netz in Betracht ziehen, das alle Muster zusammenführt, was bei den Rohsignalmustern fiktiv war. Wir könnten dies in den nächsten Artikeln behandeln.

Name	Beschreibung
wz64.mq5	Assistent Assemblierter Expert Advisor, dessen Kopfzeile die verwendeten Dateien anzeigt
SignalWZ_64.mqh	Nutzerdefinierte Signalklassendatei
64_0.onnx	Exportiertes ONNX-Modell für Feature-0
64_1.onnx	Exportierte ONNX für Feature-1
64_5.onnx	“ für Feature-5
64_6.onnx	“ für Feature-6
64_7.onnx	“ für Feature-7
64_8.onnx	' für Feature-8