MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 68): Verwendung von TRIX-Mustern und des Williams Percent Range mit einem Cosinus-Kernel-Netzwerk

Einführung

Von den zehn Signalmustern, die wir im letzten Artikel untersucht haben, waren nur 3 in der Lage, vorwärts zu gehen. Diese Muster wurden aus der Kombination von Indikatorsignalen des TRIX, einem Trendindikator, und des Williams Percent Range (WPR), einem Unterstützungs-/Widerstandsoszillator, generiert. Das Training bzw. die Optimierung des Expert Advisors wurde auf ein einziges Jahr, 2023, beschränkt, während der Vorwärtstest im darauffolgenden Jahr, 2024, durchgeführt wurde. Wir haben mit CHF JPY auf dem 4-Stunden-Zeitfenster getestet.

Bei der Erweiterung unserer Muster, die mit maschinellem Lernen vorwärts gehen, verwenden wir in der Regel Python, da es Netzwerke sehr effizient kodiert und trainiert. Das gilt auch ohne GPU. In früheren Artikeln haben wir die Funktionen von Mustern, die in der Lage waren, vorwärts zu gehen, mit Python-Implementierungen eingeleitet. In diesem Artikel werden wir uns mit den Indikator-Implementierungen in Python befassen, vor allem aber mit dem Netzwerk-Setup, das die Indikatorsignale als Eingänge verwendet. Es handelt sich um ein 1-Dim-Faltungsnetz, das den Kosinus-Kernel in seinen Entwürfen verwendet.

Indikatoren in Python

Um Indikatorsignale in Python für unser Netzwerk zu nutzen, können wir einige Python-Code-Bibliotheken verwenden oder sie selbst programmieren. Wir codieren unsere TRIX-Funktion in Python wie folgt:

def TRIX(df: pd.DataFrame, period: int) -> pd.DataFrame:
    """
    Calculate TRIX indicator and append it as 'TRIX' column to the input DataFrame.
    
    Args:
        df (pd.DataFrame): DataFrame with 'close' column
        period (int): Lookback period for EMA calculation
        
    Returns:
        pd.DataFrame: Input DataFrame with new 'TRIX' column
    """
    # Input validation
    if not all(col in df.columns for col in ['close']):
        raise ValueError("DataFrame must contain 'close' column")
    if period < 1:
        raise ValueError("Period must be positive")
        
    # Create a copy to avoid modifying the input DataFrame
    result_df = df.copy()
    
    # Calculate triple EMA
    ema1 = df['close'].ewm(span=period, adjust=False).mean()
    ema2 = ema1.ewm(span=period, adjust=False).mean()
    ema3 = ema2.ewm(span=period, adjust=False).mean()
    
    # Calculate TRIX: percentage rate of change of triple EMA
    result_df['main'] = ema3.pct_change() * 100
    
    return result_df

Der TRIX berechnet die Änderungsrate des dreifach geglätteten EMA. Unsere Eingaben sind ein Pandas-Datenframe mit einer Close-Spalte und einer Integer-Periode für EMA-Berechnungen. Die Ausgabe ist der gleiche Datenrahmen mit einer angehängten Spalte mit den Indikatorwerten. Er wird in erster Linie verwendet, um die Trendrichtung und potenzielle Umkehrungen zu erkennen, indem Kursdaten durch Hervorhebung von Momentumveränderungen geglättet werden.

Unser obiger Code beginnt mit der Definition der Funktion mit Typ-Hinweisen für ihre Eingaben, die Klarheit und Typsicherheit gewährleisten. Dann berechnen wir den ersten EMA auf Basis der Schlusskurse und glätten diese Kursdaten für eine konsistente EMA-Gewichtung. Anschließend berechnen wir den zweiten EMA mit den Daten des ersten EMA, um die Daten weiter zu glätten und das Rauschen zu reduzieren. Dadurch wird der Wert ema2 zugewiesen. Anschließend berechnen wir den dritten EMA und vervollständigen damit den dreifachen Glättungsprozess. Außerdem reagiert TRIX dadurch empfindlich auf Momentumänderungen. Unser Ergebnis ist der ema3-Wert.

Damit fügen wir unserem Pandas-Eingabedatenrahmen eine TRIX-Berechnung hinzu, die als prozentuale Veränderung des dreifachen EMA (ema3) relativ zu seinem vorherigen Wert ausgedrückt wird. Die Multiplikation mit 100 bei diesem Verfahren skaliert das Ergebnis für die Interpretierbarkeit auf den Prozentbereich 0 bis 100. Mit dieser Definition wenden wir uns dann der Williams Percent Range (WPR) zu. Dies wird in Python wie folgt codiert:

def WPR(df: pd.DataFrame, period: int) -> pd.DataFrame:
    """
    Calculate Williams %R indicator and append it as 'WPR' column to the input DataFrame.
    
    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', 'close' columns
        period (int): Lookback period for calculation
        
    Returns:
        pd.DataFrame: Input DataFrame with new 'WPR' column
    """
    # Input validation
    if not all(col in df.columns for col in ['high', 'low', 'close']):
        raise ValueError("DataFrame must contain 'high', 'low', 'close' columns")
    if period < 1:
        raise ValueError("Period must be positive")
        
    # Create a copy to avoid modifying the input DataFrame
    result_df = df.copy()
    
    # Calculate highest high and lowest low over the period
    high_max = df['high'].rolling(window=period).max()
    low_min = df['low'].rolling(window=period).min()
    
    # Calculate Williams %R
    result_df['main'] = ((high_max - df['close']) / (high_max - low_min)) * -100
    
    return result_df

Der WPR ist ein Unterstützungs-/Widerstandsoszillator, der dabei hilft, festzustellen, ob der Kurs überkauft/am Widerstand oder überverkauft/an der Unterstützung ist. Die Eingaben für unsere Funktion zur Berechnung sind ebenfalls ein Pandas-Datenframe, jedoch mit den Spalten Hoch, Tief und Schlusskurs (high, low, close) sowie einer ganzzahligen Periode zur Bestimmung des Rückblickfensters des Indikators. Die Ausgabe ist ebenfalls ein Pandas-Datenframe mit einer angehängten Spalte, die wir als WPR bezeichnen. Sie enthält Werte im Bereich [-100, 0].

Unser Code beginnt mit Typ-Hinweisen für die Eingaben, wie bei TRIX. Wir berechnen dann den höchsten Wert im angegebenen Zeitraum und bilden so eine Obergrenze für die WPR-Berechnung. Dann berechnen wir in ähnlicher Weise den niedrigsten Wert über denselben Zeitraum. Als Nächstes definieren wir den zusätzlichen Puffer, den wir an unseren Pandas-Eingabedatenrahmen anhängen wollen, und der mit „WPR“ bezeichnet wird. Dabei wird die Standard-WPR-Formel verwendet. 

Die Fähigkeit von Python, unsere Berechnungen in Puffer zu packen, ohne dabei ins Schwitzen zu kommen, ist etwas, an das sich Programmierer, die wie ich von C-Sprachen kommen, gewöhnen müssen. Es ist unglaublich.

Für beide Funktionen kann eine zusätzliche Validierung eingeführt werden, da sie davon ausgehen, dass der Eingabedatenrahmen die erforderlichen Spalten und genügend Datenzeilen enthält. Wir verwenden eine Pandas-Implementierung von Daten aus dem MetaTrader 5 Python-Modul. Das Hinzufügen einer Fehlerbehandlung nicht unbedingt für fehlende Spalten, da MetaTrader 5 immer seine Spalten hat, sondern für möglicherweise wenige Datenzeilen kann beide Funktionen verbessern. Darüber hinaus sollte bei großen Datensätzen die Optimierung durch die Vorberechnung von rollenden Fenstern oder die Verwendung von vektorisierten Operationen (wie sie von Pandas implementiert werden) im Vordergrund stehen. Beim Testen kann die Validierung der Ausgaben anhand bekannter Indikatorwerte von Plattformen wie Metatrader ebenfalls zur Gewährleistung der Genauigkeit beitragen.

Vorteile der Verwendung des Cosinus-Kernels für die Conv1D-Architektur

Ein Conv1D-Netz ist ein spezielles neuronales Faltungsnetz, das eindimensionale Faltungsoperationen auf Daten in einer Sequenz anwendet, z. B. auf finanzielle Zeitreihen oder regulären Text. Dabei wendet es Filter an, um über die Eingabedaten zu gleiten und wichtige Muster, Trends oder Motive aus den Eingabedaten zu extrahieren. Das Ergebnis dieser Extraktion reduziert die Dimensionen der Eingabesequenz von Natur aus. Jeder Filter soll jedoch ein bestimmtes/ wichtiges Merkmal der Eingabedaten ausgeben. Das Netz würde Schichten für Faltung, Aktivierung, Pooling und vollständig verbundene Schichten enthalten. Conv1D ist effizient für die Verarbeitung geordneter Daten, die zeitliche oder sequenzielle Unterschiede aufweisen.

Der Kosinuskernel hingegen ist ein Ähnlichkeitsmaß. Es berechnet den Kosinuswinkel zwischen zwei gegebenen Vektoren, indem es quantifiziert, wie sehr sich ihre Richtungen ähneln. Dies geschieht durch Normalisierung des Punktprodukts der beiden Vektoren um ihre Beträge. Die Ausgabewerte reichen von -1, was bedeutet, dass die beiden Vektoren in entgegengesetzte Richtungen weisen, bis zu +1, was bedeutet, dass die beiden Vektoren ausgerichtet sind und in dieselbe Richtung weisen. Diese Ähnlichkeit kann sehr effizient sein, wenn es um hochdimensionale Daten wie Text geht, bei denen die Größenordnung nicht so wichtig ist wie die Ausrichtung.

Die Verwendung eines Kosinus-Kerns bei der Entwicklung einer Conv1D hat einige Vorteile. Erstens bietet sie eine gleichmäßige Variation der Kernelgrößen. Die Kosinusfunktion erzeugt ein gleichmäßiges, oszillierendes Muster für die Kernelgrößen, wodurch das CNN in der Lage ist, Merkmale in unterschiedlichen Maßstäben ohne abrupte Änderungen zu erfassen. Ein weiterer Vorteil ist die adaptive Kanalprogression, da die kosinusbasierte Kanalskalierung eine schrittweise Erhöhung der Anzahl der Filter ermöglicht. Auf diese Weise wird ein Gleichgewicht zwischen Modellkomplexität und Merkmalsextraktionskapazität auf allen Ebenen hergestellt.

Der Kosinus-Kernel ermöglicht auch eine robuste Merkmalsextraktion. Dies liegt an seiner oszillatorischen Natur, die natürliche Muster in mittelwertumkehrenden Zeitreihen wie Finanzzeitreihen nachahmt. Dies kann dem CNN helfen, periodische oder zyklische Muster zu erkennen. Schließlich führt der Kosinus-Kernel aufgrund seiner unterschiedlichen Kernelgrößen und Kanäle einen Regularisierungseffekt ein. Diese „Regulierung“ verringert das Risiko einer Überanpassung, indem sie eine kontrollierte Variabilität in die Architektur einführt.

Die Verwendung eines Kosinus-Kerns mit einem Conv1D erfordert häufig, dass die Eingabedaten ein 3D-Tensor sind, der nach batch_size, input_channels und input_length geformt ist. Da wir univariate Zeitreihen verwenden, ist der Wert unserer Eingabekanäle 1. Eine ausreichende Eingabelänge ermöglicht die einfache Handhabung von Kernelgrößen ohne übermäßige Reduzierung. 

Die wichtigsten Hyperparameter, die für unser Modell abgestimmt werden müssen, sind in diesem Fall fünf. Der erste Punkt sind die base_channels. Idealerweise sollte es sich zunächst um eine kleine Anzahl von etwa 16 bis maximal 32 handeln. Die Anzahl der Schichten, der zweite Parameter, sollte in der Regel im Bereich von 3-5 liegen. Zu viele Schichten führen zum Problem des verschwindenden Gradienten oder zu übermäßigen Berechnungen. Der 3. wichtige Parameter ist die maximale Kernelgröße, die für längere Sequenzen auf 7 oder höher gesetzt werden kann. Es sollte ungerade sein, um eine Symmetrie beim Padding zu erhalten.

Der nächste Parameter ist die Frequenz, mit der die Oszillation der Kernelgrößen und Kanäle gesteuert wird. Ein Wert von 0,5 kennzeichnet die Mäßigung, während Einstellungen im Bereich von 0,1 bis 1,0 vorgenommen werden können, um schnellere bzw. langsamere Schwingungen zu erreichen. Der letzte wichtige Hyperparameter ist die Abbruchrate. Dieser Wert kann im Bereich von 0,2 bis 0,5 eingestellt werden und ist für die Regularisierung wichtig. Höhere Drop-Out-Werte verringern zwar die Überanpassung, beeinträchtigen aber das Ergebnis der Verlustfunktion, da sie Schwierigkeiten hat, ihre ideale Nullgrenze zu erreichen.

Beim Training des Modells können wir Standard-Optimierer wie Adam und einen Lernraten-Scheduler für eine schnellere und genauere Konvergenz verwenden. Auch hier sind eine ausreichende Batch-Normalisierung und Dropout entscheidend, um eine Überanpassung zu verhindern, insbesondere bei der Bearbeitung kleiner Datensätze. Die Ausgabe bei der Verwendung der Kosinusähnlichkeit für die Größe der Schichtkerne sollte idealerweise binär sein, d. h. ein einzelnes Neuron mit sigmoidaler Aktivierung. Die vollständig verknüpften Schichten sollten für andere Aufgaben, wie z. B. Mehrklassen-Klassifikation oder Regression, modifiziert werden. Anwendungsfälle sind idealerweise Zeitreihendaten, bei denen periodische oder oszillierende Muster zu erwarten sind.

Die Verwendung dieses Kerns für die Formung eines CNN hat den Nachteil, dass er nicht für alle Datensätze optimal ist. Tests mit Standard-Conv1D-Architekturen sind wichtig, um sicherzustellen, dass die Leistung gleich ist. Außerdem wird beim Global-Average-Pooling von einer festen Ausgabegröße ausgegangen. Dies eignet sich möglicherweise nicht für Aufgaben, die eine sequenzielle Ausgabe erfordern.

Das Netzwerk

Unser Netzwerk, das die Signale von TRIX und WPR als binären Eingangsvektor aufnimmt, ist ein neuronales Faltungsnetzwerk, das die Kosinusähnlichkeit für die Größe seiner Kernel verwendet, wie oben beschrieben. Wir kodieren das wie folgt:

class CosineConv1D(nn.Module):
    """
    A 1D Convolutional Neural Network with kernel sizes and channels based on cosine functions.
    Outputs a scalar float in [0,1] using sigmoid activation.
    """
    def __init__(self, input_channels: int, base_channels: int, num_layers: int, input_length: int,
                 max_kernel_size: int = 7, frequency: float = 0.5, dropout_rate: float = 0.3):
        super(CosineConv1D, self).__init__()
        
        if input_channels < 1 or base_channels < 1 or num_layers < 1:
            raise ValueError("Input channels, base channels, and num layers must be positive")
        if input_length < 1:
            raise ValueError("Input length must be positive")
        if max_kernel_size < 1:
            raise ValueError("Max kernel size must be positive")
        if not (0 <= dropout_rate < 1):
            raise ValueError("Dropout rate must be between 0 and 1")
        
        self.layers = nn.ModuleList()
        self.input_length = input_length
        current_length = input_length
        
        for i in range(num_layers):
            kernel_size = int(3 + (max_kernel_size - 3) * (1 + np.cos(2 * np.pi * frequency * i)) / 2)
            kernel_size = max(3, min(kernel_size, max_kernel_size))
            channels = int(base_channels * (1 + 0.5 * np.cos(np.pi * i / num_layers)))
            channels = max(base_channels, channels)
            padding = kernel_size // 2
            
            conv_layer = nn.Sequential(
                nn.Conv1d(
                    in_channels=input_channels if i == 0 else self.layers[-1][0].out_channels,
                    out_channels=channels,
                    kernel_size=kernel_size,
                    padding=padding
                ),
                nn.BatchNorm1d(channels),
                nn.ReLU(),
                nn.Dropout(dropout_rate)
            )
            self.layers.append(conv_layer)
            current_length = (current_length - kernel_size + 2 * padding) // 1 + 1
            
        self.global_pool = nn.AdaptiveAvgPool1d(1)
        self.fc = nn.Sequential(
            nn.Linear(channels, 1),
            nn.Sigmoid()
        )
        
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        for layer in self.layers:
            x = layer(x)
        x = self.global_pool(x)
        x = x.squeeze(-1)
        x = self.fc(x)
        return x

    def get_output_length(self) -> int:
        return self.layers[-1][0].out_channels

Als Überblick oder Zusammenfassung dieses Netzwerks verwendet dieses 1D-CNN kosinusmodulierte Kernelgrößen und Kanäle und gibt über eine sigmoidale Aktivierung einen Skalar im Bereich [0,1] aus. Es verwendet ein eigenes PyTorch-Modul, das vom nn-Modul erbt. Diese Architektur, bei der die Kernelgröße und die Anzahl der Kanäle moduliert werden, macht es anpassungsfähig an die Eingabemuster. Die Sigmoid-Aktivierung sorgt dafür, dass die Ausgabe ein wahrscheinlichkeitsförmiger Skalar im Bereich von 0-1 ist.

Die Initialisierung des Netzes ist mit einer Validierung verbunden. Dies gewährleistet gültige Eingabeparameter für die Anzahl der Kanäle, Schichten, Kernelgröße und Dropout-Rate. Dabei wird vor allem geprüft, ob die Eingänge positiv sind und ob die Ausfallrate im Bereich von 0 bis 1 liegt. Dies ist wichtig, um ungültige Konfigurationsfehler zu vermeiden, die zu Laufzeitfehlern oder schlechter Leistung führen können. Durch die Verwendung dieser anpassbaren Parameter wird auch die Flexibilität bei der Netzgestaltung erhöht. 

Bei der Implementierung sollten die Eingangskanäle in der Regel so eingestellt werden, dass sie den Dimensionen der Eingangsdaten entsprechen. Die Basiskanäle werden zur Steuerung der „Modellkapazität“ verwendet, während die Anzahl der Schichten ein Gleichgewicht zwischen der Tiefe und den Berechnungsanforderungen herstellt. Die maximale Kernelgröße und -frequenz kann abgestimmt oder angepasst werden, um die Merkmalsextraktion in jeder Phase des Vorwärtsdurchlaufs zu optimieren.

Nachdem die Initialisierung und Validierung abgeschlossen sind, fahren wir mit der Kernel-Größe und der Kanal-Skalierung fort. Wie bereits oben angedeutet, verwenden wir Kosinusfunktionen, um die Kernelgrößen und Kanalzahlen auf jeder Ebene dynamisch anzupassen. Daher berechnen wir die Kernelgröße und die Anzahl der Kanäle für jede Schicht mithilfe der Kosinusfunktionen. Die Kernelgröße würde zwischen 3 und dem Parameter für die maximale Kernelgröße liegen.  Die Kanäle skalieren vom Basiswert des Parameters Kanäle aufwärts. Sie werden ebenfalls durch die Kosinusfunktion moduliert.

Das alles ist wichtig, weil wir eine dynamische Variation der rezeptiven Felder und der Merkmalskapazität einführen, die es dem Netz ermöglicht, verschiedene Muster zu erfassen. Die Kosinusmodulation sorgt für weiche Übergänge zwischen den Kernen und vermeidet so abrupte Änderungen. Bei der Implementierung stellen wir die Frequenz ein, in der Regel im Bereich von 0,1 bis 1,0, um die Oszillation der Kernelgröße zu kontrollieren. Die Verwendung höherer Basiskanäle eignet sich häufig für komplexere/mehrdimensionale Datensätze. Es ist immer darauf zu achten, dass der Parameter für die maximale Kernelgröße mit der Länge der Eingabedaten übereinstimmt, um übermäßiges Auffüllen zu vermeiden. Damit kommen wir zur Konstruktion der Faltungsschicht. Dies geschieht mit Batch-Normalisierung, ReLU und Dropouts für mehr Robustheit.

Wir bauen jede Schicht als eine Abfolge von 1D-Faltung, Batch-Normalisierung, ReLU-Aktivierung und Dropout auf. Die erste Schicht verwendet Eingabekanäle. Nachfolgende Schichten verwenden die Ausgangskanäle der vorherigen Schicht. Das Auffüllen hilft, die Eingabelänge zu erhalten. Dieser Ansatz ist wichtig, weil jeder dieser Schichtbestandteile eine entscheidende Rolle spielt. Die Faltung dient der Merkmalsextraktion. Die Stapelnormierung wird aus Gründen der Trainingsstabilität hinzugefügt. Die ReLU-Aktivierung hilft bei der Sicherstellung der Nichtlinearität. Und schließlich hilft der Dropout bei der Regularisierung, um eine Überanpassung zu verhindern. Bei der Implementierung kann es eine gute Idee sein, eine Dropout-Rate im Bereich von 0,2 bis 0,5 zu verwenden, um das Risiko der Überanpassung zu kontrollieren. Es ist wichtig, dass die Eingangskanäle mit den Daten übereinstimmen, und das Modul „nn.ModuleList“ kann für die dynamische Verwaltung der Schichten angepasst werden. Danach kümmern wir uns um das globale Pooling und die Ausgabe.

Dabei wird das adaptive Durchschnitts-Pooling angewendet, um die räumliche Dimension auf 1 zu reduzieren. Darauf folgt eine lineare Schicht, die einen einzelnen Ausgang abbildet, und ein Sigmoid, um ihn auf den Bereich von 0 bis 1 zu beschränken. Dies ist wichtig, weil das Pooling die Merkmale in der gesamten Sequenz zusammenfasst und so unabhängig von der Eingabelänge eine Ausgabe mit fester Größe ermöglicht. Die lineare Schicht und das Sigmoid erzeugen einen Skalar für Aufgaben wie die Klassifizierung. In unserem Fall verwenden wir dieses Netz für einen einzigen Ausgang. Wenn dies der Fall ist, sollte man in der Regel sicherstellen, dass die Kanäle der letzten Schicht mit dem Eingang der linearen Schicht übereinstimmen.

Als Nächstes definieren wir unsere Funktion für den Vorwärtsdurchlauf. Diese wichtige Funktion verarbeitet die Eingaben durch Schichten, Pooling und endgültige Umwandlung der Ausgaben. Sie definiert den Vorwärtsdurchlauf des Netzes, der die Eingabe x verarbeitet. Dies geschieht durch Faltungsschichten, globales Pooling, das die räumliche Dimension verkleinert, und schließlich durch die voll verknüpfte Schicht. Die Funktion ist wichtig, weil sie den Datenfluss festlegt. Dadurch wird sichergestellt, dass die korrekten Transformationen von der Eingabe zur Ausgabe durchgeführt werden. Durch das Zusammendrücken der zusätzlichen räumlichen Dimension entfällt die singuläre Dimension aus Gründen der Kompatibilität mit der linearen Ebene. Die Implementierung sollte sicherstellen, dass die Tensorform korrekt ist. Die Fehlersuche bei Formabweichungen kann durch Überprüfung der Ebenenausgaben erfolgen.

Schließlich haben wir eine Funktion zur Kontrolle der Ausgangslänge. Diese Kontrolle gewährleistet die Kompatibilität und kann, wie oben dargelegt, auch zur Fehlersuche verwendet werden. Sie gibt die Anzahl der Ausgangskanäle der letzten Faltungsschicht zurück. Dies liefert wichtige Metadaten über die Ausgabe des Netzwerks, die für nachgelagerte Aufgaben oder die Fehlersuche nützlich sind. Diese Funktion kann auch verwendet werden, um die Kompatibilität mit nachfolgenden Schichten oder Modellen zu überprüfen. Sie ist auch erweiterbar, wenn weitere Metadaten benötigt werden, wie z. B. Daten usw.

Sequenzen und Training

Wir haben auch eine Funktion zum Erstellen von Sequenzen, um Daten für unser Netzwerk vorzubereiten. Diese Funktion dient dazu, Eingabedaten und Beschriftungen zu Sequenzen für die 1D-CNN-Vorverarbeitung aufzubereiten. Dies codieren wir in Python wie folgt:

def create_sequences(data, labels, sequence_length):
    num_samples, num_features = data.shape
    sequences = []
    seq_labels = []
    
    # Ensure labels is 1D
    labels = labels.flatten()
    
    for i in range(num_samples - sequence_length + 1):
        sequences.append(data[i:i+sequence_length].T)  # Transpose to (num_features, sequence_length)
        seq_labels.append(labels[i+sequence_length-1])  # Use label of last sample in sequence
    
    sequences = np.array(sequences)  # Shape: (num_sequences, num_features, sequence_length)
    seq_labels = np.array(seq_labels).reshape(-1, 1)  # Shape: (num_sequences, 1)
    
    return torch.tensor(sequences, dtype=torch.float32), torch.tensor(seq_labels, dtype=torch.float32)

Bei der Erstellung von Sequenzen werden zunächst aus den Eingabedaten, die in der Form [Proben, Merkmale] vorliegen, sowie den jeweiligen Labels diejenigen erstellt, deren Länge dem Eingabeparameter sequence-length entspricht. Diese Daten werden dann so umgewandelt, dass sie dem CNN-Eingabeformat [Merkmale, Sequenzlänge] entsprechen. Die Kennzeichnung stammen aus dem letzten Zeitschritt jeder Sequenz. Dies ist wichtig, weil es die Daten für 1D CNN vorbereitet, indem es sie in zusammenhängende Datentranchen strukturiert, die wir als „Sequenzen“ bezeichnen. Dies entspricht der Kompatibilitätsanforderung mit unserem obigen Netz „CosineConvID“.

Die Zuweisung der Sequenzlänge basiert auf zeitlichen Abhängigkeiten, d. h. auf dem zeitlichen Abstand, in dem Daten, z. B. in einer Zeitreihe, wiederholbare, nachvollziehbare Muster aufweisen. Es muss sichergestellt werden, dass die Anzahl der Merkmale mit der Anzahl der Eingangskanäle übereinstimmt. Der Abgleich der Kennzeichnungen muss auch bei überwachten Aufgaben mit komplexen Datensätzen überprüft werden.

Nachdem die Funktion zum Erstellen von Sequenzen definiert wurde, betrachten wir nun unsere Funktion zum Trainieren und Auswerten. Als erstes werden die Hyperparameter festgelegt. In unserem ersten 4-Code-Zeilen-Abschnitt der Funktion definieren wir die Trainings-Hyperparameter. Was wir einstellen müssen, sind die Stapelgröße für die Ministapelverarbeitung, die Eingabekanäle für lange und kurze Bedingungen, die Sequenzlänge, die Anzahl der Epochen und die Lernrate. Unsere Sequenzlänge ist auf 1 gesetzt, was bedeutet, dass sich die Preisbalken direkt und ohne Verzögerung aufeinander beziehen. Wir gehen daher von interne Musterbeziehungen mit einer Verzögerung von 1 Woche aus. Wir codieren unsere Trainingsfunktion wie folgt:

def train_and_evaluate(x_train, y_train):
    # Hyperparameters
    batch_size = 32
    input_channels = 2  # TRIX and WPR
    sequence_length = 1  # Adjustable based on your needs
    num_epochs = 10
    learning_rate = 0.0005

    # Create sequences
    X_tensor, y_tensor = create_sequences(x_train, y_train, sequence_length)
    num_sequences = X_tensor.shape[0]
    
    # Initialize model
    model = CosineConv1D(
        input_channels=input_channels,
        base_channels=128,
        num_layers=16,
        input_length=sequence_length,
        max_kernel_size=7,
        frequency=0.5,
        dropout_rate=0.03
    )
    
    # Loss and optimizer
    criterion = nn.BCELoss()
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)
    
    # Training loop
    model.train()
    for epoch in range(num_epochs):
        total_loss = 0
        for i in range(0, num_sequences, batch_size):
            batch_X = X_tensor[i:i+batch_size]  # Shape: (batch_size, 2, sequence_length)
            batch_y = y_tensor[i:i+batch_size]
            
            outputs = model(batch_X)
            loss = criterion(outputs, batch_y)
            
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            total_loss += loss.item()
        
        avg_loss = total_loss / (num_sequences // batch_size)
        print(f"Epoch [{epoch+1}/{num_epochs}], Loss: {avg_loss:.4f}")
    
    # Export model to ONNX
    model.eval()
    dummy_input = torch.randn(1, input_channels, sequence_length)
    torch.onnx.export(
        model,
        dummy_input,
        inp_model_name,
        export_params=True,
        opset_version=11,
        do_constant_folding=True,
        input_names=['input'],
        output_names=['output'],
        dynamic_axes={'input': {0: 'batch_size'}, 'output': {0: 'batch_size'}}
    )
    print("\nModel exported to: ", inp_model_name)

    # Load and verify ONNX model
    try:
        onnx_model = onnx.load(inp_model_name)
        onnx.checker.check_model(onnx_model)
        print(f" ONNX model '{inp_model_name}' has been successfully exported and validated!")

        session = ort.InferenceSession(inp_model_name)

        for i in session.get_inputs():
            print(f" Input: {i.name}, Shape: {i.shape}, Type: {i.type}")

        for o in session.get_outputs():
            print(f" Output: {o.name}, Shape: {o.shape}, Type: {o.type}")

    except onnx.onnx_cpp2py_export.checker.ValidationError as e:
        print(f" ONNX model validation failed: {e}")
    except Exception as e:
        print(f" An error occurred: {e}")
        
    
    # Evaluate on a single sample
    with torch.no_grad():
        single_input = X_tensor[0:1]  # Shape: (1, 2, 50)
        scalar_output = model(single_input).squeeze()
        print(f"\nSingle sample input shape: {single_input.shape}")
        print(f"Single sample output shape: {scalar_output.shape}")
        print(f"Single sample output value: {scalar_output.item():.4f}")

Diese Schritte sind wichtig, da die Hyperparameter die Trainingseffizienz, die Modellkapazität und die Konvergenzgeschwindigkeit steuern. Eine kleine Sequenzlänge würde die Eingabe vereinfachen, während die Lernrate die Stabilität der Optimierung beeinträchtigen würde. Oft ist es sinnvoll, eine Stapelgröße zwischen 16 und 64 zu wählen, abhängig von den Speicherbeschränkungen. Der Eingangskanal sollte, wie bereits betont, den Datenmerkmalen entsprechen. Für eine bessere Konvergenz kann auch die Anzahl der Epochen erhöht oder die Lernrate angepasst werden, idealerweise im Bereich von 0,0001 bis 0,001.

Als Nächstes wird in unserer Trainingsfunktion eine Instanz des Modells initialisiert. Wir haben uns für ein solches Modell mit 128 Basiskanälen, 16 Schichten und einer niedrigen Ausfallrate von 0,03 entschieden. Wir trainieren mit einer typischen CPU und nicht mit einer GPU. Diese Konfiguration der Netzarchitektur verarbeitet Eingaben mit Sequenzen der Länge 1 und stellt ein Gleichgewicht zwischen Komplexität und Regularisierung her.

Wir definieren dann den Verlust und den Optimierer. Dabei werden der binäre Kreuzentropieverlust für die binäre Klassifizierung und der Adam-Optimierer mit einer bestimmten Lernrate verwendet. Dies ist von entscheidender Bedeutung, da BCE-Loss für die sigmoide Ausgabe des Modells geeignet ist. Der Adam-Optimierer arbeitet effizient mit adaptiven Lernraten. BCELoss ist ideal für binäre Aufgaben, und in unserem Fall geben wir einen einzelnen Wert im Bereich von 0 bis 1 aus, was analog ist. Es können jedoch auch andere Optimierer in Betracht gezogen werden, wie z. B. SGD oder sogar angepasste Lernraten, wenn die Konvergenz zu langsam ist.

Als Nächstes kommt die Trainingsschleife. Damit wird das Modell in den Trainingsmodus versetzt, indem über Epochen und Batches iteriert wird. Es berechnet Vorhersagen, berechnet den Verlust, führt Backpropagation durch und aktualisiert die Gewichte. Anschließend wird der durchschnittliche Verlust pro Epoche ausgedruckt. Dies ist wichtig, da das Training der Kern der Logik ist, die das Modell durch Minimierung der Verluste optimiert. Der Einsatz von Batch-Verfahren erhöht die Effizienz erheblich. Dabei ist es wichtig, die Verlustwerte zu überwachen und die Konvergenzrate zu bewerten. Die Anzahl der Epochen oder die Losgröße kann dann angepasst werden, wenn Verlustplateaus auftreten. Es ist wichtig, sicherzustellen, dass zero-grad aufgerufen wird, um die Gradienten zurückzusetzen.

Danach müssen wir uns um die Validierung und den Export unseres Modells nach ONNX kümmern. Nach dem Training des deklarierten Modells erstellen wir ein ONNX-Format mit Dummy-Eingaben, validieren das Modell und erstellen dann eine ONNX-Laufzeitsitzung. Dies unterstützt dynamische Losgrößen. Der Export nach ONNX ist wichtig, da er die Bereitstellung von Modellen auf verschiedenen Plattformen ermöglicht, von denen MQL5 für uns die wichtigste ist. In diesem Schritt wird auch die Integrität des Exports überprüft, um eine Reihe von Fehlern zu vermeiden, die bei einer späteren Verwendung des Modells auftreten könnten. Beim Exportieren ist es wichtig, dass die opset-Version mit der Zielplattform kompatibel ist. 12 funktioniert gut mit MQL5, vorläufig. Validierungsfehler können durch Überprüfung der Modellkompatibilität behoben werden.

Dann haben wir einen Code für die Auswertung oder den Test unseres trainierten Modells. Dies führt die Auswertung für eine einzelne Sequenz ohne Gradientenberechnung durch und druckt die Eingabe-/Ausgabeformen und die skalare Ausgabe. Damit wird die Funktionalität des Modells auf der Grundlage der Trainingsgewichte sowie des Ausgabeformats für eine einzelne Probe überprüft. Dies kann bei der Fehlersuche nützlich sein. Sie kann auch zur Bestätigung des Modellverhaltens verwendet werden. Bei der Verwendung ist es wichtig, dass die Eingabeform mit den Trainingsdaten übereinstimmt. Der Ausgangsbereich sollte ebenfalls überprüft werden, um sicherzustellen, dass er im Bereich von 0 bis 1 liegt.

Zusammenfassend lässt sich sagen, dass diese beiden Zusatzfunktionen zu unserer Netzklasse, die Funktionen create-sequences und train-and-evaluate, die Daten vorbereiten und das CosineConv1D-Modell für die binäre Klassifizierung trainieren. Dies geschieht mit einer kosinusmodulierten Architektur. Zu den wichtigsten Schritten gehören die Erstellung einer Sequenz, die Abstimmung der Hyperparameter, das Training des Modells, der Export des Modells nach ONNX und die Auswertung. Dabei müssen zusätzliche Maßnahmen ergriffen werden, wie die Abstimmung der Sequenzlänge, der Lernrate und der Anzahl der Epochen, um eine optimale Leistung zu erzielen. Die Überprüfung des ONNX-Modells vor dem Export ist ebenfalls unerlässlich.

Implementierung in MQL5

In früheren Artikeln, in denen wir die Anwendung des maschinellen Lernens bei der Erweiterung der Verwendung von Indikatorsignalmustern betrachtet haben, haben wir die MQL5-Implementierung übergangen, da uns immer der „Platz“ auszugehen schien. Für diesen Artikel, da die Funktionsimplementierung in Python zu repetitiv wurde, dachte ich, dass wir die Aspekte abdecken, die wir auf der MQL5-Seite berücksichtigen müssen, wenn wir das exportierte ONNX-Modell importieren und verwenden. 

In der nutzerdefinierten Signalklasse, die die ONNX-Modelle importiert und über den MQL5-Assistenten zu einem Expert Advisor zusammengestellt wird, werden unsere Kauf- und Verkaufsbedingungen wie folgt gebildet:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalML_TRX_WPR::LongCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalML_TRX_WPR::ShortCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}

Wie aus diesen beiden Funktionen ersichtlich ist, beziehen wir uns häufig auf die Funktion „RunModel“. Der Code lautet wie folgt;

//+------------------------------------------------------------------+
//| Forward Feed Network, to Get Forecast State.                     |
//+------------------------------------------------------------------+
double CSignalML_TRX_WPR::RunModel(int Index, ENUM_POSITION_TYPE T, vectorf &X)
{  vectorf _y(1);
   _y.Fill(0.0);
   ResetLastError();
   if(!OnnxRun(m_handles[Index], ONNX_NO_CONVERSION, X, _y))
   {  printf(__FUNCSIG__ + " failed to get y forecast, err: %i", GetLastError());
      return(double(_y[0]));
   }
   //printf(__FUNCSIG__ + " y: "+DoubleToString(_y[0],5));
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   return(double(_y[0]));
}

Diese Ankerklasse für alle diese Funktionen erbt von der Basisklasse 'CExpertSignal' für die Signalverarbeitung von MQL5 Expert Advisors. Dies ermöglicht die Integration mit dem Ökosystem oder den Klassendateien, die von den durch den Assistenten zusammengestellten Expert Advisors verwendet werden. Wir trainieren unsere 3 Modelle für jedes der Muster, die in der Lage waren, vorwärts zu gehen; 1, 4 und 5, und beim Importieren in MQL5 zeigen uns die Testläufe die folgenden Berichte:

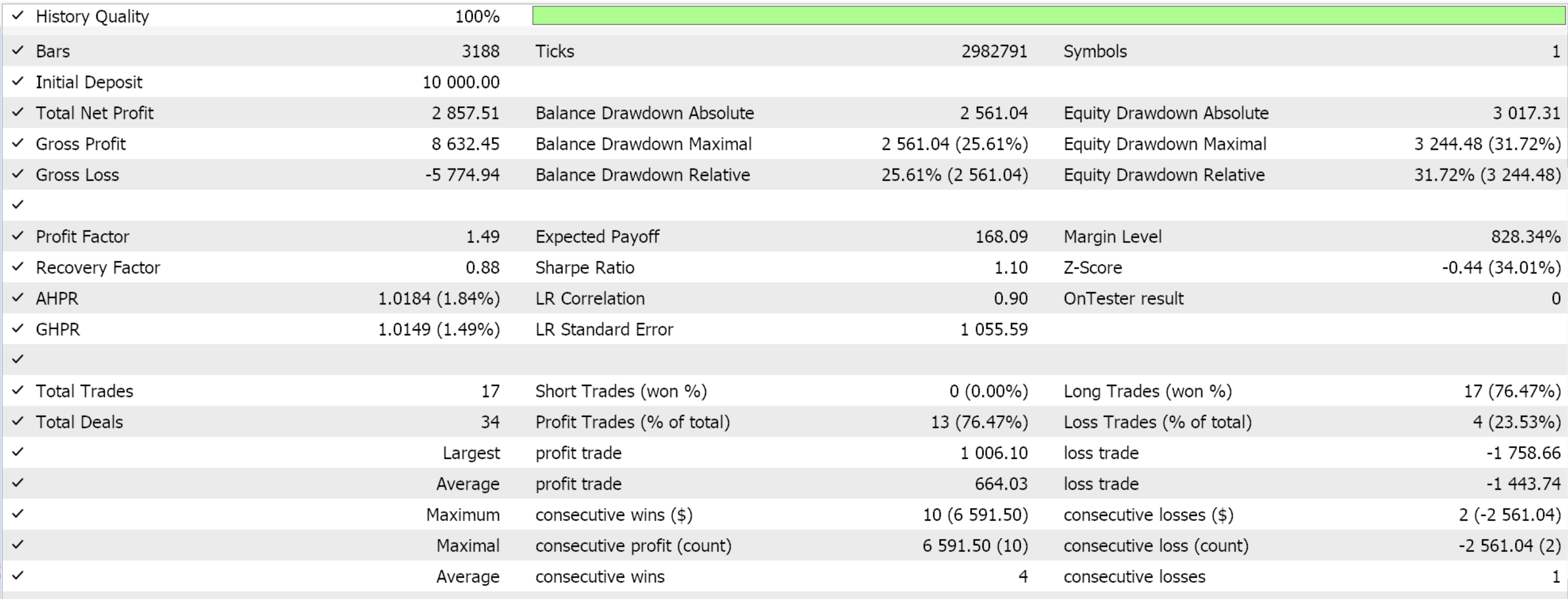
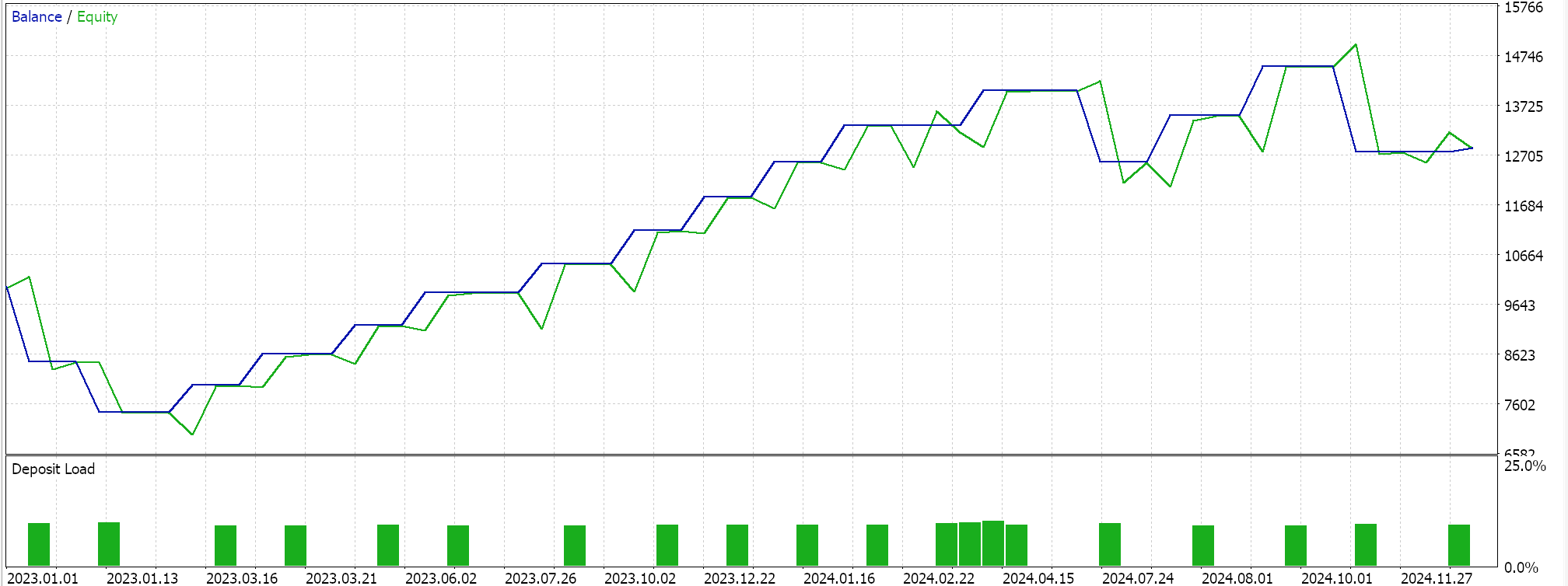
Für Pattern-1

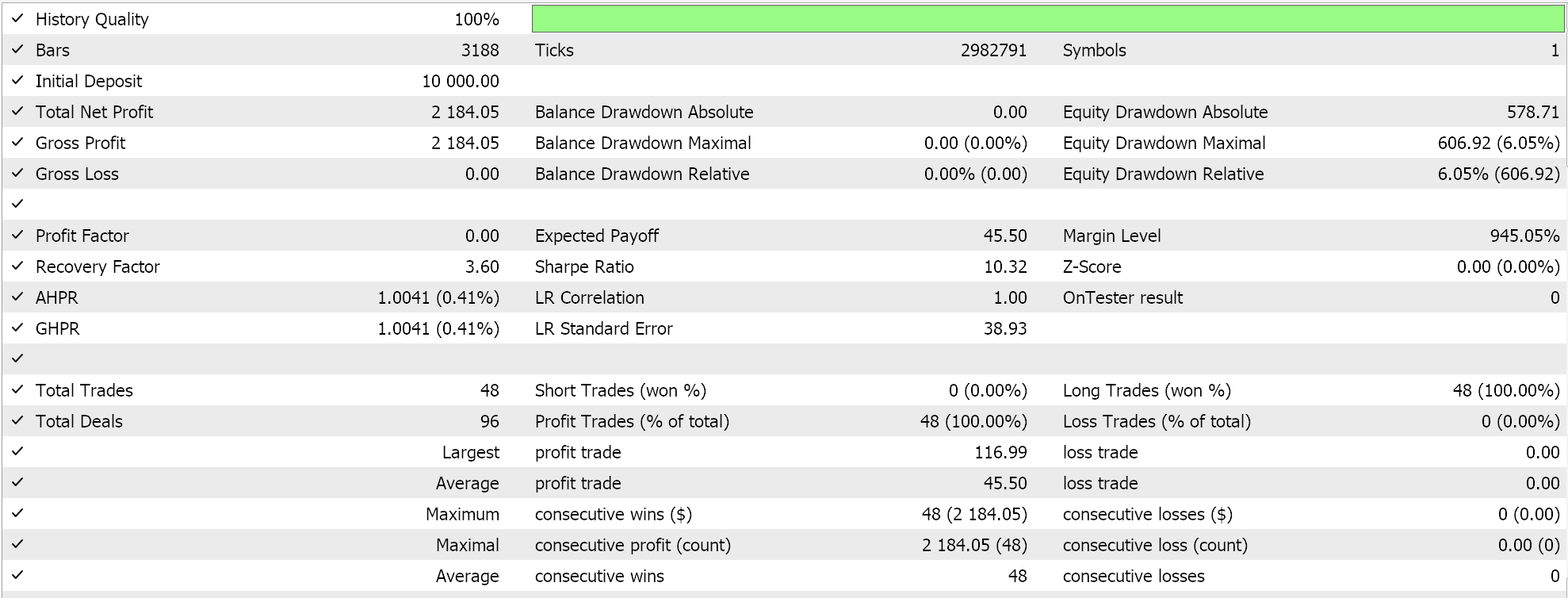
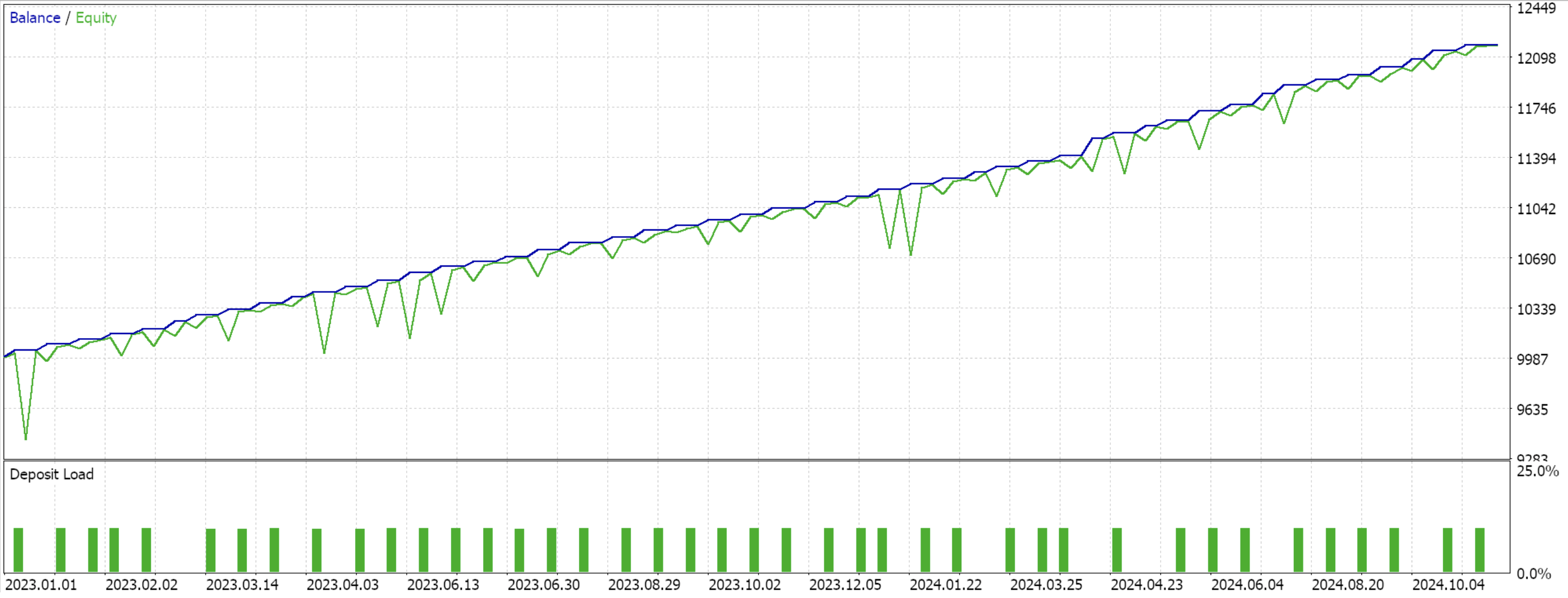
Für Pattern-4

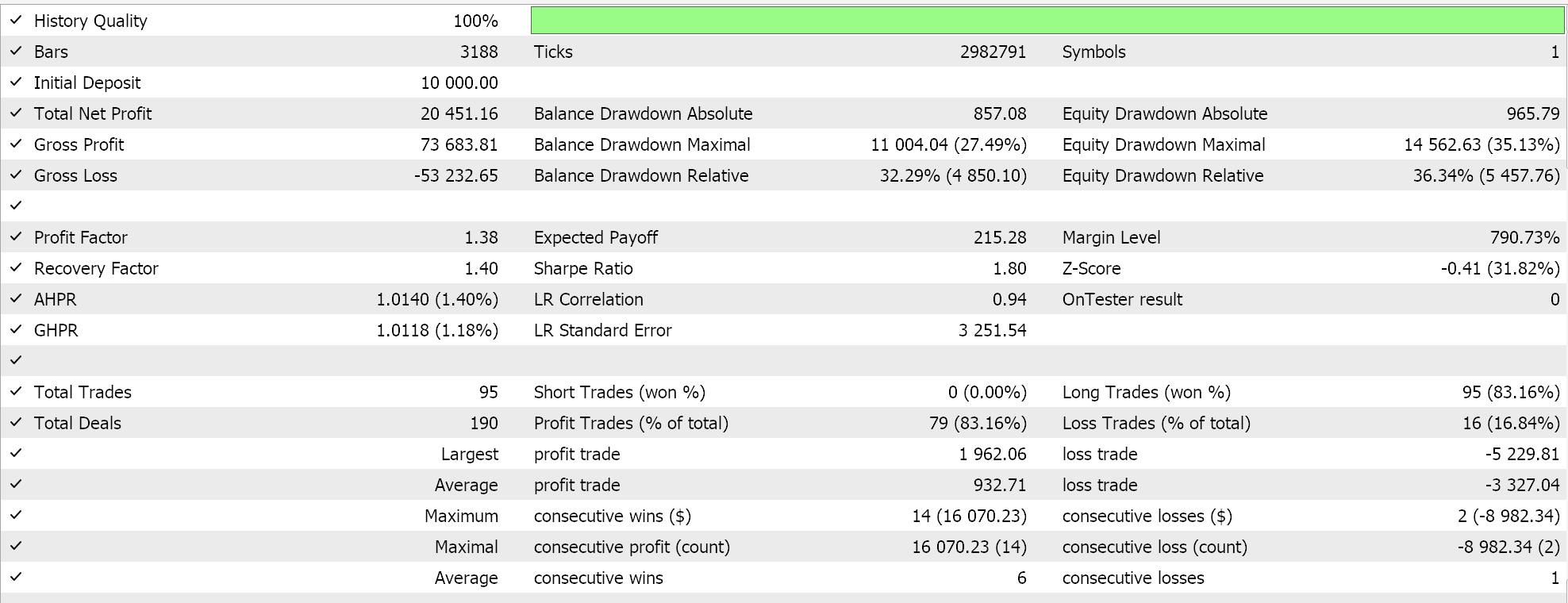
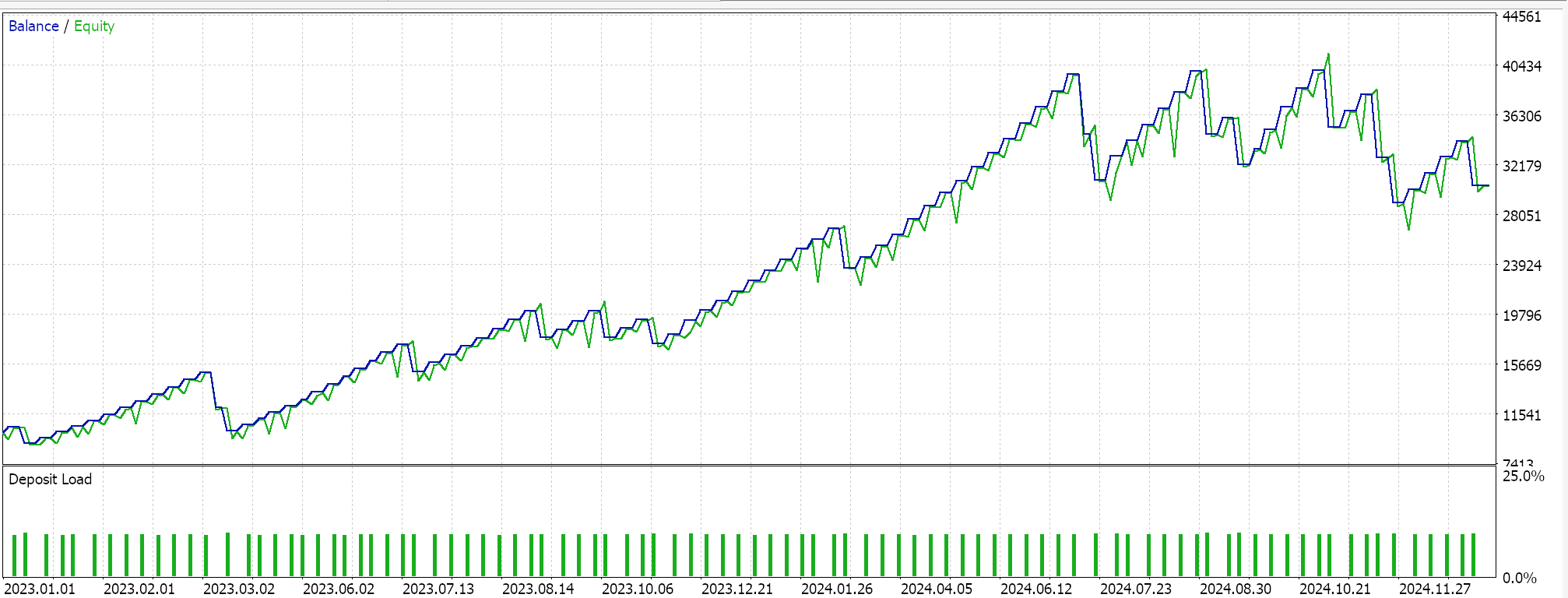
Für Pattern-5

Für neue Leser gibt es einen einführenden Leitfaden hier mit weiterführenden Links zur Verwendung des beigefügten Codes, um einen Expert Advisor über den MQL5-Assistenten zusammenzustellen. Die nutzerdefinierte Signalklasse, die wir erstellt haben, ist für eine einfache Integration mit dem MQL5-Assistenten konzipiert, und dies macht sie für verschiedene Expert Advisors wiederverwendbar. ML-Integration ist jetzt eine Sache, weil wir ONNX-Modelle verwenden können, um die Vorhersagefähigkeiten von Expert Advisor zu verbessern. Dazu ist ein robuster Satz von Trainingsdaten erforderlich. Die Validierung von Modellen mit Out-of-Sample-Tests ist wichtig, um eine Überanpassung zu vermeiden, und deshalb verwenden wir für unsere Ausstellungszwecke eine 50/50-Aufteilung unserer Daten, indem wir in einem Jahr trainieren und im nächsten Jahr weitergehen.

Aus den Testläufen geht hervor, dass alle Pattern-1, -4 und- 5 in der Lage waren, den Vorwärtstest zu machen, obwohl nur 4 anscheinend „überzeugender“ war. Diese Tests haben neben dem kurzen Zeitfenster der Tests noch weitere wichtige Vorbehalte. Dazu gehört vor allem, dass offene Positionen mit einem Take-Profit-Kursziel ohne Stop-Loss getestet werden. Die Verwendung von Limit-Aufträgen für den Einstieg macht diese Ergebnisse auch etwas rosiger, als sie es sonst wären. All dies sind Überlegungen, die der Leser berücksichtigen sollte, wenn er den beigefügten Quellcode interpretiert oder bewertet, ob er ihn weiterentwickeln soll.

Schlussfolgerung

Wir haben uns angesehen, wie die Signale des Triple Exponential Moving Average Oscillator mit dem Williams Percent Range Oscillator kombiniert und von einem maschinellen Lernmodell verarbeitet werden können, um Prognosen zu erstellen. Da die von uns betrachteten Muster bereits gelaufen waren, fungierte unser maschinelles Lernmodell im Wesentlichen als Filter für Geschäfte, von denen wir wussten, dass sie in ihrem Testjahr vorwärts laufen könnten. Die Leistung hat sich geringfügig verbessert, aber in zukünftigen Artikeln werden wir auch Tests mit ML-Mustern in Betracht ziehen, die nicht in der Lage waren, vorwärts zu laufen.

Name	Beschreibung
wz-68.mq5	Wizard assemblierte Expert Advisor, dessen Header die in der Assemblierung verwendeten Dateien umreißt
SignalWZ_68.mqh	Nutzerdefinierte Signalklassendatei, die in der Assistentengruppe verwendet wird.
68_1.mqh	Exportiertes ONNX-Modell für Pattern-1
68_4.mqh	Exportiertes ONNX-Modell für Pattern-4
68_5.mqh	Exportiertes ONNX-Modell für Pattern-5