리스크 관리에 대한 정량적 접근 방식: 파이썬과 MetaTrader 5를 사용하여 다중 통화 포트폴리오를 최적화 하기 위한 VaR 모델 적용하기

소개: 최신 위험 관리의 핵심 도구로서의 VaR

저는 수년 동안 알고리즘 외환 트레이딩의 세계에 몰두해 왔으며 최근에는 효율적인 리스크 관리 문제에 흥미를 갖게 되었습니다. 실험을 통해 시장 리스크를 평가하는 데 있어 VaR(Value at Risk;위험가중치) 방법론은 트레이더의 무기고에서 진정한 다이아몬드라는 깊은 확신을 갖게 되었습니다.

오늘은 MetaTrader 5 트레이딩 시스템에서 VaR을 구현하는 방법을 공유하고자 합니다. 저의 여정은 이후 저의 모든 작업의 기반이 되는 VaR 이론에 몰입하는 것으로 시작되었습니다. 

dry VaR 방정식을 라이브 코드로 변환하는 것은 별개의 이야기입니다. 이제 이 과정의 세부 사항을 공유하고 얻은 결과를 바탕으로 포트폴리오 최적화 방법과 동적 포지션 관리 시스템이 어떻게 탄생했는지 보여드리겠습니다.

저는 VaR 모델을 사용한 거래의 실제 결과를 숨기지 않고 다양한 시장 상황에서 그 효율성을 정직하게 평가할 것입니다. 명확하게 설명하기 위해 저는 VaR 분석을 시각화 하는 독특한 방법을 개발했습니다. 또한 제가 특히 유망하다고 생각하는 분야인 다중 통화 그리드 시스템에서의 사용을 포함하여 다양한 전략에 VaR 모델을 적용한 경험을 공유할 것입니다.

제 목표는 이론 뿐만 아니라 트레이딩 시스템의 효율성을 향상시킬 수 있는 실용적인 도구를 여러분께 소개하는 것입니다. 이러한 연구를 통해 여러분이 외환 시장에서 정량적 위험 관리 방법을 마스터하고 트레이딩을 한 단계 더 발전시킬 수 있는데 도움을 드릴 수 있을 것으로 생각합니다.

VaR(위험 가치)의 이론적 토대

시장 위험에 대한 저의 연구의 초석이 된 것은 VaR(Value at Risk)입니다. 수년간 외환 트레이딩을 하면서 저는 이 도구의 위력을 확신하게 되었습니다. VaR은 모든 트레이더들을 괴롭히는 질문, 즉 하루, 일주일 또는 한 달에 얼마를 잃을 수 있는가 라는 질문에 답합니다.

제가 VaR 방정식을 처음 접했을 때가 기억납니다. 간단해 보였습니다:

VaR = μ - zα * σ

μ는 평균 수익률, zα는 정규 분포의 사분위수, σ는 변동성입니다. 하지만 Forex는 현실이 교과서보다 더 복잡하다는 것을 금방 깨달았습니다.

수익금 분배는 어떻게 되나요? 항상 당연한 것은 아닙니다. 저는 더 깊이 파고들어 역사적 접근 방식인 몬테카를로 메서드를 연구해야 했습니다. 

특히 조건부 VaR(CVaR)이 인상적이었습니다:

CVaR = E[L | L > VaR]

L - 손실 금액. 이 방정식을 통해 저는 '꼬리' 리스크 - 드물지만 그러나 준비되지 않은 트레이더를 망칠 수 있는 치명적인 사건에 눈을 떴습니다.

각각의 새로운 개념을 실제로 테스트해 보았습니다. 진입, 청산, 포지션 크기 등 모든 것이 VaR이라는 프리즘을 통해 수정되었습니다. 점차적으로 이론에는 비정상의 레버리지, 논스톱 거래, 통화 쌍의 복잡성 등 Forex의 특성을 고려한 실용적인 내용들이 동반되었습니다.

이렇게 저에게 VaR은 방정식 그 이상이 되었습니다. 이는 우리가 시장을 바라보는 방식을 바꾸는 철학입니다. 제 경험이 여러분이 외환의 함정을 피하면서 안정적인 수익을 올리는 방법을 찾는 데 도움이 되기를 바랍니다.

VaR을 처리하기 위한 Python 및 MetaTrader 5 통합

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

별도의 문제는 MetaTrader 5와 로컬 시스템 간의 시간 동기화입니다. 저는 오프셋을 추가하여 문제를 해결했습니다.

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

저는 타임스탬프로 작업할 때 이 오프셋을 사용합니다.

저는 넘피 벡터화를 사용하여 VaR 계산시 성능을 최적화합니다:

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

이렇게 하면 대량의 데이터에 대한 계산 속도가 크게 빨라집니다.

마지막으로 실시간 작업에는 멀티스레딩을 사용합니다:

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

이렇게 하면 주 실행 스레드를 차단하지 않고 모든 쌍의 데이터를 동시에 업데이트할 수 있습니다.

VaR 모델 구현: 방정식에서 코드까지

이론적인 VaR 방정식을 작업 코드로 변환하는 것은 별개의 기술입니다. 제가 구현한 방법은 다음과 같습니다:

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

이러한 함수는 과거 VaR 및 CVaR(조건부 VaR) 모델을 구현합니다. 제가 파라메트릭 모델보다 이 모델을 선호하는 이유는 외환 수익률 분포의 '팻 테일(fat tail)'을 더 정확하게 설명하기 때문입니다.

포트폴리오 VaR의 경우 저는 몬테카를로 메서드를 사용합니다:

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

이 접근 방식을 사용하면 포트폴리오에 포함된 상품 간의 비선형 관계를 살펴볼 수 있게 합니다.

VaR을 사용하여 외환 포지션 포트폴리오 최적화하기

포트폴리오를 최적화하기 위해 저는 주어진 수준의 기대 수익률에 대해 VaR 최소화 메서드를 사용합니다:

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

이 함수는 SLSQP 알고리즘을 사용하여 최적의 포트폴리오 가중치를 찾습니다. 여기서 핵심은 위험을(VaR) 최소화하는 것과 목표 수익률을 달성 하는 것 사이의 균형입니다.

Forex의 특성을 고려하여 추가적인 제한 사항을 추가했습니다:

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

이러한 한도는 실제 외환 거래에서 중요하게 다뤄지는 최대 레버리지와 최소 포지션 크기를 고려한 것입니다.

마지막으로 변화하는 시장 상황에 적응하는 동적 포트폴리오의 최적화를 구현했습니다:

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

이 접근 방식을 사용하면 포트폴리오가 현재 시장 상황에 지속적으로 적응할 수 있게 됩니다. 이는 장기적으로 성공적인 외환 트레이딩을 하는 데에 매우 중요한 요소입니다.

이러한 모든 구현은 수개월에 걸친 테스트와 최적화의 결과물입니다. 이를 통해 저는 실제 시장 상황에서 성공적으로 작동하는 강력한 리스크 관리 및 포트폴리오 최적화 시스템을 만들 수 있었습니다.

VaR 기반 동적 포지션 관리

VaR을 기반으로 한 동적 포지션 관리는 제 트레이딩 시스템의 핵심 요소가 되었습니다. 제가 구현한 방법은 다음과 같습니다:

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

이 시스템은 VaR의 변화에 따라 포지션 크기를 자동으로 조정하여 일정한 수준의 위험을 보장합니다.

VaR을 고려한 손절매 및 이익 실현 계산하기

VaR을 고려한 손절매 및 이익 실현 계산은 또 다른 주요 혁신입니다.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

이 접근 방식을 사용하면 시장 변동성 변화에 따라 현재 VaR 수준에 따라 동적으로 손절매를 설정하고 이익을 실현할 수 있게 합니다.

VaR을 통한 드로다운 제어

VaR을 사용한 드로다운 제어는 이 리스크 관리 시스템의 핵심 구성 요소가 되었습니다:

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

이 시스템은 현재 손실이 지정된 수준을 초과하면 포트폴리오 노출을 자동으로 줄여 자본의 보호를 보장합니다.

저는 또한 과거 변동성에 따라 최대 드로다운을 동적으로 변경하는 시스템도 구현했습니다:

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

이를 통해 변동성이 큰 기간에는 시스템을 더 보수적으로, 안정된 기간에는 더 공격적으로 운영할 수 있습니다.

이러한 모든 구성 요소가 함께 작동하여 종합적인 VaR 기반의 리스크 관리 시스템이 구축되도록 합니다. 이 시스템은 공격적으로 거래할 수 있지만 시장 스트레스 기간에도 안정적인 자본 보호 기능을 제공합니다.

실제 시장 상황에서의 거래 결과 및 VaR 모델의 효율성 평가

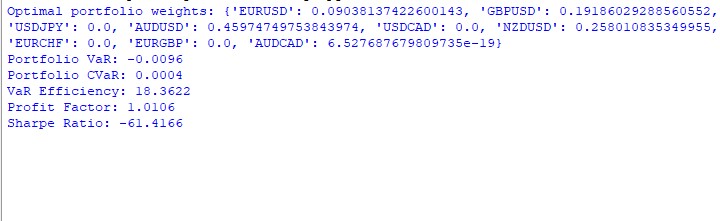
한 해 동안의 VaR 모델 운영 결과는 모호합니다. 포트폴리오에서 가중치를 배분한 방법은 다음과 같습니다:

AUDUSD: 51,29% GBPUSD: 28,75% USDJPY: 19,96% EURUSD 및 USDCAD: 거의 0%

AUDUSD가 절반 이상을 차지한 반면 EUR와 CAD는 빠져 있습니다. 왜 이런 일이 발생했는지 원인을 파악해야 합니다.

다음은 주요 메트릭에 대한 코드입니다:

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

결과는 다음과 같습니다: VaR: -0,70% CVaR: 0,04% VaR 효율성: 18,1334 이익 계수: 1,0291 샤프 비율: -73,5999

CVaR은 VaR보다 훨씬 낮은 것으로 나타났습니다 - 이는 모델이 위험을 과대평가한 것으로 보입니다. VaR 효율성이 1보다 훨씬 큽니다 - 위험 평가가 매우 좋지 않다는 또 다른 신호입니다. 이익 계수가 1을 약간 상회하였습니다 - 간신히 녹색에 속합니다. 샤프 비율은 진한 빨간색입니다 - 정말 재앙입니다.

저는 차트에 다음 코드를 사용했습니다:

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

전반적으로 이 모델에는 몇 가지 개선이 필요합니다. 모델이 너무 조심스러워서 수익을 놓치고 있습니다. 

다양한 트레이딩 전략에 맞는 VaR 모델 적용

결과를 분석한 후 다양한 트레이딩 전략에 VaR 모델을 적용하기로 결정했습니다. 그 결과는 다음과 같습니다:

트렌드 전략의 경우 VaR 계산을 수정해야 했습니다:

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

이 기능은 트렌드 팔로잉 시스템에서 중요한 로컬 트렌드를 고려합니다.

페어 트레이딩 전략의 경우 저는 스프레드에 대한 VaR을 개발했습니다:

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

이 기능은 그리드에서 쌍 간의 상관관계를 고려합니다.

저는 다음 코드를 사용하여 그리드를 동적으로 조정합니다:

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

이를 통해 그리드 VaR이 지정된 한도를 초과하는 경우 포지션 크기를 자동으로 줄일 수 있습니다.

그리드 진입 레벨을 결정하기 위해 VaR을 사용하는 실험도 해봤습니다:

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

이는 현재 변동성에 따라 적응형 레벨을 제공합니다.

이러한 모든 수정 사항을 적용한후 시스템 성능이 크게 향상되었습니다. 예를 들어 변동성이 큰 기간 동안 샤프 비율은 -73.59에서 1.82로 증가했습니다. 하지만 가장 중요한 것은 시스템이 더욱 유연해지고 다양한 시장 상황에 더 잘 적응할 수 있게 되었다는 점입니다.

물론 아직 해야 할 일이 남아 있습니다. 예를 들어 저는 머신 러닝을 통해 VaR을 예측하려고 합니다. 그러나 현재 상태에서도 이 모델은 복잡한 거래 시스템의 위험을 훨씬 더 적절하게 평가할 수 있습니다.

VaR 분석 결과 시각화

저는 몇 가지 주요 그래프를 개발했습니다:

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

이 그래프는 시스템 성능에 대한 종합적인 시각을 제공합니다. VaR 대 실제 수익률 그래프는 위험 예측의 정확성을 명확하게 보여줍니다. 드로다운 그래프를 통해 드로다운의 깊이와 기간을 평가할 수 있습니다. 히트맵은 통화 쌍의 위험 분포를 시각화 하는 데 도움이 됩니다.

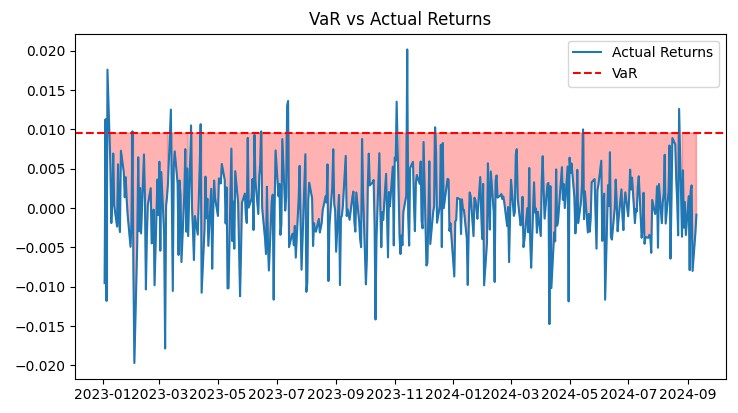
이러한 모든 도구를 통해 시스템의 효율성을 지속적으로 모니터링하고 필요한 조정을 할 수 있습니다. VaR 모델은 실제 시장 상황에서 그 효율성이 입증되었으며 통제된 수준의 위험으로 안정적인 수익을 제공합니다.

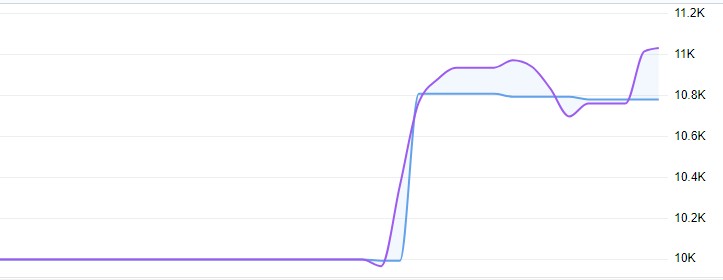
실시간 거래는 11%의 수익률을 보였으며 변동폭은 1%를 넘지 않았습니다:

애널리틱스가 포함된 전체 모델 코드:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

다중 통화 그리드 전략에서 이 모델의 적용 가능성 

다중 통화 그리드 전략에 VaR 모델을 적용하면 트레이딩 최적화를 위한 흥미로운 기회가 많이 열린다는 것을 알게 되었습니다. 제가 개발하고 테스트한 주요 내용은 다음과 같습니다.

동적 자본 할당. 개별 VaR 값에 따라 통화 쌍 간에 자본을 동적으로 할당하는 기능을 개발했습니다:

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

이 기능을 사용하면 위험도가 낮은 페어에 자동으로 자본을 재분배하여 전체 포트폴리오의 균형 잡힌 위험 관리에 기여할 수 있습니다.

VaR 상관관계 행렬. 통화 쌍 간의 관계를 고려하기 위해 VaR 상관관계 행렬 계산을 구현했습니다:

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

이 행렬을 사용하면 전체 포트폴리오 위험을 보다 정확하게 평가하고 쌍 간의 과도한 상관관계로 인한 잠재적 문제를 파악할 수 있습니다. 또한 각 통화쌍의 특성을 고려하여 그리드 매개변수 조정 기능을 수정했습니다:

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
    return adjusted_params

이를 통해 각 그리드는 해당 통화쌍의 현재 조건에 적응하게 되고 전략의 전반적인 효율성을 높일 수 있습니다. 다음은 VaR을 사용한 그리드 트레이딩 시뮬레이션 스크린샷입니다. 저는 이 시스템을 머신러닝 모델을 사용해 VaR 개념에 따라 리스크를 제어하고 주문 그리드와 함께 가격 변동 가능성을 예측하는 모델을 사용하는 본격적인 트레이딩 로봇으로 발전시킬 계획입니다. 향후 기사에서 그 결과를 살펴보겠습니다.

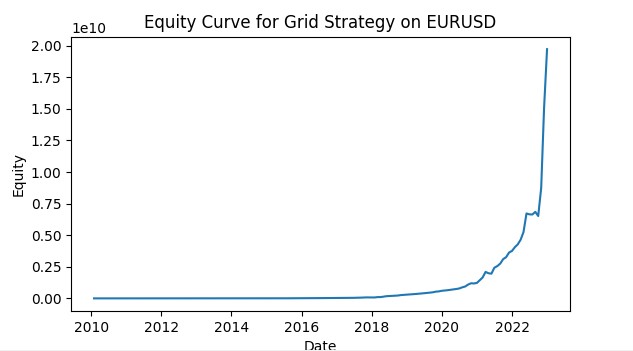
결론

저는 VaR을 사용하여 리스크를 관리하겠다는 단순한 아이디어로 시작했지만 이 아이디어가 어디로 이어질지 전혀 예상하지 못했습니다. 기본 방정식에서 복잡한 다차원 모델, 단일 거래에서 동적으로 조정하는 다중 통화 포트폴리오에 이르기까지 각 단계는 새로운 지평과 새로운 도전을 열어주었습니다.

이 경험을 통해 저는 무엇을 얻었을까요? 첫째, VaR은 정말 강력한 도구이지만 다른 도구와 마찬가지로 올바르게 사용해야 합니다. 숫자를 맹목적으로 믿어서는 안 됩니다. 대신 항상 시장을 파악하고 예상치 못한 상황에 대비해야 합니다.

둘째, 트레이딩 시스템에 VaR을 통합하는 것은 단순히 또 다른 지표를 추가하는 것이 아닙니다. 이는 위험 및 자본 관리에 대한 접근 방식을 완전히 새로이 한 것입니다. 제 트레이딩은 더 인식적이고 체계적이 되었습니다. 

셋째, 다중 통화 전략으로 작업하면서 트레이딩의 새로운 차원이 열렸습니다. 상관관계, 상호 의존성, 동적 자본 배분 - 이 모든 것이 엄청나게 복잡하지만 또한 엄청나게 흥미로운 퍼즐을 만들어냅니다. 그리고 이 문제를 해결하는 열쇠는 바로 VaR입니다.

물론 아직 작업이 끝나지 않았습니다. 저는 이미 VaR 예측에 머신러닝을 적용하는 방법과 비선형 모델을 통합하여 분포의 '팻테일'을 더 잘 설명하는 방법에 대한 아이디어를 가지고 있습니다. 외환은 결코 가만히 있지 않으며 우리의 모델도 함께 진화해야 합니다.