Approche quantitative de la gestion des risques : Application du modèle VaR pour optimiser un portefeuille multidevises en utilisant Python et MetaTrader 5

Introduction : La VaR, un outil clé de la gestion moderne des risques

Je suis plongé dans le monde du trading algorithmique sur le marché des changes depuis de nombreuses années et j'ai récemment été intrigué par la question de la gestion efficace des risques. Mes expériences m'ont conduit à une conviction profonde : la méthodologie Value at Risk (VaR) est un véritable diamant dans l'arsenal du trader pour évaluer les risques du marché.

Aujourd'hui, je souhaite partager les fruits de mes recherches sur la mise en œuvre de la VaR dans les systèmes de trading MetaTrader 5. Mon parcours a commencé par une immersion dans la théorie de la VaR - la base sur laquelle tous les travaux ultérieurs ont été construits. 

La transformation d'équations VaR sèches en code réel est une autre histoire. Je dévoilerai les détails de ce processus et montrerai comment les méthodes d'optimisation de portefeuille et le système de gestion dynamique des positions sont nés sur la base des résultats obtenus.

Je ne cacherai pas les résultats réels des transactions effectuées à l'aide de mon modèle VaR et j'évaluerai honnêtement son efficacité dans différentes conditions de marché. Pour plus de clarté, j'ai mis au point des méthodes uniques de visualisation de l'analyse de la VaR. Je partagerai également mon expérience de l'adaptation du modèle VaR à différentes stratégies, y compris son utilisation dans les systèmes de grille multidevises, un domaine que je considère comme particulièrement prometteur.

Mon objectif est de vous doter non seulement de la théorie, mais aussi d'outils pratiques pour améliorer l'efficacité de vos systèmes de trading. Je pense que ces études vous aideront à maîtriser les méthodes quantitatives de gestion des risques sur le marché des changes et à passer à la vitesse supérieure.

Fondements théoriques de la valeur à risque (VaR)

La valeur à risque (VaR) est devenue la pierre angulaire de mes recherches sur le risque de marché. Des années de pratique du Forex m'ont convaincu de la puissance de cet instrument. La VaR répond à la question qui tourmente tous les traders : combien pouvez-vous perdre en un jour, une semaine ou un mois ?

Je me souviens de la première fois que j'ai rencontré l'équation de la VaR. Cela semblait simple :

VaR = μ - zα * σ

μ est le rendement moyen, zα est le quantile de la distribution normale et σ est la volatilité. Mais le Forex a rapidement montré que la réalité est plus complexe que les manuels.

Répartition des rendements ? Elle n'est pas toujours normale. J'ai dû approfondir, étudier l'approche historique, la méthode Monte Carlo. 

J'ai été particulièrement frappé par la VaR conditionnelle (CVaR) :

CVaR = E[L | L > VaR]

L - montant de la perte. Cette équation m'a ouvert les yeux sur les risques "secondaires" - des événements rares mais dévastateurs qui peuvent ruiner un trader non préparé.

J'ai testé chaque nouveau concept dans la pratique. Entrées, sorties, taille des positions, tout a été revu à travers le prisme de la VaR. Progressivement, la théorie s'est accompagnée de développements pratiques prenant en compte les spécificités du Forex : effet de levier délirant, trading non-stop, complexité des paires de devises.

Pour moi, la VaR est devenue plus qu'une série d'équations. C'est une philosophie qui change notre façon de voir le marché. J'espère que mon expérience vous aidera à trouver votre chemin vers des profits stables tout en évitant les pièges du Forex.

Intégration de Python et de MetaTrader 5 pour la gestion de la VaR

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

La synchronisation de l'heure entre MetaTrader 5 et le système local constitue un autre problème. J'ai résolu le problème en ajoutant un décalage

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

J'utilise ce décalage lorsque je travaille avec des horodatages.

J'utilise la vectorisation numpy pour optimiser les performances lors du calcul de la VaR :

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

Cela permet d'accélérer considérablement les calculs pour de grandes quantités de données.

Enfin, j'utilise le multi-threading pour les travaux en temps réel :

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

Cela permet de mettre à jour les données de toutes les paires simultanément sans bloquer le fil d'exécution principal.

Mise en œuvre du modèle VaR : des équations au code

Convertir les équations théoriques de la VaR en code opérationnel est un art à part entière. Voici comment je l'ai mis en œuvre :

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

Ces fonctions mettent en œuvre le modèle historique de la VaR et de la CVaR (VaR conditionnelle). Je les préfère aux modèles paramétriques parce qu'ils tiennent mieux compte des "queues grasses" de la distribution des rendements du Forex.

Pour la VaR du portefeuille, j'utilise la méthode de Monte Carlo :

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

Cette approche permet de prendre en compte les relations non linéaires entre les instruments du portefeuille.

Optimisation d'un portefeuille de positions de change à l'aide de la VaR

Pour optimiser le portefeuille, j'utilise la méthode de minimisation de la VaR pour un niveau donné de rendement attendu :

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

Cette fonction utilise l'algorithme SLSQP pour trouver les pondérations optimales du portefeuille. L'élément clé est l'équilibre entre la minimisation du risque (VaR) et la réalisation de l'objectif de rendement.

J'ai ajouté des restrictions supplémentaires pour tenir compte des spécificités du Forex :

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

Ces limites tiennent compte de l'effet de levier maximal et de la taille minimale de la position, ce qui est essentiel pour le trading réel sur le marché des changes.

Enfin, j'ai mis en œuvre une optimisation dynamique du portefeuille qui s'adapte à l'évolution des conditions du marché :

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

Cette approche permet au portefeuille de s'adapter en permanence aux conditions actuelles du marché, ce qui est essentiel pour une réussite à long terme sur le Forex.

Toutes ces mises en œuvre sont le résultat de nombreux mois de tests et d'optimisation. Ils m'ont permis de créer un système robuste de gestion des risques et d'optimisation du portefeuille qui fonctionne avec succès dans des conditions de marché réelles.

Gestion dynamique des positions sur la base de la VaR

La gestion dynamique des positions basée sur la VaR est devenue un élément clé de mon système de trading. Voici comment je l'ai mis en œuvre :

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

Ce système ajuste automatiquement la taille des positions en fonction de l'évolution de la VaR, garantissant ainsi un niveau de risque constant.

Calcul des stop loss et des take profits en tenant compte de la VaR

Le calcul des stop loss et des take profits en tenant compte de la VaR est une autre innovation clé.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

Cette approche vous permet de fixer dynamiquement des stop loss et de prendre des bénéfices sur la base du niveau actuel de la VaR, en s'adaptant aux variations de la volatilité du marché.

Contrôle du Drawdown avec la VaR

Le contrôle du drawdown à l'aide de la VaR est devenu un élément essentiel de mon système de gestion des risques :

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

Ce système réduit automatiquement l'exposition du portefeuille si la baisse actuelle dépasse un niveau spécifié, assurant ainsi la protection du capital.

J'ai également mis en place un système permettant de modifier dynamiquement le max_drawdown en fonction de la volatilité historique :

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

Cela permet au système d'être plus conservateur pendant les périodes de volatilité accrue et plus agressif pendant les périodes calmes.

Tous ces éléments se conjuguent pour créer un système complet de gestion des risques basé sur la VaR. Il me permet d'effectuer des transactions agressives, tout en assurant une protection fiable du capital pendant les périodes de tensions sur les marchés.

Mes résultats de trading et l'évaluation de l'efficacité du modèle VaR dans des conditions de marché réelles

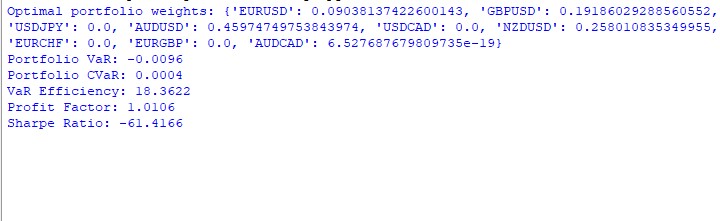
Les résultats du fonctionnement du modèle VaR pour l'année sont ambigus. Voici comment les pondérations ont été réparties dans le portefeuille :

AUDUSD : 51,29% GBPUSD : 28,75% USDJPY : 19,96% EURUSD et USDCAD : presque 0%.

Il est étrange que l'AUDUSD ait pris plus de la moitié, alors que l'EUR et le CAD ont complètement disparu. Nous devons comprendre pourquoi cela s'est produit.

Voici le code de la métrique principale :

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

Les résultats sont les suivants : VaR : -0,70% CVaR : 0,04% Efficacité de la VaR : 18,1334 Facteur de profit : 1,0291 Ratio de Sharpe : -73,5999

La CVaR s'est révélée beaucoup plus faible que la VaR - il semble que le modèle surestime les risques. L'efficacité de la VaR est nettement supérieure à 1 - un autre signe que l'évaluation du risque n'est pas très bonne. Facteur de profit légèrement supérieur à 1 - à peine dans le vert. Le ratio de Sharpe est en rouge foncé - un véritable désastre.

J'ai utilisé le code suivant pour les graphiques :

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

Dans l'ensemble, le modèle doit être sérieusement amélioré. Il est trop prudent et passe à côté de bénéfices. 

Adaptation du modèle VaR à différentes stratégies de trading

Après avoir analysé les résultats, j'ai décidé d'adapter le modèle VaR à différentes stratégies de trading. Voici ce que j'ai obtenu :

Pour les stratégies de tendance, le calcul de la VaR a dû être modifié :

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

Cette caractéristique prend en compte la tendance locale, ce qui est important pour les systèmes de suivi de tendance.

Pour les stratégies de trading par paire, j'ai développé une VaR pour le spread :

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

Cet élément prend en compte les corrélations entre les paires dans la grille.

J'utilise le code suivant pour ajuster dynamiquement la grille :

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

Cela permet de réduire automatiquement la taille des positions si la VaR de la grille dépasse une limite spécifiée.

J'ai également expérimenté l'utilisation de la VaR pour déterminer les niveaux d'entrée dans la grille :

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

Cela permet d'adapter les niveaux en fonction de la volatilité actuelle.

Toutes ces modifications ont permis d'améliorer considérablement les performances du système. Par exemple, en période de forte volatilité, le ratio de Sharpe est passé de -73,59 à 1,82. Mais l'essentiel est que le système est devenu plus flexible et s'adapte mieux aux différentes conditions du marché.

Bien sûr, il y a encore du travail à faire. Par exemple, je veux essayer d'inclure l'apprentissage automatique pour prédire la VaR. Mais même dans son état actuel, le modèle fournit une évaluation beaucoup plus adéquate des risques dans les systèmes de trading complexes.

Visualisation des résultats de l'analyse VaR

J'ai élaboré plusieurs graphiques clés :

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

Ces graphiques fournissent une vue d'ensemble des performances du système. Le graphique de la VaR par rapport aux rendements réels montre clairement la précision des prévisions de risque. Le graphique Drawdown nous permet d'évaluer la profondeur et la durée des drawdowns. La carte thermique permet de visualiser la répartition du risque entre les paires de devises.

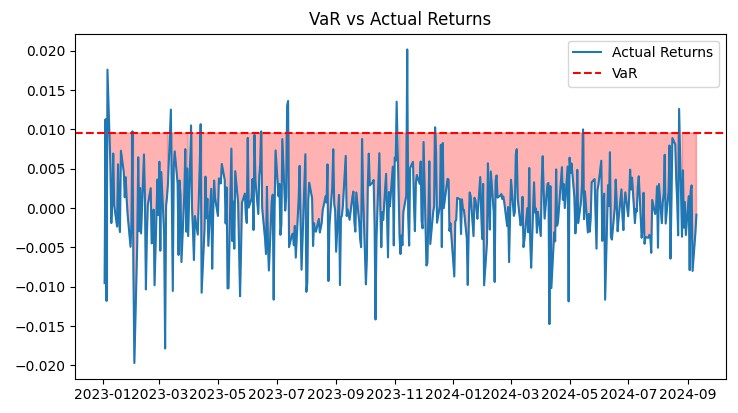
Tous ces outils me permettent de contrôler en permanence l'efficacité du système et de procéder aux ajustements nécessaires. Le modèle VaR a prouvé son efficacité dans les conditions réelles du marché, assurant une croissance stable avec un niveau de risque contrôlé.

Le trading en direct a montré un rendement de 11%, avec une baisse flottante ne dépassant pas 1% :

Code du modèle complet avec analyse :

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

Application possible de ce modèle dans les stratégies de grille multidevises 

Au cours de mes recherches, j'ai constaté que l'application du modèle VaR aux stratégies de grille multidevises ouvre un certain nombre d'opportunités intéressantes pour l'optimisation des transactions. Voici les principaux aspects que j'ai développés et testés.

Allocation dynamique des capitaux. J'ai développé une fonction pour allouer dynamiquement le capital entre les paires de devises sur la base de leurs valeurs VaR individuelles :

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

Cette fonction nous permet de réallouer automatiquement le capital en faveur de paires moins risquées, ce qui contribue à une gestion plus équilibrée du risque de l'ensemble du portefeuille.

Matrice de corrélation de la VaR. Pour tenir compte des relations entre les paires de devises, j'ai mis en œuvre le calcul de la matrice de corrélation de la VaR :

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

Cette matrice permet une évaluation plus précise du risque global du portefeuille et l'identification des problèmes potentiels liés à une corrélation excessive entre les paires. J'ai également modifié la fonction d'ajustement des paramètres de la grille pour tenir compte des spécificités de chaque paire de devises :

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
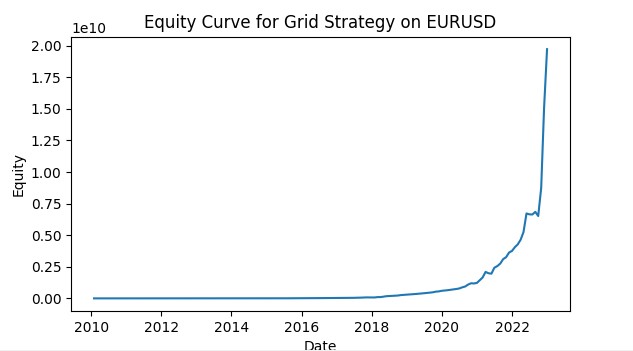
    return adjusted_params

Cela permet à chaque grille de s'adapter aux conditions actuelles de sa paire de devises, augmentant ainsi l'efficacité globale de la stratégie. Voici une capture d'écran d'une simulation de trading en grille utilisant la VaR. J'ai l'intention de développer le système pour en faire un robot de trading à part entière qui utilisera des modèles d'apprentissage automatique pour contrôler les risques selon le concept de la VaR, et des modèles pour prédire l'évolution probable des prix, couplés à une grille d'ordres. Nous examinerons les résultats dans les prochains articles.

Conclusion

En partant de l'idée simple d'utiliser la VaR pour gérer le risque, je n'avais aucune idée de ce à quoi cela me mènerait. Des équations de base aux modèles multidimensionnels complexes, des transactions uniques aux portefeuilles multidevises à adaptation dynamique, chaque étape a ouvert de nouveaux horizons et de nouveaux défis.

Qu'ai-je appris de cette expérience ? Tout d'abord, la VaR est un outil vraiment puissant, mais comme tout outil, elle doit être utilisée correctement. Il ne faut pas se fier aveuglément aux chiffres. Au contraire, vous devez toujours vous tenir au courant de l'évolution du marché et être prêt à faire face à l'imprévu.

Deuxièmement, l'intégration de la VaR dans les systèmes de trading ne se limite pas à l'ajout d'une nouvelle mesure. Il s'agit d'une refonte complète de l'approche de la gestion des risques et des capitaux. Mon activité de trading est devenue plus consciente et plus structurée. 

Troisièmement, le fait de travailler avec des stratégies multidevises m'a ouvert une nouvelle dimension dans le trading. Corrélations, interdépendances, allocation dynamique des capitaux - tout cela crée un puzzle incroyablement complexe, mais aussi incroyablement intéressant. Et la VaR est la clé pour résoudre ce problème.

Bien entendu, le travail n'est pas encore terminé. J'ai déjà des idées sur la manière d'appliquer l'apprentissage automatique à la prévision de la VaR, et sur la manière d'intégrer des modèles non linéaires pour mieux prendre en compte les "grosses queues" de la distribution. Le Forex n'est jamais figé et nos modèles doivent évoluer avec lui.