Approccio quantitativo alla gestione del rischio: Applicazione del modello VaR per ottimizzare un portafoglio multi valuta utilizzando Python e MetaTrader 5

Introduzione: Il VaR come strumento chiave della moderna gestione del rischio

Da molti anni sono immerso nel mondo del trading algoritmico sul Forex e recentemente mi sono interessato alla questione della gestione efficiente del rischio. I miei esperimenti mi hanno portato a una profonda convinzione: la metodologia Value at Risk (VaR) è un vero e proprio diamante nell'arsenale del trader per la valutazione dei rischi di mercato.

Oggi desidero condividere i frutti della mia ricerca sull'implementazione del VaR nei sistemi di trading MetaTrader 5. Il mio viaggio è iniziato con un'immersione nella teoria del VaR, la base su cui è stato costruito tutto il lavoro successivo. 

La trasformazione delle equazioni VaR secche in codice vivo è una storia a parte. Vi svelerò i dettagli di questo processo e mostrerò come, sulla base dei risultati ottenuti, sono nati i metodi di ottimizzazione del portafoglio e il sistema di gestione dinamica delle posizioni.

Non nasconderò i risultati reali del trading con il mio modello VaR e valuterò onestamente la sua efficienza in varie condizioni di mercato. Per chiarezza, ho sviluppato modi unici per visualizzare l'analisi VaR. Inoltre, condividerò la mia esperienza nell'adattamento del modello VaR a diverse strategie, compreso il suo utilizzo in sistemi a griglia multi valuta, un'area che considero particolarmente promettente.

Il mio obiettivo è quello di fornirvi non solo la teoria, ma anche gli strumenti pratici per migliorare l'efficienza dei vostri sistemi di trading. Credo che questi studi vi aiuteranno a padroneggiare i metodi quantitativi di gestione del rischio nel Forex e a portare il vostro trading al livello successivo.

Basi teoriche del Value at Risk (VaR)

Il Value at Risk (VaR) è diventato la pietra miliare della mia ricerca sul rischio di mercato. Anni di pratica nel Forex mi hanno convinto della potenza di questo strumento. Il VaR risponde alla domanda che tormenta ogni trader: quanto si può perdere in un giorno, una settimana o un mese?

Ricordo la prima volta che ho incontrato l'equazione del VaR. Sembrava semplice:

VaR = μ - zα * σ

μ è il rendimento medio, zα è il quantile della distribuzione normale e σ è la volatilità. Ma il Forex ha subito dimostrato che la realtà è più complessa dei libri di testo.

Distribuzione dei rendimenti? Non sempre è normale. Ho dovuto scavare più a fondo, studiare l'approccio storico, il metodo Monte Carlo. 

Sono rimasto particolarmente colpito dal VaR condizionato (CVaR):

CVaR = E[L | L > VaR]

L - importo della perdita. Questa equazione mi ha aperto gli occhi sui rischi di "coda", eventi rari ma devastanti che possono rovinare un trader impreparato.

Ho testato ogni nuovo concetto nella pratica. Entrate, uscite, dimensioni delle posizioni - tutto è stato rivisto attraverso il prisma del VaR. Gradualmente, la teoria è stata accompagnata da sviluppi pratici che hanno tenuto conto delle specificità del Forex: leva finanziaria pazzesca, trading non-stop, complessità delle coppie di valute.

Il VaR è diventato per me più di un insieme di equazioni. È una filosofia che cambia il modo di guardare il mercato. Spero che la mia esperienza vi aiuti a trovare la strada per ottenere profitti stabili evitando le insidie del Forex.

Integrazione di Python e MetaTrader 5 per la gestione del VaR

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

Un problema a parte è la sincronizzazione dell'ora tra MetaTrader 5 e il sistema locale. Ho risolto aggiungendo un offset

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

Utilizzo questo offset quando lavoro con i timestamp.

Utilizzo la vettorizzazione numpy per ottimizzare le prestazioni nel calcolo del VaR:

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

Questo accelera notevolmente i calcoli per grandi quantità di dati.

Infine, utilizzo il multithreading per il lavoro in tempo reale:

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

Ciò consente di aggiornare i dati di tutte le coppie contemporaneamente senza bloccare il thread di esecuzione principale.

Implementazione del modello VaR: dalle equazioni al codice

La conversione delle equazioni teoriche del VaR in codice funzionante è un'arte a parte. Ecco come l'ho implementato:

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

Queste funzioni implementano il modello VaR storico e il CVaR (Conditional VaR). Li preferisco ai modelli parametrici perché tengono conto in modo più accurato delle "code grasse" della distribuzione dei rendimenti del Forex.

Per il VaR di portafoglio, utilizzo il metodo Monte Carlo:

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

Questo approccio ci permette di tenere conto delle relazioni non lineari tra gli strumenti del portafoglio.

Ottimizzare un portafoglio di posizioni Forex utilizzando il VaR

Per ottimizzare il portafoglio, utilizzo il metodo di minimizzazione del VaR per un determinato livello di rendimento atteso:

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

Questa funzione utilizza l'algoritmo SLSQP per trovare i pesi ottimali del portafoglio. Il punto chiave è l'equilibrio tra la minimizzazione del rischio (VaR) e il raggiungimento dell'obiettivo del rendimento.

Ho aggiunto ulteriori restrizioni per tenere conto delle specificità del Forex:

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

Questi limiti tengono conto della leva massima e della dimensione minima della posizione, che è fondamentale per il trading nel Forex reale.

Infine, ho implementato un'ottimizzazione dinamica del portafoglio che si adatta alle mutevoli condizioni di mercato:

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

Questo approccio consente al portafoglio di adattarsi continuamente alle attuali condizioni di mercato, il che è fondamentale per il successo a lungo termine nel Forex.

Tutte queste implementazioni sono il risultato di molti mesi di test e ottimizzazione. Mi hanno permesso di creare un solido sistema di gestione del rischio e di ottimizzazione del portafoglio che funziona con successo in condizioni di mercato reali.

Gestione dinamica delle posizioni basata sul VaR

La gestione dinamica delle posizioni basata sul VaR è diventata un elemento chiave del mio sistema di trading. Ecco come l'ho implementato:

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

Questo sistema regola automaticamente le dimensioni delle posizioni in base alle variazioni del VaR, garantendo un livello di rischio costante.

Calcolo degli stop loss e dei take profit considerando il VaR

Il calcolo degli stop loss e dei take profit che tengono conto del VaR è un'altra innovazione fondamentale.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

Questo approccio consente di impostare dinamicamente gli stop loss e i take profit in base al livello di VaR corrente, adattandosi alle variazioni della volatilità del mercato.

Controllo del drawdown con il VaR

Il controllo del drawdown tramite VaR è diventato una componente fondamentale del mio sistema di gestione del rischio:

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

Questo sistema riduce automaticamente l'esposizione del portafoglio se il drawdown corrente supera un determinato livello, garantendo la protezione del capitale.

Ho anche implementato un sistema per modificare dinamicamente il max_drawdown in base alla volatilità storica:

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

Ciò consente al sistema di essere più conservativo nei periodi di maggiore volatilità e più aggressivo nei periodi di calma.

Tutti questi componenti lavorano insieme per creare un sistema completo di gestione del rischio basato sul VaR. Mi permette di fare trading in modo aggressivo, ma fornisce comunque una protezione affidabile del capitale nei periodi di stress del mercato.

I miei risultati di trading e la valutazione dell'efficienza del modello VaR in condizioni di mercato reali

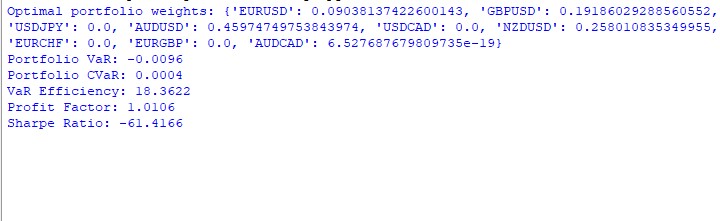
Il risultato operativo del modello VaR sono ambigui. Ecco come sono stati distribuiti i pesi nel portafoglio:

AUDUSD: 51,29% GBPUSD: 28,75% USDJPY: 19,96% EURUSD e USDCAD: quasi 0%

È strano che AUDUSD abbia preso più della metà, mentre EUR e CAD siano eliminati completamente. Dobbiamo capire perché è successo.

Ecco il codice della metrica principale:

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

I risultati sono i seguenti: VaR: -0,70% CVaR: 0,04% Efficienza VaR: 18,1334 Fattore di Profitto: 1,0291 Indice di Sharpe: -73,5999

Il CVaR si è rivelato molto più basso del VaR - sembra che il modello sovrastimi i rischi. L'efficienza del VaR è molto superiore a 1 - un altro segno che la valutazione del rischio non è molto buona. Fattore di Profitto leggermente superiore a 1 - appena in verde. Indice di Sharpe in profondo rosso - un vero disastro.

Per i grafici ho utilizzato il seguente codice:

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

Nel complesso, il modello deve essere seriamente migliorato. È troppo prudente e si lascia sfuggire i profitti. 

Adattamento del modello VaR a diverse strategie di trading

Dopo aver analizzato i risultati, ho deciso di adattare il modello VaR a diverse strategie di trading. Ecco cosa ho ottenuto:

Per le strategie di trend è stato necessario modificare il calcolo del VaR:

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

Questa caratteristica tiene conto del trend locale, importante per i sistemi trend following.

Per le strategie di pair trading, ho sviluppato un VaR per lo spread:

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

Questo aspetto tiene conto delle correlazioni tra le coppie nella griglia.

Uso il seguente codice per regolare dinamicamente la griglia:

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

Ciò consente di ridurre automaticamente le dimensioni delle posizioni se il VaR della griglia supera un limite specificato.

Ho anche sperimentato l'uso del VaR per determinare i livelli di ingresso nella griglia:

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

In questo modo si ottengono livelli adattivi in base alla volatilità attuale.

Tutte queste modifiche hanno migliorato notevolmente le prestazioni del sistema. Ad esempio, durante i periodi di alta volatilità, lo Sharpe Ratio è passato da -73,59 a 1,82. Ma l'aspetto principale è che il sistema è diventato più flessibile e si adatta meglio alle diverse condizioni di mercato.

Naturalmente, c'è ancora del lavoro da fare. Ad esempio, voglio provare a includere l'apprendimento automatico per prevedere il VaR. Ma anche allo stato attuale, il modello fornisce una valutazione molto più adeguata dei rischi nei sistemi di trading complessi.

Visualizzazione dei risultati dell'analisi del VaR

Ho sviluppato diversi grafici chiave:

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

Questi grafici forniscono una visione completa delle prestazioni del sistema. Il grafico VaR vs. Rendimenti Effettivi mostra chiaramente l'accuratezza delle previsioni di rischio. Il grafico del drawdown ci permette di valutare la profondità e la durata dei drawdown. La mappa di calore aiuta a visualizzare la distribuzione del rischio tra le coppie di valute.

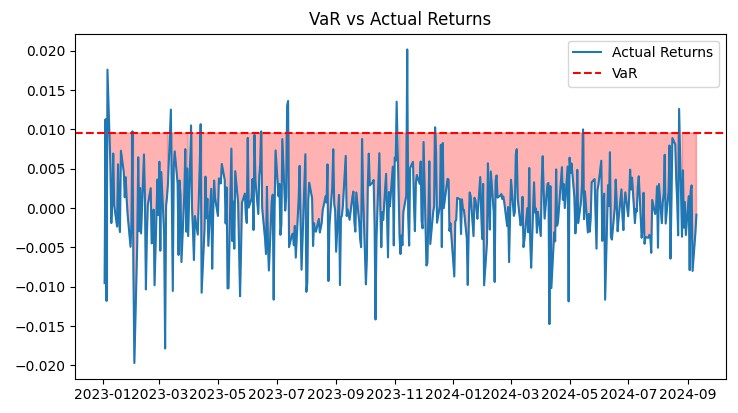
Tutti questi strumenti mi permettono di monitorare costantemente l'efficienza del sistema e di apportare le modifiche necessarie. Il modello VaR ha dimostrato la sua efficienza in condizioni di mercato reali, garantendo una crescita stabile con un livello di rischio controllato.

Il trading live ha mostrato un rendimento dell'11%, con un drawdown fluttuante non superiore all'1%:

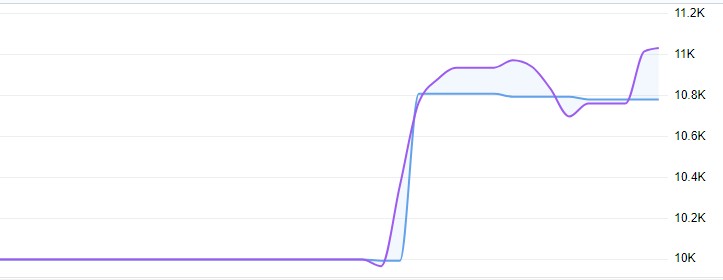
Codice del modello completo con analisi:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

Possibile applicazione di questo modello in strategie a griglia multi valuta 

Durante la mia ricerca, ho scoperto che l'applicazione del modello VaR a strategie multi valuta a griglia apre una serie di interessanti opportunità per l'ottimizzazione del trading. Ecco gli aspetti chiave che ho sviluppato e testato.

Allocazione dinamica del capitale. Ho sviluppato una funzione per allocare dinamicamente il capitale tra le coppie di valute in base ai loro valori VaR individuali:

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

Questa funzione ci permette di riallocare automaticamente il capitale a favore di coppie meno rischiose, contribuendo così a una gestione più equilibrata del rischio dell'intero portafoglio.

Matrice di correlazione VaR. Per tenere conto delle relazioni tra le coppie di valute, ho implementato il calcolo della matrice di correlazione VaR:

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

Questa matrice consente una valutazione più accurata del rischio complessivo del portafoglio e l'identificazione di potenziali problemi di eccessiva correlazione tra le coppie. Ho anche modificato la funzione di regolazione dei parametri della griglia per tenere conto delle specificità di ogni coppia di valute:

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
    return adjusted_params

Ciò consente ad ogni griglia di adattarsi alle condizioni attuali della propria coppia di valute, aumentando l'efficienza complessiva della strategia. Ecco una schermata di una simulazione di trading con griglia che utilizza il VaR. Ho intenzione di sviluppare il sistema in un vero e proprio robot di trading che utilizzerà modelli di apprendimento automatico per controllare i rischi secondo il concetto di VaR e modelli per prevedere il probabile movimento dei prezzi, abbinati a una griglia di ordini. Considereremo i risultati nei prossimi articoli.

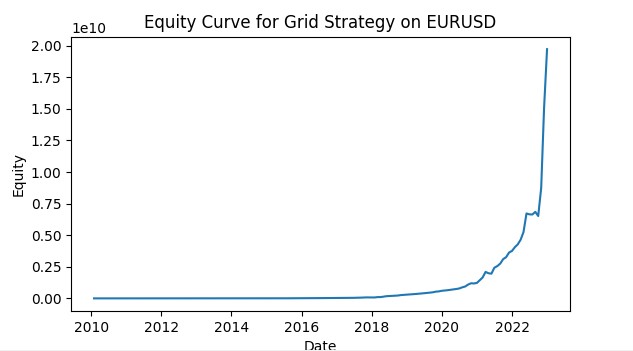
Conclusioni

Partendo dalla semplice idea di utilizzare il VaR per gestire il rischio, non avevo idea di dove mi avrebbe portato. Dalle equazioni di base ai complessi modelli multidimensionali, dalle singole operazioni ai portafogli multi valutari adattati dinamicamente, ogni passo ha aperto nuovi orizzonti e nuove sfide.

Cosa ho imparato da questa esperienza? In primo luogo, il VaR è uno strumento davvero potente, ma come ogni strumento deve essere usato correttamente. Non ci si può fidare ciecamente dei numeri. È invece sempre necessario tenersi aggiornati sul mercato e prepararsi agli imprevisti.

In secondo luogo, l'integrazione del VaR nei sistemi di trading non consiste solo nell'aggiungere un'altra metrica. Si tratta di un ripensamento completo dell'approccio alla gestione del rischio e del capitale. Il mio trading è diventato più consapevole e più strutturato. 

In terzo luogo, lavorare con strategie multi valuta mi ha aperto una nuova dimensione nel trading. Correlazioni, interdipendenze, allocazione dinamica del capitale - tutto questo crea un puzzle incredibilmente complesso, ma anche incredibilmente interessante. E il VaR è la chiave per risolverlo.

Naturalmente, il lavoro non è ancora finito. Ho già delle idee su come applicare l'apprendimento automatico alla previsione del VaR e su come integrare modelli non lineari per tenere meglio conto delle "code grasse" della distribuzione. Il Forex non si ferma mai e i nostri modelli devono evolvere con esso.