Die Gruppenmethode der Datenverarbeitung: Implementierung des mehrschichtigen iterativen Algorithmus in MQL5

Einführung

Die Group Method of Data Handling (GMDH) ist eine Familie von induktiven Algorithmen, die für die computergestützte Datenmodellierung verwendet werden. Die Algorithmen arbeiten durch automatische Konstruktion und Optimierung polynomialer neuronaler Netzmodelle aus Daten und bieten einen einzigartigen Ansatz zur Aufdeckung von Beziehungen zwischen Eingabe- und Ausgabevariablen. Traditionell bestand das GMDH-System aus vier Hauptalgorithmen: dem kombinatorischen Algorithmus (COMBI), dem kombinatorischen selektiven Algorithmus (MULTI), dem mehrschichtigen iterativen Algorithmus (MIA) und dem iterativen Relaxationsalgorithmus (RIA). In diesem Artikel werden wir die Implementierung des mehrschichtigen iterativen Algorithmus in MQL5 untersuchen, erläutern das Innenleben der Software und zeigen, wie sie zur Erstellung von Vorhersagemodellen aus Datensätzen eingesetzt werden kann.

GMDH verstehen: Die Gruppenmethode der Datenverarbeitung

Die Gruppenmethode der Datenverarbeitung ist eine Art Algorithmus, der für die Datenanalyse und -vorhersage verwendet wird. Es handelt sich um eine Technik des maschinellen Lernens, die darauf abzielt, das beste mathematische Modell zur Beschreibung eines bestimmten Datensatzes zu finden. GMDH wurde in den 1960er Jahren von dem sowjetischen Mathematiker Alexey Ivakhnenko entwickelt. Es wurde entwickelt, um die Herausforderungen zu bewältigen, die mit der Modellierung komplexer Systeme auf der Grundlage empirischer Daten verbunden sind. GMDH-Algorithmen verwenden einen datengesteuerten Ansatz zur Modellierung, bei dem Modelle auf der Grundlage von Beobachtungsdaten und nicht von vorgefassten Meinungen oder theoretischen Annahmen erstellt und verfeinert werden.

Einer der Hauptvorteile von GMDH ist, dass es den Prozess der Modellerstellung automatisiert, indem es iterativ Kandidatenmodelle generiert und bewertet, die leistungsfähigsten Modelle auswählt und sie auf der Grundlage des Datenfeedbacks verfeinert. Diese Automatisierung verringert den Bedarf an manuellen Eingriffen und Fachwissen bei der Erstellung des Modells.

Der Grundgedanke von GMDH besteht darin, durch iterative Auswahl und Kombination von Variablen eine Reihe von Modellen mit zunehmender Komplexität und Genauigkeit zu erstellen. Der Algorithmus beginnt mit einer Reihe einfacher Modelle (in der Regel lineare Modelle) und erhöht schrittweise deren Komplexität durch Hinzufügen zusätzlicher Variablen und Terme. Bei jedem Schritt bewertet der Algorithmus die Leistung der Modelle und wählt die besten aus, die die Grundlage für die nächste Iteration bilden. Dieser Prozess wird so lange fortgesetzt, bis ein zufriedenstellendes Modell erhalten wird oder bis ein Abbruchkriterium erfüllt ist.

Die GMDH eignet sich besonders gut für die Modellierung von Datensätzen mit einer großen Anzahl von Eingabevariablen und komplexen Beziehungen zwischen ihnen. GMDH-Techniken führen zu Modellen, die Eingaben mit einer Ausgabe verbinden, die durch ein unendliches Volterra–Kolmogorov–Gabor-Polynom (VKG) dargestellt werden kann. Ein Volterra-Kolmogorov-Gabor-Polynom (VKG) ist eine spezielle Art von Polynom, das bei der Modellierung nichtlinearer Systeme und der Annäherung komplexer Daten verwendet wird. Ein VKG-Polynom hat die folgende Form:

wobei:

• Yn ist der Output des Systems.
• Xi, Xj, and Xk sind die Eingangsvariablen zum Zeitpunkt i, j bzw. k.
• ai, aj, ak usw. sind die Koeffizienten des Polynoms.

Ein solches Polynom kann als polynomielles neuronales Netz (PNN) betrachtet werden. PNNs sind eine Art von künstlichen neuronalen Netzen (ANN), die polynomiale Aktivierungsfunktionen in ihren Neuronen verwenden, wobei die Struktur eines polynomialen neuronalen Netzes der anderer neuronaler Netze ähnelt, mit Eingabeknoten, versteckten Schichten und Ausgabeknoten. Die Aktivierungsfunktionen, die auf die Neuronen in PNNs angewendet werden, sind jedoch polynomielle Funktionen. Parametrische GMDH-Algorithmen wurden speziell für den Umgang mit kontinuierlichen Variablen entwickelt. Wenn das zu modellierende Objekt durch Eigenschaften gekennzeichnet ist, die in ihrer Darstellung oder Definition nicht eindeutig sind. Der mehrschichtige iterative Algorithmus ist ein Beispiel für einen parametrischen GMDH-Algorithmus.

Mehrschichtiger iterativer Algorithmus

MIA ist eine Variante des GMDH Frameworks für die Konstruktion polynomialer neuronaler Netzmodelle. Seine Struktur ist fast identisch mit der eines mehrschichtigen neuronalen Netzes mit Vorwärtskopplung. Die Informationen fließen von der Eingabeschicht über Zwischenschichten bis zur endgültigen Ausgabe. Jede Ebene führt spezifische Transformationen an den Daten durch. Im Vergleich zur allgemeinen Methode der GMDH liegt das Hauptunterscheidungsmerkmal von MIA in der Auswahl der optimalen Unterfunktionen des endgültigen Polynoms, das die Daten am besten beschreibt. Das bedeutet, dass ein Teil der durch die Ausbildung gewonnenen Informationen nach einem vorher festgelegten Kriterium verworfen wird.

Um ein Modell mit MIA zu erstellen, wird der zu untersuchende Datensatz zunächst in einen Trainings- und einen Testdatensatz unterteilt. Wir wollen so viel Vielfalt wie möglich in der Trainingsmenge haben, um die Eigenschaften des zugrunde liegenden Prozesses angemessen zu erfassen. Wir beginnen mit dem Schichtaufbau, sobald dieser abgeschlossen ist. 

Aufbau der Schichten

Ähnlich wie bei einem mehrschichtigen neuronalen Netz mit Vorwärtskopplung beginnen wir mit der Eingabeschicht, die eine Sammlung von Prädiktoren oder unabhängigen Variablen darstellt. Diese Eingaben werden jeweils zu zweit in die erste Schicht des Netzes eingespeist. Die erste Schicht besteht also aus „M Kombinationen von 2“ Knoten, wobei M die Anzahl der Prädiktoren ist.

Die obige Abbildung zeigt ein Beispiel dafür, wie die Eingabeschicht und die erste Schicht bei 4 Eingaben (bezeichnet als x1..x4) aussehen werden. In der ersten Schicht werden Teilmodelle auf der Grundlage der Eingaben eines Knotens unter Verwendung des Trainingsdatensatzes erstellt und das resultierende Teilmodell anhand des Testdatensatzes bewertet. Der Vorhersagefehler aller Teilmodelle in der Schicht wird dann verglichen. Die besten N Modelle werden notiert und zur Erzeugung der Eingaben für die nächste Schicht verwendet. Die Vorhersagefehler der obersten N Modelle einer Schicht werden auf irgendeine Weise kombiniert, um ein einziges Maß zu erhalten, das einen Hinweis auf den Gesamtfortschritt bei der Modellerstellung gibt. Diese wird mit der Zahl der vorherigen Schicht verglichen. Ist der Wert geringer, wird eine neue Ebene erstellt und der Vorgang wiederholt, adernfalls, wenn keine Verbesserung eintritt, wird die Modellerstellung gestoppt und die Daten der aktuellen Schicht werden verworfen, was bedeutet, dass das Modelltraining abgeschlossen ist.

Knotenpunkte und Teilmodelle

An jedem Knoten einer Schicht wird ein Polynom berechnet, das die Beobachtungen im Trainingsdatensatz schätzt, wenn das Paar von Eingaben von der vorherigen Schicht ausgegeben wird. Dies ist ein so genanntes Partialmodell. Ein Beispiel für eine Gleichung, die zur Modellierung der Ausgaben des Trainingssatzes unter Berücksichtigung der Eingaben des Knotens verwendet wird, ist unten dargestellt.

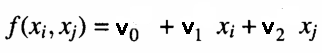
Wobei „v“ die Koeffizienten des angepassten linearen Modells sind. Die Anpassungsgüte wird durch Bestimmung des mittleren quadratischen Fehlers der Vorhersagen gegenüber den tatsächlichen Werten im Testdatensatz geprüft. Diese Fehlermessungen werden dann auf irgendeine Weise kombiniert. Entweder durch Berechnung ihres Durchschnitts oder einfach durch Auswahl des Knotens mit dem geringsten mittleren quadratischen Fehler. Diese letzte Maßnahme gibt Aufschluss darüber, ob sich die Annäherungen im Vergleich zu anderen Schichten verbessern oder nicht. Gleichzeitig werden die besten N-Knoten mit dem geringsten Vorhersagefehler notiert. Und die entsprechenden Koeffizienten werden verwendet, um die Werte eines Satzes neuer Eingaben für die nächste Schicht zu generieren. Wenn die Annäherungen der aktuellen Schicht besser (in diesem Fall schlechter) sind als die der vorherigen Schicht, wird eine neue Schicht gebildet.

Wenn das Netz vollständig ist, werden nur die Koeffizienten der Knoten mit dem besten Vorhersagefehler auf jeder Schicht beibehalten und zur Definition des endgültigen Modells verwendet, das die Daten am besten beschreibt. Im folgenden Abschnitt werden wir uns mit dem Code befassen, der das soeben beschriebene Verfahren implementiert. Der Code ist an eine C++-Implementierung der GMDH angepasst, die unter GitHub verfügbar ist.

MQL5-Implementierung

Die C++-Implementierung trainiert Modelle und speichert sie im JSON-Format in einer Textdatei zur späteren Verwendung. Es wird Parallelverarbeitung verwendet, um das Training zu beschleunigen, und es basiert auf Boost- und Eigen-Bibliotheken. Für unsere MQL5-Implementierung werden die meisten Funktionen übernommen, mit Ausnahme des Multithreading-Trainings und der Verfügbarkeit von alternativen Optionen für die QR Zerlegung zur Lösung linearer Gleichungen.

Unsere Implementierung wird aus drei Header-Dateien bestehen. Die erste ist gmdh_internal.mqh. Diese Datei enthält Definitionen für verschiedene nutzerdefinierte Datentypen. Sie beginnt mit der Definition von drei Enumerationen:

• PolynomialType - gibt die Art des Polynoms an, das zur Transformation vorhandener Variablen verwendet wird, bevor eine weitere Trainingsrunde durchgeführt wird.
  

  //+---------------------------------------------------------------------------------------------------------+
  //|  Enumeration for specifying the polynomial type to be used to construct new variables from existing ones|
  //+---------------------------------------------------------------------------------------------------------+
  enum PolynomialType
    {
     linear,
     linear_cov,
     quadratic
    };

  „PolynomialType“ stellt drei Optionen zur Verfügung, die die folgenden polymialen Funktionen darstellen, wobei x1 und x2 die Eingaben für die Funktion f(x1,x2) und v0...vN die zu findenden Koeffizienten sind. Die Enumeration steht für die Art der Gleichungen, aus denen die Lösungsmenge generiert wird:

Option	Funktion f(x1,x2)
linear	lineare Gleichung: v0 + v1*x1 + v2*x2
linear_cov	lineare Gleichung mit Kovariation: v0 + v1*x1 + v2*x2 + v3*x1*x2
quadratisch	quadratische Gleichung: v0 + v1*x1 + v2*x2 + v3*x1*x2 + v4*x1^2 + v5*x2^2

• Gleichungslöser - bestimmt die QR-Dekompositionsmethode, die zur Lösung linearer Gleichungen verwendet wird. Unsere Implementierung wird nur eine brauchbare Option haben. Die C++-Version verwendet Variationen der Householder-Methode zur QR-Dekompostierung unter Verwendung der Eigen-Bibliothek.
  

  //+-----------------------------------------------------------------------------------------------+
  //|  Enum  for specifying the QR decomposition method for linear equations solving in models.     |
  //+-----------------------------------------------------------------------------------------------+
  enum Solver
    {
     fast,
     accurate,
     balanced
    };

• CriterionType - ermöglicht es dem Nutzer, ein spezifisches externes Kriterium auszuwählen, das als Grundlage für die Bewertung der Kandidatenmodelle verwendet wird. Die Enumeration umfasst die Optionen, die man beim Training eines Modells als Abbruchkriterien verwenden kann.
  

  //+------------------------------------------------------------------+
  //|Enum for specifying the external criterion                        |
  //+------------------------------------------------------------------+
  enum CriterionType
    {
     reg,
     symReg,
     stab,
     symStab,
     unbiasedOut,
     symUnbiasedOut,
     unbiasedCoef,
     absoluteNoiseImmun,
     symAbsoluteNoiseImmun
    };

  Die verfügbaren Optionen werden in der folgenden Tabelle näher erläutert:

CriterionType	Beschreibung
reg	Regelmäßigkeit: Anwendung der regelmäßigen Summe der quadrierten Fehler (SSE) auf der Grundlage der Differenz zwischen den Zielen des Testdatensatzes und den Vorhersagen, die mit den Koeffizienten aus dem Trainingsdatensatz in Kombination mit den Prädiktoren des Testdatensatzes berechnet wurden.
symReg	symmetrische Regelmäßigkeit: ist die Summe der SSE auf der Grundlage der Differenz zwischen den Zielen des Testdatensatzes und den Vorhersagen, die mit Koeffizienten gemacht wurden, die unter Verwendung des Trainingsdatensatzes in Kombination mit den Prädiktoren des Testdatensatzes berechnet wurden, und der SSE auf der Grundlage der Differenz zwischen den Zielen des Trainingsdatensatzes und den Vorhersagen, die mit Koeffizienten gemacht wurden, die unter Verwendung des Testdatensatzes in Kombination mit den Prädiktoren des Trainingsdatensatzes berechnet wurden.
stab	Stabilität: verwendet den SSE, der auf der Differenz zwischen allen Zielen und den Vorhersagen basiert, die mit den Koeffizienten berechnet wurden, die aus dem Trainingsdatensatz in Kombination mit allen Prädiktoren stammen.
symStab	Symetrische Stabilität: Dieses Kriterium kombiniert die SSE, die ähnlich wie das Stabilitätskriterium berechnet wird, sowie die SSE, die auf der Differenz zwischen allen Zielen und Vorhersagen basiert, die mit Koeffizienten erstellt wurden, die anhand des Testdatensatzes in Kombination mit allen Prädiktoren des Datensatzes berechnet wurden.
unbiasedOut	Unbiased Outputs: ist der SSE, der auf der Differenz zwischen den Vorhersagen mit den aus dem Trainingsdatensatz berechneten Koeffizienten und den Vorhersagen mit den aus dem Testdatensatz berechneten Koeffizienten beruht, wobei beide die Prädiktoren des Testdatensatzes verwenden.
symUnbiasedOut	symmetrische unbiasedOutputs: Berechnet die SSE auf die gleiche Weise wie das Kriterium „unbiasedOutputs“, nur dass diesmal alle Prädiktoren verwendet werden.
unbiasedCoef	unverzerrte Koeffizienten: die Summe der quadrierten Differenzen zwischen den Koeffizienten, die anhand der Trainingsdaten berechnet wurden, und den Koeffizienten, die anhand der Testdaten berechnet wurden.
absoluteNoiseImmun	absolute Störfestigkeit: Bei dieser Option wird das Kriterium als Punktprodukt der Vorhersagen des auf dem gesamten Datensatz trainierten Modells minus der Vorhersagen des auf dem Trainingsdatensatz trainierten Modells bei Anwendung auf den Testdatensatz und der Vorhersagen des auf dem Testdatensatz trainierten Modells minus der Vorhersagen des auf dem Lerndatensatz trainierten Modells bei Anwendung auf den Testdatensatz berechnet.
symAbsoluteNoiseImmun	symmetrische absolute Rauschimmunität: hier ist das Kriterium das Punktprodukt der Vorhersagen des auf dem gesamten Datensatz trainierten Modells abzüglich der Vorhersagen des auf dem Trainingsdatensatz trainierten Modells bei Anwendung auf den Lerndatensatz und der Vorhersagen des auf dem gesamten Datensatz trainierten Modells und der Vorhersagen des auf dem Testdatensatz trainierten Modells bei Anwendung auf alle Beobachtungen.

Auf die Enumerationen folgen vier nutzerdefinierte Strukturen:

• BufferValues - ist eine Struktur von Vektoren zur Speicherung von Koeffizienten und vorhergesagten Werten, die auf verschiedene Weise unter Verwendung der Test- und Trainingsdatensätze berechnet wurden.
  

  //+-------------------------------------------------------------------------------------+
  //| Structure for storing coefficients and predicted values calculated in different ways|
  //+--------------------------------------------------------------------------------------+
  struct BufferValues
    {
     vector            coeffsTrain; // Coefficients vector calculated using training data
     vector            coeffsTest; // Coefficients vector calculated using testing data
     vector            coeffsAll; // Coefficients vector calculated using learning data
     vector            yPredTrainByTrain; // Predicted values for *training* data calculated using coefficients vector calculated on *training* data
     vector            yPredTrainByTest; // Predicted values for *training* data calculated using coefficients vector calculated on *testing* data
     vector            yPredTestByTrain; // Predicted values for *testing* data calculated using coefficients vector calculated on *training* data
     vector            yPredTestByTest; //Predicted values for *testing* data calculated using coefficients vector calculated on *testing* data
  
                       BufferValues(void)
       {
  
       }
  
                       BufferValues(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
       }
  
     BufferValues      operator=(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
  
        return this;
       }
  
    };

  
  
• PairDVXd - kapselt eine Datenstruktur, die einen Skalar und einen entsprechenden Vektor kombiniert.
  

  //+------------------------------------------------------------------+
  //|  struct PairDV                                                   |
  //+------------------------------------------------------------------+
  struct PairDVXd
    {
     double            first;
     vector            second;
  
                       PairDVXd(void)
       {
        first = 0.0;
        second = vector::Zeros(10);
       }
  
                       PairDVXd(double &_f, vector &_s)
       {
        first = _f;
        second.Copy(_s);
       }
  
                       PairDVXd(PairDVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairDVXd          operator=(PairDVXd& other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

  
  
• PairMVXd - ist eine Struktur, die eine Matrix und einen Vektor kombiniert. Zusammen speichern sie die Eingaben und die entsprechenden Ausgaben oder Zielwerte. Die Eingaben werden in der Matrix gespeichert, und der Vektor ist die Sammlung der Ausgaben. Jede Zeile in der Matrix entspricht einem Wert im Vektor.
  

  //+------------------------------------------------------------------+
  //| structure PairMVXd                                               |
  //+------------------------------------------------------------------+
  struct PairMVXd
    {
     matrix            first;
     vector            second;
  
                       PairMVXd(void)
       {
        first = matrix::Zeros(10,10);
        second = vector::Zeros(10);
       }
  
                       PairMVXd(matrix &_f,  vector& _s)
       {
        first = _f;
        second = _s;
       }
  
                       PairMVXd(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairMVXd          operator=(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

• SplittedData - diese Datenstruktur speichert die partitionierten Datensätze für Training und Test.
  

  //+------------------------------------------------------------------+
  //|  Structure for storing parts of a split dataset                  |
  //+------------------------------------------------------------------+
  struct SplittedData
    {
     matrix            xTrain;
     matrix            xTest;
     vector            yTrain;
     vector            yTest;
  
                       SplittedData(void)
       {
        xTrain = matrix::Zeros(10,10);
        xTest = matrix::Zeros(10,10);
        yTrain = vector::Zeros(10);
        yTest = vector::Zeros(10);
       }
  
                       SplittedData(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
       }
  
     SplittedData      operator=(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
  
        return this;
       }
    };

  
  

Nach den Structs kommen wir zu den Klassendefinitionen:

• Die Klasse Combination stellt ein Kandidatenmodell dar. Sie speichert die Bewertungskriterien, die Kombination der Eingaben und die berechneten Koeffizienten für ein Modell.
  

  //+------------------------------------------------------------------+
  //| Сlass representing the candidate model of the GMDH algorithm     |
  //+------------------------------------------------------------------+
  class Combination
    {
     vector            _combination,_bestCoeffs;
     double            _evaluation;
  public:
                       Combination(void) { _combination = vector::Zeros(10); _bestCoeffs.Copy(_combination); _evaluation = DBL_MAX; }
                       Combination(vector &comb) : _combination(comb) { _bestCoeffs=vector::Zeros(_combination.Size()); _evaluation = DBL_MAX;}
                       Combination(vector &comb, vector &coeffs) : _combination(comb),_bestCoeffs(coeffs) { _evaluation = DBL_MAX; }
                       Combination(Combination &other) { _combination = other.combination(); _bestCoeffs=other.bestCoeffs(); _evaluation = other.evaluation();}
     vector            combination(void) { return _combination;}
     vector            bestCoeffs(void)  { return _bestCoeffs; }
     double            evaluation(void)  { return _evaluation; }
  
     void              setCombination(vector &combination) { _combination = combination; }
     void              setBestCoeffs(vector &bestcoeffs) { _bestCoeffs = bestcoeffs; }
     void              setEvaluation(double evaluation)  { _evaluation = evaluation; }
  
     bool              operator<(Combination &combi) { return _evaluation<combi.evaluation();}
     Combination       operator=(Combination &combi)
       {
        _combination = combi.combination();
        _bestCoeffs = combi.bestCoeffs();
        _evaluation = combi.evaluation();
  
        return this;
       }
    };

• CVector - definiert einen nutzerdefinierten, vektorähnlichen Container, der eine Sammlung von Instanzen der Klasse Combination speichert. Es wird zu einem Container mit Kandidatenmodellen.

  //+------------------------------------------------------------------+
  //| collection of Combination instances                              |
  //+------------------------------------------------------------------+
  class CVector
    {
  protected:
     Combination       m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector(CVector &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]=other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(Combination &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, Combination &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     Combination*      operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector           operator=(CVector &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     Combination*      back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     Combination*      front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• CVector2d - ist ein weiterer nutzerdefinierter, vektorähnlicher Container, der eine Sammlung von CVector-Instanzen speichert.
  

  //+------------------------------------------------------------------+
  //| Collection of CVector instances                                  |
  //+------------------------------------------------------------------+
  class CVector2d
    {
  protected:
     CVector           m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector2d(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector2d(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector2d(CVector2d &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector2d(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(CVector &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, CVector &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     CVector*          operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector2d         operator=(CVector2d &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     CVector*          back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     CVector*          front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
  
        for(uint i = 0; i<m_array.Size(); i++)
           m_array[i].clear();
  
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• Criterion - diese Klasse implementiert die Berechnung verschiedener externer Kriterien auf der Grundlage eines ausgewählten Kriteriumstyps.
  

  //+---------------------------------------------------------------------------------+
  //|Class that implements calculations of internal and individual external criterions|
  //+---------------------------------------------------------------------------------+
  class Criterion
    {
  protected:
     CriterionType     criterionType; // Selected CriterionType object
     Solver            solver; // Selected Solver object
  
  public:
     /**
     Implements the internal criterion calculation
     param xTrain Matrix of input variables that should be used to calculate the model coefficients
     param yTrain Target values vector for the corresponding xTrain parameter
     return Coefficients vector representing a solution of the linear equations system constructed from the parameters data
     */
     vector            findBestCoeffs(matrix& xTrain,  vector& yTrain)
       {
        vector solution;
  
        matrix q,r;
  
        xTrain.QR(q,r);
  
        matrix qT = q.Transpose();
  
        vector y = qT.MatMul(yTrain);
  
        solution = r.LstSq(y);
  
  
        return solution;
       }
  
     /**
      Calculate the value of the selected external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param _criterionType Selected external criterion type
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of external criterion and calculated model coefficients
      */
     PairDVXd          getResult(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 CriterionType _criterionType, BufferValues& bufferValues)
       {
        switch(_criterionType)
          {
           case reg:
              return regularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symReg:
              return symRegularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case stab:
              return stability(xTrain, xTest, yTrain, yTest, bufferValues);
           case symStab:
              return symStability(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedOut:
              return unbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case symUnbiasedOut:
              return symUnbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedCoef:
              return unbiasedCoeffs(xTrain, xTest, yTrain, yTest, bufferValues);
           case absoluteNoiseImmun:
              return absoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symAbsoluteNoiseImmun:
              return symAbsoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
          }
  
        PairDVXd pd;
        return pd;
       }
     /**
      Calculate the regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the regularity external criterion and calculated model coefficients
      */
     PairDVXd          regularity(matrix& xTrain, matrix& xTest, vector &yTrain, vector& yTest,
                                  BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           f = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
     /**
      Calculate the symmetric regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic regularity external criterion and calculated model coefficients
      */
     PairDVXd          symRegularity(matrix& xTrain, matrix& xTest, vector& yTrain, vector& yTest,
                                     BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = regularity(xTrain,xTest,yTrain,yTest,bufferValues);
        pdv2 = regularity(xTrain,xTest,yTrain,yTest,bufferValues,true);
  
        pdsum.first = pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the stability external criterion and calculated model coefficients
      */
     PairDVXd          stability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f1,f2;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTrainByTrain.Size() == 0)
              bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTrain),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
  
           pdv.first = f1.Sum()+f2.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           if(bufferValues.yPredTestByTest.Size() == 0)
              bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTest),2.0);
           pdv.first = f1.Sum() + f2.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
  
     /**
      Calculate the symmetric stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic stability external criterion and calculated model coefficients
      */
     PairDVXd          symStability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                    BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = stability(xTrain, xTest, yTrain, yTest, bufferValues);
        pdv2 = stability(xTrain, xTest, yTrain, yTest, bufferValues, true);
  
        pdsum.first=pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedOutputs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                       BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          symUnbiasedOutputs(matrix &xTrain,  matrix &xTest,  vector &yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1,f2;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
        if(bufferValues.yPredTrainByTrain.Size() == 0)
           bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTrainByTest.Size() == 0)
           bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f1 = MathPow((bufferValues.yPredTrainByTrain - bufferValues.yPredTrainByTest),2.0);
        f2 = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f1.Sum() + f2.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the unbiased coefficients external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased coefficients external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedCoeffs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        f1 = MathPow((bufferValues.coeffsTrain - bufferValues.coeffsTest),2.0);
        pdv.first = f1.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          absoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        vector yPredTestByAll,f1,f2;
        PairDVXd pdv;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
          {
           matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
           for(ulong i = 0; i<xTrain.Rows(); i++)
              dataX.Row(xTrain.Row(i),i);
  
           for(ulong i = 0; i<xTest.Rows(); i++)
              dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
           vector dataY(yTrain.Size() + yTest.Size());
  
           for(ulong i=0; i<yTrain.Size(); i++)
              dataY[i] = yTrain[i];
  
           for(ulong i=0; i<yTest.Size(); i++)
              dataY[i+yTrain.Size()] = yTest[i];
  
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
          }
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        yPredTestByAll = xTest.MatMul(bufferValues.coeffsAll);
  
        f1 =  yPredTestByAll - bufferValues.yPredTestByTrain;
        f2 = bufferValues.yPredTestByTest - yPredTestByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          symAbsoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector yPredAllByTrain, yPredAllByTest, yPredAllByAll,f1,f2;
        matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
        for(ulong i = 0; i<xTrain.Rows(); i++)
           dataX.Row(xTrain.Row(i),i);
  
        for(ulong i = 0; i<xTest.Rows(); i++)
           dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
        vector dataY(yTrain.Size() + yTest.Size());
  
        for(ulong i=0; i<yTrain.Size(); i++)
           dataY[i] = yTrain[i];
  
        for(ulong i=0; i<yTest.Size(); i++)
           dataY[i+yTrain.Size()] = yTest[i];
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
  
        yPredAllByTrain = dataX.MatMul(bufferValues.coeffsTrain);
        yPredAllByTest = dataX.MatMul(bufferValues.coeffsTest);
        yPredAllByAll = dataX.MatMul(bufferValues.coeffsAll);
  
        f1 = yPredAllByAll - yPredAllByTrain;
        f2 = yPredAllByTest - yPredAllByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
  
       }
  
     /**
      Get k models from the given ones with the best values of the external criterion
     param combinations Vector of the trained models
     param data Object containing parts of a split dataset used in model training. Parameter is used in sequential criterion
     param func Function returning the new X train and X test data constructed from the original data using given combination of input variables column indexes. Parameter is used in sequential criterion
     param k Number of best models
     return Vector containing k best models
      */
     virtual void      getBestCombinations(CVector &combinations, CVector &bestCombo,SplittedData& data, MatFunc func, int k)
       {
        double proxys[];
        int best[];
  
        ArrayResize(best,combinations.size());
        ArrayResize(proxys,combinations.size());
  
        for(int i = 0 ; i<combinations.size(); i++)
          {
           proxys[i] = combinations[i].evaluation();
           best[i] = i;
          }
  
        MathQuickSortAscending(proxys,best,0,combinations.size()-1);
  
        for(int i = 0; i<int(MathMin(MathAbs(k),combinations.size())); i++)
           bestCombo.push_back(combinations[best[i]]);
  
       }
     /**
      Calculate the value of the selected external criterion for the given data.
      For the individual criterion this method only calls the getResult() method
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     return The value of the external criterion and calculated model coefficients
      */
     virtual PairDVXd  calculate(matrix& xTrain,  matrix& xTest,
                                 vector& yTrain,  vector& yTest)
       {
        BufferValues tempValues;
        return getResult(xTrain, xTest, yTrain, yTest, criterionType, tempValues);
       }
  
  public:
     ///  Construct a new Criterion object
                       Criterion() {};
  
     /**
      Construct a new Criterion object
     param _criterionType Selected external criterion type
     param _solver Selected method for linear equations solving
      */
                       Criterion(CriterionType _criterionType)
       {
        criterionType = _criterionType;
        solver = balanced;
       }
  
    };
  

Schließlich gibt es noch zwei Funktionen, die das Ende von gmdh_internal.mqh markieren:

validateInputData() - wird verwendet, um sicherzustellen, dass an Klassenmethoden oder andere eigenständige Funktionen übergebene Werte korrekt angegeben sind.

**
 *  Validate input parameters values
 *
 * param testSize Fraction of the input data that should be placed into the second part
 * param pAverage The number of best models based of which the external criterion for each level will be calculated
 * param threads The number of threads used for calculations. Set -1 to use max possible threads
 * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
 * param limit The minimum value by which the external criterion should be improved in order to continue training
 * param kBest The number of best models based of which new models of the next level will be constructed
 * return Method exit status
 */
int validateInputData(double testSize=0.0, int pAverage=0, double limit=0.0, int kBest=0)
  {
   int errorCode = 0;
//
   if(testSize <= 0 || testSize >= 1)
     {
      Print("testsize value must be in the (0, 1) range");
      errorCode |= 1;
     }
   if(pAverage && pAverage < 1)
     {
      Print("p_average value must be a positive integer");
      errorCode |= 4;
     }
   if(limit && limit < 0)
     {
      Print("limit value must be non-negative");
      errorCode |= 8;
     }
   if(kBest && kBest < 1)
     {
      Print("k_best value must be a positive integer");
      errorCode |= 16;
     }

   return errorCode;
  }

timeSeriesTransformation() - ist eine Hilfsfunktion, die als Eingabe eine Reihe in einem Vektor nimmt und sie in eine Datenstruktur von Eingaben und Zielen entsprechend der gewählten Anzahl von Verzögerungen transformiert.

/**
 *  Convert the time series vector to the 2D matrix format required to work with GMDH algorithms
 *
 * param timeSeries Vector of time series data
 * param lags The lags (length) of subsets of time series into which the original time series should be divided
 * return Transformed time series data
 */
PairMVXd timeSeriesTransformation(vector& timeSeries, int lags)
  {
   PairMVXd p;

   string errorMsg = "";
   if(timeSeries.Size() == 0)
      errorMsg = "time_series value is empty";
   else
      if(lags <= 0)
         errorMsg = "lags value must be a positive integer";
      else
         if(lags >= int(timeSeries.Size()))
            errorMsg = "lags value can't be greater than  time_series  size";
   if(errorMsg != "")
      return p;

   ulong last = timeSeries.Size() - ulong(lags);
   vector yTimeSeries(last,slice,timeSeries,ulong(lags));
   matrix xTimeSeries(last, ulong(lags));
   vector vect;
   for(ulong i = 0; i < last; ++i)
     {
      vect.Init(ulong(lags),slice,timeSeries,i,i+ulong(lags-1));
      xTimeSeries.Row(vect,i);
     }

   p.first = xTimeSeries;
   p.second = yTimeSeries;

   return p;
  }

Lags bezieht sich hier auf die Anzahl der vorherigen Reihenwerte, die als Prädiktoren zur Berechnung eines nachfolgenden Terms verwendet werden.

Damit ist die Beschreibung von gmdh_internal.mqh abgeschlossen. Weiter geht es mit der zweiten Header-Datei, gmdh.mqh.

Sie beginnt mit der Definition der Funktion splitData().

/**
 *  Divide the input data into 2 parts
 *
 * param x Matrix of input data containing predictive variables
 * param y Vector of the taget values for the corresponding x data
 * param testSize Fraction of the input data that should be placed into the second part
 * param shuffle True if data should be shuffled before splitting into 2 parts, otherwise false
 * param randomSeed Seed number for the random generator to get the same division every time
 * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
 */
SplittedData splitData(matrix& x,  vector& y, double testSize = 0.2, bool shuffle = false, int randomSeed = 0)
  {
   SplittedData data;

   if(validateInputData(testSize))
      return data;
   
   string errorMsg = "";
   if(x.Rows() != y.Size())
      errorMsg = " x rows number and y size must be equal";
   else
      if(round(x.Rows() * testSize) == 0 || round(x.Rows() * testSize) == x.Rows())
         errorMsg = "Result contains an empty array. Change the arrays size or the  value for correct splitting";
   if(errorMsg != "")
     {
      Print(__FUNCTION__," ",errorMsg);
      return data;
     }


   if(!shuffle)
      data = GmdhModel::internalSplitData(x, y, testSize);
   else
     {
      if(randomSeed == 0)
         randomSeed = int(GetTickCount64());
      MathSrand(uint(randomSeed));

      int shuffled_rows_indexes[],shuffled[];
      MathSequence(0,int(x.Rows()-1),1,shuffled_rows_indexes);
      MathSample(shuffled_rows_indexes,int(shuffled_rows_indexes.Size()),shuffled);

      int testItemsNumber = (int)round(x.Rows() * testSize);


      matrix Train,Test;
      vector train,test;

      Train.Resize(x.Rows()-ulong(testItemsNumber),x.Cols());
      Test.Resize(ulong(testItemsNumber),x.Cols());

      train.Resize(x.Rows()-ulong(testItemsNumber));
      test.Resize(ulong(testItemsNumber));

      for(ulong i = 0; i<Train.Rows(); i++)
        {
         Train.Row(x.Row(shuffled[i]),i);
         train[i] = y[shuffled[i]];
        }

      for(ulong i = 0; i<Test.Rows(); i++)
        {
         Test.Row(x.Row(shuffled[Train.Rows()+i]),i);
         test[i] = y[shuffled[Train.Rows()+i]];
        }

      data.xTrain = Train;
      data.xTest = Test;
      data.yTrain = train;
      data.yTest = test;
     }

   return data;
  }  

Als Eingabe dienen eine Matrix und ein Vektor, die Variablen bzw. Ziele darstellen. Der Parameter „testSize“ legt den Anteil des Datensatzes fest, der als Testsatz verwendet werden soll. „shuffle“ ermöglicht das zufällige Mischen des Datensatzes und „randomSeed“ gibt den Seed für einen Zufallszahlengenerator an, der beim Mischen verwendet wird.

Als Nächstes haben wir die Klasse „GmdhModel“, die die allgemeine Logik der GMDH-Algorithmen definiert.

//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH algorithms          |
//+------------------------------------------------------------------+

class  GmdhModel
  {
protected:

   string            modelName; // model name
   int               level; // Current number of the algorithm training level
   int               inputColsNumber; // The number of predictive variables in the original data
   double            lastLevelEvaluation; // The external criterion value of the previous training level
   double            currentLevelEvaluation; // The external criterion value of the current training level
   bool              training_complete; // flag indicator successful completion of model training
   CVector2d         bestCombinations; // Storage for the best models of previous levels

   /**
    *struct for generating vector sequence
    */
   struct unique
     {
   private:
      int            current;

      int            run(void)
        {
         return ++current;
        }

   public:
                     unique(void)
        {
         current = -1;
        }

      vector         generate(ulong t)
        {
         ulong s=0;
         vector ret(t);

         while(s<t)
            ret[s++] = run();

         return ret;
        }
     };

   /**
    *  Find all combinations of k elements from n
    *
    * param n Number of all elements
    * param k Number of required elements
    * return Vector of all combinations of k elements from n
    */
   void              nChooseK(int n, int k, vector &combos[])
     {
      if(n<=0 || k<=0 || n<k)
        {
         Print(__FUNCTION__," invalid parameters for n and or k", "n ",n , " k ", k);
         return;
        }

      unique q;

      vector comb = q.generate(ulong(k));

      ArrayResize(combos,combos.Size()+1,100);

      long first, last;

      first = 0;
      last = long(k);
      combos[combos.Size()-1]=comb;

      while(comb[first]!= double(n - k))
        {
         long mt = last;
         while(comb[--mt] == double(n - (last - mt)));
         comb[mt]++;
         while(++mt != last)
            comb[mt] = comb[mt-1]+double(1);
         ArrayResize(combos,combos.Size()+1,100);
         combos[combos.Size()-1]=comb;
        }

      for(uint i = 0; i<combos.Size(); i++)
        {
         combos[i].Resize(combos[i].Size()+1);
         combos[i][combos[i].Size()-1] = n;
        }

      return;
     }

   /**
    *  Get the mean value of extrnal criterion of the k best models
    *
    * param sortedCombinations Sorted vector of current level models
    * param k The numebr of the best models
    * return Calculated mean value of extrnal criterion of the k best models
    */
   double            getMeanCriterionValue(CVector &sortedCombinations, int k)
     {
      k = MathMin(k, sortedCombinations.size());

      double crreval=0;

      for(int i = 0; i<k; i++)
         crreval +=sortedCombinations[i].evaluation();
      if(k)
         return crreval/double(k);
      else
        {
         Print(__FUNCTION__, " Zero divide error ");
         return 0.0;
        }
     }

   /**
    *  Get the sign of the polynomial variable coefficient
    *
    * param coeff Selected coefficient
    * param isFirstCoeff True if the selected coefficient will be the first in the polynomial representation, otherwise false
    * return String containing the sign of the coefficient
    */
   string            getPolynomialCoeffSign(double coeff, bool isFirstCoeff)
     {
      return ((coeff >= 0) ? ((isFirstCoeff) ? " " : " + ") : " - ");
     }

   /**
    *  Get the rounded value of the polynomial variable coefficient without sign
    *
    * param coeff Selected coefficient
    * param isLastCoeff True if the selected coefficient will be the last one in the polynomial representation, otherwise false
    * return String containing the rounded value of the coefficient without sign
    */
   string            getPolynomialCoeffValue(double coeff, bool isLastCoeff)
     {
      string stringCoeff = StringFormat("%e",MathAbs(coeff));
      return ((stringCoeff != "1" || isLastCoeff) ? stringCoeff : "");
     }

   /**
    *  Train given subset of models and calculate external criterion for them
    *
    * param data Data used for training and evaulating models
    * param criterion Selected external criterion
    * param beginCoeffsVec Iterator indicating the beginning of a subset of models
    * param endCoeffsVec Iterator indicating the end of a subset of models
    * param leftTasks The number of remaining untrained models at the entire level
    * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
    */
   bool              polynomialsEvaluation(SplittedData& data,  Criterion& criterion,  CVector &combos, uint beginCoeffsVec,
                                           uint endCoeffsVec)
     {
      vector cmb,ytrain,ytest;
      matrix x1,x2;
      for(uint i = beginCoeffsVec; i<endCoeffsVec; i++)
        {
         cmb = combos[i].combination();
         x1 = xDataForCombination(data.xTrain,cmb);
         x2 = xDataForCombination(data.xTest,cmb);
         ytrain = data.yTrain;
         ytest = data.yTest;
         PairDVXd pd = criterion.calculate(x1,x2,ytrain,ytest);

         if(pd.second.HasNan()>0)
            {
             Print(__FUNCTION__," No solution found for coefficient at ", i, "\n xTrain \n", x1, "\n xTest \n", x2, "\n yTrain \n", ytrain, "\n yTest \n", ytest);
             combos[i].setEvaluation(DBL_MAX);
             combos[i].setBestCoeffs(vector::Ones(3));
            }
         else
            {
             combos[i].setEvaluation(pd.first);
             combos[i].setBestCoeffs(pd.second);
            } 
        }

      return true;
     }

   /**
   *  Determine the need to continue training and prepare the algorithm for the next level
   *
   * param kBest The number of best models based of which new models of the next level will be constructed
   * param pAverage The number of best models based of which the external criterion for each level will be calculated
   * param combinations Trained models of the current level
   * param criterion Selected external criterion
   * param data Data used for training and evaulating models
   * param limit The minimum value by which the external criterion should be improved in order to continue training
   * return True if the algorithm needs to continue training, otherwise fasle
   */
   bool              nextLevelCondition(int kBest, int pAverage, CVector &combinations,
                                        Criterion& criterion, SplittedData& data, double limit)
     {
      MatFunc fun = NULL;
      CVector bestcombinations;
      criterion.getBestCombinations(combinations,bestcombinations,data, fun, kBest);
      currentLevelEvaluation = getMeanCriterionValue(bestcombinations, pAverage);

      if(lastLevelEvaluation - currentLevelEvaluation > limit)
        {
         lastLevelEvaluation = currentLevelEvaluation;
         if(preparations(data,bestcombinations))
           {
            ++level;
            return true;
           }
        }
      removeExtraCombinations();
      return false;

     }

   /**
    *  Fit the algorithm to find the best solution
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param criterion Selected external criterion
    * param kBest The number of best models based of which new models of the next level will be constructed
    * param testSize Fraction of the input data that should be used to evaluate models at each level
    * param pAverage The number of best models based of which the external criterion for each level will be calculated
    * param limit The minimum value by which the external criterion should be improved in order to continue training
    * return A pointer to the algorithm object for which the training was performed
    */
   bool              gmdhFit(matrix& x,  vector& y,  Criterion& criterion, int kBest,
                             double testSize, int pAverage, double limit)
     {
      if(x.Rows() != y.Size())
        {
         Print("X rows number and y size must be equal");
         return false;
        }

      level = 1; // reset last training
      inputColsNumber = int(x.Cols());
      lastLevelEvaluation = DBL_MAX;

      SplittedData data = internalSplitData(x, y, testSize, true) ;
      training_complete = false;
      bool goToTheNextLevel;
      CVector evaluationCoeffsVec;
      do
        {
         vector combinations[];
         generateCombinations(int(data.xTrain.Cols() - 1),combinations);
         
         if(combinations.Size()<1)
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }  

         evaluationCoeffsVec.clear();

         int currLevelEvaluation = 0;
         for(int it = 0; it < int(combinations.Size()); ++it, ++currLevelEvaluation)
           {
            Combination ncomb(combinations[it]);
            evaluationCoeffsVec.push_back(ncomb);
           }

         if(!polynomialsEvaluation(data,criterion,evaluationCoeffsVec,0,uint(currLevelEvaluation)))
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }

         goToTheNextLevel = nextLevelCondition(kBest, pAverage, evaluationCoeffsVec, criterion, data, limit); // checking the results of the current level for improvement
        }
      while(goToTheNextLevel);

      training_complete = true;

      return true;
     }

   /**
    *  Get new model structures for the new level of training
    *
    * param n_cols The number of existing predictive variables at the current training level
    * return Vector of new model structures
    */
   virtual void      generateCombinations(int n_cols,vector &out[])
     {
      return;
     }


   ///  Removed the saved models that are no longer needed
   virtual void      removeExtraCombinations(void)
     {
      return;
     }

   /**
    *  Prepare data for the next training level
    *
    * param data Data used for training and evaulating models at the current level
    * param _bestCombinations Vector of the k best models of the current level
    * return True if the training process can be continued, otherwise false
    */
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations)
     {
      return false;
     }

   /**
    *  Get the data constructed according to the model structure from the original data
    *
    * param x Training data at the current level
    * param comb Vector containing the indexes of the x matrix columns that should be used in the model
    * return Constructed data
    */
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)
     {
      return matrix::Zeros(10,10);
     }

   /**
    *  Get the designation of polynomial equation
    *
    * param levelIndex The number of the level counting from 0
    * param combIndex The number of polynomial in the level counting from 0
    * return The designation of polynomial equation
    */
   virtual string    getPolynomialPrefix(int levelIndex, int combIndex)
     {
      return NULL;
     }

   /**
    *  Get the string representation of the polynomial variable
    *
    * param levelIndex The number of the level counting from 0
    * param coeffIndex The number of the coefficient related to the selected variable in the polynomial counting from 0
    * param coeffsNumber The number of coefficients in the polynomial
    * param bestColsIndexes Indexes of the data columns used to construct polynomial of the model
    * return The string representation of the polynomial variable
    */
   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector& bestColsIndexes)
     {
      return NULL;
     }

   /*
    *  Transform model data to JSON format for further saving
    *
    * return JSON value of model data
    */
   virtual CJAVal    toJSON(void)
     {
      CJAVal json_obj_model;

      json_obj_model["modelName"] = getModelName();
      json_obj_model["inputColsNumber"] = inputColsNumber;
      json_obj_model["bestCombinations"] = CJAVal(jtARRAY,"");


      for(int i = 0; i<bestCombinations.size(); i++)
        {

         CJAVal Array(jtARRAY,"");

         for(int k = 0; k<bestCombinations[i].size(); k++)
           {
            CJAVal collection;
            collection["combination"] = CJAVal(jtARRAY,"");
            collection["bestCoeffs"] = CJAVal(jtARRAY,"");
            vector combination = bestCombinations[i][k].combination();
            vector bestcoeff = bestCombinations[i][k].bestCoeffs();
            for(ulong j=0; j<combination.Size(); j++)
               collection["combination"].Add(int(combination[j]));
            for(ulong j=0; j<bestcoeff.Size(); j++)
               collection["bestCoeffs"].Add(bestcoeff[j],-15);
            Array.Add(collection);
           }

         json_obj_model["bestCombinations"].Add(Array);

        }

      return json_obj_model;

     }

   /**
    *  Set up model from JSON format model data
    *
    * param jsonModel Model data in JSON format
    * return Method exit status
    */
   virtual bool      fromJSON(CJAVal &jsonModel)
     {
      modelName = jsonModel["modelName"].ToStr();
      bestCombinations.clear();
      inputColsNumber = int(jsonModel["inputColsNumber"].ToInt());

      for(int i = 0; i<jsonModel["bestCombinations"].Size(); i++)
        {
         CVector member;
         for(int j = 0; j<jsonModel["bestCombinations"][i].Size(); j++)
           {
            Combination cb;
            vector c(ulong(jsonModel["bestCombinations"][i][j]["combination"].Size()));
            vector cf(ulong(jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size()));
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["combination"].Size(); k++)
               c[k] = jsonModel["bestCombinations"][i][j]["combination"][k].ToDbl();
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size(); k++)
               cf[k] = jsonModel["bestCombinations"][i][j]["bestCoeffs"][k].ToDbl();
            cb.setBestCoeffs(cf);
            cb.setCombination(c);
            member.push_back(cb);
           }
         bestCombinations.push_back(member);
        }
      return true;
     }



   /**
    *  Compare the number of required and actual columns of the input matrix
    *
    * param x Given matrix of input data
    */
   bool              checkMatrixColsNumber(matrix& x)
     {
      if(ulong(inputColsNumber) != x.Cols())
        {
         Print("Matrix  must have " + string(inputColsNumber) + " columns because there were " + string(inputColsNumber) + " columns in the training  matrix");
         return false;
        }

      return true;
     }
     
     

public:
   ///  Construct a new Gmdh Model object
                     GmdhModel() : level(1), lastLevelEvaluation(0) {}

   /**
   *  Get full class name
   *
   * return String containing the name of the model class
   */
   string            getModelName(void)
     {
      return modelName;
     }
   /**
     *Get number of inputs required for model
     */
    int getNumInputs(void)
     {
      return inputColsNumber;
     }

   /**
    *  Save model data into regular file
    *
    * param path Path to regular file
    */
   bool              save(string file_name)
     {

      CFileTxt modelFile;

      if(modelFile.Open(file_name,FILE_WRITE|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         CJAVal js=toJSON();
         if(modelFile.WriteString(js.Serialize())==0)
           {
            Print("failed write to ",file_name,". Error -",::GetLastError());
            return false;
           }
        }

      return true;
     }

   /**
    *  Load model data from regular file
    *
    * param path Path to regular file
    */
   bool               load(string file_name)
     {
      training_complete = false;
      CFileTxt modelFile;
      CJAVal js;

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         training_complete = fromJSON(js);
        }
      return training_complete;
     }
   /**
    *  Divide the input data into 2 parts without shuffling
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param testSize Fraction of the input data that should be placed into the second part
    * param addOnesCol True if it is needed to add a column of ones to the x data, otherwise false
    * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
    */
   static SplittedData internalSplitData(matrix& x,  vector& y, double testSize, bool addOnesCol = false)
     {
      SplittedData data;
      ulong testItemsNumber = ulong(round(double(x.Rows()) * testSize));
      matrix Train,Test;
      vector train,test;

      if(addOnesCol)
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols() + 1);
         Test.Resize(testItemsNumber, x.Cols() + 1);

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         Train.Col(vector::Ones(Train.Rows()),x.Cols());

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);

         Test.Col(vector::Ones(Test.Rows()),x.Cols());

        }
      else
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols());
         Test.Resize(testItemsNumber, x.Cols());

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);
        }

      train.Init(y.Size() - testItemsNumber,slice,y,0,y.Size() - testItemsNumber - 1);
      test.Init(testItemsNumber,slice,y,y.Size() - testItemsNumber);

      data.yTrain = train;
      data.yTest = test;

      data.xTrain = Train;
      data.xTest = Test;

      return data;
     }

   /**
    *  Get long-term forecast for the time series
    *
    * param x One row of the test time series data
    * param lags The number of lags (steps) to make a forecast for
    * return Vector containing long-term forecast
    */
   virtual vector    predict(vector& x, int lags)
     {
      return vector::Zeros(1);
     }

   /**
    *  Get the String representation of the best polynomial
    *
    * return String representation of the best polynomial
    */
   string            getBestPolynomial(void)
     {
      string polynomialStr = "";
      int ind = 0;
      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector bestColsIndexes = bestCombinations[i][j].combination();
            vector bestCoeffs = bestCombinations[i][j].bestCoeffs();
            polynomialStr += getPolynomialPrefix(i, j);
            bool isFirstCoeff = true;
            for(int k = 0; k < int(bestCoeffs.Size()); ++k)
              {
               if(bestCoeffs[k])
                 {
                  polynomialStr += getPolynomialCoeffSign(bestCoeffs[k], isFirstCoeff);
                  string coeffValuelStr = getPolynomialCoeffValue(bestCoeffs[k], (k == (bestCoeffs.Size() - 1)));
                  polynomialStr += coeffValuelStr;
                  if(coeffValuelStr != "" && k != bestCoeffs.Size() - 1)
                     polynomialStr += "*";
                  polynomialStr += getPolynomialVariable(i, k, int(bestCoeffs.Size()), bestColsIndexes);
                  isFirstCoeff = false;
                 }
              }
            if(i < bestCombinations.size() - 1 || j < (bestCombinations[i].size() - 1))
               polynomialStr += "\n";
           }//j
         if(i < bestCombinations.size() - 1 && bestCombinations[i].size() > 1)
            polynomialStr += "\n";
        }//i
      return polynomialStr;
     }

                    ~GmdhModel()
     {
      for(int i = 0; i<bestCombinations.size(); i++)
         bestCombinations[i].clear();

      bestCombinations.clear();
     }
  };


//+------------------------------------------------------------------+

Sie ist die Basisklasse, von der andere GMDH-Typen abgeleitet werden. Es bietet Methoden für das Training oder die Erstellung eines Modells und die anschließende Erstellung von Vorhersagen. Die Methoden „save“ und „load“ ermöglichen das Speichern eines Modells und das Laden aus einer Datei zur späteren Verwendung. Die Modelle werden im JSON-Format in einer Textdatei in dem für alle MetaTrader-Terminals gemeinsamen Verzeichnis gespeichert.

Die letzte Header-Datei, mia.mqh, enthält die Definition der Klasse „MIA“.

//+------------------------------------------------------------------+
//| Class implementing multilayered iterative algorithm MIA          |
//+------------------------------------------------------------------+
class MIA : public GmdhModel
  {
protected:
   PolynomialType    polynomialType; // Selected polynomial type

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,2,out);
      return;
     }
   /**
   *  Get predictions for the input data
   *
   * param x Test data of the regression task or one-step time series forecast
   * return Vector containing prediction values
   */
   virtual vector    calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         matrix xNew(1, ulong(bestCombinations[i].size()) + 1);
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector comb = bestCombinations[i][j].combination();
            matrix xx(1,comb.Size());
            for(ulong i = 0; i<xx.Cols(); ++i)
               xx[0][i] = modifiedX[0][ulong(comb[i])];
            matrix ply = getPolynomialX(xx);
            vector c,b;
            c = bestCombinations[i][j].bestCoeffs();
            b = ply.MatMul(c);
            xNew.Col(b,ulong(j));
           }
         vector n  = vector::Ones(xNew.Rows());
         xNew.Col(n,xNew.Cols() - 1);
         modifiedX = xNew;
        }

      return modifiedX.Col(0);

     }

   /**
    *  Construct vector of the new variable values according to the selected polynomial type
    *
    * param x Matrix of input variables values for the selected polynomial type
    * return Construct vector of the new variable values
    */
   matrix            getPolynomialX(matrix& x)
     {
      matrix polyX = x;
      if((polynomialType == linear_cov))
        {
         polyX.Resize(x.Rows(), 4);
         polyX.Col(x.Col(0)*x.Col(1),2);
         polyX.Col(x.Col(2),3);
        }
      else
         if((polynomialType == quadratic))
           {
            polyX.Resize(x.Rows(), 6);
            polyX.Col(x.Col(0)*x.Col(1),2) ;
            polyX.Col(x.Col(0)*x.Col(0),3);
            polyX.Col(x.Col(1)*x.Col(1),4);
            polyX.Col(x.Col(2),5) ;
           }

      return polyX;
     }

   /**
    *  Transform data in the current training level by constructing new variables using selected polynomial type
    *
    * param data Data used to train models at the current level
    * param bestCombinations Vector of the k best models of the current level
    */
   virtual void      transformDataForNextLevel(SplittedData& data,  CVector &bestCombs)
     {
      matrix xTrainNew(data.xTrain.Rows(), ulong(bestCombs.size()) + 1);
      matrix xTestNew(data.xTest.Rows(), ulong(bestCombs.size()) + 1);

      for(int i = 0; i < bestCombs.size(); ++i)
        {
         vector comb = bestCombs[i].combination();

         matrix train(xTrainNew.Rows(),comb.Size()),test(xTrainNew.Rows(),comb.Size());

         for(ulong k = 0; k<comb.Size(); k++)
           {
            train.Col(data.xTrain.Col(ulong(comb[k])),k);
            test.Col(data.xTest.Col(ulong(comb[k])),k);
           }

         matrix polyTest,polyTrain;
         vector bcoeff = bestCombs[i].bestCoeffs();
         polyTest = getPolynomialX(test);
         polyTrain = getPolynomialX(train);

         xTrainNew.Col(polyTrain.MatMul(bcoeff),i);
         xTestNew.Col(polyTest.MatMul(bcoeff),i);
        }

      xTrainNew.Col(vector::Ones(xTrainNew.Rows()),xTrainNew.Cols() - 1);
      xTestNew.Col(vector::Ones(xTestNew.Rows()),xTestNew.Cols() - 1);

      data.xTrain = xTrainNew;
      data.xTest =  xTestNew;
     }

   virtual void      removeExtraCombinations(void) override
     {

      CVector2d realBestCombinations(bestCombinations.size());
      CVector n;
      n.push_back(bestCombinations[level-2][0]);
      realBestCombinations.setAt(realBestCombinations.size() - 1,n);

      vector comb(1);
      for(int i = realBestCombinations.size() - 1; i > 0; --i)
        {
         double usedCombinationsIndexes[],unique[];
         int indexs[];
         int prevsize = 0;
         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            ArrayResize(usedCombinationsIndexes,prevsize+int(comb.Size()-1),100);
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               usedCombinationsIndexes[ulong(prevsize)+k] = comb[k];
            prevsize = int(usedCombinationsIndexes.Size());
           }
         MathUnique(usedCombinationsIndexes,unique);
         ArraySort(unique);

         for(uint it = 0; it<unique.Size(); ++it)
            realBestCombinations[i - 1].push_back(bestCombinations[i - 1][int(unique[it])]);

         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               comb[k] = ArrayBsearch(unique,comb[k]);
            comb[comb.Size() - 1] = double(unique.Size());
            realBestCombinations[i][j].setCombination(comb);
           }

         ZeroMemory(usedCombinationsIndexes);
         ZeroMemory(unique);
         ZeroMemory(indexs);
        }

      bestCombinations = realBestCombinations;
     }
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations) override
     {
      bestCombinations.push_back(_bestCombinations);
      transformDataForNextLevel(data, bestCombinations[level - 1]);
      return true;
     }
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)  override
     {
      matrix xx(x.Rows(),comb.Size());

      for(ulong i = 0; i<xx.Cols(); ++i)
         xx.Col(x.Col(ulong(comb[i])),i);

      return getPolynomialX(xx);
     }

   string            getPolynomialPrefix(int levelIndex, int combIndex)  override
     {
      return ((levelIndex < bestCombinations.size() - 1) ?
              "f" + string(levelIndex + 1) + "_" + string(combIndex + 1) : "y") + " =";
     }
   string            getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector &bestColsIndexes)  override
     {
      if(levelIndex == 0)
        {
         if(coeffIndex < 2)
            return "x" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "x" + string(int(bestColsIndexes[0]) + 1) + "*x" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "x" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      else
        {
         if(coeffIndex < 2)
            return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[0]) + 1) +
                      "*f" + string(levelIndex) + "_" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      return "";
     }


   CJAVal            toJSON(void)  override
     {
      CJAVal json_obj_model = GmdhModel::toJSON();

      json_obj_model["polynomialType"] = int(polynomialType);
      return json_obj_model;

     }

   bool              fromJSON(CJAVal &jsonModel) override
     {
      bool parsed = GmdhModel::fromJSON(jsonModel);

      if(!parsed)
         return false;

      polynomialType = PolynomialType(jsonModel["polynomialType"].ToInt());

      return true;
     }

public:
   //+------------------------------------------------------------------+
   //| Constructor                                                      |
   //+------------------------------------------------------------------+

                     MIA(void)
     {
      modelName = "MIA";
     }

   //+------------------------------------------------------------------+
   //| model a time series                                              |
   //+------------------------------------------------------------------+

   virtual bool      fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 3)
        {
         Print(__FUNCTION__," lags must be >= 3");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   //+------------------------------------------------------------------+
   //| model a multivariable data set  of inputs and targets            |
   //+------------------------------------------------------------------+

   virtual bool      fit(matrix &vars,vector &targets,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 3)
        {
         Print(__FUNCTION__," columns in vars must be >= 3");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   virtual vector     predict(vector& x, int lags)  override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;
     }



  };
//+------------------------------------------------------------------+

Es erbt von „GmdhModel“, um den mehrschichtigen iterativen Algorithmus zu implementieren.  „MIA“ hat zwei „fit()“-Überladungen, die zur Modellierung eines bestimmten Datensatzes aufgerufen werden können. Diese Methoden unterscheiden sich durch ihren ersten und zweiten Parameter. Wenn eine Zeitreihe nur mit historischen Werten modelliert werden soll, wird das unten aufgeführte „fit()“ verwendet.

fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)

Die andere ist nützlich bei der Modellierung eines Datensatzes mit abhängigen und unabhängigen Variablen. Die Parameter der beiden Methoden sind in der nächsten Tabelle dokumentiert:

Datentyp	Name des Parameters	Beschreibung
vector	time_series	stellt eine Zeitreihe dar, die in einem Vektor enthalten ist.
integer	lags	definiert die Anzahl der verzögerten Werte, die als Prädiktoren im Modell verwendet werden sollen.
matrix	vars	Matrix von Eingabedaten mit prädiktiven Variablen.
vector	targets	Vektor der Zielwerte für die entsprechenden Zeilenmitglieder von vars.
CriterionType	criterion	Die Enumerationsariable, die die externen Kriterien für den Modellbildungsprozess angibt.
integer	kBest	legt die Anzahl der besten Teilmodelle fest, auf deren Grundlage die neuen Eingänge der nachfolgenden Schicht konstruiert werden.
PolynomType	_polynomialType	Ausgewählter Polynomtyp, der verwendet werden soll, um während des Trainings neue Variablen aus vorhandenen zu konstruieren.
double	testSize	Anteil der Eingabedaten, die für die Bewertung von Modellen verwendet werden sollten.
int	pAverage	Die Anzahl der besten Teilmodelle, die bei der Berechnung der Abbruchkriterien berücksichtigt werden.
double	limit	Der Mindestwert, um den das externe Kriterium verbessert werden sollte, um die Ausbildung fortzusetzen.

Sobald ein Modell trainiert wurde, kann es zur Erstellung von Vorhersagen verwendet werden, indem „predict()“ aufgerufen wird. Die Methode erfordert einen Vektor von Eingaben und einen ganzzahligen Wert, der die gewünschte Anzahl von Vorhersagen angibt. Bei erfolgreicher Ausführung gibt die Methode einen Vektor zurück, der die berechneten Vorhersagen enthält. Andernfalls wird ein Vektor mit Nullen zurückgegeben.  Im folgenden Abschnitt sehen wir uns ein paar einfache Beispiele an, um eine bessere Vorstellung davon zu bekommen, wie der soeben beschriebene Code zu verwenden ist.

Beispiele

Wir werden drei Beispiele durchgehen, die als Skripte implementiert sind. Wie MIA in verschiedenen Szenarien angewendet werden kann. In der ersten geht es um die Erstellung eines Modells einer Zeitreihe. Dabei kann eine bestimmte Anzahl früherer Werte der Reihe verwendet werden, um die nachfolgenden Terme zu bestimmen. Dieses Beispiel ist im Skript MIA_Test.mq5 enthalten, dessen Code im Folgenden gezeigt wird.

//+------------------------------------------------------------------+
//|                                                     MIA_Test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input int NumLags = 3;
input int NumPredictions = 6;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---time series we want to model
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};
//---
   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }
//---instantiate MIA object
   MIA mia;
//---fit the series according to user defined hyper parameters
   if(!mia.fit(tms,NumLags,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---generate filename based on user defined parameter settings
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit);
//---save the trained model
   mia.save(modelname+".json");
//---inputs from original series to be used for making predictions
   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));
//---predictions made from the model
   vector out = mia.predict(in,NumPredictions);
//---output result of prediction
   Print(modelname, " predictions ", out);
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial());
  }
//+------------------------------------------------------------------+

Bei der Ausführung des Skripts kann ein Nutzer verschiedene Aspekte des Modells ändern. „NumLags“ gibt die Anzahl der vorangegangenen Reihenwerte an, aus denen der nächste Term berechnet wird. „NumPredictions“ gibt die Anzahl der Vorhersagen an, die über die angegebene Reihe hinaus gemacht werden sollen. Die übrigen vom Nutzer einstellbaren Parameter entsprechen den Argumenten, die an die Methode „fit()“ übergeben werden. Wenn ein Modell erfolgreich erstellt wurde, wird es in einer Datei gespeichert. Und es werden Vorhersagen gemacht und auf der Registerkarte Experten des Terminals ausgegeben, zusammen mit dem endgültigen Polynom, das das Modell darstellt. Die Ergebnisse der Ausführung des Skripts mit Standardeinstellungen sind unten dargestellt. Das dargestellte Polynom stellt das mathematische Modell dar, das die gegebene Zeitreihe am besten beschreibt. Angesichts der Einfachheit der Serie ist sie eindeutig unnötig kompliziert. Betrachtet man jedoch die Vorhersageergebnisse, so erfasst das Modell immer noch die allgemeine Tendenz der Reihen.

PS      0       22:37:31.246    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
OG      0       22:37:31.246    MIA_Test (USDCHF,D1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00

In einem zweiten Durchlauf des Skripts. NumLags wird auf 4 erhöht. Wir werden sehen, wie sich dies auf das Modell auswirkt.

Beachten Sie, wie viel komplexer das Modell wird, wenn ein zusätzlicher Prädiktor hinzugefügt wird. Und welche Auswirkungen dies auf die Prognosen hat. Das Polynom erstreckt sich nun über mehrere Zeilen, obwohl keine erkennbare Verbesserung der Modellvorhersagen zu verzeichnen ist.

22:37:42.921    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000005,16.00000000000007,17.00000000000011,18.00000000000015]
ML      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_1 = - 1.666667e-01*x2 + 1.166667e+00*x4 + 8.797938e-16*x2*x4 + 6.666667e-01
CO      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_2 = - 6.916614e-15*x3 + 1.000000e+00*x4 + 1.006270e-15*x3*x4 + 1.000000e+00
NN      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_3 = - 5.000000e-01*x1 + 1.500000e+00*x3 + 1.001110e-15*x1*x3 + 1.000000e+00
QR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_1 = 5.000000e-01*f1_1 + 5.000000e-01*f1_3 - 5.518760e-16*f1_1*f1_3 - 1.729874e-14
HR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_2 = 5.000000e-01*f1_1 + 5.000000e-01*f1_2 - 1.838023e-16*f1_1*f1_2 - 8.624525e-15
JK      0       22:37:42.921    MIA_Test (USDCHF,D1)    y = 5.000000e-01*f2_1 + 5.000000e-01*f2_2 - 2.963544e-16*f2_1*f2_2 - 1.003117e-14

In unserem letzten Beispiel betrachten wir ein anderes Szenario, in dem wir durch unabhängige Variablen definierte Ausgaben modellieren wollen. In diesem Beispiel versuchen wir, dem Modell beizubringen, 3 Eingaben zu addieren. Der Code für dieses Beispiel befindet sich in MIA_Multivariable_test.mq5.

//+------------------------------------------------------------------+
//|                                       MIA_miavariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---simple independent and dependent data sets we want to model
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};
//---declare MIA object     
   MIA mia;   
//---train the model based on chosen hyper parameters
   if(!mia.fit(independent,dependent,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---construct filename for generated model
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit)+"_multivars";
//---save the model
   mia.save(modelname+".json");
//---input data to be used as input for making predictions
   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};
//---make predictions and output to the terminal
  for(ulong row = 0; row<unseen.Rows(); row++)
     {
       vector in = unseen.Row(row);
       Print("inputs ", in , " prediction ", mia.predict(in,1));
     }  
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

Die Prädiktoren befinden sich in der Matrix „vars“. Jede Zeile entspricht einem Ziel aus dem Vektor „targets“. Wie im vorherigen Beispiel haben wir die Möglichkeit, verschiedene Aspekte der Trainingshyperparameter des Modells einzustellen. Die Ergebnisse des Trainings mit der Standardeinstellung sind sehr schlecht, wie unten gezeigt.

RE      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [5.999999999999997]
JQ      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [7.5]
QI      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.1]
QK      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      y = 1.900000e+00*x1 + 1.450000e+00*x2 - 9.500000e-01*x1*x2 + 3.100000e+00

Das Modell kann durch Anpassung der Trainingsparameter verbessert werden. Die besten Ergebnisse wurden mit den unten abgebildeten Einstellungen erzielt.

Mit diesen Einstellungen ist das Modell schließlich in der Lage, genaue Vorhersagen für eine Reihe von „ungesehenen“ Eingangsvariablen zu treffen. Auch wenn, wie im ersten Beispiel, das erzeugte Polynom übermäßig komplex ist.

DM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [6.999999999999998]
JI      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [8.999999999999998]
CD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.00000000000001]
OO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
IQ      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
PS      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
LO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
HN      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
PP      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
JM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
NO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
FD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15

Aus den einfachen Beispielen, die wir beobachtet haben, wird deutlich, dass der mehrschichtige iterative Algorithmus für elementare Datensätze zu viel des Guten sein kann. Die erzeugten Polynome können sehr kompliziert werden. Bei solchen Modellen besteht die Gefahr einer Überanpassung der Trainingsdaten. Der Algorithmus kann schließlich Rauschen oder Ausreißer in den Daten erfassen, was zu einer schlechten Verallgemeinerungsleistung bei ungesehenen Stichproben führt. Die Leistung von MIA- und GMDH-Algorithmen hängt im Allgemeinen stark von der Qualität und den Merkmalen der Eingabedaten ab. Verrauschte oder unvollständige Daten können die Genauigkeit und Stabilität des Modells beeinträchtigen, was zu unzuverlässigen Vorhersagen führen kann. Und schließlich ist der Trainingsprozess zwar recht einfach, aber es ist dennoch ein gewisses Maß an Hyperparameter-Abstimmung notwendig, um die besten Ergebnisse zu erzielen. Es ist nicht vollständig automatisiert.

Für unsere letzte Demonstration haben wir ein Skript, das ein Modell aus einer Datei lädt und es für Vorhersagen verwendet. Dieses Beispiel ist in LoadModelFromFile.mq5 enthalten.

//+------------------------------------------------------------------+
//|                                            LoadModelFromFile.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>
//--- input parameters
input string   JsonFileName="";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---declaration of MIA instance
    MIA mia;
//---load the model from file  
    if(!mia.load(JsonFileName))
      return;
//---get the number of required inputs for the loaded model     
    int numlags = mia.getNumInputs();
//---generate arbitrary inputs to make a prediction with  
    vector inputs(ulong(numlags),arange,21.0,1.0);
//---make prediction and output results to terminal    
    Print(JsonFileName," input ", inputs," prediction ", mia.predict(inputs,1));
//---output the model's polynomial    
    Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

Die folgende Grafik veranschaulicht die Funktionsweise des Skripts und das Ergebnis eines erfolgreichen Laufs.

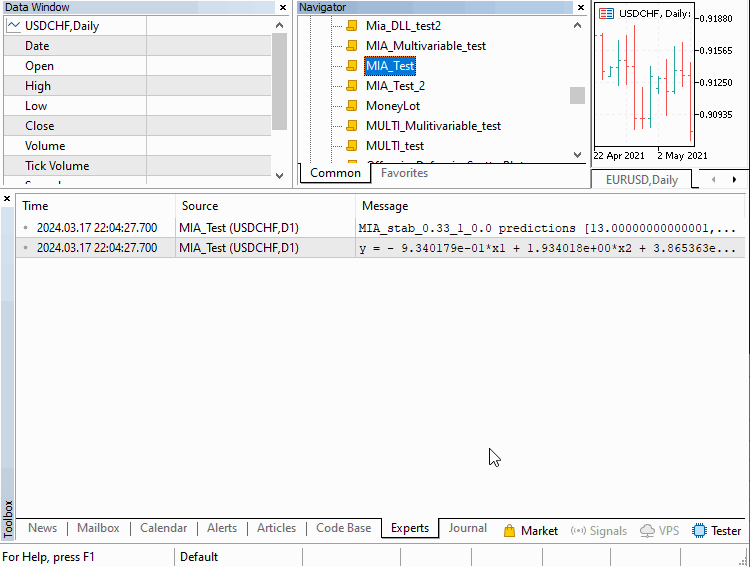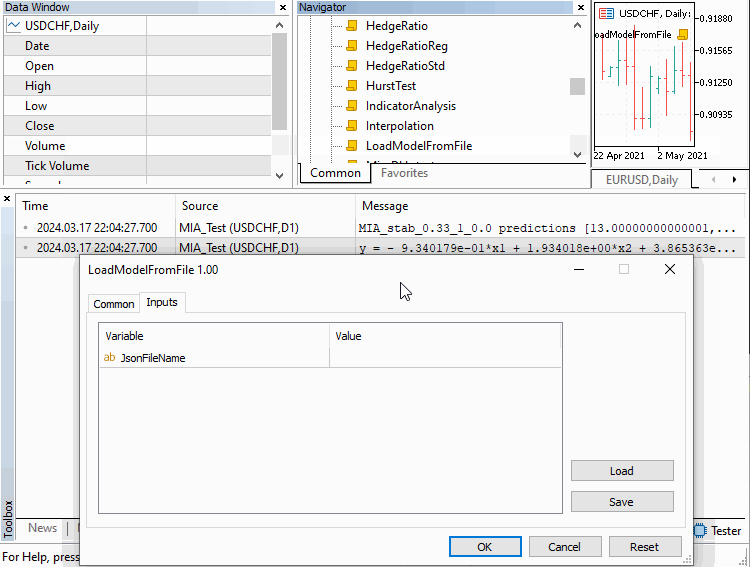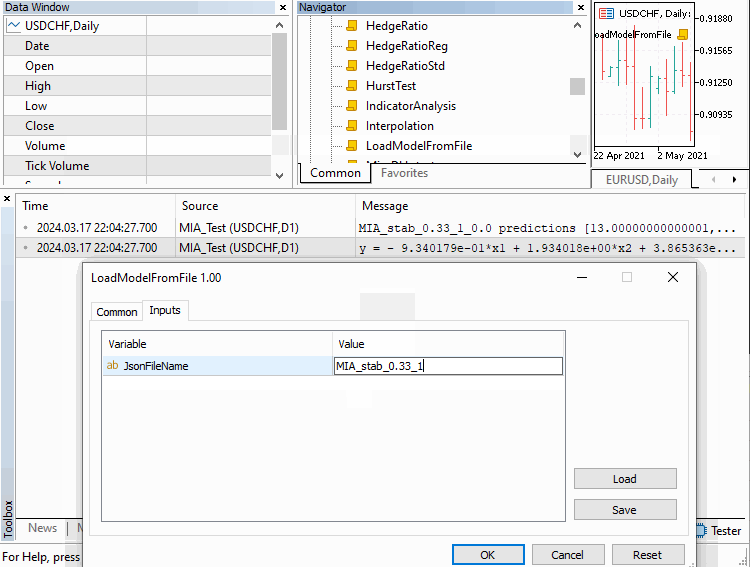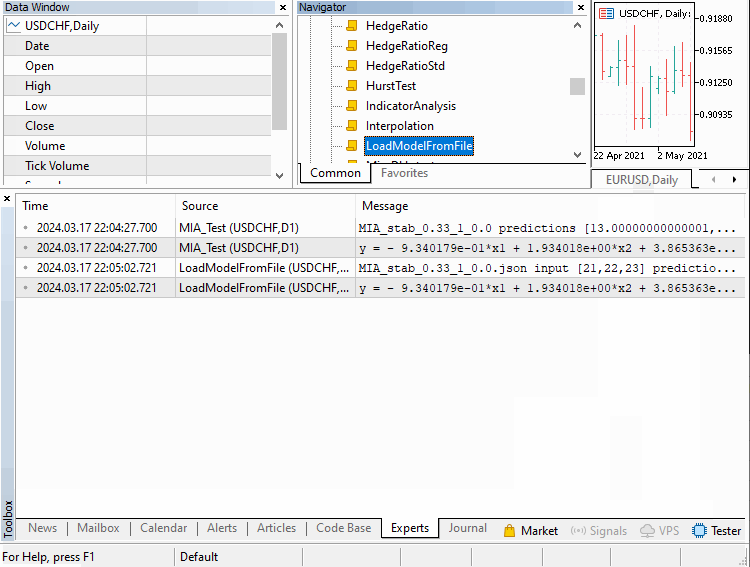
Schlussfolgerung

Die Implementierung des mehrschichtigen iterativen GMDH-Algorithmus in MQL5 bietet Händlern die Möglichkeit, das Konzept in ihren Strategien anzuwenden. Dieser Algorithmus bietet einen dynamischen Rahmen, der es den Nutzern ermöglicht, ihre Marktanalysen kontinuierlich anzupassen und zu verfeinern. Trotz der vielversprechenden Möglichkeiten ist es für Praktiker jedoch unerlässlich, die Grenzen des Systems mit Bedacht zu nutzen. Die Nutzer sollten sich der Rechenanforderungen bewusst sein, die GMDH-Algorithmen mit sich bringen, insbesondere wenn sie mit umfangreichen Datensätzen oder solchen mit hoher Dimensionalität arbeiten. Der iterative Charakter des Algorithmus erfordert mehrere Berechnungen, um die optimale Modellstruktur zu ermitteln, was einen erheblichen Zeit- und Ressourcenaufwand mit sich bringt.

In Anbetracht dieser Überlegungen werden Praktiker dazu angehalten, die Verwendung des mehrschichtigen iterativen GMDH-Algorithmus mit einem differenzierten Verständnis seiner Stärken und Grenzen anzugehen. Sie bietet zwar ein leistungsfähiges Instrument für die dynamische Marktanalyse, aber ihre Komplexität erfordert eine sorgfältige Navigation, um ihr volles Potenzial effektiv zu nutzen. Durch sorgfältige Anwendung und Berücksichtigung seiner Feinheiten können Händler den GMDH-Algorithmus nutzen, um ihre Handelsstrategien zu bereichern und wertvolle Erkenntnisse aus den Marktdaten zu gewinnen.

Der gesamte MQL5-Code ist am Ende des Artikels beigefügt.

Datei	Beschreibung
Mql5\include\VectorMatrixTools.mqh	Header-Datei mit Funktionsdefinitionen für die Bearbeitung von Vektoren und Matrizen.
Mql5\include\JAson.mqh	enthält die Definition der nutzerdefinierten Typen, die zum Parsen und Erzeugen von JSON-Objekten verwendet werden.
Mql5\include\GMDH\gmdh_internal.mqh	Header-Datei mit Definitionen der in der gmdh-Bibliothek verwendeten nutzerdefinierten Typen.
Mql5\include\GMDH\gmdh.mqh	Include-Datei mit der Definition der Basisklasse GmdhModel.
Mql5\include\GMDH\mia.mqh	enthält die Klasse MIA, die den mehrschichtigen iterativen Algorithmus implementiert.
Mql5\script\MIA_Test.mq5	ein Skript, das die Verwendung der MIA-Klasse durch die Erstellung eines Modells einer einfachen Zeitreihe demonstriert.
Mql5\script\MIA_Multivarible_test.mq5	ein weiteres Skript, das die Anwendung der MIA-Klasse zur Erstellung eines Modells für einen multivariablen Datensatz zeigt.
Mql5\script\LoadModelFromFile.mq5	Skript, das demonstriert, wie man ein Modell aus einer json-Datei lädt.