Метод группового учета аргументов: реализация многослойного итерационного алгоритма на MQL5

Введение

Метод группового учета аргументов (МГУА) — это семейство индуктивных алгоритмов для компьютерного моделирования наборов данных. Алгоритмы автоматически строят и оптимизируют модели полиномиальных нейронных сетей на основе данных и позволяют тем самым выявлять взаимосвязи между входными и выходными переменными. Традиционно структура МГУА состояла из четырех основных алгоритмов: комбинаторного, комбинаторного выборочного, многослойного итерационного и релаксационного итерационного. В этой статье мы рассмотрим реализацию многослойного итеративного алгоритма на языке MQL5. Поговорим о его внутренней работе и увидим, как его можно применять для построения прогнозных моделей на основе наборов данных.

Что такое МГУА

Метод группового учета аргументов — это тип алгоритма, используемый для анализа и прогнозирования данных. Это метод машинного обучения, целью которого является поиск лучшей математической модели для описания данного набора данных. Метод был разработан советским математиком А.И.Ивахненко в 1960-х годах. Он был разработан для решения проблем, связанных с моделированием сложных систем на основе эмпирических данных. Алгоритмы МГУА используют подход к моделированию, основанный на данных, при котором модели создаются и уточняются на основе наблюдаемых данных, а не на предвзятых представлениях или теоретических предположениях.

Одним из основных преимуществ МГУА является то, что он автоматизирует процесс построения моделей путем итеративного создания и оценки моделей-кандидатов. Он выбирает наиболее эффективные модели и дорабатывает их на основе полученных данных. Такая автоматизация снижает необходимость ручного вмешательства и специальных знаний при построении модели.

Основная идея метода заключается в построении серии моделей возрастающей сложности и точности путем итеративного выбора и комбинирования переменных. Алгоритм начинается с набора простых моделей (обычно линейных моделей) и постепенно увеличивает их сложность за счет добавления дополнительных переменных и условий. На каждом этапе алгоритм оценивает производительность моделей и выбирает наиболее эффективные из них, чтобы сформировать основу для следующей итерации. Этот процесс продолжается до тех пор, пока не будет получена удовлетворительная модель или пока не будут выполнены критерии остановки.

Алгоритм МГУА особенно хорошо подходит для моделирования наборов данных с большим количеством входных переменных и сложными взаимосвязями между ними. Методы алгоритма позволяют создавать модели, которые связывают входные данные с выходными. Такие данные можно представить в виде бесконечного полинома Вольтерры. Полином Вольтерры (а точнее, Вольтерры-Колмогорова-Габора, ВКГ) — это особый тип полинома, используемый при моделировании нелинейных систем и аппроксимации сложных данных. Полином имеет следующий вид:

Где:

• Yn — выходной параметр системы.
• Xi, Xj и Xk — входные параметры в моменты времени i, j и k соответственно.
• ai, aj, ak и т.д. — коэффициенты полинома.

Такой полином можно рассматривать как полиномиальную нейронную сеть (PNN). PNN — это тип архитектуры искусственной нейронной сети, которая использует полиномиальные функции активации в своих нейронах. Структура полиномиальной нейронной сети аналогична структуре других нейронных сетей с входными узлами, скрытыми слоями и выходными узлами. Однако функции активации, применяемые к нейронам в PNN, являются полиномиальными функциями. Параметрические алгоритмы МГУА были разработаны специально для обработки непрерывных переменных. Когда моделируемый объект характеризуется свойствами, которые не имеют двусмысленности в их представлении или определении. Многослойный итерационный алгоритм (МИА) является примером параметрического алгоритма МГУА.

Многослойный итеративный алгоритм (МИА)

МИА — это вариант структуры МГУА для построения полиномиальных нейросетевых моделей. Структура алгоритма практически идентична многослойной нейронной сети прямого распространения. Информация передается от входного слоя через промежуточные уровни к конечному выходу. Каждый уровень выполняет определенные преобразования данных. По сравнению с общим методом МГУА, ключевая дифференцирующая характеристика МИА заключается в выборе оптимальных подфункций конечного полинома, который лучше всего описывает данные. Это означает, что некоторая информация, полученная в ходе обучения, отбрасывается в соответствии с заранее определенными критериями.

Чтобы построить модель с использованием МИА, мы сначала разделяем набора данных, которые нужно изучить, на обучающую и тестовую выборки. Нам нужно как можно больше разнообразия в обучающем наборе, чтобы он адекватно отображал характеристики основного процесса. Мы начинаем с построения слоев. 

Построение слоев

Как и в многослойной нейронной сети прямого распространения, мы начинаем с входного слоя, который представляет собой набор предикторов или независимых переменных. Эти входные данные принимаются по два за раз и отправляются на первый слой сети. Таким образом, первый слой будет состоять из «M комбинаций из 2» узлов, где M — количество предикторов.

На рисунке выше показан пример того, как будут выглядеть входной слой и первый слой при работе с 4 входами (обозначенными как x1..x4). На первом слое строятся частичные модели на основе входных данных узла с использованием обучающей выборки, и полученная частичная модель затем оценивается на тестовой выборке. Затем сравниваются ошибки прогнозирования всех частичных моделей в слое. При этом N лучших моделей отмечаются и используются для генерации входов для следующего слоя. Ошибки прогнозирования N верхних моделей слоя определенным объединяются, чтобы получить единый индикатор, который дает представление об общем прогрессе в создании модели. Затем он сравнивается с рисунком предыдущего слоя. Если значение меньше, создается новый слой и процесс повторяется. В противном случае, если не будет улучшений, генерация модели останавливается, и данные текущего слоя отбрасываются, указывая на то, что обучение модели будет завершено.

Узлы и частичные модели

В каждом узле слоя вычисляется полином, который оценивает наблюдения в наборе обучающих данных с учетом пары входных данных, выходных из предыдущего слоя. Это и есть частичная модель. Ниже показан пример уравнения, используемого для моделирования выходных данных обучающего набора с учетом входных данных узла.

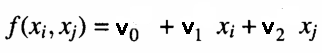
Где v — коэффициенты подобранной линейной модели. Степень соответствия проверяется через определение среднеквадратической ошибки прогнозов по сравнению с фактическими значениями в наборе тестовых данных. Эти меры ошибок затем объединяются. Для этого либо вычисляется их среднее значение, либо просто выбирается узел с наименьшей среднеквадратической ошибкой. Показатель дает представление о том, улучшаются ли аппроксимации по сравнению с другими слоями. При этом отмечаются лучшие N узлов с наименьшей ошибкой прогнозирования. Соответствующие коэффициенты используются для генерации значений набора новых входных данных для следующего слоя. Если приближения текущего слоя лучше (в данном случае хуже), чем у предыдущего слоя, будет построен новый слой.

После завершения построения сети сохраняются только коэффициенты узлов, которые имели наилучшую ошибку прогнозирования на каждом уровне. Они же используются для определения окончательной модели, которая наилучшим образом описывает данные. Далее мы рассмотрим код, реализующий этот процесс. Код адаптирован из реализации GMDH на C++, доступной в GitHub.

Реализация MQL5

В C++-реализации модели обучаются и сохраняются в формате JSON в текстовом файле для последующего использования. Для ускорения обучения используется многопоточность с использованием библиотек Boost и Eigen. Для нашей реализации на MQL5 мы перенесем большинство функций, за исключением многопоточного обучения и наличия альтернативных опций для решения линейных уравнений с QR-разложением.

Наша реализация будет состоять из трех заголовочных файлов. Первый — gmdh_internal.mqh. Файл содержит определения различных пользовательских типов данных. Он начинается с определения трех перечислений:

• PolynomialType — указывает тип полинома, используемого для преобразования существующих переменных перед выполнением следующего раунда обучения.
  

  //+---------------------------------------------------------------------------------------------------------+
  //|  Enumeration for specifying the polynomial type to be used to construct new variables from existing ones|
  //+---------------------------------------------------------------------------------------------------------+
  enum PolynomialType
    {
     linear,
     linear_cov,
     quadratic
    };

  PolynomialType содержит три параметра, которые представляют полиномиальные функции ниже, здесь x1 и x2 являются входными данными для функции f(x1,x2), а v0...vN являются коэффициентами, которые необходимо найти. Перечисление представляет собой тип уравнений, из которых будет сгенерирован набор решений:

Вариант	Функция f(x1,x2)
linear	линейное уравнение: v0 + v1*x1 + v2*x2
linear_cov	линейное уравнение с ковариацией: v0 + v1*x1 + v2*x2 + v3*x1*x2
quadratic	квадратное уравнение: v0 + v1*x1 + v2*x2 + v3*x1*x2 + v4*x1^2 + v5*x2^2

• Solver — определяет метод QR-разложения, используемый для решения линейных уравнений. В нашей реализации будет только один подходящий вариант. В версии C++ используются вариации метода Хаусхолдера для QR-разложения с использованием библиотеки Eigen.
  

  //+-----------------------------------------------------------------------------------------------+
  //|  Enum  for specifying the QR decomposition method for linear equations solving in models.     |
  //+-----------------------------------------------------------------------------------------------+
  enum Solver
    {
     fast,
     accurate,
     balanced
    };

• CriterionType — позволяет пользователям выбрать определенный внешний критерий, который будет использоваться в качестве основы для оценки моделей-кандидатов. Перечисление содержит варианты, которые можно использовать в качестве критериев останова при обучении модели.
  

  //+------------------------------------------------------------------+
  //|Enum for specifying the external criterion                        |
  //+------------------------------------------------------------------+
  enum CriterionType
    {
     reg,
     symReg,
     stab,
     symStab,
     unbiasedOut,
     symUnbiasedOut,
     unbiasedCoef,
     absoluteNoiseImmun,
     symAbsoluteNoiseImmun
    };

  Доступные варианты более подробно описаны в таблице ниже:

CriterionType	Описание
reg	Регулярность — применяет обычную сумму квадратов ошибок (SSE) на основе разницы между целевыми значениями тестового набора данных и прогнозами по коэффициентам, вычисленным с использованием обучающего набора данных в сочетании с предикторами тестового набора данных
symReg	Симметричная регулярность — представляет собой суммирование SSE на разнице между целевыми значениями тестового набора данных и прогнозами по коэффициентам, вычисленным с использованием обучающего набора данных в сочетании с предикторами тестового набора данных, и SSE на разнице между целевыми значениями обучающего набора данных и прогнозами по коэффициентам, вычисленным с использованием тестового набора данных в сочетании с предикторами обучающего набора данных.
stab	Стабильность — использует SSE на основе разницы между всеми целями и прогнозами по коэффициентам, рассчитанным с использованием обучающего набора данных в сочетании со всеми предикторами
symStab	Симметричная устойчивость — этот критерий объединяет SSE, рассчитанные аналогично критерию stability, а также SSE на разнице между всеми целями и прогнозами по коэффициентам, рассчитанным с использованием тестового набора данных в сочетании со всеми предикторами набора данных
unbiasedOut	Несмещенные результаты — SSE на разнице между прогнозами по коэффициентам, рассчитанным с использованием обучающего набора данных, и прогнозам по коэффициентам, рассчитанным с использованием тестового набора данных, оба из которых используют предикторы тестового набора данных.
symUnbiasedOut	Симметричные несмещенные выходы — вычисляет SSE таким же образом, как критерий unbiasedOutputs, только здесь мы используем все предикторы
unbiasedCoef	Несмещенные коэффициенты — сумма квадратов разностей между коэффициентами, вычисленными с использованием обучающих данных, и коэффициентами, вычисленными с использованием тестовых данных.
absoluteNoiseImmun	Абсолютная устойчивость к шумам — при использовании этой опции критерий вычисляется как скалярное произведение предсказаний модели, обученной на всем наборе данных, за вычетом предсказаний модели, обученной на обучающем наборе данных, при применении к тестовому набору данных, и предсказаний модели, обученной на тестовом наборе данных, за вычетом предсказаний модели, обученной на обучающем наборе данных, при применении к тестовому набору данных.
symAbsoluteNoiseImmun	Симметричная абсолютная устойчивость к шумам — здесь критерием является скалярное произведение предсказаний модели, обученной на всем наборе данных, за вычетом предсказаний модели, обученной на обучающем наборе данных, при применении к обучающему набору данных, и предсказаний модели, обученной на всем наборе данных, и предсказаний модели, обученной на проверочном наборе данных, при применении ко всем наблюдениям.

За перечислениями идут четыре пользовательские структуры:

• BufferValues — это структура векторов, используемая для хранения коэффициентов и прогнозируемых значений, рассчитанных различными способами с использованием тестовых и обучающих наборов данных.
  

  //+-------------------------------------------------------------------------------------+
  //| Structure for storing coefficients and predicted values calculated in different ways|
  //+--------------------------------------------------------------------------------------+
  struct BufferValues
    {
     vector            coeffsTrain; // Coefficients vector calculated using training data
     vector            coeffsTest; // Coefficients vector calculated using testing data
     vector            coeffsAll; // Coefficients vector calculated using learning data
     vector            yPredTrainByTrain; // Predicted values for *training* data calculated using coefficients vector calculated on *training* data
     vector            yPredTrainByTest; // Predicted values for *training* data calculated using coefficients vector calculated on *testing* data
     vector            yPredTestByTrain; // Predicted values for *testing* data calculated using coefficients vector calculated on *training* data
     vector            yPredTestByTest; //Predicted values for *testing* data calculated using coefficients vector calculated on *testing* data
  
                       BufferValues(void)
       {
  
       }
  
                       BufferValues(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
       }
  
     BufferValues      operator=(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
  
        return this;
       }
  
    };

  
  
• PairDVXd — инкапсулирует структуру данных, объединяющую скаляр и соответствующий вектор.
  

  //+------------------------------------------------------------------+
  //|  struct PairDV                                                   |
  //+------------------------------------------------------------------+
  struct PairDVXd
    {
     double            first;
     vector            second;
  
                       PairDVXd(void)
       {
        first = 0.0;
        second = vector::Zeros(10);
       }
  
                       PairDVXd(double &_f, vector &_s)
       {
        first = _f;
        second.Copy(_s);
       }
  
                       PairDVXd(PairDVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairDVXd          operator=(PairDVXd& other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

  
  
• PairMVXd — это структура, объединяющая матрицу и вектор. Вместе они хранят входные данные и соответствующие выходные данные или целевые значения. Входные данные хранятся в матрице, а вектор представляет собой совокупность выходных данных. Каждая строка матрицы соответствует значению в векторе.
  

  //+------------------------------------------------------------------+
  //| structure PairMVXd                                               |
  //+------------------------------------------------------------------+
  struct PairMVXd
    {
     matrix            first;
     vector            second;
  
                       PairMVXd(void)
       {
        first = matrix::Zeros(10,10);
        second = vector::Zeros(10);
       }
  
                       PairMVXd(matrix &_f,  vector& _s)
       {
        first = _f;
        second = _s;
       }
  
                       PairMVXd(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairMVXd          operator=(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

• SplittedData — эта структура данных хранит разделенные наборы данных для обучения и тестирования.
  

  //+------------------------------------------------------------------+
  //|  Structure for storing parts of a split dataset                  |
  //+------------------------------------------------------------------+
  struct SplittedData
    {
     matrix            xTrain;
     matrix            xTest;
     vector            yTrain;
     vector            yTest;
  
                       SplittedData(void)
       {
        xTrain = matrix::Zeros(10,10);
        xTest = matrix::Zeros(10,10);
        yTrain = vector::Zeros(10);
        yTest = vector::Zeros(10);
       }
  
                       SplittedData(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
       }
  
     SplittedData      operator=(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
  
        return this;
       }
    };

  
  

После структур переходим к определениям классов:

• Класс Combination представляет собой модель-кандидат. Он хранит критерии оценки, комбинацию входных данных и рассчитанные коэффициенты для модели.
  

  //+------------------------------------------------------------------+
  //| Сlass representing the candidate model of the GMDH algorithm     |
  //+------------------------------------------------------------------+
  class Combination
    {
     vector            _combination,_bestCoeffs;
     double            _evaluation;
  public:
                       Combination(void) { _combination = vector::Zeros(10); _bestCoeffs.Copy(_combination); _evaluation = DBL_MAX; }
                       Combination(vector &comb) : _combination(comb) { _bestCoeffs=vector::Zeros(_combination.Size()); _evaluation = DBL_MAX;}
                       Combination(vector &comb, vector &coeffs) : _combination(comb),_bestCoeffs(coeffs) { _evaluation = DBL_MAX; }
                       Combination(Combination &other) { _combination = other.combination(); _bestCoeffs=other.bestCoeffs(); _evaluation = other.evaluation();}
     vector            combination(void) { return _combination;}
     vector            bestCoeffs(void)  { return _bestCoeffs; }
     double            evaluation(void)  { return _evaluation; }
  
     void              setCombination(vector &combination) { _combination = combination; }
     void              setBestCoeffs(vector &bestcoeffs) { _bestCoeffs = bestcoeffs; }
     void              setEvaluation(double evaluation)  { _evaluation = evaluation; }
  
     bool              operator<(Combination &combi) { return _evaluation<combi.evaluation();}
     Combination       operator=(Combination &combi)
       {
        _combination = combi.combination();
        _bestCoeffs = combi.bestCoeffs();
        _evaluation = combi.evaluation();
  
        return this;
       }
    };

• CVector — определяет пользовательский вектороподобный контейнер, в котором хранится коллекция экземпляров Combination. То есть это контейнер моделей-кандидатов.

  //+------------------------------------------------------------------+
  //| Collection of Combination instances                              |
  //+------------------------------------------------------------------+
  class CVector
    {
  protected:
     Combination       m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector(CVector &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]=other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(Combination &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, Combination &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     Combination*      operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector           operator=(CVector &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     Combination*      back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     Combination*      front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• CVector2d — еще один пользовательский вектороподобный контейнер, который хранит коллекцию экземпляров CVector.
  

  //+------------------------------------------------------------------+
  //| Collection of CVector instances                                  |
  //+------------------------------------------------------------------+
  class CVector2d
    {
  protected:
     CVector           m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector2d(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector2d(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector2d(CVector2d &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector2d(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(CVector &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, CVector &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     CVector*          operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector2d         operator=(CVector2d &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     CVector*          back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     CVector*          front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
  
        for(uint i = 0; i<m_array.Size(); i++)
           m_array[i].clear();
  
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• Criterion — этот класс реализует расчет различных внешних критериев на основе выбранного типа критерия.
  

  //+---------------------------------------------------------------------------------+
  //|Class that implements calculations of internal and individual external criterions|
  //+---------------------------------------------------------------------------------+
  class Criterion
    {
  protected:
     CriterionType     criterionType; // Selected CriterionType object
     Solver            solver; // Selected Solver object
  
  public:
     /**
     Implements the internal criterion calculation
     param xTrain Matrix of input variables that should be used to calculate the model coefficients
     param yTrain Target values vector for the corresponding xTrain parameter
     return Coefficients vector representing a solution of the linear equations system constructed from the parameters data
     */
     vector            findBestCoeffs(matrix& xTrain,  vector& yTrain)
       {
        vector solution;
  
        matrix q,r;
  
        xTrain.QR(q,r);
  
        matrix qT = q.Transpose();
  
        vector y = qT.MatMul(yTrain);
  
        solution = r.LstSq(y);
  
  
        return solution;
       }
  
     /**
      Calculate the value of the selected external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param _criterionType Selected external criterion type
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of external criterion and calculated model coefficients
      */
     PairDVXd          getResult(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 CriterionType _criterionType, BufferValues& bufferValues)
       {
        switch(_criterionType)
          {
           case reg:
              return regularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symReg:
              return symRegularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case stab:
              return stability(xTrain, xTest, yTrain, yTest, bufferValues);
           case symStab:
              return symStability(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedOut:
              return unbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case symUnbiasedOut:
              return symUnbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedCoef:
              return unbiasedCoeffs(xTrain, xTest, yTrain, yTest, bufferValues);
           case absoluteNoiseImmun:
              return absoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symAbsoluteNoiseImmun:
              return symAbsoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
          }
  
        PairDVXd pd;
        return pd;
       }
     /**
      Calculate the regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the regularity external criterion and calculated model coefficients
      */
     PairDVXd          regularity(matrix& xTrain, matrix& xTest, vector &yTrain, vector& yTest,
                                  BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           f = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
     /**
      Calculate the symmetric regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic regularity external criterion and calculated model coefficients
      */
     PairDVXd          symRegularity(matrix& xTrain, matrix& xTest, vector& yTrain, vector& yTest,
                                     BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = regularity(xTrain,xTest,yTrain,yTest,bufferValues);
        pdv2 = regularity(xTrain,xTest,yTrain,yTest,bufferValues,true);
  
        pdsum.first = pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the stability external criterion and calculated model coefficients
      */
     PairDVXd          stability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f1,f2;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTrainByTrain.Size() == 0)
              bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTrain),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
  
           pdv.first = f1.Sum()+f2.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           if(bufferValues.yPredTestByTest.Size() == 0)
              bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTest),2.0);
           pdv.first = f1.Sum() + f2.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
  
     /**
      Calculate the symmetric stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic stability external criterion and calculated model coefficients
      */
     PairDVXd          symStability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                    BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = stability(xTrain, xTest, yTrain, yTest, bufferValues);
        pdv2 = stability(xTrain, xTest, yTrain, yTest, bufferValues, true);
  
        pdsum.first=pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedOutputs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                       BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          symUnbiasedOutputs(matrix &xTrain,  matrix &xTest,  vector &yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1,f2;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
        if(bufferValues.yPredTrainByTrain.Size() == 0)
           bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTrainByTest.Size() == 0)
           bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f1 = MathPow((bufferValues.yPredTrainByTrain - bufferValues.yPredTrainByTest),2.0);
        f2 = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f1.Sum() + f2.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the unbiased coefficients external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased coefficients external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedCoeffs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        f1 = MathPow((bufferValues.coeffsTrain - bufferValues.coeffsTest),2.0);
        pdv.first = f1.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          absoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        vector yPredTestByAll,f1,f2;
        PairDVXd pdv;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
          {
           matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
           for(ulong i = 0; i<xTrain.Rows(); i++)
              dataX.Row(xTrain.Row(i),i);
  
           for(ulong i = 0; i<xTest.Rows(); i++)
              dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
           vector dataY(yTrain.Size() + yTest.Size());
  
           for(ulong i=0; i<yTrain.Size(); i++)
              dataY[i] = yTrain[i];
  
           for(ulong i=0; i<yTest.Size(); i++)
              dataY[i+yTrain.Size()] = yTest[i];
  
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
          }
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        yPredTestByAll = xTest.MatMul(bufferValues.coeffsAll);
  
        f1 =  yPredTestByAll - bufferValues.yPredTestByTrain;
        f2 = bufferValues.yPredTestByTest - yPredTestByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          symAbsoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector yPredAllByTrain, yPredAllByTest, yPredAllByAll,f1,f2;
        matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
        for(ulong i = 0; i<xTrain.Rows(); i++)
           dataX.Row(xTrain.Row(i),i);
  
        for(ulong i = 0; i<xTest.Rows(); i++)
           dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
        vector dataY(yTrain.Size() + yTest.Size());
  
        for(ulong i=0; i<yTrain.Size(); i++)
           dataY[i] = yTrain[i];
  
        for(ulong i=0; i<yTest.Size(); i++)
           dataY[i+yTrain.Size()] = yTest[i];
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
  
        yPredAllByTrain = dataX.MatMul(bufferValues.coeffsTrain);
        yPredAllByTest = dataX.MatMul(bufferValues.coeffsTest);
        yPredAllByAll = dataX.MatMul(bufferValues.coeffsAll);
  
        f1 = yPredAllByAll - yPredAllByTrain;
        f2 = yPredAllByTest - yPredAllByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
  
       }
  
     /**
      Get k models from the given ones with the best values of the external criterion
     param combinations Vector of the trained models
     param data Object containing parts of a split dataset used in model training. Parameter is used in sequential criterion
     param func Function returning the new X train and X test data constructed from the original data using given combination of input variables column indexes. Parameter is used in sequential criterion
     param k Number of best models
     return Vector containing k best models
      */
     virtual void      getBestCombinations(CVector &combinations, CVector &bestCombo,SplittedData& data, MatFunc func, int k)
       {
        double proxys[];
        int best[];
  
        ArrayResize(best,combinations.size());
        ArrayResize(proxys,combinations.size());
  
        for(int i = 0 ; i<combinations.size(); i++)
          {
           proxys[i] = combinations[i].evaluation();
           best[i] = i;
          }
  
        MathQuickSortAscending(proxys,best,0,combinations.size()-1);
  
        for(int i = 0; i<int(MathMin(MathAbs(k),combinations.size())); i++)
           bestCombo.push_back(combinations[best[i]]);
  
       }
     /**
      Calculate the value of the selected external criterion for the given data.
      For the individual criterion this method only calls the getResult() method
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     return The value of the external criterion and calculated model coefficients
      */
     virtual PairDVXd  calculate(matrix& xTrain,  matrix& xTest,
                                 vector& yTrain,  vector& yTest)
       {
        BufferValues tempValues;
        return getResult(xTrain, xTest, yTrain, yTest, criterionType, tempValues);
       }
  
  public:
     ///  Construct a new Criterion object
                       Criterion() {};
  
     /**
      Construct a new Criterion object
     param _criterionType Selected external criterion type
     param _solver Selected method for linear equations solving
      */
                       Criterion(CriterionType _criterionType)
       {
        criterionType = _criterionType;
        solver = balanced;
       }
  
    };
  

Наконец, у нас есть две функции, которыми заканчивается файл gmdh_internal.mqh:

validateInputData() — используется для обеспечения корректности значений, передаваемых методам класса или другим автономным функциям.

**
 *  Validate input parameters values
 *
 * param testSize Fraction of the input data that should be placed into the second part
 * param pAverage The number of best models based of which the external criterion for each level will be calculated
 * param threads The number of threads used for calculations. Set -1 to use max possible threads
 * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
 * param limit The minimum value by which the external criterion should be improved in order to continue training
 * param kBest The number of best models based of which new models of the next level will be constructed
 * return Method exit status
 */
int validateInputData(double testSize=0.0, int pAverage=0, double limit=0.0, int kBest=0)
  {
   int errorCode = 0;
//
   if(testSize <= 0 || testSize >= 1)
     {
      Print("testsize value must be in the (0, 1) range");
      errorCode |= 1;
     }
   if(pAverage && pAverage < 1)
     {
      Print("p_average value must be a positive integer");
      errorCode |= 4;
     }
   if(limit && limit < 0)
     {
      Print("limit value must be non-negative");
      errorCode |= 8;
     }
   if(kBest && kBest < 1)
     {
      Print("k_best value must be a positive integer");
      errorCode |= 16;
     }

   return errorCode;
  }

timeSeriesTransformation() — вспомогательная функция, которая принимает в качестве входных данных ряд в векторе и преобразует его в структуру данных входных данных и целей в соответствии с выбранным числом лагов.

/**
 *  Convert the time series vector to the 2D matrix format required to work with GMDH algorithms
 *
 * param timeSeries Vector of time series data
 * param lags The lags (length) of subsets of time series into which the original time series should be divided
 * return Transformed time series data
 */
PairMVXd timeSeriesTransformation(vector& timeSeries, int lags)
  {
   PairMVXd p;

   string errorMsg = "";
   if(timeSeries.Size() == 0)
      errorMsg = "time_series value is empty";
   else
      if(lags <= 0)
         errorMsg = "lags value must be a positive integer";
      else
         if(lags >= int(timeSeries.Size()))
            errorMsg = "lags value can't be greater than  time_series  size";
   if(errorMsg != "")
      return p;

   ulong last = timeSeries.Size() - ulong(lags);
   vector yTimeSeries(last,slice,timeSeries,ulong(lags));
   matrix xTimeSeries(last, ulong(lags));
   vector vect;
   for(ulong i = 0; i < last; ++i)
     {
      vect.Init(ulong(lags),slice,timeSeries,i,i+ulong(lags-1));
      xTimeSeries.Row(vect,i);
     }

   p.first = xTimeSeries;
   p.second = yTimeSeries;

   return p;
  }

Здесь lags относятся к числу значений предыдущего ряда, используемых в качестве предикторов для вычисления последующего члена.

На этом мы заканчиваем рассмотрение файла gmdh_internal.mqh. Переходим ко второму заголовочному файлу, gmdh.mqh.

Он начинается с определения функции splitData().

/**
 *  Divide the input data into 2 parts
 *
 * param x Matrix of input data containing predictive variables
 * param y Vector of the taget values for the corresponding x data
 * param testSize Fraction of the input data that should be placed into the second part
 * param shuffle True if data should be shuffled before splitting into 2 parts, otherwise false
 * param randomSeed Seed number for the random generator to get the same division every time
 * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
 */
SplittedData splitData(matrix& x,  vector& y, double testSize = 0.2, bool shuffle = false, int randomSeed = 0)
  {
   SplittedData data;

   if(validateInputData(testSize))
      return data;
   
   string errorMsg = "";
   if(x.Rows() != y.Size())
      errorMsg = " x rows number and y size must be equal";
   else
      if(round(x.Rows() * testSize) == 0 || round(x.Rows() * testSize) == x.Rows())
         errorMsg = "Result contains an empty array. Change the arrays size or the  value for correct splitting";
   if(errorMsg != "")
     {
      Print(__FUNCTION__," ",errorMsg);
      return data;
     }


   if(!shuffle)
      data = GmdhModel::internalSplitData(x, y, testSize);
   else
     {
      if(randomSeed == 0)
         randomSeed = int(GetTickCount64());
      MathSrand(uint(randomSeed));

      int shuffled_rows_indexes[],shuffled[];
      MathSequence(0,int(x.Rows()-1),1,shuffled_rows_indexes);
      MathSample(shuffled_rows_indexes,int(shuffled_rows_indexes.Size()),shuffled);

      int testItemsNumber = (int)round(x.Rows() * testSize);


      matrix Train,Test;
      vector train,test;

      Train.Resize(x.Rows()-ulong(testItemsNumber),x.Cols());
      Test.Resize(ulong(testItemsNumber),x.Cols());

      train.Resize(x.Rows()-ulong(testItemsNumber));
      test.Resize(ulong(testItemsNumber));

      for(ulong i = 0; i<Train.Rows(); i++)
        {
         Train.Row(x.Row(shuffled[i]),i);
         train[i] = y[shuffled[i]];
        }

      for(ulong i = 0; i<Test.Rows(); i++)
        {
         Test.Row(x.Row(shuffled[Train.Rows()+i]),i);
         test[i] = y[shuffled[Train.Rows()+i]];
        }

      data.xTrain = Train;
      data.xTest = Test;
      data.yTrain = train;
      data.yTest = test;
     }

   return data;
  }  

В качестве входных данных принимает матрицу и вектор, представляющие переменные и цели соответственно. Параметр testSize определяет долю набора данных, которая будет использоваться в качестве тестового набора. Параметр shuffle включает случайное перемешивание набора данных, а randomSeed указывает начальное число для генератора случайных чисел, используемого в процессе перемешивания.

Далее идет класс GmdhModel, который определяет общую логику алгоритмов GMDH.

//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH algorithms          |
//+------------------------------------------------------------------+

class  GmdhModel
  {
protected:

   string            modelName; // model name
   int               level; // Current number of the algorithm training level
   int               inputColsNumber; // The number of predictive variables in the original data
   double            lastLevelEvaluation; // The external criterion value of the previous training level
   double            currentLevelEvaluation; // The external criterion value of the current training level
   bool              training_complete; // flag indicator successful completion of model training
   CVector2d         bestCombinations; // Storage for the best models of previous levels

   /**
    *struct for generating vector sequence
    */
   struct unique
     {
   private:
      int            current;

      int            run(void)
        {
         return ++current;
        }

   public:
                     unique(void)
        {
         current = -1;
        }

      vector         generate(ulong t)
        {
         ulong s=0;
         vector ret(t);

         while(s<t)
            ret[s++] = run();

         return ret;
        }
     };

   /**
    *  Find all combinations of k elements from n
    *
    * param n Number of all elements
    * param k Number of required elements
    * return Vector of all combinations of k elements from n
    */
   void              nChooseK(int n, int k, vector &combos[])
     {
      if(n<=0 || k<=0 || n<k)
        {
         Print(__FUNCTION__," invalid parameters for n and or k", "n ",n , " k ", k);
         return;
        }

      unique q;

      vector comb = q.generate(ulong(k));

      ArrayResize(combos,combos.Size()+1,100);

      long first, last;

      first = 0;
      last = long(k);
      combos[combos.Size()-1]=comb;

      while(comb[first]!= double(n - k))
        {
         long mt = last;
         while(comb[--mt] == double(n - (last - mt)));
         comb[mt]++;
         while(++mt != last)
            comb[mt] = comb[mt-1]+double(1);
         ArrayResize(combos,combos.Size()+1,100);
         combos[combos.Size()-1]=comb;
        }

      for(uint i = 0; i<combos.Size(); i++)
        {
         combos[i].Resize(combos[i].Size()+1);
         combos[i][combos[i].Size()-1] = n;
        }

      return;
     }

   /**
    *  Get the mean value of extrnal criterion of the k best models
    *
    * param sortedCombinations Sorted vector of current level models
    * param k The numebr of the best models
    * return Calculated mean value of extrnal criterion of the k best models
    */
   double            getMeanCriterionValue(CVector &sortedCombinations, int k)
     {
      k = MathMin(k, sortedCombinations.size());

      double crreval=0;

      for(int i = 0; i<k; i++)
         crreval +=sortedCombinations[i].evaluation();
      if(k)
         return crreval/double(k);
      else
        {
         Print(__FUNCTION__, " Zero divide error ");
         return 0.0;
        }
     }

   /**
    *  Get the sign of the polynomial variable coefficient
    *
    * param coeff Selected coefficient
    * param isFirstCoeff True if the selected coefficient will be the first in the polynomial representation, otherwise false
    * return String containing the sign of the coefficient
    */
   string            getPolynomialCoeffSign(double coeff, bool isFirstCoeff)
     {
      return ((coeff >= 0) ? ((isFirstCoeff) ? " " : " + ") : " - ");
     }

   /**
    *  Get the rounded value of the polynomial variable coefficient without sign
    *
    * param coeff Selected coefficient
    * param isLastCoeff True if the selected coefficient will be the last one in the polynomial representation, otherwise false
    * return String containing the rounded value of the coefficient without sign
    */
   string            getPolynomialCoeffValue(double coeff, bool isLastCoeff)
     {
      string stringCoeff = StringFormat("%e",MathAbs(coeff));
      return ((stringCoeff != "1" || isLastCoeff) ? stringCoeff : "");
     }

   /**
    *  Train given subset of models and calculate external criterion for them
    *
    * param data Data used for training and evaulating models
    * param criterion Selected external criterion
    * param beginCoeffsVec Iterator indicating the beginning of a subset of models
    * param endCoeffsVec Iterator indicating the end of a subset of models
    * param leftTasks The number of remaining untrained models at the entire level
    * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
    */
   bool              polynomialsEvaluation(SplittedData& data,  Criterion& criterion,  CVector &combos, uint beginCoeffsVec,
                                           uint endCoeffsVec)
     {
      vector cmb,ytrain,ytest;
      matrix x1,x2;
      for(uint i = beginCoeffsVec; i<endCoeffsVec; i++)
        {
         cmb = combos[i].combination();
         x1 = xDataForCombination(data.xTrain,cmb);
         x2 = xDataForCombination(data.xTest,cmb);
         ytrain = data.yTrain;
         ytest = data.yTest;
         PairDVXd pd = criterion.calculate(x1,x2,ytrain,ytest);

         if(pd.second.HasNan()>0)
            {
             Print(__FUNCTION__," No solution found for coefficient at ", i, "\n xTrain \n", x1, "\n xTest \n", x2, "\n yTrain \n", ytrain, "\n yTest \n", ytest);
             combos[i].setEvaluation(DBL_MAX);
             combos[i].setBestCoeffs(vector::Ones(3));
            }
         else
            {
             combos[i].setEvaluation(pd.first);
             combos[i].setBestCoeffs(pd.second);
            } 
        }

      return true;
     }

   /**
   *  Determine the need to continue training and prepare the algorithm for the next level
   *
   * param kBest The number of best models based of which new models of the next level will be constructed
   * param pAverage The number of best models based of which the external criterion for each level will be calculated
   * param combinations Trained models of the current level
   * param criterion Selected external criterion
   * param data Data used for training and evaulating models
   * param limit The minimum value by which the external criterion should be improved in order to continue training
   * return True if the algorithm needs to continue training, otherwise fasle
   */
   bool              nextLevelCondition(int kBest, int pAverage, CVector &combinations,
                                        Criterion& criterion, SplittedData& data, double limit)
     {
      MatFunc fun = NULL;
      CVector bestcombinations;
      criterion.getBestCombinations(combinations,bestcombinations,data, fun, kBest);
      currentLevelEvaluation = getMeanCriterionValue(bestcombinations, pAverage);

      if(lastLevelEvaluation - currentLevelEvaluation > limit)
        {
         lastLevelEvaluation = currentLevelEvaluation;
         if(preparations(data,bestcombinations))
           {
            ++level;
            return true;
           }
        }
      removeExtraCombinations();
      return false;

     }

   /**
    *  Fit the algorithm to find the best solution
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param criterion Selected external criterion
    * param kBest The number of best models based of which new models of the next level will be constructed
    * param testSize Fraction of the input data that should be used to evaluate models at each level
    * param pAverage The number of best models based of which the external criterion for each level will be calculated
    * param limit The minimum value by which the external criterion should be improved in order to continue training
    * return A pointer to the algorithm object for which the training was performed
    */
   bool              gmdhFit(matrix& x,  vector& y,  Criterion& criterion, int kBest,
                             double testSize, int pAverage, double limit)
     {
      if(x.Rows() != y.Size())
        {
         Print("X rows number and y size must be equal");
         return false;
        }

      level = 1; // reset last training
      inputColsNumber = int(x.Cols());
      lastLevelEvaluation = DBL_MAX;

      SplittedData data = internalSplitData(x, y, testSize, true) ;
      training_complete = false;
      bool goToTheNextLevel;
      CVector evaluationCoeffsVec;
      do
        {
         vector combinations[];
         generateCombinations(int(data.xTrain.Cols() - 1),combinations);
         
         if(combinations.Size()<1)
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }  

         evaluationCoeffsVec.clear();

         int currLevelEvaluation = 0;
         for(int it = 0; it < int(combinations.Size()); ++it, ++currLevelEvaluation)
           {
            Combination ncomb(combinations[it]);
            evaluationCoeffsVec.push_back(ncomb);
           }

         if(!polynomialsEvaluation(data,criterion,evaluationCoeffsVec,0,uint(currLevelEvaluation)))
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }

         goToTheNextLevel = nextLevelCondition(kBest, pAverage, evaluationCoeffsVec, criterion, data, limit); // checking the results of the current level for improvement
        }
      while(goToTheNextLevel);

      training_complete = true;

      return true;
     }

   /**
    *  Get new model structures for the new level of training
    *
    * param n_cols The number of existing predictive variables at the current training level
    * return Vector of new model structures
    */
   virtual void      generateCombinations(int n_cols,vector &out[])
     {
      return;
     }


   ///  Removed the saved models that are no longer needed
   virtual void      removeExtraCombinations(void)
     {
      return;
     }

   /**
    *  Prepare data for the next training level
    *
    * param data Data used for training and evaulating models at the current level
    * param _bestCombinations Vector of the k best models of the current level
    * return True if the training process can be continued, otherwise false
    */
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations)
     {
      return false;
     }

   /**
    *  Get the data constructed according to the model structure from the original data
    *
    * param x Training data at the current level
    * param comb Vector containing the indexes of the x matrix columns that should be used in the model
    * return Constructed data
    */
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)
     {
      return matrix::Zeros(10,10);
     }

   /**
    *  Get the designation of polynomial equation
    *
    * param levelIndex The number of the level counting from 0
    * param combIndex The number of polynomial in the level counting from 0
    * return The designation of polynomial equation
    */
   virtual string    getPolynomialPrefix(int levelIndex, int combIndex)
     {
      return NULL;
     }

   /**
    *  Get the string representation of the polynomial variable
    *
    * param levelIndex The number of the level counting from 0
    * param coeffIndex The number of the coefficient related to the selected variable in the polynomial counting from 0
    * param coeffsNumber The number of coefficients in the polynomial
    * param bestColsIndexes Indexes of the data columns used to construct polynomial of the model
    * return The string representation of the polynomial variable
    */
   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector& bestColsIndexes)
     {
      return NULL;
     }

   /*
    *  Transform model data to JSON format for further saving
    *
    * return JSON value of model data
    */
   virtual CJAVal    toJSON(void)
     {
      CJAVal json_obj_model;

      json_obj_model["modelName"] = getModelName();
      json_obj_model["inputColsNumber"] = inputColsNumber;
      json_obj_model["bestCombinations"] = CJAVal(jtARRAY,"");


      for(int i = 0; i<bestCombinations.size(); i++)
        {

         CJAVal Array(jtARRAY,"");

         for(int k = 0; k<bestCombinations[i].size(); k++)
           {
            CJAVal collection;
            collection["combination"] = CJAVal(jtARRAY,"");
            collection["bestCoeffs"] = CJAVal(jtARRAY,"");
            vector combination = bestCombinations[i][k].combination();
            vector bestcoeff = bestCombinations[i][k].bestCoeffs();
            for(ulong j=0; j<combination.Size(); j++)
               collection["combination"].Add(int(combination[j]));
            for(ulong j=0; j<bestcoeff.Size(); j++)
               collection["bestCoeffs"].Add(bestcoeff[j],-15);
            Array.Add(collection);
           }

         json_obj_model["bestCombinations"].Add(Array);

        }

      return json_obj_model;

     }

   /**
    *  Set up model from JSON format model data
    *
    * param jsonModel Model data in JSON format
    * return Method exit status
    */
   virtual bool      fromJSON(CJAVal &jsonModel)
     {
      modelName = jsonModel["modelName"].ToStr();
      bestCombinations.clear();
      inputColsNumber = int(jsonModel["inputColsNumber"].ToInt());

      for(int i = 0; i<jsonModel["bestCombinations"].Size(); i++)
        {
         CVector member;
         for(int j = 0; j<jsonModel["bestCombinations"][i].Size(); j++)
           {
            Combination cb;
            vector c(ulong(jsonModel["bestCombinations"][i][j]["combination"].Size()));
            vector cf(ulong(jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size()));
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["combination"].Size(); k++)
               c[k] = jsonModel["bestCombinations"][i][j]["combination"][k].ToDbl();
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size(); k++)
               cf[k] = jsonModel["bestCombinations"][i][j]["bestCoeffs"][k].ToDbl();
            cb.setBestCoeffs(cf);
            cb.setCombination(c);
            member.push_back(cb);
           }
         bestCombinations.push_back(member);
        }
      return true;
     }



   /**
    *  Compare the number of required and actual columns of the input matrix
    *
    * param x Given matrix of input data
    */
   bool              checkMatrixColsNumber(matrix& x)
     {
      if(ulong(inputColsNumber) != x.Cols())
        {
         Print("Matrix  must have " + string(inputColsNumber) + " columns because there were " + string(inputColsNumber) + " columns in the training  matrix");
         return false;
        }

      return true;
     }
     
     

public:
   ///  Construct a new Gmdh Model object
                     GmdhModel() : level(1), lastLevelEvaluation(0) {}

   /**
   *  Get full class name
   *
   * return String containing the name of the model class
   */
   string            getModelName(void)
     {
      return modelName;
     }
   /**
     *Get number of inputs required for model
     */
    int getNumInputs(void)
     {
      return inputColsNumber;
     }

   /**
    *  Save model data into regular file
    *
    * param path Path to regular file
    */
   bool              save(string file_name)
     {

      CFileTxt modelFile;

      if(modelFile.Open(file_name,FILE_WRITE|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         CJAVal js=toJSON();
         if(modelFile.WriteString(js.Serialize())==0)
           {
            Print("failed write to ",file_name,". Error -",::GetLastError());
            return false;
           }
        }

      return true;
     }

   /**
    *  Load model data from regular file
    *
    * param path Path to regular file
    */
   bool               load(string file_name)
     {
      training_complete = false;
      CFileTxt modelFile;
      CJAVal js;

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         training_complete = fromJSON(js);
        }
      return training_complete;
     }
   /**
    *  Divide the input data into 2 parts without shuffling
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param testSize Fraction of the input data that should be placed into the second part
    * param addOnesCol True if it is needed to add a column of ones to the x data, otherwise false
    * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
    */
   static SplittedData internalSplitData(matrix& x,  vector& y, double testSize, bool addOnesCol = false)
     {
      SplittedData data;
      ulong testItemsNumber = ulong(round(double(x.Rows()) * testSize));
      matrix Train,Test;
      vector train,test;

      if(addOnesCol)
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols() + 1);
         Test.Resize(testItemsNumber, x.Cols() + 1);

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         Train.Col(vector::Ones(Train.Rows()),x.Cols());

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);

         Test.Col(vector::Ones(Test.Rows()),x.Cols());

        }
      else
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols());
         Test.Resize(testItemsNumber, x.Cols());

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);
        }

      train.Init(y.Size() - testItemsNumber,slice,y,0,y.Size() - testItemsNumber - 1);
      test.Init(testItemsNumber,slice,y,y.Size() - testItemsNumber);

      data.yTrain = train;
      data.yTest = test;

      data.xTrain = Train;
      data.xTest = Test;

      return data;
     }

   /**
    *  Get long-term forecast for the time series
    *
    * param x One row of the test time series data
    * param lags The number of lags (steps) to make a forecast for
    * return Vector containing long-term forecast
    */
   virtual vector    predict(vector& x, int lags)
     {
      return vector::Zeros(1);
     }

   /**
    *  Get the String representation of the best polynomial
    *
    * return String representation of the best polynomial
    */
   string            getBestPolynomial(void)
     {
      string polynomialStr = "";
      int ind = 0;
      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector bestColsIndexes = bestCombinations[i][j].combination();
            vector bestCoeffs = bestCombinations[i][j].bestCoeffs();
            polynomialStr += getPolynomialPrefix(i, j);
            bool isFirstCoeff = true;
            for(int k = 0; k < int(bestCoeffs.Size()); ++k)
              {
               if(bestCoeffs[k])
                 {
                  polynomialStr += getPolynomialCoeffSign(bestCoeffs[k], isFirstCoeff);
                  string coeffValuelStr = getPolynomialCoeffValue(bestCoeffs[k], (k == (bestCoeffs.Size() - 1)));
                  polynomialStr += coeffValuelStr;
                  if(coeffValuelStr != "" && k != bestCoeffs.Size() - 1)
                     polynomialStr += "*";
                  polynomialStr += getPolynomialVariable(i, k, int(bestCoeffs.Size()), bestColsIndexes);
                  isFirstCoeff = false;
                 }
              }
            if(i < bestCombinations.size() - 1 || j < (bestCombinations[i].size() - 1))
               polynomialStr += "\n";
           }//j
         if(i < bestCombinations.size() - 1 && bestCombinations[i].size() > 1)
            polynomialStr += "\n";
        }//i
      return polynomialStr;
     }

                    ~GmdhModel()
     {
      for(int i = 0; i<bestCombinations.size(); i++)
         bestCombinations[i].clear();

      bestCombinations.clear();
     }
  };


//+------------------------------------------------------------------+

Это базовый класс, из которого будут выведены другие типы МГУА. Он содержит методы обучения или построения модели и последующего составления прогнозов с ее помощью. Методы "save" и "load" позволяют сохранить модель и загрузить ее из файла для последующего использования. Модели сохраняются в формате JSON в текстовом файле в общем каталоге всех терминалов MetaTrader.

Последний заголовочный файл mia.mqh содержит определение класса MIA.

//+------------------------------------------------------------------+
//| Class implementing multilayered iterative algorithm MIA          |
//+------------------------------------------------------------------+
class MIA : public GmdhModel
  {
protected:
   PolynomialType    polynomialType; // Selected polynomial type

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,2,out);
      return;
     }
   /**
   *  Get predictions for the input data
   *
   * param x Test data of the regression task or one-step time series forecast
   * return Vector containing prediction values
   */
   virtual vector    calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         matrix xNew(1, ulong(bestCombinations[i].size()) + 1);
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector comb = bestCombinations[i][j].combination();
            matrix xx(1,comb.Size());
            for(ulong i = 0; i<xx.Cols(); ++i)
               xx[0][i] = modifiedX[0][ulong(comb[i])];
            matrix ply = getPolynomialX(xx);
            vector c,b;
            c = bestCombinations[i][j].bestCoeffs();
            b = ply.MatMul(c);
            xNew.Col(b,ulong(j));
           }
         vector n  = vector::Ones(xNew.Rows());
         xNew.Col(n,xNew.Cols() - 1);
         modifiedX = xNew;
        }

      return modifiedX.Col(0);

     }

   /**
    *  Construct vector of the new variable values according to the selected polynomial type
    *
    * param x Matrix of input variables values for the selected polynomial type
    * return Construct vector of the new variable values
    */
   matrix            getPolynomialX(matrix& x)
     {
      matrix polyX = x;
      if((polynomialType == linear_cov))
        {
         polyX.Resize(x.Rows(), 4);
         polyX.Col(x.Col(0)*x.Col(1),2);
         polyX.Col(x.Col(2),3);
        }
      else
         if((polynomialType == quadratic))
           {
            polyX.Resize(x.Rows(), 6);
            polyX.Col(x.Col(0)*x.Col(1),2) ;
            polyX.Col(x.Col(0)*x.Col(0),3);
            polyX.Col(x.Col(1)*x.Col(1),4);
            polyX.Col(x.Col(2),5) ;
           }

      return polyX;
     }

   /**
    *  Transform data in the current training level by constructing new variables using selected polynomial type
    *
    * param data Data used to train models at the current level
    * param bestCombinations Vector of the k best models of the current level
    */
   virtual void      transformDataForNextLevel(SplittedData& data,  CVector &bestCombs)
     {
      matrix xTrainNew(data.xTrain.Rows(), ulong(bestCombs.size()) + 1);
      matrix xTestNew(data.xTest.Rows(), ulong(bestCombs.size()) + 1);

      for(int i = 0; i < bestCombs.size(); ++i)
        {
         vector comb = bestCombs[i].combination();

         matrix train(xTrainNew.Rows(),comb.Size()),test(xTrainNew.Rows(),comb.Size());

         for(ulong k = 0; k<comb.Size(); k++)
           {
            train.Col(data.xTrain.Col(ulong(comb[k])),k);
            test.Col(data.xTest.Col(ulong(comb[k])),k);
           }

         matrix polyTest,polyTrain;
         vector bcoeff = bestCombs[i].bestCoeffs();
         polyTest = getPolynomialX(test);
         polyTrain = getPolynomialX(train);

         xTrainNew.Col(polyTrain.MatMul(bcoeff),i);
         xTestNew.Col(polyTest.MatMul(bcoeff),i);
        }

      xTrainNew.Col(vector::Ones(xTrainNew.Rows()),xTrainNew.Cols() - 1);
      xTestNew.Col(vector::Ones(xTestNew.Rows()),xTestNew.Cols() - 1);

      data.xTrain = xTrainNew;
      data.xTest =  xTestNew;
     }

   virtual void      removeExtraCombinations(void) override
     {

      CVector2d realBestCombinations(bestCombinations.size());
      CVector n;
      n.push_back(bestCombinations[level-2][0]);
      realBestCombinations.setAt(realBestCombinations.size() - 1,n);

      vector comb(1);
      for(int i = realBestCombinations.size() - 1; i > 0; --i)
        {
         double usedCombinationsIndexes[],unique[];
         int indexs[];
         int prevsize = 0;
         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            ArrayResize(usedCombinationsIndexes,prevsize+int(comb.Size()-1),100);
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               usedCombinationsIndexes[ulong(prevsize)+k] = comb[k];
            prevsize = int(usedCombinationsIndexes.Size());
           }
         MathUnique(usedCombinationsIndexes,unique);
         ArraySort(unique);

         for(uint it = 0; it<unique.Size(); ++it)
            realBestCombinations[i - 1].push_back(bestCombinations[i - 1][int(unique[it])]);

         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               comb[k] = ArrayBsearch(unique,comb[k]);
            comb[comb.Size() - 1] = double(unique.Size());
            realBestCombinations[i][j].setCombination(comb);
           }

         ZeroMemory(usedCombinationsIndexes);
         ZeroMemory(unique);
         ZeroMemory(indexs);
        }

      bestCombinations = realBestCombinations;
     }
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations) override
     {
      bestCombinations.push_back(_bestCombinations);
      transformDataForNextLevel(data, bestCombinations[level - 1]);
      return true;
     }
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)  override
     {
      matrix xx(x.Rows(),comb.Size());

      for(ulong i = 0; i<xx.Cols(); ++i)
         xx.Col(x.Col(ulong(comb[i])),i);

      return getPolynomialX(xx);
     }

   string            getPolynomialPrefix(int levelIndex, int combIndex)  override
     {
      return ((levelIndex < bestCombinations.size() - 1) ?
              "f" + string(levelIndex + 1) + "_" + string(combIndex + 1) : "y") + " =";
     }
   string            getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector &bestColsIndexes)  override
     {
      if(levelIndex == 0)
        {
         if(coeffIndex < 2)
            return "x" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "x" + string(int(bestColsIndexes[0]) + 1) + "*x" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "x" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      else
        {
         if(coeffIndex < 2)
            return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[0]) + 1) +
                      "*f" + string(levelIndex) + "_" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      return "";
     }


   CJAVal            toJSON(void)  override
     {
      CJAVal json_obj_model = GmdhModel::toJSON();

      json_obj_model["polynomialType"] = int(polynomialType);
      return json_obj_model;

     }

   bool              fromJSON(CJAVal &jsonModel) override
     {
      bool parsed = GmdhModel::fromJSON(jsonModel);

      if(!parsed)
         return false;

      polynomialType = PolynomialType(jsonModel["polynomialType"].ToInt());

      return true;
     }

public:
   //+------------------------------------------------------------------+
   //| Constructor                                                      |
   //+------------------------------------------------------------------+

                     MIA(void)
     {
      modelName = "MIA";
     }

   //+------------------------------------------------------------------+
   //| model a time series                                              |
   //+------------------------------------------------------------------+

   virtual bool      fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 3)
        {
         Print(__FUNCTION__," lags must be >= 3");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   //+------------------------------------------------------------------+
   //| model a multivariable data set  of inputs and targets            |
   //+------------------------------------------------------------------+

   virtual bool      fit(matrix &vars,vector &targets,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 3)
        {
         Print(__FUNCTION__," columns in vars must be >= 3");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   virtual vector     predict(vector& x, int lags)  override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;
     }



  };
//+------------------------------------------------------------------+

Он наследуется от класса GmdhModel для реализации многослойного итерационного алгоритма. Класс MIA содержит две перегрузки функции fit(), которые вызываются для моделирования заданного набора данных. Эти методы различаются по первому и второму параметрам. При моделировании временного ряда с использованием только исторических значений используется функция fit(), показанная ниже.

fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)

Второй метод используется при моделировании набора данных зависимых и независимых переменных. Параметры обоих методов показаны в таблице:

Тип данных	Название параметра	Описание
вектор	time_series	представляет собой временной ряд, содержащийся в векторе
integer	lags	определяет количество запаздывающих значений, которые будут использоваться в качестве предикторов в модели
матрица	vars	матрица входных данных, содержащая предиктивные переменные
вектор	targets	вектор целевых значений для соответствующих членов-строк vars
CriterionType	criterion	перечисление, определяет внешние критерии для процесса построения модели
integer	kBest	определяет количество лучших частичных моделей, на основе которых будут построены новые входы последующего слоя
PolynomialType	_polynomialType	выбранный тип полинома, который будет использоваться для построения новых переменных из существующих во время обучения
double	testSize	доля входных данных, которая должна использоваться для оценки моделей
int	pAverage	Число лучших частичных моделей, которые следует учитывать при расчете критериев остановки
double	limit	Минимальное значение, на которое внешний критерий должен улучшаться для продолжения обучения

После обучения модели ее можно использовать для составления прогнозов. Для этого вызываем метод predict(). Для этого метода требуется вектор входных данных и целочисленное значение, указывающее желаемое количество прогнозов. При успешном выполнении метод возвращает вектор, содержащий вычисленные прогнозы. В противном случае возвращается вектор нулей. В следующем разделе мы рассмотрим несколько простых примеров, чтобы лучше понять, как использовать только что описанный код.

Примеры

Рассмотрим три примера, реализованных в виде скриптов. Увидим, как применять его в различных сценариях. В первом скрипте у нас будет построение модели временного ряда. В этом скрипте определенное количество предыдущих значений ряда можно использовать для определения последующих членов. Этот пример содержится в файле MIA_Test.mq5, код показан ниже.

//+------------------------------------------------------------------+
//|                                                     MIA_Test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input int NumLags = 3;
input int NumPredictions = 6;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---time series we want to model
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};
//---
   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }
//---instantiate MIA object
   MIA mia;
//---fit the series according to user defined hyper parameters
   if(!mia.fit(tms,NumLags,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---generate filename based on user defined parameter settings
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit);
//---save the trained model
   mia.save(modelname+".json");
//---inputs from original series to be used for making predictions
   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));
//---predictions made from the model
   vector out = mia.predict(in,NumPredictions);
//---output result of prediction
   Print(modelname, " predictions ", out);
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial());
  }
//+------------------------------------------------------------------+

При запуске скрипта пользователь может изменять различные параметры модели. NumLags — количество значений предыдущего ряда для расчета следующего члена. NumPredictions — количество прогнозов, которые будут сделаны за пределами указанной серии. Остальные параметры соответствуют аргументам, передаваемым методу fit(). После успешного построения модели она сохраняется в файле. Прогнозы делаются и выводятся на вкладку «Эксперты» терминала вместе с окончательным полиномом, представляющим модель. Результаты выполнения скрипта с настройками по умолчанию показаны ниже. Показанный полином представляет собой математическую модель, которая, как выяснилось, наилучшим образом описывает заданный временной ряд. Очевидно, что все это излишне усложнено, если учесть простоту временного ряда. Хотя, учитывая результаты прогнозирования, модель все же улавливает общую тенденцию ряда.

PS      0       22:37:31.246    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
OG      0       22:37:31.246    MIA_Test (USDCHF,D1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00

Во втором прогоне скрипта: Значение NumLags увеличим до 4. Давайте посмотрим, как это повлияет на модель.

Обратите внимание, насколько усложняется модель при добавлении дополнительного предиктора. А также на влияние, которое это оказывает на прогнозы. Полином теперь охватывает несколько линий, несмотря на отсутствие заметного улучшения в прогнозах модели.

22:37:42.921    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000005,16.00000000000007,17.00000000000011,18.00000000000015]
ML      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_1 = - 1.666667e-01*x2 + 1.166667e+00*x4 + 8.797938e-16*x2*x4 + 6.666667e-01
CO      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_2 = - 6.916614e-15*x3 + 1.000000e+00*x4 + 1.006270e-15*x3*x4 + 1.000000e+00
NN      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_3 = - 5.000000e-01*x1 + 1.500000e+00*x3 + 1.001110e-15*x1*x3 + 1.000000e+00
QR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_1 = 5.000000e-01*f1_1 + 5.000000e-01*f1_3 - 5.518760e-16*f1_1*f1_3 - 1.729874e-14
HR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_2 = 5.000000e-01*f1_1 + 5.000000e-01*f1_2 - 1.838023e-16*f1_1*f1_2 - 8.624525e-15
JK      0       22:37:42.921    MIA_Test (USDCHF,D1)    y = 5.000000e-01*f2_1 + 5.000000e-01*f2_2 - 2.963544e-16*f2_1*f2_2 - 1.003117e-14

В нашем последнем примере рассмотрим другой сценарий, в котором будем моделировать результаты, определяемые независимыми переменными. В этом примере мы пытаемся научить модель складывать три входных сигнала. Код этого примера находится в файле MIA_Multivariable_test.mq5.

//+------------------------------------------------------------------+
//|                                       MIA_miavariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---simple independent and dependent data sets we want to model
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};
//---declare MIA object     
   MIA mia;   
//---train the model based on chosen hyper parameters
   if(!mia.fit(independent,dependent,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---construct filename for generated model
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit)+"_multivars";
//---save the model
   mia.save(modelname+".json");
//---input data to be used as input for making predictions
   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};
//---make predictions and output to the terminal
  for(ulong row = 0; row<unseen.Rows(); row++)
     {
       vector in = unseen.Row(row);
       Print("inputs ", in , " prediction ", mia.predict(in,1));
     }  
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

Предикторы находятся в матрице vars. Каждая строка соответствует цели в векторе targets. Как и в предыдущем примере, мы можем задать различные аспекты гиперпараметров для обучения модели. Результаты обучения с настройками по умолчанию получились очень плохими:

RE      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [5.999999999999997]
JQ      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [7.5]
QI      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.1]
QK      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      y = 1.900000e+00*x1 + 1.450000e+00*x2 - 9.500000e-01*x1*x2 + 3.100000e+00

Модель можно улучшить, скорректировав параметры обучения. Наилучшие результаты были достигнуты при использовании таких настроек:

С этими настройками модель наконец-то способна делать точные прогнозы по набору незнакомых входных переменных. Хотя, как и в первом примере, сгенерированный полином слишком сложен.

DM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [6.999999999999998]
JI      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [8.999999999999998]
CD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.00000000000001]
OO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
IQ      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
PS      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
LO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
HN      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
PP      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
JM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
NO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
FD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15

Из рассмотренных простых примеров видно, что многослойный итеративный алгоритм может оказаться излишним для элементарных наборов данных. Сгенерированные полиномы могут оказаться чрезвычайно сложными. Подобные модели подвержены переобучению. Алгоритм может наткнуться на шум или выбросы в данных, что приведет к снижению эффективности обобщения на неизвестных образцах. Эффективность алгоритмов МИА (MIA) и МГУА (GMDH) в целом во многом зависит от качества и характеристик входных данных. Неполные или зашумленные данные могут отрицательно повлиять на точность и стабильность модели, что может привести к ненадежным прогнозам. Наконец, хотя процесс обучения довольно прост, для получения наилучших результатов все равно требуется определенный уровень настройки гиперпараметров. При этом процесс не полностью автоматизирован.

Для последней демонстрации у нас есть скрипт, который загружает модель из файла и использует ее для составления прогнозов. Этот пример доступен в файле LoadModelFromFile.mq5.

//+------------------------------------------------------------------+
//|                                            LoadModelFromFile.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>
//--- input parameters
input string   JsonFileName="";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---declaration of MIA instance
    MIA mia;
//---load the model from file  
    if(!mia.load(JsonFileName))
      return;
//---get the number of required inputs for the loaded model     
    int numlags = mia.getNumInputs();
//---generate arbitrary inputs to make a prediction with  
    vector inputs(ulong(numlags),arange,21.0,1.0);
//---make prediction and output results to terminal    
    Print(JsonFileName," input ", inputs," prediction ", mia.predict(inputs,1));
//---output the model's polynomial    
    Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

На следующем рисунке показан принцип работы скрипта и результат его успешного выполнения.

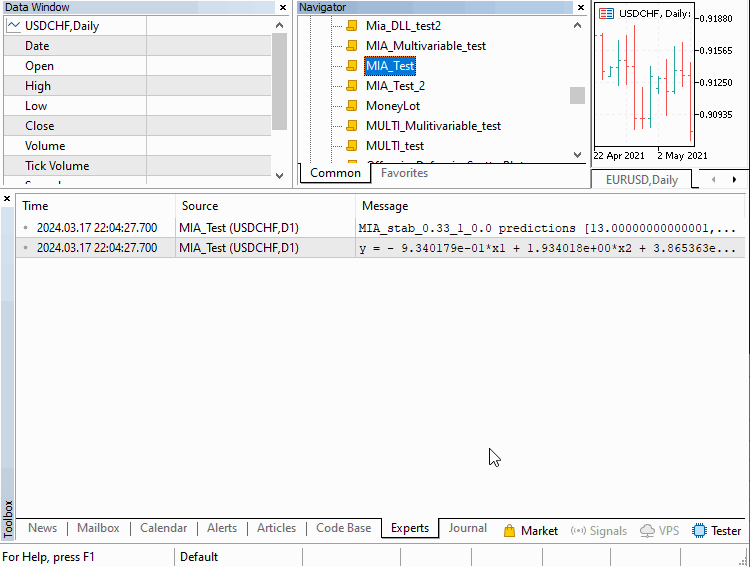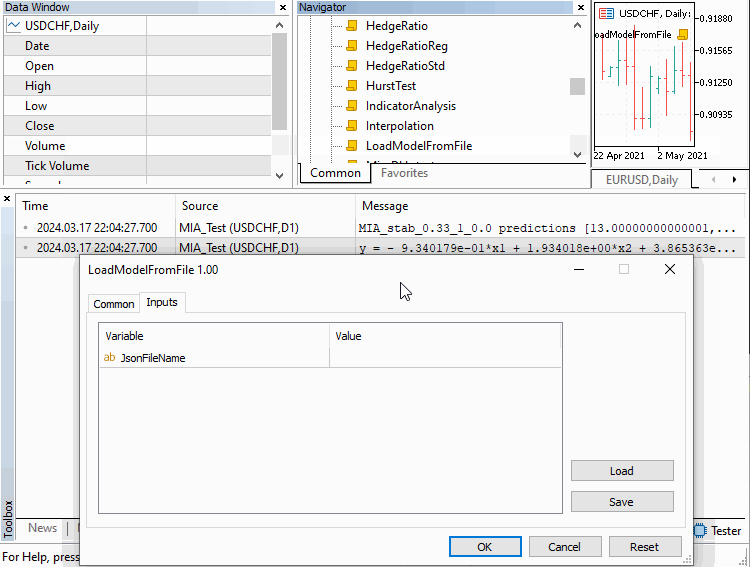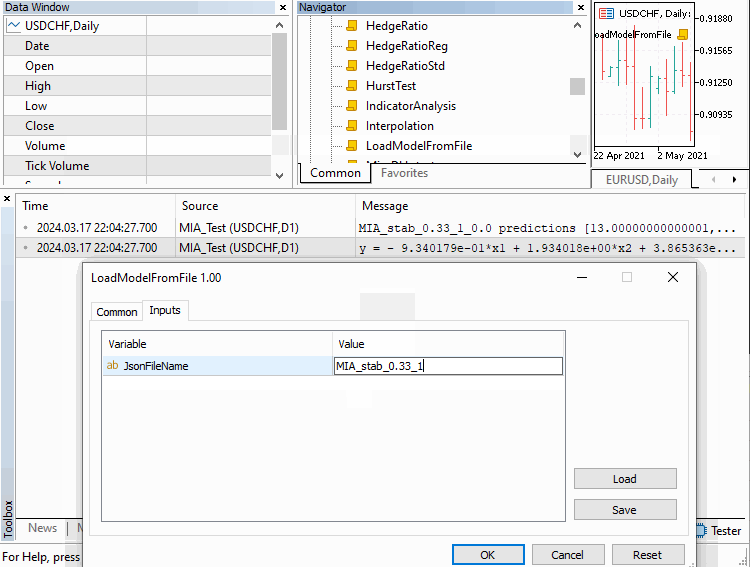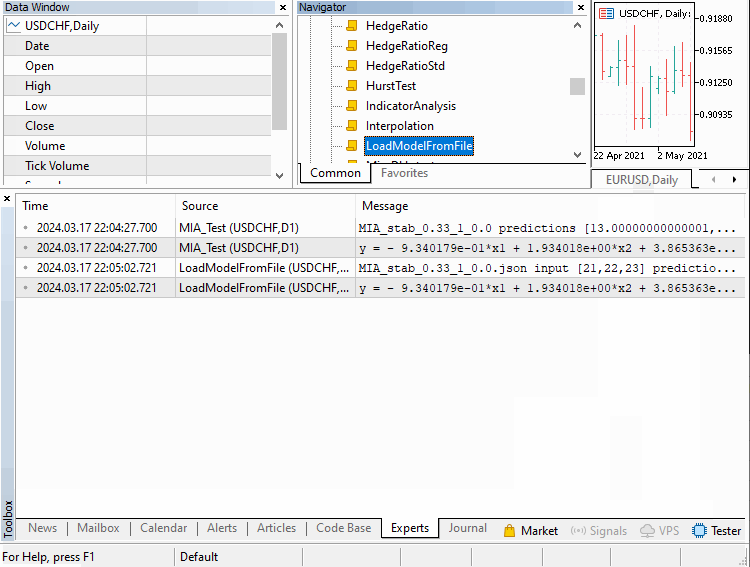
Заключение

Реализация многослойного итеративного алгоритма МГУА (GMDH) в MQL5 предоставляет трейдерам возможность применять эту концепцию в своих стратегиях. Алгоритм имеет динамическую структуру и позволяет пользователям постоянно адаптировать и совершенствовать анализ рынка. Однако, несмотря на все перспективы, важно понимать его ограничения. Нужно помнить о вычислительных требованиях, присущих алгоритмам МГУА, особенно при работе с большими наборами данных или с данными высокой размерности. Итеративный характер алгоритма требует проведения множественных вычислений для определения оптимальной структуры модели, что требует значительных затрат времени и ресурсов.

В свете этих соображений настоятельно рекомендуется подходить к использованию алгоритма МГУА с пониманием его сильных сторон и ограничений. Хотя он предлагает мощный инструмент для динамического анализа рынка, его сложность требует осторожного использования. При разумном применении и учете всех тонкостей алгоритма трейдеры могут использовать его для улучшения торговых стратегий и извлечения ценной информации из рыночных данных.

Все MQL5-коды приложены в конце статьи.

Файл	Описание
Mql5\include\VectorMatrixTools.mqh	Заголовочный файл определений функций, используемых для работы с векторами и матрицами
Mql5\include\JAson.mqh	Содержит определение пользовательских типов, используемых для анализа и генерации объектов JSON
Mql5\include\GMDH\gmdh_internal.mqh	Заголовочный файл, содержащий определения пользовательских типов, используемых в библиотеке gmdh
Mql5\include\GMDH\gmdh.mqh	Файл include с определением базового класса GmdhModel
Mql5\include\GMDH\mia.mqh	Содержит класс MIA, реализующий многослойный итерационный алгоритм
Mql5\script\MIA_Test.mq5	Скрипт, демонстрирующий использование класса MIA через построение модели простого временного ряда
Mql5\script\MIA_Multivarible_test.mq5	Еще один скрипт, демонстрирующий применение класса MIA для построения модели многомерного набора данных
Mql5\script\LoadModelFromFile.mq5	Скрипт, демонстрирующий, как загрузить модель из файла json