The Group Method of Data Handling: Implementing the Multilayered Iterative Algorithm in MQL5

Introduction

The Group Method of Data Handling (GMDH) is a family of inductive algorithms used for computer-based data modeling. The algorithms operate by automatically constructing and optimizing polynomial neural network models from data, offering a unique approach to uncovering relationships between input and output variables.Traditionally, the GMDH frame work consisted of four main algorithms: the combinatorial algorithm (COMBI), the combinatorial selective algorithm (MULTI), the multilayered iterative algorithm (MIA) and the relaxation iterative algorithm (RIA). In this article we will explore the implementation of the multilayered iterative algorithim in MQL5. Discuss its inner workings and also demonstrate ways it can be applied to build predictive models from datasets.

Understanding the GMDH

The Group Method of Data Handling  is a type of algorithm used for data analysis and prediction. It is a machine learning technique that aims to find the best mathematical model to describe a given dataset. GMDH was developed by the Soviet mathematician Alexey Ivakhnenko in the 1960s. It was developed to address the challenges associated with modeling complex systems based on empirical data. GMDH algorithms employ a data-driven approach to modeling, where models are generated and refined based on observed data rather than preconceived notions or theoretical assumptions.

One of the main advantages of GMDH is that it automates the process of model building by iteratively generating and evaluating candidate models. Selecting the best-performing models and refining them based on feedback from the data. This automation reduces the need for manual intervention and expertise in the construction of the model.

The key idea behind GMDH is to build a series of models of increasing complexity and accuracy by iteratively selecting and combining variables. The algorithm starts with a set of simple models (usually linear models) and gradually increases their complexity by adding additional variables and terms. At each step, the algorithm evaluates the performance of the models and selects the best-performing ones to form the basis for the next iteration. This process continues until a satisfactory model is obtained or until a stopping criteria is met.

The GMDH is particularly well-suited to modelling datasets with a large number of input variables and complex relationships between them. GMDH techniques result in models that relate inputs to an output that can be represented by an infinite Volterra–Kolmogorov–Gabor (VKG) polynomial. A Volterra-Kolmogorov-Gabor (VKG) polynomial is a specific type of polynomial used in modeling nonlinear systems and approximating complex data. A VKG polynomial takes the following form:

where:

• Yn is the output of the system.
• Xi, Xj, and Xk are the input variables at times i, j, and k, respectively.
• ai, aj, ak, etc. are the coefficients of the polynomial.

Such a polynomial can be thought of as a polynomial neural network (PNN). PNNs are a type of artificial neural network (ANN) architecture that uses polynomial activation functions in its neurons.The structure of a polynomial neural network is similar to that of other neural networks, with input nodes, hidden layers, and output nodes. However, the activation functions applied to the neurons in PNNs are polynomial functions. Parametric GMDH algorithms were developed specifically to handle continuous variables. Where the object being modelled is characterized by properties that lack ambiguity in their representation or definition. The multilayered iterative algorithm is an example of a parametric GMDH algorithm.

Multilayered Iterative Algorithm

MIA is a variant of the GMDH framework for constructing polynomial neural network models. Its structure is almost identical to a multilayer feedforward neural network. Information flows from the input layer through intermediate layers to the final output. With each layer performing specific transformations on the data. Relative to the general method of the GMDH, the key differentiating characteristic of MIA lies in the selection of optimal subfunctions of the final polynomial that best describes the data. Meaning that some information gained through training is discarded in accordance with a predefined criteria.

To construct a model using MIA, we begin by partitioning the dataset we want to study,  into training and test sets. We want to have as much variety as possible in the training set, to adequately capture the characteristics of the underlying process. We commence with layer construction once it's done . 

Layer construction

Similar to a multilayer feedforward neural network, we start with the input layer, which is the collection of predictors or independent variables. These inputs are taken two at a time and sent into the first layer of the network. The first layer will therefore be made up of "M combinations of 2"  nodes , where M is the number of predictors.

The illustration above depicts an example of what the input layer and first layer will look like if dealing with 4 inputs (denoted as x1..x4). In the first layer, partial models will be built based on a node's inputs using the training dataset and the resulting partial model evaluated against the test dataset. The prediction error from all partial models in the layer are then compared. With the best N models being noted and used to generate the inputs for the next layer. The prediction error of the top N models of a layer are combined in some manner to come up with a single measure that gives an indication of overall progress in model generation. Which is compared with the figure of the previous layer. If it is less, a new layer is created and the process is repeated. Otherwise, if there is no improvement. Model generation is stopped and data from the current layer is discarded, indicating that model training would be complete.

Nodes and partial models

At each node of a layer, a polynomial that estimates observations in the training dataset given the pair of inputs output from the previous layer is calculated. This is what is referred to as a partial model. An example of an equation used to model outputs of the training set given the node's inputs is shown below.

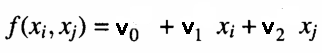
Where 'v's are the coefficients of the fitted linear model. The goodness of fit is tested by determining the mean square error of predictions against actual values , in the test dataset. These error measures are then combined in some manner. Either by calculating their average or simply selecting the node with the least mean square error. This final measure gives an indication of whether approximations are improving or not relative to other layers. At the same time the best N nodes with the least prediction error are noted. And the corresponding coefficients are used to generate the values of a set of new inputs for the next layer. If approximations of the current layer are better (in this case less) than that of the previous layer, a new layer will be constructed.

Once the network is complete, only the coefficients of nodes that had the best prediction error at each layer, are retained and used to define the final model that best describes the data. In the following section, we delve into code that implements the procedure just described. The code is adapted from a C++ implementation of the GMDH available on GitHub.

MQL5 implementation

The C++ implementation trains models and saves them in JSON format to a text file for later use. It leverages multithreading to speed up training and is built using Boost and Eigen libraries. For our MQL5 implementation, most of the features will be carried over except for multithreaded training and the availability of alternate options for QR decomposition to solve linear equations.

Our implementation will consist of three header files. The first being gmdh_internal.mqh. This file contains definitions for various custom datatypes. It starts by defining three enumerations:

• PolynomialType - specifies the type of polynomial used to transform existing variables before undertaking another round of training.
  

  //+---------------------------------------------------------------------------------------------------------+
  //|  Enumeration for specifying the polynomial type to be used to construct new variables from existing ones|
  //+---------------------------------------------------------------------------------------------------------+
  enum PolynomialType
    {
     linear,
     linear_cov,
     quadratic
    };

  "PolynomialType" exposes three options which represent the polymial functions below, here x1 and x2 are the inputs to the function f(x1,x2) and v0...vN are the  coefficients to be found. The enumeration represents the type of equations from which the set of solutions will be generated:

Option	Function f(x1,x2)
linear	linear equation: v0 + v1*x1 + v2*x2
linear_cov	linear equation with covariation: v0 + v1*x1 + v2*x2 + v3*x1*x2
quadratic	quadratic equation: v0 + v1*x1 + v2*x2 + v3*x1*x2 + v4*x1^2 + v5*x2^2

• Solver - determines QR decompostion method used to solve linear equations. Our implementation will only have one useable option. The C++ version employs variations  of the Householder method for QR decompostion using the Eigen library.
  

  //+-----------------------------------------------------------------------------------------------+
  //|  Enum  for specifying the QR decomposition method for linear equations solving in models.     |
  //+-----------------------------------------------------------------------------------------------+
  enum Solver
    {
     fast,
     accurate,
     balanced
    };

• CriterionType - allows users to select a specific external criterion that will be used as the basis for evaluating candidate models. The enumeration captures the options one can use as stopping critieria when training a model.
  

  //+------------------------------------------------------------------+
  //|Enum for specifying the external criterion                        |
  //+------------------------------------------------------------------+
  enum CriterionType
    {
     reg,
     symReg,
     stab,
     symStab,
     unbiasedOut,
     symUnbiasedOut,
     unbiasedCoef,
     absoluteNoiseImmun,
     symAbsoluteNoiseImmun
    };

  The options available are explained further in the table that follows:

CriterionType	Description
reg	regularity: applies the regular sum of squared errors (SSE) based on the difference between the test dataset's targets and predictions made with coefficients computed using the training dataset in combination with the predictors of the test dataset
symReg	symmetric regularity: is the summation of the SSE based on the difference between the test dataset's targets and predictions made with coefficients computed using the training dataset in combination with the predictors of the test dataset and the SSE  based on the difference between the training dataset's targets and predictions made with coefficients computed using the test dataset in combination with the predictors of the training dataset
stab	stability: uses the SSE based on difference between all the targets and predictions made with coefficients calculated using the training dataset in combination with all the predictors
symStab	symetric stabitlity: this criterion combines the SSE calculated similarly to the 'stability' criterion as well as the SSE based on the difference between all the targets and predictions made with coefficients calculated using the test dataset in combination with all the predictors of the dataset
unbiasedOut	unbiased outputs: is the SSE based on the difference between the predictions made with coefficients calculated using the training dataset and predictions made with coefficients calculated using the test dataset both using the predictors of the test dataset
symUnbiasedOut	symmetric unbiased outputs: computes the SSE in the same manner as the 'unbiasedOutputs' criterion, only this time we use all the predictors
unbiasedCoef	unbiased Coefficients:  the sum of squared differences between the coefficients computed using the training data and coefficients calculated using the test data
absoluteNoiseImmun	absolute noise immunity: using this option the criterion is calculated as the dot product of  the predictions of the model trained on the entire data set minus the predictions of the model trained on the training data set when applied to the testing data set and the predictions of the model trained on the testing data set minus the predictions of the model trained on the learning data set when applied to the testing data set
symAbsoluteNoiseImmun	symmetric absolute noise immunity: here the criterion is the dot product of the predictions of the model trained on the entire data set minus the predictions of the model trained on the training data set when applied to the learning data set and the predictions of the model trained on the entire data set and the predictions of the model trained on the testing data set when applied to all the observations

The enumerations are followed by four custom structs:

• BufferValues - is a structure of vectors used to store coefficients and predicted values calculated in various ways using both the test and training datasets.
  

  //+-------------------------------------------------------------------------------------+
  //| Structure for storing coefficients and predicted values calculated in different ways|
  //+--------------------------------------------------------------------------------------+
  struct BufferValues
    {
     vector            coeffsTrain; // Coefficients vector calculated using training data
     vector            coeffsTest; // Coefficients vector calculated using testing data
     vector            coeffsAll; // Coefficients vector calculated using learning data
     vector            yPredTrainByTrain; // Predicted values for *training* data calculated using coefficients vector calculated on *training* data
     vector            yPredTrainByTest; // Predicted values for *training* data calculated using coefficients vector calculated on *testing* data
     vector            yPredTestByTrain; // Predicted values for *testing* data calculated using coefficients vector calculated on *training* data
     vector            yPredTestByTest; //Predicted values for *testing* data calculated using coefficients vector calculated on *testing* data
  
                       BufferValues(void)
       {
  
       }
  
                       BufferValues(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
       }
  
     BufferValues      operator=(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
  
        return this;
       }
  
    };

  
  
• PairDVXd - encapsulates a data structure combining a scalar and a corresponding vector.
  

  //+------------------------------------------------------------------+
  //|  struct PairDV                                                   |
  //+------------------------------------------------------------------+
  struct PairDVXd
    {
     double            first;
     vector            second;
  
                       PairDVXd(void)
       {
        first = 0.0;
        second = vector::Zeros(10);
       }
  
                       PairDVXd(double &_f, vector &_s)
       {
        first = _f;
        second.Copy(_s);
       }
  
                       PairDVXd(PairDVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairDVXd          operator=(PairDVXd& other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

  
  
• PairMVXd - is a structure combining a matrix and vector. Together they store the inputs and the corresponding outputs or target values. The inputs are kept in the matrix and the vector is the collection of outputs. Each row in the matrix corresponds to a value in the vector.
  

  //+------------------------------------------------------------------+
  //| structure PairMVXd                                               |
  //+------------------------------------------------------------------+
  struct PairMVXd
    {
     matrix            first;
     vector            second;
  
                       PairMVXd(void)
       {
        first = matrix::Zeros(10,10);
        second = vector::Zeros(10);
       }
  
                       PairMVXd(matrix &_f,  vector& _s)
       {
        first = _f;
        second = _s;
       }
  
                       PairMVXd(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairMVXd          operator=(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

• SplittedData - this data structure stores the partitioned datasets for training and testing.
  

  //+------------------------------------------------------------------+
  //|  Structure for storing parts of a split dataset                  |
  //+------------------------------------------------------------------+
  struct SplittedData
    {
     matrix            xTrain;
     matrix            xTest;
     vector            yTrain;
     vector            yTest;
  
                       SplittedData(void)
       {
        xTrain = matrix::Zeros(10,10);
        xTest = matrix::Zeros(10,10);
        yTrain = vector::Zeros(10);
        yTest = vector::Zeros(10);
       }
  
                       SplittedData(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
       }
  
     SplittedData      operator=(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
  
        return this;
       }
    };

  
  

After the structs, we get to the class definitions:

• The class Combination represents a candidate model. It stores the evaluation criteria, the combination of inputs and the calculated coefficients for a model.
  

  //+------------------------------------------------------------------+
  //| Сlass representing the candidate model of the GMDH algorithm     |
  //+------------------------------------------------------------------+
  class Combination
    {
     vector            _combination,_bestCoeffs;
     double            _evaluation;
  public:
                       Combination(void) { _combination = vector::Zeros(10); _bestCoeffs.Copy(_combination); _evaluation = DBL_MAX; }
                       Combination(vector &comb) : _combination(comb) { _bestCoeffs=vector::Zeros(_combination.Size()); _evaluation = DBL_MAX;}
                       Combination(vector &comb, vector &coeffs) : _combination(comb),_bestCoeffs(coeffs) { _evaluation = DBL_MAX; }
                       Combination(Combination &other) { _combination = other.combination(); _bestCoeffs=other.bestCoeffs(); _evaluation = other.evaluation();}
     vector            combination(void) { return _combination;}
     vector            bestCoeffs(void)  { return _bestCoeffs; }
     double            evaluation(void)  { return _evaluation; }
  
     void              setCombination(vector &combination) { _combination = combination; }
     void              setBestCoeffs(vector &bestcoeffs) { _bestCoeffs = bestcoeffs; }
     void              setEvaluation(double evaluation)  { _evaluation = evaluation; }
  
     bool              operator<(Combination &combi) { return _evaluation<combi.evaluation();}
     Combination       operator=(Combination &combi)
       {
        _combination = combi.combination();
        _bestCoeffs = combi.bestCoeffs();
        _evaluation = combi.evaluation();
  
        return this;
       }
    };

• CVector - defines a custom vector-like container that stores a collection of Combination instances. Making it a container of candidate models.

  //+------------------------------------------------------------------+
  //| collection of Combination instances                              |
  //+------------------------------------------------------------------+
  class CVector
    {
  protected:
     Combination       m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector(CVector &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]=other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(Combination &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, Combination &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     Combination*      operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector           operator=(CVector &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     Combination*      back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     Combination*      front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• CVector2d - is another custom vector-like container , that stores a collection of CVector instances.
  

  //+------------------------------------------------------------------+
  //| Collection of CVector instances                                  |
  //+------------------------------------------------------------------+
  class CVector2d
    {
  protected:
     CVector           m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector2d(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector2d(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector2d(CVector2d &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector2d(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(CVector &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, CVector &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     CVector*          operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector2d         operator=(CVector2d &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     CVector*          back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     CVector*          front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
  
        for(uint i = 0; i<m_array.Size(); i++)
           m_array[i].clear();
  
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• Criterion - this class implements the calculation of various external criteria based on a selected criterion type.
  

  //+---------------------------------------------------------------------------------+
  //|Class that implements calculations of internal and individual external criterions|
  //+---------------------------------------------------------------------------------+
  class Criterion
    {
  protected:
     CriterionType     criterionType; // Selected CriterionType object
     Solver            solver; // Selected Solver object
  
  public:
     /**
     Implements the internal criterion calculation
     param xTrain Matrix of input variables that should be used to calculate the model coefficients
     param yTrain Target values vector for the corresponding xTrain parameter
     return Coefficients vector representing a solution of the linear equations system constructed from the parameters data
     */
     vector            findBestCoeffs(matrix& xTrain,  vector& yTrain)
       {
        vector solution;
  
        matrix q,r;
  
        xTrain.QR(q,r);
  
        matrix qT = q.Transpose();
  
        vector y = qT.MatMul(yTrain);
  
        solution = r.LstSq(y);
  
  
        return solution;
       }
  
     /**
      Calculate the value of the selected external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param _criterionType Selected external criterion type
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of external criterion and calculated model coefficients
      */
     PairDVXd          getResult(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 CriterionType _criterionType, BufferValues& bufferValues)
       {
        switch(_criterionType)
          {
           case reg:
              return regularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symReg:
              return symRegularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case stab:
              return stability(xTrain, xTest, yTrain, yTest, bufferValues);
           case symStab:
              return symStability(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedOut:
              return unbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case symUnbiasedOut:
              return symUnbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedCoef:
              return unbiasedCoeffs(xTrain, xTest, yTrain, yTest, bufferValues);
           case absoluteNoiseImmun:
              return absoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symAbsoluteNoiseImmun:
              return symAbsoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
          }
  
        PairDVXd pd;
        return pd;
       }
     /**
      Calculate the regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the regularity external criterion and calculated model coefficients
      */
     PairDVXd          regularity(matrix& xTrain, matrix& xTest, vector &yTrain, vector& yTest,
                                  BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           f = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
     /**
      Calculate the symmetric regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic regularity external criterion and calculated model coefficients
      */
     PairDVXd          symRegularity(matrix& xTrain, matrix& xTest, vector& yTrain, vector& yTest,
                                     BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = regularity(xTrain,xTest,yTrain,yTest,bufferValues);
        pdv2 = regularity(xTrain,xTest,yTrain,yTest,bufferValues,true);
  
        pdsum.first = pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the stability external criterion and calculated model coefficients
      */
     PairDVXd          stability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f1,f2;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTrainByTrain.Size() == 0)
              bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTrain),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
  
           pdv.first = f1.Sum()+f2.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           if(bufferValues.yPredTestByTest.Size() == 0)
              bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTest),2.0);
           pdv.first = f1.Sum() + f2.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
  
     /**
      Calculate the symmetric stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic stability external criterion and calculated model coefficients
      */
     PairDVXd          symStability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                    BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = stability(xTrain, xTest, yTrain, yTest, bufferValues);
        pdv2 = stability(xTrain, xTest, yTrain, yTest, bufferValues, true);
  
        pdsum.first=pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedOutputs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                       BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          symUnbiasedOutputs(matrix &xTrain,  matrix &xTest,  vector &yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1,f2;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
        if(bufferValues.yPredTrainByTrain.Size() == 0)
           bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTrainByTest.Size() == 0)
           bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f1 = MathPow((bufferValues.yPredTrainByTrain - bufferValues.yPredTrainByTest),2.0);
        f2 = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f1.Sum() + f2.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the unbiased coefficients external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased coefficients external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedCoeffs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        f1 = MathPow((bufferValues.coeffsTrain - bufferValues.coeffsTest),2.0);
        pdv.first = f1.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          absoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        vector yPredTestByAll,f1,f2;
        PairDVXd pdv;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
          {
           matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
           for(ulong i = 0; i<xTrain.Rows(); i++)
              dataX.Row(xTrain.Row(i),i);
  
           for(ulong i = 0; i<xTest.Rows(); i++)
              dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
           vector dataY(yTrain.Size() + yTest.Size());
  
           for(ulong i=0; i<yTrain.Size(); i++)
              dataY[i] = yTrain[i];
  
           for(ulong i=0; i<yTest.Size(); i++)
              dataY[i+yTrain.Size()] = yTest[i];
  
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
          }
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        yPredTestByAll = xTest.MatMul(bufferValues.coeffsAll);
  
        f1 =  yPredTestByAll - bufferValues.yPredTestByTrain;
        f2 = bufferValues.yPredTestByTest - yPredTestByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          symAbsoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector yPredAllByTrain, yPredAllByTest, yPredAllByAll,f1,f2;
        matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
        for(ulong i = 0; i<xTrain.Rows(); i++)
           dataX.Row(xTrain.Row(i),i);
  
        for(ulong i = 0; i<xTest.Rows(); i++)
           dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
        vector dataY(yTrain.Size() + yTest.Size());
  
        for(ulong i=0; i<yTrain.Size(); i++)
           dataY[i] = yTrain[i];
  
        for(ulong i=0; i<yTest.Size(); i++)
           dataY[i+yTrain.Size()] = yTest[i];
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
  
        yPredAllByTrain = dataX.MatMul(bufferValues.coeffsTrain);
        yPredAllByTest = dataX.MatMul(bufferValues.coeffsTest);
        yPredAllByAll = dataX.MatMul(bufferValues.coeffsAll);
  
        f1 = yPredAllByAll - yPredAllByTrain;
        f2 = yPredAllByTest - yPredAllByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
  
       }
  
     /**
      Get k models from the given ones with the best values of the external criterion
     param combinations Vector of the trained models
     param data Object containing parts of a split dataset used in model training. Parameter is used in sequential criterion
     param func Function returning the new X train and X test data constructed from the original data using given combination of input variables column indexes. Parameter is used in sequential criterion
     param k Number of best models
     return Vector containing k best models
      */
     virtual void      getBestCombinations(CVector &combinations, CVector &bestCombo,SplittedData& data, MatFunc func, int k)
       {
        double proxys[];
        int best[];
  
        ArrayResize(best,combinations.size());
        ArrayResize(proxys,combinations.size());
  
        for(int i = 0 ; i<combinations.size(); i++)
          {
           proxys[i] = combinations[i].evaluation();
           best[i] = i;
          }
  
        MathQuickSortAscending(proxys,best,0,combinations.size()-1);
  
        for(int i = 0; i<int(MathMin(MathAbs(k),combinations.size())); i++)
           bestCombo.push_back(combinations[best[i]]);
  
       }
     /**
      Calculate the value of the selected external criterion for the given data.
      For the individual criterion this method only calls the getResult() method
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     return The value of the external criterion and calculated model coefficients
      */
     virtual PairDVXd  calculate(matrix& xTrain,  matrix& xTest,
                                 vector& yTrain,  vector& yTest)
       {
        BufferValues tempValues;
        return getResult(xTrain, xTest, yTrain, yTest, criterionType, tempValues);
       }
  
  public:
     ///  Construct a new Criterion object
                       Criterion() {};
  
     /**
      Construct a new Criterion object
     param _criterionType Selected external criterion type
     param _solver Selected method for linear equations solving
      */
                       Criterion(CriterionType _criterionType)
       {
        criterionType = _criterionType;
        solver = balanced;
       }
  
    };
  

Lastly, we have two functions that mark the end of gmdh_internal.mqh:

validateInputData() - is used to ensure that values passed to class methods or other stand alone functions are correctly specified.

**
 *  Validate input parameters values
 *
 * param testSize Fraction of the input data that should be placed into the second part
 * param pAverage The number of best models based of which the external criterion for each level will be calculated
 * param threads The number of threads used for calculations. Set -1 to use max possible threads
 * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
 * param limit The minimum value by which the external criterion should be improved in order to continue training
 * param kBest The number of best models based of which new models of the next level will be constructed
 * return Method exit status
 */
int validateInputData(double testSize=0.0, int pAverage=0, double limit=0.0, int kBest=0)
  {
   int errorCode = 0;
//
   if(testSize <= 0 || testSize >= 1)
     {
      Print("testsize value must be in the (0, 1) range");
      errorCode |= 1;
     }
   if(pAverage && pAverage < 1)
     {
      Print("p_average value must be a positive integer");
      errorCode |= 4;
     }
   if(limit && limit < 0)
     {
      Print("limit value must be non-negative");
      errorCode |= 8;
     }
   if(kBest && kBest < 1)
     {
      Print("k_best value must be a positive integer");
      errorCode |= 16;
     }

   return errorCode;
  }

timeSeriesTransformation() -  is a utility function that takes as input a series in a vector and transforms it into a data structure of inputs and targets according to the chosen number of lags.

/**
 *  Convert the time series vector to the 2D matrix format required to work with GMDH algorithms
 *
 * param timeSeries Vector of time series data
 * param lags The lags (length) of subsets of time series into which the original time series should be divided
 * return Transformed time series data
 */
PairMVXd timeSeriesTransformation(vector& timeSeries, int lags)
  {
   PairMVXd p;

   string errorMsg = "";
   if(timeSeries.Size() == 0)
      errorMsg = "time_series value is empty";
   else
      if(lags <= 0)
         errorMsg = "lags value must be a positive integer";
      else
         if(lags >= int(timeSeries.Size()))
            errorMsg = "lags value can't be greater than  time_series  size";
   if(errorMsg != "")
      return p;

   ulong last = timeSeries.Size() - ulong(lags);
   vector yTimeSeries(last,slice,timeSeries,ulong(lags));
   matrix xTimeSeries(last, ulong(lags));
   vector vect;
   for(ulong i = 0; i < last; ++i)
     {
      vect.Init(ulong(lags),slice,timeSeries,i,i+ulong(lags-1));
      xTimeSeries.Row(vect,i);
     }

   p.first = xTimeSeries;
   p.second = yTimeSeries;

   return p;
  }

Here lags refers to the number of previous series values used as predictors to compute a subsequent term.

That completes the description of gmdh_internal.mqh. We move on to the second header file, gmdh.mqh.

It starts with the definition of the splitData() function.

/**
 *  Divide the input data into 2 parts
 *
 * param x Matrix of input data containing predictive variables
 * param y Vector of the taget values for the corresponding x data
 * param testSize Fraction of the input data that should be placed into the second part
 * param shuffle True if data should be shuffled before splitting into 2 parts, otherwise false
 * param randomSeed Seed number for the random generator to get the same division every time
 * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
 */
SplittedData splitData(matrix& x,  vector& y, double testSize = 0.2, bool shuffle = false, int randomSeed = 0)
  {
   SplittedData data;

   if(validateInputData(testSize))
      return data;
   
   string errorMsg = "";
   if(x.Rows() != y.Size())
      errorMsg = " x rows number and y size must be equal";
   else
      if(round(x.Rows() * testSize) == 0 || round(x.Rows() * testSize) == x.Rows())
         errorMsg = "Result contains an empty array. Change the arrays size or the  value for correct splitting";
   if(errorMsg != "")
     {
      Print(__FUNCTION__," ",errorMsg);
      return data;
     }


   if(!shuffle)
      data = GmdhModel::internalSplitData(x, y, testSize);
   else
     {
      if(randomSeed == 0)
         randomSeed = int(GetTickCount64());
      MathSrand(uint(randomSeed));

      int shuffled_rows_indexes[],shuffled[];
      MathSequence(0,int(x.Rows()-1),1,shuffled_rows_indexes);
      MathSample(shuffled_rows_indexes,int(shuffled_rows_indexes.Size()),shuffled);

      int testItemsNumber = (int)round(x.Rows() * testSize);


      matrix Train,Test;
      vector train,test;

      Train.Resize(x.Rows()-ulong(testItemsNumber),x.Cols());
      Test.Resize(ulong(testItemsNumber),x.Cols());

      train.Resize(x.Rows()-ulong(testItemsNumber));
      test.Resize(ulong(testItemsNumber));

      for(ulong i = 0; i<Train.Rows(); i++)
        {
         Train.Row(x.Row(shuffled[i]),i);
         train[i] = y[shuffled[i]];
        }

      for(ulong i = 0; i<Test.Rows(); i++)
        {
         Test.Row(x.Row(shuffled[Train.Rows()+i]),i);
         test[i] = y[shuffled[Train.Rows()+i]];
        }

      data.xTrain = Train;
      data.xTest = Test;
      data.yTrain = train;
      data.yTest = test;
     }

   return data;
  }  

It takes as input a matrix and a vector representing variables and targets respectively. "testSize" parameter defines the fraction of the dataset to be used as the test set. "shuffle" enables random shuffling of the dataset and "randomSeed" specifies the seed for a random number generator used in shuffling process.

Next we have the "GmdhModel" class, which defines the general logic of GMDH algorithms.

//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH algorithms          |
//+------------------------------------------------------------------+

class  GmdhModel
  {
protected:

   string            modelName; // model name
   int               level; // Current number of the algorithm training level
   int               inputColsNumber; // The number of predictive variables in the original data
   double            lastLevelEvaluation; // The external criterion value of the previous training level
   double            currentLevelEvaluation; // The external criterion value of the current training level
   bool              training_complete; // flag indicator successful completion of model training
   CVector2d         bestCombinations; // Storage for the best models of previous levels

   /**
    *struct for generating vector sequence
    */
   struct unique
     {
   private:
      int            current;

      int            run(void)
        {
         return ++current;
        }

   public:
                     unique(void)
        {
         current = -1;
        }

      vector         generate(ulong t)
        {
         ulong s=0;
         vector ret(t);

         while(s<t)
            ret[s++] = run();

         return ret;
        }
     };

   /**
    *  Find all combinations of k elements from n
    *
    * param n Number of all elements
    * param k Number of required elements
    * return Vector of all combinations of k elements from n
    */
   void              nChooseK(int n, int k, vector &combos[])
     {
      if(n<=0 || k<=0 || n<k)
        {
         Print(__FUNCTION__," invalid parameters for n and or k", "n ",n , " k ", k);
         return;
        }

      unique q;

      vector comb = q.generate(ulong(k));

      ArrayResize(combos,combos.Size()+1,100);

      long first, last;

      first = 0;
      last = long(k);
      combos[combos.Size()-1]=comb;

      while(comb[first]!= double(n - k))
        {
         long mt = last;
         while(comb[--mt] == double(n - (last - mt)));
         comb[mt]++;
         while(++mt != last)
            comb[mt] = comb[mt-1]+double(1);
         ArrayResize(combos,combos.Size()+1,100);
         combos[combos.Size()-1]=comb;
        }

      for(uint i = 0; i<combos.Size(); i++)
        {
         combos[i].Resize(combos[i].Size()+1);
         combos[i][combos[i].Size()-1] = n;
        }

      return;
     }

   /**
    *  Get the mean value of extrnal criterion of the k best models
    *
    * param sortedCombinations Sorted vector of current level models
    * param k The numebr of the best models
    * return Calculated mean value of extrnal criterion of the k best models
    */
   double            getMeanCriterionValue(CVector &sortedCombinations, int k)
     {
      k = MathMin(k, sortedCombinations.size());

      double crreval=0;

      for(int i = 0; i<k; i++)
         crreval +=sortedCombinations[i].evaluation();
      if(k)
         return crreval/double(k);
      else
        {
         Print(__FUNCTION__, " Zero divide error ");
         return 0.0;
        }
     }

   /**
    *  Get the sign of the polynomial variable coefficient
    *
    * param coeff Selected coefficient
    * param isFirstCoeff True if the selected coefficient will be the first in the polynomial representation, otherwise false
    * return String containing the sign of the coefficient
    */
   string            getPolynomialCoeffSign(double coeff, bool isFirstCoeff)
     {
      return ((coeff >= 0) ? ((isFirstCoeff) ? " " : " + ") : " - ");
     }

   /**
    *  Get the rounded value of the polynomial variable coefficient without sign
    *
    * param coeff Selected coefficient
    * param isLastCoeff True if the selected coefficient will be the last one in the polynomial representation, otherwise false
    * return String containing the rounded value of the coefficient without sign
    */
   string            getPolynomialCoeffValue(double coeff, bool isLastCoeff)
     {
      string stringCoeff = StringFormat("%e",MathAbs(coeff));
      return ((stringCoeff != "1" || isLastCoeff) ? stringCoeff : "");
     }

   /**
    *  Train given subset of models and calculate external criterion for them
    *
    * param data Data used for training and evaulating models
    * param criterion Selected external criterion
    * param beginCoeffsVec Iterator indicating the beginning of a subset of models
    * param endCoeffsVec Iterator indicating the end of a subset of models
    * param leftTasks The number of remaining untrained models at the entire level
    * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
    */
   bool              polynomialsEvaluation(SplittedData& data,  Criterion& criterion,  CVector &combos, uint beginCoeffsVec,
                                           uint endCoeffsVec)
     {
      vector cmb,ytrain,ytest;
      matrix x1,x2;
      for(uint i = beginCoeffsVec; i<endCoeffsVec; i++)
        {
         cmb = combos[i].combination();
         x1 = xDataForCombination(data.xTrain,cmb);
         x2 = xDataForCombination(data.xTest,cmb);
         ytrain = data.yTrain;
         ytest = data.yTest;
         PairDVXd pd = criterion.calculate(x1,x2,ytrain,ytest);

         if(pd.second.HasNan()>0)
            {
             Print(__FUNCTION__," No solution found for coefficient at ", i, "\n xTrain \n", x1, "\n xTest \n", x2, "\n yTrain \n", ytrain, "\n yTest \n", ytest);
             combos[i].setEvaluation(DBL_MAX);
             combos[i].setBestCoeffs(vector::Ones(3));
            }
         else
            {
             combos[i].setEvaluation(pd.first);
             combos[i].setBestCoeffs(pd.second);
            } 
        }

      return true;
     }

   /**
   *  Determine the need to continue training and prepare the algorithm for the next level
   *
   * param kBest The number of best models based of which new models of the next level will be constructed
   * param pAverage The number of best models based of which the external criterion for each level will be calculated
   * param combinations Trained models of the current level
   * param criterion Selected external criterion
   * param data Data used for training and evaulating models
   * param limit The minimum value by which the external criterion should be improved in order to continue training
   * return True if the algorithm needs to continue training, otherwise fasle
   */
   bool              nextLevelCondition(int kBest, int pAverage, CVector &combinations,
                                        Criterion& criterion, SplittedData& data, double limit)
     {
      MatFunc fun = NULL;
      CVector bestcombinations;
      criterion.getBestCombinations(combinations,bestcombinations,data, fun, kBest);
      currentLevelEvaluation = getMeanCriterionValue(bestcombinations, pAverage);

      if(lastLevelEvaluation - currentLevelEvaluation > limit)
        {
         lastLevelEvaluation = currentLevelEvaluation;
         if(preparations(data,bestcombinations))
           {
            ++level;
            return true;
           }
        }
      removeExtraCombinations();
      return false;

     }

   /**
    *  Fit the algorithm to find the best solution
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param criterion Selected external criterion
    * param kBest The number of best models based of which new models of the next level will be constructed
    * param testSize Fraction of the input data that should be used to evaluate models at each level
    * param pAverage The number of best models based of which the external criterion for each level will be calculated
    * param limit The minimum value by which the external criterion should be improved in order to continue training
    * return A pointer to the algorithm object for which the training was performed
    */
   bool              gmdhFit(matrix& x,  vector& y,  Criterion& criterion, int kBest,
                             double testSize, int pAverage, double limit)
     {
      if(x.Rows() != y.Size())
        {
         Print("X rows number and y size must be equal");
         return false;
        }

      level = 1; // reset last training
      inputColsNumber = int(x.Cols());
      lastLevelEvaluation = DBL_MAX;

      SplittedData data = internalSplitData(x, y, testSize, true) ;
      training_complete = false;
      bool goToTheNextLevel;
      CVector evaluationCoeffsVec;
      do
        {
         vector combinations[];
         generateCombinations(int(data.xTrain.Cols() - 1),combinations);
         
         if(combinations.Size()<1)
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }  

         evaluationCoeffsVec.clear();

         int currLevelEvaluation = 0;
         for(int it = 0; it < int(combinations.Size()); ++it, ++currLevelEvaluation)
           {
            Combination ncomb(combinations[it]);
            evaluationCoeffsVec.push_back(ncomb);
           }

         if(!polynomialsEvaluation(data,criterion,evaluationCoeffsVec,0,uint(currLevelEvaluation)))
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }

         goToTheNextLevel = nextLevelCondition(kBest, pAverage, evaluationCoeffsVec, criterion, data, limit); // checking the results of the current level for improvement
        }
      while(goToTheNextLevel);

      training_complete = true;

      return true;
     }

   /**
    *  Get new model structures for the new level of training
    *
    * param n_cols The number of existing predictive variables at the current training level
    * return Vector of new model structures
    */
   virtual void      generateCombinations(int n_cols,vector &out[])
     {
      return;
     }


   ///  Removed the saved models that are no longer needed
   virtual void      removeExtraCombinations(void)
     {
      return;
     }

   /**
    *  Prepare data for the next training level
    *
    * param data Data used for training and evaulating models at the current level
    * param _bestCombinations Vector of the k best models of the current level
    * return True if the training process can be continued, otherwise false
    */
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations)
     {
      return false;
     }

   /**
    *  Get the data constructed according to the model structure from the original data
    *
    * param x Training data at the current level
    * param comb Vector containing the indexes of the x matrix columns that should be used in the model
    * return Constructed data
    */
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)
     {
      return matrix::Zeros(10,10);
     }

   /**
    *  Get the designation of polynomial equation
    *
    * param levelIndex The number of the level counting from 0
    * param combIndex The number of polynomial in the level counting from 0
    * return The designation of polynomial equation
    */
   virtual string    getPolynomialPrefix(int levelIndex, int combIndex)
     {
      return NULL;
     }

   /**
    *  Get the string representation of the polynomial variable
    *
    * param levelIndex The number of the level counting from 0
    * param coeffIndex The number of the coefficient related to the selected variable in the polynomial counting from 0
    * param coeffsNumber The number of coefficients in the polynomial
    * param bestColsIndexes Indexes of the data columns used to construct polynomial of the model
    * return The string representation of the polynomial variable
    */
   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector& bestColsIndexes)
     {
      return NULL;
     }

   /*
    *  Transform model data to JSON format for further saving
    *
    * return JSON value of model data
    */
   virtual CJAVal    toJSON(void)
     {
      CJAVal json_obj_model;

      json_obj_model["modelName"] = getModelName();
      json_obj_model["inputColsNumber"] = inputColsNumber;
      json_obj_model["bestCombinations"] = CJAVal(jtARRAY,"");


      for(int i = 0; i<bestCombinations.size(); i++)
        {

         CJAVal Array(jtARRAY,"");

         for(int k = 0; k<bestCombinations[i].size(); k++)
           {
            CJAVal collection;
            collection["combination"] = CJAVal(jtARRAY,"");
            collection["bestCoeffs"] = CJAVal(jtARRAY,"");
            vector combination = bestCombinations[i][k].combination();
            vector bestcoeff = bestCombinations[i][k].bestCoeffs();
            for(ulong j=0; j<combination.Size(); j++)
               collection["combination"].Add(int(combination[j]));
            for(ulong j=0; j<bestcoeff.Size(); j++)
               collection["bestCoeffs"].Add(bestcoeff[j],-15);
            Array.Add(collection);
           }

         json_obj_model["bestCombinations"].Add(Array);

        }

      return json_obj_model;

     }

   /**
    *  Set up model from JSON format model data
    *
    * param jsonModel Model data in JSON format
    * return Method exit status
    */
   virtual bool      fromJSON(CJAVal &jsonModel)
     {
      modelName = jsonModel["modelName"].ToStr();
      bestCombinations.clear();
      inputColsNumber = int(jsonModel["inputColsNumber"].ToInt());

      for(int i = 0; i<jsonModel["bestCombinations"].Size(); i++)
        {
         CVector member;
         for(int j = 0; j<jsonModel["bestCombinations"][i].Size(); j++)
           {
            Combination cb;
            vector c(ulong(jsonModel["bestCombinations"][i][j]["combination"].Size()));
            vector cf(ulong(jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size()));
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["combination"].Size(); k++)
               c[k] = jsonModel["bestCombinations"][i][j]["combination"][k].ToDbl();
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size(); k++)
               cf[k] = jsonModel["bestCombinations"][i][j]["bestCoeffs"][k].ToDbl();
            cb.setBestCoeffs(cf);
            cb.setCombination(c);
            member.push_back(cb);
           }
         bestCombinations.push_back(member);
        }
      return true;
     }



   /**
    *  Compare the number of required and actual columns of the input matrix
    *
    * param x Given matrix of input data
    */
   bool              checkMatrixColsNumber(matrix& x)
     {
      if(ulong(inputColsNumber) != x.Cols())
        {
         Print("Matrix  must have " + string(inputColsNumber) + " columns because there were " + string(inputColsNumber) + " columns in the training  matrix");
         return false;
        }

      return true;
     }
     
     

public:
   ///  Construct a new Gmdh Model object
                     GmdhModel() : level(1), lastLevelEvaluation(0) {}

   /**
   *  Get full class name
   *
   * return String containing the name of the model class
   */
   string            getModelName(void)
     {
      return modelName;
     }
   /**
     *Get number of inputs required for model
     */
    int getNumInputs(void)
     {
      return inputColsNumber;
     }

   /**
    *  Save model data into regular file
    *
    * param path Path to regular file
    */
   bool              save(string file_name)
     {

      CFileTxt modelFile;

      if(modelFile.Open(file_name,FILE_WRITE|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         CJAVal js=toJSON();
         if(modelFile.WriteString(js.Serialize())==0)
           {
            Print("failed write to ",file_name,". Error -",::GetLastError());
            return false;
           }
        }

      return true;
     }

   /**
    *  Load model data from regular file
    *
    * param path Path to regular file
    */
   bool               load(string file_name)
     {
      training_complete = false;
      CFileTxt modelFile;
      CJAVal js;

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         training_complete = fromJSON(js);
        }
      return training_complete;
     }
   /**
    *  Divide the input data into 2 parts without shuffling
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param testSize Fraction of the input data that should be placed into the second part
    * param addOnesCol True if it is needed to add a column of ones to the x data, otherwise false
    * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
    */
   static SplittedData internalSplitData(matrix& x,  vector& y, double testSize, bool addOnesCol = false)
     {
      SplittedData data;
      ulong testItemsNumber = ulong(round(double(x.Rows()) * testSize));
      matrix Train,Test;
      vector train,test;

      if(addOnesCol)
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols() + 1);
         Test.Resize(testItemsNumber, x.Cols() + 1);

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         Train.Col(vector::Ones(Train.Rows()),x.Cols());

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);

         Test.Col(vector::Ones(Test.Rows()),x.Cols());

        }
      else
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols());
         Test.Resize(testItemsNumber, x.Cols());

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);
        }

      train.Init(y.Size() - testItemsNumber,slice,y,0,y.Size() - testItemsNumber - 1);
      test.Init(testItemsNumber,slice,y,y.Size() - testItemsNumber);

      data.yTrain = train;
      data.yTest = test;

      data.xTrain = Train;
      data.xTest = Test;

      return data;
     }

   /**
    *  Get long-term forecast for the time series
    *
    * param x One row of the test time series data
    * param lags The number of lags (steps) to make a forecast for
    * return Vector containing long-term forecast
    */
   virtual vector    predict(vector& x, int lags)
     {
      return vector::Zeros(1);
     }

   /**
    *  Get the String representation of the best polynomial
    *
    * return String representation of the best polynomial
    */
   string            getBestPolynomial(void)
     {
      string polynomialStr = "";
      int ind = 0;
      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector bestColsIndexes = bestCombinations[i][j].combination();
            vector bestCoeffs = bestCombinations[i][j].bestCoeffs();
            polynomialStr += getPolynomialPrefix(i, j);
            bool isFirstCoeff = true;
            for(int k = 0; k < int(bestCoeffs.Size()); ++k)
              {
               if(bestCoeffs[k])
                 {
                  polynomialStr += getPolynomialCoeffSign(bestCoeffs[k], isFirstCoeff);
                  string coeffValuelStr = getPolynomialCoeffValue(bestCoeffs[k], (k == (bestCoeffs.Size() - 1)));
                  polynomialStr += coeffValuelStr;
                  if(coeffValuelStr != "" && k != bestCoeffs.Size() - 1)
                     polynomialStr += "*";
                  polynomialStr += getPolynomialVariable(i, k, int(bestCoeffs.Size()), bestColsIndexes);
                  isFirstCoeff = false;
                 }
              }
            if(i < bestCombinations.size() - 1 || j < (bestCombinations[i].size() - 1))
               polynomialStr += "\n";
           }//j
         if(i < bestCombinations.size() - 1 && bestCombinations[i].size() > 1)
            polynomialStr += "\n";
        }//i
      return polynomialStr;
     }

                    ~GmdhModel()
     {
      for(int i = 0; i<bestCombinations.size(); i++)
         bestCombinations[i].clear();

      bestCombinations.clear();
     }
  };


//+------------------------------------------------------------------+

It is the base class from which other GMDH types will be derived. It provides methods for training or building a model and subsequently making predictions with it. the "save" and "load" methods allow one to save a model and load it from file for later use. Models are saved in JSON format to a text file in the directory common to all MetaTrader terminals.

The last header file, mia.mqh contains the definition of the "MIA" class.

//+------------------------------------------------------------------+
//| Class implementing multilayered iterative algorithm MIA          |
//+------------------------------------------------------------------+
class MIA : public GmdhModel
  {
protected:
   PolynomialType    polynomialType; // Selected polynomial type

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,2,out);
      return;
     }
   /**
   *  Get predictions for the input data
   *
   * param x Test data of the regression task or one-step time series forecast
   * return Vector containing prediction values
   */
   virtual vector    calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         matrix xNew(1, ulong(bestCombinations[i].size()) + 1);
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector comb = bestCombinations[i][j].combination();
            matrix xx(1,comb.Size());
            for(ulong i = 0; i<xx.Cols(); ++i)
               xx[0][i] = modifiedX[0][ulong(comb[i])];
            matrix ply = getPolynomialX(xx);
            vector c,b;
            c = bestCombinations[i][j].bestCoeffs();
            b = ply.MatMul(c);
            xNew.Col(b,ulong(j));
           }
         vector n  = vector::Ones(xNew.Rows());
         xNew.Col(n,xNew.Cols() - 1);
         modifiedX = xNew;
        }

      return modifiedX.Col(0);

     }

   /**
    *  Construct vector of the new variable values according to the selected polynomial type
    *
    * param x Matrix of input variables values for the selected polynomial type
    * return Construct vector of the new variable values
    */
   matrix            getPolynomialX(matrix& x)
     {
      matrix polyX = x;
      if((polynomialType == linear_cov))
        {
         polyX.Resize(x.Rows(), 4);
         polyX.Col(x.Col(0)*x.Col(1),2);
         polyX.Col(x.Col(2),3);
        }
      else
         if((polynomialType == quadratic))
           {
            polyX.Resize(x.Rows(), 6);
            polyX.Col(x.Col(0)*x.Col(1),2) ;
            polyX.Col(x.Col(0)*x.Col(0),3);
            polyX.Col(x.Col(1)*x.Col(1),4);
            polyX.Col(x.Col(2),5) ;
           }

      return polyX;
     }

   /**
    *  Transform data in the current training level by constructing new variables using selected polynomial type
    *
    * param data Data used to train models at the current level
    * param bestCombinations Vector of the k best models of the current level
    */
   virtual void      transformDataForNextLevel(SplittedData& data,  CVector &bestCombs)
     {
      matrix xTrainNew(data.xTrain.Rows(), ulong(bestCombs.size()) + 1);
      matrix xTestNew(data.xTest.Rows(), ulong(bestCombs.size()) + 1);

      for(int i = 0; i < bestCombs.size(); ++i)
        {
         vector comb = bestCombs[i].combination();

         matrix train(xTrainNew.Rows(),comb.Size()),test(xTrainNew.Rows(),comb.Size());

         for(ulong k = 0; k<comb.Size(); k++)
           {
            train.Col(data.xTrain.Col(ulong(comb[k])),k);
            test.Col(data.xTest.Col(ulong(comb[k])),k);
           }

         matrix polyTest,polyTrain;
         vector bcoeff = bestCombs[i].bestCoeffs();
         polyTest = getPolynomialX(test);
         polyTrain = getPolynomialX(train);

         xTrainNew.Col(polyTrain.MatMul(bcoeff),i);
         xTestNew.Col(polyTest.MatMul(bcoeff),i);
        }

      xTrainNew.Col(vector::Ones(xTrainNew.Rows()),xTrainNew.Cols() - 1);
      xTestNew.Col(vector::Ones(xTestNew.Rows()),xTestNew.Cols() - 1);

      data.xTrain = xTrainNew;
      data.xTest =  xTestNew;
     }

   virtual void      removeExtraCombinations(void) override
     {

      CVector2d realBestCombinations(bestCombinations.size());
      CVector n;
      n.push_back(bestCombinations[level-2][0]);
      realBestCombinations.setAt(realBestCombinations.size() - 1,n);

      vector comb(1);
      for(int i = realBestCombinations.size() - 1; i > 0; --i)
        {
         double usedCombinationsIndexes[],unique[];
         int indexs[];
         int prevsize = 0;
         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            ArrayResize(usedCombinationsIndexes,prevsize+int(comb.Size()-1),100);
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               usedCombinationsIndexes[ulong(prevsize)+k] = comb[k];
            prevsize = int(usedCombinationsIndexes.Size());
           }
         MathUnique(usedCombinationsIndexes,unique);
         ArraySort(unique);

         for(uint it = 0; it<unique.Size(); ++it)
            realBestCombinations[i - 1].push_back(bestCombinations[i - 1][int(unique[it])]);

         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               comb[k] = ArrayBsearch(unique,comb[k]);
            comb[comb.Size() - 1] = double(unique.Size());
            realBestCombinations[i][j].setCombination(comb);
           }

         ZeroMemory(usedCombinationsIndexes);
         ZeroMemory(unique);
         ZeroMemory(indexs);
        }

      bestCombinations = realBestCombinations;
     }
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations) override
     {
      bestCombinations.push_back(_bestCombinations);
      transformDataForNextLevel(data, bestCombinations[level - 1]);
      return true;
     }
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)  override
     {
      matrix xx(x.Rows(),comb.Size());

      for(ulong i = 0; i<xx.Cols(); ++i)
         xx.Col(x.Col(ulong(comb[i])),i);

      return getPolynomialX(xx);
     }

   string            getPolynomialPrefix(int levelIndex, int combIndex)  override
     {
      return ((levelIndex < bestCombinations.size() - 1) ?
              "f" + string(levelIndex + 1) + "_" + string(combIndex + 1) : "y") + " =";
     }
   string            getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector &bestColsIndexes)  override
     {
      if(levelIndex == 0)
        {
         if(coeffIndex < 2)
            return "x" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "x" + string(int(bestColsIndexes[0]) + 1) + "*x" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "x" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      else
        {
         if(coeffIndex < 2)
            return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[0]) + 1) +
                      "*f" + string(levelIndex) + "_" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      return "";
     }


   CJAVal            toJSON(void)  override
     {
      CJAVal json_obj_model = GmdhModel::toJSON();

      json_obj_model["polynomialType"] = int(polynomialType);
      return json_obj_model;

     }

   bool              fromJSON(CJAVal &jsonModel) override
     {
      bool parsed = GmdhModel::fromJSON(jsonModel);

      if(!parsed)
         return false;

      polynomialType = PolynomialType(jsonModel["polynomialType"].ToInt());

      return true;
     }

public:
   //+------------------------------------------------------------------+
   //| Constructor                                                      |
   //+------------------------------------------------------------------+

                     MIA(void)
     {
      modelName = "MIA";
     }

   //+------------------------------------------------------------------+
   //| model a time series                                              |
   //+------------------------------------------------------------------+

   virtual bool      fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 3)
        {
         Print(__FUNCTION__," lags must be >= 3");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   //+------------------------------------------------------------------+
   //| model a multivariable data set  of inputs and targets            |
   //+------------------------------------------------------------------+

   virtual bool      fit(matrix &vars,vector &targets,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 3)
        {
         Print(__FUNCTION__," columns in vars must be >= 3");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   virtual vector     predict(vector& x, int lags)  override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;
     }



  };
//+------------------------------------------------------------------+

It  inherits from "GmdhModel" to implement the multilayer iterative algorithm.  "MIA" has two "fit()" overloads that can be called to model a given dataset. These methods are distinguished by their first and second parameters. When looking to model a time series using historical values only , the "fit()"  listed below is used.

fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)

Whilst the other is useful when modeling a dataset of dependent and independent variables. The parameters of both methods are documented in the next table:

Data type	Parameter name	Description
vector	time_series	represents a time series contained in a vector
integer	lags	defines the number of lagged values to use as predictors in the model
matrix	vars	matrix of input data containing predictive variables
vector	targets	vector of the target values for corresponding row members of vars
CriterionType	criterion	enumeration variable that specifies the external criteria for the model building process
integer	kBest	defines the number of the best partial models based on which new inputs of subsequent layer will be constructed
PolynomialType	_polynomialType	Selected polynomial type to be used to construct new variables from existing ones during training
double	testSize	Fraction of the input data that should be used to evaluate models
int	pAverage	The number of the best partial models based to be considered in the calculation of the stopping criteria
double	limit	The minimum value by which the external criterion should be improved in order to continue training

Once a model has been trained, it can be used to make predictions, by calling "predict()". The method requires a vector of inputs and an integer value that specifies the desired number of predictions. On successful execution, the method returns a vector containing the computed predictions. Otherwise a vector of zeros is returned.  In the section that follows we look at a  few simple examples, to get a better idea of how to use the code just described.

Examples

We will go over three examples implemented as scripts. Covering how MIA can be applied in different scenarios. The first deals with building a model of a time series. Where a certain number of previous values of the series can be used to determine subsequent terms. This example is contained in the script MIA_Test.mq5, whose code is shown below.

//+------------------------------------------------------------------+
//|                                                     MIA_Test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input int NumLags = 3;
input int NumPredictions = 6;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---time series we want to model
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};
//---
   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }
//---instantiate MIA object
   MIA mia;
//---fit the series according to user defined hyper parameters
   if(!mia.fit(tms,NumLags,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---generate filename based on user defined parameter settings
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit);
//---save the trained model
   mia.save(modelname+".json");
//---inputs from original series to be used for making predictions
   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));
//---predictions made from the model
   vector out = mia.predict(in,NumPredictions);
//---output result of prediction
   Print(modelname, " predictions ", out);
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial());
  }
//+------------------------------------------------------------------+

When running the script, a user can change various aspects of the model. "NumLags" specifies the number of previous series values to calculate the next term. "NumPredictions" indicates the number of predictions to be made beyond the specified series. The rest of the user adjustable parameters correspond to the arguments passed to the method "fit()". When a model has been successfully built, it is saved to file. And predictions are made and output to the terminal's Experts tab, along with the final polynimial representing the model. The results of running the script with default settings are shown below. The polynomial shown represents the mathematical model found to be the best at describing the given time series. It is clearly unnecessarily overcomplicated when considering the simplicity of the series. Although, considering the prediction results, the model still captures the general tendency of the series.

PS      0       22:37:31.246    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
OG      0       22:37:31.246    MIA_Test (USDCHF,D1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00

In a second run of the script. NumLags is increased to 4. Lets see what effect this has on the model.

Notice how much more complexity is introduced to the model by adding an extra  predictor. As well as the impact this has on predictions. The polynomial now spans several lines, despite there being no discernible improvement in model predictions.

22:37:42.921    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000005,16.00000000000007,17.00000000000011,18.00000000000015]
ML      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_1 = - 1.666667e-01*x2 + 1.166667e+00*x4 + 8.797938e-16*x2*x4 + 6.666667e-01
CO      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_2 = - 6.916614e-15*x3 + 1.000000e+00*x4 + 1.006270e-15*x3*x4 + 1.000000e+00
NN      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_3 = - 5.000000e-01*x1 + 1.500000e+00*x3 + 1.001110e-15*x1*x3 + 1.000000e+00
QR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_1 = 5.000000e-01*f1_1 + 5.000000e-01*f1_3 - 5.518760e-16*f1_1*f1_3 - 1.729874e-14
HR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_2 = 5.000000e-01*f1_1 + 5.000000e-01*f1_2 - 1.838023e-16*f1_1*f1_2 - 8.624525e-15
JK      0       22:37:42.921    MIA_Test (USDCHF,D1)    y = 5.000000e-01*f2_1 + 5.000000e-01*f2_2 - 2.963544e-16*f2_1*f2_2 - 1.003117e-14

For our last example we look at a different scenario, where we want to model outputs defined by independent variables. In this example we are attempting to teach the model to add 3 inputs together. The code for this example is in MIA_Multivariable_test.mq5.

//+------------------------------------------------------------------+
//|                                       MIA_miavariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---simple independent and dependent data sets we want to model
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};
//---declare MIA object     
   MIA mia;   
//---train the model based on chosen hyper parameters
   if(!mia.fit(independent,dependent,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---construct filename for generated model
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit)+"_multivars";
//---save the model
   mia.save(modelname+".json");
//---input data to be used as input for making predictions
   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};
//---make predictions and output to the terminal
  for(ulong row = 0; row<unseen.Rows(); row++)
     {
       vector in = unseen.Row(row);
       Print("inputs ", in , " prediction ", mia.predict(in,1));
     }  
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

The predictors are in the matrix "vars". Each row corresponds to a target in the vector "targets". As in the previous example we have the option to set various aspects of the model's training hyper parameters. The results from training with the default setting are very poor, as shown below.

RE      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [5.999999999999997]
JQ      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [7.5]
QI      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.1]
QK      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      y = 1.900000e+00*x1 + 1.450000e+00*x2 - 9.500000e-01*x1*x2 + 3.100000e+00

The model can be improved by adjusting so training parameters. The best results were attained by using the settings depicted below.

Using these settings the model is able to finally make accurate predictions on set of "unseen" input variables. Even though, just as in the first example, the generated polynomial is overly complex.

DM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [6.999999999999998]
JI      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [8.999999999999998]
CD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.00000000000001]
OO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
IQ      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
PS      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
LO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
HN      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
PP      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
JM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
NO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
FD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15

Its clear from the simple examples we have observed, that the multilayered iterative algorithm may be overkill for elementary datasets. The polynomials generated can become fiercely complicated. Such models  run the risk of overfitting the training data. The algorithm may end up capturing noise or outliers in the data, leading to poor generalization performance on unseen samples. The performance of MIA and GMDH algorithms in general, is highly dependent on the quality and characteristics of the input data. Noisy or incomplete data can adversely affect the model's accuracy and stability, potentially leading to unreliable predictions. Lastly, whilst the training process is fairly simple, there is still some level of hyper parameter tuning necessay to get the best results. Its not completely automated.

For our last demonstration, we have a script that  loads a model from file and uses it to make predictions. This example is given in LoadModelFromFile.mq5.

//+------------------------------------------------------------------+
//|                                            LoadModelFromFile.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>
//--- input parameters
input string   JsonFileName="";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---declaration of MIA instance
    MIA mia;
//---load the model from file  
    if(!mia.load(JsonFileName))
      return;
//---get the number of required inputs for the loaded model     
    int numlags = mia.getNumInputs();
//---generate arbitrary inputs to make a prediction with  
    vector inputs(ulong(numlags),arange,21.0,1.0);
//---make prediction and output results to terminal    
    Print(JsonFileName," input ", inputs," prediction ", mia.predict(inputs,1));
//---output the model's polynomial    
    Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

The following graphic illustrates how the script works and the result from a successful run.

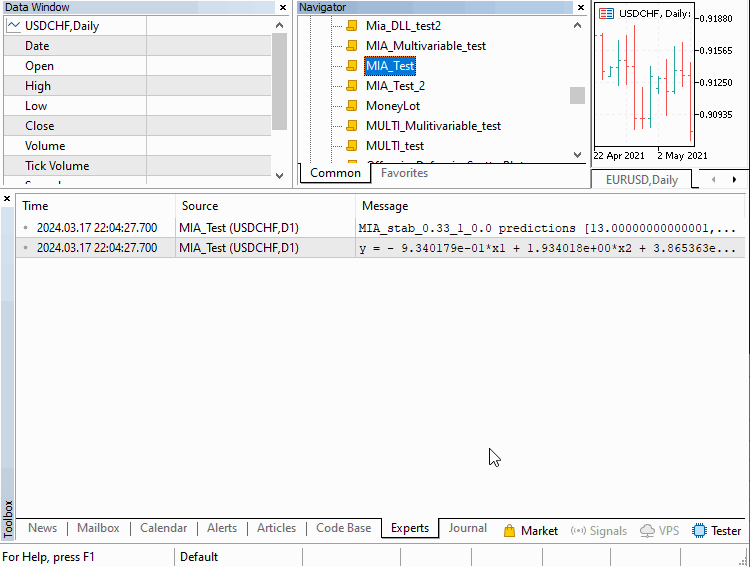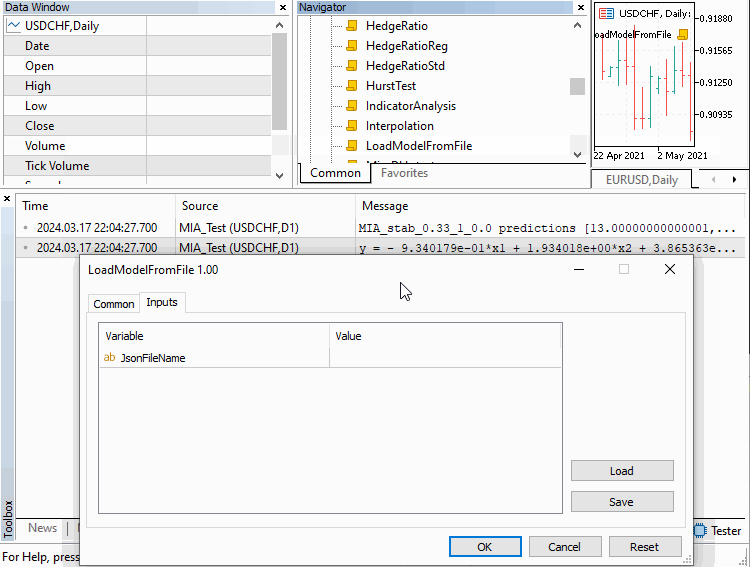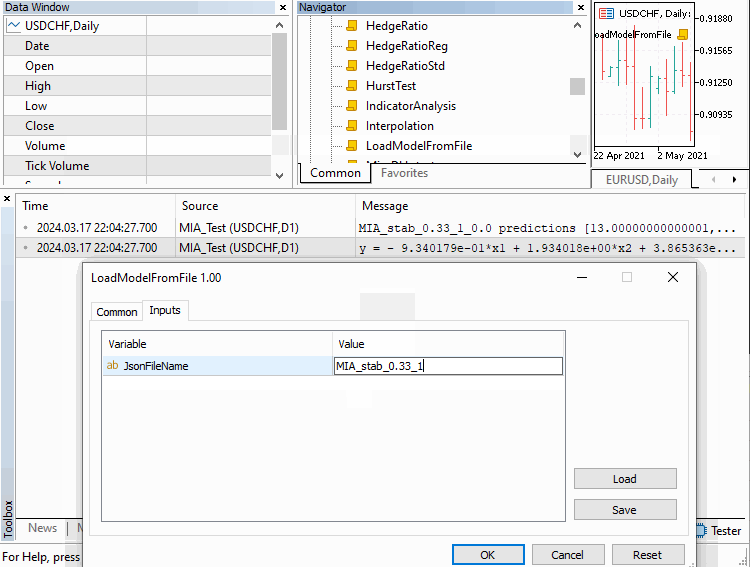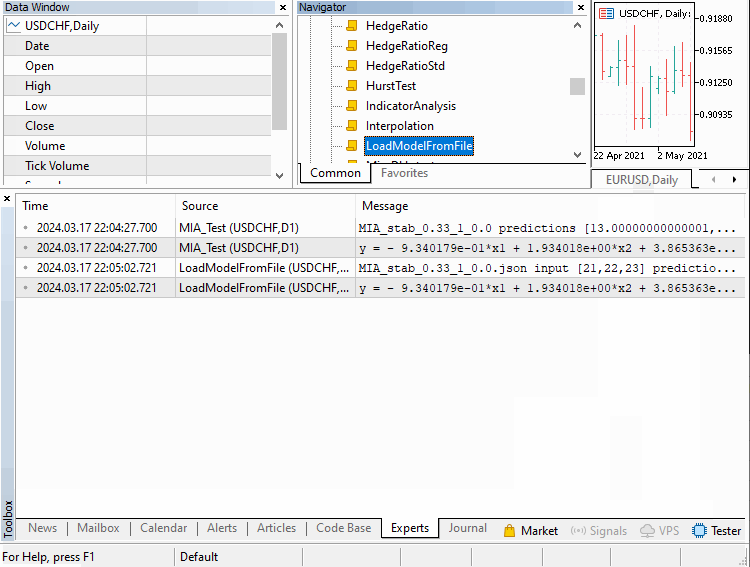
Conclusion

The implementaion of the GMDH multilayer iterative algorithm in MQL5 presents an opportunity for traders to apply the concept in their strategies. Offering a dynamic framework, this algorithm empowers users with the capability to adapt and refine their market analyses continually. However, despite its promise, it's essential for practitioners to navigate its limitations judiciously. Users should be mindful of the computational demands inherent in GMDH algorithms, particularly when dealing with extensive datasets or those with high dimensionality. The algorithm's iterative nature necessitates multiple computations to ascertain the optimal model structure, consuming significant time and resources in the process.

In light of these considerations, practitioners are urged to approach the use of the GMDH multilayer iterative algorithm with a nuanced understanding of its strengths and limitations. While it offers a powerful tool for dynamic market analysis, its complexities warrant careful navigation to unlock its full potential effectively. Through thoughtful application and consideration of its intricacies, traders can leverage the GMDH algorithm to enrich their trading strategies and glean valuable insights from market data.

All MQL5 code is attached at the end of the article.

File	Description
Mql5\include\VectorMatrixTools.mqh	header file of function definitions used for manipulating vectors and matrices
Mql5\include\JAson.mqh	contains the definition of the custom types used for parsing and generating JSON objects
Mql5\include\GMDH\gmdh_internal.mqh	header file containing definitions of custom types used in gmdh library
Mql5\include\GMDH\gmdh.mqh	include file with definition of the base class GmdhModel
Mql5\include\GMDH\mia.mqh	contains the class MIA which implements the multilayer iterative algorithm
Mql5\script\MIA_Test.mq5	a script that demonstrates use of the MIA class by building a model of a simple time series
Mql5\script\MIA_Multivarible_test.mq5	another script showing the application of the MIA class to build a model of a multivariable dataset
Mql5\script\LoadModelFromFile.mq5	script demonstrating how to load a model from a json file