Selbstoptimierende Expert Advisors in MQL5 erstellen
319
0
Einführung
Selbstoptimierende, automatisierte Systeme sind auf den dynamischen Finanzmärkten von heute unerlässlich. Im digitalen Zeitalter sind die Märkte aufgrund der weit verbreiteten Einführung des algorithmischen Handels, insbesondere durch Hochfrequenzhändler, deutlich volatiler geworden. Laut diesem Arbeitspapier der SEC über das High-Frequency Trading, machen Hochfrequenzhändler fast die Hälfte aller Geschäfte in Europa und den USA aus.
Entgegen mancher Meinung ist MQL5 ideal für diese Aufgabe geeignet. Seine API bietet umfangreiche Matrix- und Vektorfunktionen, die die Erstellung kompakter Modelle für maschinelles Lernen ermöglichen. Diese Einführung legt den Schwerpunkt auf die Verwendung von MQL5 zur Erstellung selbstoptimierender Bots. Ein objektorientierter Programmieransatz reduziert die sich wiederholende Codierung und verbessert die Anpassungsfähigkeit über verschiedene Zeitrahmen und Marktbedingungen hinweg.
Die Entscheidung für die Matrix- und Vektorfähigkeiten von MQL5 gegenüber Alternativen wie ONNX und Python hat erhebliche Vorteile. Die Verwendung eines ONNX-Modells würde separate Modellinstanzen für jedes Handelssymbol und neue Modelle für jede geringfügige Parameteränderung, wie z. B. Zeitrahmenanpassungen, erfordern. MQL5 hingegen bietet Anpassungsfähigkeit, ohne dass zahlreiche Modelle für unterschiedliche Bedingungen verwaltet werden müssen.
Zielvorgabe: Entwicklung selbstoptimierender Expert Advisors
Wir brauchen einen Rahmen, um zu bewerten, wie effektiv unser Expertenberater arbeitet. Sobald eine endgültige Leistungskennzahl definiert ist, können wir die von uns gewählte Kennzahl entsprechend maximieren oder minimieren. Bei der Entwicklung von überwachten maschinellen Lernmodellen für die Preisvorhersage besteht unser Ziel darin, den Fehler zwischen den vorhergesagten Werten und den tatsächlichen Beobachtungen zu minimieren. Bei Verstärkungslernproblemen hingegen ist das Ziel die Maximierung der gesamten diskontierten erwarteten Belohnungen.
In diesem Artikel werden wir die Differenz zwischen dem von unserem Expertenberater prognostizierten zukünftigen Kurs und dem tatsächlich beobachteten Kurs in der Zukunft minimieren. Dies kann durch Berechnung der absoluten Differenzen zwischen diesen Preisen erreicht werden.
Dieser Artikel befasst sich mit den grundlegenden Aspekten des Aufbaus eines selbstoptimierenden Expertenberaters. Künftige Artikel werden sich mit fortgeschritteneren Methoden zur Erstellung selbstoptimierender Expert Advisors befassen, die erweiterte Funktionen der MQL5-API nutzen.
Nach der Lektüre dieses Artikels wird der Leser verstehen:
- Eine Auswahl an nützlichen Matrix- und Vektorfunktionen
- Grundlegende Konzepte der objektorientierten Programmierung in MQL5
- Ein Rahmen für den Aufbau von dynamischen und selbstanpassenden Expertenberatern in MQL5
Selbstoptimierung mit Gradientenabstieg
Unser Ziel ist es, einen Expert Advisor zu entwickeln, der in der Lage ist, sich ständig an die aktuellen Marktbedingungen anzupassen. Um dies zu erreichen, werden wir den Gradientenabstiegsalgorithmus in MQL5 implementieren. Für Leser, die mit dem Algorithmus des Gradientenabstiegs nicht vertraut sind, könnte es hilfreich sein, den Algorithmus mit dem Prozess zu vergleichen, mit dem ein DJ seine Musikanlage aufstellt. Stellen Sie sich vor, Sie sind ein DJ und bereiten sich auf ein Konzert vor. Sie schalten Ihre Geräte ein und die Lautstärke ist viel zu laut. Was würden Sie als Nächstes tun? Wahrscheinlich würden Sie die Lautstärke reduzieren. Aber jetzt ist die Lautstärke zu leise, und deshalb werden Sie sie erhöhen. Dieses Hin und Her zwischen Lauter und Leiser geschieht so lange, bis Sie ein ausgeglichenes Niveau gefunden haben.
Der Gradientenabstiegsalgorithmus funktioniert auf ähnliche Weise. Wir beginnen mit Zufallskoeffizienten im Modell des Marktes, in dem wir uns befinden. Dann messen wir den Fehler, der durch unsere aktuellen Koeffizienten entsteht. Ähnlich wie der DJ passen wir die Koeffizienten unseres Modells iterativ in die entgegengesetzte Richtung der Fehlerzunahme an. Wir nehmen Ableitungen in Bezug auf Eingaben, wie z. B. Koeffizienten in einem linearen Modell, um abzuleiten, in welche Richtung der Fehler zunimmt.
Darüber hinaus ist neben den Koeffizienten ein weiterer entscheidender Parameter des Gradientenabstiegs die Lernrate: Die Lernrate entspricht der Lautstärkeänderung, die der DJ bei jeder Anpassung des Lautstärkereglers vornimmt. Die Lernrate bestimmt die Größe des Schritts, den wir jedes Mal machen, wenn wir die Parameter unseres Modells anpassen. Wenn unsere Lernrate zu groß oder zu klein ist, wird unser Modell nicht optimal lernen.
Der ideale Ansatz besteht darin, unseren Expertenberater so zu konzipieren, dass er die Lernraten und -koeffizienten für jedes Marktszenario dynamisch optimiert, selbst wenn wir Zeitrahmen und Datenumfang ändern. Diese Anpassungsfähigkeit wird uns hoffentlich in die Lage versetzen, effektiv auf der richtigen Seite des Marktes zu stehen und das volle Potenzial nativer Lösungen für den Handel ohne Einschränkungen zu nutzen.
Handelsstrategie
Unsere Handelsstrategie wird ein hybrider Ansatz sein, der technische Analyse und maschinelles Lernen einsetzt. Wir werden einen gleitenden Durchschnitt verwenden, um den vorherrschenden Markttrend zu bestimmen. Liegt der Kurs über dem gleitenden Durchschnitt, gehen wir davon aus, dass der vorherrschende Trend nach oben gerichtet ist. Liegt der Kurs hingegen unter dem gleitenden Durchschnitt, gehen wir davon aus, dass der Markttrend nach unten gerichtet ist. Sobald wir den Markttrend abgeleitet haben, suchen wir nach einer Bestätigung durch 2 unterstützende Indikatoren. Der Relative Strength Index (RSI) und der William's Percent Range (WPR).
Der RSI-Indikator zeigt Werte zwischen 0 und 100 an. Wenn der RSI-Wert über 70 liegt, gilt das Wertpapier in der Regel als überkauft und sollte verkauft werden, und wenn der RSI-Wert unter 30 liegt, gilt das Wertpapier als überverkauft und sollte gekauft werden Diese Strategie eignet sich gut für den Handel mit Wertpapieren, die nur in begrenzter Stückzahl existieren, wie Aktien oder Rohstoffe. Währungen können weder überverkauft noch überkauft sein, die Zentralbanken können so viel oder so wenig Geld schaffen, wie sie es für nötig halten. Wenn der RSI-Wert über 50 liegt, werden wir kaufen, anstatt zu verkaufen, und wenn der RSI-Wert unter 50 liegt, werden wir verkaufen, anstatt zu kaufen.
Der WPR-Indikator zeigt Werte zwischen 0 und -100 an. Wie der RSI zeigt auch der WPR-Indikator überkaufte und überverkaufte Bereiche an. Allerdings können Währungen nicht überkauft oder überverkauft sein, das Angebot an Währungen ist unbegrenzt, daher werden wir in unserer Strategie den WPR etwas anders interpretieren. Wenn der WPR-Indikator über -20 liegt, wird dies als Kaufsignal registriert, und wenn der WPR-Indikator unter -80 liegt, wird dies als Verkaufssignal registriert.
Wenn sich alle 3 Indikatoren auf der gleichen Seite des Marktes befinden, werden wir unser Modell zur Vorhersage des zu erwartenden Preises in der Zukunft heranziehen. Wenn die Vorhersage unseres Modells mit unserer Einschätzung aus der Analyse unserer Indikatoren übereinstimmt, eröffnen wir die Position, andernfalls, wenn unser Modell und unsere Indikatoren widersprüchliche Signale geben, warten wir, bis sie übereinstimmen.
Unsere Take-Profit- und Stop-Loss-Niveaus werden ebenfalls dynamisch auf der Grundlage der aktuellen Marktvolatilität festgelegt, wobei wir den absoluten Wert der Differenz zwischen dem Preis und dem gleitenden Durchschnitt nehmen. Unser Stop-Loss und Take-Profit wird das 2-fache des absoluten Wertes der Höhe zwischen dem gleitenden Durchschnitt und dem Schlusskurs sein. Unser Grundgedanke ist, dass unter trägen Marktbedingungen unser Stop-Loss und Take-Profit knapp bemessen sein wird und an volatilen Markttagen unser Stop-Loss und Take-Profit ausreichend weit sein wird. Kurz gesagt, unser gesamtes System passt sich dynamisch an, ohne dass wir eingreifen müssen.
Implementierung in MQL5
Um zu beginnen, müssen wir zunächst eine Klasse für unser maschinelles Lernmodell definieren. Die Verwendung von objektorientierter Programmierung (OOP) hat viele Vorteile, insbesondere bei datenwissenschaftlichen Projekten. Stellen Sie sich vor, Sie hätten ein Modell für maschinelles Lernen entwickelt und diesen Code dann einfach manuell kopiert und in jeden Ihrer Expert Advisors eingefügt. Tage später bemerken Sie einen Fehler, den Sie in einer der Funktionen in Ihrem Code gemacht haben. Wenn Sie keine OOP-Entwurfsprinzipien verwenden würden, müssten Sie jede Instanz des kopierten Codes manuell durchgehen und die Korrekturen einzeln vornehmen. Wenn Sie jedoch OOP-Entwurfsprinzipien anwenden, müssen Sie nur die Klasse korrigieren und dann die anderen Programme neu zu kompilieren. Kurz gesagt, die OOP-Entwurfsprinzipien können Ihnen eine eindeutige und präzise Kontrolle über Tausende von verschiedenen Instanzen Ihres Codes geben.
Wir beginnen mit der Erstellung einer neuen Klasse in unserem MetaTrader 5 Editor.
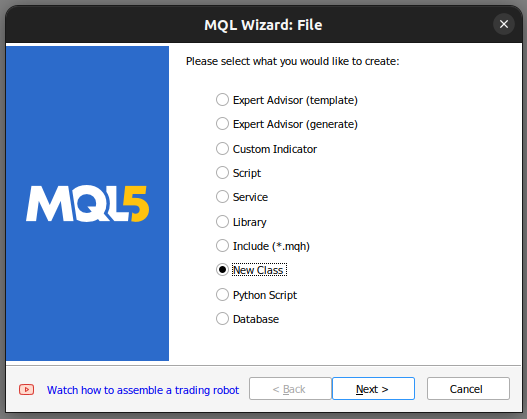
Abb. 1: Erstellen einer neuen Klasse in MQL5.
Von dort aus legen wir den Namen der Klasse fest. Vergewissern Sie sich, dass Ihre Klasse im Ordner „Include“ gespeichert wird, außerdem empfehle ich Ihnen, jeder Klasse einen eigenen Ordner zuzuweisen und diesem Ordner denselben Namen wie der Klasse zu geben, damit Sie diese Klassen in Zukunft leichter wiederfinden.
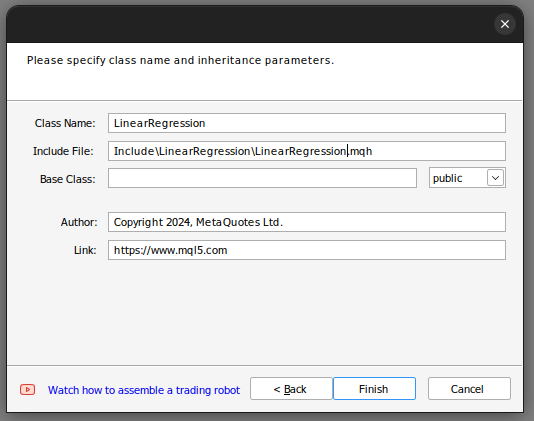
Abb. 2: Aufbau unserer Klasse für die lineare Regression.
Wenn Sie die obigen Schritte befolgt haben, können Sie mit dem MQL5-Assistenten einen ähnlichen Code erstellen.
class LinearRegegression { private: public: LinearRegegression(); ~LinearRegegression(); }; LinearRegegression::LinearRegegression() { } LinearRegegression::~LinearRegegression() { }
Wenn Sie zum ersten Mal mit OOP in MQL5 zu tun haben, lassen Sie uns gemeinsam den obigen Code durchgehen. Ganz oben steht die Klassendefinition. Das Schlüsselwort class definiert den gesamten Code als Klasse, nach dem Schlüsselwort class folgt der Name der Klasse. Von dort aus gelangen wir in den Hauptteil der Klasse. Das Schlüsselwort „private“ definiert Variablen und Funktionen, auf die außerhalb der Klasse nicht zugegriffen werden kann, während das Schlüsselwort „public“ Variablen und Funktionen definiert, auf die von außerhalb der Klasse zugegriffen werden kann. Beachten Sie, dass wir bereits 2 Funktionen in unseren Klassendefinitionen haben.
Die erste Funktion „LinearRegression()“ wird als Konstruktor bezeichnet. Dies ist die erste Funktion, die aufgerufen wird, wenn wir eine neue Instanz unserer Klasse starten, und die letzte Funktion „~LinearRegression()“ ist der Destruktor. Der Destruktor ist die letzte Funktion, die aufgerufen wird, wenn wir die Klasse unseres Diagramms entfernen.
Wir können nun zur Definition der Variablen übergehen, die wir zur Berechnung unseres linearen Regressionsmodells verwenden werden.
- max_earning_ate_ower legt fest, wie hoch wir nach einer guten Lernrate suchen.
- Fetch ist einfach die Anzahl der Kerzen, die wir auf dem Markt analysieren wollen.
- Start und predict legen fest, wann wir mit dem Abruf von Daten beginnen und von welchem Punkt aus wir unsere Vorhersage treffen.
- Look_head legt fest, wie viele Schritte in die Zukunft wir prognostizieren wollen.
- mae_array ist das Array, in dem unsere Fehlermessung gespeichert wird.
- Trained ist ein Flag, das uns anzeigt, ob unser Modell trainiert wurde und einsatzbereit ist.
- epochs_power definiert die Anzahl der Epochen, die wir zum Trainieren unseres Modells verwenden werden.
- Wir haben 2 Vektoren mae_train und mae_validation, die unsere Fehlermetriken aus Training und Validierung speichern.
- Wir haben 4 Vektoren: x_- und y_validation, x_- und y_train. Diese Vektoren enthalten unsere Trainings- und Validierungsdaten.
- Die Vektoren m und b enthalten Schätzungen für die entsprechenden m- und b-Koeffizienten für unser Modell.
- forecast, ein double-Wert, ist einfach die Vorhersage unseres Modells.
- Learning_rate_power ist die Potenz, auf die wir 0,1 erhöhen, um unsere Lernrate zu definieren.
- Epochs ist die Anzahl der Male, die wir das Modell trainieren werden.
- n ist die Anzahl der Zeilen in unseren Daten, sie ist immer gleich fetch.
- “output_end,output_start,input_end,input_start“ definieren unsere Aufteilung in Training und Test.
private: //This is the highest power that we will raise ten to, as we are searching for coefficients ulong max_learning_rate_power; //This is how many bars we should fetch int fetch; //This is where we will start collecting data, it is the end of our validation data set. datetime start,predict; //This is how many steps into the future we want to forecast int look_ahead; //This is the array that will contain our MAE readings from testing different learning rates on the validation data double mae_array[30]; //Trained flag to inform us if the model has been fit and optimised succesfuly and is ready for use bool trained; //The number to raise the power of 10 buy when calculating the number of epochs int epochs_power; //Our error metrics vector mae_train,mae_validation; //This vector contains our inputs validation and training set vector x_validation,x_train; //This vector contains our outputs validation and training set vector y_validation,y_train; //This vector contains our predictions on the validation set vector y_hat_validation,y_hat_train; //This vector contains our gradient coefficient vector m; //This vector contains our model bias vector b; //This is our model's forecast double forecast; //This is our current learning rate power ulong learning_rate_power; //This is the learning rate power we are currently evaluating int lr_error_index; //This is our current learning rate double learning_rate; //This is the number of rounds we will allow whilst training our model double epochs; //This is used in calculations, it is the number of rows in our data, or the fetch size. ulong n; //These are the times for our input and output data datetime output_end,output_start,input_end,input_start; //These are the index times for our input and output data int index_output_end,index_output_start,index_input_end,index_input_start; //This is the value we will use to scale our data double first_reading; bool allowed_to_evaluate; //Update the learning rate bool UpdateLearningRate(void); //Update the number of epochs bool UpdateEpochs(void); //Set the number of epochs bool SetEpochs(int _epochs_power); //Reset the number of epochs bool ResetEpochs(void); //Reset the learning rate bool ResetLearningRate(void); //This function will fit the coeffeicients bool Fit(void); //This function evaluates the current settings bool Evaluate(ulong _index,int _epochs_power); //This function will scale the input data bool ScaleInputs(void); //This function sets the learning rate bool SetLearningRate(ulong _learning_rate_power);
Nun gehen wir zu den öffentlichen Definitionen in unserer Klasse über.
public: //Constructor LinearRegression(); //Fetch Current Validation Data bool GetCurrentValidationData(void); //Initialise the LinearRegressor Model void Init(int _fetch,int _look_ahead); //Function to determine if the model has been trained and is ready for use. bool Trained(void); //A function to train the model using the best learning rate and the most recent prices bool Train(void); //A function to predict future price using the current price. double Predict(void); //Destructor ~LinearRegression();
Der obige Code definiert die Funktionen, die wir in unserer Klasse haben, und die Signatur jeder Funktion, aber wir sind noch nicht jede Funktion zu implementieren. Beginnen wir mit der Implementierung des Konstruktors.
Beachten Sie, dass unser Konstruktor keine Eingaben benötigt; dies wird als Standard- oder nicht-parametrischer Konstruktor bezeichnet. Beachten Sie außerdem, dass der Konstruktor keinen Rückgabetyp hat, nicht einmal void
LinearRegression::LinearRegression()
{
Print("Current Symbol: ",_Symbol);
}
Unser Konstruktor führt außer der Anzeige des aktuellen Handelssymbols keine weiteren Aktionen aus. Diese bewusste Entscheidung ermöglicht es uns, Eingaben aus den Eingaben unseres Expertenberaters abzurufen und sie zur Initialisierung unseres linearen Regressionsobjekts auf der Grundlage dieser Eingaben zu verwenden. Insbesondere setzt der Konstruktor keine Variablen oder Standardwerte, eine Aufgabe, die einer separaten Methode, der „Init()“-Funktion, vorbehalten ist. Kurz gesagt, die Trennung des Konstruktors von der Funktion Init() erweist sich als äußerst vorteilhaft, da sie es uns ermöglicht, dynamisch Eingaben aus den Einstellungen des Expertenberaters zu sammeln. Wäre der Konstruktor für die Variableninitialisierung zuständig gewesen, wäre diese dynamische Erfassung von Eingaben eingeschränkt worden.
Definieren wir nun die Funktion Init(), die für die Initialisierung unserer Variablen auf ihre Standardwerte zuständig ist. Nach der Initialisierung unserer Variablen wird die Methode Init automatisch versuchen, die Eingaben zu skalieren und das Modell für uns zu trainieren.
void LinearRegression::Init(int _fetch,int _look_ahead) { //Clear The Chart ObjectsDeleteAll(0); //Allow evaluations allowed_to_evaluate = true; //Epochs power epochs_power =4; //Set the number of epochs epochs = 5 * MathPow(10,epochs_power); //Has the model been trained? trained = false; //Set the maximum learning rate power max_learning_rate_power = 30; //Set the end of our validation data start = iTime(_Symbol,PERIOD_CURRENT,1); //This is how much data we're going to fetch this.fetch = _fetch - 1; //This is how far into the future we want to forecast this.look_ahead = _look_ahead + 1; //Set the gradient coefficient to a random value m = vector::Zeros(1); //Set the bias to a random value b = vector::Zeros(1); //Set the forecast to 0 forecast = 0; //Our model's learning rate will start at 0 learning_rate_power = 0; //This is the learning rate we are evaluting lr_error_index = 0; mae_train = vector::Full(1,MathPow(10,100)); mae_validation = vector::Full(30,MathPow(10,10000)); //Set the initial learning rate learning_rate = MathPow(0.1,(learning_rate_power)); //Set the number of rows n = fetch; if(GetCurrentValidationData()) { //Scale the data ScaleInputs(); //Fit the model Fit(); } }
Die Funktion Predict ist so konzipiert, dass sie einen Double-Datentyp ohne Parameter zurückgibt, daher hat sie eine keine Eingabeparameter. Um eine Funktion als Klassenmitglied zu bezeichnen, wird ihr der Klassenname vorangestellt, gefolgt von zwei Doppelpunkten und dem Funktionsnamen.
Die Funktion Predict überprüft zunächst, ob das Modell trainiert wurde, indem sie die Funktion „Trainiert()“ aufruft. Sobald der Trainingsstatus des Modells bestätigt ist, sammeln wir Echtzeitdaten, insbesondere den aktuellen Kurs und den Schlusskurs, sowie Zeitstempeldaten für den Vorhersagekontext. Wir berechnen den voraussichtlichen Preis, indem wir den aktuellen Preis mit m multiplizieren und b hinzufügen. Wir geben dann die Prognose zurück oder 0, wenn das Modell nicht trainiert wurde.
double LinearRegression::Predict(void) { if(Trained()) { double _current_reading = iClose(_Symbol,PERIOD_CURRENT,0); predict = iTime(_Symbol,PERIOD_CURRENT,0); double prediction = (m[0]*_current_reading)+b[0]; if(prediction > _current_reading) { Comment("Buy, forecast: ",prediction); } else if(prediction < _current_reading) { Comment("Sell, forecast: ",prediction); } ObjectCreate(0,"prediction point",OBJ_VLINE,0,predict,0); ObjectCreate(0,"forecast",OBJ_HLINE,0,predict,prediction); return(prediction); } return(0); }
Unsere nächste Funktion hat die Aufgabe, Trainings- und Validierungsdaten zu sammeln, wobei wir immer die neuesten verfügbaren Marktdaten abrufen. Dies geschieht mit der Funktion copy_rates vector, die speziell für die Übertragung historischer Preisdaten in einen Vektor entwickelt wurde.
Nach dem Abrufen der Daten müssen wir sicherstellen, dass die Vektoren die gleiche Größe haben, indem wir die Funktion Vektorgröße verwenden.
bool LinearRegression::GetCurrentValidationData(void) { //Indexes index_output_end = 1; index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Get the output data if(!y_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Get the input data if(!x_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Print the vectors we have if(x_validation.Size() != y_validation.Size()) { Print("Failed to get market data: Our vectors aren't the same length."); return(false); } //Print the vectors and plot the data points Print("X validation: ",x_validation); ObjectCreate(0,"X validation end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X validation start",OBJ_VLINE,0,input_start,0); //Print the vectors and plot the data points Print("y validation: ",y_validation); ObjectCreate(0,"y validation end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y validation start",OBJ_VLINE,0,output_start,0); //Set the training data index_output_end = index_input_start + (look_ahead * 2); index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Copy the training data if(!y_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Copy the training data if(!x_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Check if the data matches if(x_train.Size() != y_train.Size()) { Print("Error fetching training dataL: The x and y vectors are not the same size"); } //Print the vectors and plot the data points Print("X training: ",x_train); ObjectCreate(0,"X training end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X training start",OBJ_VLINE,0,input_start,0); Print("y training: ",y_train); ObjectCreate(0,"y training end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y training start",OBJ_VLINE,0,output_start,0); return(true); }
Wir definieren nun unsere Anpassungsfunktion. Die Funktion beginnt mit der Verwendung der aktuellen Werte von m und b, um Vorhersagen für die Trainingsdaten zu erstellen. Anschließend wird der Fehler innerhalb der Trainingsdaten bewertet, indem die absoluten Differenzen zwischen den tatsächlichen Y-Beobachtungen und den von uns vorhergesagten Y-Beobachtungen berechnet werden.
Sobald der Fehler bestimmt ist, berechnen wir den mittleren Fehler mit Hilfe einer anderen effizienten Vektor-Funktion, „Mean“, um das arithmetische Mittel des Fehlervektors zu berechnen.
Anschließend implementieren wir nun den Gradientenabstiegsalgorithmus, indem wir die Ableitungen unseres Fehlers bezüglich m und b approximieren. Diese Ableitungsannäherungen leiten uns bei der Aktualisierung unserer Koeffizienten durch einen Bruchteil der abgeleiteten Ableitungen.
Nach der Aktualisierung der Koeffizienten ist es unbedingt erforderlich, die neuen Koeffizienten zu validieren, da bestimmte Szenarien ungültige Koeffizienten wie NaN oder unendlich ergeben können. Dieser Validierungsschritt ist entscheidend, um die Integrität und Verwendbarkeit der aktualisierten Koeffizienten zu gewährleisten.
bool LinearRegression::Fit() { Print("Fitting a linear regression on the training set with learning rate ",learning_rate_power); Print("Evalutaions: ",allowed_to_evaluate); for(int i =0; i < epochs;i++) { //Measure error y_hat_train = (m[0]*x_train) + b[0]; vector y_minus_y_hat = (y_train - y_hat_train); vector y_minus_y_hat_sqaured = MathAbs((y_train - y_hat_train)); mae_train.Set(0,( y_minus_y_hat_sqaured.Mean())); vector x_times_y_minus_y_hat = (x_train*(y_train -y_hat_train)); //Aproximate the derivatives double derivative_m = (-2.0/n) * x_times_y_minus_y_hat.Sum(); double derivative_b = (-2.0/n) * y_minus_y_hat.Sum(); //Update the linear parameters m[0] = m[0] - (learning_rate * derivative_m); b[0] = b[0] - (learning_rate * derivative_b); } //Finished fitting the coefficients Print("Fit on training data complete.\nm: ",m[0]," b: ",b[0]," mae ",mae_train[0],"\nlearning rate: ",learning_rate); if(allowed_to_evaluate) { Evaluate(learning_rate_power,epochs_power); } //Return true return(true); }
Fahren wir fort mit der Definition unserer Evaluierungsfunktion. Die Funktion ist für die Auswahl der besten Lernrate für jedes von uns gehandelte Symbol verantwortlich. Wir beginnen mit der Überprüfung der Gültigkeit unserer Koeffizienten. Wenn die Koeffizienten Null sind oder NaN-Werte enthalten, werden sie zurückgesetzt.
Der Grundgedanke hinter diesem Validierungsprozess ist die sorgfältige Auswahl von Koeffizienten, die bei unterschiedlichen Lernraten den geringsten Validierungsfehler ergeben. Ungültige Koeffizienten, die durch hohe Validierungsfehler gekennzeichnet sind, werden in der Phase der Koeffizientenauswahl nicht berücksichtigt. Umgekehrt werden gültige Koeffizienten für weitere Analysen gespeichert.
Anschließend verwenden wir diese gespeicherten Koeffizienten, um Vorhersagen für unsere Validierungsdaten zu erstellen und den Fehler zu bewerten. Dieser iterative Prozess umfasst die Aktualisierung der Lernraten, die Anpassung des Modells und die Bewertung der Fehler. Die maximale Iterationsgrenze wurde auf 30 festgelegt, was der maximalen Lernleistung entspricht.
Während der gesamten Evaluierungsfunktion wird durch eine kontinuierliche Überprüfung sichergestellt, dass der Index innerhalb der Grenzen der maximalen Lernratenleistung bleibt. Wir fassen die absoluten Fehlerdaten in einem Vektor zusammen, um sie effizient verarbeiten zu können, und verwenden Vektorfunktionen wie vector.Min() und Argmin(), um die mit dem niedrigsten Validierungsfehler verbundene Lernrate zu ermitteln.
//This function evaluates the current coefficient settings and learning rate bool LinearRegression::Evaluate(ulong _index) { Print("Evaluating the coefficients m:",m[0]," b: ",b[0]," at learning rate: ",learning_rate); //First check if the coefficient and learning rate are valid if((m.HasNan() > 0 || b.HasNan() > 0 || m[0] == 0 || b[0] == 0 || _index > max_learning_rate_power) && (_index < max_learning_rate_power)) { Print("Coefficients are invalid"); m[0] = 0; b[0] = 0 ; mae_array[_index] = MathPow(10,100000); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } else { //Validation predictions if(_index < max_learning_rate_power) { Print("Coefficients are valid, solution at index ",_index); y_hat_validation = (m[0] * x_validation) + b[0]; vector y_minus_y_hat_squared = MathAbs(y_validation - y_hat_validation); //If everything is fine, let's assess the validation mae mae_array[_index] = (1.0/n) * y_minus_y_hat_squared.Sum(); //What was the validation error? Print("Validation error: ",(1.0/n) * y_minus_y_hat_squared.Sum()); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } } if(_index == max_learning_rate_power) { for(int i = 0; i < max_learning_rate_power;i++) { mae_validation[i] = mae_array[i]; } allowed_to_evaluate = false; trained = true; Print("Validation mae: \n",mae_validation); Print("Lowest validation mae: ",mae_validation.Min()); ulong chosen_learning_rate = mae_validation.ArgMin(); Print("Chosen learning rate ",MathPow(0.1,(chosen_learning_rate))); SetLearningRate(chosen_learning_rate); Fit(); } return(true); }
Wir werden auch eine Funktion zur Skalierung unserer Eingaben definieren. Diese Funktion ist einfach zu verstehen: Sie teilt alle unsere Eingaben durch den ersten Eintrag in unserem Trainingsvektor.
//This function will scale our inputs bool LinearRegression::ScaleInputs(void) { //Set the first reading first_reading = x_train[0]; x_train = x_train / first_reading; x_validation = x_validation / first_reading; return(true); }
Von dort aus definieren wir den Destrcutor, der alle Koeffizienten, die wir gerade optimiert haben, zurücksetzt.
LinearRegression::~LinearRegression()
{
ResetLearningRate();
ResetLastError();
} Die Funktionen, die vom Destruktor aufgerufen werden, sind wie folgt definiert:
bool LinearRegression::ResetLearningRate(void) { learning_rate_power = 0; learning_rate = MathPow(0.1,learning_rate_power); return(true); }
Wenn wir alles zusammennehmen, ergibt sich daraus unsere Klassendefinition:
#property copyright "Gamuchirai Ndawana" #property link "https://www.mql5.com" #property version "1.00" class LinearRegression { private: //This is the highest power that we will raise ten to, as we are searching for coefficients ulong max_learning_rate_power; //This is how many bars we should fetch int fetch; //This is where we will start collecting data, it is the end of our validation data set. datetime start,predict; //This is how many steps into the future we want to forecast int look_ahead; //This is the array that will contain our MAE readings from testing different learning rates on the validation data double mae_array[30]; //Trained flag to inform us if the model has been fit and optimised succesfuly and is ready for use bool trained; //The number to raise the power of 10 buy when calculating the number of epochs int epochs_power; //Our error metrics vector mae_train,mae_validation; //This vector contains our inputs validation and training set vector x_validation,x_train; //This vector contains our outputs validation and training set vector y_validation,y_train; //This vector contains our predictions on the validation set vector y_hat_validation,y_hat_train; //This vector contains our gradient coefficient vector m; //This vector contains our model bias vector b; //This is our model's forecast double forecast; //This is our current learning rate power ulong learning_rate_power; //This is the learning rate power we are currently evaluating int lr_error_index; //This is our current learning rate double learning_rate; //This is the number of rounds we will allow whilst training our model double epochs; //This is used in calculations, it is the number of rows in our data, or the fetch size. ulong n; //These are the times for our input and output data datetime output_end,output_start,input_end,input_start; //These are the index times for our input and output data int index_output_end,index_output_start,index_input_end,index_input_start; //This is the value we will use to scale our data double first_reading; bool allowed_to_evaluate; //Update the learning rate bool UpdateLearningRate(void); //Update the number of epochs bool UpdateEpochs(void); //Set the number of epochs bool SetEpochs(int _epochs_power); //Reset the number of epochs bool ResetEpochs(void); //Reset the learning rate bool ResetLearningRate(void); //This function will fit the coeffeicients bool Fit(void); //This function evaluates the current settings bool Evaluate(ulong _index); //This function will scale the input data bool ScaleInputs(void); //This function sets the learning rate bool SetLearningRate(ulong _learning_rate_power); public: //Constructor LinearRegression(); //Fetch Current Validation Data bool GetCurrentValidationData(void); //Initialise the LinearRegressor Model void Init(int _fetch,int _look_ahead); //Function to determine if the model has been trained and is ready for use. bool Trained(void); //A function to train the model using the best learning rate and the most recent prices bool Train(void); //A function to predict future price using the current price. double Predict(void); //Destructor ~LinearRegression(); }; bool LinearRegression::UpdateEpochs(void) { epochs_power = epochs_power + 1; epochs = MathPow(10,epochs_power); return(true); } bool LinearRegression::ResetEpochs(void) { epochs_power = 0 ; epochs = MathPow(10,epochs_power); return(true); } bool LinearRegression::SetEpochs(int _epochs_power) { epochs_power = _epochs_power; epochs = MathPow(10,epochs_power); return(true); } double LinearRegression::Predict(void) { if(Trained()) { double _current_reading = iClose(_Symbol,PERIOD_CURRENT,0); predict = iTime(_Symbol,PERIOD_CURRENT,0); double prediction = (m[0]*_current_reading)+b[0]; if(prediction > _current_reading) { Comment("Buy, forecast: ",prediction); } else if(prediction < _current_reading) { Comment("Sell, forecast: ",prediction); } ObjectCreate(0,"prediction point",OBJ_VLINE,0,predict,0); ObjectCreate(0,"forecast",OBJ_HLINE,0,predict,prediction); return(prediction); } return(0); } bool LinearRegression::GetCurrentValidationData(void) { //Indexes index_output_end = 1; index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Get the output data if(!y_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Get the input data if(!x_validation.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Failed to get market data: ",GetLastError()); return(false); } //Print the vectors we have if(x_validation.Size() != y_validation.Size()) { Print("Failed to get market data: Our vectors aren't the same length."); return(false); } //Print the vectors and plot the data points Print("X validation: ",x_validation); ObjectCreate(0,"X validation end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X validation start",OBJ_VLINE,0,input_start,0); //Print the vectors and plot the data points Print("y validation: ",y_validation); ObjectCreate(0,"y validation end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y validation start",OBJ_VLINE,0,output_start,0); //Set the training data index_output_end = index_input_start + (look_ahead * 2); index_output_start = index_output_end + fetch; index_input_end = index_output_end + look_ahead; index_input_start = index_output_start + look_ahead; //Assigning time stamps output_end = iTime(Symbol(),PERIOD_CURRENT,index_output_end); output_start = iTime(Symbol(),PERIOD_CURRENT,index_output_start); input_end = iTime(Symbol(),PERIOD_CURRENT,index_input_end); input_start = iTime(Symbol(),PERIOD_CURRENT,index_input_start); //Copy the training data if(!y_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,output_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Copy the training data if(!x_train.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,input_end,fetch)) { Print("Error fetching training data ",GetLastError()); } //Check if the data matches if(x_train.Size() != y_train.Size()) { Print("Error fetching training dataL: The x and y vectors are not the same size"); } //Print the vectors and plot the data points Print("X training: ",x_train); ObjectCreate(0,"X training end",OBJ_VLINE,0,input_end,0); ObjectCreate(0,"X training start",OBJ_VLINE,0,input_start,0); Print("y training: ",y_train); ObjectCreate(0,"y training end",OBJ_VLINE,0,output_end,0); ObjectCreate(0,"y training start",OBJ_VLINE,0,output_start,0); return(true); } bool LinearRegression::Train(void) { m = vector::Zeros(1); //Set the bias to a random value b = vector::Zeros(1); forecast = 0; if(GetCurrentValidationData()) { if(Fit()) { Print("Model last updated: ",iTime(_Symbol,PERIOD_CURRENT,0)); return(true); } } return(false); } void LinearRegression::Init(int _fetch,int _look_ahead) { //Clear The Chart ObjectsDeleteAll(0); //Allow evaluations allowed_to_evaluate = true; //Epochs power epochs_power =4; //Set the number of epochs epochs = 5 * MathPow(10,epochs_power); //Has the model been trained? trained = false; //Set the maximum learning rate power max_learning_rate_power = 30; //Set the end of our validation data start = iTime(_Symbol,PERIOD_CURRENT,1); //This is how much data we're going to fetch this.fetch = _fetch - 1; //This is how far into the future we want to forecast this.look_ahead = _look_ahead + 1; //Set the gradient coefficient to a random value m = vector::Zeros(1); //Set the bias to a random value b = vector::Zeros(1); //Set the forecast to 0 forecast = 0; //Our model's learning rate will start at 0 learning_rate_power = 0; //This is the learning rate we are evaluting lr_error_index = 0; mae_train = vector::Full(1,MathPow(10,100)); mae_validation = vector::Full(30,MathPow(10,10000)); //Set the initial learning rate learning_rate = MathPow(0.1,(learning_rate_power)); //Set the number of rows n = fetch; if(GetCurrentValidationData()) { //Scale the data ScaleInputs(); //Fit the model Fit(); } } bool LinearRegression::Trained(void) { return(trained); } bool LinearRegression::SetLearningRate(ulong _learning_rate_power) { learning_rate_power = _learning_rate_power; learning_rate = MathPow(0.1,(learning_rate_power)); return(true); } bool LinearRegression::UpdateLearningRate(void) { learning_rate_power = learning_rate_power + 1; learning_rate = MathPow(0.1,(learning_rate_power)); Print("New learning rate: ",learning_rate," learning rate power: ",learning_rate_power); return(true); } bool LinearRegression::ResetLearningRate(void) { learning_rate_power = 0; learning_rate = MathPow(0.1,learning_rate_power); return(true); } LinearRegression::LinearRegression() { Print("Current Symbol: ",_Symbol); } bool LinearRegression::Fit() { Print("Fitting a linear regression on the training set with learning rate ",learning_rate_power); Print("Evalutaions: ",allowed_to_evaluate); for(int i =0; i < epochs;i++) { //Measure error y_hat_train = (m[0]*x_train) + b[0]; vector y_minus_y_hat = (y_train - y_hat_train); vector y_minus_y_hat_sqaured = MathAbs((y_train - y_hat_train)); mae_train.Set(0,( y_minus_y_hat_sqaured.Mean())); vector x_times_y_minus_y_hat = (x_train*(y_train -y_hat_train)); //Aproximate the derivatives double derivative_m = (-2.0/n) * x_times_y_minus_y_hat.Sum(); double derivative_b = (-2.0/n) * y_minus_y_hat.Sum(); //Update the linear parameters m[0] = m[0] - (learning_rate * derivative_m); b[0] = b[0] - (learning_rate * derivative_b); } //Finished fitting the coefficients Print("Fit on training data complete.\nm: ",m[0]," b: ",b[0]," mae ",mae_train[0],"\nlearning rate: ",learning_rate); if(allowed_to_evaluate) { Evaluate(learning_rate_power); } //Return true return(true); } //This function evaluates the current coefficient settings and learning rate bool LinearRegression::Evaluate(ulong _index) { Print("Evaluating the coefficients m:",m[0]," b: ",b[0]," at learning rate: ",learning_rate); //First check if the coefficient and learning rate are valid if((m.HasNan() > 0 || b.HasNan() > 0 || m[0] == 0 || b[0] == 0 || _index > max_learning_rate_power) && (_index < max_learning_rate_power)) { Print("Coefficients are invalid"); m[0] = 0; b[0] = 0 ; mae_array[_index] = MathPow(10,100000); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } else { //Validation predictions if(_index < max_learning_rate_power) { Print("Coefficients are valid, solution at index ",_index); y_hat_validation = (m[0] * x_validation) + b[0]; vector y_minus_y_hat_squared = MathAbs(y_validation - y_hat_validation); //If everything is fine, let's assess the validation mae mae_array[_index] = (1.0/n) * y_minus_y_hat_squared.Sum(); //What was the validation error? Print("Validation error: ",(1.0/n) * y_minus_y_hat_squared.Sum()); //Update the learning rate UpdateLearningRate(); //Fit the model again Fit(); } } if(_index == max_learning_rate_power) { for(int i = 0; i < max_learning_rate_power;i++) { mae_validation[i] = mae_array[i]; } allowed_to_evaluate = false; trained = true; Print("Validation mae: \n",mae_validation); Print("Lowest validation mae: ",mae_validation.Min()); ulong chosen_learning_rate = mae_validation.ArgMin(); Print("Chosen learning rate ",MathPow(0.1,(chosen_learning_rate))); SetLearningRate(chosen_learning_rate); Fit(); } return(true); } //This function will scale our inputs bool LinearRegression::ScaleInputs(void) { //Set the first reading first_reading = x_train[0]; x_train = x_train / first_reading; x_validation = x_validation / first_reading; return(true); } LinearRegression::~LinearRegression() { ResetLearningRate(); ResetEpochs(); ResetLastError(); }
Nachdem wir nun unsere Klasse LinearRegression definiert haben, können wir sie in unserem Expert Advisor verwenden.
Wir beginnen mit der Erstellung eines neuen Expertenberaters und der Aufnahme der Klasse in unseren Expertenberater.
#property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com" #property version "1.00" //Include our linear regression class #include <LinearRegression/LinearRegression.mqh> LinearRegression ExtLinearRegression;
Der obige Code ruft den Standardkonstruktor unserer Klasse LinearRegression auf.
Von dort aus schließen wir auch andere nützliche Klassen ein.
//Include the trade class #include <Trade/Trade.mqh> CTrade Trade;
Wir definieren die Eingaben, die unser Expertenberater benötigt.
//Inputs int input look_ahead = 10; //How many steps into the future should we forecast? int input fetch_data = 100; //How much data should we fetch? int input ma_period = 10; //Moving Average Period int input rsi_period = 10; //RSI Period int input wr_period = 10; //Williams Percent R Period
Wir werden auch andere Variablen definieren, die für die technische Analyse nützlich sind, z. B. das zulässige Mindesthandelsvolumen und Vektoren zum Speichern unserer Indikatorpuffer.
//Technical Analysis double min_volume =SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); //Indicator Handlers int ma_handler,rsi_handler,wr_handler,total_time; vector ma_vector,rsi_vector,wr_vector; double _price; ulong _ticket;
Nach der Fertigstellung sind wir nun bereit, den OnInit() für unseren Expert Advisor zu schreiben. Unser Handler initialisiert unser lineares Regressionsobjekt mit den Parametern, die der Nutzer dem Expert Advisor übergeben hat, und richtet dann unsere technischen Indikatoren ein.
int OnInit() { //Setup our model ExtLinearRegression.Init(fetch_data,look_ahead); //Keep Track Of Time total_time = 0; //Set up our technical indicators ma_handler = iMA(_Symbol,PERIOD_CURRENT,ma_period,0,MODE_EMA,PRICE_CLOSE); rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,rsi_period,PRICE_CLOSE); wr_handler = iWPR(_Symbol,PERIOD_CURRENT,wr_period); return(INIT_SUCCEEDED); }
Wir kommen nun zur Funktion OnTick(). Die Funktion OnTick() verfolgt die Zeit und ermöglicht es uns, bestimmte Aktionen nach jeder neuen Kerze und einige Aktionen nach jedem Tick durchzuführen. Wenn bei jeder neuen Kerze die Gesamtzahl der verstrichenen Kerzen größer ist als der vom Nutzer gewählte Prognosehorizont, müssen wir unser Modell mit der von uns implementierten Funktion Train erneut trainieren. Außerdem möchten wir die gespeicherten Indikatorwerte aktualisieren, indem wir eine andere nützliche Vektor-Funktion CopyIndicatorBuffer verwenden. Wir haben eine Funktion geschaffen, die für diese Aufgabe zuständig ist. Wenn wir eine offene Stelle haben, haben wir eine Funktion geschaffen, die für die Verwaltung der offenen Stellen zuständig ist.
void OnTick() { //--- static datetime time_stamp; datetime current_time = iTime(_Symbol,PERIOD_CURRENT,0); if(time_stamp != current_time) { //Update the values of the indicators update_vectors(); total_time += 1; if(total_time > look_ahead) { total_time = 0; //Let the model adapt to the market dynamically ExtLinearRegression.Train(); } //If our model is ready then let's start trading if(ExtLinearRegression.Trained()) { if(PositionsTotal() == 0) { analyse_indicators(); } } if(PositionsTotal() == 1) { //Get position ticket _ticket = PositionGetTicket(0); //Manage the position manage_position(_ticket); } time_stamp = current_time; } }
Diese Funktion ist verantwortlich für das Abrufen der aktuellsten Balken, die von unserem Broker verfügbar sind.
void update_vectors(void) { //Get the current reading of our indicators ma_vector.CopyIndicatorBuffer(ma_handler,0,1,1); rsi_vector.CopyIndicatorBuffer(rsi_handler,0,1,1); wr_vector.CopyIndicatorBuffer(wr_handler,0,1,1); _price = iClose(_Symbol,PERIOD_CURRENT,1); }
Diese Funktion ist für die Interpretation unserer Indikatoren und der Prognosen unseres Modells verantwortlich. Wenn sie alle ausgerichtet sind, können wir einen Handel eröffnen, andernfalls warten wir, bis sie sich ausgerichtet haben.
void analyse_indicators(void) { double forecast = ExtLinearRegression.Predict(); Comment("Forecast: ",forecast," Price: ",_price); //If price is above the moving average, check if the other indicators also confirm the buy signal if(_price - ma_vector[0] > 0) { if(rsi_vector[0] > 50) { if(wr_vector[0] > -20) { if(forecast > _price) { Trade.Buy(min_volume,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0); } } } } //If price is below the moving average, check if the other indicators also confirm the sell signal if(_price - ma_vector[0] < 0) { if(rsi_vector[0] < 50) { if(wr_vector[0] < -80) { if( forecast < _price) { Trade.Sell(min_volume,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0); } } } }
Diese Funktion ist verantwortlich für die Verwaltung aller offenen Positionen, die wir haben, und für die dynamische Einrichtung von Stop-Loss und Take-Profit auf der Grundlage der aktuellen Volatilitätsniveaus im Markt. Beachten Sie, dass die Position nur geändert wird, wenn die Position keinen Stop-Loss oder Take-Profit hat.
void manage_position(ulong m_ticket) { if(PositionSelectByTicket(m_ticket)) { double volatility = 2 * MathAbs(ma_vector[0] - _price); double entry = PositionGetDouble(POSITION_PRICE_OPEN); double current_sl = PositionGetDouble(POSITION_SL); double current_tp = PositionGetDouble(POSITION_TP); if(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY) { double new_sl = _price - volatility; double new_tp = _price + volatility; if(current_sl == 0 || current_tp == 0) { Trade.PositionModify(m_ticket,new_sl,new_tp); } } if(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL) { double new_sl = _price + volatility; double new_tp = _price - volatility; if(current_sl == 0 || current_tp == 0) { Trade.PositionModify(m_ticket,new_sl,new_tp); } } } }
Unser Expert Advisor sieht nun wie folgt aus:
Abb. 3: Selbstoptimierender Experten-EA.
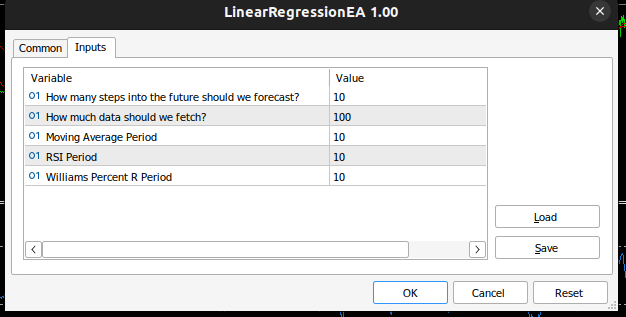
Abb. 4: Inputs für unseren selbstoptimierenden EA.
Wenn Sie den Experten auf ein Symbol anwenden, können Sie die Berechnungen, die er für Sie durchführt, auf der Registerkarte „Experten“ sehen
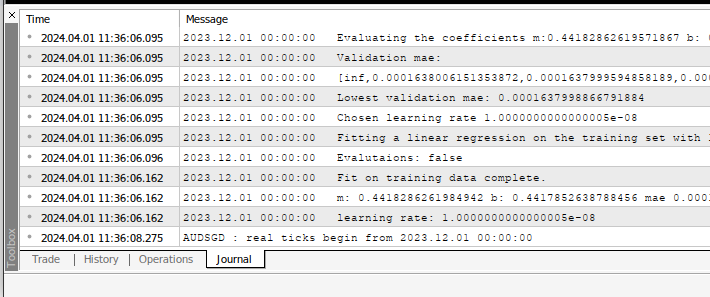
Abb. 5: Die Berechnungen unseres Expert Advisors.
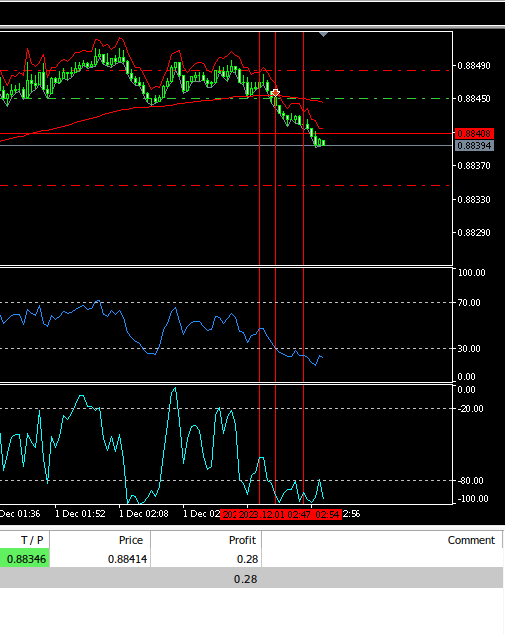
FIg 6: Backtesting unseres EA.
Empfehlungen
In diesem Artikel wurde die einfachste Methode zur Erstellung selbstoptimierender EAs vorgestellt. Dies ist jedoch nicht der bestmögliche Ansatz, das wäre eine manuelle Suche nach Optimalitätskoeffizienten. Die ideale Lösung würde fortschrittlichere Matrix- und Vektorberechnungen einsetzen, um automatisch die optimalen Koeffizienten zu finden. Wenn wir Matrix- und Vektorfunktionen verwenden, können wir unser lineares Regressionsmodell erstellen, ohne jemals eine einzige for-Schleife zu verwenden. Unser Code wird kompakter und unsere Koeffizienten werden numerisch stabiler sein. Die manuelle Suche garantiert nicht immer eine Lösung.
Schlussfolgerung
Der Aufbau von selbstanpassenden Expert Advisors in MQL5 ist dank der leistungsstarken Matrix- und Vektorfunktionen in der MQL5-API einfach. In Wahrheit ist das, was wir in MQL5 bauen können, nur durch unser Verständnis der API begrenzt.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/14630
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 15): Support-Vektor-Maschinen mit dem Newtonschen Polynom
MQL5-Assistent - Techniken, die Sie kennen sollten (14): Zeitreihenvorhersage mit mehreren Zielvorgaben durch STF
Entwicklung eines MQTT-Clients für MetaTrader 5: ein TDD-Ansatz — Finale
Die Gruppenmethode der Datenverarbeitung: Implementierung des mehrschichtigen iterativen Algorithmus in MQL5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.