Techniken des MQL5-Assistenten, die Sie kennen sollten (Teil 05): Markov-Ketten
Einführung
Markow-Ketten sind ein leistungsfähiges mathematisches Werkzeug, das zur Modellierung und Vorhersage von Zeitreihendaten in verschiedenen Bereichen, einschließlich des Finanzwesens, verwendet werden kann. In der Finanzzeitreihenmodellierung und -prognose werden Markov-Ketten häufig zur Modellierung der zeitlichen Entwicklung von Finanzwerten wie Aktienkursen oder Wechselkursen verwendet. Einer der Hauptvorteile von Markov-Kettenmodellen ist ihre Einfachheit und Nutzerfreundlichkeit. Sie beruhen auf einem einfachen probabilistischen Modell, das die Entwicklung eines Systems im Laufe der Zeit beschreibt, und erfordern keine komplexen mathematischen Annahmen oder Annahmen über die statistischen Eigenschaften der Daten. Dies macht sie besonders nützlich für die Modellierung und Vorhersage von Finanzzeitreihen, die sehr komplex sein können und ein nicht-stationäres Verhalten aufweisen.
Die Modellierung von Markov-Kettenmodellen lässt sich in vier Haupttypen einteilen: zeitdiskrete Markov-Ketten, zeitkontinuierliche Markov-Ketten, Hidden-Markov-Modelle und Switching-Markov-Modelle. Die wichtigsten davon sind: zeitdiskrete Markov-Ketten, die zur Modellierung der Entwicklung eines Systems über eine Reihe von diskreten Zeitschritten verwendet werden, und zeitkontinuierliche Markov-Ketten, die zur Modellierung der Entwicklung eines Systems über ein kontinuierliches Zeitintervall verwendet werden. Beide können zur Modellierung und Prognose von Finanzzeitreihen verwendet werden.
Die Wahrscheinlichkeitsschätzung für ein Markov-Kettenmodell aus Finanzzeitreihendaten kann auf verschiedene Weise erfolgen. Ich werde 8 davon aufführen, von denen die Erwartungsmaximierung die wichtigste ist. Dies ist die von alglib implementierte Methode, die von meiner MQL5-Codebibliothek übernommen wurde.
Sobald die Wahrscheinlichkeit (oder die Parameter eines Markov-Kettenmodells) geschätzt wurden, kann das Modell verwendet werden, um Prognosen über zukünftige Zustände oder Ereignisse zu erstellen. Bei finanziellen Zeitreihendaten könnte beispielsweise ein Markov-Kettenmodell verwendet werden, um künftige Aktienkurse oder Wechselkurse auf der Grundlage des aktuellen Marktzustands und der Übergangswahrscheinlichkeiten zwischen verschiedenen Marktzuständen vorherzusagen.
Modellierung der Ketten
Eine Markov-Kette ist ein mathematisches System, das nach bestimmten probabilistischen Regeln von einem Zustand in einen anderen übergeht. Eine Markov-Kette zeichnet sich dadurch aus, dass die Wahrscheinlichkeit des Übergangs in einen bestimmten Zustand ausschließlich vom aktuellen Zustand und der verstrichenen Zeit abhängt, unabhängig davon, wie das System in seinen aktuellen Zustand gelangt ist. Eine Markov-Kette kann mit Hilfe eines Zustandsdiagramms dargestellt werden, wobei jeder Knoten im Diagramm einen Zustand darstellt und die Kanten zwischen den Knoten die Übergänge zwischen den Zuständen repräsentieren. Die Wahrscheinlichkeit, von einem Zustand in einen anderen zu wechseln, wird durch das Gewicht der entsprechenden Kante dargestellt.
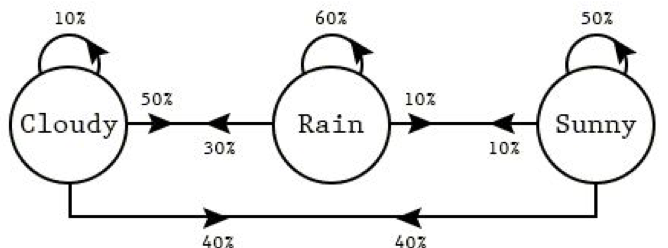
Die Pfeile im Diagramm (auch Markov-Kette genannt) stellen Übergänge zwischen den Zuständen dar. Die Wahrscheinlichkeit des Übergangs vom Zustand „rainy“ (Regenwetter) zum Zustand „sunny“ (Sonnenschein) kann durch das Gewicht der Kante zwischen den beiden Knoten dargestellt werden (in diesem Fall 0,1), und ähnlich verhält es sich mit den anderen Übergängen.
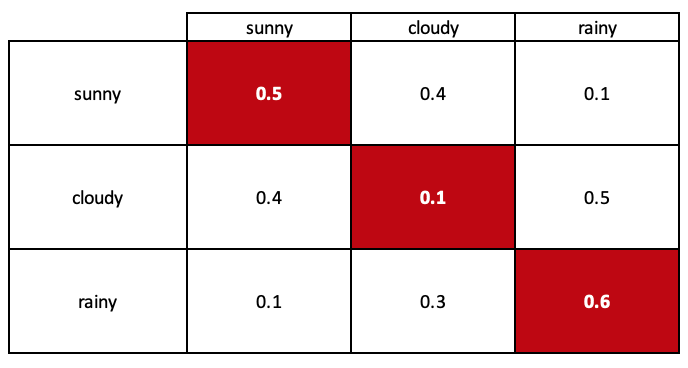
Mit diesem Zustandsdiagramm können wir die Wahrscheinlichkeiten des Übergangs zwischen den Zuständen des Systems modellieren. Das von uns erstellte Modell wird besser als Übergangsmatrix bezeichnet und ist oben abgebildet.
Eine wichtige Annahme einer Markov-Kette ist, dass das zukünftige Verhalten des Systems nur vom aktuellen Zustand und der verstrichenen Zeit abhängt, nicht aber von der Vergangenheit des Systems. Dies wird als die „gedächtnislose“ Eigenschaft einer Markov-Kette bezeichnet. Dies bedeutet, dass die Wahrscheinlichkeit, von einem Zustand in einen anderen überzugehen, die gleiche ist, unabhängig davon, wie viele Zwischenzustände das System durchlaufen hat, um seinen aktuellen Zustand zu erreichen.
Markov-Ketten können zur Modellierung einer Vielzahl von Systemen verwendet werden, darunter Finanzsysteme, Wettersysteme und biologische Systeme. Sie sind besonders nützlich für die Modellierung von Systemen, die zeitliche Abhängigkeiten aufweisen, bei denen der aktuelle Zustand des Systems von seinen vergangenen Zuständen abhängt, wie z. B. bei Zeitreihen.
Markov-Ketten werden häufig zur Modellierung von Zeitreihendaten verwendet, d. h. einer Reihe von Datenpunkten, die im Laufe der Zeit in regelmäßigen Abständen erfasst werden. Zeitreihendaten sind in vielen verschiedenen Bereichen zu finden, z. B. im Finanzwesen, in der Wirtschaft, in der Meteorologie und in der Biologie.
Um eine Markov-Kette zur Modellierung von Zeitreihendaten zu verwenden, müssen zunächst die Zustände des Systems und die Übergänge zwischen ihnen definiert werden. Die Übergangswahrscheinlichkeiten zwischen den Zuständen können anhand der Daten mit Techniken wie der Maximum-Likelihood-Schätzung oder der Erwartungsmaximierung geschätzt werden. Sobald die Übergangswahrscheinlichkeiten geschätzt wurden, kann die Markov-Kette verwendet werden, um auf der Grundlage des aktuellen Zustands und der verstrichenen Zeit Vorhersagen über zukünftige Zustände oder Ereignisse zu treffen.
Es gibt mehrere Möglichkeiten, wie Markov-Ketten zur Modellierung von Zeitreihenanalyse verwendet werden können:
-
Markov-Kette: Eine zeitdiskrete Markov-Kette ist ein mathematisches Modell, das zur Beschreibung der Entwicklung eines zeitdiskreten stochastischen Prozesses über eine Reihe von Zeitschritten verwendet wird. Sie kann dazu verwendet werden, eine Abfolge von Ereignissen oder Zuständen zu modellieren, bei denen die Wahrscheinlichkeit des Übergangs in einen bestimmten Zustand zu einem bestimmten Zeitpunkt nur vom aktuellen Zustand abhängt.
- Wettervorhersage: Eine zeitdiskrete Markov-Kette könnte verwendet werden, um das tägliche Wetter an einem bestimmten Ort zu modellieren. Die Zustände der Markov-Kette könnten verschiedene Wetterbedingungen darstellen, z. B. sonnig, bewölkt, regnerisch oder verschneit. Die Übergangswahrscheinlichkeiten könnten anhand historischer Wetterdaten geschätzt werden, und die Markov-Kette könnte verwendet werden, um auf der Grundlage der aktuellen Wetterlage Prognosen für das Wetter des nächsten Tages zu erstellen.
- Aktienkursbewegungen: Eine zeitdiskrete Markov-Kette könnte verwendet werden, um die täglichen Bewegungen eines bestimmten Aktienkurses zu modellieren. Die Zustände der Markov-Kette könnten verschiedene Stufen der Preisbewegung darstellen, wie z. B. nach oben, nach unten oder unverändert. Die Übergangswahrscheinlichkeiten könnten anhand historischer Aktienkursdaten geschätzt werden, und die Markov-Kette könnte verwendet werden, um Prognosen über die Richtung des Aktienkurses für den nächsten Tag auf der Grundlage der aktuellen Kursbewegung zu erstellen.
- Verkehrsmuster: Eine zeitdiskrete Markov-Kette könnte verwendet werden, um die täglichen Verkehrsmuster auf einer bestimmten Straße oder Autobahn zu modellieren. Die Zustände der Markov-Kette könnten verschiedene Stufen der Verkehrsüberlastung darstellen, wie z. B. leicht, mittel oder schwer. Die Übergangswahrscheinlichkeiten könnten anhand historischer Verkehrsdaten geschätzt werden, und die Markov-Kette könnte verwendet werden, um auf der Grundlage des aktuellen Verkehrsaufkommens Prognosen über das Ausmaß der Verkehrsüberlastung am nächsten Tag zu erstellen.
-
Kontinuierliche Markov-Kette: Hier erfolgen die Übergänge zwischen den Zuständen kontinuierlich und nicht in diskreten Zeitschritten. Das bedeutet, dass die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen von der Zeit abhängt, die seit dem letzten Übergang verstrichen ist. Zeitkontinuierliche Markov-Ketten werden häufig verwendet, um Systeme zu modellieren, die sich über verschiedene Zeitspannen hinweg kontinuierlich verändern, wie z. B. der Verkehrsfluss auf einer bestimmten Autobahn oder die Geschwindigkeit chemischer Reaktionen in einer chemischen Anlage. Einer der Hauptunterschiede zwischen zeitdiskreten und zeitkontinuierlichen Markov-Ketten besteht darin, dass die Übergangswahrscheinlichkeiten in einer zeitkontinuierlichen Markov-Kette durch Übergangsraten gekennzeichnet sind, d. h. die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen pro Zeiteinheit. Diese Übergangsraten werden verwendet, um die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen innerhalb eines bestimmten Zeitintervalls zu berechnen.
-
Hidden Markov Model: Ein verborgenes (hidden) Markov-Modell (HMM) ist ein statistisches Modell, eine Art Markov-Kette, bei der die Zustände des Systems nicht direkt beobachtbar sind, sondern aus einer Folge von Beobachtungen abgeleitet werden. Hier einige Beispiele dafür, wie ein verborgenes Markov-Modell verwendet werden könnte, um alltägliche Ereignisse zu modellieren:
- Spracherkennung: Ein verstecktes Markov-Modell könnte verwendet werden, um die beim Sprechen erzeugten Laute zu modellieren und gesprochene Wörter zu erkennen. In diesem Fall könnten die Zustände des HMM verschiedene Phoneme (Sprachlaute) darstellen, und die Beobachtungen könnten eine Folge von Schallwellen sein, die die gesprochenen Wörter repräsentieren. Das HMM könnte auf einem großen Datensatz von gesprochenen Wörtern und den dazugehörigen Schallwellen trainiert werden und zur Erkennung neuer gesprochener Wörter verwendet werden, indem die wahrscheinlichste Phonemfolge aus den beobachteten Schallwellen abgeleitet wird.
- Handschrifterkennung: Ein verstecktes Markov-Modell könnte verwendet werden, um die Abfolge der Stiftstriche während des Schreibens zu modellieren und handgeschriebene Wörter zu erkennen. In diesem Fall könnten die Zustände des HMM verschiedene Stiftstriche darstellen, und die Beobachtungen könnten eine Folge von Bildern handgeschriebener Wörter sein. Das HMM könnte auf einem großen Datensatz von handgeschriebenen Wörtern und den dazugehörigen Bildern trainiert werden und zur Erkennung neuer handgeschriebener Wörter verwendet werden, indem die wahrscheinlichste Abfolge von Stiftstrichen aus den beobachteten Bildern abgeleitet wird.
- Erkennung von Aktivitäten: Ein verstecktes Markov-Modell könnte zur Erkennung menschlicher Aktivitäten auf der Grundlage einer Abfolge von Beobachtungen, z. B. von Sensormesswerten oder Videobildern, verwendet werden. Ein HMM könnte zum Beispiel zur Erkennung von Aktivitäten wie Gehen, Laufen oder Springen verwendet werden.
-
Markov-Modell: Ein Markov-Switching-Modell (MSM) ist eine Art von Markov-Kette, bei der sich die Zustände des Systems im Laufe der Zeit ändern oder „umschalten“ können, und zwar auf der Grundlage bestimmter Bedingungen. Hier sind einige Beispiele dafür, wie ein Markov-Switching-Modell verwendet werden könnte, um alltägliche Ereignisse zu modellieren:
- Verbraucherverhalten: Ein Markov-Switching-Modell könnte verwendet werden, um das Kaufverhalten der Verbraucher zu modellieren. Die Zustände des MSM könnten verschiedene Arten des Kaufverhaltens darstellen, z. B. hochfrequentes oder niedrigfrequentes Kaufverhalten. Die Übergänge zwischen den Zuständen könnten auf bestimmten Bedingungen beruhen, wie z. B. Einkommensänderungen oder die Einführung neuer Produkte. Das MSM könnte verwendet werden, um das zukünftige Kaufverhalten auf der Grundlage des aktuellen Zustands und der Übergangswahrscheinlichkeiten zwischen den Zuständen vorherzusagen.
- Wirtschaftliche Indikatoren: Ein Markov-Switching-Modell könnte zur Modellierung von Wirtschaftsindikatoren wie dem BIP oder der Arbeitslosenquote verwendet werden. Die Zustände des MSM könnten verschiedene wirtschaftliche Bedingungen darstellen, wie z. B. Expansion oder Rezession, und die Übergänge zwischen den Zuständen könnten auf bestimmten Bedingungen beruhen, wie z. B. Änderungen in der Geldpolitik oder dem Konjunkturzyklus. Das MSM könnte zur Vorhersage künftiger wirtschaftlicher Bedingungen auf der Grundlage des aktuellen Zustands und der Übergangswahrscheinlichkeiten zwischen den Zuständen verwendet werden.
- Verkehrsmuster: Ein Markov-Switching-Modell könnte verwendet werden, um die Verkehrsmuster auf einer bestimmten Straße oder Autobahn zu modellieren. Die Zustände des MSM könnten verschiedene Stufen der Verkehrsüberlastung darstellen, z. B. leicht, mittel oder schwer, und die Übergänge zwischen den Zuständen könnten auf bestimmten Bedingungen basieren, z. B. der Tageszeit oder dem Wochentag. Das MSM könnte verwendet werden, um zukünftige Verkehrsmuster auf der Grundlage des aktuellen Zustands und der Übergangswahrscheinlichkeiten zwischen den Zuständen vorherzusagen.
Hier sind einige Beispiele, wie eine zeitdiskrete Markov-Kette zur Modellierung von täglichen Ereignissen verwendet werden könnte:
Wie bei jeder Hypothese gibt es immer zugrundeliegende Annahmen, die dazu führen, dass die Idee in irgendeiner Form eingeschränkt wird. Markov-Ketten bilden da keine Ausnahme. Hier sind einige der Annahmen:
-
Stationarität: Eine der wichtigsten Annahmen einer Markov-Kette ist, dass die Übergangswahrscheinlichkeiten zwischen den Zuständen über die Zeit konstant sind. Diese Annahme wird als Stationarität bezeichnet. Wenn die Übergangswahrscheinlichkeiten im Laufe der Zeit nicht konstant sind, ist das Markov-Kettenmodell möglicherweise nicht genau.
-
Markov-Eigenschaft: Eine weitere Annahme einer Markov-Kette ist, dass die zukünftige Entwicklung des Systems nur vom aktuellen Zustand und der verstrichenen Zeit abhängt und nicht von der Vergangenheit des Systems über den aktuellen Zustand hinaus beeinflusst wird. Diese Annahme trifft in der Praxis nicht immer zu, insbesondere bei Datensätzen mit komplexen Abhängigkeiten oder Langzeitspeicher.
-
Endlicher Zustandsraum: Eine Markov-Kette ist in der Regel auf einem endlichen Zustandsraum definiert, was bedeutet, dass es eine endliche Anzahl möglicher Zustände gibt, die das System annehmen kann. Dies ist für Datensätze mit einer großen Anzahl von Zuständen oder kontinuierlichen Variablen möglicherweise nicht geeignet.
-
Zeit-Homogenität: Bei einer Markov-Kette wird in der Regel davon ausgegangen, dass sie zeithomogen ist, d. h. dass die Übergangswahrscheinlichkeiten zwischen den Zuständen nicht von dem Zeitpunkt abhängen, zu dem der Übergang stattfindet. Wenn die Übergangswahrscheinlichkeiten von der Zeit abhängen, zu der der Übergang stattfindet, ist das Markov-Kettenmodell möglicherweise nicht genau.
-
Ergodizität: Bei einer Markov-Kette wird in der Regel davon ausgegangen, dass sie ergodisch ist, d. h. es ist möglich, jeden Zustand von jedem anderen Zustand aus in einer endlichen Anzahl von Schritten zu erreichen. Wenn diese Annahme nicht erfüllt ist, ist das Markov-Kettenmodell möglicherweise nicht genau.
Im Allgemeinen eignen sich Markov-Kettenmodelle am besten für Datensätze mit relativ einfachen Abhängigkeiten und einer geringen Anzahl von Zuständen oder Variablen. Wenn der Datensatz komplexe Abhängigkeiten oder eine große Anzahl von Zuständen oder Variablen aufweist, sind andere Modellierungstechniken möglicherweise besser geeignet.
Schätzung der Wahrscheinlichkeit
Sobald eine Markov-Kette modelliert ist, müssen wir die Wahrscheinlichkeiten für den Übergang von jedem Zustand zu einem anderen schätzen. Es gibt eine Reihe von Methoden, die verwendet werden können, und es wird hilfreich sein, sie durchzugehen, um ein besseres Gefühl für den Umfang und die Möglichkeiten von Markov-Ketten zu bekommen. Es gibt mehrere Methoden zur Schätzung von Wahrscheinlichkeiten für den Übergang zwischen Zuständen in Markov-Ketten, darunter:
- Maximum-Likelihood-Schätzung: Bei der Maximum-Likelihood-Wahrscheinlichkeitsschätzung (MLE) besteht das Ziel darin, die Wahrscheinlichkeit eines Ereignisses oder einer Folge von Ereignissen auf der Grundlage der beobachteten Daten zu schätzen. Im Zusammenhang mit Markov-Ketten bedeutet dies, dass wir die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen auf der Grundlage einer Reihe von beobachteten Übergängen schätzen wollen.
Um MLE für Markov-Ketten zu implementieren, müssen wir zunächst eine Reihe von beobachteten Übergängen sammeln. Dies kann durch eine Simulation oder durch das Sammeln von Daten aus der Praxis geschehen. Sobald wir die beobachteten Übergänge haben, können wir sie verwenden, um die Übergangswahrscheinlichkeiten zu schätzen.
Um die Übergangswahrscheinlichkeiten abzuschätzen, können wir die folgenden Schritte anwenden:
- Definieren einer Matrix zur Speicherung der Übergangswahrscheinlichkeiten. Die Matrix sollte die Dimensionen num_states x num_states haben, wobei num_states die Anzahl der Zustände in der Markov-Kette ist.
- Initialisieren der Matrix mit allen Wahrscheinlichkeiten, die auf 0 gesetzt sind. Dies kann mit einer verschachtelten Schleife geschehen, die über alle Elemente der Matrix iteriert.
- Iterieren der beobachteten Übergänge und aktualisieren der Übergangswahrscheinlichkeiten. Für jeden beobachteten Übergang von Zustand i nach Zustand j wird die Wahrscheinlichkeit transition_probs[i][j] um 1 erhöht.
- Normalisieren der Übergangswahrscheinlichkeiten, sodass sie in der Summe 1 ergeben. Dazu wird jedes Element der Matrix durch die Summe der Elemente in der entsprechenden Zeile dividiert.
Sobald die Übergangswahrscheinlichkeiten geschätzt wurden, können wir sie verwenden, um die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen vorherzusagen. Wenn wir zum Beispiel die Wahrscheinlichkeit des Übergangs von Zustand i zu Zustand j vorhersagen wollen, können wir die Formel P(j | i) = transition_probs[i][j] verwenden.
. - Bayes‘sche Wahrscheinlichkeit: Bei dieser Methode wird das Bayes'sche Theorem verwendet, um zu aktualisieren. die Wahrscheinlichkeitsverteilung über die Modellparameter auf der Grundlage neuer Daten zu aktualisieren. Um die Bayes'sche Wahrscheinlichkeitsschätzung mit einer Markov-Kette anzuwenden, müssen wir zunächst eine Prioritätsverteilung über die Zustände der Markov-Kette definieren. Diese Prioritätsverteilung stellt unsere anfängliche Annahme über die Wahrscheinlichkeiten der verschiedenen Zustände in der Kette dar. Mit Hilfe der Bayes'schen Aktualisierung können wir dann unsere Überzeugungen über die Wahrscheinlichkeiten der Zustände aktualisieren, wenn neue Informationen verfügbar werden. Nehmen wir zum Beispiel an, wir haben eine Markov-Kette mit drei Zuständen: A, B und C. Wir beginnen mit einer Prioritätsverteilung über die Zustände, die wie folgt dargestellt werden kann:
P(A) = 0,4 P(B) = 0,3 P(C) = 0,3
Das bedeutet, dass wir anfangs glauben, dass die Wahrscheinlichkeit, in Zustand A zu sein, 40 % beträgt, die Wahrscheinlichkeit, in Zustand B zu sein, 30 % und die Wahrscheinlichkeit, in Zustand C zu sein, 30 %.
Nehmen wir nun an, wir beobachten, dass das System vom Zustand A in den Zustand B übergeht. Wir können diese neuen Informationen nutzen, um unsere Überzeugungen über die Wahrscheinlichkeiten der Zustände mithilfe der Bayes'schen Wahrscheinlichkeitsschätzung zu aktualisieren. Dazu müssen wir die Übergangswahrscheinlichkeiten zwischen den Zuständen kennen. Nehmen wir an, dass die Übergangswahrscheinlichkeiten wie folgt sind:
P(A -> B) = 0.8
P(A -> C) = 0.2
P(B -> A) = 0.1
P(B -> B) = 0.7
P(B -> C) = 0.2
P(C -> A) = 0.2
P(C -> B) = 0.3
P(C -> C) = 0.5
Diese Übergangswahrscheinlichkeiten geben an, wie wahrscheinlich der Übergang von einem Zustand in einen anderen ist. Die Wahrscheinlichkeit des Übergangs von Zustand A zu Zustand B beträgt beispielsweise 0,8, während die Wahrscheinlichkeit des Übergangs von Zustand A zu Zustand C 0,2 beträgt.
Anhand dieser Übergangswahrscheinlichkeiten können wir nun unsere Überzeugungen über die Wahrscheinlichkeiten der Zustände mithilfe der Bayes'schen Wahrscheinlichkeitsschätzung aktualisieren. Insbesondere können wir die Bayes‘sche Regel verwenden, um die Posterior-Verteilung über die Zustände zu berechnen, wenn wir die neue Information erhalten, dass das System vom Zustand A in den Zustand B übergegangen ist. Diese Posterior-Verteilung stellt unsere aktualisierte Überzeugung über die Wahrscheinlichkeiten der Zustände dar, wobei wir die neuen Informationen berücksichtigen, die wir erhalten haben.
Mit Hilfe der Bayes'schen Regel können wir beispielsweise die posteriore Wahrscheinlichkeit, sich im Zustand A zu befinden, wie folgt berechnen:
P(A | A -> B) = P(A -> B | A) * P(A) / P(A -> B)
Setzt man die Werte aus unserer Vorabverteilung und die Übergangswahrscheinlichkeiten ein, erhält man:
P(A | A -> B) = (0.8 * 0.4) / (0.8 * 0.4 + 0.1 * 0.3 + 0.2 * 0.3) = 0.36
In ähnlicher Weise können wir die posterioren Wahrscheinlichkeiten für die Zustände B und C wie folgt berechnen:
P(B | A -> B) = (0.1 * 0.3) / (0.8 * 0.4 + 0.1 * 0.3 + 0.2 * 0.3) = 0.09
. - EM-Algorithmus: Um EM für die Wahrscheinlichkeitsschätzung mit einer Markov-Kette zu verwenden, müssten wir die Übergänge zwischen den Zuständen der Markov-Kette über einen bestimmten Zeitraum beobachten. Anhand dieser Daten könnten wir den EM-Algorithmus verwenden, um die Übergangswahrscheinlichkeiten zu schätzen, indem wir Ihre Schätzungen auf der Grundlage der beobachteten Daten iterativ verfeinern. Der EM-Algorithmus arbeitet abwechselnd in zwei Schritten: dem Erwartungsschritt (E-Schritt) und dem Maximierungsschritt (M-Schritt). Im E-Schritt schätzen wir den Erwartungswert der vollständigen Datenlog-Likelihood, wenn die aktuellen Schätzungen der Parameter vorliegen. Im M-Schritt maximieren wir den Erwartungswert der vollständigen Datenlog-Likelihood in Bezug auf die Parameter, um aktualisierte Schätzungen der Parameter zu erhalten. Anschließend wiederholen wir diese Schritte, bis die Schätzungen der Parameter zu einem stabilen Wert konvergieren. Wenn wir beispielsweise eine Markov-Kette mit drei Zuständen (A, B und C) beobachten und die Übergangswahrscheinlichkeiten zwischen den Zuständen schätzen möchten, können wir den EM-Algorithmus verwenden, um Ihre Schätzungen der Übergangswahrscheinlichkeiten auf der Grundlage der beobachteten Daten iterativ zu verfeinern.
Der Hauptvorteil der Verwendung von EM für Wahrscheinlichkeitsschätzungen besteht darin, dass es mit unvollständigen oder verrauschten Daten umgehen kann und die Parameter eines statistischen Modells auch dann schätzen kann, wenn die zugrunde liegende Verteilung nicht vollständig bekannt ist. EM kann jedoch empfindlich auf die Initialisierung reagieren und konvergiert möglicherweise nicht immer zum globalen Maximum der Log-Likelihood-Funktion. Sie kann auch sehr rechenintensiv sein, da sie die wiederholte Auswertung der Log-Likelihood-Funktion und ihres Gradienten erfordert.
- Parametrische Statistik: Um die parametrische Wahrscheinlichkeitsschätzung mit einer Markov-Kette zu verwenden, müssen wir die Übergänge zwischen den Zuständen der Markov-Kette über einen bestimmten Zeitraum beobachten. Ausgehend von diesen Daten könnte man ein parametrisches Modell an die Übergangswahrscheinlichkeiten anpassen, indem man annimmt, dass die zugrunde liegende Verteilung einer bestimmten Verteilung folgt, z. B. einer Normalverteilung oder einer Binomialverteilung. Anhand dieses Modells können wir dann die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen abschätzen. Wenn wir beispielsweise eine Markov-Kette mit drei Zuständen (A, B und C) beobachten und feststellen, dass der Übergang von Zustand A zu Zustand B 10 Mal von insgesamt 20 Übergängen auftritt, können wir ein Binomialmodell an die Daten anpassen und es zur Schätzung der Wahrscheinlichkeit des Übergangs von Zustand A zu Zustand B verwenden.
Der Hauptvorteil parametrischer Wahrscheinlichkeitsschätzungen besteht darin, dass sie genauer sein können als nicht-parametrische Methoden, die keine Annahmen über die zugrunde liegende Verteilung machen. Sie erfordert jedoch Annahmen über die zugrunde liegende Verteilung, die nicht immer angemessen sind oder zu verzerrten Schätzungen führen können. Außerdem können parametrische Methoden weniger flexibel und weniger robust sein als nicht-parametrische Methoden, da sie empfindlich auf Abweichungen von der angenommenen Verteilung reagieren.
- Relative Häufigkeit: Um eine nichtparametrische Wahrscheinlichkeitsschätzung mit einer Markov-Kette zu verwenden, müssen wir die Übergänge zwischen den Zuständen der Markov-Kette über einen bestimmten Zeitraum beobachten. Anhand dieser Daten können wir die Wahrscheinlichkeit des Übergangs von einem Zustand in einen anderen abschätzen, indem wir die Anzahl der Übergänge zählen und durch die Gesamtzahl der Übergänge dividieren. Wenn wir beispielsweise eine Markov-Kette mit drei Zuständen (A, B und C) beobachten und feststellen, dass der Übergang von Zustand A zu Zustand B 10 Mal von insgesamt 20 Übergängen auftritt, könnten wir die Wahrscheinlichkeit des Übergangs von Zustand A zu Zustand B auf 0,5 schätzen.
Diese Methode der Wahrscheinlichkeitsschätzung wird als empirische Verteilungsmethode bezeichnet und kann zur Schätzung der Wahrscheinlichkeiten einer beliebigen Menge von Ereignissen, nicht nur von Übergängen in einer Markov-Kette, verwendet werden. Der Hauptvorteil der nichtparametrischen Wahrscheinlichkeitsschätzung besteht darin, dass sie keine Annahmen über die zugrunde liegende Verteilung erfordert, was sie zu einer flexiblen und robusten Methode zur Schätzung von Wahrscheinlichkeiten macht. Sie kann jedoch weniger genau sein als parametrische Methoden, die Annahmen über die zugrunde liegende Verteilung machen, um Wahrscheinlichkeiten genauer zu schätzen.
- Bootstrapping: Dies ist eine allgemeine Technik, die zur Schätzung von Wahrscheinlichkeiten in einer Markov-Kette oder in jedem anderen probabilistischen Modell verwendet werden kann. Die Grundidee besteht darin, eine kleine Anzahl von Beobachtungen zu verwenden, um die Wahrscheinlichkeitsverteilung über die Zustände des Systems zu schätzen, und dann diese Verteilung zu verwenden, um eine große Anzahl von synthetischen Beobachtungen zu erzeugen. Die synthetischen Beobachtungen können dann verwendet werden, um die Wahrscheinlichkeitsverteilung genauer zu schätzen, und der Prozess kann so lange wiederholt werden, bis der gewünschte Genauigkeitsgrad erreicht ist.
Um das Bootstrapping für die Wahrscheinlichkeitsschätzung in einer Markov-Kette zu verwenden, müssen wir zunächst eine anfängliche Markov-Kette mit ihren Zuständen haben. Wie die Bayes'sche Methode aktualisiert und verbessert das Bootstrapping bestehende Markov-Ketten. Jeder Zustand in der Kette ist mit einer Übergangswahrscheinlichkeit zu anderen Zuständen verbunden, und die Übergangswahrscheinlichkeiten zwischen verschiedenen Paaren von Zuständen sind unabhängig von der Geschichte des Systems. Sobald wir die ursprüngliche Markov-Kette haben, können wir Bootstrapping verwenden, um die Wahrscheinlichkeitsverteilung über ihre Zustände zu schätzen. Dazu beginnt man mit einer kleinen Anzahl von Beobachtungen des Systems, z. B. mit einigen Anfangszuständen oder einer kurzen Folge von Übergängen zwischen Zuständen. Anhand dieser Beobachtungen können wir dann die Wahrscheinlichkeitsverteilung über die Zustände des Systems schätzen.
Wenn wir z. B. eine Markov-Kette mit drei Zuständen A, B und C haben und beobachtet haben, dass das System einige Male vom Zustand A in den Zustand B und einige Male vom Zustand B in den Zustand C übergeht, können wir diese Beobachtungen verwenden, um die Wahrscheinlichkeit des Übergangs vom Zustand A in den Zustand B und vom Zustand B in den Zustand C zu schätzen.
Sobald wir die Wahrscheinlichkeitsverteilung über die Zustände des Systems geschätzt haben, können wir sie verwenden, um eine große Anzahl synthetischer Beobachtungen des Systems zu erzeugen. Dies kann durch Zufallsstichproben aus der Wahrscheinlichkeitsverteilung geschehen, um Übergänge zwischen Zuständen zu simulieren. Wir können dann die synthetischen Beobachtungen verwenden, um die Wahrscheinlichkeitsverteilung genauer zu schätzen, und den Vorgang so lange wiederholen, bis wir den gewünschten Genauigkeitsgrad erreicht haben.
Das Bootstrapping kann eine nützliche Technik für die Schätzung von Wahrscheinlichkeiten in einer Markov-Kette sein, da es uns ermöglicht, eine kleine Anzahl von Beobachtungen zu verwenden, um eine große Anzahl von synthetischen Beobachtungen zu erzeugen, was die Genauigkeit Ihrer Schätzungen erhöhen kann. Es ist auch relativ einfach zu implementieren und kann mit einer breiten Palette von probabilistischen Modellen verwendet werden. Es ist jedoch zu beachten, dass die Genauigkeit der mit Bootstrapping gewonnenen Schätzungen von der Qualität der ursprünglichen Beobachtungen und des zugrunde liegenden probabilistischen Modells abhängt und möglicherweise nicht immer so genau ist wie andere Schätzverfahren.
- Jackknife-Methode: Bei dieser Methode werden mehrere Simulationen der Markov-Kette durchgeführt, wobei jedes Mal ein anderer Zustand oder eine andere Gruppe von Zuständen ausgelassen wird. Die Wahrscheinlichkeit des Eintretens des Ereignisses wird dann geschätzt, indem die Wahrscheinlichkeiten des Eintretens des Ereignisses in jeder der Simulationen gemittelt werden. Hier finden wir eine genauere Erläuterung des Verfahrens:
- Einrichten der Markov-Kette und definieren des Ereignisses, das uns interessiert. Das Ereignis kann zum Beispiel das Erreichen eines bestimmten Zustands in der Kette oder der Übergang zwischen zwei bestimmten Zuständen sein.
- Durchführen mehrerer Simulationen der Markov-Kette, wobei wir jedes Mal einen anderen Zustand oder eine andere Gruppe von Zuständen auslassen. Dies kann dadurch geschehen, dass die ausgeschlossenen Zustände bei der Simulation einfach nicht berücksichtigt werden oder dass ihre Übergangswahrscheinlichkeiten auf Null gesetzt werden.
- Berechnen der Wahrscheinlichkeit für das Eintreten des Ereignisses für jede Simulation. Dies kann durch eine detaillierte Saldenanalyse oder durch Techniken wie Monte-Carlo-Stichproben oder Matrixmultiplikation geschehen.
- Mitteln der Wahrscheinlichkeiten für das Eintreten des Ereignisses in jeder der Simulationen, um eine Schätzung der Wahrscheinlichkeit für das Eintreten des Ereignisses in der vollständigen Markov-Kette zu erhalten.
Die Verwendung der Jackknife-Methode für Wahrscheinlichkeitsschätzungen in Markov-Ketten hat mehrere Vorteile. Ein Vorteil ist, dass sie eine genauere Schätzung der Wahrscheinlichkeit des Eintretens des Ereignisses ermöglicht, da sie die Auswirkungen jedes einzelnen Zustands auf die Gesamtwahrscheinlichkeit berücksichtigt. Ein weiterer Vorteil ist, dass es relativ einfach zu implementieren ist und leicht automatisiert werden kann. Die Jackknife-Methode weist jedoch auch einige Einschränkungen auf. Eine Einschränkung besteht darin, dass mehrere Simulationen der Markov-Kette durchgeführt werden müssen, was bei großen oder komplexen Ketten rechenintensiv sein kann. Außerdem kann die Genauigkeit der Schätzung von der Anzahl und der Auswahl der Zustände abhängen, die bei den Simulationen ausgeschlossen werden.
- Kreuzvalidierung: Mit dieser Methode lässt sich die Wahrscheinlichkeit des Eintretens eines bestimmten Ereignisses innerhalb einer Markov-Kette schätzen. Dabei werden die Daten in eine Reihe von Falten oder Teilmengen unterteilt und jede Falte als Testmenge verwendet, um die Leistung des Modells für diese Teilmenge zu bewerten. Um die Wahrscheinlichkeitsschätzung der Kreuzvalidierung mit Markov-Ketten zu verwenden, müssen wir zunächst die Markov-Kette mit den gewünschten Zuständen und Übergängen einrichten. Dann würden wir die Daten in die gewünschte Anzahl von Faltungen aufteilen. Als Nächstes würden wir jede Falte durchlaufen und sie als Testmenge verwenden, um die Leistung des Modells für diese Teilmenge zu bewerten. Dabei wird die Markov-Kette verwendet, um die Wahrscheinlichkeit des Auftretens jedes Ereignisses in der Testmenge zu schätzen, und diese Schätzungen werden mit den tatsächlichen Ergebnissen in der Testmenge verglichen.
Schließlich würden wir die Leistung über alle Faltungen hinweg mitteln, um eine Gesamtschätzung der Leistung des Modells zu erhalten. Dies kann nützlich sein, um die Leistung des Modells zu bewerten und die Parameter der Markov-Kette fein abzustimmen, um ihre Genauigkeit zu verbessern. Es ist wichtig zu beachten, dass die Daten unabhängig und identisch verteilt sein müssen, um eine Wahrscheinlichkeitsschätzung der Kreuzvalidierung mit einer Markov-Kette verwenden zu können, was bedeutet, dass jede Teilmenge von Daten repräsentativ für den gesamten Datensatz sein sollte.
Jede dieser Methoden hat ihre eigenen Stärken und Grenzen, und die Wahl der Methode hängt von den spezifischen Merkmalen der Daten und den Zielen der Analyse ab.
Implementierung mit dem MQL5-Assistenten
Zur Programmierung einer Signalklasse, die Markov-Ketten implementiert, verwenden wir die Klasse „CMarkovCPD“ in der Datei „dataanalysis.mqh“ im Ordner „alglib“. Wir werden die Ketten also als zeitdiskrete Ketten modellieren. Diese zeitdiskrete Kette wird 5 Zustände haben, die einfach die letzten 5 Änderungen des Schlusskurses darstellen. Der Zeitrahmen, in dem der Experte getestet oder ausgeführt wird, definiert also die diskrete Zeiteinheit. Um die Übergangswahrscheinlichkeiten zwischen den Zuständen zu schätzen, müssen der Klasse „CMarkovCPD“ Spuren hinzugefügt werden, um das Modell zu trainieren. Die Anzahl der hinzugefügten Spuren ist ein optimierbarer Eingabeparameter ‚m_signal_tracks‘. Auf diese Weise würden wir den Modus initialisieren und die Spuren (Trainingsdaten) hinzufügen.
CMCPDState _s; CMatrixDouble _xy,_p; CMCPDReport _rep; int _k=m_signal_tracks; _xy.Resize(m_signal_tracks,__S_STATES); m_close.Refresh(-1); for(int t=0;t<m_signal_tracks;t++) { for(int s=0;s<__S_STATES;s++) { _xy[t].Set(s,GetState(Close(Index+t+s)-Close(Index+t+s+1),Close(Index+t+s+1)-Close(Index+t+s+2))); } }
Die Schlusskursdaten sind um 1,0 normalisiert. Ist die Änderung eines Schlusskurses negativ, so sind die Eingabedaten kleiner als 1,0, ist sie dagegen positiv, so ist die Eingabe größer als 1,0, und keine Änderung ergibt genau 1,0. Diese Normalisierung wird durch die unten dargestellte Funktion „GetState“ erreicht.
//+------------------------------------------------------------------+ //| Normalizer. | //+------------------------------------------------------------------+ double CSignalMC::GetState(double NewChange,double OldChange) { double _state=0.0; double _norm=fabs(NewChange)/fmax(m_symbol.Point(),fabs(NewChange)+fabs(OldChange)); if(NewChange>0.0) { _state=_norm+1.0; } else if(NewChange<0.0) { _state=1.0-_norm; } return(_state); }
Sobald wir unsere Daten hinzugefügt haben, müssen wir eine Instanz der Klasse „CMCPDState“ initialisieren, da dies das Objekt ist, das alle unsere Modelldaten verarbeitet und bei der Berechnung der Wahrscheinlichkeitsschätzungen hilft. Wir tun dies auf diese Weise:
CPD.MCPDCreate(__S_STATES,_s); CPD.MCPDAddTrack(_s,_xy,_k); CPD.MCPDSetTikhonovRegularizer(_s,m_signal_regulizer); CPD.MCPDSolve(_s); CPD.MCPDResults(_s,_p,_rep);
Der Eingangsparameter „m_signal_regulazier“ sollte idealerweise kein abstrakter reeller Wert sein, sondern ein reeller Wert, der für die Größe der verfolgten Daten repräsentativ ist. Mit anderen Worten, er sollte proportional zu den verfolgten Daten sein, die mit der Funktion „GetState“ ermittelt wurden. Das heißt, wenn wir ihn idealerweise auf einen Wert zwischen 0,5 und 0,0 optimieren, sollten wir ihn mit der Größe der größten Spurdaten multiplizieren, wenn wir den Tichonow-Regulator verwenden.
Die Matrix „_p“ ist unsere Übergangsmatrix mit allen Wahrscheinlichkeiten für den Übergang zwischen den Zuständen. Der vollständige Code der Signalklasse ist am Ende des Artikels beigefügt.
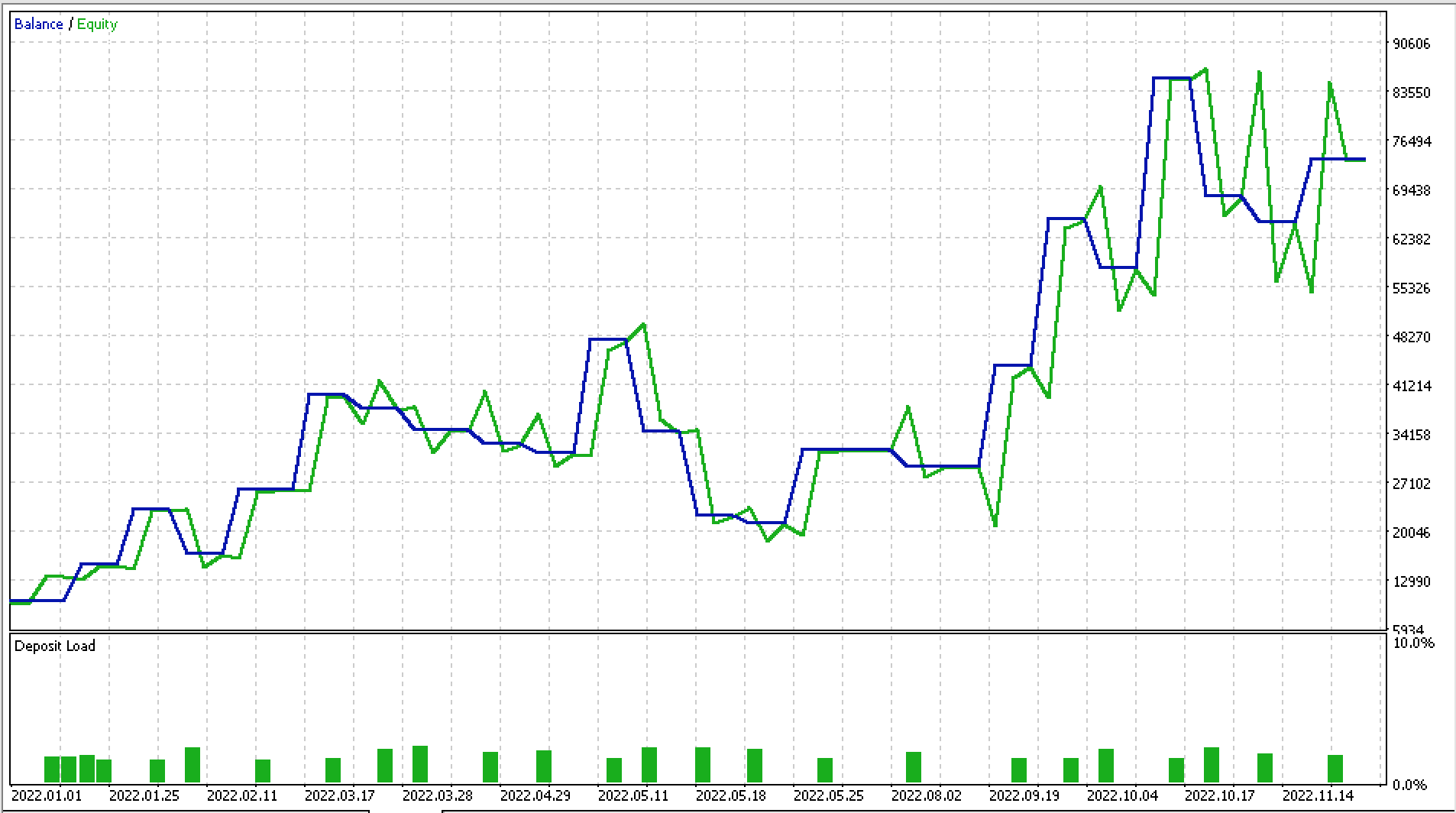
Ich habe einige Testläufe für EURJPY für das Jahr 2022 auf dem täglichen Zeitrahmen durchgeführt, und unten finden Sie einen Teil des Berichts und die dazugehörige Aktienkurve.
Schlussfolgerung
Markov-Ketten sind ein mathematisches Werkzeug, das zur Modellierung des Verhaltens von Finanzmärkten verwendet werden können. Sie sind besonders nützlich, weil sie es den Händlern ermöglichen, die Wahrscheinlichkeit künftiger Marktzustände auf der Grundlage des aktuellen Marktzustands zu analysieren. Dies kann beim Handel sehr nützlich sein, da es den Händlern ermöglicht, fundierte Entscheidungen darüber zu treffen, welche Geschäfte zu welchem Zeitpunkt zu tätigen sind.
Einer der Hauptvorteile des Einsatzes von Markov-Ketten auf den Finanzmärkten besteht darin, dass sie es den Händlern ermöglichen, die Entwicklung der Markttrends im Laufe der Zeit zu analysieren und vorherzusagen. Dies ist besonders wichtig auf schnelllebigen Märkten, auf denen sich Trends schnell ändern können und es schwierig ist, das Verhalten des Marktes vorherzusagen. Durch die Verwendung von Markov-Ketten können Händler die wahrscheinlichsten Wege, die der Markt nehmen wird, identifizieren und diese Informationen nutzen, um fundierte Handelsentscheidungen zu treffen.
Ein weiterer Vorteil von Markov-Ketten ist, dass sie zur Analyse des mit verschiedenen Geschäften verbundenen Risikos verwendet werden können. Durch die Analyse der Wahrscheinlichkeiten verschiedener Marktzustände können Händler das mit verschiedenen Geschäften verbundene Risiko bestimmen und die Geschäfte auswählen, die am ehesten erfolgreich sein werden. Dies kann besonders auf volatilen Märkten nützlich sein, wo das Verlustrisiko höher ist.
Zusammenfassend lässt sich sagen, dass Markov-Ketten ein unverzichtbares Instrument für Händler auf den Finanzmärkten sind, da sie es ihnen ermöglichen, das Verhalten des Marktes zu analysieren und vorherzusagen, die wahrscheinlichsten Pfade zu identifizieren, die der Markt einschlagen wird, und das mit verschiedenen Geschäften verbundene Risiko zu bewerten.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11930
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 MQL5 Kochbuch — Dienste
MQL5 Kochbuch — Dienste
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
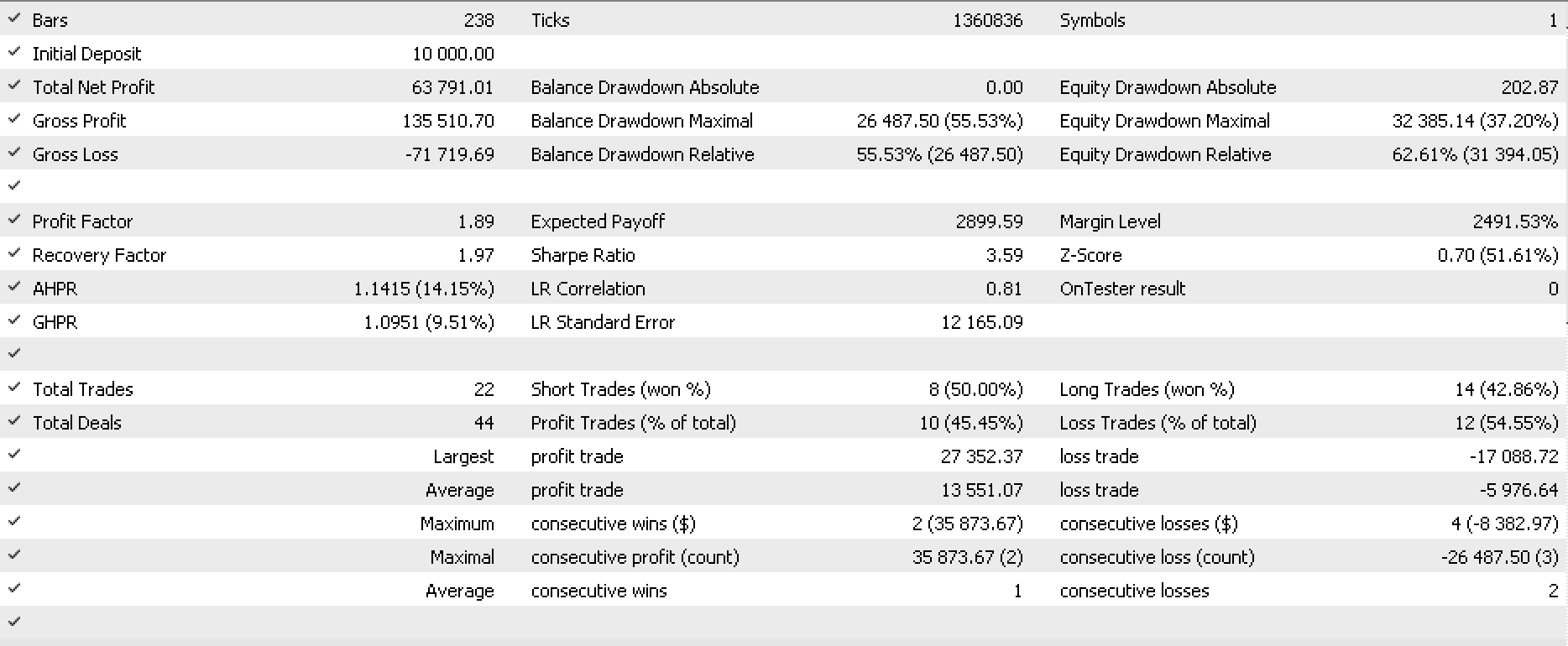
Können Sie uns das Ea auf dem Bild nennen?
Der Code funktioniert nicht
Hallo Stephen,
ich erhalte interessante Ergebnisse mit dieser MC-Klasse. Allerdings erhalte ich auf der Registerkarte "Journal" viele Zeilen mit Meldungen, wie diese: "CAp::Assert CMarkovCPD::MCPDAddTrack: XY enthält unendliche oder NaN-Elemente". Woran liegt das? Sollte ich mir Sorgen machen? Was würden Sie empfehlen, um solche Meldungen loszuwerden?
Vielen Dank!