
Neuronale Netze leicht gemacht (Teil 19): Assoziationsregeln mit MQL5
Inhalt
- Einführung
- 1. Wie die Methode im Handel eingesetzt werden kann
- 2. Implementierung des FP Growth-Algorithmus
- 3. Tests
- Schlussfolgerung
- Liste der Referenzen
- Programme, die im diesem Artikel verwendet werden
Einführung
Im vorangegangenen Artikel haben wir damit begonnen, Algorithmen zur Ermittlung von Assoziationsregeln zu erlernen, die zu den unüberwachten Lernmethoden gehören. Wir haben zwei Algorithmen für die Lösung dieser Art von Problemen in Betracht gezogen: Apriori und FP-Wachstum. Der Engpass des Apriori-Algorithmus ist die große Anzahl von Datenbankaufrufen zur Bestimmung der Unterstützung von Frequent-Pattern-Kandidaten. Die FP Growth-Methode löst dieses Problem, indem sie einen Baum erstellt, der die gesamte Datenbank umfasst. Alle weiteren Operationen werden mit dem FP-Baum durchgeführt, ohne auf die Datenbank zuzugreifen. Dies erhöht die Problemlösungsgeschwindigkeit, da sich der FP-Baum im RAM befindet. Der Zugriff darauf ist viel schneller als eine vollständige Iteration der Datenbank.
1. Wie die Methode im Handel eingesetzt werden kann
Bevor wir mit der Konstruktion des Algorithmus für das Assoziationsregel-Mining mit MQL5 fortfahren, sollten wir darüber nachdenken, wie sie im Handel verwendet werden können.
Assoziationsregel-Algorithmen wurden entwickelt, um nach stabilen Abhängigkeiten zwischen binären Merkmalen (features) in der Datenbank zu suchen. Daher können solche Algorithmen verwendet werden, um einige stabile Beziehungen zwischen verschiedenen Merkmalen zu finden. Dabei kann es sich um verschiedene Muster handeln, die aus mehreren Indikatoren und/oder Instrumenten bestehen. Der Algorithmus kümmert sich nicht darum, ob jedes einzelne Merkmal verschiedene Metriken darstellt oder ob es sich um die Werte derselben Metrik in verschiedenen Zeitintervallen handelt. Der Algorithmus wertet jedes Merkmal als unabhängig. Wir können also versuchen, diesen Algorithmus mit den Entwicklungen bei den überwachten Lernmethoden zu kombinieren. Fügen wir der Trainingsstichprobe der historischen Daten einige Zielmerkmale hinzu. Der Algorithmus soll Assoziationsregeln finden, die zur Bildung unserer Zielwerte führen.
Wir haben einen Algorithmus und eine Idee, wie wir ihn zur Lösung unserer praktischen Probleme einsetzen können. Schauen wir uns an, wie dies mit MQL5 umgesetzt werden kann. Dann werden wir die Idee in der Praxis testen.
2. Implementierung des FP Growth-Algorithmus
Um den im vorigen Artikel betrachteten FP Growth-Algorithmus zu implementieren, sei daran erinnert, dass seine Konstruktion auf einem Entscheidungsbaum basiert. Die MQL5-Standardbibliothek verfügt über die Klasse CTree zum Aufbau eines Binärbaums. Leider ist die Option des Binärbaums für uns nicht ganz bequem, da die Anzahl der Verzweigungen von einem Knoten eines FP-Baums mehr als 2 betragen kann (das Maximum, das in der binären Implementierung verfügbar ist). Bevor wir also den Algorithmus selbst erstellen, wollen wir die Klasse CMyTreeNode erstellen, um einen Baumknoten mit mehreren Zweigen zu implementieren.
2.1. Implementierung der Baumknotenklasse
Diese Klasse wird von der Standard-MQL5-Klasse eines dynamischen Arrays von Objekten CArrayObj abgeleitet. Diese Klasse wurde als übergeordnete Klasse ausgewählt, weil sie die erforderlichen Funktionen für die Erstellung und Pflege eines dynamischen Arrays von Objekten besitzt, die in unserem Fall die Zweigknoten sind.
Um die für den Algorithmus erforderlichen Funktionen zu implementieren, wurden drei neue Variablen in die Klasse aufgenommen:
- m_cParent — ein Zeiger auf das Objekt des vorherigen übergeordneten Knotens. Für die Wurzel des Baumes wird sie leer sein
- m_iIndex — Index eines Merkmals in der Quelldatenbank; wird zur Identifizierung von Merkmalen verwendet
- m_dSupport — eine Variable, die den Wert der Merkmalsunterstützung erhält
class CMyTreeNode : public CArrayObj { protected: CMyTreeNode *m_cParent; ulong m_iIndex; double m_dSupport; public: CMyTreeNode(); ~CMyTreeNode(); }
Im Klassenkonstruktor setzen wir die Anfangswerte der Variablen und löschen das dynamische Array. Wir lassen den Destruktor der Klasse leer.
CMyTreeNode::CMyTreeNode() : m_iIndex(ULONG_MAX), m_dSupport(0) { Clear(); }
Um mit versteckten Klassenvariablen zu arbeiten, werden wir eine Reihe von Methoden erstellen, die bei der Erstellung des FP Growth-Algorithmus verwendet werden. Ich werde die Zwecke der Methode zusammen mit ihrer Verwendung erläutern.
class CMyTreeNode : public CArrayObj { ........ public: ........ //--- methods of access to protected data CMyTreeNode* Parent(void) const { return(m_cParent); } void Parent(CMyTreeNode *node) { m_cParent = node; } void IncreaseSupport(double support) { m_dSupport += support; } double GetSupport(void) { return m_dSupport; } void SetSupport(double support) { m_dSupport = support; } ulong ID(void) { return m_iIndex; } void ID(ulong ID) { m_iIndex = ID; } };
Um das Konfidenzniveau zu berechnen, erstellen wir die Methode GetConfidence. Darin wird zunächst der Zeiger auf den Vorgängerknoten geprüft und, falls er gültig ist, die aktuelle Knotenunterstützung durch die Unterstützung des übergeordneten Knotens geteilt.
Beachten Sie, dass der FP-Baumbildungsalgorithmus so organisiert ist, dass die Unterstützung eines Knotens nicht größer sein kann als die Unterstützung des Elternknotens. Daher wird das Ergebnis der Methodenoperationen immer positiv sein und nicht größer als 1 sein.
Es gibt keine Nullteilungskontrollen, da die Baumknoten auf der Grundlage bestehender Transaktionen hinzugefügt werden. Wenn sich also ein Knoten im Baum befindet, dann ist sein Merkmal mindestens einmal in der Datenbank aufgetaucht und er hat die Mindestunterstützung.
double CMyTreeNode::GetConfidence(void) { CMyTreeNode *parent = Parent(); if(!parent) return 1; //--- double result = m_dSupport / parent.GetSupport(); return result; }
Außerdem fügen wir eine Methode hinzu, die einen neuen Zweigknoten AddNode erstellt. In den Methodenparametern übergeben wir die Merkmals-ID in der Quelldatenbank der Trainingsstichprobe und die Unterstützung des Knotens. Die Methode gibt einen Zeiger auf das erstellte Objekt zurück.
Im Methodenrumpf wird eine neue Instanz des Baumknotens erstellt und das Ergebnis der Operation sofort überprüft. Wenn ein Fehler auftritt, wird ein ungültiger Objektzeiger zurückgegeben.
Als Nächstes geben wir die ID des erstellten Knotens an und übergeben ihm einen Zeiger auf das aktuelle Objekt als übergeordnetes Objekt.
Hinzufügen eines neuen Objekts zum dynamischen Array des aktuellen Knotens und Überprüfung des Ergebnisses der Operation. Wenn beim Hinzufügen eines Objekts zum Array ein Fehler auftritt, wird das erstellte Objekt gelöscht und die Methode beendet, wobei ein ungültiger Zeiger zurückgegeben wird.
Am Ende der Methode speichern wir die in den Parametern angegebene Unterstützung in dem neuen Objekt und beenden die Methode.
CMyTreeNode *CMyTreeNode::AddNode(const ulong ID, double support = 0) { CMyTreeNode *node = new CMyTreeNode(); if(!node) return node; node.ID(ID); if(!Add(node)) { delete node; return node; } node.Parent(GetPointer(this)); //--- if(support > 0) node.SetSupport(support); return node; }
Wenn wir ein neues Objekt erstellt haben, sollten wir es auch wieder löschen können. Die Methode zum Löschen eines Objekts nach seinem Index in einem dynamischen Array existiert bereits in der übergeordneten Klasse. Um die Funktionalität zu erweitern, erstellen wir die Methode DeleteNode zum Löschen eines Knotens anhand der Merkmals-ID.
Die Methode erhält die ID des zu löschenden Merkmals und gibt das boolesche Ergebnis der Operation zurück.
Im Methodenrumpf implementieren wir eine Schleife, um einen Knoten mit der angegebenen ID im dynamischen Array des aktuellen Knotens zu finden. Die Schleife durchläuft die Elemente im Bereich von 0 bis zum Wert der Variablen m_data_total. Die Variable enthält die Anzahl der aktiven Elemente des dynamischen Arrays und wird von der übergeordneten Klasse gesteuert.
Im Methodenrumpf extrahieren wir aus dem dynamischen Array das nächste Element und validieren den Zeiger. Ein Element mit einem ungültigen Zeiger wird sofort gelöscht, indem die Delete-Methode der Elternklasse mit dem angegebenen Index des zu löschenden Elements aufgerufen wird.
Beachten Sie, dass die Methode Delete das boolesche Ergebnis der Operation zurückgibt. Wenn ein Element erfolgreich aus dem dynamischen Array gelöscht wurde, verringern wir den Zähler der Schleifeniterationen und gehen zum nächsten Array über. Wir dekrementieren nur den Iterationszähler der Schleife und ändern den Wert der Variablen m_data_total nicht. Dies liegt daran, dass sein Wert bereits in der Methode der übergeordneten Klasse Delete geändert wird.
Wenn beim Entfernen eines ungültigen Elements aus dem dynamischen Array ein Fehler auftritt, gehen wir einfach zum nächsten Element des Arrays über. Wir brechen die Methode nicht mit dem falschen Ergebnis ab, da die Aufgabe der Methode nicht darin besteht, das dynamische Array von ungültigen Objekten zu befreien. Dies ist nur eine Hilfsfunktion. Die Hauptaufgabe der Methode besteht darin, ein bestimmtes Element zu löschen. Daher setzen wir die Ausführung der Methode fort, bis das gewünschte Element gefunden ist.
Wenn das gewünschte Element des dynamischen Arrays gefunden wurde, rufen wir die zuvor erwähnte Methode Delete der übergeordneten Klasse auf. Diesmal beenden wir die Methode, während wir das Ergebnis der Objektlöschung zurückgeben.
Wenn das Element nach einer vollständigen Iteration durch alle Elemente des dynamischen Arrays nicht gefunden wird, wird die Methode mit einem falseverlassen.
bool CMyTreeNode::DeleteNode(const ulong ID) { for(int i = 0; i < m_data_total; i++) { CMyTreeNode *temp = m_data[i]; if(!temp) { if(!Delete(i)) continue; return DeleteNode(ID); } if(temp.ID() != ID) continue; return Delete(i); } //--- return false; }
Wenn wir nun über die Methoden der neuen Klasse des Baumknotens CMyTreeNode sprechen, möchte ich Ihre Aufmerksamkeit auf die Methode Mining lenken. Diese Methode ist dafür verantwortlich, Pfade in unserem FP-Baum bis zu dem zu analysierenden Merkmal zu finden. Bevor wir zur Beschreibung des Algorithmus der Methode übergehen, muss ich sagen, dass er unter Berücksichtigung der beabsichtigten Verwendung im Handel erstellt wurde. Daher weicht er leicht vom Grundalgorithmus ab.
Zunächst einmal werden wir nicht für alle Merkmale Assoziationsregeln festlegen, sondern nur für unsere Zielwerte. Beim Aufbau von Regelbäumen ist es daher sehr wahrscheinlich, dass das gewünschte Merkmal kein Blatt ist, sondern ein Knoten, der die nachfolgenden Elemente entlang des Pfades enthält. Aber wir können nachfolgende Knoten nicht ignorieren, da sie die Wahrscheinlichkeit eines Zielergebnisses erhöhen können. Daher sollten sie bei der Auswahl der Pfade zum analysierten Merkmal berücksichtigt werden.
Ein weiterer Punkt, auf den ich bei der Entwicklung dieser Methode geachtet habe, ist der folgende. Gemäß dem Algorithmus müssen wir zunächst alle Pfade zu dem analysierten Merkmal im FP-Baum finden. Danach können wir die Unterstützungswerte für jedes Merkmal in den ausgewählten Pfaden berechnen. Ich habe beschlossen, diese beiden Teilaufgaben innerhalb einer Methode durchzuführen.
Bitte beachten Sie, dass zum Aufbau eines FP-Baums nur die Instanzen der Klasse CMyTreeNode vorgesehen sind. Um eine Tiefensuche durchzuführen, verwenden wir daher einen rekursiven Methodenaufruf.
Schauen wir uns nun die Umsetzung dieser Aufgaben in der Mining-Methode unserer Klasse an. In den Methodenparametern übergeben wir Zeiger auf einen Vektor zum Schreiben der Elementunterstützungswerte, eine Matrix zum Schreiben der Pfade, einen Bezeichner des zu analysierenden Merkmals und ein minimales Vertrauensniveau. Die Methode gibt das boolesche Ergebnis der Operation zurück.
Prüfen wir im Methodenrumpf zunächst, ob der analysierte Knoten das gewünschte Merkmal ist. Dazu vergleichen wir die ID unseres Knotens mit der ID des gewünschten Knotens, die wir in den Parametern erhalten haben. Wenn sie gleich sind, prüfen wir den Vertrauensgrad des Knotens im aktuellen Zweig. Das Niveau wird mit Hilfe der bereits erwähnten Methode GetConfidence ermittelt. Das Konfidenzniveau darf nicht unter dem zulässigen Mindestwert liegen. Andernfalls verlassen wir die Methode mit dem Ergebnis false.
bool CMyTreeNode::Mining(vector &supports, matrix &paths, const ulong ID, double min_conf) { if(ID == m_iIndex) if(GetConfidence() < min_conf) return true;
Der nächste Block führt eine weitere Suche in Richtung Baumtiefe durch. Hier wird zunächst der Unterstützungswert des aktuellen Knotens in einer lokalen Variablen gespeichert. Dann durchlaufen wir in einer Schleife alle Zweige vom aktuellen Knoten bis zur Tiefe des Baums. Die Methode wird für alle Zweige rekursiv aufgerufen.
Beachten Sie, dass wir bei der rekursiven Methode nur den gewünschten Identifikator übergeben, bis wir den entsprechenden Knoten finden. Danach übergeben wir die Konstante ULONG_MAX in die Baumtiefe, anstatt des gewünschten Identifikators. Der Grund dafür ist, dass aufgrund der Besonderheiten der FP-Baumkonstruktion die Konfidenz des Musters wahrscheinlich weniger als 100 % beträgt, bevor wir den Pfad zum gewünschten Element finden. Je weiter wir auf dem Pfad fortschreiten, desto größer wird die Wahrscheinlichkeit, dass das gewünschte Merkmal zu 100 % auftritt. Andernfalls hätten wir einen anderen Pfad gebaut, der den gewünschten Knoten umgeht.
Natürlich ist eine solche Situation ausgeschlossen, wenn wir einen nutzerdefinierten Algorithmus verwenden. Wenn wir die Regeln für alle Merkmale festlegen, ist jedes dieser Merkmale zu dem Zeitpunkt, zu dem wir in unserem FP-Baum mit der Arbeit beginnen, ein Blatt ohne nachfolgende Knoten. Dies liegt daran, dass alle Merkmale mit geringerer Unterstützung verarbeitet und aus dem Baum gelöscht wurden.
Wenn wir also vom Algorithmus abweichen, müssen wir die Auswirkungen der Änderungen auf den gesamten Prozess bewerten und entsprechende Anpassungen am Algorithmus vornehmen. In diesem Fall müssen wir alle Pfade, die das gewünschte Merkmal enthalten, in die Liste aufnehmen. Dies ist der Pfad von dem gewünschten Merkmal zur Baumwurzel und alle Pfade von einem der nachfolgenden Knoten zur Baumwurzel, die durch das gewünschte Merkmal führen. Zu diesem Zweck müssen wir weiteren Knoten mitteilen, dass das gewünschte Merkmal zwischen dem Knoten und der Wurzel gefunden wurde. Ein solches Flag tritt auf, wenn die ID des gewünschten Merkmals auf die Konstante ULONG_MAX wechselt.
Nach dem positiven Ergebnis der rekursiven Methode subtrahieren wir für den nächsten Knoten den Unterstützungswert von der lokalen Variablen, die vor der Schleife mit der Unterstützung des aktuellen Knotens erstellt wurde. Wenn die nächste Knoten-ID gleich der gewünschten ist, löschen wir den bearbeiteten Knoten.
double support = m_dSupport; for(int i = 0; i < m_data_total; i++) { CMyTreeNode *temp = m_data[i]; if(!temp) { if(Delete(i)) i--; continue; } if(!temp.Mining(supports, paths, (ID == m_iIndex ? ULONG_MAX : ID), min_conf)) return false; support -= temp.GetSupport(); if(temp.ID() == ID) if(Delete(i)) i--; }
Wie man sehen kann, haben wir im vorherigen Block dieselbe Methode nur rekursiv für nachfolgende Knoten aufgerufen, aber die gefundenen Pfade nicht gespeichert. Das Speichern wird im nächsten Methodenblock durchgeführt. Dieser Block wird für Knoten mit dem gewünschten Attribut und für nachfolgende Knoten ausgeführt. Dazu müssen wir die ID des aktuellen Knotens und die in den Parametern erhaltene ID überprüfen. Außerdem muss die Unterstützung des aktuellen Knotens nach der Ausführung von rekursiven Methoden größer als "0" sein. Außerdem kann der aktuelle Knoten nicht die Wurzel sein. Das bedeutet, dass er mindestens einen Vorgängerknoten haben muss. Das liegt daran, dass wir etwas als Vorgeschichte für die Regel verwenden müssen.
Wird die Kontrolle erfolgreich übergeben, so wird die Pfadmatrix um eine Zeile vergrößert und die hinzugefügte Zeile mit Nullwerten gefüllt.
Als Nächstes implementieren wir eine Fortpflanzungsschleife vom aktuellen Knoten zur Baumwurzel. Dem aktuellen und allen Vorgängerknoten wird die verbleibende Unterstützung des aktuellen Knotens in unserer Pfadlinie zugewiesen. Außerdem fügen wir denselben Wert in den kumulativen Unterstützungsvektor für die entsprechenden Elemente ein.
Nachdem die übergeordnete Iteration abgeschlossen ist, wird die Methode mit einem positiven Ergebnis beendet.
if(ID == m_iIndex || ID == ULONG_MAX) if(support > 0 && !!m_cParent) { CMyTreeNode *parent = m_cParent; ulong row = paths.Rows(); if(!paths.Resize(row + 1, paths.Cols())) return false; if(!paths.Row(vector::Zeros(paths.Cols()), row)) return false; supports[m_iIndex] += support; while(!!parent) { if(parent.ID() != ULONG_MAX) { supports[parent.ID()] += support; paths[row, parent.ID()] = support; } parent = parent.Parent(); } } //--- return true; }
Ich möchte die Funktionsweise der Methode anhand eines kleinen Beispiels erläutern, da ihr Aufbau den Rahmen des oben beschriebenen PF-Growth-Algorithmus etwas sprengt. Angenommen, die Quelldatenbank hat die folgenden Transaktionen: 2 Mal "AB", 1 Mal "ABC", 3 Mal "ABCD" 1 Mal "ABCDE". Infolgedessen hat sich im FP-Baum der folgende Pfad gebildet: "A7-B7-C5-D4-E1". Bei der Analyse des Elements "C" müssen wir alle Pfade, die dieses Element enthalten, aus dem Baum wiederherstellen.
Wir beginnen mit dem Aufruf einer Methode auf dem Wurzelelement "A" und weisen sie an, das "C" zu finden. Hier rufen wir die Methode für den Knoten "B" rekursiv auf. Wir gehen weiter bis zum Blatt "E". Da das Blatt "E" keine Nachfolgeknoten hat, beginnen wir mit der Verarbeitung im Block 2 unserer Methode und schreiben die Pfade. Hier speichern wir zunächst den Pfad "ABCDE" und schreiben für alle Knoten die Unterstützung 1. Das bedeutet, dass es in der Quelldatenbank 1 solchen Pfad gab. Dann verlassen wir die Methode und übergeben die Kontrolle an eine höhere Ebene.
Speichern wir auf der Ebene des Knotens "D" den Pfad "ABCD". Von der Unterstützung des Knotens "D" ziehen wir die Unterstützung des Blattes "E" ab (4-1=3). Den resultierenden Wert registrieren wir als Unterstützung für alle Elemente dieses Pfads. Wie wir sehen können, entspricht dies den ursprünglichen Daten, bei denen wir 3 identische Transaktionen in der Trainingsstichprobe hatten. Anstatt die Transaktion dreimal zu wiederholen, verwenden wir die Unterstützwerte der Elemente.
In ähnlicher Weise speichern wir den Pfad "ABC" mit der Unterstützung von 1. Der Pfad "AB" wird nicht gespeichert, da er das analysierte Merkmal nicht enthält.
Den gesamten Code aller Klassenmethoden finden wir in der unten angehängten Datei MyTreeNode.mqh.
2.2. Implementierung der Assoziationsregel-Mining-Klasse
Fahren wir fort mit dem Aufbau des FP Growth Assoziationsregel-Mining-Algorithmus. Die wichtigsten Funktionen werden in einer anderen Klasse CAssocRules beschrieben. Die Struktur dieser Klasse ist im Folgenden aufgelistet. Wie wir sehen können, sind die meisten Methoden "unter der Haube" versteckt. Aber das Wichtigste zuerst.
class CAssocRules : public CObject { protected: CMyTreeNode m_cRoot; CMyTreeNode m_cBuyRules; CMyTreeNode m_cSellRules; vector m_vMin; vector m_vStep; int m_iSections; matrix m_mPositions; matrix m_BuyPositions; matrix m_SellPositions; //--- bool NewPath(CMyTreeNode *root, matrix &path); CMyTreeNode *CheckPath(CMyTreeNode *root, vector &path); //--- bool PrepareData(matrix &data, matrix &bin_data, vector &buy, vector &sell, const int sections = 10, const double min_sup = 0.03); matrix CreatePath(vector &bin_data, matrix &positions); matrix CreatePositions(vector &support, const double min_sup = 0.03); bool GrowsTree(CMyTreeNode *root, matrix &bin_data, matrix &positions); double Probability(CMyTreeNode *root, vector &data, matrix &positions); public: CAssocRules(); ~CAssocRules(); //--- bool CreateRules(matrix &data, vector &buy, vector &sell, int sections = 10, double min_freq = 0.03, double min_prob = 0.3); bool Probability(vector &data, double &buy, double &sell); //--- methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); virtual bool Save(const string file_name); virtual bool Load(const string file_name); };
Unter den Klassenvariablen gibt es drei Instanzen der oben beschriebenen Baumknoten:
- m_cRoot — wir werden es verwenden, um unseren FP-Baum aufzuschreiben
- m_cBuyRules — hier werden die Kaufregeln eingetragen
- m_cSellRules — für Verkaufsregeln
Die Matrizen m_mPositions, m_BuyPositions und m_SellPositions enthalten Merkmale und ihre Unterstützungswerte in absteigender Reihenfolge.
Beim Testen aller vorherigen Modelle haben wir die Möglichkeit geprüft, ein Fraktal vor der Bildung der 3. Kerze des Musters zu bestimmen. Daher werde ich zwei Regelbäume festlegen, um Kauf- und Verkaufsfraktale zu definieren. Wenn wir aufgrund unseres Problems Regeln für eine größere Anzahl von Zielmerkmalen definieren müssen, dann müssen wir mehr private Regelbäume erstellen.
Wir können zum Beispiel mehrere Zielkauf- und -verkaufsniveaus haben. Leider arbeiten die Algorithmen zur Ermittlung von Assoziationsregeln nur mit binären Tabellen. Daher müssen wir für jede Zielebene ein eigenes Element erstellen und dafür Assoziationsregeln finden. Wir können dynamische Arrays verwenden, um eine große Anzahl von privaten Variablen auszuschließen.
Der Methodenkonstruktor und der Destruktor sind leer, da ich in dieser Klasse keine dynamischen Zeiger auf baumbildende Objekte verwendet habe.
Wie bereits erwähnt, arbeiten die Algorithmen zur Ermittlung von Assoziationsregeln nur mit binären Matrizen. Die Daten über die Marktlage sind jedoch nur schwer als solche zu klassifizieren. Daher müssen sie vor der Verwendung aufbereitet werden.
Um die weitere Nutzung der Klasse zu vereinfachen, erfordert der Algorithmus keine Vorverarbeitung der Daten durch den Nutzer. Stattdessen wird sie in der PrepareData-Methode implementiert. Als Parameter erhält die Methode Zeiger auf 2 Matrizen, 2 Vektoren und 2 Konstanten. Eine Matrix enthält die Originaldaten, die zweite wird zum Schreiben der verarbeiteten Binärdaten verwendet. Die Vektoren enthalten die Zielwerte. In unserem Fall werden sie durch binäre Daten dargestellt, sodass sie nicht vorverarbeitet werden müssen. Die Quelldaten müssen vorverarbeitet werden.
Um die skalaren Einheiten der Ausgangsdaten in binäre Einheiten umzuwandeln, verwenden wir den Wertebereich für jedes Merkmal und unterteilen ihn in mehrere Intervalle. Die Anzahl der Intervalle wird durch den Parameter "Abschnitte" festgelegt. Die Mindestwerte und die Schrittweite für jedes Merkmal werden in den entsprechenden Vektoren m_vMin und m_vStep gespeichert. Die Vektoren werden dann in der Praxis zur Umwandlung von Quelldaten in Binärdaten verwendet.
Hier bereiten wir die binäre Matrix vor, indem wir die erforderliche Größe einstellen und mit Nullen füllen. Wir können auch den Identifikator für Zielmerkmale angeben, die später als letzte Spalten in eine Matrix eingefügt werden.
bool CAssocRules::PrepareData(matrix &data, matrix &bin_data, vector &buy, vector &sell, const int sections = 10, const double min_sup = 0.03) { //--- m_iSections = sections; m_vMin = data.Min(0); vector max = data.Max(0); vector delt = max - m_vMin; m_vStep = delt / sections + 1e-8; m_cBuyRules.ID(data.Cols() * m_iSections); m_cSellRules.ID(m_cBuyRules.ID() + 1); bin_data = matrix::Zeros(data.Rows(), m_cSellRules.ID() + 1);
Als Nächstes implementieren wir eine Schleife über alle Zeilen der Eingabedatenmatrix. Wir ziehen im Schleifenkörper den Vektor der Mindestwerte von jeder Zeile ab und teilen das Ergebnis durch die Schrittweite. Um Daten, die außerhalb des Bereichs liegen, auszuschließen, müssen wir die unteren und oberen Werte der Vektorelemente begrenzen. Als Ergebnis dieser Operationen zeigt der ganzzahlige Teil der Zahl in jedem Element des Vektors an, in welchen Wertebereich wir das entsprechende Element der Quelldaten aufnehmen müssen. Jeder Bereich für unsere binäre Matrix wird ein separates Merkmal sein.
Führen wir eine verschachtelte Schleife aus und füllen die entsprechende Zeile der binären Matrix. Wenn das Merkmal aktiv ist, ändern wir seinen Wert auf "1". Inaktive Merkmale bleiben mit Nullwerten erhalten.
for(ulong r = 0; r < data.Rows(); r++) { vector pos = (data.Row(r) - m_vMin) / m_vStep; if(!pos.Clip(0, m_iSections - 1)) return false; for(ulong c = 0; c < pos.Size(); c++) bin_data[r, c * sections + (int)pos[c]] = 1; } if(!bin_data.Col(buy, m_cBuyRules.ID()) || !bin_data.Col(sell, m_cSellRules.ID())) return false;
Nach dem Ausfüllen der binären Matrix können wir sofort die Unterstützungen für jedes Merkmal berechnen und sie in absteigender Reihenfolge in der Methode CreatePositions sortieren. Wir beenden die Methode nach dem Sortieren mit einem positiven Ergebnis.
vector supp = bin_data.Sum(0) / bin_data.Rows(); m_mPositions = CreatePositions(supp, min_sup); //--- return true; }
Da wir die Sortiermethode des Merkmals CreatePositions erwähnt haben, wollen wir ihren Algorithmus betrachten. Die Methode empfängt einen Unterstützungsvektor und ein minimales Unterstützungsniveau als Parameter.
Der Methodenkorpus wird ein wenig Vorarbeit enthalten. Dies liegt daran, dass die empfangenen Unterstützungswerte durch einen Vektor dargestellt werden, in dem die Elementwerte Unterstützungswerte enthalten. Die Indizes der Elemente geben die Merkmale an. Bei einer einfachen Sortierung der Vektorelemente würden wir die Verbindung zu den Merkmalen der Ausgangsdaten verlieren. Daher müssen wir Paare "Merkmals-ID - Unterstützung" erstellen. Die Daten des Paares werden in einer Matrix gespeichert.
Dazu erstellen wir zunächst eine Identitätsmatrix mit 2 Spalten und der Anzahl der Zeilen, die der Anzahl der Merkmale in der ursprünglichen Stichprobe entspricht. Dann berechnen wir die kumulierten Summen der Posten nach Spalten und reduzieren die Werte der resultierenden Matrix um "1". So erhalten wir eine Matrix, in der die Spalten Werte in aufsteigender Reihenfolge ab "0" enthalten, was dem Zeilenindex entspricht. Wir müssen nur eine Spalte durch den resultierenden Stützvektor ersetzen. Auf diese Weise erhalten wir eine Matrix: Jede Zeile enthält eine Merkmalskennung und einen entsprechenden Unterstützungswert.
matrix CAssocRules::CreatePositions(vector &support, const double min_sup = 0.03) { matrix result = matrix::Ones(support.Size(), 2); result = result.CumSum(0) - 1; if(!result.Col(support, 1)) return matrix::Zeros(0, 0);
Wir müssen nur die Zeilen der Matrix in der absteigenden Reihenfolge der Unterstützung sortieren. Dazu implementieren wir eine Schleife mit einem Bubble-Sort-Algorithmus.
bool change = false; do { change = false; ulong total = result.Rows() - 1; for(ulong i = 0; i < total; i++) { if(result[i, 1] >= result[i + 1, 1]) continue; if(result.SwapRows(i, i + 1)) change = true; } } while(change);
Nach Beendigung der Schleife haben wir eine Matrix mit sortierten Merkmalen. Wir müssen nur die Merkmale aus dieser Matrix entfernen, die die Mindestanforderungen an die Unterstützung nicht erfüllen. Suchen wir dazu das erste Merkmal unterhalb des Mindestunterstützungsniveaus und "schneiden" alle Merkmale unterhalb dieses Niveaus ab.
int i = 0; while(result[i, 1] >= min_sup) i++; if(!result.Resize(i, 2)) return matrix::Zeros(0, 0); //--- return result; }
Nach erfolgreicher Größenänderung der Matrix beenden wir die Methode und geben die resultierende Matrix zurück.
Bevor wir zu den öffentlichen Methoden übergehen, wollen wir uns einige weitere Methoden ansehen, in denen einige der sich wiederholenden Funktionen ausgeführt werden. Wir müssen einen Pfad für die Übertragung von Binärdaten in den FP-Baum erstellen. Diese Funktionalität wird in der Methode CreatePath ausgeführt. Die Methode erhält Zeiger auf den Vektor der Binärdaten und die Matrix der sortierten Merkmale. Es wird dann eine Pfadmatrix zurückgegeben, die Paare "Merkmals-ID - Unterstützung" enthält, die dem FP-Baum hinzugefügt werden sollen.
Achten wir auf den Unterschied zwischen der sortierten Merkmalsmatrix, die wir bei der Aufbereitung der Daten erhalten haben, und der Matrix für das Hinzufügen des Pfades zum FP-Baum. Beide Matrizen enthalten die Paare "Merkmalsidentifikator - Unterstützung". Die erste Matrix enthält jedoch alle in den Quelldaten vorhandenen Merkmale und deren Unterstützung in der Trainingsstichprobe. Die Pfadmatrix enthält nur die Merkmale, die in der analysierten Transaktion vorhanden sind, und die in der Binärmatrix angegebenen Unterstützungen dieser Transaktion.
Da wir es mit einer binären Matrix zu tun haben, müssen die Unterstützungswerte der Merkmale in jeder Transaktion gleich sein. Später werden wir die gleiche Methode verwenden, um private Regelbäume zu erstellen. Bei der Beschreibung der Methode CMyTreeNode::Mining haben wir bereits ein Beispiel besprochen. Anstatt einen Pfad zu wiederholen, haben wir in diesem Beispiel mehrere Unterstützungsebenen verwendet. Um die Vorgänge zu vereinheitlichen, werden wir also 1 Methode in 2 Teilprozessen verwenden. In diesem Fall ist die Einführung des Unterstützungsniveaus sehr nützlich.
Zu Beginn der Methode speichern wir in lokalen Variablen die Größen des Quelldatenvektors und die Anzahl der analysierten Merkmale, die um die Anzahl der Zufallsmerkmale mit Unterstützung unterhalb des Minimums kleiner ist als die Größe des Quelldatenvektors.
Außerdem bereiten wir eine Matrix vor, in die wir die Ergebnisse eintragen. Sie kann nicht größer sein als die analysierte Merkmalsmatrix. Außerdem führen wir eine Variable ein, die die Größe unseres Pfades angibt. In diesem Stadium ist sie gleich "0".
Als Nächstes führen wir eine Schleife durch alle analysierten Merkmale in absteigender Reihenfolge ihrer Unterstützung durch. Im Schleifenkörper wird die Kennung des nächsten geprüften Merkmals extrahiert. Wir überprüfen seinen Wert im binären Quelldatenvektor. Wenn das Merkmal nicht aktiv ist, fahren wir mit dem nächsten Merkmal fort.
Wenn das Merkmal aktiv ist, fügen wir die Merkmals-ID und seine Unterstützung aus dem binären Quelldatenvektor zur Pfadmatrix hinzu. Danach erhöhen wir die Variable für die Pfadgröße.
Nach dem Verlassen der Schleife reduzieren wir die Größe der Pfadmatrix auf die Anzahl der gefüllten Elemente und beenden die Methode.
matrix CAssocRules::CreatePath(vector &bin_data, matrix &positions) { ulong size = bin_data.Size(); //--- ulong total = positions.Rows(); int vect_pos = 0; matrix path = matrix::Zeros(2, total); for(ulong c = 0; c < total; c++) { ulong pos = (ulong)positions[c, 0]; if(pos >= size) continue; if(bin_data[pos] == 0) continue; path[0, vect_pos] = (double)pos; path[1, vect_pos] = bin_data[pos]; vect_pos++; } if(!path.Resize(2, vect_pos)) return matrix::Zeros(0, 0); //--- return path; }
Eine weitere Methode, die wir benötigen, ist das Hinzufügen eines Pfades zu unserem FP-Baum: NewPath. Die Methode erhält einen Zeiger auf den Wurzelknoten des Baums und die zuvor erstellte Pfadmatrix. Dann wird das boolesche Ergebnis der Operation zurückgegeben. Im Hauptteil der Methode wird zunächst die Größe des resultierenden Pfads überprüft. Er sollte größer als 0 sein. Dann erhöhen wir die Unterstützung des Wurzelknotens und führen eine Schleife durch alle Elemente des Pfades.
Im Schleifenkörper überprüfen wir das Vorhandensein des nächsten Knotens mit der gewünschten ID und legen gegebenenfalls einen neuen Knoten an. Dann erhöhen wir die Größe der Knotenunterstützung und fahren mit der Suche nach dem nächsten Knoten im Pfad fort.
Nachdem alle Elemente des Pfades durchlaufen wurden, beenden wir die Methode.
bool CAssocRules::NewPath(CMyTreeNode *root, matrix &path) { ulong total = path.Cols(); if(total <= 0) return false; CMyTreeNode *parent = root; root.IncreaseSupport(path[1, 0]); for(ulong i = 0; i < total; i++) { CMyTreeNode *temp = parent.GetNext((ulong)path[0, i]); if(!temp) { temp = parent.AddNode((int)path[0, i], 0); if(!temp) return false; } temp.IncreaseSupport(path[1, i]); parent = temp; } //--- return true; }
Und schließlich gehen wir zu der Methode über, die den FP-Baum wachsen lässt: GrowsTree. Als Parameter erhält sie einen Zeiger auf den Wurzelknoten des Baums, eine binäre Matrix der Quelldaten und eine Matrix der sortierten analysierten Merkmale. Innerhalb der Methode gehen wir mit einer Schleife durch alle Zeilen der Quelldaten.
In der Schleife erfassen wir die nächste Transaktion aus dem Trainingsbeispiel und erstellen mit der Methode CreatePath einen Pfad, der dem Baum hinzugefügt wird. Wir prüfen, ob der empfangene Teil größer als 0 ist. Dann rufen wir die Methode NewPath auf, um den erstellten Pfad zu unserem FP-Baum hinzuzufügen. Vergessen wir nicht, die Ergebnisse der Ausführung der Operation zu überprüfen.
Nach einer erfolgreichen Iteration durch alle Transaktionen aus den Quelldaten wird die Methode mit einem positiven Ergebnis beendet.
bool CAssocRules::GrowsTree(CMyTreeNode * root, matrix & bin_data, matrix &positions) { ulong rows = bin_data.Rows(); for(ulong r = 0; r < rows; r++) { matrix path = CreatePath(bin_data.Row(r), positions); ulong size = path.Cols(); if(size <= 0) continue; if(!NewPath(root, path)) return false; } //--- return true; }
Fassen wir nun alle oben beschriebenen Methoden in der öffentlichen Methode CreateRules zusammen. In den Methodenparametern übergeben wir eine Matrix skalarer Quelldaten (nicht binär), binäre Vektoren von Zielwerten, die Anzahl der Intervalle für die Umwandlung skalarer Werte in binäre Werte, minimale Unterstützung und minimale Konfidenz.
Im Hauptteil der Methode werden zunächst die empfangenen Quelldaten geprüft. Wir prüfen in erster Linie die Übereinstimmung zwischen den Dimensionen der erhaltenen Matrixvektoren und der Anzahl der Intervalle, die größer als 0 sein muss.
Nach dem Prüfblock werden die skalaren Quelldaten in eine binäre Form umgewandelt. Dies geschieht mit der oben beschriebenen PrepareData-Methode.
bool CAssocRules::CreateRules(matrix &data, vector &buy, vector &sell, int sections = 10, double min_sup = 0.03, double min_conf = 0.3) { if(data.Rows() <= 0 || data.Cols() <= 0 || sections <= 0 || data.Rows() != buy.Size() || data.Rows() != sell.Size()) return false; //--- matrix binary_data; if(!PrepareData(data, binary_data, buy, sell, sections)) return false;
Um auf die Ebene der relativen Einheiten zu gelangen, teilen wir die Werte der binären Matrix durch die Anzahl der Transaktionen in der Trainingsstichprobe und erstellen den FP-Baum mit der GrowsTree-Methode.
double k = 1.0 / (double)(binary_data.Rows()); if(!GrowsTree(GetPointer(m_cRoot), binary_data * k, m_mPositions)) return false;
Nachdem wir den FP-Baum erstellt haben, können wir mit der Erstellung der Regeln fortfahren. Zunächst bereiten wir einen Vektor zum Schreiben von Stützen und eine Matrix zum Schreiben von Pfaden vor. Dann rufen wir die Methode Mining unseres FP-Baums auf , um alle Pfade mit dem Merkmal Kaufen zu finden.
vector supports = vector::Zeros(binary_data.Cols()); binary_data = matrix::Zeros(0, binary_data.Cols()); if(!m_cRoot.Mining(supports, binary_data, m_cBuyRules.ID(),min_conf)) return false;
Nachdem wir alle Pfade erfolgreich extrahiert haben, setzen wir die Unterstützung für das Merkmal "Kaufen" zurück und entfernen es damit aus der Verarbeitung aller Pfade. Wir sortieren auch private Unterstützungen in absteigender Reihenfolge. Wir rufen die Methode CreatePositions auf und schreiben das Ergebnis in die Matrix m_BuyPositions. Wenn wir nach dem Sortieren der Merkmale immer noch in der Lage sind, Regeln zu erstellen (die sortierte Matrix enthält immer noch Merkmale, die als Antezedens für die Regel verwendet werden können), dann rufen wir die Baumwachstumsmethode auf und geben die zuvor ausgewählten Pfade in sie ein.
Als Ergebnis dieser Operationen erhalten wir einen privaten Regelbaum mit einer Wurzel am Knoten m_cBuyRules.
supports[m_cBuyRules.ID()] = 0; m_BuyPositions = CreatePositions(supports, min_sup); if(m_BuyPositions.Rows() > 0) if(!GrowsTree(GetPointer(m_cBuyRules), binary_data, m_BuyPositions)) return false;
Auf ähnliche Weise erstellen wir einen Regelbaum für Sell-Merkmale.
supports = vector::Zeros(binary_data.Cols()); binary_data = matrix::Zeros(0, binary_data.Cols()); if(!m_cRoot.Mining(supports, binary_data, m_cSellRules.ID(),min_conf)) return false; supports[m_cSellRules.ID()] = 0; m_SellPositions = CreatePositions(supports, min_sup); if(m_SellPositions.Rows() > 0) if(!GrowsTree(GetPointer(m_cSellRules), binary_data, m_SellPositions)) return false; //--- m_cRoot.Clear(); //--- return true; }
Nachdem wir alle Regeln ausgewählt haben, löschen wir das FP-Quellbaumobjekt, um Computerressourcen freizugeben. Dann verlassen wir die Methode mit einem positiven Ergebnis.
Die Methode „Probability“ (Wahrscheinlichkeit) wurde für den praktischen Gebrauch entwickelt. Als Parameter erhält die Methode einen skalaren Vektor von Quelldaten und Zeiger auf zwei Variablen vom Typ double, die zur Speicherung des jeweiligen Vertrauensmusters verwendet werden. Der Methodenalgorithmus verwendet alle oben genannten Methoden. Sie können sie in der Anlage sehen.
Der gesamte Code aller Klassen und Methoden befindet sich in der Anlage.
3. Tests
Ich habe einen Expert Advisor (assocrules.mq5) erstellt, um die Klasse mit echten Daten zu testen. Der EA wurde unter Einhaltung aller in früheren Tests verwendeten Parameter getestet. Ich kann nicht sagen, dass die Methode alle Fraktale fehlerfrei ermittelt hat. Aber der erstellte EA zeigte interessante Ergebnisse, die im folgenden Screenshot zu sehen sind.
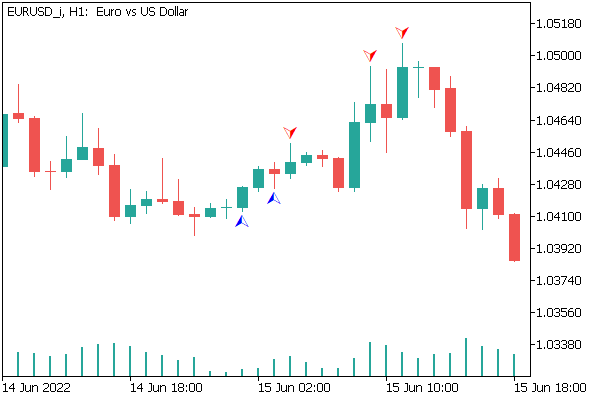
Schlussfolgerung
In diesem Artikel haben wir eine andere Art von Problemen gewidmet, die durch unüberwachte Lernmethoden gelöst werden: Assoziationsregel-Mining. Wir haben eine Klasse für die Erstellung von Assoziationsregeln unter Verwendung des FP Growth-Algorithmus erstellt. Es wurde mit einem Expert Advisor getestet, der interessante Ergebnisse zeigte. Daraus lässt sich schließen, dass solche Algorithmen zur Lösung praktischer Probleme im Handel verwendet werden können.
Liste der Referenzen
- Neuronale Netze leicht gemacht (Teil 14): Datenclustering
- Neuronale Netze leicht gemacht (Teil 15): Datenclustering mit MQL5
- Neuronale Netze leicht gemacht (Teil 16): Praktische Anwendung des Clustering
- Neuronale Netze leicht gemacht (Teil 17): Dimensionsreduktion.
- Neuronale Netze leicht gemacht (Teil 18): Assoziationsregeln
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | assocrules.mq5 | Expert Advisor | Expert Advisor zum Trainieren und Testen des Modells |
| 2 | AssocRules.mqh | Klassenbibliothek | Klassenbibliothek für die Organisation des FP Growth Algorithmus |
| 3 | MyTreeNode.mqh | Klassenbibliothek | Klassenbibliothek zur Organisation von Baumknoten |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/11141
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Lernen Sie, wie man ein Handelssystem mit dem DeMarker entwickelt
Lernen Sie, wie man ein Handelssystem mit dem DeMarker entwickelt
 Erfahren Sie, wie Sie ein Handelssystem anhand des Relative Vigor Index entwickeln können
Erfahren Sie, wie Sie ein Handelssystem anhand des Relative Vigor Index entwickeln können
 Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 21): Neues Auftragssystem (IV)
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 21): Neues Auftragssystem (IV)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo Lehrer
ich habe versucht, das Programm zu starten, aber ohne Erfolg.
Fragen Sie nach den Parametern, die zum Ausführen verwendet werden.
Mit freundlichen Grüßen
Anan Seti
Hallo Lehrer
ich habe versucht, das Programm zu starten, aber ohne Erfolg.
Fragen Sie nach den Parametern, die zum Ausführen verwendet werden.
Mit freundlichen Grüßen
Anan Seti
Sie haben EA im Tester ausgeführt. Zum Lernen müssen Sie den EA in Echtzeit ausführen. Machen Sie sich keine Sorgen. EA erstellt keinen Auftrag.
Hallo Dmitriy
Dieser Code kompiliert gut, aber wenn ich den EA auf einen Graphen setze, schließt der MT5 diesen EA ohne Fehler aus
2022.12.01 10:24:01.046 Experten Experte assocrules(EURUSD,H1) erfolgreich geladen
2022.12.01 10:24:03.843 Experten Experten-Assocrules (EURUSD,H1) entfernt
Ich habe alle Dateien in allen Verzeichnissen aktualisiert, aber ich konnte diesen EA nicht ausführen
Danke, dass Sie
Rogerio
Hallo Dmitrij
Dieser Code kompiliert gut, aber wenn ich den EA auf einen Graphen setze, schließt der MT5 diesen EA ohne Fehler aus
2022.12.01 10:24:01.046 Experten Experte assocrules (EURUSD,H1) erfolgreich geladen
2022.12.01 10:24:03.843 Experten Experten-Assocrules (EURUSD,H1) entfernt
Ich habe alle Dateien in allen Verzeichnissen aktualisiert, aber ich konnte diesen EA nicht ausführen
Danke, dass Sie
Rogerio
Hallo Rogerto.
Es ist nur ein Demo-EA. Und es werden keine Aufträge erstellt.