您应当知道的 MQL5 向导技术（第 54 部分）：搭配混合 SAC 和张量的强化学习

MetaTrader 5 — 积分 | 1 十二月 2025, 09:23

257

Stephen Njuki

概述

软性参与者-评论者（SAC）是训练神经网络时常用的强化学习算法之一。回想一下，强化学习是机器学习中一种新兴的训练方法，与监督式学习和无监督式学习并列。

回放缓冲区

回放缓冲区是强化学习中 SAC 非政策算法中很重要的组成部分，它维持过去的状态、动作、奖励、以及下一个状态和完成标志（记录是否完成、或正在进行的事件）的经验到小批量样本中用于训练。其主要目的是去相关化各种经验，令智代能够从更多样化的经验中学习，其倾向有助于提升学习稳定性、和样本效率。

在实现 SAC 时，我们能够使用 MQL5 语言，但所创建的网络训练效率不如用 Python 开源库创建的网络，像是 TensorFlow 或 PyTorch。因此，正如我们在上一篇强化学习文章中看到的，其中 Python 用来为一个基础的 SAC 网络建模，我们继续使用 Python，但这次考察如何探索和利用其张量图形。理论上，在 Python 中实现回放缓冲区有两条途径。手工或基于张量的方式。

按手动方式时，用到的是基本 Python 数据结构，像是列表或 NumPy 数组。然而，若按张量方法的深度学习框架，像是 TensorFlow 或 PyTorch，因该方式与神经网络训练流水线无缝集成，故 GPU 加速更高效。在手工方式中，回放缓冲区由 “NumPy” 数组组成，对于小规模问题这样做既简单又有效。其处理可能如下：

import numpy as np

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.actions = np.zeros((max_size, action_dim), dtype=np.float32)
        self.rewards = np.zeros(max_size, dtype=np.float32)
        self.next_states = np.zeros((max_size, state_dim), dtype=np.float32)
        self.dones = np.zeros(max_size, dtype=np.float32)
        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
             
        ...

    def sample(self, batch_size):
        idx = np.random.randint(0, self.size, size=batch_size)
        return (
            self.states[idx],
            ...

             self.dones[idx],
        )

虽然这种方式实现起来直截了当，也与我们之前 SAC 文章中所用非常相似，但或许它无法很好地扩展到更大的问题、或由 GPU 加速。

采用基于张量的方法，回放缓冲区即可用 PyTorch 亦或 TensorFlow 编码。根据我的经验（到目前为止），后者看似有点问题。我能设置一个 GPU 来运行 TensorFlow，但当需用特定 GPU 时，其所需配备的驱动链，和相关软件函数库版本的特殊性质，让人感到不知所措，不光 TensorFlow 这样，Python 也如此。

后来我试了 PyTorch，或许归功于早前有 TensorFlow 的经验，整个过程要顺畅得多。PyTorch 能将神经网络训练与 GPU 加速无缝集成，一个近百万行的数据集，投喂到一个相当复杂的一千万参数网络时，在很基础的 NVIDIA T4 上单局次大约 4 分钟就能运行完毕。我们能够用 Python 进行如下基础实现：

import torch

class ReplayBuffer:
    def __init__(self, max_size, state_dim, action_dim):
        self.max_size = max_size
        self.states = torch.zeros((max_size, state_dim), dtype=torch.float32)
        ...

        self.ptr = 0
        self.size = 0

    def add(self, state, action, reward, next_state, done):
        self.states[self.ptr] = torch.tensor(state, dtype=torch.float32)
        self.actions[self.ptr] = torch.tensor(action, dtype=torch.float32)
        self.rewards[self.ptr] = torch.tensor(reward, dtype=torch.float32)
        self.next_states[self.ptr] = torch.tensor(next_state, dtype=torch.float32)
        self.dones[self.ptr] = torch.tensor(done, dtype=torch.float32)
        self.ptr = (self.ptr + 1) % self.max_size
        self.size = min(self.size + 1, self.max_size)

    def sample(self, batch_size):
        idx = torch.randint(0, self.size, (batch_size,))
        return (
            self.states[idx],
            self.actions[idx],
            self.rewards[idx],
            self.next_states[idx],
            self.dones[idx],
        )

该方法非常高效，因为它直接集成了 PyTorch 的自动分级，和优化流水线。故汇总手工和张量之间的比较，手工方式优点是实现简单，不依赖深度学习框架。缺点则是，其它方面的可扩展性有限，且无 GPU 加速。基于张量的方式，优点是能与神经网络、GPU 加速、和大规模问题无缝集成，缺点是需要熟知 TensorFlow/PyTorch 的复杂实现。

如是结果，在挑拣方案时通常应考虑问题的规模和硬件可用性；对于大规模问题、或 GPU 训练，基于张量的方法则更受青睐。进而，如果您的环境有像图像那样可变大小的状态，那么基于张量的方法就更适合。此外，SAC 还可以通过优先经验回放（PER）来强化，该回放缓冲区抽样基于缓冲区中每个状态的相对重要性，通过衡量时差的误差、或其它关键量值。基于张量的回放缓冲区的 PER 实现更容易，因为它允许高效的优先级更新和采样。

如任何代码清单一样，部署前先行测试和调试始终是个好主意，通过回放缓冲区，能够通过添加仿造数据，并验证采样工作是否正确来实现。此外，还应确保回放缓冲区能处理如空载、或满载、等边际情况。可用 Python 断言、或单元测试来验证功能。一旦回放缓冲区准备就绪，接下来就是在 SAC 训练循环中集成每个训练步骤后的存储经验，然后小批量抽样进行更新。

设置回放缓冲区时通常需要权衡，因为它应足够大，以便存储多样化的经验，但又不能过大，以免拖慢采样过程。通过使用高效的数据结构，如 PyTorch 张量，可以优化回放缓冲区，从而提升速度和内存；避免不必要的数据复制；以及为缓冲区预分配内存。剖析回放缓冲区，有助于辨别和解决性能瓶颈。

故总体上，一个实现良好的 SAC 缓冲区，对于 SAC 和许多非政策算法的成功至关重要。它通过提供多样性、去相关性的经验，确保训练的稳定和高效。

评论者网络

在 SAC 算法中，评论者网络在表述当前环境状态，及参与者选择下一步动作时，估算 Q-值（或状态动作值，或参与者下一步采取的动作）。SAC 会结合两个这样的评论者网络，以降低偏差高估，并提升学习稳定性。作为一个神经网络，其输入为参与者网络的动作分布概率，以及环境状态“坐标”的2个压缩数据集，选择使用 NumPy 亦或张量取决于问题规模（由网络大小、和训练数据体量来定义），以及硬件可用性。

按照手工非张量实现评论者网络，NumPy 在矩阵运算和梯度更新中都能派上用场。若网络每层大小不超过 15 层，或用于教育和示范目的，这可能是一个可行的解决方案。按该方式，前向和后向传播通验都经手工实现，这可能容易出错，且在扩充大规模训练数据集时效率不佳。这是手工 Python 实现可能的样子：

import numpy as np

class CriticNetwork:
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        self.state_dim = state_dim
        self.action_dim = action_dim
        self.hidden_dim = hidden_dim

        # Initialize weights and biases
        self.W1 = np.random.randn(state_dim + action_dim, hidden_dim)
        self.b1 = np.zeros(hidden_dim)
        self.W2 = np.random.randn(hidden_dim, hidden_dim)
        self.b2 = np.zeros(hidden_dim)
        self.W3 = np.random.randn(hidden_dim, 1)
        self.b3 = np.zeros(1)

    def forward(self, state, action):
        x = np.concatenate([state, action], axis=-1)
        x = np.maximum(0, x @ self.W1 + self.b1)  # ReLU activation
        x = np.maximum(0, x @ self.W2 + self.b2)  # ReLU activation
        q_value = x @ self.W3 + self.b3
        return q_value

    def update(self, states, actions, targets, learning_rate=1e-3):
        # Manual gradient descent (simplified)
        q_values = self.forward(states, actions)
        error = q_values - targets
        # Backpropagation and weight updates (not shown for brevity)

如前所述，这种方式无法扩展大型网络或数据集，且缺乏 GPU 加速。另一方面，如果我们选择使用张量，配合 PyTorch，我们就能驾驭自动微分、和 GPU 加速。这些属性对于大规模问题、及生产层面的实现来说是有利的预兆。一个非常基础的编码示例如下：

import torch
import torch.nn as nn
import torch.nn.functional as F

class CriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(CriticNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, 1)

    def forward(self, state, action):
        x = torch.cat([state, action], dim=-1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        q_value = self.fc3(x)
        return q_value

尤其是 PyTorch，随同少量关键函数库，分别是网络优化的 “torch.optim”，和设置网络架构的 “torch.nn”。这一切都以高度可扩展、且高效的方式实现。

故此，如上方示例所示，手工方式是可行的，且其提供了简单且无需依赖深度学习框架的优点，但其无法扩展、甚至无法有效利用 GPU 是个阻碍。

在评论者网络中使用张量也会带来类似的优缺点，正如前面回放缓冲区所涵盖的，这大致意味着，手工方法往往适合在问题规模非常小的状况下使用，且其重点是示范、或“教授”神经网络的复杂性。在实践中，针对已分享的原因，张量更实用。

如果我们回忆一下，SAC 网络用到两个评论者网络（通常称为 Q1 和 Q2）来减轻高估偏差。目标 Q值由此判定为网络产生的两个 Q-值中的最小者。作为示范，评论者网络像是参与者网络输出的一部分，会产生一个向量，并估算每个可用动作的奖励。

故此，在每个这样的向量中，肯定是最高数值的索引/动作会预测出最高的奖励。评论者网络的主要目的是保守地判定反向传播到参与者网络的梯度。

在参与者网络更新期间，计算目标函数的梯度，并从两个 Q-值中的最小值反向传播至参与者网络。最小选择确保依据评论者高估误差更具健壮性的动作来优化参与者。

这些为更新参与者网络提供目标函数梯度的评论者网络，也需要训练。但既然它们是在估算来自动作的未来奖励，它们的训练目标是如何确立的？答案是对于评论者更新，SAC 并未直接取用两个 Q-值中的最小值。取而代之，每个评论者（Q1 和 Q2）执行更新时，都使用软性贝尔曼（Bellman）方程推导的目标。

class DoubleCriticNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(DoubleCriticNetwork, self).__init__()
        self.Q1 = CriticNetwork(state_dim, action_dim, hidden_dim)
        self.Q2 = CriticNetwork(state_dim, action_dim, hidden_dim)

    def forward(self, state, action):
        q1 = self.Q1(state, action)
        q2 = self.Q2(state, action)
        return q1, q2

此外，SAC 中的目标网络是另一组分离的网络（分别对应每个评论者 Q1 和 Q2），即用于计算这些评论者网络反向传播中关键的目标 Q-值。它们自己通过多重平均法慢慢更新，以确保训练期间的稳定性。目标网络的使用源于需要为贝尔曼方程提供一个稳定的目标，否则评论者网络的 Q-值估算将因 Q-值与目标之间的反馈环路而发散或振荡。

for target_param, param in zip(target_critic.parameters(), critic.parameters()):
    target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)
```
where `tau` is the polyak averaging coefficient (e.g., 0.005).

对批评者来说，损失函数将是预测 Q-值与目标 Q-值之间的均方误差（MSE），由贝尔曼方程借助上述目标网络判定。

target_q_value = reward + (1 - done) * gamma * min(Q1_target(next_state, next_action), Q2_target(next_state, next_action))
```
where `gamma` is the discount factor.

故此，为了训练评论者，会从回放缓冲区抽取一个小批量，并计算目标 Q-值。据此，评者论网络将按梯度下降进行更新。如 Adam 这样的优化器可用来提高训练效率。

optimizer = torch.optim.Adam(critic.parameters(), lr=learning_rate)

执行调试和测试可以投喂仿造输入，并验证输出形状和数值。应确保网络能够针对小数据集过度拟合。如前所述，Python 断言可用来验证输入数据。评论者网络集成在 SAC 训练环路中，计算 Q-值、更新评论损失、并同步目标网络。确保评论网络与演员网络和值网络同步更新非常重要，这也是为什么张量，尤其是GPU的使用在这里非常重要。

评论者网络还可以采用一些额外的优化提示，首先包括批量归一化、或层归一化。其次，试验不同的激活函数，如 ReLU 或 Leaky，这样能根据测试数据和所用网络的性质产生不同结果。此外，学习率和网络深度等超参数也能进行优调。训练期间对评论者损失的监测，对于发现过度拟合和不稳定性等问题非常重要。

总之，评论者网络是 SAC 的关键组成部分，对于估算 Q-值、以及指导参与者的政策更新必不可少。一个完善的评论者网络确保了稳定高效的学习。

价值网络

这个网络也称为状态值函数，是 SAC 的一个可选部分，我们可以选择使用它。其目的是利用软性价值函数，估算当前政策下状态的预期累计奖励。而价值网络的使用是“可选”的，如果实现得当，它会带来许多优势。首先，由于软性价值函数明确协同熵，它鼓励政策更高效、更有效地探索。软性值函数动作倾向于为训练提供更平滑的目标，其有助于稳定学习过程。

这种稳定性在面对高维输入数据时非常有益（输入数据向量较大，大小 > 10），或动作空间是连续性的（例如动作选项为（0.14，0.67，1.51），而非（买入、卖出、持有）），或当数据环境面临多个局部最优解（即多种不同网络权重配置，在不同数据集训练时似乎都能获得不错结果的状况或环境，但这些权重配置都无法在更广阔的数据集上普适或维持其性能）。

总结 SAC 中的价值网络，它们用于估算状态的预期回报，独立于任何动作，通过提供软性目标，帮助降低 Q-值估算的方差。张量与手工对比，论调与上面给出的评论者网络非常相似。大多数现代 SAC 网络不实现价值网络，而是依赖额外的 2 个目标网络，来辅助两个评论者网络设定训练目标。

除了使用上述单一值网络来温和调节评论者网络训练目标外，我们还能使用两个数值的网络。在这种状况下，价值网络和价值目标网络都被用来估算价值函数，其预测来自任一给定状态的预期回报（累计回报）。特别是目标值网络用于稳定训练，不仅在该情况下，也适用于深度 Q-网络。作为价值网络的复本，其更新频率较低，并为训练提供了稳定的目标。

参与者网络

这是主网络，也称为政策网络。它取环境状态作为输入，而输出是两个向量：均值和标准差，作为覆盖动作的概率分布参数，其可用于随机采样。两个评论者网络、其配套目标网络以及价值网络（如果用到）都有助于该网络的反向传播和训练。

作为一个网络，鉴于张量在 SAC 中的核心作用，我们理应从其应用中获益良多。此外，由于上述所有网络都与该网络 — 参与者网络的训练相关，因此利用 GPU 并行化，允许这些多个网络并发训练是值得探索的，因为这会带来极大的效率。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributions as dist

class ActorNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(ActorNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc_mean = nn.Linear(hidden_dim, action_dim)
        self.fc_log_std = nn.Linear(hidden_dim, action_dim)

    def forward(self, state):
        x = F.relu(self.fc1(state))
        x = F.relu(self.fc2(x))
        mean = self.fc_mean(x)
        log_std = self.fc_log_std(x)
        return mean, log_std

    def sample_action(self, state):
        mean, log_std = self.forward(state)
        std = torch.exp(log_std)
        normal = dist.Normal(mean, std)
        action = normal.rsample()  # Reparameterization trick
        return torch.tanh(action), normal.log_prob(action).sum(dim=-1, keepdim=True)

正如我们在上一篇 SAC 文章中提到的，参与者网络输出两个关键“向量”数据：均值、以及高斯分布的标准差。这两者结合起来，随机行事判定下一步动作，这对于连续动作空间中的探索和优化非常重要。均值代表作用扩散、或分布的中心，而标准差则控制分布的扩散或随机性。这两者定义了一个高斯分布，可以从中选择动作。下面的 Python 代码帮助实现了这一点。

import torch

def select_action(mean, log_std):
    """
    Given the SAC actor's output (mean and log_std), this function selects an action index.
    
    Args:
        mean (torch.Tensor): Mean of the action distribution, shape (n_actions,)
        log_std (torch.Tensor): Log standard deviation, shape (n_actions,)

    Returns:
        int: The index of the selected action.
    """
    std = log_std.exp()  # Convert log standard deviation back to standard deviation
    ....  
    return selected_index

# Example inputs
mean = torch.tensor([0.2, -0.5, 1.0, 0.3])  # Example mean values for 4 actions
log_std = torch.tensor([-1.0, -0.7, -0.2, -0.5])  # Example log std values

# Select action
action_index = select_action(mean, log_std)
print("Selected Action Index:", action_index)

实际上，尽管我们必须在 MQL5 中运行这个函数，因为在用 Python 训练模型后，它会导出为 ONNX 文件，而作为 ONNX，它的任何前向通验输出都与 Python 训练时类似。故此，由于在 MQL5 中会接收这两个输出，因此该动作选择函数也必须含在 MQL5 之中。

这两个输出定义了一个高斯分布、或正态分布，可从中选择动作。动作的选择是随机进行的，以便鼓励探索，令智代在给定状态下不会始终选择相同的动作。在反向传播时，为了提高效率，采用了重新参数化，令梯度能够贯穿采样过程流动。

另外，来自于我们上面提到的 Python 函数，由于现世应用中的大多数动作都有作用域或边界，SAC 会应用 Tanh 函数来压缩采样动作，令其范围在 -1 到 +1 之间。这确保了动作在可控范围内，同时避免过程的随机性质。

智代

SAC 中的智代，我们在此处以 Python 表述智代类，结合了政策优化（参与者网络）、和价值函数近似（两个配对的评论者网络：价值网络、和目标价值网络）。该智代应具备较高的采样效率，并能够处理连续动作空间。这是因为它不仅将这些网络汇聚在一起，还有回放缓冲区，目标是学习“最优政策”，或适合参与者网络的权重和乖离。

鉴于智代的高级概览性质，如果要执行高效网络训练，张量或许是必不可少的。下面是 Python 如何行事的运作分解：

import torch
import torch.nn.functional as F
import torch.optim as optim

class SACAgent:
    def __init__(self, state_dim, action_dim, hidden_dim=256, replay_buffer_size=1e6, batch_size=256, gamma=0.99, tau=0.005, alpha=0.2):
        self.state_dim = state_dim
        ...

        self.alpha = alpha

        # Initialize networks and replay buffer
        self.actor = ActorNetwork(state_dim, action_dim, hidden_dim)
        ....

        self.value_optimizer = optim.Adam(self.value_network.parameters(), lr=3e-4)

    def select_action(self, state):
        state = torch.FloatTensor(state).unsqueeze(0)
        action, _ = self.actor.sample_action(state)
        return action.detach().numpy()[0]

    def update(self):
        # Sample a batch from the replay buffer
        states, actions, rewards, next_states, dones = self.replay_buffer.sample(self.batch_size)

        # Convert to tensors
        states = torch.FloatTensor(states)
        ...

        dones = torch.FloatTensor(dones).unsqueeze(1)

        # Update value network
        target_value = self.target_value_network(next_states)
        ...

        # Update critic networks
        q1_value = self.critic1(states, actions)
             
        ...

        self.critic2_optimizer.step()

        # Update actor network
        new_actions, log_probs = self.actor.sample_action(states)
             
        ...

        self.actor_optimizer.step()

        # Update target networks
        for target_param, param in zip(self.target_value_network.parameters(), self.value_network.parameters()):
            target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)

由于我们正用张量，配合 PyTorch，重点要强调，如果有 GPU 设备，手工分配设备能极大地确保张量的高效运行和执行。

环境

环境是训练和目标/动作数据集定义之所在。它本质上定义了智代试图解决的问题，基于智代动作，为其提供状态、奖励和终止信号。环境能够手工实现（即从第一原则出发），也可以通过继承，使用像 OpenAI 的 Gym 这样的函数库来实现标准化环境。基于张量的环境可实现如下：

import torch

class TensorEnvironment:
    def __init__(self):
        self.state_space = 4  # Example: state dimension
        self.action_space = 2  # Example: action dimension
        self.state = torch.zeros(self.state_space)  # Initial state

    def reset(self):
        self.state = torch.randn(self.state_space)  # Reset to a random state
        return self.state

    def step(self, action):
        # Define transition dynamics and reward function
        next_state = self.state + action  # Simple transition
        ...

        self.state = next_state
        return next_state, reward, done, {}

    def render(self):
        print(f"State: {self.state}")

然后使用循环收集经验，并定期更新智代：

for episode in range(num_episodes):
    state = env.reset()
    episode_reward = 0
    for step in range(max_steps):
        action = agent.select_action(state)
        next_state, reward, done, _ = env.step(action)
        agent.replay_buffer.add(state, action, reward, next_state, done)
        state = next_state
        episode_reward += reward
        if len(agent.replay_buffer) > batch_size:
            agent.update()
        if done:
            break
    print(f"Episode {episode}, Reward: {episode_reward}")

向导汇编与测试

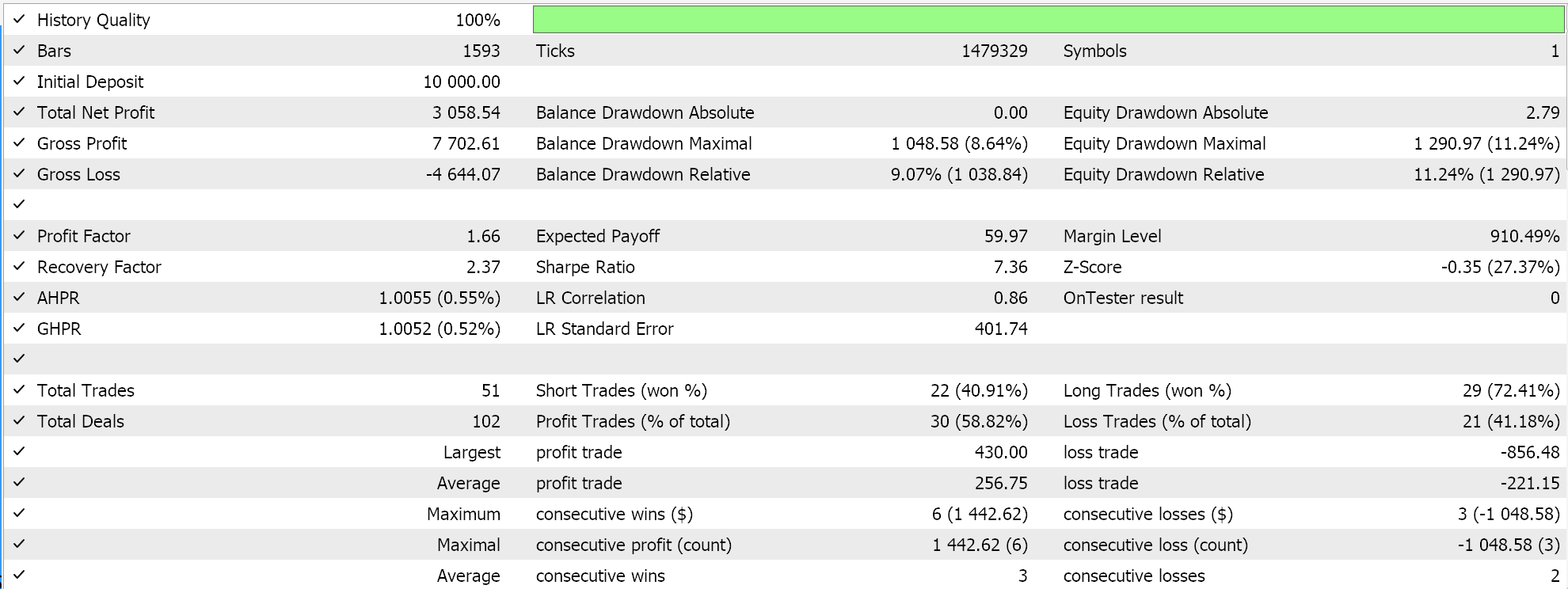
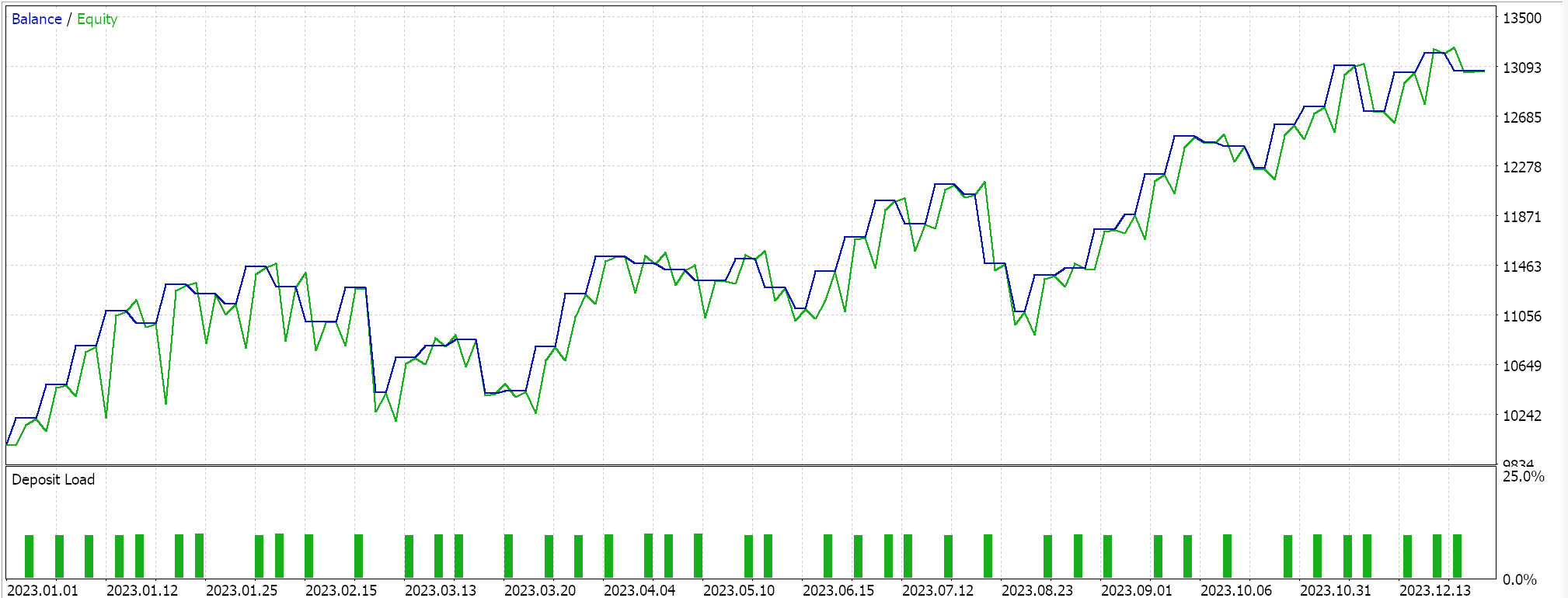
我们测试基于张量的混合 SAC，除了拥有参与者网络、和两个评论者网络外，还用到价值网络、和目标值网络来替代训练评论者的两个目标网络。我们依据 EURUSD 货币对 2023 年 H4 时间帧。

TensorFlow 和 PyTorch 不仅允许模型训练，还支持交叉验证。TensorFlow 允许把验证 x 和 y 的数据值传递给适应度函数，而 PyTorch 则本质上允许将相同数据传递给 data_loader。测试运行 MQL5 编译的智能系统，不执行交叉验证（或推断），为我们给出以下 EURUSD 覆盖 2023 年的结果：

我们取上一篇 SAC 文章所述的、由 Python 导出的 ONNX 模型，并将其导入 MQL5。我们曾与 5 个神经网络打过交道，但只有一个能做出我们需要的预测，其它 4 个则只是帮助反向传播。我们需要并导出的网络是参与者网络。尽管该网络的输出不是一个，而是两个向量，正如前面提到的。均值和标准差。因此，在我们于 MQL5 中使用 ONNX 模型之前，需要准确定义该模型的输出形状。输入形状很直接了当。我们在 MQL5 中设置如下形状：

//+------------------------------------------------------------------+
//| Validation arch protected data.                                  |
//+------------------------------------------------------------------+
bool CSignalSAC::ValidationSettings(void)
{  if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   if(m_period != PERIOD_H4)
   {  Print(" time frame should be H4 ");
      return(false);
   }
   if(m_actor_handle == INVALID_HANDLE)
   {  Print("Actor OnnxCreateFromBuffer error ", GetLastError());
      return(false);
   }
   // Set input shapes
   const long _actor_in_shape[] = {1, __STATES};
   // Set output shapes
   const long _actor_out_shape[] = {1, __ACTIONS};
   if(!OnnxSetInputShape(m_actor_handle, ONNX_DEFAULT, _actor_in_shape))
   {  Print("Actor OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 0, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
   if(!OnnxSetOutputShape(m_actor_handle, 1, _actor_out_shape))
   {  Print("Actor OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//read best weights
//--- ok
   return(true);
}

这在我们自定义信号类的验证函数中处理，因为 ONNX 模型只在这些形状被准确定义时才会运行。新读者可以在这里和这里找到如何从自定义信号 *.*mqh 文件汇编智能系统的指南。

结束语

我们以 Python 并借助张量，实现了软性参与者-评论者强化学习算法。张量在机器学习中至关重要，因为它们在训练模型时能带来巨大的效率提升，这一层面对交易者尤为重要。训练数据集的规模、以及对更复杂网络的需求，往往导致训练过程变慢。因此，这一倒退不仅能通过由张量来解决，还可利用 GPU 的强大性能来实现。

名称	描述
hybrid_sac.mq5	向导汇编的智能系统，头文件显示所用文件
SignlWZ_54.mqh	自定义信号类文件
model.onnx	ONNX 网络文件

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/17159

附加的文件 |

下载ZIP

model.onnx (271.1 KB)

SignalWZ_54.mqh (8.44 KB)

hybrid_sac.mq5 (6.24 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

前往讨论

百年数学函数如何革新您的交易策略？

本文聚焦R德马赫（Rademacher）函数与沃尔什（Walsh）函数。探讨如何将这两类诞生于20世纪初的数学工具应用于金融时间序列分析，并揭示其在交易策略中的创新应用场景。

圆搜索算法（CSA）

本文提出一种基于圆几何特性的新型元启发式优化算法——圆搜索算法（CSA）。该算法通过模拟切线方向上的点移动机制，在解空间中实现全局探索与局部开发的协同优化。

在 IBM 量子计算机上分析所有价格变动选项

我们将使用 IBM 的量子计算机来发现所有价格变动选项。听起来像科幻小说？欢迎来到用于交易的量子计算世界！

在MQL5中创建交易管理面板（第九部分）：代码组织（5）：分析面板（AnalyticsPanel）类

在本文中，我们将探讨如何获取实时市场数据和交易账户信息，执行各种计算，并将结果展示在自定义面板上。为此，我们将深入开发一个分析面板（AnalyticsPanel）类，该类封装了所有这些功能，包括面板创建功能。这项工作是我们正在进行的新建管理面板智能交易系统（EA）扩展工作的一部分，旨在运用模块化设计原则和代码组织的最佳实践来引入高级功能。