您应当知道的 MQL5 向导技术（第 55 部分）：配备优先经验回放的 SAC

神经网络模型日益复杂，受我们处理海量数据能力的驱动。传统机器学习的效率陷入困顿，而神经网络，如 DeepSeek、Grok 和 ChatGPT 等平台，则提供了强力解决方案。

然而，训练这些模型存在挑战，尤其是在历史数据有限的情况下。过度拟合是一个主要问题，在于模型学习噪声来替代有意义形态的风险。传统训练往往优先损失函数最小化，这可能导致普适能力不佳。

强化学习（RL）通过平衡利用（优化权重）和探索（测试替代方案）来解决这个问题。优先经验回放（PER）等技术强化了学习效率，缓解交易等领域中数据稀缺问题，其中月度经济数据点有限。

强化学习的关键考虑因素包括设计有效的奖励函数、选择正确的算法，以及在基于数值的（如 Q-学习、DQN）和基于政策的方法（如 PPO、TRPO）之间做出选择。参与者-评论者方法（如 A3C、SAC）在稳定性和效率之间取得了平衡。政策性方法（PPO、A3C）确保稳定学习，而非政策方法（DQN、SAC）则最大化数据效率。

强化学习的适应性令其成为机器学习通路中宝贵的补充，填补了传统方式。在据有限数据训练复杂模型时，优先权重更新压倒损失最小化，促成更好佳普适性和健壮性。

优先经验回放

优先经验回放（PER）缓冲区和典型的回放缓冲区（针对随机抽样）两者都在强化学习中用到，并配合非政策算法如 DQN 和 SAC，因为它们允许存储和抽样以往的经验。PER 不同于典型的回放缓冲区，体现在以往经验的优先和抽样。 

在典型的回放缓冲区内，会均匀且随机地抽样经验，这意味着任何以往经历都会被等概率选中，无关其对学习过程的重要性或相关性。遵照 PER，以往的经验会基于其“优先级”抽样，这一属性往往按时态差值误差的量级来量化。这个误差可作为学习潜力的代表。每个经验都会被赋予一个误差值，经验值越高就会被更频繁地抽样。这种优先级能够利用比例或基于排位的方式实现。

典型的回放缓冲区也不会引入或使用任何乖离。PER 会这样做，这可能会不公平地扭曲学习过程，这就是为何要纠正这一点，PER 采用重要性抽样权重来调整每个所抽经验的影响。因此典型的回放缓冲区抽样效率更高，因为它们在后台完成的事情远少于 PER。另一折面，PER 提供了更专注、更具建设性的学习，而典型的缓冲区则无法做到。

因此，无需多言，实现 PER 比典型的回放缓冲区更复杂；不过此处强调这一点的原因在于，PER 需要额外的类来维护常称为“总和树”的优先级队列。这种数据结构允许基于优先级更高效地进行经验抽样。PER 倾向导致更快的收敛、及更佳性能，在于它专注于对智代更具信息量、或更具挑战性的经验。

在模型中实现

我们 Python 版本的 PER 类使用初始化来验证构造函数参数，特别是模式参数。我可能记错了，但我觉得在 C/MQL5 沙箱之外它是无法做到的。我们如下声明 __init__ 函数：

        def __init__(self, capacity, alpha=0.6, beta=0.4, beta_increment=0.001, mode='proportional'):
                self.capacity = capacity
                self.alpha = alpha
                self.beta = beta
                self.beta_increment = beta_increment
                self.mode = mode

                if mode == 'proportional':
                        self.tree = SumTree(capacity)
                elif mode == 'rank':
                        self.priorities = []
                        self.data = []
                else:
                        raise ValueError("Invalid mode. Choose 'proportional' or 'rank'.")

在类中声明了一个重要函数，它应包含一个将经验添加到缓冲区的方法。我们实现如下： 

    def add(self, error, sample):
        p = self._get_priority(error)
        if self.mode == 'proportional':
            self.tree.add(p, sample)
        elif self.mode == 'rank':
            heapq.heappush(self.priorities, -p)
            if len(self.data) < self.capacity:
                self.data.append(sample)
            else:
                heapq.heappop(self.priorities)
                heapq.heappush(self.data, sample)

注意，在这种经验添补中，抽样方式是关键，因为如果我们正在基于误差比例选择经验，只需将其附加到总和树中;但如果我们基于误差量级的排位选择，则会使用导入的模块 heapq，即上述我们以样本的更新。因此，在按比例抽样中用到总和树类，而非排位。以下是如何实现：

class SumTree:
    def __init__(self, capacity):
        self.capacity = capacity
        self.tree = np.zeros(2 * capacity - 1)
        self.data = np.zeros(capacity, dtype=object)
        self.write = 0
        self.n_entries = 0

    def _propagate(self, idx, change):
        parent = (idx - 1) // 2
        self.tree[parent] += change
        if parent != 0:
            self._propagate(parent, change)

    def _retrieve(self, idx, s):
        left = 2 * idx + 1
        right = left + 1

        if left >= len(self.tree):
            return idx

        if s <= self.tree[left]:
            return self._retrieve(left, s)
        else:
            return self._retrieve(right, s - self.tree[left])

    def total(self):
        return self.tree[0]

    def add(self, p, data):
        idx = self.write + self.capacity - 1

        self.data[self.write] = data
        self.update(idx, p)

        self.write += 1
        if self.write >= self.capacity:
            self.write = 0

        if self.n_entries < self.capacity:
            self.n_entries += 1

    def update(self, idx, p):
        change = p - self.tree[idx]
        self.tree[idx] = p
        self._propagate(idx, change)

    def get(self, s):
        idx = self._retrieve(0, s)
        data_idx = idx - self.capacity + 1
        return (idx, self.tree[idx], self.data[data_idx])

定义了这个关键类后，另一个关键组件是抽样函数本身，它是 PER 类的一部分。 

def sample(self, batch_size):
        batch = []
        idxs = []
        segment = self.tree.total() / batch_size if self.mode == 'proportional' else len(self.data) / batch_size
        priorities = []

        self.beta = np.min([1., self.beta + self.beta_increment])

        for i in range(batch_size):
            a = segment * i
            b = segment * (i + 1)

            if self.mode == 'proportional':
                s = random.uniform(a, b)
                (idx, p, data) = self.tree.get(s)
                priorities.append(p)
                batch.append(data)
                idxs.append(idx)
            elif self.mode == 'rank':
                idx = random.randint(0, len(self.data) - 1)
                priorities.append(-self.priorities[idx])
                batch.append(self.data[idx])
                idxs.append(idx)

        sampling_probabilities = np.array(priorities) / self.tree.total() if self.mode == 'proportional' else np.array(priorities) / sum(self.priorities)
        is_weights = np.power(len(self.data) * sampling_probabilities, -self.beta)
        is_weights /= is_weights.max()

        return batch, idxs, is_weights

再次强调，基于比例还是基于排位抽样于此是关键考虑因素。这两种方式为每个经验分配优先级，同时考虑到 TD 误差，略有细微差别。TD 误差的量级和 TD 误差的排位。TD 误差实际上是经验输出与实际或目标值之间的差值。它从未采用原生状态来为经验加权，但会被转换为优先级值，如清单所示：

def _get_priority(self, error):
        return (error + 1e-5) ** self.alpha

正是这个优先级值的量级（对于比例抽样）、或排位（对于排位抽样），会在训练模型时用来选择经验。PER 由 Shaul 等人于 2015 年提出。经验的优先级越高会被更频繁地抽中，从而在强化学习环境中提升了抽样效率和学习速度。学习之后会更新优先级。重要性抽样权重被用来纠正因非均匀优先级抽样带来的乖离。这在上述 PER 类的抽样函数中有所指示。我们来深入探讨这两种抽样方式。

比例优先权

如上所述，优先级与时态差值误差（∣δ∣）成正比。经验 i 的优先级计算为：

pi=∣δi∣+ϵ

其中 ε 大于零，是一个小常数，确保所有经验呢的优先级不为零。因此，该经验的抽样概率为：

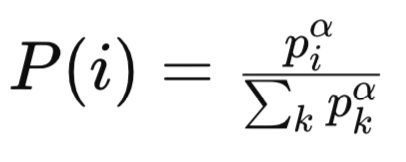
其中：

• pi 是回放缓冲区中第 i 个经验的优先级。优先级典型情况下基于该经验的时态差值（TD）误差的量级。较大 TD 误差的经验被认为更重要，并被赋予更高的优先级。

• α 是一个控制优先级程度的超参数。当（α = 0）时，所有经验均被均匀抽样（无优先级）。当（α = 1）时，抽样完全基于优先级。

• 所有 k 个优先级的 Sigma/sum 是归一化项，确保概率总和为 1。它将回放缓冲区中所有经验的优先级汇总，提升至（ α）次幂。

• P(i)  是第（i）次经验的抽样概率。它与经验的优先级（Piα）成正比，据所有优先级的总和进行归一化，提升至（α）次幂。

然后可用总和树或类似形式的数据结构，按 piα 的比例高效地抽取经验。按优先级比例的抽样分布是连续的，且与 TD 误差量级直接绑定。经验值 TD 误差越高，趋于优先级明显较高，导致尾部分布偏重。

这可能导致某些经验被过度频繁抽样（如果 TD 误差为异常值，就会成为主要问题），而另一些则因误差较小而罕被抽样。训练误差的敏感性在不同训练阶段的任务中可能有所不同，但对于 TD 误差中的异常值，比例优先级存在一定脆弱性，因为大数值可能会主导抽样分布。

举例，假设一个场景，其经验与目标差距为 1000，而其它都在 1 附近，显而易见这个大数值被抽中的次数会不成比例。这一特征可能导致对噪声或异常值经验的过度拟合，尤其是在奖励、或Q-值数据变异较大的环境之中。一种可能的缓解举措是裁剪或 TD 误差归一化。举例：

pi=min⁡(∣δi∣,δmax)+ϵ

本质上，经验的优先级设置为其自身 TD 误差与该段落内所有经历中最高 TD 误差加上一个小的非零值 ε 之间的最小值。当计算每个经验的优先级时，，若与总和树打交道时，操作时间复杂度是直接的，因每个经验都达到 O(1)。优先级的抽样和更新每次操作达到 O(log n)，其中 n 为缓冲区大小。由于没有额外的排序和排位开销，这令更新计算更高效。

比例优先级（PP）在 TD 误差在不同训练阶段变化显著的情况下，可能导致训练不稳定，因为抽样分布会快速变化。它对超参数也很敏感，故此 α 和 ε 的选择需要谨慎，从而平衡探索和利用。对于具有“良好行为”误差的任务，PP 收敛速度可能更快，这反映了学习价值，且在噪声和非静止环境中必然会遇到困境。

PP 适合 TD 误差可接受，且能直接反映学习潜力/价值的任务。在低噪声和稳定 Q-值，且 TD 误差与重要经验呈直接成正比的环境中，成效斐然。例如，Atari 游戏中奖励结构稳定，连续控制任务中伴随数值平滑函数。

由于重尾抽样分布，PP 的重要性抽样权重往往会变化。低优先级权重，则 P(i) 值较低（即抽中经验 i 的概率）也较低，这导致 wi 权重较大（调整权重即意味着校正偏乖离）。这种设置有可能带来意外的后果，比如梯度放大，并破坏训练的稳定性。因此，意味着 β 也需要被仔细调校，在偏置矫正与稳定性之间取得平衡。

总结 PP 的适宜任务，当 TD 误差表现良好、且与学习值相关时；数据环境噪声低、且 Q-值稳定；计算效率至关重要，这意味着排序和排位开销是不可接受的。超参数 α、β 和 ε 的优调有助于处理异常值，并管理不稳定性。

基于排位的优先级

在这种模式下，优先级基于 TD 误差经排序后列表中的排位索引值。经验 i 的排位，是由所有经验按时态差值误差的量级降序排列后设定的。为什么是降序？因为直观上，这样的列表能解释经验的重要性。在列表中越高，经验就越重要。其次，立足于计算，将最常被引用的经验放在堆的低索引处是合理的，因为算法无需遍历整个堆来获得大部分训练都会用到的经验。经验 i 的优先级通常计算为：

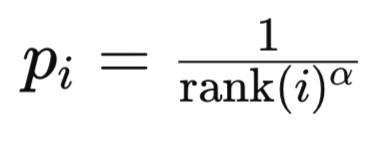
其中：

- rank(i) 是第 i 处经验的等级。

- alpha 是控制优先级强度的超参数。

该经验的抽样概率采用了与我们之前在比例优先级中讨论过的类似公式。

基于排位优先级（RP）的抽样分布是离散的，且基于排位。这令其偏向对 TD 误差的绝对尺度不那么敏感。经验的选择是基于它们的排位，而非误差量级。这就令抽样时给出的分布更为均匀，即不同经验之间的优先级差异几乎是“标准”的，因为它受控于各自的排位（如 1/1、1/2、1/3、等等...）进而，RP 不易过度拟合异常值，因为任何经验的最高优先级都固定在 1/1，无关其 TD 误差量级。尽然，这种健壮性被经验的低采样所掩盖，如果基于排位的优先级函数衰减过快，TD 误差就会非常高。

然而，除了关键经验低抽中率风险外，RP 的主要瑕疵仍是计算复杂度。整个缓冲区进行排序以判定排位，对于大小为 n 的整个缓冲区，运算的计算复杂度为 O(nlogn) 量级。实践中，能通过维护已排序的数据结构（如二叉搜索树、或堆）来避免这种排序，但计算每个经验仍需 O(logn) 运算。抽样和更新仍保持在 O(logn)，亦如按比例抽样般节省。总体而言，RP 相比 PP，计算开销明显更高。

训练 RP 时更稳定，因为抽样分布对 TD 误差量级变化的敏感度较低。因排位是相对的，且较少受噪声和异常值影响，它也倾向于随时间提供一致的抽样概率。对于有些任务，如绝对 TD 误差至关重要，或训练过程信息量更高，它收敛速度或许更慢，因为它不会激进地优先采用高量级误差。它的优调（调整超参数）也稍微容易一些，因为基于排位的优先级函数对尺度敏感度较低。

RP 适合奖励稀疏的环境，或奖励延迟、或奖励变化较大的任务。RP 是一种首选模式，即使在收敛速度较慢的情况下，稳定性和均衡抽样也至关重要。

由于 PP 和 RP 两者都引入了偏置，造成抽样方法不均匀，如上文所述、及源码中所示。其基本公式为：

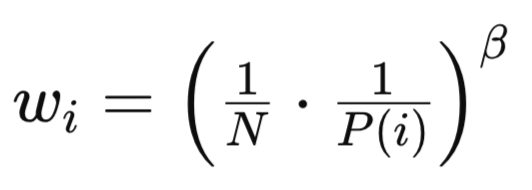
其中：

- N 是回放缓冲区中的经验总数。

- P(i) 是第 i 个经验的抽样概率。

- β（β∈[0,1]）是控制重要性抽样校正强度的超参数。

尽管公式相似，RP 和 PP 的 wi 权重在关键方面存在差异。对于 RP，重要性抽样权重更加均匀，因为分布倾斜较低。wi 值的较低变化导致训练更稳定，对 β 的敏感性降低。此外，偏差校正更容易管控，因为基于排位的分布本质上更为平衡。

测试信号类

如果我们使用上面的代码清单，并修改上一篇文章的 SAC 模型代码，用 PER 代替典型的简单回放缓冲区，我们就能训练模型，并导出一个含有权重的网络，作为 ONNX 文件。我们在上一篇文章中讲解了如何管理这种导出，这里也有关于如何从 Python 导出 ONNX 模型的指导说明。ONNX 模型可由 MQL5 所用，编译时将其嵌入为资源。 

在 MQL5 端的 IDE 中，我们的自定义信号类，严格来说与上一篇 SAC 文章中的内容无异，应当能由 MQL5 向导汇编，对于新读者，这里和这里有相关指南，教您如何实现这一点。无交叉验证测试依据 USDJPY 的 2023 年日线时间帧运行，为我们呈现以下报告：

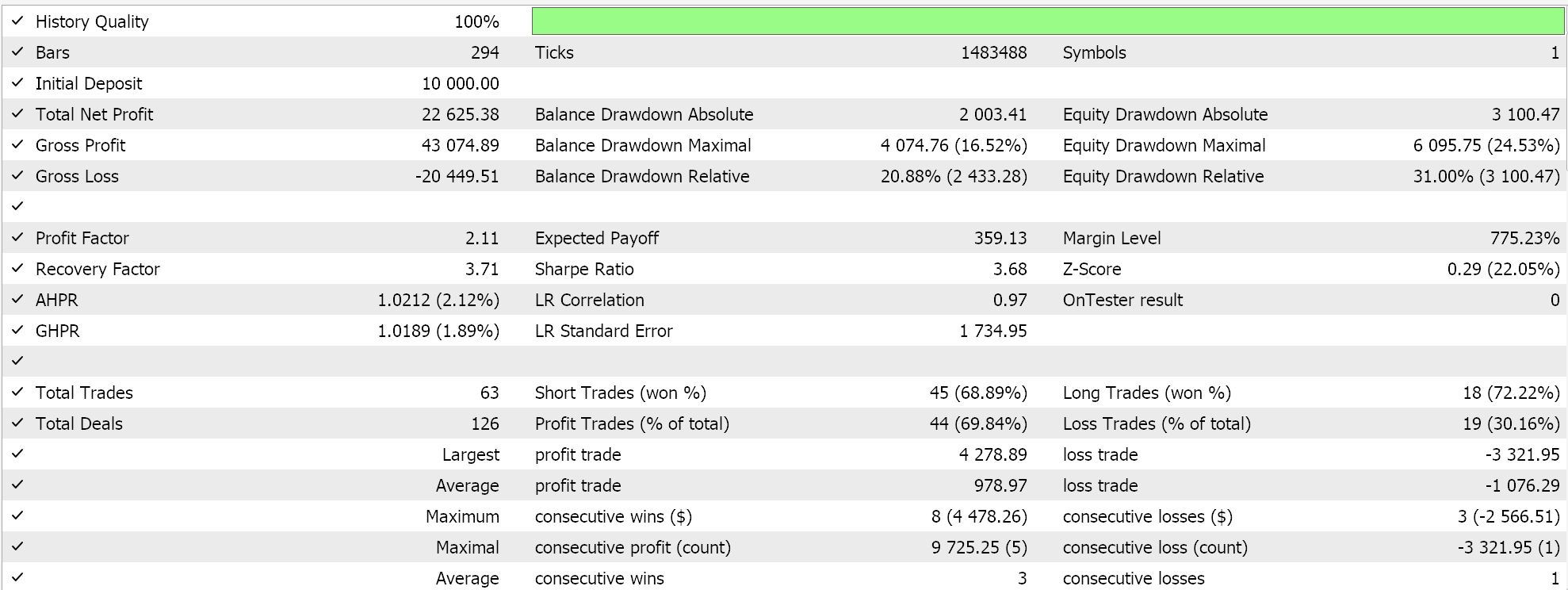
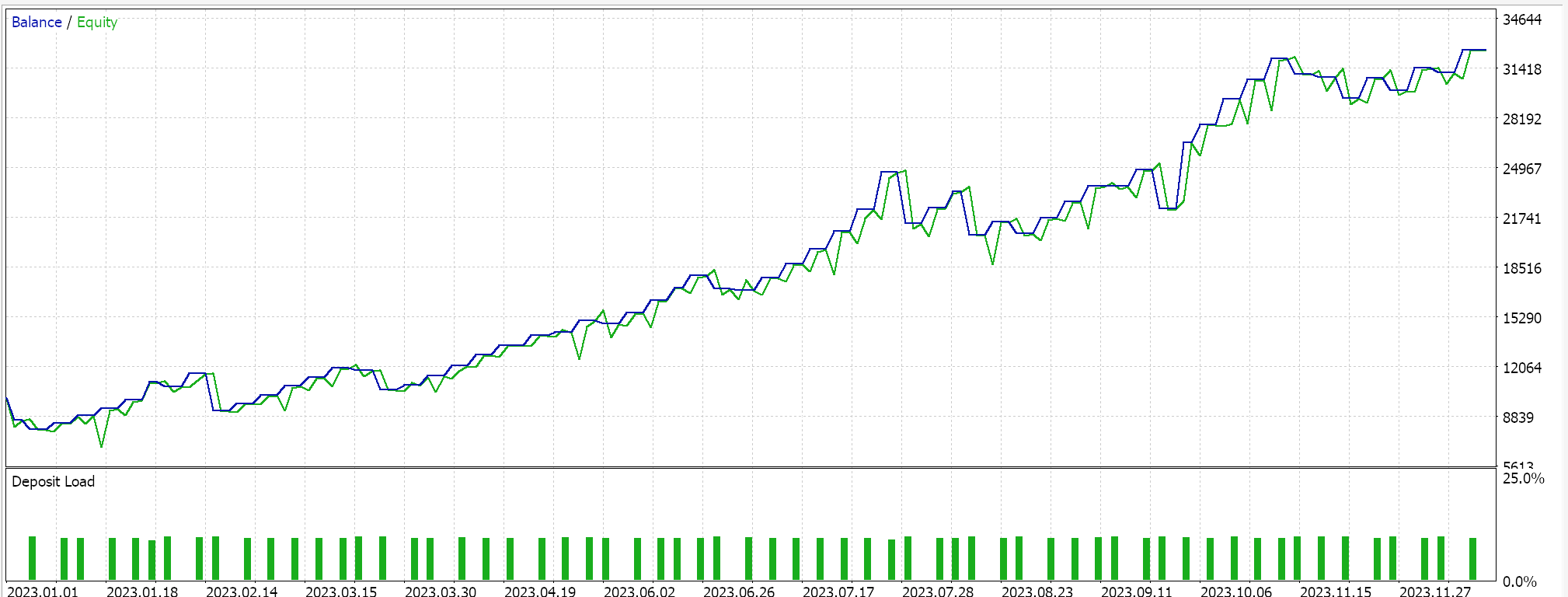
迈向未来，利用 Python 进行模型交叉验证能够非常高效地完成，故我以后大概会开始在这些文章中加入一些。然而，一如既往，过去的表现并不保证未来成果，读者在选择使用、或部署本文分享的任何系统前，始终要自行勤加努力。

结束语

我们重新审视了强化学习的案例，重申了为何在当今复杂模型和受限历史测试数据的环境中，将获得合适网络权重的过程置于低损失函数得分之上的重要性。过程很重要。为此，我们专门为强化学习设立了一个备用回放缓冲区，一个优先级经验回放缓冲区，不仅保留近期经验可供训练抽样，还令该缓冲区的样本与网络需要训练的相关性和程度成正比。

文件	描述
wz_55.mq5	向导汇编的智能系统，头文件显示所用文件
SignlWZ_55.mqh	自定义信号类文件
USDJPY.onnx	ONNX 网络文件