您应当知道的 MQL5 向导技术（第 59 部分）：配以移动平均和随机振荡器形态的强化学习（DDPG）

概述

在上一篇文章中，我们讲述了 DDPG，一种强化学习算法，并考察了其三个关键类是如何以 Python 实现的。回放缓冲区类、参与者网络类和评论者网络类。未涵盖的是 DDPG 智代类；MetaTrader 5 价格数据导入 Python；MA 和随机振荡器的函数；一个获取形态的函数，将来自两个指标的数据并拢到一个二元向量，作为监督学习网络的输入（已在早期监督学习文章中实现了 MQL5 版本）；最后是一个环境模拟环路，训练参与者和评论者网络。

所有这些都是强化学习（RL）的一部分，我们正在考察从监督学习（SL）到推理学习（IL）、或无监督学习的过渡。这些模式中的任何一种都能单方面用于训练、及模型运用，不过这些文章试图举证它们能够统合运用，来构建更有趣的东西。故此我们继续考察强化学习，并与非常重要的 DDPG 智代类打交道。

DDPG 智代

该类的核心架构和初始化能够如下定义：

def __init__(self, state_dim, action_dim):

    # Actor networks
    self.actor = Actor(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.actor_target = Actor(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.actor_target.load_state_dict(self.actor.state_dict())
    self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=LR_ACTOR)
   
    # Critic networks  
    self.critic = Critic(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.critic_target = Critic(state_dim, action_dim, HIDDEN_DIM).to(device)
    self.critic_target.load_state_dict(self.critic.state_dict())
    self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=LR_CRITIC)

    self.replay_buffer = ReplayBuffer(BUFFER_SIZE)

至关重要的组件于此是双网络架构、优化器设置、和经验管理。双架构维护一个单独的政策（参与者网络）和一个单独的数值（评论者网络），来自两个主政策和数值网络。两者都实现了目标网络，这对训练时的稳定性很重要。各自目标的初始化，按其主网络的相同权重进行。

优化器设置中，参与者网络和评论者网络分别采用了单独的 Adam 优化器。此外，正如典型情况，我们针对政策和数值网络采用单独的学习率。最后，对于经验管理，我们确保回放缓冲区存储了无政策学习的过渡，并通过修复缓冲区大小来预防内存无界限地使用。我们协同探索如下选择动作：

def select_action(self, state, noise_scale=0.1):
    state = torch.FloatTensor(state).unsqueeze(0).to(device)
    action = self.actor(state).cpu().data.numpy().flatten()
    action += noise_scale * np.random.randn(self.action_dim)
    return np.clip(action, -1, 1)

此处的关键机制是状态处理、探索策略、和设备管理。状态处理监视 NumPy 数组转换为正确的张量格式，附加批处理维度（通过取消压缩），最后确保计算在正确的设备上。

探索策略在判定性政策输出中加入了高斯噪声。噪声标尺控制探索量级，而削波维持一个有效的动作范围。设备管理确保 GPU 与 CPU 之间的高效移动（如适用）。此外，为了环境兼容性，由函数返回的最终输出是 NumPy 数组。学习更新机制如下：

def update(self):

    if len(self.replay_buffer) < BATCH_SIZE:

        return

该 if-从句作为一个更新门槛，其在收集到足够多的批量数据之前，会略过更新。这就确保了有意义的批量统计数据。两个评论者网络的更新如下：

# Sample batch

states, actions, rewards, next_states, dones = self.replay_buffer.sample(BATCH_SIZE)

# Target Q calculation
next_actions = self.actor_target(next_states)
target_q = self.critic_target(next_states, next_actions)
target_q = rewards + (1 - dones) * GAMMA * target_q

# Current Q estimation
current_q = self.critic(states, actions)

# Loss computation and backpropagation
critic_loss = nn.MSELoss()(current_q, target_q.detach())
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()

该段代码解决的关键层面是目标值计算、损失计算、和梯度管理。目标值计算利用目标网络来获得稳定的 Q-目标。它实现了Bellman 方程，终端处理时按照经验参数 ‘dones’ 的设定。GAMMA 的折扣因子控制未来奖励的重要性。

至于损失计算，判定当前 Q-值与目标 Q-值之间的均方误差。detach() 方法预防目标梯度流动（或被张量携带进行转移）。并且，应用了标准的时态差分学习。梯度管理简单地确保所有梯度都重置为零，而评论者网络的优化则是一个单独步骤。参与者网络更新也如下执行：

actor_loss = -self.critic(states, self.actor(states)).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()

政略梯度于此打交道的是经由最小化负 Q-值而来的最大化 Q-值，经由参与者和评论者网络进行微分，以及应用无对数概率的纯政策梯度方式（判定性）。目标网络的更新如下：

for target, param in zip(self.actor_target.parameters(), self.actor.parameters()):

    target.data.copy_(TAU * param.data + (1 - TAU) * target.data)

for target, param in zip(self.critic_target.parameters(), self.critic.parameters()):

    target.data.copy_(TAU * param.data + (1 - TAU) * target.data)

这种软性更新机制采用了 polyak 平均，所依 TAU 典型情况小于 1。网络权重的跟踪速度较慢，在于这样可提供周期性硬性更新的替代方案。整体上，该过程既维持了稳定性，而又允许从中学习。我们的模型需要持久。它应当能够加载之前保存的网络权重，且也能在训练后保存。我们按如下方式完成这一点：

def save(self, filename):

    torch.save({
        'actor': self.actor.state_dict(),

        'critic': self.critic.state_dict(),

        'actor_target': self.actor_target.state_dict(),

        'critic_target': self.critic_target.state_dict(),
    }, filename)


def load(self, filename):

    checkpoint = torch.load(filename)
    self.actor.load_state_dict(checkpoint['actor'])
    self.critic.load_state_dict(checkpoint['critic'])
    self.actor_target.load_state_dict(checkpoint['actor_target'])
    self.critic_target.load_state_dict(checkpoint['critic_target'])

我们上述列出的关键功能是：我们保存/加载所有网络状态；我们维持目标网络的一致性；允许持续训练；并支持模型评估。汇总智代类，当实现 DDPG 智代时，需要做出一些至关重要的设计选择。这些大致可落于三个类别，称为：选择 DDPG 专用组件、驾驭实现力度、以及打造潜在强化。

所使用 DDPG 组件主要是目标网络、判定性政策，和单独学习率。当与连续动作空间打交道时，目标网络依据所采取动作（Q-学习）奖励进行稳定学习非常重要。连续空间的运用令这一点至关重要。这种判定性政策就此需要外部的噪声探索，以便建立韧性。采用单独学习率也是典型应用，其中政略（参与者网络）的学习率慢于数值网络。

这一相对强势实现选择是清晰的“关注点分离”，其中我们有良好定义的方法，用来动作选择、及更新。此外，这个设备感知能确保 GPU 与 CPU 过渡处理一致。还采用批处理来令张量操作更高效，最后在多个点检查形状安全，以确保张量维度一致。

潜在的强化可能是：梯度削波以避免梯度膨胀；采用学习率规划表以便细化和更好地控制学习过程；使用优先回放来实现高效抽样，诚然这与上一篇文章中提到的回放缓冲区有关；最后是并行探索，其中可利用多个参与者实例来加快数据收集。

还有少量训练动态值得注意，这些所做都做配合更新序列、并参照超参数。更新序列功能，先要更新评论者网络。这是因为更准确的 Q-值能指导政策提升。为了引入一些额外的稳定性，也可实现政策更新延迟。最后，会频繁执行目标更新，以减缓跟踪已学习的参数（网络权重）。

超参数的参照应包括 TAU，因为它控制目标网络速度，因此是整体学习过程稳定性的关键驱动力。这应当使用允许随时间衰减的噪声标量。缓冲区大小也至关重要，因为它影响学习效率，且批量大小会影响更新的变化幅度。

MA 与随机振荡器函数

这两个函数都是针对强化学习（RL）以 Python 实现的，不同于我们在监督学习文章中所做的以 MQL5 来实现，且简单地导出网络输入数据至 Python 来训练。在此处我们的实现中，我们使用 MetaTrader 的 Python 模块连接到运行中的终端实例，然后提取价格数据。此处的文档里有如何做到这一点的指南。下面的指标函数将原初价格数据变换到技术指标数据，在转换/归一化为二元形态向量之前，其作为我们监督学习模型的输入。 

监督学习模型的输出就是我们所投放的状态，因为本质上它们是在预测价格动作中的变化。这些状态随后被用作 DDPG 强化学习智代的输入。我们的 MA 函数从 MetaTrader 5 Python 模块获取价格数据帧。该数据框架需要如下进行验证和准备：

p = np.asarray(p).flatten()  # Convert to 1D array if not already

if len(p) < window:

    raise ValueError("Window size cannot be larger than the number of prices.")

我们于此正在做的是标准化数组，确保无论输入形状如何，都能保持一维输入格式一致。我们还有错误处理，可避免导致计算错误的无效窗口大小。数据完整性还能贯穿进程流水线维持数据流通畅。计算机制如下

return np.convolve(p, np.ones(window), 'valid') / window

该实现使用卷积，以便平均滚动计算高效。使用 “valid” 输入参数确保仅有完全计算完的窗口才会返回。归一化还会按窗口大小进行，以便生成真实的平均值。整个运算均是矢量化，以便优化性能。其金融学意义在于它平滑价格数据，有助于识别趋势，而所用窗口大小（即均化周期）决定了对价格变化的敏感度。随机振荡器函数如下验证其输入：

p = np.asarray(p).flatten()

if len(p) < k_window:
    raise ValueError("Window size for %K cannot be larger than the number of prices.")

此处设计考虑到 MA 函数的输入格式一致。对于 %K 计算窗口需要单独验证，对于无效参数，会提早抛出失败错误。%K 的计算方法如下：

for i in range(k_window - 1, len(p)):

    current_close = p[i]
    lowest_low = min(p[i - k_window + 1:i + 1])
    highest_high = max(p[i - k_window + 1:i + 1])
    K = ((current_close - lowest_low) / (highest_high - lowest_low)) * 100
    K_values.append(K)

此粗重要的组件包括滚动窗口分析、市场境况、和整体实现。滚动窗口分析需要实证覆盖一段回顾区间的价格范围。这有助于识别当前收盘价的相对位置，而应用的标准比例为 0 到 100。市场境况帮助我们评估超买/超卖的条件。接近 100 的数值暗示可能逆转向下，而接近 0 的数值则表示转头向上。出于清晰，整体实现采用显式环路，使用相应的窗口索引处理边缘情况，并保留结果的时态顺序。%D 的计算如下：

D_values = MA(K_values, d_window)

本质上，这是一种信号细化，其中用到了 %K 移动平均线的平滑版本。平均周期的典型赋值是 3，而这就是我们正用的。该附加缓冲区为 %K 的摆动提供确认，从而帮助降低来自原初 %K 的假信号。

获取形态函数

该函数把来自上述两个指标缓冲区的数据整合到学习流水线之中。它扮演的是特征工程的角色。这是原因：它有助于降维，它将原初价格变换为更有意义的信号；它有助于平稳提升，因为指标往往比原初价格更稳定；最后，它允许时态-境况-捕捉，即窗口计算维持时间依赖性（比如说生成的输入向量 [1,0,0,1] 能够关联其生成时间，就像任何指标值、或原初价格也标注它们的生成时间一样）。

然而，它主要用于监督学习的准备。它输出的特征以 0 和 1 的二进制向量，训练模型预测下一个价格变化。MA 提供趋势信息，STO 函数为我们给出动量和逆转信息。我们在第 57 篇文章中涵盖了这两个指标的组合互补形态。输出的预测价格变化随后作为强化学习的状态表示。

这意味着我们的监督学习模型的预测，变成 DDPG 的状态输入。我们所用的 MA 和 STO 指标最终帮助 DDPG 智代，为其提供特定市场境况，助其理解给定的市场形势。这降低了定义状态时对原初历史价格的需求。

实现强度包括来自验证输入以预防无声故障的健壮性、维度处理确保数组形状一致，甚至在不当使用时也能清晰传递错误消息。此外，考虑尽可能使用矢量化运算、显式环路、以及来自流式友好设计的内存效率。对于交易者来说它依维持相关性，不会被技术细节淹没。这是因为行业标准指标被用来生成状态。这两个指标是互补的，因为它们携带了趋势和动量量值，且状态输出处于归一化范围，这对一致性非常重要。

潜在的强化包括计算 %K 时实现了向量化，优化了计算，利用 numba 加速（从 JIT 导入）来为 STO 函数中的环路提速，以及中间计算的高速缓存。还可经由加入额外验证 NaN/inf 值，来扩展功能。实现搭配 DDPG 的强化学习代码较大，且在其中针对关键部分已提供了相应注释，我将把未覆盖部分附在本文的末尾。其中最重要的就是这个获取形态函数。

测试

在第 57 篇文章中测试了监督学习 10 个形态，只有 7 个能在一年的前想漫游测试中盈利，且之前已经接受过为期一年的训练。由于每个形态本身就是个独立网络，我们只得为每个形态生成强化学习网络和环境。我们在第 57 篇文章中遵循类似方法，依据 EURUSD 货币对的 2023年日线时间帧训练。在这种情况下，我们通过模拟 2023 年作为“实时市场”环境来训练强化学习网络。正如前两篇文章的论调，强化学习系统立足支持和保护已建立、且训练好的模型，在我们的案例中，其为我们在第 57 篇文章中训练的监督学习网络。 

在生产环境、或实时环境中，它进行反向传播，而非仅靠历史数据。由于从 MQL5 反向传播 ONNX 网络不可行，我们“模拟”了一个实时环境，我们的情况仍是 2023 年。

与其问我们在监督学习中"下一步价格走向何方"？我们问这样一个问题：鉴于即将到来的价格变化，交易者应采取什么动作。因此，我们按照上述概括执行 2023 年的模拟训练，然后在 2024 年进行前向漫游测试，其中我们略微调整了入场条件。

与其依据价格下一步走向来建仓做多或做空，我们还要考虑需要采取什么实际动作来应对价格下一步走向。我们还要考虑的因素就是奖励能否有利可图。在第 57 篇文章中前向漫游的 7 个形态中，进有 3 个在运用强化学习时有意义。用我们的 10 个索引，从 0 到 9，这些形态分别是 1、2 和 5。它们的报告呈现如下：

对于形态-1：

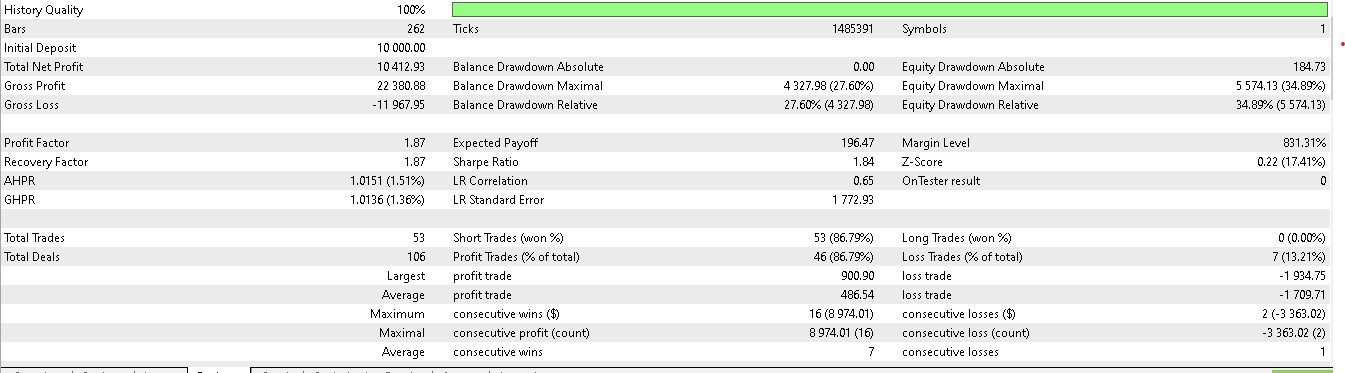
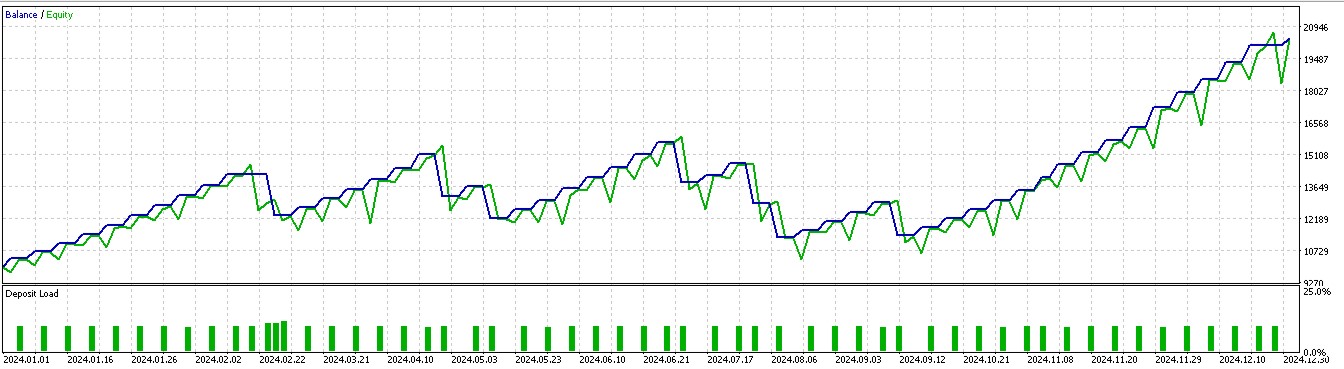
对于形态-2：

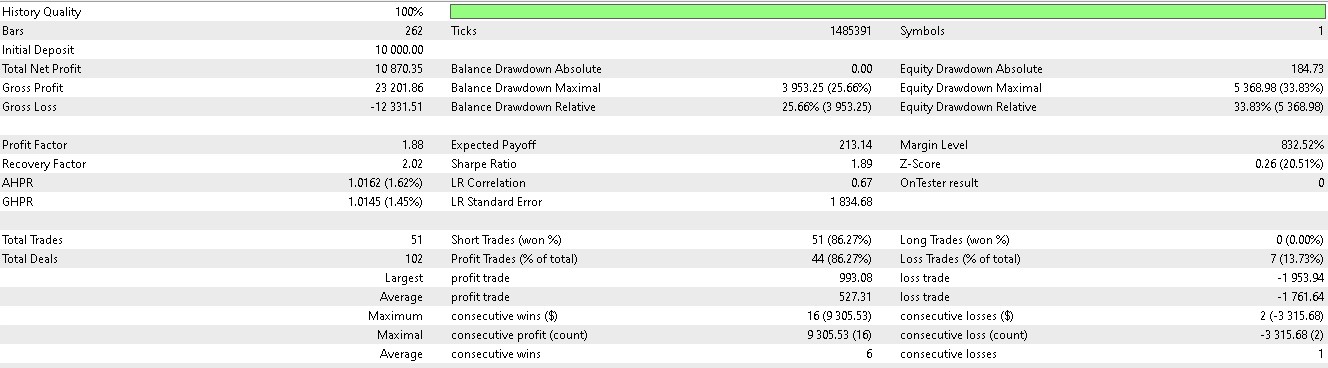
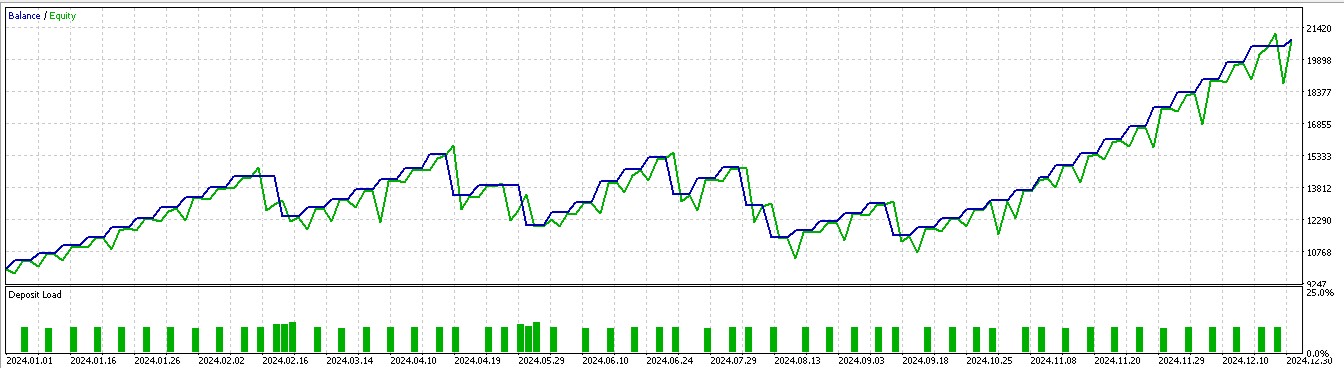
对于形态-5：

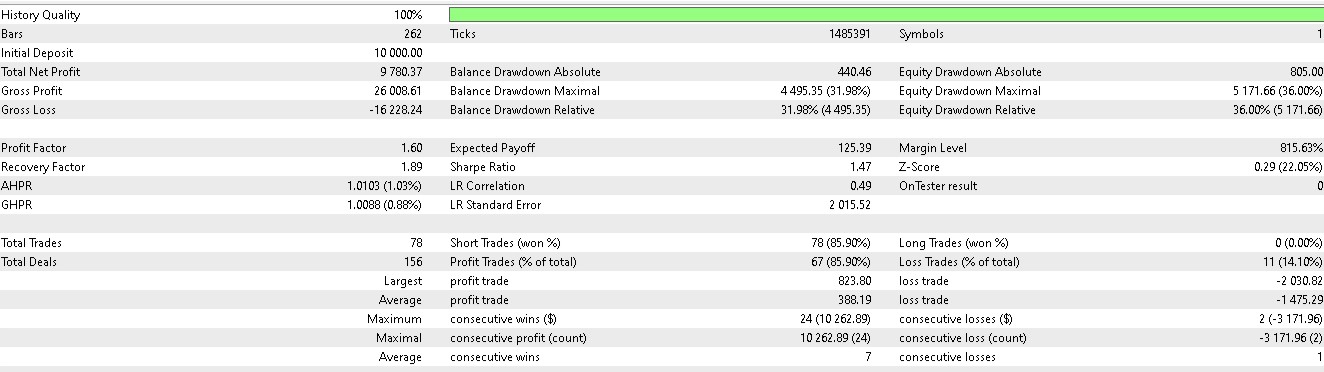
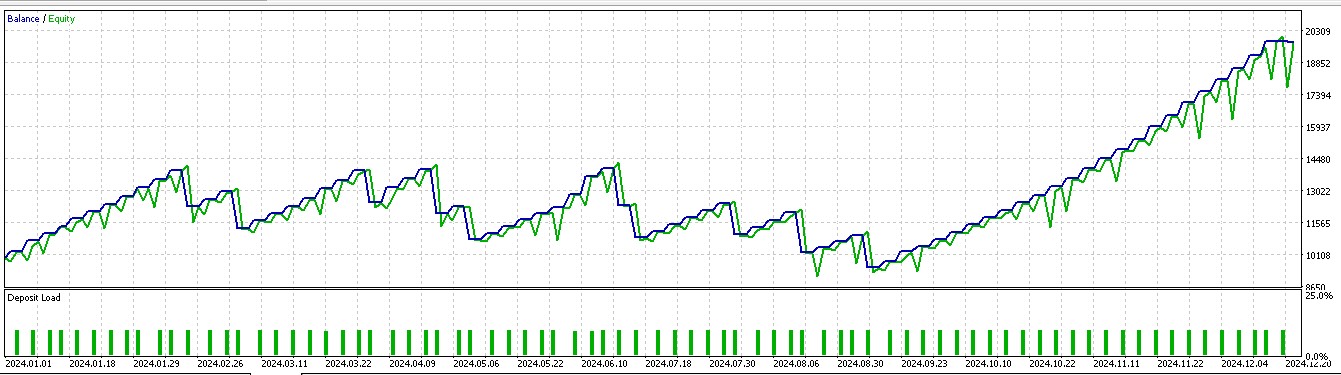
所测试智能系统一如既往地搭配自定义信号类构建，其代码附于下方。我们修改了第 57 篇文章中的信号类文件，将函数 “IsPattern” 重命名为 “Supervise”。此外，我们引入了一个新函数 “Reinforce”。以下分享这两者的代码：

//+------------------------------------------------------------------+
//| Supervised Learning Model Forward Pass.                          |
//+------------------------------------------------------------------+
double CSignal_DDPG::Supervise(int Index, ENUM_POSITION_TYPE T)
{  vectorf _x = Get(Index, m_time.GetData(X()), m_close, m_ma, m_ma_lag, m_sto);
   vectorf _y(1);
   _y.Fill(0.0);
   int _i=Index;
   if(_i==8)
   {  _i -= 2;
   }
   ResetLastError();
   if(!OnnxRun(m_handles[_i], ONNX_NO_CONVERSION, _x, _y))
   {  printf(__FUNCSIG__ + " failed to get y forecast, err: %i", GetLastError());
      return(double(_y[0]));
   }
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   return(double(_y[0]));
}
//+------------------------------------------------------------------+
//| Reinforcement Learning Model Forward Pass.                       |
//+------------------------------------------------------------------+
double CSignal_DDPG::Reinforce(int Index, ENUM_POSITION_TYPE T, double State)
{  vectorf _x(1);
   _x.Fill(float(State));
   vectorf _y(1);
   _y.Fill(0.0);
   vectorf _y_state(1);
   _y_state.Fill(float(State));
   vectorf _y_action(1);
   _y_action.Fill(0.0);
   vectorf _z(1);
   _z.Fill(0.0);
   int _i=Index;
   if(_i==8)
   {  _i -= 2;
   }
   ResetLastError();
   if(!OnnxRun(m_handles_a[_i], ONNX_NO_CONVERSION, _x, _y))
   {  printf(__FUNCSIG__ + " failed to get y action forecast, err: %i", GetLastError());
   }
   _y_action[0] = _y[0];
   ResetLastError();
   if(!OnnxRun(m_handles_c[_i], ONNX_NO_CONVERSION, _y_state, _y_action, _z))
   {  printf(__FUNCSIG__ + " failed to get z reward forecast, err: %i", GetLastError()); 
   }
   //normalize action output & check for state-action alignment
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   else
   {  _y[0] = 0.0f;
   }
   return(double(_y[0]*_z[0]));
}

这个自定义信号类文件是经由 MQL5 向导汇编成智能系统的，对于新读者，可在这里和这里找到相关指导。

结束语

我们研究了在部署/生产环境中应用强化学习模型的案例。我们的强化学习采用了深度判定性政策梯度算法，该实现包含了如本文及上一篇文章所述的回放缓冲区、参与者、评论者、和智代等类。部署/生产中的强化学习既能令模型专注于监督学习阶段（探索）所学内容，也考察未来制定决策时应考虑的环境、或市场条件中新的未知变化（利用）。按此正确行事，我们本质上必须在使用模型时反向传播和训练。 

然而，由于 MQL5 中不支持 ONNX 模型训练，我们选择在历史数据上模拟实时交易条件。模拟后，我们依据训练之年下一年的历史数据测试了所训练强化学习模型，7 个只有 3 个形态能够前像漫游，而且交易结果偏颇，因为仓位大多仅持有多头或空头。正如我们在第 57 篇文章中的论调，这很可能是由于测试窗口较小，意即扩展训练和测试覆盖更多的数据量，应当就能解决这个问题。现在我们来考察下一步推断。

类型	描述
*.*onnx 文件	在 Python 子文件夹中的 ONNX 模型文件，位于自定义信号类文件的所在
*.*MQH 文件	自定义信号类文件，文件含有处理输入网络数据（57_X）的函数
*.*MQ5 文件	向导汇编的智能系统，其头文件显示用到的文件。