
Применение нечеткой логики в трейдинге средствами MQL4
Введение
В современном трейдинге все чаще используются системы автоматической торговли — торговые эксперты или роботы. Суть их работы в том, что они имеют четкую, жестко заданную систему, а именно — торговую стратегию и систему управления финансами (мани-менеджмент). Преимущества таких систем в том, что они исключают человеческий фактор, строго действуют по определенному алгоритму. Недостатки автоматической торговли заключаются в отсутствии гибкости применяемой торговой стратегии, она всегда будет работать в одних и тех же рамках, с одними и теми же жестко разбитыми на категории параметрами. Проще говоря, система будет груба: средний тренд — входит одним лотом, сильный тренд — двойным, и точка!
Как бы торговал человек, мышлению которого, в отличие от машины, как раз присуща нечеткость категорий, различное мнение при схожих сигналах на вход? Он бы пытался оценить тренд, задаваться вопросами: "А насколько он средний? Может быть, он ближе к сильному? Или, может быть, тренд сильный, но не настолько, чтобы открывать позицию двойным лотом по стратегии?" Все это может описать нечеткая логика. Она не ставит жестких границ между категориями, она их как бы размывает и тем самым делает торговую систему более гибкой, сочетая в себе дисциплину робота и гибкость человеческого мышления. В этой статье предлагаются примеры применения системы нечеткой логики в трейдинге средствами MQL4.
Описание функций принадлежности
Для ознакомления с общими понятиями теории нечеткой логики рекомендуется прочесть статью Введение в теорию нечеткой логики и изучить основы работы библиотеки FuzzyNet для MQL4, так как она будет использована для реализации примеров.
Рассмотрим функции принадлежности, которые будут использоваться в статье.
Треугольная функция принадлежности
Функция принадлежности в форме треугольника. Эта простая и наиболее часто применяемая функция задается следующей аналитической формулой:
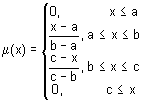
Как правило, используется для задания неопределенностей типа: «приблизительно равно», «среднее значение», «расположен в интервале», «подобен объекту», «похож на предмет» и т.п. Параметры треугольной функции принадлежности обычно интерпретируются так:
- [a, c] — диапазон изменения переменной;
- b — наиболее возможное значение переменной.
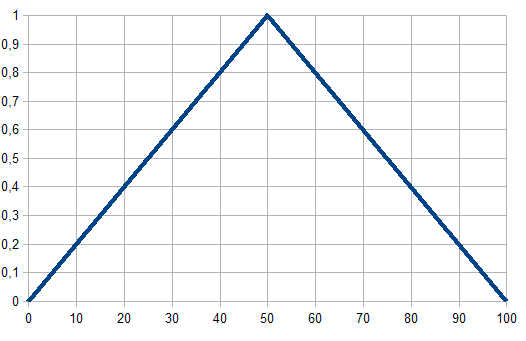
Рис. 1. Треугольная функция принадлежности
Трапециевидная функция принадлежности
Функция принадлежности в форме трапеции. Задается в виде следующей формулы:
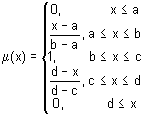
Параметры трапециевидной функции принадлежности интерпретируются следующим образом:
- [a, d] — носитель нечеткого множества, пессимистическая оценка значений переменной;
- [b, c] — ядро нечеткого множества, оптимистическая оценка значений переменной.
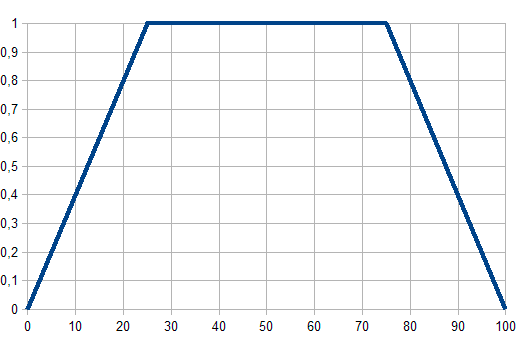
Рис. 2. Трапециевидная функция принадлежности
Колоколообразная функция принадлежности
Функция принадлежности в виде симметричной кривой в форме колокола. Данная функция задается формулой:
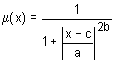
Значения параметров которой интерпретируются так:
- a — коэффициент концентрации функции принадлежности;
- b — коэффициент крутизны функции принадлежности;
- c — координата максимума функции принадлежности.
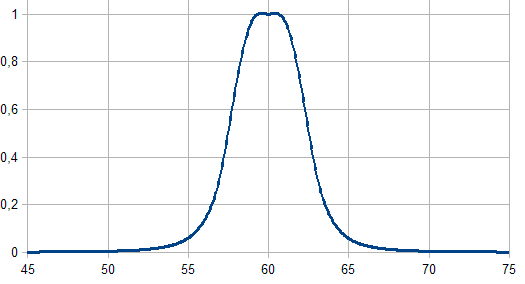
Рис. 3. Колоколообразная функция принадлежности
Сигмоидная функция принадлежности
Задается следующей формулой и применяется для задания монотонных функций принадлежности:
![]()
Ее параметры следует интерпретировать следующим образом:
- a — коэффициент крутизны функции принадлежности;
- с — координата перегиба функции принадлежности.
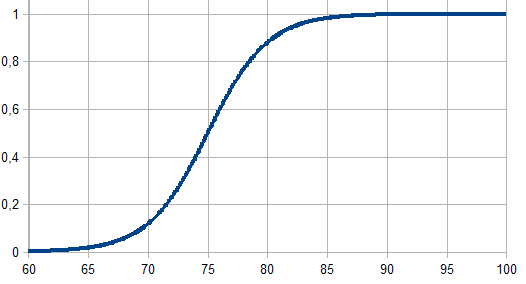
Рис. 4. Сигмоидная функция принадлежности
Пример реализации индикатора средствами библиотеки FuzzyNet для MQL4
В качестве примера я решил использовать индекс Среднего Направления Движения (Average Directional Movement Index) или ADX. Это трендовый индикатор, показывающий силу текущего тренда (зеленая толстая линия). Для начала введем четкие категории силы тренда (рис. 5), а именно:- Weak Trend — значение основной зеленой линии находится в диапазоне от 30 до 50. Показатели в этом жестко заданном диапазоне мы будем классифицировать как слабый тренд.
- Average Trend — значение основной зеленой линии находится в диапазоне 50-70. Показания в этом коридоре значений мы будем классифицировать как умеренный или средний тренд.
- Strong Trend — значение основной зеленой линии находится выше 70, вплоть до максимального в 100. Это признак сильного тренда.
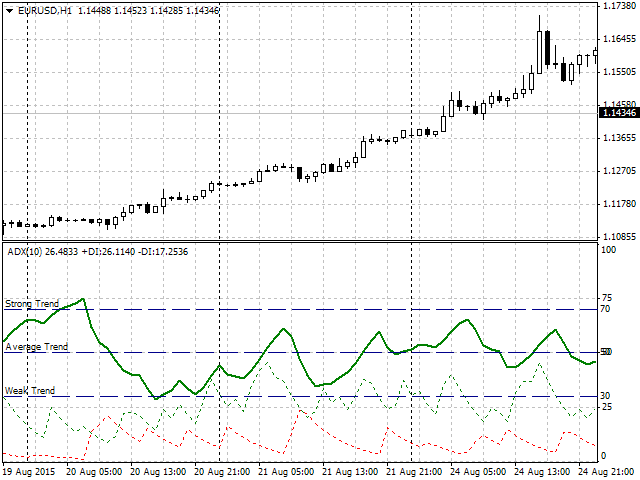
Рис. 5. Пример работы и выбранная градация по силе тренда
В данных трех жестко заданных категориях присутствуют следующие недостатки, обусловленные тем, что они заданы четкой, строгой логикой классификации:
- Первый недостаток — это субъективность мнения. Кто-то может задать вполне резонный вопрос: а почему пограничные значения — 30, 50, 70? Может быть, лучше задать 25, 50, 75 или какие-либо другие? Отчасти он будет прав, равно как и любой другой трейдер, предлагающий свои варианты пограничных значений. Тем не менее, результаты этих различных мнений могут привести к диаметрально противоположным результатам применения ADX в трейдинге.
- Вторая проблема заключается в пограничных областях выбранных категорий. Например значение 50 — это граница между слабым и умеренным трендом. Выходит, что значения 48, 49 — это слабый тренд, а 50 и 51 — средний. Возникает проблема с определением перехода от 49 к 50. Разница между значениями — в единицу, такая же, как и между 48 и 49, но в этом месте происходит резкий переход уже в другую категорию.
Что же предлагает нечеткая логика для исправления этих недостатков?
Происходит следующее: заданные границы размываются, становятся нечеткими. То есть в приграничных зонах жестко заданных категорий появляется двойственность — сила тренда относится сразу к двум понятиям, но с разной степенью принадлежности. Это можно описать так: сила тренда в данный момент в меньшей степени (30%) похожа на слабый тренд, но в большей (70%) — на средний. Человек охарактеризовал бы это так: тренд скорее средний, чем слабый. Я считаю, именно в этом состоит главное преимущество нечеткой логики — гибкость и вариативность оценки какого-либо изначально жестко заданного параметра. Для нашего примера с ADX я выбрал следующие описанные выше функции принадлежности:
- Трапециевидная функция для описания понятия слабого тренда.
- Колоколообразная функция для описания понятия среднего или умеренного тренда.
- Сигмоидная функция для сильного тренда.
Более сложные системы с большим количеством категорий можно описывать и другими доступными в библиотеке FuzzyNet. В данный момент их там более десятка. Итак, вот что в итоге получилось:
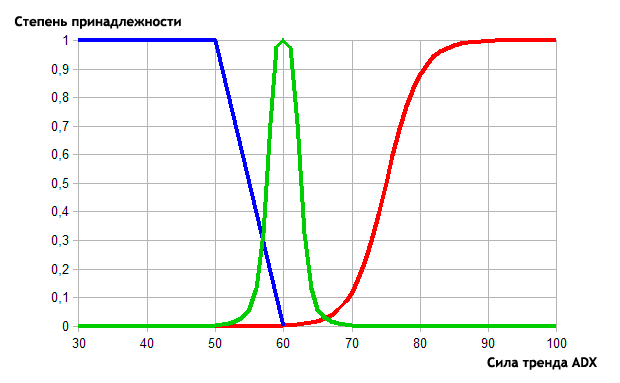
Рис. 6. Описание силы тренда средствами нечеткой логики
Как видно на графике, теперь мы видим области, в которых одновременно присутствуют 2 категории тренда. В зоне 50-60 это одновременно слабый и средний тренд, а в области 60-70 — средний и сильный. Таким образом, для трех категорий мы определили терм-множество с заданными функциями принадлежности. Теперь, имея входные значения ADX, описанные функциями принадлежности, нам нужно определиться с тем, что же будет выходным значением, результатом дефаззификации, и выбрать алгоритм нечеткого логического вывода.
Для нашего примера выходным значением я выбрал значение процента риска депозита относительно нечеткой переменной силы тренда, заданной на входе. То есть, чем сильнее тренд, тем выше риск и процент используемого депозита в трейдинге. В качестве алгоритма логического вывода мной выбран Мамдани.
Так же, как и для силы тренда, введем три четкие категории по степени риска:
- Низкий риск (Low) — диапазон от 2 до 4% от депозита.
- Нормальный риск (Normal) — 4-5%.
- Высокий риск(High) — от 5 до максимального значения в 10% от депозита.
По аналогии с силой тренда опишем категории риска с помощью функций принадлежности:
- Трапециевидная для низкого риска.
- Треугольная для нормального риска.
- Сигмоидная для высокого риска.
В итоге получим следующее графическое описание средствами нечеткой логики:
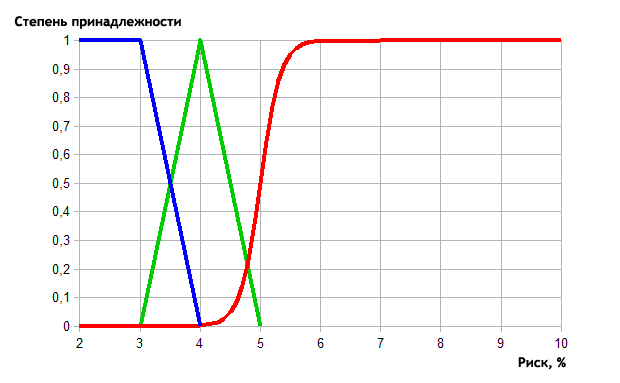
Рис. 7. Описание степени риска средствами нечеткой логики
Реализуем описанные данные с помощью библиотеки FuzzyNet для MQL4:
//+------------------------------------------------------------------+ //| ADX_Fuzzy.mq4 | //| Alexander Fedosov | //| https://www.mql5.com/ru/users/alex2356 | //+------------------------------------------------------------------+ #property copyright "Alexander Fedosov" #property link "https://www.mql5.com/ru/users/alex2356" #property version "1.00" #property strict #property indicator_separate_window #property indicator_buffers 2 #property indicator_color1 Green #property indicator_color2 Red #property indicator_minimum 0 #property indicator_maximum 10 //+------------------------------------------------------------------+ //| Connecting libraries | //+------------------------------------------------------------------+ #include <Math\FuzzyNet\MamdaniFuzzySystem.mqh> //--- input parameters input string p1="==== Parameters ===="; input int visual=100; // Visual Period input int adx_period=10; // ADX Period //--- double Buffer1[],Buffer2[],adx,adx_di_minus,adx_di_plus; int limit; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexStyle(0,DRAW_HISTOGRAM,0,2); SetIndexBuffer(0,Buffer1); SetIndexEmptyValue(0,0.0); //--- SetIndexStyle(1,DRAW_HISTOGRAM,0,2); SetIndexBuffer(1,Buffer2); SetIndexEmptyValue(1,0.0); //--- ArrayResize(Buffer1,visual); ArrayResize(Buffer2,visual); ArrayInitialize(Buffer1,0.0); ArrayInitialize(Buffer2,0.0); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int count_bars=IndicatorCounted(); //--- if(count_bars<0) return(-1); //--- if(Bars-1<adx_period) return(0); //--- for(int i=0; i<visual;i++) { adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits); adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits); adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits); //--- double r=(adx_di_plus-adx_di_minus); if(MathAbs(r)>10 && adx>=30.0) if(r>0) Buffer1[i]=mamdani(adx); else if(r<0) Buffer2[i]=mamdani(adx); } return(rates_total); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double mamdani(double v) { double res=0; //--- Mamdani Fuzzy System MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem(); //--- Create input variables for the system FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0); //--- fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(20.0, 30.0, 50.0, 60.0))); fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0))); fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0))); fsRisk.Input().Add(fsTrend); //--- Create Output FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0); fvRisk.Terms().Add(new FuzzyTerm("low", new TrapezoidMembershipFunction(1.0, 2.0, 3.0, 4.0))); fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0))); fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0))); fsRisk.Output().Add(fvRisk); //--- Create three Mamdani fuzzy rules MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low"); MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal"); MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high"); //--- Add three Mamdani fuzzy rules in the system fsRisk.Rules().Add(rule1); fsRisk.Rules().Add(rule2); fsRisk.Rules().Add(rule3); //--- Set input value CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsTrend,v); in.Add(p_od_in); //--- Get result CList *result; Dictionary_Obj_Double *p_od_out; result=fsRisk.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits); //--- delete in; delete result; delete fsRisk; return res; } //+------------------------------------------------------------------+
Визуальной реализацией нашей системы зависимости степени риска от силы тренда я сделал простой индикатор в виде гистограмм (зеленого цвета при бычьем тренде и красного цвета при медвежьем), высота которых показывает численное значение степени риска при силе тренда в пределах, описанных ранее. Рассмотрим код более подробно.
Вначале установим 2 буфера для применяемых гистограмм, их цвет и диапазон по оси ординат от нуля до максимально заданного значения риска, равного 10%.
#property indicator_separate_window #property indicator_buffers 2 #property indicator_color1 Green #property indicator_color2 Red #property indicator_minimum 0 #property indicator_maximum 10
Далее подключаем библиотеки для создания систем по алгоритму Мамдани, а также добавляем переменные для визуализации количества баров, начиная с нулевого, и настраиваемое значение периода индикатора ADX.
//+------------------------------------------------------------------+ //| Connecting libraries FuzzyNet | //+------------------------------------------------------------------+ #include <Math\FuzzyNet\MamdaniFuzzySystem.mqh> //--- input parameters input string p1="==== Parameters ===="; input int visual=100; // Visual Period input int adx_period=10; // ADX Period
При инициализации устанавливаем, что наш индикатор будет в виде гистограмм.
//+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexStyle(0,DRAW_HISTOGRAM,0,2); SetIndexBuffer(0,Buffer1); SetIndexEmptyValue(0,0.0); //--- SetIndexStyle(1,DRAW_HISTOGRAM,0,2); SetIndexBuffer(1,Buffer2); SetIndexEmptyValue(1,0.0); //--- ArrayResize(Buffer1,visual); ArrayResize(Buffer2,visual); ArrayInitialize(Buffer1,0.0); ArrayInitialize(Buffer2,0.0); //--- return(INIT_SUCCEEDED); }
В основном коде определяем основные показания индикатора ADX, а также в переменной r находим разницу между двумя индикаторами направленности тренда +DI и -DI. Вводим фильтр присутствия тренда как разницу по модулю значений +DI и -DI выше 10 и основное значение силы тренда выше 30 (нижняя граница слабого тренда). Далее определяем направление тренда исходя из знака переменной r и помещаем значение функции mamdani() в заданный заранее массив.
int count_bars=IndicatorCounted(); //--- if(count_bars<0) return(-1); //--- if(Bars-1<adx_period) return(0); //--- for(int i=0; i<visual;i++) { adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits); adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits); adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits); //--- double r=(adx_di_plus-adx_di_minus); if(MathAbs(r)>10 && adx>=30.0) if(r>0) Buffer1[i]=mamdani(adx); else if(r<0) Buffer2[i]=mamdani(adx); }
Описание функции mamdani:
1. Создаем новую систему нечеткой логики типа Мамдани *fsRisk.
2. Добавляем в нее входную переменнную *fsTrend с установленным именем trend, минимальным и максимальным значениями 30 и 100.
//--- Mamdani Fuzzy System MamdaniFuzzySystem *fsRisk=new MamdaniFuzzySystem(); //--- Create input variables for the system FuzzyVariable *fsTrend=new FuzzyVariable("trend",30.0,100.0);
3. Далее добавляем в нее нечеткие термы, описанные выше (рис. 6), с выбранными для каждой категории функциями принадлежности.
fsTrend.Terms().Add(new FuzzyTerm("weak", new TrapezoidMembershipFunction(30.0, 40.0, 50.0, 60.0))); fsTrend.Terms().Add(new FuzzyTerm("average", new GeneralizedBellShapedMembershipFunction(2.5,2.0,60.0))); fsTrend.Terms().Add(new FuzzyTerm("strong",new SigmoidalMembershipFunction(0.4,75.0))); fsRisk.Input().Add(fsTrend);
4. Проделаем пункты 2-3 для выходного значения: создаем переменную *fvRisk с именем risk и минимальными и максимальными значениями риска 2% и 10%.
//--- Create Output FuzzyVariable *fvRisk=new FuzzyVariable("risk",2.0,10.0); fvRisk.Terms().Add(new FuzzyTerm("low", new TriangularMembershipFunction(2.0, 3.0, 4.0))); fvRisk.Terms().Add(new FuzzyTerm("normal", new TriangularMembershipFunction(3.0, 4.0, 5.0))); fvRisk.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,5.0))); fsRisk.Output().Add(fvRisk);
5. Создадим теперь набор нечетких правил, которые будут представлять нашу систему, а именно три правила:
- Если тренд слабый, то риск низкий.
- Если тренд средний, то риск нормальный.
- Если тренд сильный, то риск высокий.
//--- Create three Mamdani fuzzy rules MamdaniFuzzyRule *rule1 = fsRisk.ParseRule("if (trend is weak) then risk is low"); MamdaniFuzzyRule *rule2 = fsRisk.ParseRule("if (trend is average) then risk is normal"); MamdaniFuzzyRule *rule3 = fsRisk.ParseRule("if (trend is strong) then risk is high");
6. Добавляем наши правила в систему:
//--- Add three Mamdani fuzzy rules in the system
fsRisk.Rules().Add(rule1);
fsRisk.Rules().Add(rule2);
fsRisk.Rules().Add(rule3);
7. Создаем списки для входных и выходных переменных и добавляем входной параметр v, который служит аргументом функции mamdani. То есть для всей функции mamdani создается система нечеткой логики с установленными входными и выходными нечеткими перемененными, а на вход подается значение индикатора ADX.
//--- Set input value CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsTrend,v); in.Add(p_od_in); //--- Get result CList *result=new CList; Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; result=fsRisk.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits);
8. Значением функции и результатом является переменная res, на основе которой и строится гистограмма.
adx=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MAIN,i),_Digits); adx_di_plus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_PLUSDI,i),_Digits); adx_di_minus=NormalizeDouble(iADX(_Symbol,PERIOD_CURRENT,adx_period,PRICE_CLOSE,MODE_MINUSDI,i),_Digits); //--- double r=(adx_di_plus-adx_di_minus); if(MathAbs(r)>10 && adx>=30.0) if(r>0) Buffer1[i]=mamdani(adx); else if(r<0) Buffer2[i]=mamdani(adx);
В итоге мы сможем наблюдать следующий визуальный результат работы индикатора:
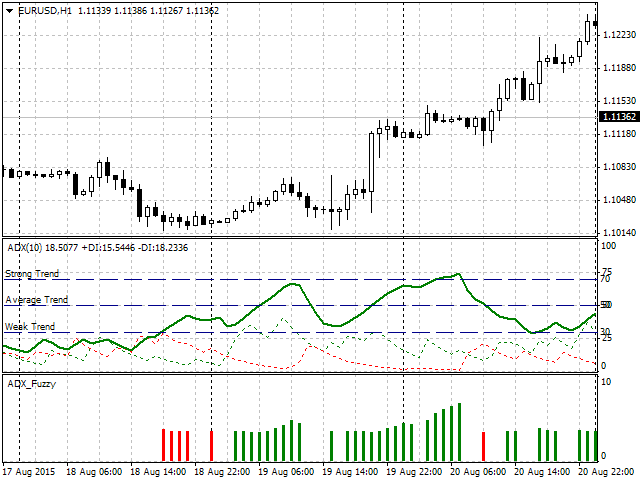
Рис. 8. Работа индикатора
Как видно из его работы, при наличии тренда индикатор в виде гистограммы определенного цвета указывает на это, а высота показывает рекомендуемый процент риска от депозита. Вполне очевиден вопрос — а в чем же была бы разница, если бы этот же индикатор был реализован как обычно, с четкими интервалами? Для этого рассмотрим более детально следующий участок (рис. 9). На нем зеленой стрелкой указан столбец гистограммы, а слева — его численное значение и значение силы тренда ADX. Как определено нами ранее, значение ADX больше 70 — это сильный тренд, а при сильном тренде значение риска предлагается выше 5%. Но на рис. 9 мы прекрасно видим, что ADX = 69.7923, т.е. по строгим условиям это был бы еще средний тренд, и риск обязан быть ниже 5%, а здесь — 5,6406, т.е. выше.
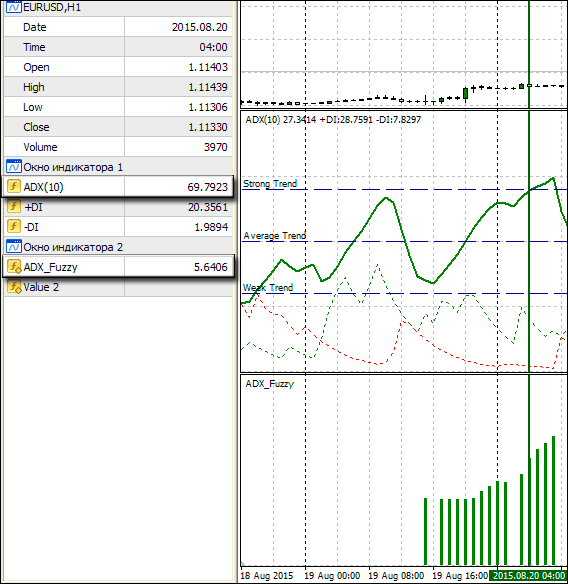
Рис. 9. Демонстрация отличия нечеткой логики от стандартной
Это и есть работа нечеткой логики в действии — она определила, что хоть значение и ниже 70, но тренд в этой области больше похож на сильный, чем средний. В этом можно убедиться, посмотрев на рис. 6, где отлично видно, что при значении на оси абсцисс равном 69,7923 функция принадлежности сильного тренда имеет значение выше, чем функция среднего тренда. Поэтому наша система и предложила риск выше 5%, подойдя к оценке на границе категорий сильного и умеренного тренда более гибко, чем это сделала бы система с четкой логикой.
Пример реализации торгового эксперта средствами библиотеки FuzzyNet для MQL4
В примере реализации эксперта я хотел бы показать разницу его работы при четко сформулированных условиях и при использовании элементов нечеткой логики. Для будущей полноты сравнения я решил взять пример эксперта из другой своей статьи — "Торговые идеи на основе направления и скорости движения цен". В ней достаточно подробно описана суть работы торгового робота, и чтобы не повторяться здесь, возьмем его за основу, но сделаем следующие изменения:
- Итак. Логика работы этого эксперта основана на идее инерционности движения цены. Параметры движения описаны следующими индикаторами: RSI (в качестве индикатора скорости) и AC (индикатор ускорения). Оценка скорости и ускорения производится с помощью индексации интервалов значений этих индикаторов. А теперь применим теорию нечетких множеств к показаниям и расчету индекса RSI. В итоге на входе нашей системы будут значения RSI, а на выходе — нечеткий индекс скорости, который будет иметь значения не только целые 1-4, а, например, 1,3 или 3,85.
- В свою очередь, значение нечеткого индекса будет входом для другой системы, выходом которой я решил взять значения прибыли. То есть показатель, который в исходном советнике вообще неизменен: тейк-профит.
Смысл связи достаточно прост. Если RSI и AC — это параметры движения, то чем выше скорость, тем выше будет инерция данного движения, а значит, логично поставить тейк-профит побольше. Соответственно, при низкой скорости, т.е. несильном движении, нужно делать цели для прибыли скромнее, чтобы в стремлении получить больше, получить откат или смену тенденции и получить убыток. На рис. 10 представлена блок-схема для более ясного понимания применения нечеткой логики в данном торговом эксперте.
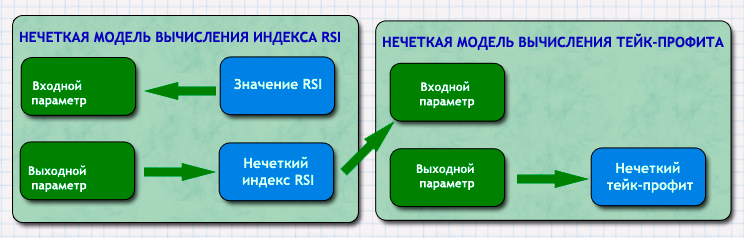
Рис. 10. Блок-схема применения нечеткой логики в советнике
Так же, как и в примере с индикатором, опишем функции принадлежности для обеих нечетких моделей. Первая — это нечеткая модель вычисления индекса RSI, где на вход подается само значение индикатора, поэтому разобьем интересующие нас значения на три категории:
- Weak. Первая категория. Характеризует слабый тренд. Значение RSI: 60-70.
- Average. Вторая категория. Это средний тренд. Диапазон RSI: 70-80.
- Strong. Третья категория, относящаяся к сильному тренду. Диапазон будет 80-85.
Выберем функции принадлежности, чтобы описать заданные категории:
- Weak. Сигмоидная фунцкия с коэффициентом крутизны -0,75 и точкой перегиба 67,5.
- Average. Гауссовская функция с координатой максимума в точке 72,5 и коэффициентом концентрации, равным 2,2.
- Strong. Гауссовская функция с координатой максимума в точке 80 и коэффициентом концентрации, равным 1,4.
Визуальное представление таково:
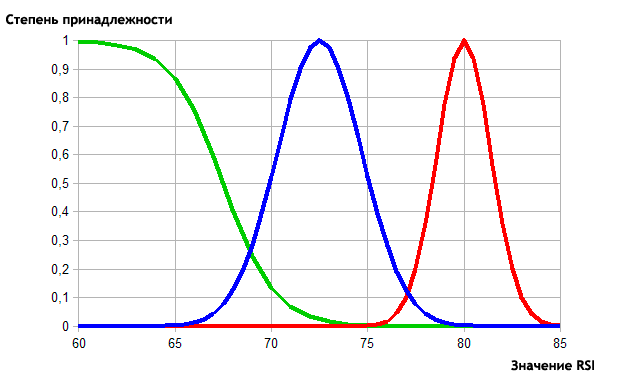
Рис. 11. Описание функциями принадлежности категорий значений RSI
Выходным параметром данной нечеткой модели у нас является индекс RSI. Для его описания были использованы следующие категории и функции принадлежности:
- Low. Низкий индекс, в который входит диапазон 1-2. Функция принадлежности — сигмоидная с крутизной -11 и перегибом в точке 1,5.
- Normal. Средний индекс с диапазоном 2-3. Функция принадлежности — гауссовская с максимумом в точке 2 и коэффициентом концентрации 0,3.
- High. Высокое значение индекса и его диапазон 3-4. Функция принадлежности — сигмоидная с крутизной 6 и точкой перегиба 3.
В итоге мы получим следующую визуализацию:
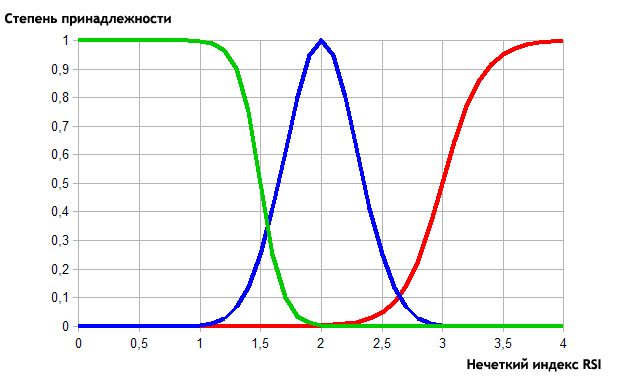
Рис. 12. Описание функциями принадлежности категорий значений индекса RSI
Далее опишем вторую нечеткую модель из рис. 10 — нечеткую модель вычисления тейк-профита. Входные параметры этой модели уже описаны как выходные первой модели, а именно — нечеткого индекса RSI. Выходным же будет значение самого тейк-профита. Определим для него четкие категории:
- Minimal. Категория минимального тейк-профита в диапазоне 30-40.
- Average. Категория среднего значения тейк-профита в диапазоне 40-60.
- Maximal. Категроия высокого значения и диапазон 60-70.
Теперь опишем функциями принадлежности:
- Minimal. Функция принадлежности — сигмоидная с крутизной -0,8 и перегибом в точке 37,5.
- Average. Функция принадлежности — гауссовская функция с координатой максимума в точке 50 и коэффициентом концентрации, равным 3.
- Maximal. Функция принадлежности — сигмоидная с крутизной 0,8 и перегибом в точке 62,5.
Соответственно, графическая реализация будет следующая:
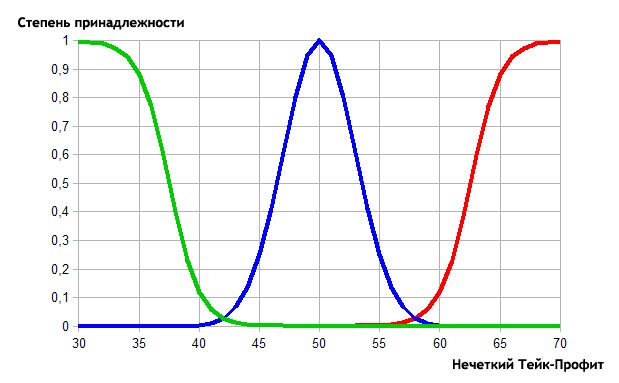
Рис. 13. Описание функциями принадлежности категорий значений тейк-профита
Итак, мы определились со всеми параметрами, осталось реализовать это в торговом эксперте, в который мы добавим две нечеткие модели последовательного расчета значения тейк-профита и стоп-лосса, исходя из показаний индикатора RSI.
//+------------------------------------------------------------------+ //| tester.mq4 | //| Alexander Fedosov | //| | //+------------------------------------------------------------------+ #property copyright "Alexander Fedosov" #property strict #include "trading.mqh" //вспомогательная библиотека для торговых операций //+------------------------------------------------------------------+ //| Connecting libraries | //+------------------------------------------------------------------+ #include <Math\FuzzyNet\MamdaniFuzzySystem.mqh> //+------------------------------------------------------------------+ //| Параметры советника | //+------------------------------------------------------------------+ input bool Lot_perm=false; // Лот от баланса? input double Risk = 2; // Риск депозита, % input double lt=0.01; // Лот input int magic=2356; // Маджик input int period=14; // Период индикатора RSI input ENUM_TIMEFRAMES tf=PERIOD_CURRENT; // Рабочий таймфрейм //--- int index_rsi,index_ac; double tkp,stl; double rs,mdm; CTrading tr; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { tr.Trading(magic,5,lt,Lot_perm,Risk); tr.exp_name="Tester Fuzzy Logic"; return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Главная функция расчета | //+------------------------------------------------------------------+ void OnTick() { //--- проверка на то, что нет уже открытых ордеров if(!tr.isOpened(magic)) { depth_trend(); speed_ac(); rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2); //--- проверка условий на покупку if(Buy() && rs<=85.0) { mdm = mamdani_rsi(rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_BUY,lt,(int)tkp,(int)stl)) Print("RSI равно ",rs," TP равно ",tkp," SL равно ",stl); } //--- проверка условий на продажу if(Sell() && rs>=15.0) { mdm = mamdani_rsi(100-rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_SELL,lt,(int)tkp,(int)stl)) Print("RSI равно ",rs," TP равно ",tkp," SL равно ",stl); } } //--- есть открытые ордера? if(tr.isOpened(magic)) { //--- проверяем и закрываем те ордера на продажу, которые удовлетворяют условиям закрытия if(Sell_close()) tr.ClosePosAll(OP_SELL); //--- проверяем и закрываем те ордера на покупку, которые удовлетворяют условиям закрытия if(Buy_close()) tr.ClosePosAll(OP_BUY); } } //+------------------------------------------------------------------+ //| Функция определения глубины тренда | //+------------------------------------------------------------------+ void depth_trend() { //--- определение индекса на вход в рынок double rsi=iRSI(_Symbol,tf,period,PRICE_CLOSE,0); //--- index_rsi=0; if(rsi>90.0) index_rsi=4; else if(rsi>80.0) index_rsi=3; else if(rsi>70.0) index_rsi=2; else if(rsi>60.0) index_rsi=1; else if(rsi<10.0) index_rsi=-4; else if(rsi<20.0) index_rsi=-3; else if(rsi<30.0) index_rsi=-2; else if(rsi<40.0) index_rsi=-1; } //+------------------------------------------------------------------+ //| Функция определения скорости тренда | //+------------------------------------------------------------------+ void speed_ac() { double ac[]; ArrayResize(ac,5); ArrayInitialize(ac,0.0); for(int i=0; i<5; i++) ac[i]=iAC(_Symbol,tf,i); //--- index_ac=0; //--- индексы на покупку if(ac[0]>ac[1]) index_ac=1; else if(ac[0]>ac[1] && ac[1]>ac[2]) index_ac=2; else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3]) index_ac=3; else if(ac[0]>ac[1] && ac[1]>ac[2] && ac[2]>ac[3] && ac[3]>ac[4]) index_ac=4; //--- индексы на продажу else if(ac[0]<ac[1]) index_ac=-1; else if(ac[0]<ac[1] && ac[1]<ac[2]) index_ac=-2; else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3]) index_ac=-3; else if(ac[0]<ac[1] && ac[1]<ac[2] && ac[2]<ac[3] && ac[3]<ac[4]) index_ac=-4; } //+------------------------------------------------------------------+ //| Функция проверки условия на покупку | //+------------------------------------------------------------------+ bool Buy() { return (((index_rsi==2 && index_ac>=1) || (index_rsi==3 && index_ac==1))?true:false); } //+------------------------------------------------------------------+ //| Функция проверки условия на продажу | //+------------------------------------------------------------------+ bool Sell() { return (((index_rsi==-2 && index_ac<=-1) || (index_rsi==-3 && index_ac==-1))?true:false); } //+------------------------------------------------------------------+ //| Функция проверки условия закрытия позиции на покупку | //+------------------------------------------------------------------+ bool Buy_close() { return ((index_rsi>2 && index_ac<0)?true:false); } //+------------------------------------------------------------------+ //| Функция проверки условия закрытия позиции на продажу | //+------------------------------------------------------------------+ bool Sell_close() { return ((index_rsi<-2 && index_ac>0)?true:false); } //+------------------------------------------------------------------+ //| Функция нечеткой модели вычисления индекса RSI | //+------------------------------------------------------------------+ double mamdani_rsi(double rsi) { double res=0; //--- Mamdani Fuzzy System MamdaniFuzzySystem *fsRSI=new MamdaniFuzzySystem(); //--- создание входных переменных для системы и определение термов FuzzyVariable *fsTrend=new FuzzyVariable("rsi",60.0,85.0); //--- fsTrend.Terms().Add(new FuzzyTerm("weak", new SigmoidalMembershipFunction(-0.75,67.5))); fsTrend.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(72.5,2.2))); fsTrend.Terms().Add(new FuzzyTerm("strong", new NormalMembershipFunction(80.0,1.4))); fsRSI.Input().Add(fsTrend); //--- создание выходных переменных для системы и определение термов FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0); fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5))); fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3))); fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0))); fsRSI.Output().Add(fsIndex); //--- создание нечетких правил и добавление их в систему MamdaniFuzzyRule *rule1 = fsRSI.ParseRule("if (rsi is weak) then (index is low)"); MamdaniFuzzyRule *rule2 = fsRSI.ParseRule("if (rsi is average) then (index is normal)"); MamdaniFuzzyRule *rule3 = fsRSI.ParseRule("if (rsi is strong) then (index is high)"); fsRSI.Rules().Add(rule1); fsRSI.Rules().Add(rule2); fsRSI.Rules().Add(rule3); //--- настройка входных значений CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsTrend,rsi); in.Add(p_od_in); //--- вывод результата CList *result=new CList; Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; result=fsRSI.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits); //--- delete in; delete result; delete fsRSI; return res; } //+------------------------------------------------------------------+ //| Функция нечеткой модели вычисления индекса Тейк-Профита | //+------------------------------------------------------------------+ double mamdani_tp(double ind_rsi) { double res=0; //--- Mamdani Fuzzy System MamdaniFuzzySystem *fsTP=new MamdaniFuzzySystem(); //--- создание входных переменных для системы и определение термов FuzzyVariable *fsIndex=new FuzzyVariable("index",1.0,4.0); fsIndex.Terms().Add(new FuzzyTerm("low", new SigmoidalMembershipFunction(-11.0,1.5))); fsIndex.Terms().Add(new FuzzyTerm("normal", new NormalMembershipFunction(2.0,0.3))); fsIndex.Terms().Add(new FuzzyTerm("high", new SigmoidalMembershipFunction(6.0,3.0))); fsTP.Input().Add(fsIndex); //--- создание выходных переменных для системы и определение термов FuzzyVariable *fsProfit=new FuzzyVariable("TP",30.0,70.0); fsProfit.Terms().Add(new FuzzyTerm("minimal", new SigmoidalMembershipFunction(-0.8,37.5))); fsProfit.Terms().Add(new FuzzyTerm("average", new NormalMembershipFunction(50.0,3.0))); fsProfit.Terms().Add(new FuzzyTerm("maximal", new SigmoidalMembershipFunction(0.8,62.5))); fsTP.Output().Add(fsProfit); //--- создание нечетких правил и добавление их в систему MamdaniFuzzyRule *rule1 = fsTP.ParseRule("if (index is low) then (TP is minimal)"); MamdaniFuzzyRule *rule2 = fsTP.ParseRule("if (index is normal) then (TP is average)"); MamdaniFuzzyRule *rule3 = fsTP.ParseRule("if (index is high) then (TP is maximal)"); fsTP.Rules().Add(rule1); fsTP.Rules().Add(rule2); fsTP.Rules().Add(rule3); //--- настройка входных значений CList *in=new CList; Dictionary_Obj_Double *p_od_in=new Dictionary_Obj_Double; p_od_in.SetAll(fsIndex,ind_rsi); in.Add(p_od_in); //--- вывод результата CList *result=new CList; Dictionary_Obj_Double *p_od_out=new Dictionary_Obj_Double; result=fsTP.Calculate(in); p_od_out=result.GetNodeAtIndex(0); res=NormalizeDouble(p_od_out.Value(),_Digits); //--- delete in; delete result; delete fsTP; return res; } //+------------------------------------------------------------------+
Теперь разберем основные изменения, которые были внесены в советник:
- Главное дополнение — это, конечно, реализация двух нечетких моделей в виде функций mamdani_rsi и mamdani_tp.
- Соответственно, были убраны такие параметры советника, как стоп-лосс и тейк-профит. Они теперь рассчитываются с помощью нечеткой логики.
- Рассмотрим, каким образом реализуется этот расчет:
if(OrdersTotal()<1) { depth_trend(); speed_ac(); rs=tr.ND(iRSI(_Symbol,tf,period,PRICE_CLOSE,0),2); //--- проверка условий на покупку if(Buy() && rs<=85.0) { mdm = mamdani_rsi(rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_BUY,lt,tkp,stl)) Print("RSI равно ",rs," TP равно ",tkp," SL равно ",stl); } //--- проверка условий на продажу if(Sell() && rs>=15.0) { mdm = mamdani_rsi(100-rs); tkp = MathCeil(mamdani_tp(mdm)); stl = MathCeil(tkp*0.43); if(tr.OpnOrd(OP_SELL,lt,tkp,stl)) Print("RSI равно ",rs," TP равно ",tkp," SL равно ",stl); } }
Если нет открытых ордеров с маджиком советника, то система с помощью функций depth_trend() и speed_ac() отслеживает параметры движения на рынке и при соответствии Buy() или Sell() входит. Далее, в момент удовлетворения условиям переменной mdm присваивается значение результата работы нечеткой модели, у которой на входе — текущее значение RSI, а на выходе — нечеткий индекс. В свою очередь, значение нечеткого индекса подается на вход второй нашей системы, выходом которой является тейк-профит в пунктах. Значение тейк-профита присваивается переменной tkp.
Коэффицинет 0,43 я взял исходя из максимального значения профита в 70 пунктов и взял стоп-лосс для него в 30. При успешном открытии ордера наш советник также показывает значения RSI, при котором он был открыт, а также вычисленные от его значения параметры стоп-лосс и тейк-профит. Это сделано лишь для удобства тестирования.
Стоит пояснить следущие моменты:
- При условии на продажу переменной mdm присваивается mamdani_rsi(100-rs). Сделано это потому, что диапазоны и их границы относительно минимума и максимума значения RSI (0 и 100) зеркальны.
- Второй момент — это два дополнительных условия: при покупке rs<=85 и аналогично при продаже rs>=15. Это сделано потому, что при создании входных переменных нечеткой модели вычисления индекса RSI границы установлены в 60-85, соответственно, зеркально для продажи крайнее значение как раз 15.
Пример работы советника изображен на рис. 14, где можно убедиться в том, что при различных значениях индикатора RSI происходит пересчет значений стопа и тейка.
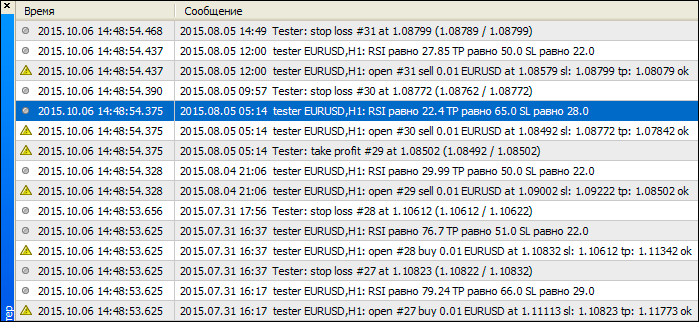
Рис. 14. Результаты работы торгового эксперта
Заключение
В данной статье были рассмотрены примеры реализации теории нечетких множеств в трейдинге с помощью библиотеки FuzzyNet средствами MQL4. Было продемонстрировано, что системы, основанные на нечеткой логике, более гибко подходят к проблеме четких категорий, таких как классификация тренда или разграничение риска. В торговом эксперте было продемонстрировано, как система на нечеткой логике анализирует силу торгового сигнала, исходя из своей торговой стратегии, и сама определяет значения ограничения убытков и значения целевой прибыли. Думаю, системы торговли, основанные на нечеткой логике — это симбиоз лучших качеств, необходимых в успешной торговле, таких как дисциплинированность торгового робота и гибкость человеческого мышления.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Оценка и выбор переменных для моделей машинного обучения
Оценка и выбор переменных для моделей машинного обучения
 Обработка ошибок и логирование в MQL5
Обработка ошибок и логирование в MQL5
 Индикатор для построения графика "шпинделей" (веретён)
Индикатор для построения графика "шпинделей" (веретён)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
работа проделана огромная, но есть ошибки в советнике,
- утечка памяти,
- вот здесь у вас определение функции:
bool ClosePosAll(int magik,int OrdType=-1);
а вызываете вы зту функцию так:
tr.ClosePosAll(OP_BUY);
грамматически все прошло гладко, но у вас нет маджика равного OP_BUY...
надо так:
по плодотворности применения нечетких множеств не могу ничего сказать, надо все это фундаментально изучать...
Автору большой респект за проделанную работу... НО! ;-)
Это ведь только половина теории нечеткой логики... Я в свое время застрял на реализации и понимании именно механизма нечеткого вывода... Нечеткий вывод предназначен как раз для создания какого-то результата совмещения двух и более нечетких правил. В итоге у меня работа застопорилась...
Идея была такая:
Сделал связку метатрейдер + база данных на 1С. (1С - потому что очень удобно и быстро можно сконфигурировать базу данных любой сложности и при этом ее видеть и управлять данными)
В метатрейдере скрипт передавал данные в 1С (через файлы) и получал команды на торговлю.
В БД 1С была создана стройная система: Входные данные -> Термы лингвистических переменных -> Лингвистические переменные -> Нечеткие правила -> Нечеткие выводы (это мне не удалось)
Правила, как оказалось, можно создавать любой сложности и направления: не только тренд, но и время в сделке, прирост прибыли/убытка сделки, просадка внутри сделки, анализ любых индикаторов (как ADX у автора) , динамика отдельных стратегий и прочее. Да, система была многовалютной и много системной :) Начинал на евро, потом пробовал подключать еще несколько инструментов для наработки статистики. Но в итоге несколько остыл, т.к. через полгода занятий по вечерам, не увидел продвижения... Сейчас занят похожей системой, но с другими принципами.
Если у кого-то есть какие-то еще наработки: делитесь, тема очень интересна, как мне кажется...
Вопрос к автору - как работает система (прибыль убыток) и перспективы есть или нет? Можно в личку, т.к. здесь бываю не очень часто.
Спасибо, но я специально указывал что это тестерный советник. Он не учитывает и половины боевых условий, но показывает суть работы в системе нечетких множеств.