
Нейросети в трейдинге: Интеллектуальный конвейер прогнозов (Time-MoE)
Введение
Прогнозирование временных рядов остаётся одной из ключевых задач, на которой строится современный алгоритмический трейдинг. От точности модели зависит не только успех торговой стратегии, но и её способность адаптироваться к постоянно меняющемуся характеру рынка. Большинство моделей разрабатывались под конкретную задачу, теряя устойчивость при малейших изменениях рыночной среды. В последнее время наблюдается стремительное развитие фундаментальных моделей (foundation models). Одна из таких моделей была представлена в работе "Time-MoE: Billion-Scale Time Series Foundation Models with Mixture of Experts".
Time-MoE — это Decoder-Only Transformer нового поколения, разработанный специально для временных последовательностей. В его основе лежат принципы разреженного обучения, модульности и прогнозирования на множестве масштабов. Авторы фреймворка демонстрируют, как можно перенести масштабируемость и гибкость крупных моделей в область временных рядов, не жертвуя вычислительной эффективностью. Представленная ими архитектура модели позволяет поддерживать произвольные длины анализируемых последовательностей и горизонтов планирования. При этом, модель способна обрабатывать потоки данных в режиме реального времени.
Первым звеном архитектуры выступает точечная токенизация временного ряда (Point-Wise Tokenization). В отличие от оконных или агрегированных подходов, здесь каждый временной шаг преобразуется в отдельный токен. Это свойство может оказаться полезным в высокочастотной торговле, где даже один тик может изменить картину. В среде MQL5 токены можно формировать на основе баров, тиков и производных индикаторов, включая волатильность, объёмы и сигналы от пользовательских стратегий.
После токенизации данные проходят через эмбеддинговый слой с активацией SwiGLU, которая представляет собой гибрид Swish и Gated Linear Unit. Она позволяет формировать более гладкие и устойчивые представления анализируемой информации, что особенно полезно при наличии рыночного шума и нестабильных трендов.
Сердцем модели является стек из N повторяющихся блоков, каждый из которых сочетает каузальное многоголовое внимание (Causal Multi-Head Self-Attention) и разреженную смесь экспертов (Sparse MoE). Внимание строго ориентировано в прошлое, что гарантирует честную хронологию — модель не видит будущего, а значит, применима в реальных рыночных условиях. MoE добавляет к архитектуре масштабируемость: вместо активации всех параметров модели, для каждого токена выбирается ограниченное число специализированных подмоделей (экспертов). Одни из них учатся лучше работать с импульсными движениями, другие — с фазами консолидации или флетами. Адаптивный механизм принимает решение о маршрутизации токенов.
Но модель не останавливается на уровне обработки данных. Одной из ключевых особенностей TIME-MOE является многомасштабное прогнозирование (Multiscale Forecasting). Во время обучения модель получает задание делать прогнозы одновременно на разных временных горизонтах. Это реализуется через параллельные выходные модули (головы), каждый из которых обучается на своей целевой метке: краткосрочной, среднесрочной или долгосрочной. Такая архитектура позволяет одновременно учитывать микродинамику и макроповедение рынка. И модель способна переключаться между ними в зависимости от рыночного контекста.
Во время инференса вступает в игру динамический выбор головы прогноза (Dynamic Head Scheduling). В зависимости от волатильности, силы тренда или уверенности модели, активируются различные прогнозные модули. Такой адаптивный подход делает Time-MoE особенно ценной в трейдинге, где поведение рынка может меняться мгновенно.
Важно подчеркнуть, что Time-MoE оптимизирован для обучения на масштабных наборах временных рядов. Авторами фреймворка модель была обучена на Time-300B — крупнейшем открытом датасете, содержащем более 300 миллиардов точек временных данных из девяти доменов. Это позволило добиться высокой универсальности модели, устойчивости к смещениям распределения и способности к обобщению на неизвестные задачи. При этом Time-MoE масштабируется до 2.4 миллиардов параметров, активируя только часть из них в процессе инференса, что делает её производительной и экономной одновременно.
Алгоритм Time-MoE
В основе Time-MoE лежит идея создания единой, масштабируемой модели для прогнозирования временных рядов, способной адаптироваться к любым условиям анализируемой окружающей среды и при этом, сохранять управляемую нагрузку на вычислительные ресурсы. Алгоритм фреймворка начинается с точечной токенизации (Point-Wise Tokenization), где фиксируются все важные признаки каждого шага временного ряда. Такой подход гарантирует, что ни один нюанс не потеряется при агрегации.
Преобразование сырых токенов в информативное скрытое пространство осуществляется средствами SwiGLU-эмбеддинга.
![]()
где матрицы W и V обучаются вместе с моделью. Поэлементное умножение ⨂ усиливает значимые признаки, а сочетание функции Swish и механизма врат (Gated Linear Unit) формирует более выразительные эмбеддинги, способные кодировать сложные нелинейные зависимости.
После эмбеддинга токены поступают в стек из N идентичных трансформерных блоков. Каждый блок состоит из трех этапов:
- Нормализация и каузальное внимание: на вход подаются векторы ht,l-1, которые сначала проходят нормализацию, а затем анализируются многоголовым Self-Attention, ограниченным маской, исключающей информацию о будущих значениях. Токен буквально поворачивает голову назад, оглядываясь на всю пройденную историю, но при этом не может заглянуть вперёд, словно следуя строгому правилу: настоящие решения базируются только на прошлом опыте.
- Повторная нормализация позволяет избежать чрезмерной реакции на редкие аномалии.
- Разреженный слой Mixture-of-Experts. Здесь мы направляем каждое историческое окно к группе экспертов — Mixture‑of‑Experts. Адаптивный роутер решает, какие K экспертов из N активировать. Один эксперт (общий N+1) всегда участвует через сигмоидальную весовую функцию. Активные эксперты обрабатывают данные независимо и возвращают свои прогнозы. Итоговый выход блока складывается с исходным сигналом.
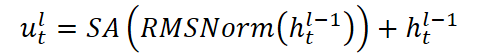
где SA — Self-Attention с H головами, каждая из которых анализирует предыдущие t-1 позиций. Такая конструкция позволяет модели следить за важными событиями в истории, сохраняя причинно-следственные связи.
![]()
![]()
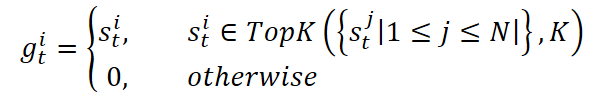
![]()
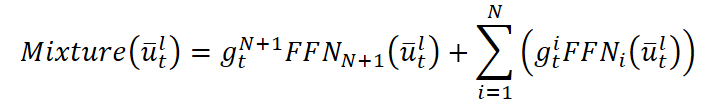
![]()
Эта структура обеспечивает динамический выбор специализации: в периоды высокой волатильности токены перенаправляются к экспертам, обученным распознавать импульсные движения, тогда как в спокойные моменты — к тем, кто лучше знает тренды или флэты. Top-K отбор экспертов позволяет ограничить число активных подсетей, сохраняя основной массив параметров в спящем состоянии. Это позволяет масштабировать модель до миллиардов параметров при постоянном бюджетe инференса.
Когда токен xT проходит через все N слоёв, мы получаем контекстный вектор hT,L, содержащий всю историю и паттерны рынка. Для Multi-Resolution Forecasting из него формируются P прогнозов на горизонты p1,…,pP через однослойные FFN.
![]()
Такая архитектура позволяет одновременно выдавать прогнозы на разные временные отрезки, сохраняя единое скрытое представление.
При обучении модель сталкивается с задачей одновременно прогнозировать несколько временных горизонтов: от ближайших минутных колебаний до отложенных трендов в днях и неделях. Для каждого прогноза авторы фреймворка применяют Huber loss, которая сочетает мягкость квадратичной составляющей и устойчивость линейной части. При малых ошибках Huber loss ведёт себя как классический MSE, аккуратно штрафуя за небольшие отклонения, а при больших, постепенно переходит в L1, снижая влияние редких выбросов и предотвращая взрыв градиентов. Далее модель аккумулирует потери по всем головам прогнозирования.
Благодаря такой схеме, модель учится одновременно ловить краткосрочные импульсы и удерживать долгосрочные тренды, сохраняя цельность прогноза на всех уровнях.
Однако, использование разреженных экспертов (MoE) порождает риск неравномерной загрузки: одни эксперты могут оказаться перегруженными, а другие — без работы. С целью устранения этого эффекта, была добавлена вспомогательная регуляризация, измеряющая дисбаланс. Финальной целью обучения становится сумма основной и вспомогательной частей.
Конечный результат — единый, скоординированный конвейер: от тонкой токенизации до динамической маршрутизации по экспертам, многоуровневого прогноза и сбалансированного обучения.
Авторская визуализация фреймворка Time-MoE представлена ниже.
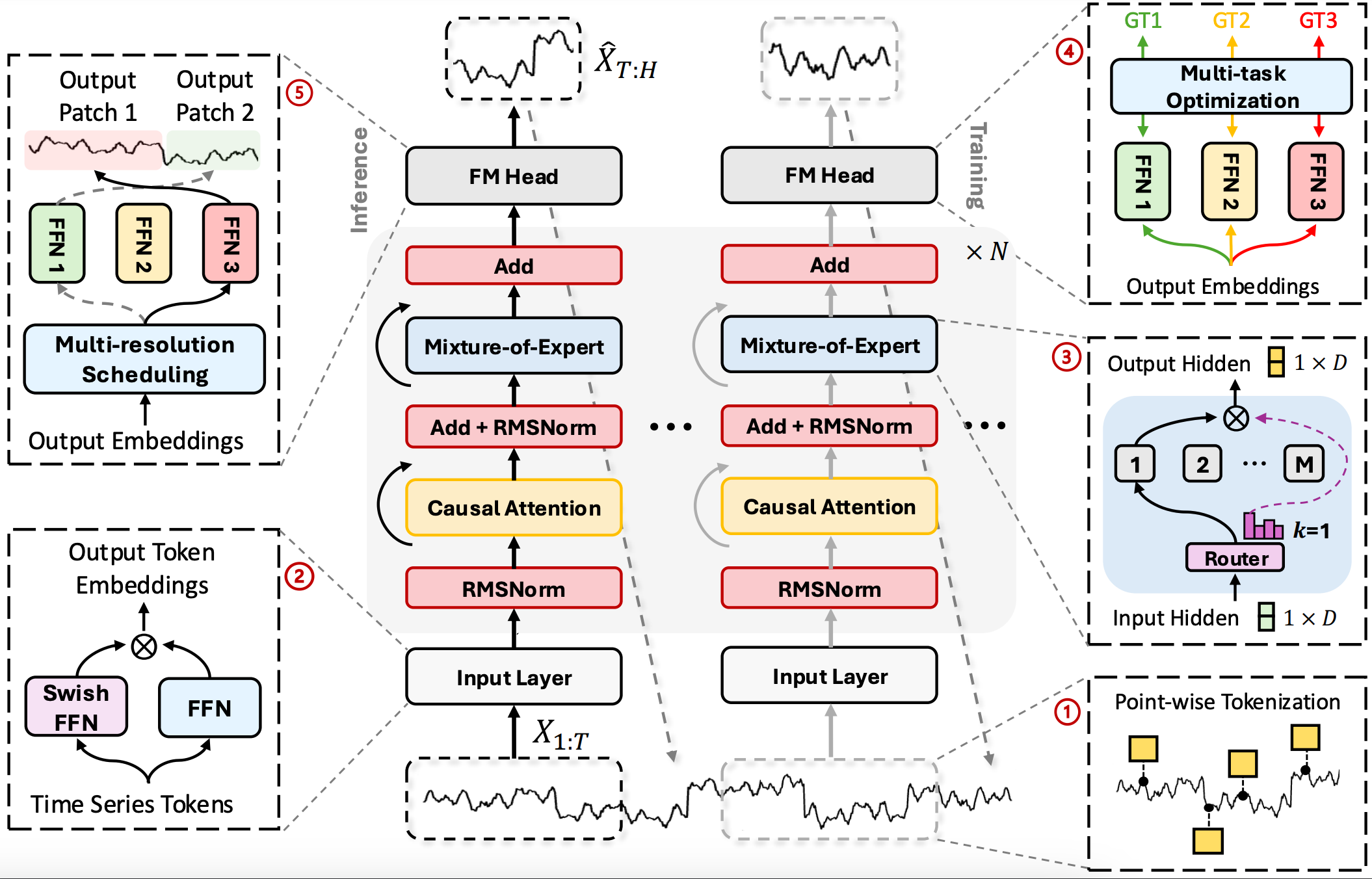
Реализация средствами MQL5
После того как мы подробно рассмотрели теорию и ключевые аспекты фреймворка Time-MoE, пора перейти к практической части нашей работы и оживить теорию в коде. Однако, чтобы не пытаться охватить необъятное сразу, мы разобьем всю систему на логические блоки. И, следуя информационному потоку, будем реализовывать фреймворк шаг за шагом средствами MQL5. Такой поэтапный, практико-ориентированный подход не только облегчит тестирование и отладку каждого блока, но и позволит собрать из них живую, отзывчивую реализацию Time-MoE, готовую к мощной и эффективной работе в реальных условиях рынка.
Согласно первоначальной задумке авторов Time-MoE, все исходные данные проходят через модуль Point-Wise Tokenization, который можно эффективно реализовать средствами существующего сверточного слоя. По сути, каждый бар или тик подаётся на вход короткому 1D-свёрточному фильтру, и результат свёртки — это не что иное, как атомарный токен с набором признаков. Такой приём даёт нам два важных преимущества: во-первых, мы сохраняем информацию о каждом моменте времени без потерь, связанных с агрегацией; во-вторых, свёртка сразу же выявляет локальные паттерны.
Далее данные передаются в SwiGLU-эмбеддинг, над которым нам уже предстоит поработать.
SwiGLU-эмбеддинг
После формирования токенов они отправляются на второй этап — модуль SwiGLU-эмбеддинга, который превращает сырые признаки в ёмкие векторы скрытого пространства. SwiGLU-слой выполняет над ним двойное преображение:
- сначала токен проходит через линейную проекцию и мягкую, плавную функцию Swish;
- затем, через другую проекцию и селективную Gated Linear Unit (GLU).
На выходе два результата сплетаются поэлементным умножением.
![]()
Swish придаёт эмбеддингу плавность, позволяя модели не пропустить тонкие сигналы, а GLU открывает или закрывает отдельные компоненты вектора, подчёркивая действительно важные паттерны.
В нашей реализации слой SwiGLU будет представлен в виде класса CNeuronSwiGLUOCL, унаследованного от базового объекта нейронных слоёв. Внутри этого класса мы создадим два специальных свёрточных слоя, которые выполняют двойную проекцию анализируемого вектора и выдают две версии сигнала. Структура нового объекта представлена ниже.
class CNeuronSwiGLUOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL caProjections[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSwiGLUOCL(void) {}; ~CNeuronSwiGLUOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint window_out, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSwiGLUOCL; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; };
Все внутренние объекты нашего нового класса объявлены статически. Поэтому конструктор и деструктор остаются пустыми. Инициализация всех проекций, параметров свёртки и связи с OpenCL-контекстом возлагается на метод Init. Именно в параметрах этой функции пользователем задаются размеры свёрточного окна, шаг сдвига, число фильтров и указатель на OpenCL-контекст. Все это позволяет осуществить полную настройку слоя перед эксплуатацией.
bool CNeuronSwiGLUOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint window_out, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * window_out * variables, optimization_type, batch)) return false; SetActivationFunction(None);
Внутри метода мы делегируем всю базовую подготовку наверх — на уровень родительского класса, где уже реализованы точки контроля и настройка общих интерфейсов. Для этого достаточно вызвать одноименный метод родительского класса. Это позволяет нам не дублировать низкоуровневые операции и быть уверенными в надёжности среды исполнения.
Тут же мы явно отключаем функцию активации нашего слоя на уровне интерфейсов, так как все нелинейности создаются внутренними объектами.
Когда инфраструктурные детали отработаны, мы приступаем к тонкой настройке своего слоя. Здесь следует обратить внимание, что оба внутренних свёрточных слоя спроектированы так, чтобы выдавать векторы одного и того же размера — это критически важно. Ведь только при совпадающих измерениях мы сможем корректно перемножить их поэлементно. Единственное отличие между ними заключается в последующем применении разных функций активации.
Поэтому на этапе подготовки мы запускаем инициализацию этих слоёв в цикле, автоматически задавая каждому одинаковую конфигурацию свёрточного окна, количество фильтров и шаг сдвига. Это позволяет избежать дублирования кода и гарантирует, что обе проекции всегда остаются синхронными по размерности.
for(uint i = 0; i < caProjections.Size(); i++) { if(!caProjections[i].Init(0, i, OpenCL, window, step, window_out, units_count, variables, optimization, iBatch)) return false; }
После того, как размеры и базовые параметры выверены, мы отдельно настраиваем для каждого слоя собственную функцию активации, чтобы в итоговых эмбеддингах возникало сочетание плавных и селективных признаков. Такой приём упрощает поддержку кода и обеспечивает чёткое разделение ролей внутри SwiGLU-слоя.
caProjections[0].SetActivationFunction(GELU); caProjections[1].SetActivationFunction(None); //--- return true; }
Теперь мы можем завершить работу метода инициализации SwiGLU-слоя, вернув логический результат выполнения операций вызывающей программе.
Когда все настройки слоя завершены, пора завести мотор и пропустить анализируемые данные через наши две проекционные свёртки. Приступаем к построению алгоритма прямого прохода, который реализован в методе feedForward.
bool CNeuronSwiGLUOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { for(uint i = 0; i < caProjections.Size(); i++) if(!caProjections[i].FeedForward(NeuronOCL)) return false;
Как обычно, в параметрах данного метода мы получаем указатель на объект исходных данных. Именно его мы должны передать в оба наших слоя проекции данных. Данную операцию мы выполняем в цикле. Такую возможность предоставляет нам объявление массива объектов.
Именно благодаря тому, что оба слоя выдают тензоры одинаковой размерности, мы можем мгновенно перемножить их поэлементно, не заботясь о несоответствии размерностей. В результате получается единый выходной тензор, где каждое значение — это продукт мненийSwish- и GLU-проекций. Такой приём, основанный на циклической передаче указателя на данные внутрь массива слоёв, обеспечивает компактность кода и позволяет легко масштабировать количество «голосов» внутри слоя, просто меняя длину массива.
if(!ElementMult(caProjections[0].getOutput(), caProjections[1].getOutput(), Output)) return false; //--- return true; }
Полученные результаты сохраняем в буфер результатов внешнего интерфейса и завершаем работу метода, вернув логический результат вызывающей программе.
Когда прямая передача данных через SwiGLU-слой отработала, наступает время по-следить за тем, куда ушла каждая капля ошибки, — организовать обратный проход. Суть в том, чтобы распылить градиент от уровня результатов обратно к исходным данным, аккуратно пройдя через оба наших свёрточных проектора. Данный процесс организован в методе calcInputGradients.
bool CNeuronSwiGLUOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
В теле метода мы получаем указатель на объект исходных данных. Тот же, который использовали при прямом проходе. Только на это раз нам необходимо вернуть в него градиент ошибки, в соответствии с влиянием исходных данных на итоговый результат. Разумеется, что для корректной передачи данных нам необходим действительный объект. Поэтому, перед началом дальнейших операций мы проверяем актуальность полученного указателя.
Во внешних интерфейсах нашего слоя мы уже имеем разницу между текущим прогнозом и желаемым значением. Далее, благодаря совпадающим размерам векторов, мы легко выделяем долю ошибки, которая пришлась на каждый из внутренних фильтров.
if(!ElementMultGrad(caProjections[0].getOutput(), caProjections[0].getGradient(), caProjections[1].getOutput(), caProjections[1].getGradient(), Gradient, caProjections[0].Activation(), caProjections[1].Activation() )) return false;
Эти две струи мы отправляем в соответствующие свёрточные нейроны. Благодаря тому, что оба слоя хранят у себя собственные буферы для градиентов, каждый из них получает свой вектор, идентичный по размеру исходным данным.
После этого, каждый внутренний свёрточный объект самостоятельно разложит свою порцию ошибки дальше. Но на этот раз мы не можем в цикле передать значения на уровень объекта исходных данных. Проблема в том, что каждая последующая операция перезапишет данные, удалив ранее сохранённые. Нам же необходимо аккумулировать значения всех информационных потоков. Поэтому мы сначала передаем градиенты ошибки от первого проекционного слоя.
if(!NeuronOCL.calcHiddenGradients(caProjections[0].AsObject())) return false;
Затем, сохраним указатель на буфер градиентов ошибки объекта исходных данных в локальную переменную. А его место займет другой свободный буфер данных такого же размера.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(caProjections[1].AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false) ) return false; //--- return true; }
И теперь мы можем безопасно передать данные по второму информационному потоку. После чего, суммируем значения, полученные от двух проекционных слоёв. Такой приём гарантирует, что каждая частичка ошибки от разных информационных потоков сохранится и правильно агрегируется, давая нам точное и стабильное обновление весов в последующем шаге оптимизации.
В завершение, вернем указатели на буферы данных в исходное состояние и завершим работу метода, вернув логический результат выполнения операций вызывающей программе.
Алгоритм обратного прохода, как обычно, делится на два логических этапа. Первый этап — распределение градиента ошибки — мы уже рассмотрели подробно. Это ключевой шаг, который позволяет корректно передать ошибку от выхода слоя к исходным данным, соблюдая все особенности мультимагистрального потока информации.
Второй этап — оптимизация параметров, направленная на снижение общей ошибки — остаётся за рамками текущей статьи. Не потому, что он не важен, а потому, что его реализация строго инкапсулирована внутри каждого из свёрточных объектов. Это даёт нам важное преимущество: интерфейс нашего класса не перегружается избыточными деталями, а соблюдает архитектурную чистоту и модульность.
Все необходимые шаги по коррекции весов уже реализованы внутри каждого слоя проекции. Поэтому для выполнения всего цикла оптимизации нам достаточно последовательно вызвать соответствующие методы всех внутренних объектов. Благодаря этому подходу, основной класс остаётся компактным, а логика обновления параметров — надёжной и протестированной в изоляции.
Полный исходный код класса CNeuronSwiGLUOCL и всех его методов, включая функции прямого и обратного прохода, представлен во вложении и может быть изучен для более глубокого понимания всех внутренних механизмов работы.
Мы завершили реализацию компонента SwiGLU-эмбеддинга, и теперь можем смело переходить к следующему этапу — реализации основной части фреймворка Time-MoE — модифицированному блоку Transformer. Этот шаг открывает новую страницу в построении модели, поскольку именно в блоке трансформера происходит формирование высокоуровневого понимания последовательности: модель учится улавливать долгосрочные зависимости, анализировать контекст и прогнозировать вероятную динамику развития событий.
Передача преобразованного временного ряда из SwiGLU-блока в модуль Transformer — это не просто передача данных, а, по сути, передача знаний. Эмбеддинги, сжатые и насыщенные информацией о локальных паттернах, теперь становятся материалом для глубокой аналитики. Однако, архитектура трансформера в Time-MoE существенно отличается от классической реализации. И первое, что бросается в глаза, — это отсутствие привычного FeedForward-блока, который обычно следует сразу за механизмом внимания в каждом слое.
Вместо стандартного модуля, авторы предложили использовать так называемую разреженную смесь экспертов (Sparse Mixture of Experts, или просто MoE). Это архитектурное решение не только добавляет интеллектуальную гибкость модели, но и делает её обучение более осмысленным и контекстно-зависимым. Основная идея MoE — разбить один универсальный слой на множество узкоспециализированных подмодулей (экспертов), каждый из которых обучается обрабатывать определённый тип исходных данных. Такой подход позволяет каждому токену входной последовательности обращаться только к тем экспертам, которые наиболее подходят для обработки его особенностей, оставляя другие в спящем режиме.
Адаптивный механизм выбора экспертов осуществляется с помощью роутера — отдельного подблока, который на основании исходного представления токена принимает решение, какие эксперты будут задействованы. В оригинальной статье подчёркивается важный момент: используется разреженная маршрутизация, при которой каждый токен направляется не ко всем экспертам сразу, а лишь к нескольким (например, двум из десяти возможных). Это значительно снижает вычислительные затраты, позволяя использовать MoE даже в больших масштабах без критической нагрузки на ресурсы.
Такой подход даёт модели множество преимуществ. Во-первых, она учится разделять задачи между экспертами: одни подстраиваются под краткосрочные ценовые колебания, другие — под трендовые движения или волатильность. Во-вторых, модель получает возможность обобщать знания: за счёт разного опыта у разных экспертов можно моделировать более сложные взаимодействия, чем в традиционной одноуровневой архитектуре.
Таким образом, использование Sparse Mixture of Experts в трансформере Time-MoE можно рассматривать как центральную инновацию фреймворка. Это не просто архитектурный эксперимент — это фундаментальный пересмотр подхода к обработке временных последовательностей.
И перед нами становится вопрос: как перенести эти архитектурные идеи в практическую плоскость? Мы ведь не просто теоретизируем, а шаг за шагом создаём рабочую систему. Если вспомнить предыдущие этапы наших исследований, то мы уже сталкивались с концепцией Mixture of Experts (MoE) в рамках разработки фреймворка DUET. Тогда мы реализовали простейший прототип, который помог лучше понять, как работает маршрутизация и агрегирование экспертных решений. Однако ту реализацию сложно назвать по-настоящему разреженной. Скорее, это была имитация механизма выбора — в ней все эксперты вычисляли свои выходы одновременно, а затем их результаты просто умножались на соответствующие маски.
С математической точки зрения итоговый результат выглядел правдоподобно: маски позволяли обнулить выходы ненужных экспертов, формируя тем самым управляемую суперпозицию. Однако, с точки зрения вычислительной эффективности — мы, откровенно говоря, проигрывали. Ведь каждый эксперт в этом случае всё равно выполнял полный объём своей работы, вне зависимости от того, будет ли его результат использован или нет. Таким образом, вычислительная сложность росла линейно с числом экспертов, что сводило на нет одно из ключевых преимуществ архитектуры MoE — её способность масштабироваться без экспоненциального роста затрат.
Такой подход, конечно, допустим для небольших моделей, где количество экспертов и их размерность невелики, а требования к производительности не столь критичны. Однако в реальных сценариях — например, при работе с глубокими и широкими трансформерами, где MoE используется в каждом втором слое, а количество экспертов может достигать десятков — подобное решение становится попросту нежизнеспособным. Вычислительная нагрузка стремительно выходит за пределы разумного, особенно если мы хотим использовать модель в условиях реального времени — например, при алгоритмической торговле на финансовых рынках.
Кроме того, с ростом числа экспертов усложняется и сама процедура маршрутизации. Если мы и дальше будем использовать все сразу, то неизбежно столкнёмся с перегрузкой видеопамяти и потерей эффективности в OpenCL. И тут становится особенно важным придерживаться философии настоящей разреженности: пусть работает лишь небольшая часть сети, но именно та, что необходима здесь и сейчас. Такой подход не только экономит ресурсы, но и делает саму модель более адаптивной и устойчивой к шуму.
В текущей реализации мы решили не ограничиваться лишь формальной маскировкой, а пойти дальше — и построить по-настоящему разреженный алгоритм, соответствующий философии фреймворка Time-MoE. Безусловно, перед нами стоит объёмная задача, охватывающая несколько уровней архитектуры. Здесь важно не просто запрограммировать очередной модуль, а выстроить логическую систему, в которой маршрутизация, активация, агрегация и оптимизация параметров работают слаженно — точно так, как это задумано в оригинальном алгоритме. Поэтому, на данном этапе, я предлагаю сделать небольшой перерыв.
Мы сделали серьёзный шаг вперёд: реализовали собственный SwiGLU-эмбеддинг, наладили информационный поток и подготовили архитектурную почву для подключения Mixture of Experts. Это уже мощный фундамент, на котором мы сможем выстроить следующий уровень модели. Но чтобы не размывать фокус и не перегружать материал, логично будет выделить построение разреженного MoE в отдельную статью. Это позволит нам не только рассмотреть все детали максимально полно, но и избежать фрагментарности в коде и логике.
Так что на этом логичном этапе мы завершаем текущую часть и приглашаем вас продолжить наше путешествие в следующей статье — уже с разреженным MoE на борту.
Заключение
В данной статье мы познакомились с архитектурой Time-MoE — прогрессивным фреймворком, предложенным авторами статьи "Time-MoE: Temporal Mixture of Experts for Long-Term Time Series Forecasting". Эта модель удачно сочетает преимущества Transformer-подхода с идеей разреженной смеси экспертов (Sparse Mixture of Experts), позволяя улучшать качество прогнозирования за счёт адаптивной маршрутизации вычислений. Одним из главных достоинств Time-MoE является способность эффективно обрабатывать как краткосрочные, так и долгосрочные зависимости во временных рядах. А введение модулей SwiGLU делает модель более гибкой.
В практической части мы начали реализацию собственного видения предложенных подходов средствами MQL5, шаг за шагом превращая теоретические концепты в реальный код. В рамках текущего этапа был реализован блок SwiGLU-эмбединга, построенный на основе двух сверточных проекций с поэлементным умножением. Мы уделили внимание вопросам прямого и обратного прохода, корректному распределению градиента и обработке информации внутри сверточных слоев.
Таким образом, фундамент заложен, и мы готовы двигаться дальше. В следующей части мы сосредоточимся на построении действительно разреженного блока MoE, который требует более сложной логики маршрутизации и управления экспертами. Эта часть будет ключевой в архитектуре Time-MoE, и её реализация потребует как аккуратного планирования, так и оригинальных инженерных решений.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 4 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 5 | Test.mq5 | Советник | Советник для тестирования модели |
| 6 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 7 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 8 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Гауссовcкие процессы в машинном обучении: регрессионная модель в MQL5
Гауссовcкие процессы в машинном обучении: регрессионная модель в MQL5
 Самооптимизирующийся советник на языках MQL5 и Python (Часть VI): Использование преимуществ глубокого двойного спуска
Самооптимизирующийся советник на языках MQL5 и Python (Часть VI): Использование преимуществ глубокого двойного спуска
 Оптимизация на основе биогеографии — Biogeography-Based Optimization (BBO)
Оптимизация на основе биогеографии — Biogeography-Based Optimization (BBO)
 Разработка системы репликации (Часть 76): Новый Chart Trade (III)
Разработка системы репликации (Часть 76): Новый Chart Trade (III)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования