MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português
preview
Переосмысливаем классические стратегии (Часть VII): Анализ валютных рынков и суверенного долга на USDJPY

Переосмысливаем классические стратегии (Часть VII): Анализ валютных рынков и суверенного долга на USDJPY

MetaTrader 5 — Примеры | 18 марта 2025, 11:07
440 0
Gamuchirai Zororo Ndawana
Gamuchirai Zororo Ndawana

Искусственный интеллект обладает потенциалом создания новых торговых стратегий для современного инвестора. Маловероятно, что у какого-либо отдельного инвестора будет достаточно времени, чтобы тщательно оценить каждую возможную стратегию, прежде чем решить, какой из них доверить свой капитал. В этой серии статей мы стремимся предоставить вам информацию, необходимую для принятия обоснованного решения о том, какая стратегия лучше всего подходит вам как инвестору.


Краткий обзор торговой стратегии

Ценные бумаги с фиксированным доходом — это инвестиции, которые позволяют безопасно диверсифицировать портфель. Это класс инвестиций, приносящих фиксированную или плавающую доходность до погашения. По истечении срока основная сумма вклада инвестору возвращается, и никаких дальнейших выплат инвестору не производится. Существует множество различных типов ценных бумаг с фиксированным доходом, таких как облигации (bonds) и депозитные сертификаты (Certificates of Deposit).

Облигации являются одной из самых популярных форм ценных бумаг с фиксированным доходом. Именно их мы и рассмотрим здесь. Облигации могут выпускаться корпорацией или правительством. Государственные облигации являются одними из самых надежных инвестиций в мире. Если инвестор желает приобрести конкретную государственную облигацию, он должен сделать это в валюте государства-эмитента. Если конкретная государственная облигация пользуется большим спросом на международном уровне, каждый инвестор, желающий приобрести облигацию, сначала конвертирует свою национальную валюту в желаемую валюту. Это, в свою очередь, может изменить представления рынка относительно справедливой оценки обменного курса двух валют. 

Эффективность облигации измеряется ее доходностью. Между доходностью облигации и уровнем спроса на эту облигацию существует обратная зависимость. Другими словами, по мере падения спроса на конкретную облигацию доходность облигации растет, что стимулирует спрос на нее. Некоторые успешные трейдеры на валютных рынках включают этот фундаментальный анализ в свою торговую стратегию. Сравнивая доходность среднесрочных государственных облигаций двух стран по любому обменному курсу, валютные трейдеры могут получить представление об экономических условиях двух рассматриваемых стран.

Как правило, облигации, предлагающие инвесторам более высокие процентные ставки, будут более популярными, и в соответствии со стратегией валюта страны-эмитента также будет укрепляться с течением времени, а валюта страны, выпускающей облигации с более низкими процентными ставками, будет обесцениваться с течением времени. 


Краткое изложение методологии

Для оценки стратегии мы обучаем различные модели прогнозировать цену закрытия обменного курса USDJPY. У нас было 3 набора предикторов для моделей:

  1. Данные по ценам открытия (Open), максимумам (High), минимумам (Low), закрытию (Close), тиковому объему (OHLCV) с рынка USDJPY.
  2. Данные OHLCV по 10-летним облигациям правительства Японии и 10-летним казначейским облигациям правительства США.
  3. Супернабор из первых двух.

Нашей целью было определить, какой набор предикторов позволит создать модель с наименьшим среднеквадратичным отклонением (RMSE) на невидимых данных. Хотя уровни корреляции между историческими ценами облигаций и парой USDJPY были весьма сильными, -0,85 для обеих государственных облигаций, самый низкий уровень ошибок тестирования был получен для моделей, обученных на основе первого набора предикторов.

Лучшей моделью оказалась линейная регрессия (linear regression, LR). Однако у него нет параметров, которые мы могли бы настроить. Поэтому в качестве нашего решения мы выбрали линейный опорный векторный регрессор (Linear Support Vector Regressor, LSVR). Мы успешно выполнили настройку гиперпараметров на модели LSVR без переобучения обучающей выборки. Более того, наша индивидуальная модель LSVR смогла превзойти эталонную производительность, установленную более простой моделью LR на проверочных данных. Модели обучались и сравнивались с использованием перекрестной проверки временных рядов без случайного перемешивания.

После успешной настройки нашей модели мы экспортировали ее в формат ONNX и интегрировали в наш настроенный советник. 


Извлечение данных

Для начала импортируем необходимые нам библиотеки.

#Import the libraries we need
import pandas as pd
import numpy as np
import MetaTrader5 as mt5
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
import sklearn
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split

Вот версии библиотек, которые мы используем.

#Show library versions
print(f"Pandas version: {pd.__version__}")
print(f"Numpy version: {np.__version__}")
print(f"MetaTrader 5 version: {mt5.__version__}")
print(f"Matplotlib version: {matplotlib.__version__}")
print(f"Seaborn version: {sns.__version__}")
print(f"Scikit-learn version: {sklearn.__version__}")

Pandas: 1.5.3

Numpy: 1.24.4

MetaTrader 5: 5.0.45

Matplotlib: 3.7.1

Seaborn: 0.13.0

Scikit-learn: 1.2.2

Инициализируем наш терминал.

#Initialize the terminal
mt5.initialize()

True

Определим, насколько далеко в будущее мы хотим заглянуть.

#Define how far ahead into the future we should forecast
look_ahead = 20

Извлекаем необходимые нам данные временного ряда из терминала MetaTrader 5.

#Fetch historical market data 
usa_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("UST10Y_U4",mt5.TIMEFRAME_M1,0,100000))
jpn_10y_bond = pd.DataFrame(mt5.copy_rates_from_pos("JGB10Y_U4",mt5.TIMEFRAME_M1,0,100000))
usd_jpy      = pd.DataFrame(mt5.copy_rates_from_pos("USDJPY",mt5.TIMEFRAME_M1,0,100000))

Столбец времени фрейма данных необходимо отформатировать.

#Convert the time from seconds
usa_10y_bond["time"] = pd.to_datetime(usa_10y_bond["time"],unit="s")
jpn_10y_bond["time"] = pd.to_datetime(jpn_10y_bond["time"],unit="s")
usd_jpy["time"] = pd.to_datetime(usd_jpy["time"],unit="s")

Нам следует установить столбец времени в качестве индекса, это упростит нам объединение трех фреймов данных в один.

#Prepare to merge the data
usa_10y_bond.set_index("time",inplace=True)
jpn_10y_bond.set_index("time",inplace=True)
usd_jpy.set_index("time",inplace=True)

Объединение фреймов данных.

#Merge the data
merged_data = usa_10y_bond.merge(jpn_10y_bond,how="inner",left_index=True,right_index=True,suffixes=(" usa"," japan"))
merged_data = merged_data.merge(usd_jpy,left_index=True,right_index=True)


Разведочный анализ данных


Создадим копию фрейма данных, которую будем использовать для построения графика.

data_visualization = merged_data

Нам необходимо сбросить индекс данных визуализации.

#Reset the index
data_visualization.reset_index(inplace=True)

Масштабируем все значения столбцов так, чтобы они начинались с единицы.

#Let's scale the data so all the first values in the column are one
for i in np.arange(1,data_visualization.shape[1]):
    data_visualization.iloc[:,i] = data_visualization.iloc[:,i] / data_visualization.iloc[0,i]

Построим график трех временных рядов, чтобы увидеть, есть ли какие-либо наблюдаемые взаимосвязи.

#Let's create a plot
plt.figure(figsize=(10, 5))
plt.plot(data_visualization.loc[:,"open usa"])
plt.plot(data_visualization.loc[:,"open japan"])
plt.plot(data_visualization.loc[:,"open"])
plt.legend(["USA 10Y T-Note","JGB 10Y Bond","USDJPY Fx Rate"])

Наши рыночные данные.

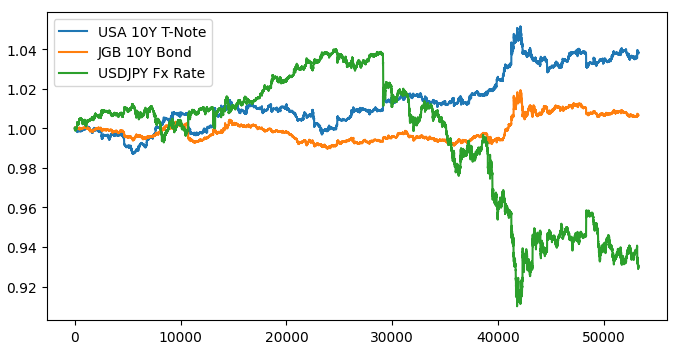
Рис. 1. Визуализация рыночных данных

При наложении трех рынков не наблюдается никакой заметной взаимосвязи. Давайте попробуем сделать график более удобным для чтения, построив график спреда между американскими и японскими облигациями. Таким образом, нам нужно будет учитывать только обменный курс USDJPY и спред по 10-летним облигациям США и Японии. Или, другими словами, три кривые, которые мы нарисовали выше, можно полностью представить всего лишь двумя кривыми.

Сначала нам необходимо рассчитать спред между облигациями.

#Let's create a new feature to show the spread between the securities
data_visualization["spread"] = data_visualization["open usa"] - data_visualization["open japan"]

На левой стороне графика мы видим образец обменного курса USDJPY: всякий раз, когда обменный курс превышает 1, доллар демонстрирует лучшие результаты, чем иена. Когда обменный курс падает ниже 1, ситуация обратная. Более того, всякий раз, когда спред поднимается выше 0, американские облигации показывают лучшие результаты, чем японские. Обратное верно, когда спред падает ниже 0. Таким образом, когда спред ниже 0, что означает, что японские облигации демонстрируют лучшие результаты на рынке, мы также ожидаем увидеть смещение равновесного обменного курса в пользу иены. Однако, визуально осматривая участки, мы можем быстро заметить, что это ожидание не всегда оправдывается.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,2,sharex=True,sharey=False,figsize=(8,4))
columns = ["open","spread"]

for i,ax in enumerate(axs.flat):
    ax.plot(data_visualization.loc[:,columns[i]])
    ax.set_title(columns[i])

Визуализация спреда по обменному курсу.

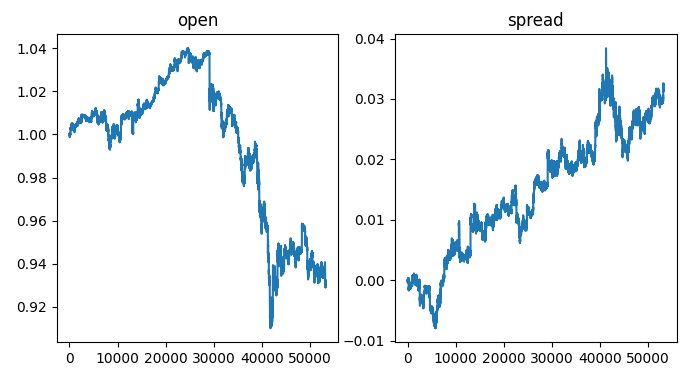
Рис. 2. Визуализация спреда облигаций по обменному курсу

Теперь маркируем наши данные. 

#Label the data
merged_data["target"] = merged_data["close"].shift(-look_ahead)
merged_data["binary target"] = np.nan
merged_data.loc[merged_data["close"] > merged_data["target"],"binary target"] = 0
merged_data.loc[merged_data["close"] < merged_data["target"],"binary target"] = 1
merged_data.dropna(inplace=True)
merged_data.reset_index(inplace=True)
merged_data


Наши маркированные данные

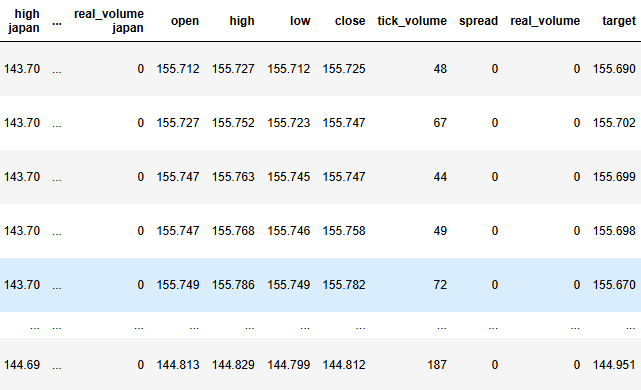
Рис. 3. Текущее состояние нашего фрейма данных

Теперь нам нужно определить нашу цель и входные параметры.

#Define the predictors and target
target = "target"
ohlc_predictors = ['open', 'high', 'low', 'close','tick_volume']
bonds_predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan']
predictors = ['open usa','high usa','low usa','close usa','tick_volume usa','open japan','high japan', 'low japan', 'close japan','tick_volume japan','open', 'high', 'low', 'close','tick_volume']

Проанализируем уровни корреляции в нашем наборе данных.

#Analyze correlation levels
plt.subplots(figsize=(8,6))
sns.heatmap(merged_data.loc[:,predictors].corr(),annot=True)


Наша корреляционная матрица


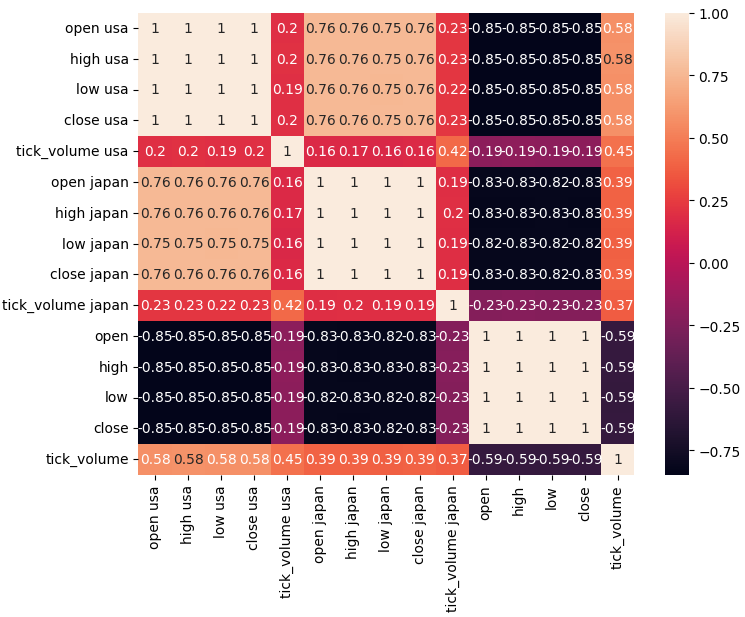
Рис. 4. Наша корреляционная матрица

Как мы можем видеть, между американскими и японскими облигациями наблюдается высокая корреляция — 0,76. Более того, как американские, так и японские облигации имеют сильные отрицательные уровни корреляции с обменным курсом USDJPY. 

Диаграммы рассеяния позволяют нам визуализировать взаимосвязи между переменными в двух измерениях. Создадим диаграммы рассеяния, используя данные, которые мы собрали на рынке облигаций. Начнем с создания диаграммы рассеяния начальной цены американских казначейских облигаций по сравнению с начальной ценой обменного курса USDJPY.

Диаграмма рассеяния 1

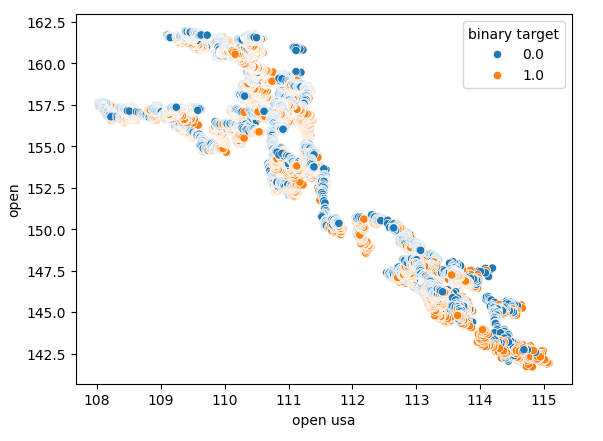
Рис. 5. Диаграмма рассеяния цены открытия облигаций США по отношению к цене открытия пары USDJPY

Как можно заметить, диаграмма рассеяния не выявляет четкой закономерности или зависимости. Похоже, что обменный курс может вырасти или упасть независимо от изменений, происходящих на рынке облигаций.

Мы также построили еще одну диаграмму рассеяния, используя начальную цену японских государственных облигаций по оси X и начальную цену обменного курса USDJPY по оси Y. К сожалению, видимой взаимосвязи в данных по-прежнему не обнаружено.

Диаграмма рассеяния 2

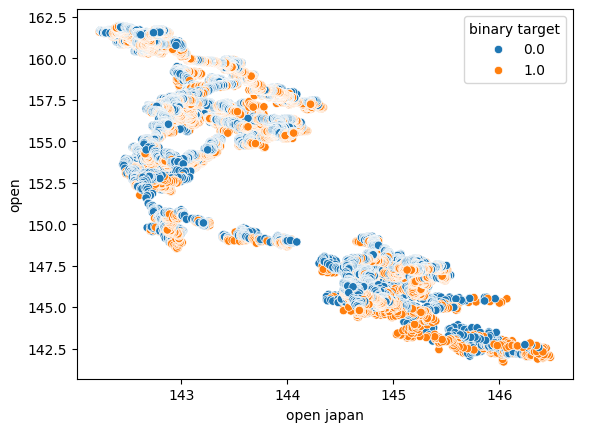
Рис. 6. Диаграмма рассеяния цены открытия японских государственных облигаций в зависимости от цены открытия USDJPY

Мы также попытались создать еще одну диаграмму рассеяния, на этот раз используя обе государственные облигации на каждой оси. Мы отложили начальную цену японских государственных облигаций по оси X, а американские казначейские облигации — по оси Y. Наша диаграмма рассеяния не выявила никаких интересных закономерностей в данных. Это может указывать на то, что могут быть и другие переменные, которые мы не учитываем, но которые также влияют на данные.

Диаграмма рассеяния 3

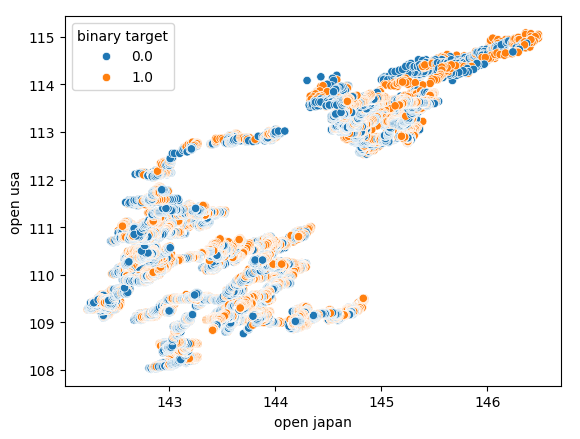
Рис. 7. Диаграмма рассеяния цены открытия японских государственных облигаций по сравнению с ценой открытия американских государственных облигаций

Давайте также проверим, существует ли какая-либо связь между тиковым объемом американского рынка облигаций и ценой закрытия обменного курса USDJPY. К сожалению, на диаграмме рассеяния нет четкого разделения. Мы наблюдаем много случаев, когда цена росла и падала при одном и том же значении тикового объема.

Диаграмма рассеяния 4

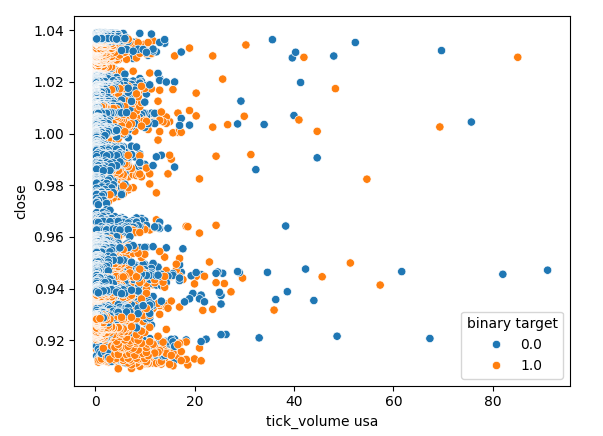
Рис. 8. Диаграмма рассеяния тикового объема американских государственных облигаций в зависимости от цены закрытия USDJPY


Моделирование данных

Теперь мы готовы приступить к моделированию наших данных. Начнем с масштабирования и стандартизации нашего набора данных. Это позволит нашим моделям машинного обучения обучаться эффективно.

#Scale the data
scaled_data = pd.DataFrame(RobustScaler().fit_transform(merged_data.loc[:,predictors]),columns=predictors)

Затем мы разделим наш набор данных на две половины: одна половина будет использоваться для обучения и оптимизации наших моделей, а вторая — для проверки наших моделей и проверки на переобучение.

#Partition the data
train_X , test_X, train_y, test_y = train_test_split(scaled_data,merged_data.loc[:,target],shuffle=False,test_size=0.5)

Для эффективного тестирования различных моделей мы будем хранить их в списке, чтобы иметь возможность последовательно перебирать их и проверять эффективность каждой из них. Нам также потребуется создать 3 фрейма данных:

  1. Первый фрейм данных будет хранить наши уровни ошибок при использовании только обычных данных OHLCV с рынка USDJPY.
  2. Во втором фрейме данных будут храниться наши уровни ошибок, когда мы полагаемся только на данные OHCLV с обоих рынков облигаций.
  3. А последний фрейм данных будет хранить наши уровни ошибок при включении всех доступных нам данных.

#Model selection
from sklearn.linear_model import LinearRegression , Lasso , SGDRegressor
from sklearn.svm import LinearSVR
from sklearn.ensemble import GradientBoostingRegressor , RandomForestRegressor , BaggingRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error 
from sklearn.model_selection import TimeSeriesSplit

#Define the columns
columns = [
    "Linear Model",
    "Lasso",
    "SGD",
    "Linear SV",
    "Gradient Boost",
    "Random Forest",
    "Bagging",
    "K Neighbors",
    "Neural Network"
]

#Define the models
models = [
    LinearRegression(),
    Lasso(),
    SGDRegressor(),
    LinearSVR(),
    GradientBoostingRegressor(),
    RandomForestRegressor(),
    BaggingRegressor(),
    KNeighborsRegressor(),
    MLPRegressor(hidden_layer_sizes=(100,40,20,10),shuffle=False)
]

#Create 2 dataframes to store our error on the training and test sets respectively
ohlc_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
ohlc_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
bonds_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_training_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
all_validation_loss = pd.DataFrame(index=np.arange(0,5),columns=columns)
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Теперь мы проведем перекрестную проверку каждой из наших моделей. Внешний цикл будет проходить по каждой доступной нам модели, в то время как внутренний цикл будет выполнять перекрестную проверку каждой модели и сохранять наши соответствующие уровни ошибок обучения и тестирования. Обратите внимание, что мы проводим перекрестную проверку моделей только на обучающем наборе.

#Now perform cross validation
for j in np.arange(0,len(models)):
    model = models[j]
    for i,(train,test) in enumerate(tscv.split(train_X)):
        model.fit(train_X.loc[train[0]:train[-1],predictors],train_y.loc[train[0]:train[-1]])
        all_training_loss.iloc[i,j] = mean_squared_error(train_y.loc[train[0]:train[-1]],model.predict(train_X.loc[train[0]:train[-1],predictors]))
        all_validation_loss.iloc[i,j] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],predictors]))

Давайте теперь рассмотрим наши уровни ошибок при использовании обычных данных OHLCV с рынка USDJPY. Как мы видим, линейная модель и регрессор линейного опорного вектора показали себя особенно хорошо в данной конкретной настройке.

#Our results using the OHLC data
ohlc_validation_loss

Наши уровни ошибок OHLCV

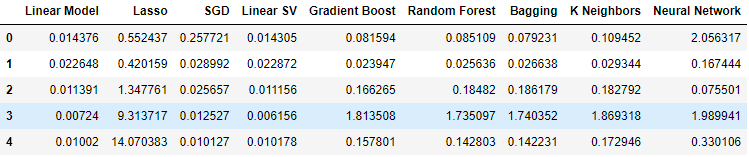
Рис. 9. Уровни ошибок OHLCV

Визуализируем результаты. Начнем с линейного графика эффективности каждой модели в нашей 5-кратной процедуре перекрестной проверки.

#Visualizing the results of using the OHLC predictors
plt.plot(ohlc_validation_loss)
plt.legend(columns)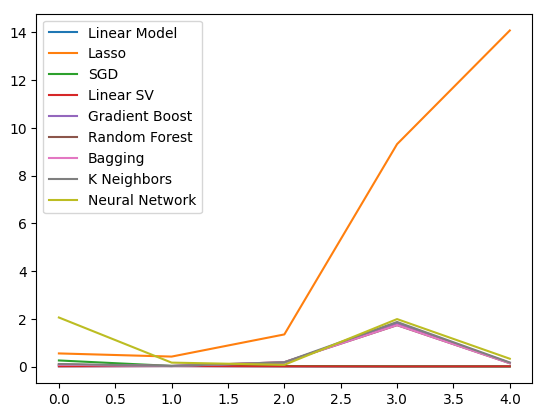

Наши значения ошибок OHLCV

Рис. 10. Линейные графики значений ошибок OHLCV 

Мы ясно видим, что Lasso оказалась наихудшей моделью, ее показатель ошибок проверки оказался самым высоким со значительным отрывом. Однако неясно, какая модель достигает наименьшего уровня ошибок. Для ответа на этот вопрос можно использовать диаграммы размаха.

Диаграммы размаха помогают нам быстро определить, какие модели хорошо справляются с данной конкретной задачей. Как видно из диаграммы ниже, линейная регрессия имеет самые низкие средние уровни ошибок, кроме того, она выглядит стабильной и имеет самые низкие выбросы.

#Visualizing the results of using the OHLC predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(ohlc_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

Уровни ошибок при использовании данных USDJPY OHLCV

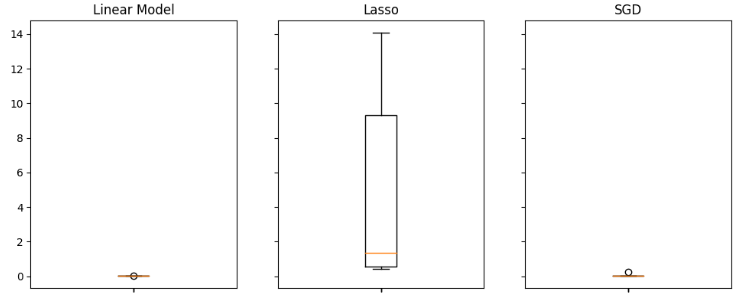
Рис. 11. Некоторые из уровней ошибок при использовании обычного USDJP OHLCV

Когда мы использовали данные, связанные с государственными облигациями, наши показатели производительности упали по всем направлениям. Однако линейный опорный векторный регрессор (Linear SVR), по-видимому, способен достаточно хорошо обрабатывать эти данные.

#Our results using the bonds data
bonds_validation_loss

Ошибки возникают при использовании данных по облигациям

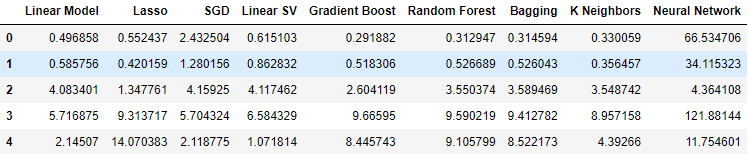
Рис. 12. Уровни ошибок при использовании данных по облигациям

Визуализируем результаты.

#Visualizing the results of using the bonds predictors
plt.plot(bonds_validation_loss)
plt.legend(columns)

Уровни ошибок при использовании данных по облигациям

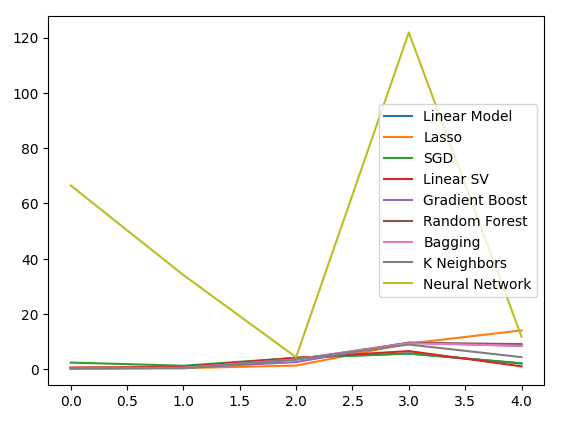
Рис. 13. Линейный график нашей ошибки проверки при использовании данных по облигациям для прогнозирования обменного курса USDJPY

Мы также можем использовать диаграммы размаха для оценки уровня ошибок.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(bonds_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

Уровни ошибок при использовании данных по облигациям

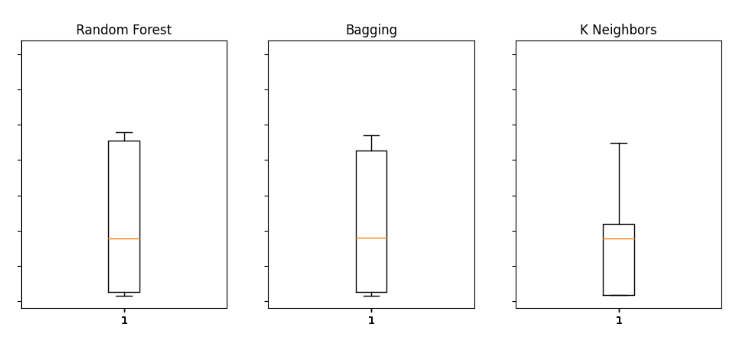
Рис. 14. Некоторые из наших уровней ошибок при использовании данных OHLCV с рынка облигаций для прогнозирования будущей цены закрытия пары USDJPY

Наконец, когда мы включили все доступные данные, наши уровни ошибок улучшились по сравнению с предыдущим шагом, однако они оказались не столь удовлетворительными по сравнению с нашими уровнями ошибок, использовавшими только рыночные котировки на рынке USDJPY.

#Our results using all the data we have
all_validation_loss

Наши уровни ошибок при использовании всех имеющихся у нас данных

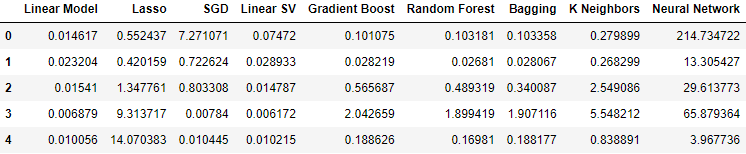
Рис. 15. Уровни ошибок при использовании всех имеющихся у нас данных

Визуализируем нашу работу.

#Visualizing the results of using the bonds predictors
plt.plot(all_validation_loss)
plt.legend(columns)

Наши уровни ошибок при прогнозировании закрытия USDJPY с использованием всех имеющихся у нас данных.

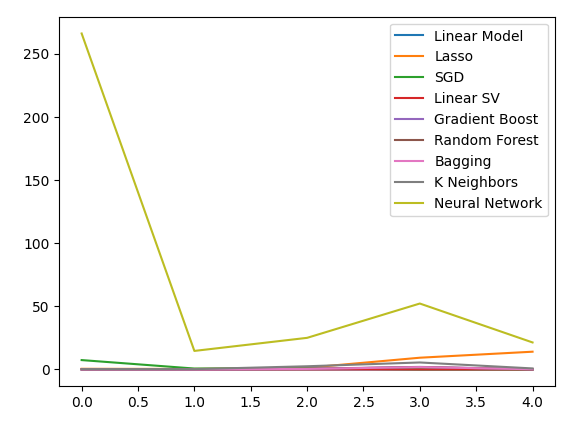
Рис. 16. Уровни ошибок при прогнозировании закрытия USDJPY с использованием всех имеющихся у нас данных

Модель линейной регрессии, безусловно, является здесь наилучшим вариантом. Однако она не содержит гиперпараметров, представляющих для нас интерес. Поэтому мы выберем вторую лучшую модель, линейную SVR, и попытаемся настроить ее так, чтобы она превзошла линейную модель, не переобучаясь при этом обучающему набору. Прежде чем оптимизировать модель, давайте оценим, какие характеристики важны для модели. Если наша стратегия жизнеспособна, мы ожидаем, что наши алгоритмы исключения признаков сохранят столбец. В противном случае, если данные по облигациям будут отброшены, у нас могут появиться основания пересмотреть стратегию.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(2,4,sharex=True,sharey=True,figsize=(16,10))

for i,ax in enumerate(axs.flat):
    ax.boxplot(all_validation_loss.iloc[:,i])
    ax.set_title(columns[i])

Наши уровни ошибок при использовании всех имеющихся у нас данных

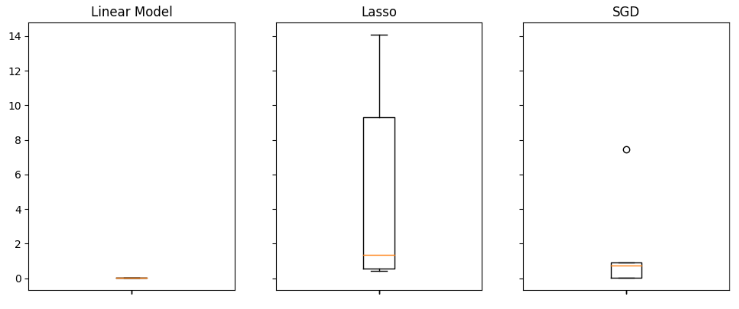
Рис. 17. Наша линейная модель показала наилучшие результаты при использовании всех доступных данных



Выбор признаков

Давайте сначала вычислим значения Шепли (SHAP). Значения SHAP — это метрика, призванная информировать нас о влиянии каждого входного параметра на прогнозы нашей модели по сравнению с базовым значением для каждого столбца. Например, рассмотрим модель, прогнозирующую вероятность получения водителем штрафа за превышение скорости. Если бы мы хотели оценить, способна ли наша модель делать обоснованные прогнозы, мы могли бы спросить: "Как наша модель интерпретирует высокий уровень алкоголя в крови водителя?"

Очевидно, мы ожидаем, что наша модель будет предсказывать более высокую вероятность получения штрафа за превышение скорости при пьяной езде. Значения SHAP помогают нам отвечать на вопросы такого рода, перефразируя вопрос для включения базового значения: "Как наша модель интерпретирует тот факт, что уровень алкоголя в крови водителя превышает допустимую норму?"

Включив установленный законом предел, мы определили базовый уровень. Таким образом, мы рассчитываем наши значения SHAP, выполняя расчеты на основе разницы между прогнозами модели, когда уровень алкоголя в крови водителя ниже и выше допустимых норм. 


Импортируем библиотеку SHAP. 
#Feature selection
import shap

Теперь нам нужно обучить нашу модель.

#The SVR performed quite well, let's inspect it further
model = LinearSVR()
model.fit(train_X,train_y)

Давайте применим пояснение SHAP.

#Calculate SHAP Values
explainer = shap.Explainer(model.predict,test_X)
shap_values = explainer(test_X)

Давайте рассмотрим график SHAP.

shap.plots.beeswarm(shap_values)

Наши значения SHAP

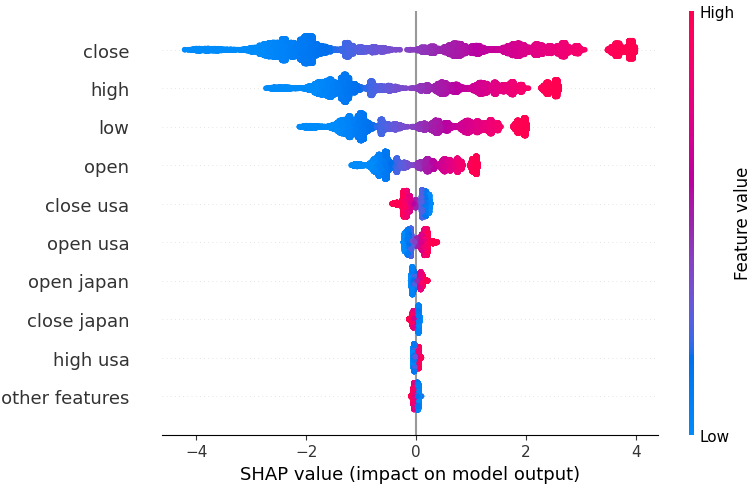
Рис. 18. Наши значения SHAP из нашей линейной модели SVR

Функции расположены по порядку, начиная с самых важных сверху. Таким образом, по объяснениям SHAP, наиболее важной характеристикой является значение закрытия пары USDJPY. Более того, мы также видим, что наши данные, относящиеся к государственным облигациям, были получены сразу после всех данных о ценах валютной пары. Это хорошее доказательство в поддержку нашей стратегии: наши значения SHAP учитывают, что данные по облигациям важнее, чем тиковый объем самого рынка USDJPY.

Однако все объяснения модели следует воспринимать с долей скепсиса. Они не застрахованы от ошибок.

Рассмотрим также обратный отбор. Алгоритм обратного выбора начинается с подгонки полной модели и последовательно исключает признаки до тех пор, пока ошибку теста уже невозможно будет улучшить. 

Давайте импортируем библиотеку mlxtend.

#Let's also perform backward selection
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs

Инициализируем модель.

#Reinitialize the model
model = LinearSVR()

Создадим объект селектора признаков.

#Prepare the feature selector
sfs = SFS(model,
         k_features=(1,train_X.shape[1]),
         forward=False,
          n_jobs = -1,
          scoring="neg_mean_squared_error",
          cv=5)

Установим селектор функций.

#Fit the feature selector
sfs_results = sfs.fit(train_X,train_y)

Давайте посмотрим на выбранные функции.

#The best features we identified
sfs_results.k_feature_names_

('open usa',

 'high usa',

 'tick_volume usa',

 'open japan',

 'low japan',

 'close',

 'tick_volume')

Наш алгоритм обратного исключения придал большее значение данным рынка облигаций, чем нашим значениям SHAP. Таким образом, мы можем обоснованно заключить, что между нашими данными по облигациям и будущим обменным курсом пары USDJPY может существовать надежная связь.


Отобразим результаты на графике.

#Prepare the plot
fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev")
plt.title("Backward Selection on our Linear SVR")
plt.grid()

Результаты обратного исключения

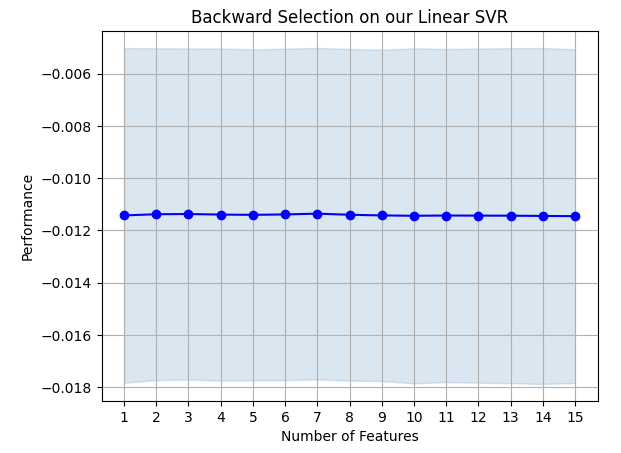
Рис. 19. Результаты обратного исключения

Похоже, что коэффициенты ошибок нашей модели не подвержены резким колебаниям, а это значит, что наша модель может быть стабильной даже в условиях ограниченных данных. Помните, что алгоритм устраняет признаки один за другим до тех пор, пока коэффициент ошибок не станет неустранимым, если удалить любой из признаков, выбранных алгоритмом.


Настройка гиперпараметров

Давайте теперь оптимизируем нашу модель, чтобы она превзошла линейную регрессию.

Сначала импортируем необходимые нам библиотеки.

#Parameter tuning 
from sklearn.model_selection import RandomizedSearchCV

Инициализируем модель.

#Reinitialize the model
model = LinearSVR()

Определим объект тюнера.

tuner = RandomizedSearchCV(model,
                          {
                              "epsilon":[0,0.001,0.01,0.1,25,50,100],
                              "tol": [0.1,0.01,0.001,0.0001,0.00001],
                              "C" : [1,5,10,50,100,1000,10000,100000],
                              "loss":["epsilon_insensitive", "squared_epsilon_insensitive"],
                              "fit_intercept": [False,True]
                          },
                           n_jobs=-1,
                           n_iter=100,
                           scoring="neg_mean_squared_error"
                          )

Настроим модель.

tuner_results = tuner.fit(train_X,train_y)

Интересно отметить, что наши наилучшие параметры практически идентичны настройкам по умолчанию. Однако давайте посмотрим на разницу в производительности.

tuner_results.best_params_

{'tol': 0.0001,

 'loss': 'epsilon_insensitive',

 'fit_intercept': True,

 'epsilon': 0,

 'C': 1}


Проверка на переобучение

Давайте теперь проверим, не переобучаем ли мы обучающий набор. Создадим экземпляры наших моделей. 
#Testing for overfitting
baseline_model = LinearRegression()
default_model =  LinearSVR()
customized_model = LinearSVR(tol=0.0001,loss='epsilon_insensitive',fit_intercept=True,epsilon=0,C=1)

Теперь займемся подгонкой всех трех моделей.

#Fit the models
baseline_model.fit(train_X,train_y)
default_model.fit(train_X,train_y)
customized_model.fit(train_X,train_y)

Подготовка к перекрестной проверке эффективности каждой модели.

#Create a list of models
models = [
    baseline_model,
    default_model,
    customized_model
]

columns = [
    "Linear Regression",
    "Default Linear SVR",
    "Customized Linear SVR"
]

We need to reset the index of our datasets.
#Let's assess our new accuracy levels
test_y = test_y.reset_index()
test_X.reset_index(inplace=True)

Переопределим объект разделения временного ряда и создадим фрейм данных для хранения нашей ошибки проверки.

#Create our time-series test object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
overfitting_error = pd.DataFrame(columns=columns,index=np.arange(0,5))

Cross-validate each model.
for j in np.arange(0,len(columns)):
    model = models[j]
    for i , (train,test) in enumerate(tscv.split(test_X)):
        model.fit(test_X.loc[train[0]:train[-1],predictors],test_y.loc[train[0]:train[-1],"target"])
        overfitting_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"target"],model.predict(test_X.loc[test[0]:test[-1],predictors]))

Посмотрим на результаты.

#Visualizing the results of using the bonds predictors
fig,axs = plt.subplots(1,3,sharex=True,sharey=True,figsize=(8,4))

for i,ax in enumerate(axs.flat):
    ax.boxplot(overfitting_error.iloc[:,i])
    ax.set_title(columns[i])

Наши уровни ошибок на невидимых данных.

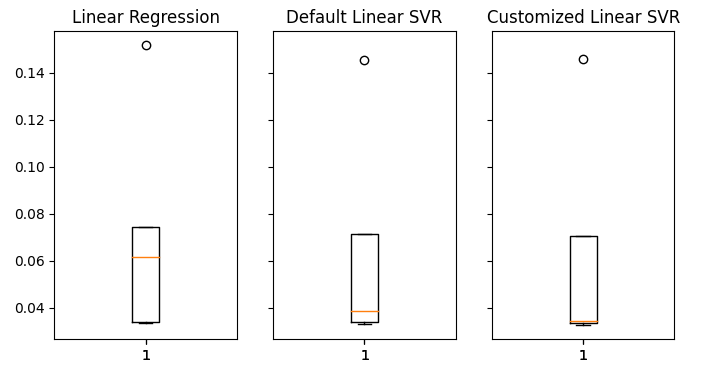
Рис. 20: Уровни ошибок на невидимых данных

Мы ясно видим, что наша модель LinearSVR показала самую низкую среднюю ошибку при проверке. Таким образом, нам удалось превзойти эталон, установленный линейной моделью. Более того, мы также превзошли стандартный уровень ошибок без переобучения обучающей выборки.


Экспорт в ONNX

Теперь давайте подготовимся к экспорту нашей модели в формат ONNX, чтобы мы могли легко интегрировать ее в нашу MQL5-программу.

Прежде чем двигаться дальше, нам необходимо стандартизировать наши данные таким образом, чтобы их можно было воспроизвести в MQL5. Этого можно добиться, вычитая среднее значение столбца из каждого соответствующего значения столбца, а затем разделив каждый столбец на его стандартное отклонение.

Давайте запишем соответствующие значения в CSV-файл на пути к файлу нашего терминала.

#Create scaling factors
scaling_factors = pd.DataFrame(index=("mean","standard deviation"),columns=predictors)

#Write our the values
for i in np.arange(0,scaling_factors.shape[1]):
    scaling_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
    scaling_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std()
    merged_data.loc[:,predictors[i]] = ((merged_data.loc[:,predictors[i]] - scaling_factors.iloc[0,i]) / scaling_factors.iloc[1,i])

scaling_factors

Коэффициенты масштабирования

Рис. 21. Коэффициенты масштабирования

Теперь сохраним CSV-файл.

#Save the scaling factors
scaling_factors.to_csv("C:\\Enter \\Your\\Path\\Here\\MetaQuotes\\Terminal\\D0E82094358C8CF3394F550E51FF075\\MQL5\\Files\\usdjpy scaling factors.csv")

Давайте обучим нашу модель на всех имеющихся у нас данных.

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,"target"])

Импортируем необходимые нам библиотеки.

#Let's import the libraries we need
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import netron
import onnx

Определите тип и форму входных данных нашей ONNX-модели.

#Define the initial input types
initial_types = [('float_input',FloatTensorType([1,len(predictors)]))]

Создадим ONNX-модель.

#Create an ONNX representation of the model
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

Сохраним ONNX-модель в файл с расширением .onnx.

#Save the ONNX model
onnx_name = "USDJPY M1 FLOAT.onnx"
onnx.save(onnx_model,onnx_name)

Визуализируем модель в netron.

#Visualize the model
netron.start(onnx_name)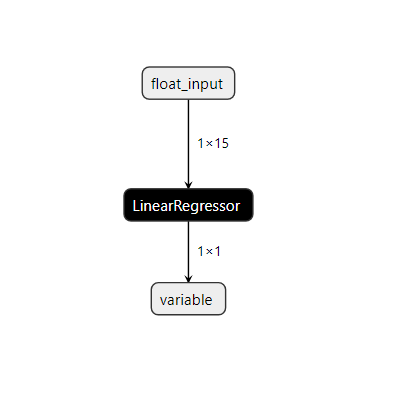

Наша модель LinearSVR

Рис. 22. Визуализация модели Linear SVR


Метаданные нашей модели ONNX

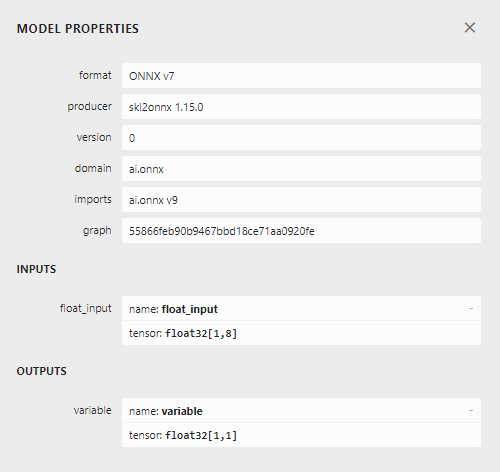
Рис. 23. Форма входных и выходных данных нашей модели ONNX

Входные и выходные данные нашей модели соответствуют нашим спецификациям. Приступим к созданию советника.


Реализация средствами MQL5

Сначала нам понадобится наша модель ONNX как ресурс, который будет скомпилирован в нашу программу. 
//+------------------------------------------------------------------+
//|                                                 USDJPY Bonds.mq5 |
//|                                               Gamuchirai Ndawana |
//|                    https://www.mql5.com/en/users/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Resources                                                        |
//+------------------------------------------------------------------+
#resource "\\Files\\USDJPY M1 FLOAT.onnx" as const uchar onnx_model_buffer[];

Теперь давайте определим несколько глобальных переменных, которые нам понадобятся в нашей программе.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long onnx_model;
float mean_values[15],std_values[15];
vector model_output = vector::Zeros(1);
int state = 0;
int prediction = 0;

Импортируем торговую библиотеку, чтобы легко открывать позиции и управлять ими.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Теперь определим вспомогательные функции для нашего советника. Нам нужна функция, которая загрузит нашу модель ONNX и определит ее входные и выходные формы. Если в какой-либо момент произойдет сбой, наша функция вернет флаг, который прервет инициализацию.

//+------------------------------------------------------------------+
//| Load our onnx file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the model from the buffer
   onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT);

//--- Set the input shape
   ulong input_shape [] = {1,15};

//--- Check if the input shape is valid
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model));
      return(false);
     }

//--- Set the output shape
   ulong output_shape [] = {1,1};

//--- Check if the output shape is valid
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model));
      return(false);
     }
//--- Everything went fine
   return(true);
  }

Нам также нужна функция для чтения CSV-файла, содержащего значения масштабирования, и сохранения их в массиве для дальнейшего использования в нашей функции прогнозирования. Обратите внимание, что первая строка содержит только заголовки столбцов. Первая запись во второй строке — это метка индекса, а вторая запись во второй строке — среднее значение первого столбца. Поэтому наша функция будет проверять текущую итерацию цикла, чтобы отслеживать, где она находится и какие значения важны.

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
void load_scaling_factors(void)
    {
//--- Read in the file
   string file_name = "usdjpy scaling factors.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). 

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file
      
      int counter = 0;
      string value = "";
      
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end 
       {
       
         if (counter > 100) //if you aim to read 10 values set a break point after 10 elements have been read
           break; //stop the reading progress
         
         value = FileReadString(result);
         Print("Trying to read string: ",value," count value: ",counter);
         
         //--- Check where we are
         if((counter >= 17) && (counter < 32))
            {
               mean_values[counter - 17] = (float) value;
            }   
         //--- Check where we are
         if((counter >= 33) && (counter < 48))
            {
               std_values[counter - 33] = (float) value;
            }   
         //--- Reading a new row
         if(FileIsLineEnding(result))
           { 
             Print("row++");
           }
         
         counter++;
       }
      //---Close the file
      ArrayPrint(mean_values);
      ArrayPrint(std_values);
      FileClose(result);
     }
//--- We failed to find the file
else 
   {
      Print("Failed to find the file");
   }

  }

Функция извлечет входные значения нашей модели и стандартизирует их перед получением прогноза от нее. Впоследствии прогноз модели будет сохранен как двоичное состояние, 1 — бычий прогноз, 2 — медвежий. Это поможет нам определить, когда наша модель предсказывает разворот.

//+------------------------------------------------------------------+
//| Obtain a prediction from our model                               |
//+------------------------------------------------------------------+
void model_predict(void)
   {
     //--- Fetch input values
      string symbols[3] = {"UST10Y_U4","JGB10Y_U4","USDJPY"};
      vectorf model_inputs = {iOpen(symbols[0],PERIOD_CURRENT,0),iHigh(symbols[0],PERIOD_CURRENT,0),iLow(symbols[0],PERIOD_CURRENT,0),iClose(symbols[0],PERIOD_CURRENT,0),iTickVolume(symbols[0],PERIOD_CURRENT,0),
                      iOpen(symbols[1],PERIOD_CURRENT,0),iHigh(symbols[1],PERIOD_CURRENT,0),iLow(symbols[1],PERIOD_CURRENT,0),iClose(symbols[1],PERIOD_CURRENT,0),iTickVolume(symbols[1],PERIOD_CURRENT,0),
                      iOpen(symbols[2],PERIOD_CURRENT,0),iHigh(symbols[2],PERIOD_CURRENT,0),iLow(symbols[2],PERIOD_CURRENT,0),iClose(symbols[2],PERIOD_CURRENT,0),iTickVolume(symbols[2],PERIOD_CURRENT,0)
                     };
     //--- Normalize and scale our inputs
     for(int i=0;i < 15;i++)
         {
            model_inputs[i] = ((model_inputs[i] - mean_values[i])/std_values[i]);
         }
     //--- Show the inputs
     Print("Model inputs: ",model_inputs);
     //--- Fetch a forecast from our model
     OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
     //--- Give the user feedback
     Comment("Model forecast: ",model_output[0]);
     
     //--- Store the prediction
     if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 1;
         }
     else if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
         {
            prediction = 2;
         }       
   }

Для процедуры инициализации сначала потребуется успешно загрузить файл ONNX, а затем считать значения масштабирования и, наконец, проверить работоспособность нашей модели.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
  
//--- Load the ONNX file
   if(!load_onnx_file())
     {
      //--- We failed to load our onnx model
      return(INIT_FAILED);
     }
     
//--- Load scaling factors
load_scaling_factors();

//--- Test if our ONNX model works
model_predict();

//--- Everything worked out
   return(INIT_SUCCEEDED);
   
  }

Всякий раз, когда наша программа больше не используется, мы должны освободить ресурсы.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we used for our onnx model
   OnnxRelease(onnx_model);
//--- Release the expert advisor
   ExpertRemove();
  }

Наконец, всякий раз, когда у нас происходят изменения в уровнях цен, мы сначала получаем прогноз с помощью нашей модели. Если у нас нет открытых позиций, мы следуем прогнозу нашей модели и сохраняем флаг, представляющий нашу текущую открытую позицию. В противном случае, если у нас уже есть открытые позиции, мы проверим, соответствует ли прогноз нашей модели нашим открытым позициям, и в случае, если это не так, закроем наши открытые позиции.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
      //--- Obtain a forecast from our model
      model_predict();
      
      //--- Check if we have any positions
      if(PositionsTotal() == 0)
         {
            //--- Reset the state of our system
            state = 0;
            
            //--- Check for an entry
            if(model_output[0] > iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Buy(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_ASK),SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,"USDJPY Bonds AI");
                  state = 1;
               }
            
             if(model_output[0] < iClose("USDJPY",PERIOD_CURRENT,0))
               {
                  Trade.Sell(0.3,"USDJPY",SymbolInfoDouble("USDJPY",SYMBOL_BID),SymbolInfoDouble("USDJPY",SYMBOL_ASK)+2,SymbolInfoDouble("USDJPY",SYMBOL_ASK)-2,"USDJPY Bonds AI");
                  state = 2;
               }
         }
         
      //--- Check for reversals
      if(state != prediction)
         {
            Alert("Reversal detected by the AI system!");
            Trade.PositionClose("USDJPY");
         }
  }
//+------------------------------------------------------------------+

Наша программа в действии

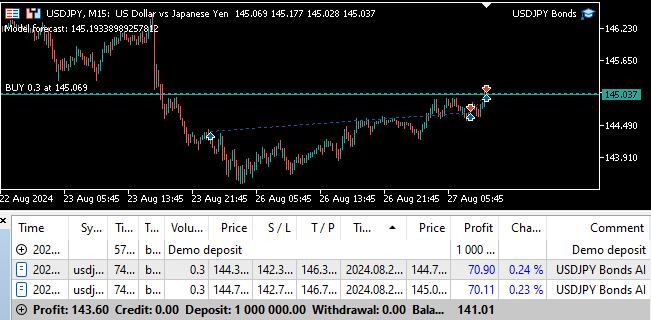
Рис. 24. Форвард-тестирование программы

Наша модель ИИ обнаружила разворот

Рис. 25. Советник может автоматически закрывать позиции при обнаружении разворота


Заключение

В этой статье мы продемонстрировали, как можно использовать ИИ, чтобы вдохнуть новую жизнь в классическую торговую стратегию. Вопрос о том, оправдывает ли наша стратегия ее сложность, остается спорным: мы могли бы получить более низкие уровни точности, используя более простую модель. Таким образом, мы можем сделать обоснованный вывод, что если не потратить больше времени на преобразование характеристик для лучшего выявления взаимосвязи, то, возможно, нам лучше будет использовать более простую стратегию, используя лишь обычные рыночные котировки. 

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15719

Прикрепленные файлы |
Загрузить ZIP
USDJPY_M1_FLOAT.onnx (0.33 KB)
USDJPY_Sovereign_Debt.ipynb (1264.27 KB)
USDJPY_Bonds.mq5 (8.22 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
От начального до среднего уровня: Массив (I) От начального до среднего уровня: Массив (I)
Данная статья является переходом между тем, что рассматривалось до этого, и новым этапом исследований. Чтобы понять эту статью, необходимо прочитать предыдущие. Представленные здесь материалы предназначены только для обучения. Ни в коем случае нельзя рассматривать это приложение как окончательное, цели которого будут иные, кроме изучения представленных концепций.
Разработка системы репликации (Часть 69): Настройка времени (II) Разработка системы репликации (Часть 69): Настройка времени (II)
Сегодня мы рассмотрим, зачем нам нужна функция iSpread. Одновременно с этим мы поймем, как система информирует нас об оставшемся времени бара, когда для этого нет ни одного доступного тика. Представленные здесь материалы предназначены только для обучения. Ни в коем случае не рассматривайте его как окончательное приложение, целью которого не является изучение представленных концепций.
Пример сетевого анализа причинно-следственных связей (CNA) и модели векторной авторегресси для прогнозирования рыночных событий Пример сетевого анализа причинно-следственных связей (CNA) и модели векторной авторегресси для прогнозирования рыночных событий
В настоящей статье представлено подробное руководство по реализации сложной торговой системы с использованием сетевого анализа причинно-следственных связей (CNA) и векторной авторегрессии (VAR) в MQL5. В ней излагаются теоретические основы этих методов, предлагаются подробные объяснения ключевых функций торгового алгоритма, а также приводится пример кода для реализации.
Арбитражный трейдинг Forex: Панель оценки взаимосвязей Арбитражный трейдинг Forex: Панель оценки взаимосвязей
Рассмотрим создание арбитражной панели на языке MQl5. Как получать справедливые курсы валют на Forex разными способами? Создадим индикатор для получения отклонений рыночных цен от справедливых курсов, а также для оценки выгоды от арбитражных путей обмена одной валюты на другую (как в треугольном арбитраже).