Нейросети в трейдинге: Выявление аномалий в частотной области (CATCH)

Введение

Современные финансовые рынки работают в режиме реального времени, где каждую секунду обрабатываются гигантские массивы данных. Котировки акций, валютные курсы, объёмы торгов, процентные ставки — всё это образует сложные многомерные временные ряды. Анализ таких данных критически важен для трейдеров и инвесторов. Он помогает прогнозировать предстоящее движения рынка и выявлять скрытые закономерности.

Одной из главных задач анализа временных рядов является обнаружение аномалий. Неожиданные скачки цен, резкие изменения ликвидности, подозрительные торговые активности могут сигнализировать о рыночных манипуляциях или инсайдерской торговле. Если их вовремя не заметить, последствия могут быть катастрофическими — от больших убытков, до краха целых финансовых институтов.

Аномалии бывают двух типов: точечные и в виде подпоследовательностей. Точечные аномалии — это резкие выбросы, например, внезапный всплеск объёма сделок на одной акции. Их легко обнаружить с помощью стандартных методов. Аномалии подпоследовательностей более сложные — это изменения, которые выглядят нормальными, но нарушают привычные рыночные паттерны. Например, долгосрочный сдвиг в корреляции между акциями, или аномально плавный рост цены на фоне нестабильного рынка. Такие аномалии особенно важны, ведь они могут сигнализировать о скрытых рисках.

Один из наиболее эффективных подходов к их выявлению — перевод данных в частотную область. В этом представлении разные типы аномалий проявляют себя в определённых частотных диапазонах. Например, краткосрочные всплески волатильности влияют на высокочастотные компоненты, а глобальные изменения трендов — на низкочастотные. Однако, стандартные методы часто теряют важные детали, особенно в высоких частотах, где скрываются малозаметные, но критически важные сигналы.

Также важно учитывать связи между различными рыночными активами. Например, если фьючерсы на нефть резко падают, а акции нефтяных компаний остаются стабильными, это может быть сигналом о несоответствии в рынке. Однако, классические модели либо игнорируют такие взаимосвязи, либо учитывают их слишком жёстко, что снижает точность прогнозов.

Одни из вариантов решения указанных проблем предложен в работе "CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching". Её авторы предложили новый фреймворк CATCH, который использует преобразование Фурье для анализа рыночных данных в частотной области. С целью лучшего обнаружения сложных аномалий авторы фреймворка разработали механизм частотного патчинга, который помогает моделировать нормальное поведение активов с высокой точностью. Адаптивный модуль взаимосвязей позволяет автоматически выявлять важные корреляции между рыночными инструментами, игнорируя шум.

Алгоритм CATCH

Архитектура CATCH состоит из трех ключевых модулей:

• Forward Module,
• Channel Fusion Module (CFM),
• Time-Frequency Reconstruction Module (TFRM).

Данная архитектура была разработана с учетом необходимости детального анализа временных и частотных характеристик данных, а также выявления скрытых закономерностей между каналами. Такой подход позволяет эффективно детектировать аномалии даже в сложных многомерных временных рядах.

Первый этап обработки данных — Forward Module. Он включает нормализацию данных, преобразование временного ряда в частотную область с помощью быстрого преобразования Фурье (FFT), а затем разбиение на частотные фрагменты (патчи). Преобразование Фурье позволяет представить временные данные в виде ортогональных тригонометрических функций, сохраняя вещественные и мнимые части частотного спектра анализируемого временного ряда.

Далее выполняется разбиение на L частотных патчей размера P с шагом S. Патчингу подвергаются данные вещественной и мнимой части частотного спектра с одинаковыми параметрами, после чего, данные конкатенируются, объединяя вещественную и мнимую части спектра каждого сегмента в едином тензоре.

На следующем этапе патчи переводятся в скрытое пространство с помощью слоя проекции:

Этот процесс играет важную роль, так как позволяет снизить размерность данных, сохраняя при этом наиболее важные признаки для дальнейшего анализа. Благодаря этому, удается улучшить обобщающую способность модели и повысить точность обнаружения аномалий.

Вторым используется Channel Fusion Module (CFM), который выявляет взаимозависимости между каналами в каждом частотном диапазоне. Для этого применяется механизм Channel-Masked Transformer (CMT). Здесь маска каналов M создается с помощью Mask Generator (MG). MG строит вероятностные матрицы D, которые затем бинаризуются с помощью ресемплинга Бернулли.Таким образом, высокие значения в D приводят к единицам в M, указывая на наличие связи между каналами.

CMT обрабатывает патчи с учетом маскированного внимания, которое можно представить в виде следующих математических выражений:

Для достижения эффективной оптимизации в контексте генерации масок и корректировки механизмов внимания, важно разработать четкие цели оптимизации, которые позволят повысить качество получаемых масок. В данном случае, ключевым аспектом является явное повышение коэффициентов внимания между релевантными каналами, которые были определены с помощью маски. Это позволяет выровнять механизм внимания с наиболее актуальной и оптимальной корреляцией каналов, что в свою очередь, способствует улучшению качества модели.

Одним из важнейших преимуществ такого подхода является возможность избежать негативных эффектов, возникающих при включении нерелевантных каналов в процесс внимания. Маскированный механизм, с учетом корректировки связей, эффективно фокусирует внимание на наиболее значимых каналах, минимизируя влияние помех и искажений. Такой подход позволяет достичь устойчивости механизма внимания, что значительно повышает точность и эффективность модели в условиях изменяющихся данных.

Следующим шагом является итеративная оптимизация генератора масок, направленная на более точное уточнение корреляций между каналами. Этот процесс включает в себя настройку механизма внимания в слое маскированного Transformer в разрезе каналов, что позволяет полноценно захватить и обработать все возможные взаимосвязи между каналами.

Для оптимизации механизма маскирования авторы фреймворка предлагают использовать функцию потерь ClusteringLoss:

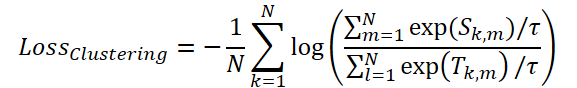
На завершающем этапе Time-Frequency Reconstruction Module (TFRM) выполняет обратное преобразование Фурье (iFFT) для восстановления временного ряда:

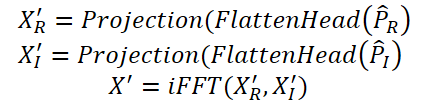
Аномалии выявляются на основе ошибки реконструкции.

Благодаря использованию комплексного анализа данных, основанного на временных и частотных характеристиках, модель CATCH обеспечивает надежное выявление аномалий.

Авторская визуализация фреймворка CATCH представлена ниже.

Реализация средствами MQL5

После рассмотрения теоретических аспектов фреймворка CATCH, мы переходим к практической части нашей статьи, в которой реализуем собственное видение предложенных подходов средствами MQL5.

Прежде всего, следует обратить особое внимание на тот факт, что в данном фреймворке практически все операции выполняются в частотной области анализируемых данных. Это ключевая особенность, которая определяет подход к обработке данных и выбор математических методов.

Как известно, представление сигнала в частотной области осуществляется с использованием комплексных чисел. Следовательно, для корректного функционирования системы необходимо обеспечить эффективную обработку комплексных данных, включая арифметические операции.

Подобная задача уже частично решалась нами в процессе работы над фреймворком ATFNet. Тогда были заложены принципы обработки спектральных данных и выработаны методологические подходы, которые теперь могут быть использованы при создании текущего решения. Эти наработки позволяют нам значительно упростить реализацию основных функций.

Сверточный слой комплексных данных

Начнем нашу работу с разработки сверточного слоя для работы с комплексными значениями. Как показывает практика, сверточные слои являются одним из наиболее эффективных инструментов для обработки многомерных последовательностей. Именно по этой причине мы уделяем первоочередное внимание построению данного компонента.

Как обычно, сначала мы построим алгоритмы функционирования нового объекта на стороне OpenCL-контекста. Вынос всех ключевых операций на уровень GPU позволяет нам добиться максимального параллелизма, что критически важно при обработке многомерных данных. В отличие от последовательных вычислений на CPU, здесь каждое ядро GPU выполняет часть общей задачи, что приводит к значительному ускорению работы модели. Как в процессе обучения, так и во время промышленной эксплуатации.

Операции прямого прохода реализуем в кернеле FeedForwardComplexConv. В параметрах данного кернела передаются указатели на 3 буфера данных и ряд констант, определяющих структуру данных.

Следует обратить особое внимание на то, что все буферы данных используют векторный тип float2. Этот выбор обусловлен необходимостью эффективной обработки комплексных чисел, где каждая величина представлена парой значений: действительной и мнимой частью.

Использование float2 дает нам несколько ключевых преимуществ:

• Оптимизация загрузки и сохранения данных: благодаря векторному представлению, мы можем одновременно извлекать из буферов и записывать в них сразу два значения, что сокращает количество операций чтения и записи.
• Аппаратное ускорение: OpenCL предоставляют аппаратную поддержку работы с векторными типами, что позволяет ускорить выполнение арифметических операций.
• Единообразное представление данных: использование float2 делает код более читаемым и логичным, так как каждая переменная явно соответствует комплексному числу.

__kernel void FeedForwardComplexConv(__global const float2 *matrix_w,
                                     __global const float2 *matrix_i,
                                     __global float2 *matrix_o,
                                     const int inputs,
                                     const int step,
                                     const int window_in,
                                     const int activation
                                    )
  {
   const size_t i = get_global_id(0);
   const size_t units = get_global_size(0);
   const size_t out = get_global_id(1);
   const size_t w_out = get_global_size(1);
   const size_t var = get_global_id(2);
   const size_t variables = get_global_size(2);

Работа данного кернела предполагается в трехмерном пространстве задач. По-первому измерению мы указываем количество элементов последовательности. По-второму — количество фильтров. А третье измерение пространства задач указывает на число независимых унитарных последовательностей в общем тензоре исходных данных. В теле кернела мы сразу идентифицируем текущий поток операций в пространстве задач по всем измерениям. Полученные значения сохраняем в локальные константы.

Далее, на основании результатов идентификации потока операций определяем смещения в буферах данных. Данная операция полностью идентична алгоритму, используемом в ранее созданном сверточном нейронном слое действительных значений, что стало возможным, благодаря использованию векторного типа данных для представления комплексных величин.

int w_in = window_in;
int shift_out = w_out * (i + units * var);
int shift_in = step * i + inputs * var;
int shift = (w_in + 1) * (out + var * w_out);
int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in)) + inputs * var;

На этом завершается подготовительная работа, и мы переходим непосредственно к операции сверкти. В данном случае, исходные данные и обучаемые параметры фильтров являются комплексными величинами. Результат операций тоже будет представлен комплексной величиной. А все математические операции мы будем осуществлять с помощью ранее созданных функций базовых операций с комплексными величинами.

Вначале объявим локальную переменную для временного хранения промежуточных результатов и перенесем в нее значение обучаемого элемента смещенения.

   float2 sum = ComplexMul((float2)(1, 0), matrix_w[shift + w_in]);
#pragma unroll
   for(int k = 0; k <= stop; k ++)
      sum += IsNaNOrInf2(ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]), (float2)0);

А затем, организуем цикл умножения вектора исходных данных на соответствующий вектор фильтра, с суммированием результатов в локальной переменной.

Затем, нам остается лишь применить необходимую функцию активации и сохранить полученное значение в буфер результатов.

   switch(activation)
     {
      case 0:
         sum = ComplexTanh(sum);
         break;
      case 1:
         sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum));
         break;
      case 2:
         if(sum.x < 0)
           {
            sum.x *= 0.01f;
            sum.y *= 0.01f;
           }
         break;
      default:
         break;
     }
   matrix_o[out + shift_out] = sum;
  }

Следующим этапом переходим к построению алгоритмов обратного прохода. Рассмотрим кернел распределения градиента ошибки CalcHiddenGradientComplexConv. Здесь мы используем тот же подход представления комплексных чисел в виде векторной величины. При этом в параметрах метода добавляем буферы градиентов ошибки на соответствующих уровнях операций.

__kernel void CalcHiddenGradientComplexConv(__global const float2 * matrix_w,
                                            __global const float2 * matrix_g,
                                            __global const float2 * matrix_o,
                                            __global float2 * matrix_ig,
                                            const int outputs,
                                            const int step,
                                            const int window_in,
                                            const int window_out,
                                            const int activation,
                                            const int shift_out
                                           )
  {
   const size_t i = get_global_id(0);
   const size_t inputs = get_global_size(0);
   const size_t var = get_global_id(1);
   const size_t variables = get_global_size(1);

Следует обратить внимание, что целью данной операции является передача градиента ошибки на уровень исходных данных в соответствии с их влиянием на результат работы модели. Это и повлияло на изменения пространства задач работы кернела. В своей реализации мы используем двух мерное пространство задач. Первое измерение указывает на элемент в последовательности исходных данных, а второе — на унитарную последовательность многомерного ряда.

В теле кернела мы, как и ранее, сначала идентифицируем текущий поток операций во всех измерениях пространства задач. Подученные значения сохраняем в виде локальных констант.

Далее, определяем смещения в буферах данных. Здесь стоит обратить внимание, что один элемент исходных данных в зависимости от используемого шага окна свертки может участвовать в нескольких операциях свертки. Следовательно, нам предстоит собрать градиент ошибки по всем таким операциям. Поэтому мы определяем границы диапазонов, в которых будем собирать градиент ошибки.

float2 sum = (float2)0;
float2 out = matrix_o[i];
int start = i - window_in + step;
start = max((start - start % step) / step, 0) + var * inputs;
int stop = (i + step - 1) / step;
if(stop > (outputs / window_out))
   stop = outputs / window_out;
stop += var * outputs;

После завершения подготовительной работы организуем цикл прохода по ранее определенным диапазонам с заданным шагом и суммируем градиенты ошибки с учетом соответствующих весовых коэффициентов.

#pragma unroll
   for(int h = 0; h < window_out; h ++)
     {
      for(int k = start; k < stop; k++)
        {
         int shift_g = k * window_out + h;
         int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1);
         if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out)
            break;
         sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]);
        }
     }
   sum = IsNaNOrInf2(sum, (float2)0);

Полученное значение скорректируем на производную функции активации исходных данных.

   switch(activation)
     {
      case 0:
         sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out));
         break;
      case 1:
         sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out));
         break;
      case 2:
         if(out.x < 0.0f)
           {
            sum.x *= 0.01f;
            sum.y *= 0.01f;
           }
         break;
      default:
         break;
     }
   matrix_ig[i] = sum;
  }

Результат операций сохраняем в соответствующем элементе глобального буфера данных.

Полный код представленных выше кернелов вы можете найти во вложении к статье. Там же представлен полный код кернелов оптимизации обучаемых параметров фильтров, которые я предлагаю оставить для самостоятельного изучения. А мы переходим к организации процессов на стороне основной программы.

Здесь мы создаем новый объект CNeuronComplexConvOCL, структура которого представлена ниже.

class CNeuronComplexConvOCL    :  public CNeuronConvOCL
  {
protected:
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronComplexConvOCL(void)   {  activation = None;   }
                    ~CNeuronComplexConvOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint window_out, 
                          uint units_count, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronComplexConvOCL;   }
  };

Вполне закономерно, что в качестве родительского класса используется объект сверточного слоя действительных величин. Это позволяет нам полностью использовать инфраструктуру родительского класса, включая внутренние объекты и интерфейсы. Тем не менее, некоторые корректировки в работу унаследованных методов нам предстоит внести.

Прежде всего, конечно, это методы прямого и обратного проходов. Мы переопределяем их на работу с новыми кернелами OpenCL-программы, алгоритмы которых были описаны выше. Алгоритм постановки указанных кернелов в очередь выполнения остается стандартной. Поэтому мы не будем останавливаться на детальном рассмотрении этих методов. Оставим их для самостоятельного изучения, полный код представлен во вложении.

Однако, уделим немного времени рассмотрению алгоритма метода инициализации нового объекта. Ведь работа с комплексными величинами ведет к изменениям буферов данных. Здесь стоит отметить, что, хотя MQL5 поддерживает работу с комплексными величинами, мы не стали вводить новые объекты буферов данных. А лишь увеличили размер существующих. Это делает наше решение боле универсальным и не требует внесение сложных доработок в работе методов.

Структура параметров метода инициализации полностью унаследована от родительского класса.

bool CNeuronComplexConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint window_out, 
                                 uint units_count, uint variables, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * window_out * variables,
                                                                         optimization_type, batch))
      return false;

В теле метода сначала вызываем одноименный метод полносвязного слоя, который является родительским классом всех объектов нейронных слоев в нашей библиотеке. В том числе и сверточного слоя. Мы не можем воспользоваться одноименным методом прямого родительского класса ввиду несоответствия размеров буферов данных.

Обратите внимание, что при определении размера объекта, создаваемого средствами метода родительского класса, мы указываем размер слоя в 2 раза больше расчётного. Как не сложно догадаться, это вызвано необходимостью хранения действительной и мнимой частью комплексной величины.

Затем сохраним константы архитектуры объекта во внутренние переменные.

iWindow = (int)window;
iStep = MathMax(step, 1);
activation = None;
iWindowOut = window_out;
iVariables = variables;

Следующим этапом переходим к инициализации унаследованных буферов данных. Первым проверим актуальность и, при необходимости, создадим новый объект буфера обучаемых параметров.

if(CheckPointer(WeightsConv) == POINTER_INVALID)
  {
   WeightsConv = new CBufferFloat();
   if(CheckPointer(WeightsConv) == POINTER_INVALID)
      return false;
  }

При определении размеров буфера обучаемых параметров, следует учесть, что здесь мы так же используем комплексные величины. Поэтому размер буфера увеличиваем в 2 раза от расчетного значения.

int count = (int)(2 * (iWindow + 1) * iWindowOut * iVariables);
if(!WeightsConv.Reserve(count))
   return false;

И инициализируем буфер случайными значениями.

float k = (float)(1 / sqrt(iWindow + 1));
for(int i = 0; i < count; i++)
  {
   if(!WeightsConv.Add((GenerateWeight() * 2 * k - k)*WeightsMultiplier))
    return false;
  }
if(!WeightsConv.BufferCreate(OpenCL))
   return false;

Далее, в зависимости от метода оптимизации параметров, инициализируем нужное количество буферов для сохранения данных моментов оптимизации параметров. Начальная инициализация этих буферов осуществляется нулевыми значениями.

   if(optimization == SGD)
     {
      if(CheckPointer(DeltaWeightsConv) == POINTER_INVALID)
        {
         DeltaWeightsConv = new CBufferFloat();
         if(CheckPointer(DeltaWeightsConv) == POINTER_INVALID)
            return false;
        }
      if(!DeltaWeightsConv.BufferInit(count, 0.0))
         return false;
      if(!DeltaWeightsConv.BufferCreate(OpenCL))
         return false;
     }
   else
     {
      if(CheckPointer(FirstMomentumConv) == POINTER_INVALID)
        {
         FirstMomentumConv = new CBufferFloat();
         if(CheckPointer(FirstMomentumConv) == POINTER_INVALID)
            return false;
        }
      if(!FirstMomentumConv.BufferInit(count, 0.0))
         return false;
      if(!FirstMomentumConv.BufferCreate(OpenCL))
         return false;
      //---
      if(CheckPointer(SecondMomentumConv) == POINTER_INVALID)
        {
         SecondMomentumConv = new CBufferFloat();
         if(CheckPointer(SecondMomentumConv) == POINTER_INVALID)
            return false;
        }
      if(!SecondMomentumConv.BufferInit(count, 0.0))
         return false;
      if(!SecondMomentumConv.BufferCreate(OpenCL))
         return false;
     }
//---
   return true;
  }

После чего, завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.

На этом мы завершаем рассмотрение алгоритмов организации работы объекта сверточного слоя работы с комплексными величинами. Полный код данного объекта и всех его методов представлен во вложении к статье.

Объект маскированного внимания к комплексным величинам

Следующим, довольно крупным, блоком нашей работы будет создание объекта маскированного внимания к комплексным величинам, который ляжет в основу Channel Fusion Module.

Ранее мы уже создавали объекты маскированного внимания, работающие с действительными величинами. Сейчас же нам предстоит построить алгоритм работы с комплексными величинами и, конечно, добавить некоторые особенности фреймворка CATCH.

Как всегда, работу над новым объектом мы начинаем с построения процессов на стороне OpenCL-контекста. Алгоритм прямого прохода реализуем в кернеле MaskAttentionComplex. В параметрах кернела будем передавать указатели на 5 буферов данных и 2 константы, определяющие структуру анализируемых данных. Так как предполагается работа с комплексными величинами, то буфера, которые предназначены для передачи исходных данных и получения результатов, получили векторный тип float2. Однако, буфер матрицы маскирования и коэффициентов внимания по-прежнему содержат действительные числа, поскольку представляют собой вероятностное распределение.

__kernel void MaskAttentionComplex(__global const float2 *q,
                                   __global const float2 *kv,
                                   __global float2 *scores,
                                   __global const float *masks,
                                   __global float2 *out,
                                   const int dimension,
                                   const int heads_kv
                                  )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_local_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_local_size(1);
   const int heads = get_global_size(2);

Работа кернела предполагается в трехмерном пространстве задач. Первое измерение отвечает за размерность тензора Query и указывает на количество анализируемых элементов. Второе измерение укажет размерность тензора Key — количество элементов для поиска зависимостей. По этому измерению мы объединяем потоки в рабочие группы. А третье измерение укажет на количество голов внимания. В теле кернела мы сразу идентифицируем поток по всем измерениям пространства задач и сохраняем полученные значения в локальные константы.

На основании данных констант мы определяем смещение во всех буферах данных.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;

И тут же сохраняем значение маски в локальной переменной.

   const float mask = IsNaNOrInf(masks[shift_s], 0);

Здесь следует обратить внимание, что на вход кернела мы ожидаем тензор маскирования с учетом голов внимания. Иными словами, каждая голова внимания имеет свою матрицу маскирования каналов.

Далее объявим массив в локальной памяти OpenCL-контекста, который будем использовать для обмена данными в рамках группы.

   const uint ls = min((uint)kunits, (uint)LOCAL_ARRAY_SIZE);
   float2 koef = (float2)(fmax((float)sqrt((float)dimension), (float)1), 0);
   __local float2 temp[LOCAL_ARRAY_SIZE];

На этом мы завершаем подготовительную работу и переходим непосредственно к процессу вычислений. Вначале нам предстоит определить коэффициенты внимания. Для этого организуем цикл умножения советующих векторов Query и Key. Экспоненциальное значение полученного произведения умножаем на маску.

//--- Score
   float score = 0;
   float2 score2 = (float2)0;
   if(ComplexAbs(mask) >= 0.01)
     {
      for(int d = 0; d < dimension; d++)
         score2 = IsNaNOrInf2(ComplexMul(q[shift_q + d], kv[shift_k + d]), (float2)0);
      score = IsNaNOrInf(ComplexAbs(ComplexExp(ComplexDiv(score, koef))) * mask, 0);
     }

Обратите внимание, данную операцию мы выполняем только в случае, если коэффициент маскирования, больше или равен пороговому значению. Тем самым, мы исключаем влияние неактуальных каналов.

Далее нам необходимо нормализовать полученные значения, переведя их вероятностное измерение с помощью функции SoftMax. Для этого мы организуем процесс суммирования полученных значений в рамках рабочей группы. Вначале организуем цикл частичного суммирования значений в элементах локального массива.

//--- sum of exp
#pragma unroll
   for(int i = 0; i < kunits; i += ls)
     {
      if(k >= i && k < (i + ls))
         temp[k % ls].x = (i == 0 ? 0 : temp[k % ls].x) + score;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

А затем, суммируем значение элементов нашего массива.

   uint count = ls;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k].x += (k < count && (k + count) < kunits ? temp[k + count].x : 0);
      if(k + count < ls)
         temp[k + count].x = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

В результате выполнения всех итераций циклов, в первом элементе локального массива содержится сумма всех значений в рамках рабочей группы. И теперь нам необходимо разделить значение коэффициента внимания, полученного в каждом потоке операций, на посчитанное суммарное значение для получения желаемого нормализованного представления. Результат операций сохраняем в соответствующем элементе глобального буфера.

//--- score
   if(temp[0].x > 0)
      score = score / temp[0].x;
   scores[shift_s] = score;

Теперь нам остается определить итоговое представление анализируемого элемента с учетом влияния других каналов. Для этого нам необходимо умножить вектор полученных коэффициентов внимания на матрицу Value. Данный процесс усложняется необходимостью выполнения операций в параллельных потоках рабочей группы, ведь каждый поток содержит только один коэффициент внимания. Поэтому мы создаем целую систему циклов. Внешний цикл перебирает элементы соответствующей строки матрицы Value.

//--- out
#pragma unroll
   for(int d = 0; d < dimension; d++)
     {
      float2 val = (score > 0 ? ComplexMul(kv[shift_v + d], (float2)(score,0)) : (float2)0);

И в теле цикла мы сразу сохраняем текущее значение из глобального буфера данных, умноженное на соответствующий коэффициент внимания в локальной переменной. Однако, с целью сокращения количества дорогих операций обращения к глобальной памяти, данная операций выполняется только при наличии коэффициента внимания больше "0". В противном случае мы безболезненно можем инициализировать переменную нулевым значением без обращения к глобальному буферу данных.

Далее нам необходимо суммировать значения, полученные в параллельных потоках операций рабочей группы. Здесь мы организуем процесс, аналогичный суммированию коэффициентов внимания. Сначала суммируем отдельные значения в элементах локального массива.

#pragma unroll
      for(int i = 0; i < kunits; i += ls)
        {
         if(k >= i && k < (i + ls))
            temp[k % ls] = (i == 0 ? (float2)0 : temp[k % ls]) + val;
         barrier(CLK_LOCAL_MEM_FENCE);
        }

А затем суммируем значения элементов локального массива.

      uint count = ls;
#pragma unroll
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : (float2)0);
         if((k + count) < ls)
            temp[k + count] = (float2)0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

Для сохранения полученного значения в глобальном буфере данных нам достаточно одного информационного потока.

      //---
      if(k == 0)
         out[shift_q + d] = temp[0];
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

Здесь мы в обязательном порядке синхронизуем работу потоков рабочей группы и переходим к следующей итерации цикла.

После успешного выполнения всех итераций системы циклов, завершаем работу кернела.

Следующим этапом нашей работы является построение процесса распределения градиента ошибки через операции маскированного внимания к комплексным величинам. Его мы реализуем в кернеле MaskAttentionGradientsComplex.

__kernel void MaskAttentionGradientsComplex(__global const float2 *q, __global float2 *q_g,
                                            __global const float2 *kv, __global float2 *kv_g,
                                            __global const float *scores,
                                            __global const float *mask, __global float *mask_g,
                                            __global const float2 *gradient,
                                            const int kunits, const int heads_kv
                                           )
  {
//--- init
   const int q_id = get_global_id(0);
   const int d = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int dimension = get_global_size(1);
   const int heads = get_global_size(2);

Структура параметров кернела во многом напоминает кернел прямого прохода. Мы лишь добавили глобальные буфера данных соответствующих градиентов ошибки. Однако, мы несколько изменили структуру пространства задач. По-прежнему используется трехмерное пространство задач, только второе измерение теперь указывает на размерность внутренних векторов, и отсутствует объединение потоков в рабочие группы.

В теле кернела идентифицируем текущий поток операций по всем измерением пространства задач с сохранением полученных значений в локальные константы. Как и ранее, их мы используем для определения смещений в глобальных буферах данных.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h) + d;
   const int shift_s = (q_id * heads + h) * kunits;
   const int shift_g = h * dimension + d;
   float2 koef = (float2)(fmax(sqrt((float)dimension), (float)1), 0);

После завершения подготовительной работы, переходим непосредственно к сбору градиентов ошибки. Вначале определим погрешность на уровне тензора Value.

Здесь следует вспомнить, что тензор Value используется для генерации всех элементов результирующей последовательности путем умножения на матрицу коэффициентов внимания. Следовательно, перенесем градиенты ошибки результатов внимания на уровень тензора Value с учетом соответствующих коэффициентов внимания. Для этого организуем систему циклов.

//--- Calculating Value's gradients
   int step_score = kunits * heads;
   if(h < heads_kv)
     {
#pragma unroll
      for(int v = q_id; v < kunits; v += qunits)
        {
         float2 grad = (float2)0;
         for(int hq = h; hq < heads; hq += heads_kv)
           {
            int shift_score = hq * kunits + v;
            for(int g = 0; g < qunits; g++)
              {
               float sc = IsNaNOrInf(scores[shift_score + g * step_score], 0);
               if(sc > 0)
                  grad += ComplexMul(gradient[shift_g + dimension * (hq - h + g  * heads)],
                                     (float2)(sc, 0));
              }
           }
         int shift_v = dimension * (2 *  heads_kv * v + heads_kv + h) + d;
         kv_g[shift_v] = grad;
        }
     }

Следующим этапом нам предстоит распределить градиент ошибки до уровня тензора Query. Очевидно, что каждый элемент данного тензора влияет только на один элемент в тензоре результатов. Значит мы можем сохранить значение соответствующего градиента ошибки в локальную переменную, чтобы сократить количество обращений к глобальной памяти.

//--- Calculating Query's gradients
   float2 grad = 0;
   float2 out_g = IsNaNOrInf2(gradient[shift_g + q_id * dimension], (float2)0);
   int shift_val = (heads_kv + h_kv) * dimension + d;
   int shift_key = h_kv * dimension + d;
#pragma unroll
   for(int k = 0; (k < kunits && ComplexAbs(out_g) != 0); k++)
     {
      float2 sc_g = 0;
      float2 sc = (float2)(scores[shift_s + k], 0);
      for(int v = 0; v < kunits; v++)
         sc_g += IsNaNOrInf2(ComplexMul(
                                ComplexMul((float2)(scores[shift_s + v], 0),
                                           out_g * kv[shift_val + 2 * v * heads_kv * dimension]),
                                ((float2)(k == v, 0) - sc)), (float2)0);
      float m = mask[shift_s + k];
      mask_g[shift_s + k] = IsNaNOrInf(sc.x / m * sc_g.x + sc.y / m * sc_g.y, 0);
      grad += IsNaNOrInf2(ComplexMul(sc_g, kv[shift_key + 2*k*heads_kv*dimension]), (float2)0);
     }
   q_g[shift_q] = IsNaNOrInf2(ComplexDiv(grad, koef), (float2)0);

Однако, при формировании результирующего значения, осуществляется взаимодействие с целым рядом значений тензоров Key и Value. И для получения требуемого значения ошибки, мы сначала спускаем градиент до матрицы коэффициентов внимания, и лишь затем переносим на тензор Query.

Обратите внимание, что тут же мы переносим градиент ошибки и на матрицу маскирования каналов.

На заключительном этапе, мы аналогичным образом переносим градиент ошибки на уровень тензора Key. Алгоритм практически полностью повторяет распределение градиента ошибки на уровень Query, только в данном случае,  двигаемся по столбцу матрицы внимания.

//--- Calculating Key's gradients
   if(h < heads_kv)
     {
#pragma unroll
      for(int k = q_id; k < kunits; k += qunits)
        {
         int shift_k = dimension * (2 *  heads_kv * k + h_kv) + d;
         grad = 0;
         for(int hq = h; hq < heads; hq++)
           {
            int shift_score = hq * kunits + k;
            float2 val = IsNaNOrInf2(kv[shift_k + heads_kv * dimension], (float2)0);
            for(int scr = 0; scr < qunits; scr++)
              {
               float2 sc_g = (float2)0;
               int shift_sc = scr * kunits * heads;
               float2 sc = (float2)(IsNaNOrInf(scores[shift_sc + k], 0), 0);
               if(ComplexAbs(sc) == 0)
                  continue;
               for(int v = 0; v < kunits; v++)
                  sc_g += IsNaNOrInf2(
                             ComplexMul(
                                ComplexMul((float2)(scores[shift_sc + v], 0),
                                           gradient[shift_g + scr * dimension]),
                                ComplexMul(val, ((float2)(k == v, 0) - sc))),
                             (float2)0);
               grad += IsNaNOrInf2(ComplexMul(sc_g, q[shift_q + scr * dimension]), (float2)0);
              }
           }
         kv_g[shift_k] = IsNaNOrInf2(ComplexDiv(grad, koef), (float2)0);
        }
     }
  }

На этом мы завершаем рассмотрение алгоритмов построения процессов маскированного внимания в области комплексных значений на стороне OpenCL-контекста. С полным кодом представленных кернелов можно ознакомиться во вложении.

Следующим этапом нашей работы будет реализация алгоритмов маскирования внимания комплексных значений на стороне основной программы. Но об этом поговорим уже в следующей статье.

Заключение

Мы познакомились с теоретическими аспектами фреймворка CATCH, который объединяет преобразование Фурье и механизм частотного патчинга для детектирования аномалий в многомерных временных рядах. Его ключевое преимущество — способность выявлять сложные рыночные паттерны, которые остаются незамеченными при анализе только во временной области.

Использование частотного представления позволяет глубже понимать динамику рынка, а механизм частотного патчинга адаптирует анализ к изменяющимся условиям. Кроме того, CATCH учитывает взаимосвязи между активами, что делает его более чувствительным к системным рыночным аномалиям. В отличие от традиционных методов, он не только фиксирует очевидные скачки и выбросы, но и распознаёт сложные, скрытые зависимости, которые могут предвещать изменения рыночных трендов.

В практической части начата работа по имплементации средствами MQL5 собственного видения подходов, предложенных авторами фреймворка. В следующей статье мы продолжим начатую работу, в завершении которой оценим эффективность реализованных решений на реальных исторических данных.

Ссылки

• CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы