Теория категорий в MQL5 (Часть 22): Другой взгляд на скользящие средние

Введение

В центре внимания в этой серии статей всегда была теория категорий. Мы много говорили о прогнозировании временных рядов, потому что оно актуально для большинства трейдеров, а они составляют большинство участников этой платформы. Однако другие соответствующие приложения, помимо этого, включают оценку, риск, распределение портфеля и многие другие. Если кратко остановиться на примере оценки, мы увидим множество способов применения теории категорий для оценки акций. Например, если мы возьмем ключевые показатели акции так, чтобы каждый из них был объектом в категории, то морфизмы (или пути графа), связывающие эти разные показатели (например, доходы, долг и т. д.), можно отнести к разным классам оценки (скажем, A+, A, B и т. д.). При этом, получив показатели конкретной акции, мы можем определить ее принадлежность к определенному классу. Это упрощенный подход, который призван служить лишь подсказкой о том, что можно сделать в этой области.

Но вернемся к временным рядам. Многие считают скользящие средние излишне упрощенным представлением. Тем не менее, они очень важны для технического анализа, прежде всего потому, что их концепция лежит в основе многих других индикаторов, например, полос Боллинджера, MACD и т. д. Их можно рассматривать как менее волатильный взгляд на ценовое действие Это важно, учитывая количество белого шума на рынках.

В этой статье мы продолжим рассматривать естественные преобразования. В предыдущей статье мы изучали способность естественных преобразований преодолевать разрыв между связанными наборами данных разных измерений. Понятие "измерения" здесь используются для представления количества столбцов в наборе данных. Итак, как и раньше, мы сталкиваемся с двумя категориями: одна — с "простым" рядом необработанных цен, а другая — со "сложным" рядом скользящих средних цен. Нашей целью будет показать использование теории категорий для прогнозирования временных рядов с областью действия всего трех функторов.

Общие сведения

Итак, для начала давайте рассмотрим некоторые основные определения того, что мы здесь рассматриваем. Функтор — это функция, отображающая две категории. Здесь мы будем иметь дело с тремя. Категории схематично представлены ниже:

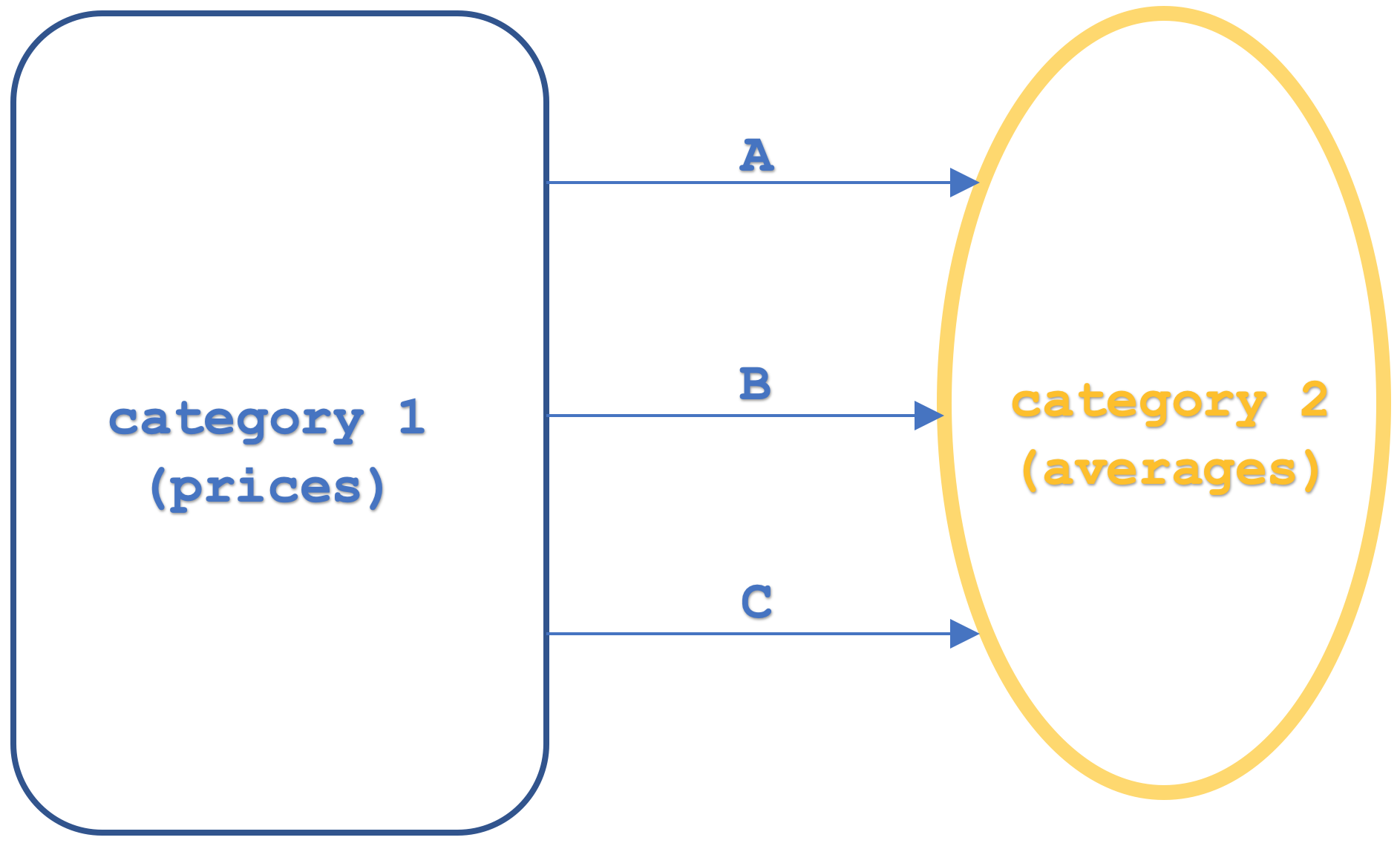
В нашей категории домена есть объекты со значениями цен в заданные интервалы времени, а также объекты кодомена со значениями цен скользящего среднего также в аналогичные интервалы времени. У нас выделены три функтора, а именно A, B и C. В недавних статьях мы представляли функторы, связывающие категории. Новым здесь является добавление третьего функтора. Это служит нашим целям, потому что показывает естественные преобразования в "вертикальном" расположении. "Вертикальная" установка указана на схеме, но во избежание любой двусмысленности в будущем "вертикальная" относится к естественным преобразованиям между функторами, которые имеют одну и ту же категорию домена и кодомена. Это означает, что если бы категории были схематически расположены вертикально, а наши естественные преобразования, казалось бы, указывали бы в горизонтальном направлении, естественные преобразования все равно находились бы в "вертикальном" расположении.

Скользящие средние обычно используются в качестве торговых индикаторов, отслеживая точки их пересечения. Это могут быть места, где они пересекают базовую цену, так что пересечение вершины является медвежьим, поскольку представляет собой барьер сопротивления, а пересечение дна является бычьим, поскольку указывает на поддержку. Однако чаще всего эти точки пересечения находятся между двумя скользящими средними разных периодов. Таким образом, обычно, когда средняя с более коротким периодом пересекает более длинную, у нас возникает бычья установка, поскольку более длинная и, следовательно, менее волатильная скользящая средняя указывает на поддержку, и наоборот, если средняя с более коротким периодом прорвется ниже, тем дольше оно будет медвежьим. С этой целью в этой модели каждый функтор представляет определенный период усреднения. Таким образом, функтор A будет самым коротким из всех трех, тогда как период функтора B будет промежуточным, а функтор C будет иметь самый длинный период усреднения.

Если мы посмотрим на рассматриваемые нами категории, возможно, будет полезно обрисовать, почему эти два временных ряда соответствуют аксиомам категорий. Напомним, мы уже рассмотрели, как ордера (к которым временные ряды более близки) могут быть истолкованы как категории, тем не менее аксиомами категории являются объекты, морфизмы, морфизмы тождеств и ассоциации. Категории домена и кодомена представляют собой временные ряды цен, поэтому иллюстрации с одной из них легко вывести из другой. Таким образом, если мы сосредоточимся на категории необработанных цен (области), каждая ценовая точка представляет собой объект, состоящий из двух элементов - времени и цены. Морфизмы представляют собой последовательные отображения между ценовыми точками, поскольку каждая ценовая точка следует за другой ценовой точкой. Тождественный морфизм в каждой ценовой точке можно рассматривать как скользящую среднюю за период, равный единице. Это то же самое, что и ценовой ряд, но средняя за один период обеспечивает отношение тождества. Наконец, легко подразумевается композиция с ассоциацией, поскольку даны три последовательные ценовые точки L, M и N.

L o (M o N) = (L o M) o N

Цена после морфизма из M в N, когда она связана с морфизмом из L, такая же, как цена в N, когда она связана с результатом морфизма из L в M.

Категории и функторы

Наша категория 1, которая будет доменной категорией для всех функторов, как уже упоминалось, будет содержать необработанный временной ряд цен, из которого функторы отображают свои средние значения.

Таким образом, в этой категории будет всего 4 функтора, из которых только 3 представляют для нас интерес. Первое, о чем стоит упомянуть, — это функтор тождества. Это связано с тем, что категории и функторы ведут себя во многом подобно объектам и морфизмам, поэтому необходимо наличие тождества. Остальные три функтора, которые, как уже упоминалось, представляют различные реализации скользящего среднего, будут иметь каждый из периодов, заданный целочисленными входными параметрами, а именно m_functor_a, m_functor_b и m_functor_c для функторов A, B и C соответственно.

Вторая категория, которая составляет кодомен для наших трех функторов, будет иметь три объекта, каждый со скользящими средними ценами во временном ряду. Таким образом, каждый функтор из необработанного ценового ряда в категории 1 будет сопоставляться со своим собственным объектом в категории 2.

Категория 2 будет иметь единственный начальный функтор, который, как уже упоминалось, будет тождественным. Морфизмы между этими объектами будут эквивалентны естественным преобразованиям согласно определениям, которые мы рассматривали в наших последних статьях. Все это можно суммировать с помощью немного более подробной схемы ниже:

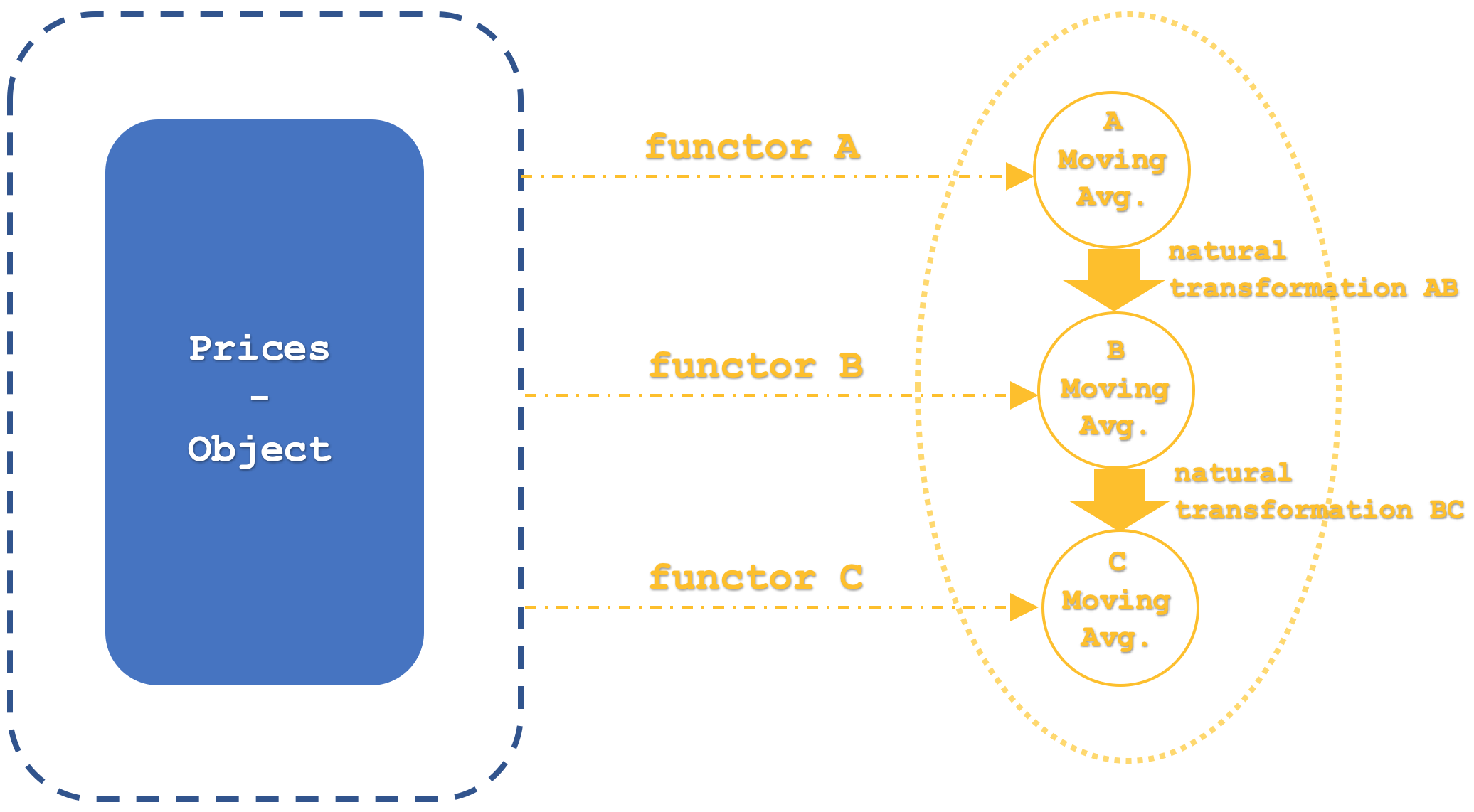
Наше отображение функторов для этой статьи не использует сторонние алгоритмы, такие как многослойный перцептрон, лес случайного распределения или линейный дискриминантный анализ, как мы использовали в последних статьях. Скорее, это алгоритм скользящего среднего, и естественные преобразования будут даже проще, поскольку они будут представлять собой арифметическую разность между конечными значениями двух рассматриваемых функторов.

Естественные трансформации

Определение естественных преобразований в контексте финансов похоже на исследование новых территорий. Материалов и ссылок по теме немного. Часто используются или рассматриваются другие методы, такие как корреляция, которая имеет две основные реализации - Пирсона и Спирмена. Существуют и другие методы, которые можно использовать для сравнения, но в этой статье мы будем использовать корреляцию Спирмена как часть нашего алгоритма генерации сигналов.

Итак, естественное преобразование между двумя функторами — это чистая разница целевых объектов функторов. В нашем случае у нас есть 3 функтора, что подразумевает 3 возможных естественных преобразования. Однако мы сосредоточимся только на двух преобразованиях, а именно на преобразовании между функтором A и функтором B, который мы можем называть AB, и между функтором B и функтором C, который мы назовем BC. Используя эти два функтора, мы хотим создать для каждого два буфера данных. Итак, мы будем отслеживать соответствующую разницу в скользящих средних и регистрировать их в соответствующих массивах, создавая таким образом два буфера данных. Мы отслеживаем коэффициент корреляции буферов. Отслеживание этого значения представляет собой суть нашего торгового сигнала. Положительное значение должно указывать на то, что рынки находятся в тренде, тогда как отрицательное значение указывает на флэт.

Таким образом, наш сигнал будет соответствовать сумме всех дополнительных изменений скользящих средних с указанным сигналом. Таким образом, если значение положительное, это указывает на бычий настрой, и наоборот, если оно отрицательное, то на медвежий. Этот сигнал, который всегда будет давать значение на каждом баре, будет фильтроваться, как упоминалось выше, с помощью корреляции между двумя естественными буферами преобразования. Иными словами, наша система спрашивает, есть ли какая-либо дополнительная польза от отслеживания естественных преобразований, учитывая, что мы уже установили тренды для каждого скользящего среднего.

Вертикальная композиция естественных преобразований

В рамках теории категорий понятие "вертикальная композиция" и ее противоположность "горизонтальная композиция" естественных преобразований иногда могут меняться значениями в зависимости от контекста и авторских конвенций. В некоторых источниках естественные преобразования функторов с общими категориями домена и кодомена называются "горизонтальными композициями". Но мы не будем использовать такое определение. В этой и, возможно, последующих статьях вертикальной композицией будут называться естественные преобразования функторов с общими категориями домена и кодомена.

Итак, в чем же значение вертикальной композиции? Она проще горизонтальной, а также предоставляет возможность взглянуть на два относительно простых набора данных (которые можно рассматривать как категории) и установить между ними особые отношения, которые можно легко упустить из виду при работе с несколькими категориями в более сложных условиях.

Хорошая иллюстрация - выбор набора данных ценовых рядов и набора данных скользящего среднего для этой статьи. Помимо торговли, более показательным примером может быть кулинария. Рассмотрим список кулинарных ингредиентов (категория домена) и несколько меню (категория кодомена). Наши функторы просто соединяли бы ингредиенты с соответствующими меню. Естественные преобразования, такие как функторы и морфизмы, сохраняют определения и структуру своего происхождения. Казалось бы, обычное дело, но это краеугольный камень теории категорий. Таким образом, при наличии элементов и структуры объекта (т. е. меню и их позиций) естественные преобразования между разными меню могут помочь измерить и оценить относительное время, необходимое для приготовления каждого блюда, или стоимость каждого блюда, а также множество других параметров в зависимости от того, что интересует шеф-повара/ресторан. Вооружившись этой информацией, можно использовать изоморфизм и исследовать получение ингредиентов с учетом набора различных меню. Хотя это можно сделать с помощью других методов и систем, теория категорий обеспечивает сохранение структуры и подход, поддающийся количественной оценке.

Прогнозирование изменения цен

При использовании вертикальной структуры прогнозирование изменений цен осуществляется путем регистрации и анализа коэффициентов корреляции наших двух естественных буферов трансформации. Эти массивы необходимо инициализировать, поскольку при первом запуске эксперта загружается недостаточно данных для выполнения корреляции. Обработка такого поведения показано ниже:

//+------------------------------------------------------------------+
//| Get Direction function from Natural Transformations.             |
//+------------------------------------------------------------------+
void CSignalCT::Init(void)
   {
      if(!m_init)
      {
         m_close.Refresh(-1);
         
         int _x=StartIndex();
         
         m_o_prices.Cardinality(m_functor_c+m_functor_c);
         for(int i=0;i<m_functor_c+m_functor_c;i++)
         {
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,m_close.GetData(_x+i));m_o_prices.Set(i,m_e_price);
         }
         
         m_o_average_a.Cardinality(m_transformations+1);
         m_o_average_b.Cardinality(m_transformations+1);
         m_o_average_c.Cardinality(m_transformations+1);
         
         for(int i=0;i<m_transformations+1;i++)
         {
            double _a=0.0;
            for(int ii=i;ii<m_functor_a+i;ii++)
            {
               _a+=m_close.GetData(_x+ii);
            }
            _a/=m_functor_a;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_a);m_o_average_a.Set(i,m_e_price);
            //
            double _b=0.0;
            for(int ii=i;ii<m_functor_b+i;ii++)
            {
               _b+=m_close.GetData(_x+ii);
            }
            _b/=m_functor_b;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_b);m_o_average_b.Set(i,m_e_price);
            //
            double _c=0.0;
            for(int ii=i;ii<m_functor_c+i;ii++)
            {
               _c+=m_close.GetData(_x+ii);
            }
            _c/=m_functor_c;
            m_e_price.Let();m_e_price.Cardinality(1);m_e_price.Set(0,_c);m_o_average_c.Set(i,m_e_price);
         }
         //
         ArrayResize(m_natural_transformations_ab,m_transformations);ArrayInitialize(m_natural_transformations_ab,0.0);
         ArrayResize(m_natural_transformations_bc,m_transformations);ArrayInitialize(m_natural_transformations_bc,0.0);
         
         for(int i=m_transformations-1;i>=0;i--)
         {
            double _a=0.0;
            m_e_price.Let();m_e_price.Cardinality(1);m_o_average_a.Get(i,m_e_price);m_e_price.Get(0,_a);
            double _b=0.0;
            m_e_price.Let();m_e_price.Cardinality(1);m_o_average_b.Get(i,m_e_price);m_e_price.Get(0,_b);
            double _c=0.0;
            m_e_price.Let();m_e_price.Cardinality(1);m_o_average_c.Get(i,m_e_price);m_e_price.Get(0,_c);
            
            m_natural_transformations_ab[i]=_a-_b;
            m_natural_transformations_bc[i]=_b-_c;
         }
         
         m_init=true;
      }
   }

Мы объявили три маркера скользящего среднего для каждого функтора, и нам необходимо обновить их, прежде чем считывать из них какие-либо значения. Период каждой скользящей средней является входным параметром, поэтому у нас есть m_functor_a, m_functor_b и m_functor_c для хэндлов m_ma_a, m_ma_b и m_ma_c соответственно. У нас также есть два буфера для каждого естественного преобразования, а именно m_natural_transformations_ab и m_natural_transformations_bc. Размер этих массивов задается входным параметром m_transformations, поэтому вначале размеры обоих массивов необходимо изменить до его значения. Объекты в категории кодомена, а именно m_o_average_a, m_o_average_b и m_o_average_c, также должны быть изменены до этого значения плюс один, чтобы иметь возможность получить все приращения изменений.

Таким образом, влияние различных периодов скользящего среднего на возможность прогнозирования с помощью этой системы будет оцениваться при появлении сигналов, генерируемых в результате сопоставления изменений скользящего среднего, когда корреляция естественных буферов преобразования больше нуля. Поведение реализовано в функции GetDirection:

//+------------------------------------------------------------------+
//| Get Direction function from Natural Transformations.             |
//+------------------------------------------------------------------+
double CSignalCT::GetDirection()
   {
      double _r=0.0;
      
      Refresh();
      
      MathCorrelationSpearman(m_natural_transformations_ab,m_natural_transformations_bc,_r);
      
      return(_r);
   }

Каждая из функций CheckOpenLong и CheckOpenShort, которые вычисляют наш "тренд". Этот тренд задает направление сигнала, при этом "направление" действует как фильтр для флэтовых рынков. Реализация показана ниже:

      m_ma_a.Refresh(-1);
      m_ma_b.Refresh(-1);
      m_ma_c.Refresh(-1);
      
      int _x=StartIndex();
      
      double _trend= (m_ma_a.GetData(0,_x)-m_ma_a.GetData(0,_x+1))+
                     (m_ma_b.GetData(0,_x)-m_ma_b.GetData(0,_x+1))+
                     (m_ma_c.GetData(0,_x)-m_ma_c.GetData(0,_x+1));

Нам также нужна функция для обновления этих значений, очень похожая на функцию Init. Полный исходный код приложен в конце статьи.

В ходе тестирования на истории форекс-пары USDJPY с 1999.01.01 по 2020.01.01 на дневном таймфрейме мы получили приведенный ниже отчет с некоторыми из наших идеальных настроек:

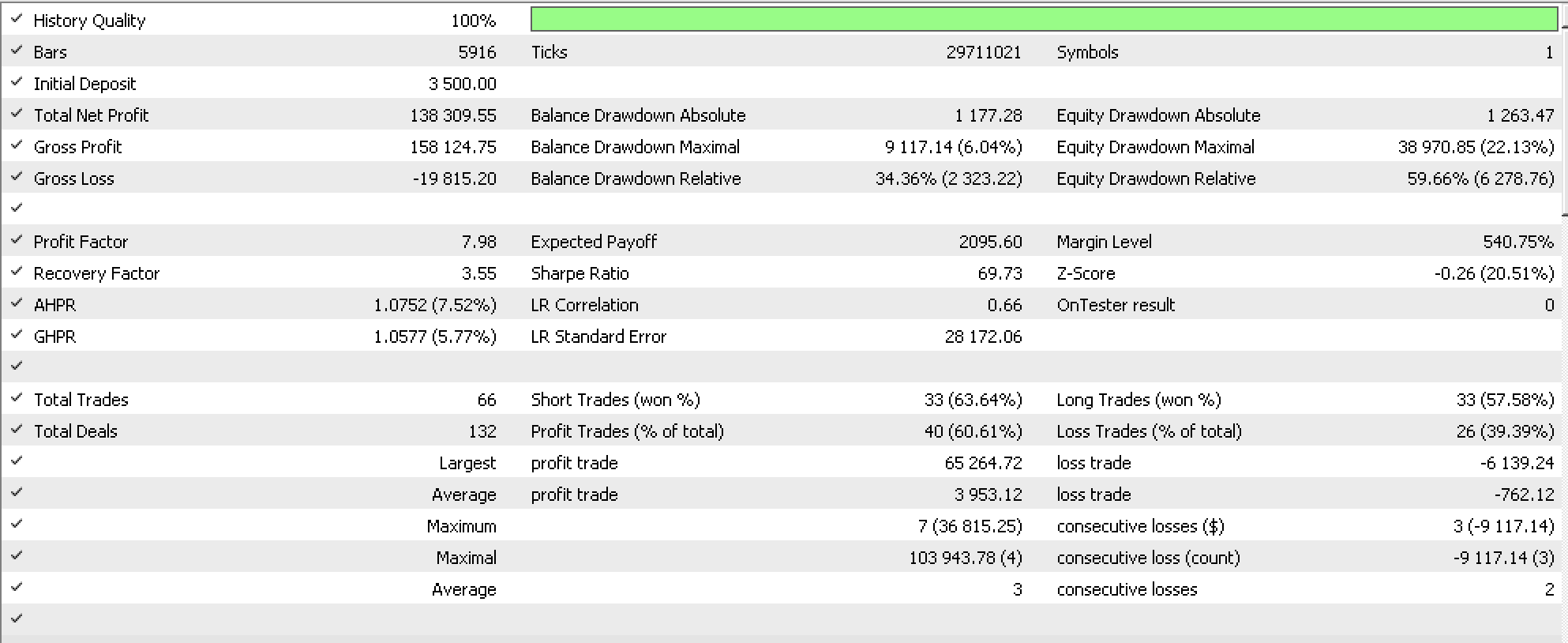
Если мы попытаемся продолжить тестирование с этими настройками с 2020.01.01 по 2023.08.01, мы получим следующий отчет:

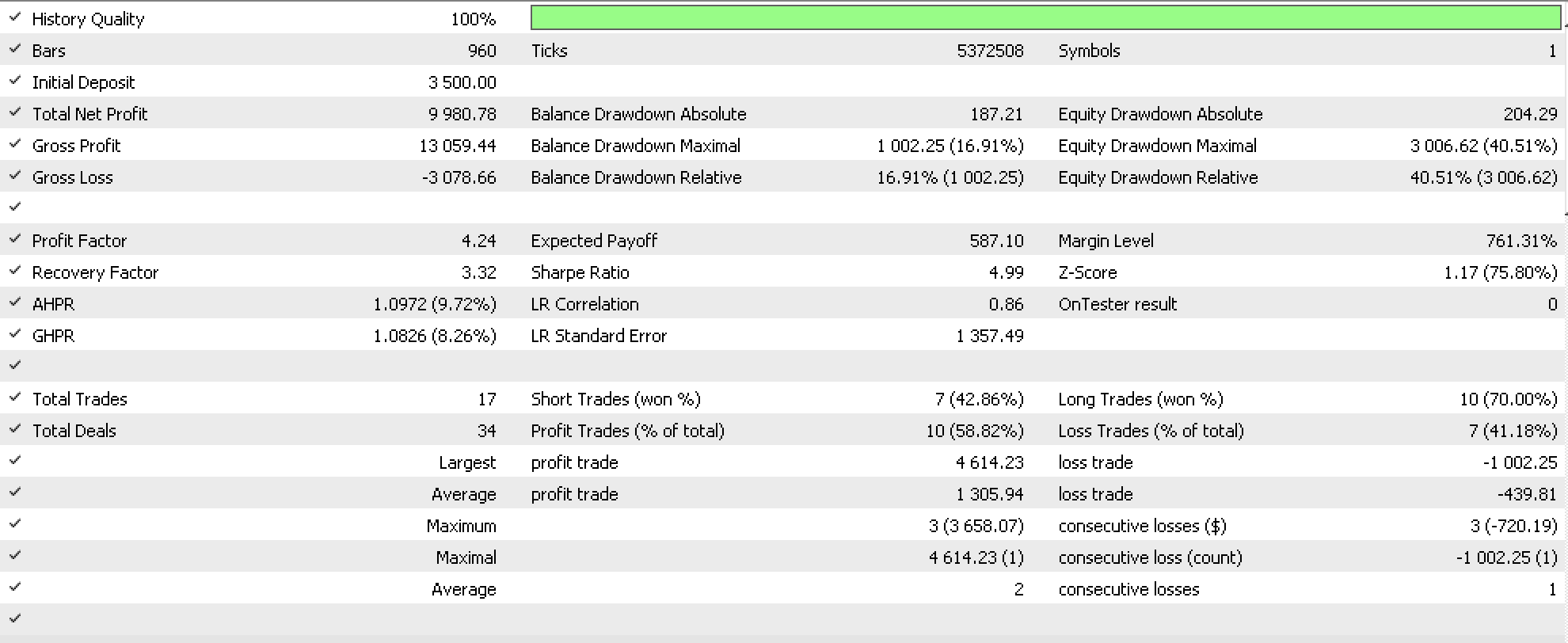
Как обычно, положительные результаты не означают, что у нас есть работающая система, а скорее, что у нас может быть что-то, что можно протестировать на более длительных периодах, чтобы подтвердить наши ранние выводы.

Тестирование при разработке торговой системы

Класс сигналов можно легко интегрировать в новую или существующую торговую систему благодаря Мастеру MQL5. Все, что нам нужно сделать, это собрать нового советника с этим классом сигналов в качестве одного из других сигналов, которые трейдер либо всегда использует, либо хочет испытать. Типичный входной параметр Signal_XXX_Weight (где XXX - имя класса сигнала), значение которого обычно находится в диапазоне от 0,0 до 1,0, можно оптимизировать для всех сигналов, чтобы определить подходящий вес для каждого.

Оценка такой торговой системы должна основываться на потребностях трейдера. Обычно это колебание между ростом и сохранением капитала. Говоря проще, я бы отметил, что AHPR (среднее арифметическое сделки) — лучший показатель роста, в то время как коэффициент восстановления — показатель безопасности. Это все приблизительные оценки, поэтому трейдерам придется приложить больше усилий, чтобы найти то, что подойдет им.

При наличии системы оценки эффективности следующим и, возможно, не менее важным будет метод постепенного улучшения стратегии без ущерба для ее предпосылок и способности двигаться вперед. При этом не существует шаблонного метода, кроме постоянной проверки производительности на основе бэк-тестов и продвижения вперед с каждой итерацией или модификацией системы.

Как всегда, существует возможность иметь экземпляр завершающего класса, основанного на этой модели. Нам придется внести несколько изменений, но суть останется неизменной. Во-первых, наши скользящие средние вместо того, чтобы использовать цену закрытия в качестве прикладной цены, будут использовать что-то, что склоняется к волатильности, это может быть типичная цена или, возможно, медианная цена. Во-вторых, направление прогноза по-прежнему будет указывать на корреляции между двумя буферами естественных преобразований, но в этом случае мы будем отслеживать текущее изменение диапазона баров, чтобы оно действовало как наш "тренд". Таким образом, уменьшение диапазона должно быть подкреплено положительной корреляцией (значениями больше нуля). То же самое относится и к увеличению волатильности. Если корреляция равна нулю или отрицательна, это будет означать, что наша модель указывает на то, что любые текущие изменения волатильности можно игнорировать. Реализация прилагается в конце статьи.

Заключение

Подводя итог, можно сказать, что влияние естественных преобразований в вертикальной композиции звучит слишком академично и архаично, чтобы вызвать какой-либо интерес у большинства людей. И все же, рассматривая иллюстрации с распространенными индикаторами, такими как скользящая средняя, в этой статье, мы выявили несколько закономерностей, из которых смогли прочитать сигналы подтверждения при прогнозировании временного ряда.

Использование полученных знаний для разработки надежной торговой системы всегда происходит там, где теория встречается с практикой, и для ее реализации требуется немного больше работы со стороны трейдера. Тем не менее, в Интернете, достаточно вспомогательных материалов, чтобы заинтересованный трейдер мог довести дело до конца.

Я призываю к дальнейшему изучению этих концепций за пределами прогнозирования временных рядов и в других областях торговли и финансов, таких как оценка или риск.

Ссылки

В основном использованы статьи из Викиедии.

Ресурсы для реализации концепций теории категорий, изложенных в этой статье, прикреплены ниже. Это файл класса по теории категорий ct_22.mq5 и файл трейлинга TraillingCT_22_r1.mqh. Файл класса следует поместить в папку include, а файл с трейлингом — в папку Include\Expert\Trailling. Читатели, незнакомые с Мастером MQL5, могут обратиться к этой статье, так как файл сигнала предназначен для сборке в Мастере.