Возможности Мастера MQL5, которые вам нужно знать (Часть 3): Энтропия Шеннона
1 211
1
1.0. Введение
В 1948 году Клод Шеннон представил свою статью "Математическая теория связи", в которой была выдвинута идея об информационной энтропии. Энтропия — понятие, пришедшее из физики. Это мера степени активности частиц внутри объекта. Например, если мы рассмотрим три состояния воды - лед, жидкость и газ, мы увидим, что кинетическая энергия частицы наибольшая в газообразном состоянии и наименьшая в виде льда. Понятие применяется в математике применительно к вероятности. Рассмотрим следующие три набора.
Набор 1:
Набор 2:
Набор 3:
Какой из этих наборов имеет наибольшую энтропию?
Если вы выбрали последний вариант, то вы правы, но как мы можем подтвердить правильность этого ответа? Самый простой способ ответить на этот вопрос — взять количество способов реорганизации каждого набора в качестве оценки энтропии, игнорируя при этом совпадения по цвету. Таким образом, для первого набора существует только один способ "реорганизовать" его. Однако если мы после этого посмотрим на наборы, то увидим, что количество перестановок относительно цвета значительно увеличивается, поэтому мы можем утверждать, что последний набор имеет самую высокую энтропию.
Существует более точный способ определения энтропии, основанный на информации. Если бы вы произвольно выбрали шар из первого набора до того, как взяли бы его в руки, что бы вы узнали о нем? Поскольку в наборе только синие шары, вы можете быть уверены, что это будет синий шар. Таким образом, можно сказать, что у нас есть полная информация о том, что мы собираемся выбрать из набора 1. В случае с наборами 2 и 3 наша информация становится все менее и менее полной. Таким образом, в математике энтропия обратно пропорциональна информации. Чем выше энтропия, тем больше неизвестных.
Так как же нам вывести формулу для вычисления энтропии? Если мы еще раз рассмотрим наборы, то увидим, что чем больше разнообразие типов шаров в наборе, тем выше энтропия. Наиболее чувствительным фактором при измерении имеющейся у нас информации о шаре до его выбора может быть вероятность выбора каждого шара в наборе. Итак, если мы должны рассмотреть каждый набор в целом и найти вероятность выбора 8 шаров с каждым цветом, выбираемым так часто, как он появляется в своем наборе, при условии, что выбор каждого шара является независимым событием, тогда вероятность (и, следовательно, "известная информация") для каждого набора является произведением отдельных вероятностей для каждого шара.
Набор 1:
(1,0 x 1,0 x 1,0 x 1,0 x 1,0 x 1,0 x 1,0 x 1,0) = 1,0
Набор 2:
(0,625 x 0,625 x 0,625 x 0,625 x 0,625 x 0,375 x 0,375 x 0,375) ~ 0,0050
Набор 3:
(0,375 x 0,375 x 0,375 x 0,25 x 0,25 x 0,25 x 0,25 x 0,125) ~ 0,000025
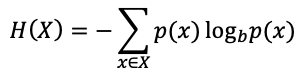
Набор 1:
-(8 x 0,125 x log2(1,0)) = 0,0
Набор 2:
(-(0,625 x log2(0,625)) - (0,375 x log2(0,375))) ~ 0,9544
Набор 3:
(- (0,375 x log2(0,375)) - (2 x 0,25 x log2(0,25)) - (0,125 x log2(0,125))) ~ 1,906
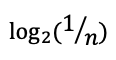
2.0. Создание класса
В этой статье мы будем использовать класс Decision Forest ("лес решений") из библиотеки MQL5. В частности, мы будем абстрагироваться от идеи случайных лесов (Random Forest) при изучении эффективности сигнала энтропии Шеннона. Эта статья не о случайных лесах, а об энтропии Шеннона.
Давайте еще раз вернемся к классу Decision Forest, поскольку он является основой модели случайного леса. Мы все, сознательно или бессознательно, периодически пользуемся деревом решений, и поэтому сама концепция не кажется нам странной.
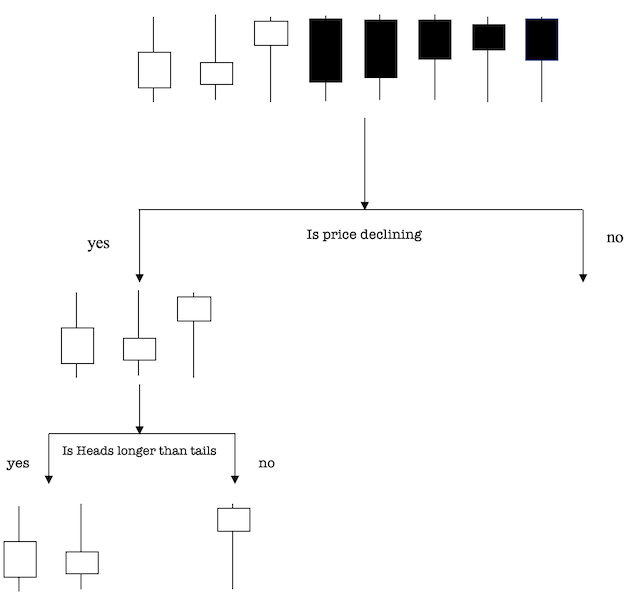
Давайте рассмотрим пример, чтобы лучше проиллюстрировать, как она работает.
Предположим, что наш набор данных состоит из ценовых баров, как указано выше. У нас есть три падающих и пять восходящих свечей (возьмем медвежьи и бычьи рынки в качестве наших классов), и мы хотим разделить классы, используя их атрибуты. Атрибутами являются направление цены и сравнение длины головы и хвоста, поскольку они могут быть предвестниками изменения направления. Итак, как мы можем это сделать?
Направление цены кажется простым атрибутом для разделения, поскольку белый цвет представляет медвежьи свечи, а синий — бычьи. Итак, мы можем использовать вопрос "Снижается ли цена?", чтобы отделить первый узел. Узлом на дереве является точка, в которой ветвь разделяется на две — ветви "Да" и "Нет".
У всех ответвлений "Нет" (восходящие свечи) хвосты длиннее голов, но на ответвлении "Да" картина другая, поэтому предстоит проделать дополнительную работу. При использовании второго атрибута мы спрашиваем: "Голова длиннее хвоста?", чтобы сделать второе разделение.
Две падающие свечи с более длинными головами относятся к подветви "Да", а одна падающая свеча с более длинным хвостом относится к правой подветви. Это дерево решений смогло использовать два атрибута для идеального разделения данных в соответствии с нашими критериями.
В реальных торговых системах для построения более полного дерева решений можно использовать тиковый объем, время суток и множество других торговых индикаторов. Тем не менее, центральная предпосылка каждого вопроса в узле состоит в том, чтобы найти один атрибут, который разбивает (или классифицирует) приведенные выше данные на два непохожих набора, при этом созданные элементы каждого набора похожи.
Как следует из названия, Random Forest ("случайный лес") состоит из огромного количества отдельных деревьев решений, которые работают как группа. Для каждого дерева в случайном лесу делается прогноз класса, и класс с наибольшим количеством голосов выбирается в качестве прогноза модели. Основную концепцию случайного леса легко упустить из виду, но она очень мощная, так как выражает мудрость масс. Делая прогнозы, некоррелированные деревья превосходят отдельные деревья, независимо от того, на каком количестве данных производится обучение. Вся суть - в низкой корреляции. Причина этого в том, что деревья защищают друг друга от индивидуальных ошибок согласно Тону (до тех пор, пока они не ошибаются постоянно в одном и том же направлении). Чтобы случайные леса работали, сигнал прогнозирования должен быть лучше среднего, а предсказания/ошибки каждого дерева должны иметь низкую корреляцию друг с другом.
Например, если у вас есть две торговые системы, в первой из которых вы можете разместить до тысячи маржинальных ордеров на один доллар в год, а в другой - только один маржинальный ордер на 1000 долларов, какую из них вы предпочтете, учитывая одинаковое матожидание? Большинство выберут первую систему, поскольку она дает трейдеру "больше контроля".
Так каким же образом алгоритмы случайного леса гарантируют, что характеристика каждого отдельного дерева не слишком коррелирует с характеристикой любого другого дерева в лесу? Ответ на этот вопрос можно свести к двум особенностям:
2.0.1. Бэггинг
Деревья решений очень чувствительны к обучающим данным, и небольшие изменения могут привести к значительному изменению леса. Случайные леса используют это, когда каждое дерево случайным образом выбирает набор данных при замене, в результате чего получаются разные деревья. Этот процесс известен как бэггинг (сокращение от "бутстреп-агрегирование" - bootstrap aggregating).
При бэггинге мы не заменяем тренировочные данные меньшими наборами, а вместо исходных тренировочных данных берем случайную выборку размера N с некоторыми заменами. Начальный размер набора N сохраняется. Например, если наши обучающие данные были [U, V, W, X, Y, Z], то мы могли бы дать одному из наших деревьев следующий список [U, U, V, X, X, Z]. В обоих списках сохраняется размер N (шесть), а в случайно выбранных данных повторяются "U" и "X".
2.0.2. Функция случайности (Feature Randomness)
Обычно в дереве решений разделение узла включает в себя рассмотрение всех возможных признаков и выбор того, который дает наибольшее различие между наблюдениями в конечном левом узле и наблюдениями в конечном правом узле. С другой стороны, в случайном лесу каждое дерево может выбирать только из случайного подмножества признаков. Это, как правило, приводит к большей изменчивости внутри леса и в конечном итоге ведет к снижению корреляции между деревьями и большей диверсификации.
Давайте рассмотрим наглядный пример — на картинке выше традиционное дерево решений (обозначено синим цветом) может выбирать из всех четырех атрибутов при принятии решения о том, как разделить узел. Оно решает использовать Атрибут 1 (черный и подчеркнутый), поскольку при этом данные разбиваются на максимально разделенные группы.
Теперь давайте посмотрим на наш случайный лес. В этом примере мы рассмотрим только два дерева леса. Когда мы проверяем Дерево 1, мы обнаруживаем, что оно может учитывать только Атрибуты 2 и 3 (выбранные случайным образом) при принятии решения о разделении узлов. Из нашего традиционного дерева решений (обозначено синим цветом) мы знаем, что Атрибут 1 лучше всего подходит для разделения, но Дерево 1 не может видеть Атрибут 1, поэтому оно вынуждено использовать Атрибут 2 (черный и подчеркнутый). Дерево 2, с другой стороны, может видеть только Атрибуты 1 и 3, поэтому оно может выбрать Атрибут 1.
Итак, в случайных лесах деревья не только обучаются на наборах данных (благодаря бэггингу), но и используют различные функции при принятии решений.
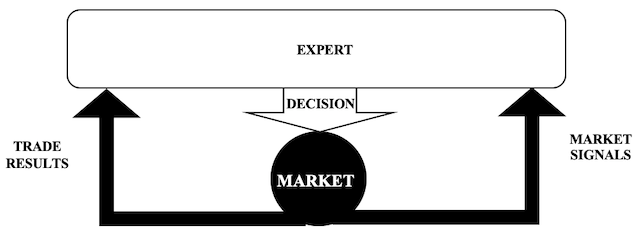
При использовании случайных лесов наш советник обрабатывает прошлые результаты торговли и рыночные сигналы, чтобы принять решение о покупке или продаже. При получении сигнала, а не просто скринера из энтропии, мы будем рассматривать отдельно энтропию положительных ценовых баров и энтропию отрицательных ценовых баров в пределах недавнего набора.
Построение и обучение случайных лесов будет происходить только при оптимизации одним потоком.
2.1. Сигнальный класс советника
// wizard description start //+------------------------------------------------------------------+ //| Description of the class | //| Title=Signals of'Shannon Entropy' | //| Type=SignalAdvanced | //| Name=Shannon Entropy | //| ShortName=SE | //| Class=CSignalSE | //| Page=signal_se | //| Parameter=Reset,bool,false,Reset Training | //| Parameter=Trees,int,50,Trees number | //| Parameter=Regularization,double,0.15,Regularization Threshold | //| Parameter=Trainings,int,21,Trainings number | //+------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| Class CSignalSE. | //| Purpose: Class of generator of trade signals based on | //| the 'Shannon Entropy' signals. | //| Is derived from the CExpertSignal class. | //+------------------------------------------------------------------+ class CSignalSE : public CExpertSignal { public: //Decision Forest objects. CDecisionForest DF; //Decision Forest CMatrixDouble DF_SIGNAL; //Decision Forest Matrix for inputs and output CDFReport DF_REPORT; //Decision Forest Report for results int DF_INFO; //Decision Forest feedback double m_out_calculations[2], m_in_calculations[__INPUTS]; //Decision Forest calculation arrays //--- adjusted parameters bool m_reset; int m_trees; double m_regularization; int m_trainings; //--- methods of setting adjustable parameters void Reset(bool value){ m_reset=value; } void Trees(int value){ m_trees=value; } void Regularization(double value){ m_regularization=value; } void Trainings(int value){ m_trainings=value; } //Decision Forest FUZZY system objects CMamdaniFuzzySystem *m_fuzzy; CFuzzyVariable *m_in_variables[__INPUTS]; CFuzzyVariable *m_out_variable; CDictionary_Obj_Double *m_in_text[__INPUTS]; CDictionary_Obj_Double *m_out_text; CMamdaniFuzzyRule *m_rule[__RULES]; CList *m_in_list; double m_signals[][__INPUTS]; CNormalMembershipFunction *m_update; datetime m_last_time; double m_last_signal; double m_last_condition; CSignalSE(void); ~CSignalSE(void); //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); bool m_random; bool m_read_forest; int m_samples; //--- method of initialization of the oscillator bool InitSE(CIndicators *indicators); double Data(int Index){ return(Close(StartIndex()+Index)-Close(StartIndex()+Index+1)); } void ReadForest(); void WriteForest(); void SignalUpdate(double Signal); void ResultUpdate(double Result); double Signal(void); double Result(void); bool IsNewBar(void); };
2.1.1. Сигналы
Эта энтропия будет взвешена по индексу для определения новизны.
if(_data>0.0) { _long_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); } else if(_data<0.0) { _short_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); }
Также она будет взвешена по величине ценовых баров.
if(_data>0.0) { _long_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); } else if(_data<0.0) { _short_entropy-=((1.0/__SIGNALS[i])*((__SIGNALS[i]-s)/__SIGNALS[i])*(fabs(_data)/_range)*(log10(1.0/__SIGNALS[i])/log10(2.0))); }
Генерируемый сигнал будет представлять собой отрицательную энтропию баров минус положительную энтропию баров. Причина здесь в том, что если энтропия отрицательных баров превышает энтропию положительных , то у нас меньше информации об отрицательных барах и, следовательно, короткой позиции, чем при положительных барах, которые подразумевают длинную позицию. На первый взгляд кажется, что на выходе мы получаем "опасную" систему следования за трендом! Однако из-за весов, приложенных выше при вычислении энтропии, это впечатление может оказаться неверным.
Сигналы будут обновляться, когда состояние длинной или короткой позиции превысит порог открытия, поскольку это означает открытие позиции. Это произойдет по таймеру, поэтому мы изменим советник, собранный Мастером, чтобы учесть это.
//+------------------------------------------------------------------+ //| "Timer" event handler function | //+------------------------------------------------------------------+ void OnTimer() { if(PositionSelect(Symbol()) && Signal_ThresholdClose<=fabs(filter0.m_last_condition)) { filter0.ResultUpdate(filter0.Result()); } // if(!PositionSelect(Symbol()) && Signal_ThresholdOpen<=fabs(filter0.m_last_condition)) { filter0.SignalUpdate(filter0.m_last_signal); } ExtExpert.OnTimer(); }
Как уже говорилось, исходная функция в классе будет работать только при оптимизации.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalSE::SignalUpdate(double Signal) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { m_samples++; DF_SIGNAL.Resize(m_samples,__INPUTS+2); for(int i=0;i<__INPUTS;i++) { DF_SIGNAL[m_samples-1].Set(i,m_signals[0][i]); } // DF_SIGNAL[m_samples-1].Set(__INPUTS,Signal); DF_SIGNAL[m_samples-1].Set(__INPUTS+1,1-Signal); } }
2.1.2. Результаты
Результаты будут основаны на прибыли последней закрытой позиции.
if(HistorySelect(0,m_symbol.Time())) { int _deals=HistoryDealsTotal(); for(int d=_deals-1;d>=0;d--) { ulong _deal_ticket=HistoryDealGetTicket(d); if(HistoryDealSelect(_deal_ticket)) { if(HistoryDealGetInteger(_deal_ticket,DEAL_ENTRY)==DEAL_ENTRY_OUT) { _result=HistoryDealGetDouble(_deal_ticket,DEAL_PROFIT); break; } } } } return(_result);
Они будут обновляться, когда состояние длинной или короткой позиции превысит порог закрытия, поскольку это означает закрытие позиции. Это также произойдет по таймеру. При этом функция класса лишь обновит файлы леса решений при оптимизации.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalSE::ResultUpdate(double Result) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { int _err; if(Result<0.0) { double _odds = MathRandomUniform(0,1,_err); // DF_SIGNAL[m_samples-1].Set(__INPUTS,_odds); DF_SIGNAL[m_samples-1].Set(__INPUTS+1,1-_odds); } } }
2.1.3. Написание Forest
Лес будет записан на тике перед чтением, поэтому мы модифицируем советника, собранного Мастером, чтобы учесть это.
//+------------------------------------------------------------------+ //| "Tick" event handler function | //+------------------------------------------------------------------+ void OnTick() { if(!signal_se.m_read_forest) signal_se.WriteForest(); ExtExpert.OnTick(); }
2.1.4. Чтение Forest
Лес будет записан в тестере в конце прогона, поэтому мы модифицируем советника, собранного Мастером, чтобы учесть это.
//+------------------------------------------------------------------+ //| "Tester" event handler function | //+------------------------------------------------------------------+ double OnTester() { signal_se.ReadForest(); return(0.0); }
2.2. Денежный класс советника
В этой статье мы также рассмотрим создание кастомного класса изменения размера позиции для использования с Мастером. Используем класс Money Size Optimized и изменим его, чтобы нормализовать размеры позиций на основе энтропии Шеннона. Наш новый интерфейс будет выглядеть так:
// wizard description start //+------------------------------------------------------------------+ //| Description of the class | //| Title=Trading with 'Shannon Entropy' optimized trade volume | //| Type=Money | //| Name=SE | //| Class=CMoneySE | //| Page=money_se | //| Parameter=ScaleFactor,int,3,Scale factor | //| Parameter=Percent,double,10.0,Percent | //+------------------------------------------------------------------+ // wizard description end //+------------------------------------------------------------------+ //| Class CMoneySE. | //| Purpose: Class of money management with 'Shannon Entropy' optimized volume. | //| Derives from class CExpertMoney. | //+------------------------------------------------------------------+ class CMoneySE : public CExpertMoney { protected: int m_scale_factor; public: double m_absolute_condition; CMoneySE(void); ~CMoneySE(void); //--- void ScaleFactor(int scale_factor) { m_scale_factor=scale_factor; } void AbsoluteCondition(double absolute_condition) { m_absolute_condition=absolute_condition; } virtual bool ValidationSettings(void); //--- virtual double CheckOpenLong(double price,double sl); virtual double CheckOpenShort(double price,double sl); protected: double Optimize(double lots); };
Переменная m_absolute_condition является абсолютным значением целых чисел, возвращаемых функциями LongCondition и ShortCondition. Поскольку это нормализованное значение, мы можем использовать его размер для определения размера нашей позиции. Эта переменная будет передана из сигнального класса в денежный класс с помощью модификаций советника, собранного Мастером.
//+------------------------------------------------------------------+ //| Global expert object | //+------------------------------------------------------------------+ CExpert ExtExpert; CSignalSE *signal_se; CMoneySE *money_se;
Сделаем то же самое в тиковой функции:
//+------------------------------------------------------------------+ //| "Tick" event handler function | //+------------------------------------------------------------------+ void OnTick() { if(!signal_se.m_read_forest) signal_se.WriteForest(); money_se.AbsoluteCondition(fabs(signal_se.m_last_condition)); ExtExpert.OnTick(); }
Основные изменения будут внесены в функцию Optimize:
//+------------------------------------------------------------------+ //| Optimizing lot size for open. | //+------------------------------------------------------------------+ double CMoneySE::Optimize(double lots) { double lot=lots; //--- normalize lot size based on magnitude of condition lot*=(20*m_scale_factor/fmax(20.0,((100.0-m_absolute_condition)/100.0)*20.0*m_scale_factor*m_scale_factor)); //--- reduce lot based on number of losses orders without a break if(m_scale_factor>0) { //--- select history for access HistorySelect(0,TimeCurrent()); //--- int orders=HistoryDealsTotal(); // total history deals int losses=0; // number of consequent losing orders CDealInfo deal; //--- for(int i=orders-1;i>=0;i--) { deal.Ticket(HistoryDealGetTicket(i)); if(deal.Ticket()==0) { Print("CMoneySE::Optimize: HistoryDealGetTicket failed, no trade history"); break; } //--- check symbol if(deal.Symbol()!=m_symbol.Name()) continue; //--- check profit double profit=deal.Profit(); if(profit>0.0) break; if(profit<0.0) losses++; } //--- if(losses>1){ lot*=m_scale_factor; lot/=(losses+m_scale_factor); lot=NormalizeDouble(lot,2);} } //--- normalize and check limits double stepvol=m_symbol.LotsStep(); lot=stepvol*NormalizeDouble(lot/stepvol,0); //--- double minvol=m_symbol.LotsMin(); if(lot<minvol){ lot=minvol; } //--- double maxvol=m_symbol.LotsMax(); if(lot>maxvol){ lot=maxvol; } //--- return(lot); }
3.0. Мастер MQL5
Мы соберем два советника: один только с созданным нами классом сигналов плюс торговля минимальным объемом для управления капиталом, а второй — с созданными нами классами сигналов и управления капиталом.
4.0. Тестер стратегий
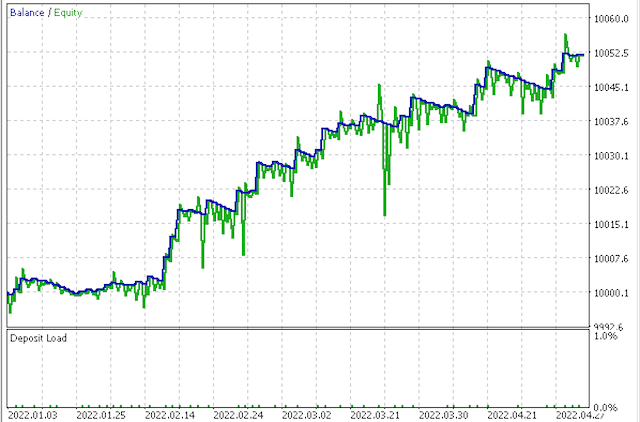
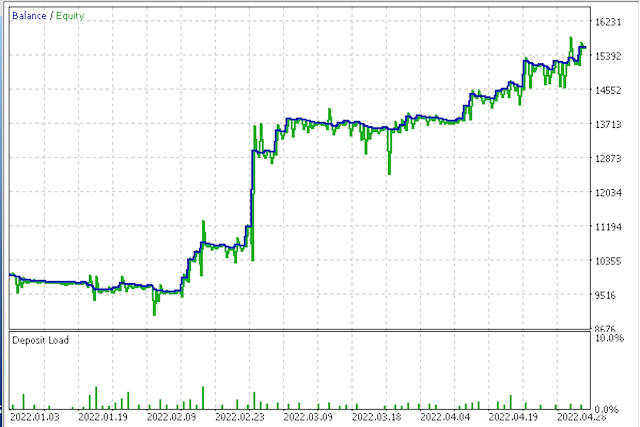
Оптимизация первого советника дает профит-фактор 2,89 и коэффициент Шарпа 4,87. При оптимизации второго советника получаем профит-фактор 3,65 и коэффициент Шарпа 5,79.
Первый отчет
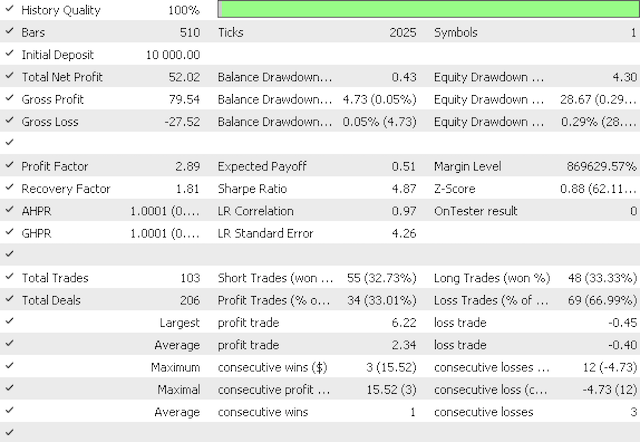
Первая кривая эквити
Второй отчет
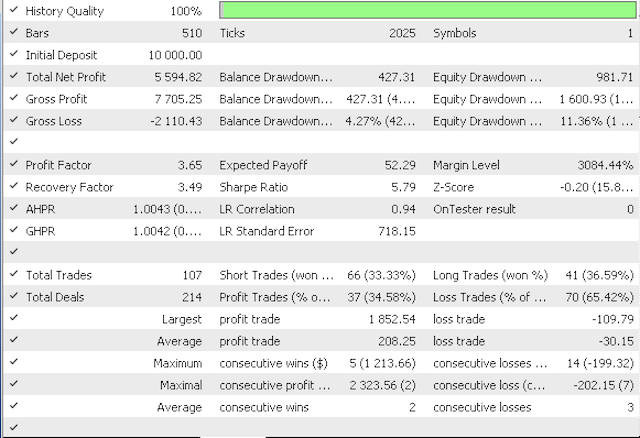
Вторая кривая эквити
5.0. Заключение
Приложенные советники были оптимизированы по ценам открытия 4-часового таймфрейма для идеальных уровней тейк-профита и стоп-лосса. Это означает, что вы не сможете воспроизвести эти результаты на реальном счете или даже в тестере стратегий в режиме каждого тика. Но смысл статьи не в этом. Вместо того, чтобы пытаться придумать грааль, который каждый должен воспроизвести, эта серия статей стремится раскрыть различные идеи, которые каждый трейдер может приспособить под свои нужды. Рынки в целом все еще слишком сильно коррелированы, поэтому поиск преимущества может сослужить вам хорошую службу в условиях высокой волатильности. Спасибо за внимание!
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/11487
Разработка торговой системы на основе индикатора VIDYA
Нейросети — это просто (Часть 32): Распределенное Q-обучение
Управление рисками и капиталом с помощью советников
Магия временных торговых интервалов с инструментом Frames Analyzer
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Прочитал статью, но толком не понял:
1. Что подаёте на вход случайному лесу.
2. Как считаете энтропию - по истории классификации леса?
Перевод статьи не высокого качества, к сожалению, что осложняет понимание.
Иногда кажется, что не хватает иллюстраций к статье, хотя в тексте идёт о них речь:
"
Давайте рассмотрим наглядный пример — на картинке выше традиционное дерево решений (обозначено синим цветом) может выбирать из всех четырех атрибутов при принятии решения о том, как разделить узел. Оно решает использовать Атрибут 1 (черный и подчеркнутый), поскольку при этом данные разбиваются на максимально разделенные группы.
"