Aplicação prática das correlações na negociação

MetaTrader 5 — Estatística e análise | 7 março 2019, 07:12

4 119

Alexander Fedosov

Índice

Introdução

A essência da negociação está ligada à necessidade de prever o futuro do movimento do mercado e, portanto, o lucro em potencial depende fortemente da precisão de tal previsão. No começo do meu artigo Ideias de negociação com base na direção dos preços e na velocidade do movimento, eu descrevi a seguinte ideia: cada movimento é caracterizado por sua direção, aceleração e velocidade. O mesmo é aplicável ao movimento de preços em forex e outros mercados.

Qualquer movimento tem certas características que indicam o começo do movimento, uma certa velocidade, inércia e fim. Estratégias de negociação bem-sucedidas são aquelas que podem detectar o início do movimento o mais cedo possível e se posicionar no mercado, bem como identificar de forma clara o fim desse movimento. No entanto, nenhuma estratégia pode determinar os pontos de entrada e saída com uma probabilidade absoluta. Esta é uma questão de probabilidade e chances favoráveis. Portanto, neste artigo, nós vamos considerar uma das ferramentas da teoria da probabilidade — a correlação, que será aplicada no âmbito dos mercados financeiros.

O conceito de correlação

Correlação é uma relação estatística entre duas ou mais variáveis aleatórias (ou quantidades que podem ser consideradas aleatórias com algum grau aceitável de precisão). Mudanças em uma ou mais variáveis levam a mudanças sistemáticas em outras variáveis relacionadas. A métrica matemática da correlação de duas variáveis aleatórias é o coeficiente de correlação. Se uma alteração em uma variável aleatória não levar a uma alteração regular na outra variável aleatória, mas levar a uma mudança em outra característica estatística dessa variável aleatória, tal relação não é considerada como correlacionada, embora a mesma seja estatística.

Os valores do coeficiente de correlação podem variar de -1 a +1. Quanto mais próximo de 1 for o valor da correlação, maior a interdependência entre as variáveis estudadas. E se o valor tende para 1, a correlação é considerada positiva. Se o valor tender para -1, a correlação é negativa. Durante a correlação positiva, o aumento em uma das variáveis leva ao aumento do segundo. No caso da correlação negativa, o aumento do valor de um leva a diminuição do segundo.

Em outros palavras, as correlações ajudam a identificar a dependência da primeira variável com a segunda, com base nos dados disponíveis. Como a correlação pode ajudar na negociação do mercado financeiro?

Vejamos a Fig.1 e a zona de tendência de baixa que foi marcada.

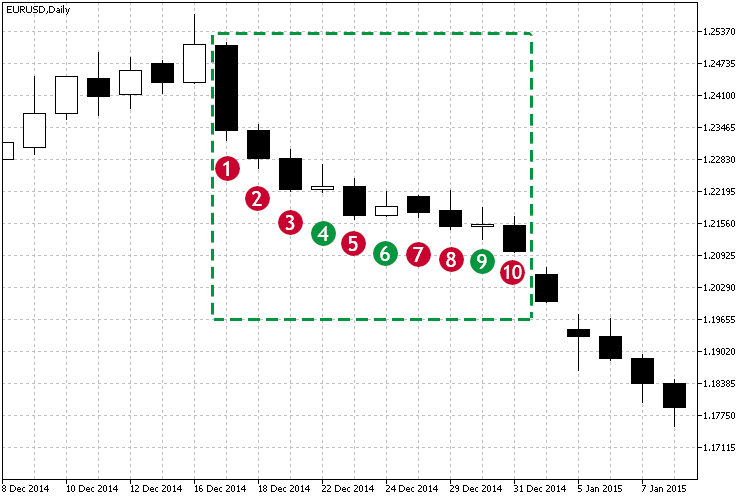
Fig.1 Exemplo de uma tendência de baixa.

Como pode ser visto na área marcada, começando com a vela #1, a maioria dos preços de fechamento estão abaixo do preço de abertura, e cada preço de fechamento está abaixo do preço anterior. Desse modo, o preço está caindo. Pode-se verificar de forma visual, que há uma tendência de baixa. Mas como você pode entender se há uma dependência forte entre eles? Além disso, a tendência não é perfeita: houve pequenas tentativas de movimentos de alta nas velas 4, 6 e 9. Como a correlação pode ser útil aqui? Nesse caso, o coeficiente de correlação indicará a força do movimento atual. Com base nas observações dos coeficientes de correlação ao longo do tempo, nós podemos tirar várias conclusões:

A força da tendência atual - diretamente com base no valor atual da correlação.
A duração da tendência - com base na observação do valor limitante selecionado ao longo do tempo. Por exemplo, o limite é superior a 0.75 e não se enquadra entre as velas 3-4.

Tipos de correlações

Os seguintes tipos de correlação ajudam na definição da dependência entre as variáveis analisadas:

Linear e não linear. A correlação linear refere-se a uma dependência, na qual um valor aumenta ou diminui, e o segundo se altera de maneira correspondente. Na dependência não-linear, as alterações em uma variável não levam a uma alteração direta na outra, mas podem ser descritas por outras funções.
A correlação positiva e negativa refere-se ao caráter dessa dependência. No caso da correlação positiva, o crescimento de uma das variáveis leva ao crescimento da outra.

Veja a Fig. 1, que mostra um exemplo da correlação negativa linear. Em seguida, nós consideramos vários tipos de cálculo e métodos para determinar a interdependência das duas variáveis.

Coeficiente de correlação linear (coeficiente de correlação de Pearson)

Este método de cálculo permite identificar a relação direta entre as variáveis com base em seus valores absolutos. O cálculo é organizado de modo que, se a relação entre as variáveis for linear, o coeficiente de Pearson será exibido. No contexto dos mercados financeiros, essa relação significaria a presença de movimento em uma ou outra direção no tempo. A correlação de Pearson é calculada de acordo com a seguinte fórmula:

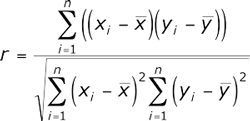
Agora vamos calcular o coeficiente de correlação de Pearson para os dados apresentados na Fig.1 e medir a dependência dos preços de fechamento ao longo do tempo. Para fazer isso, vamos inserir os dados na tabela:

Preço de fechamento	Número da vela
1.23406	1
1.22856	2
1.22224	3
1.22285	4
1.21721	5
1.21891	6
1.21773	7
1.21500	8
1.21546	9
1.20995	10

Todo o cálculo é exibido na próxima figura.

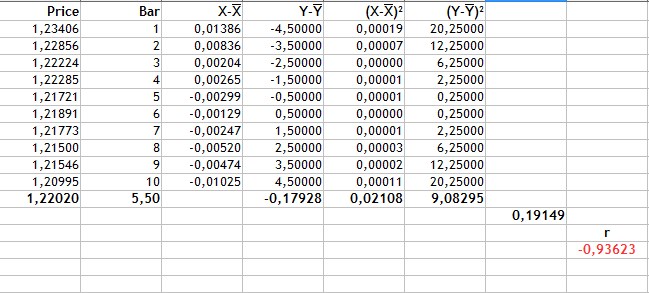
Fig.2 Cálculo do coeficiente de correlação de Pearson.

O cálculo é realizado na seguinte sequencia:

Primeiro, calcula-se os valores médios do Preço e do número de velas. Esses são 1.22020 e 5.5 respectivamente.
Então, nós encontramos o desvio da média para cada tipo de variável (colunas 3-4).
O valor de -0.17928 é a soma do produto dos desvios do preço e o número da vela. Ele é o numerador da fórmula.
As colunas 5 e 6 são os desvios quadrados. Os valores de 0.02108 e 9.08295 são as raízes quadradas da soma dos desvios quadrados.
O denominador na fórmula ou o produto da soma dos desvios quadrados é igual a 0.19149.
Então, o coeficiente de correlação de Pearson é igual a -0.93623.

Esses resultados mostram que há uma forte dependência linear negativa.

Coeficiente de correlação de postos de Spearman

Este método de cálculo permite a determinação de uma relação linear direta entre variáveis aleatórias. A avaliação baseia-se não nos valores numéricos dos elementos analisados, mas nos postos correspondentes. Seus valores também podem variar de -1 a 1. O valor absoluto caracteriza a proximidade da interconexão, enquanto o sinal denota a direção dessa conexão entre os dois elementos. Ele é calculado usando a seguinte fórmula:

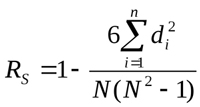
Onde Di é a diferença dos postos das características estudadas. Vamos considerar um exemplo do cálculo da correlação de postos para os dados apresentados na Fig.1 e inserir os valores na nova tabela:

Preço de fechamento	Número da vela	Posto do preço de fechamento	Posto do número da vela
1.23406	1	10	1
1.22856	2	9	2
1.22224	3	7	3
1.22285	4	8	4
1.21721	5	4	5
1.21891	6	6	6
1.21773	7	5	7
1.21500	8	2	8
1.21546	9	3	9
1.20995	10	1	10

Como pode ser visto na tabela, nós classificamos os valores do preço de fechamento: o posto 1 é atribuído ao valor mais baixo e assim por diante. Usando a fórmula, nós calculamos a diferença dos níveis D das características estudadas e substituímos os valores obtidos na fórmula.

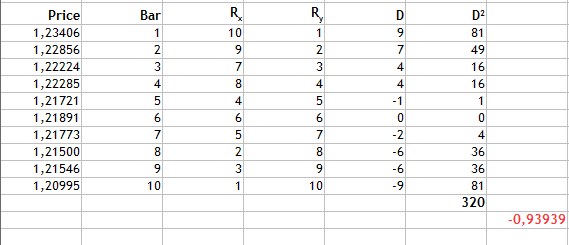
Fig.3 Cálculo do coeficiente de correlação de postos de Spearman.

Como pode ser visto na Fig.3, nós encontramos a diferença dos postos e, então, encontramos a soma dos quadrados das diferenças resultantes e obtemos 320. Substitua os valores obtidos pela fórmula e obtenha o resultado de -0.93939.

Com base no valor resultante do coeficiente de correlação, nós podemos chegar à mesma conclusão: uma forte dependência linear negativa. Nesse caso, a proximidade da conexão é comparável ao coeficiente de correlação de Pearson. No entanto, o seguinte fato deve ser levado em consideração: este método de cálculo tem uma desvantagem. Valores incomparáveis de diferenças podem corresponder aos mesmos valores das diferenças de postos. Por exemplo, os postos das barras são comparáveis, enquanto que os valores dos níveis de preços não são uniformes, embora a variação do preço seja bem pequena e difere por milésimos. Portanto, esse método calculado é apropriado neste caso.

Coeficiente de correlação por postos de Kendall

Como o coeficiente de Spearman, o coeficiente de correlação por postos de Kendall é a medida da relação linear entre as variáveis aleatórias. Os valores dos elementos analisados são classificados de maneira semelhante, embora o método de cálculo seja diferente. A seguinte fórmula do cálculo do coeficiente é aplicada aqui:

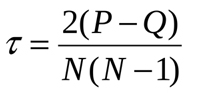
Onde P é a soma das correspondências e Q é a soma das inversões. Para entender o significado acima, vamos mais uma vez ver o exemplo na Fig.1. Vamos ordenar primeiro os dados da tabela da seguinte forma:

Preço de fechamento	Número da vela	Posto do preço de fechamento	Posto do número da vela
1.20995	10	1	10
1.21500	8	2	8
1.21546	9	3	9
1.21721	5	4	5
1.21773	7	5	7
1.21891	6	6	6
1.22224	3	7	3
1.22285	4	8	4
1.22856	2	9	2
1.23406	1	10	1

Portanto, a tabela é ordenada pelo posto do preço de fechamento. Após isso, vamos determinar o número de postos acima do atual, começando com a primeira linha no campo 'Posto do número da vela'. O primeiro valor é 10, então vamos verificar - não há postos acima de um. Então visualizamos 8 e encontramos um posto mais acima de 9. E assim por diante. Estes serão os valores correspondentes de P.

Então nós calculamos os postos mais baixos. Para 10, haverá 9 níveis mais baixos, porque ele é o mais alto. Para 8, haverá sete postos mais baixos — 5,7,6,3,4,2,1. Estes serão as inversões de Q. Vamos adicionar o valor resultante a uma tabela e calcular o coeficiente:

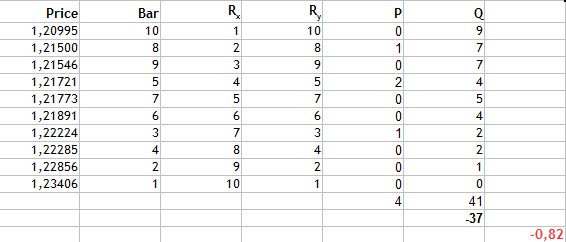
Figura 4 Cálculo do coeficiente de correlação por postos de Kendall.

Em seguida, nós somamos os valores correspondentes e os valores de inversão resultantes. Sua diferença é igual à -37. Ao inserir este valor na fórmula, nós obtemos o coeficiente de Kendall igual a -0.82. Novamente, há uma forte correlação negativa. No entanto, o resultado sugere que esse método é mais seletivo do que os dois anteriores, porque o valor absoluto é menor.

O coeficiente de correlação dos sinais de Fechner

Este método baseia-se na avaliação do grau de consistência nas direções dos desvios do valor da média e no cálculo dos sinais dos desvios correspondentes aos valores. A fórmula de cálculo é muito simples:

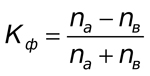
Aqui Na é o número de correspondências pelo sinal, Nb é o número de disparidade. Agora vamos calcular o coeficiente de correlação para o nosso exemplo da fig.1.

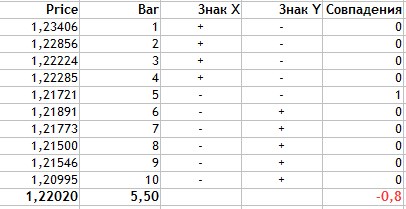
Fig.4 Cálculo do coeficiente de correlação de Fechner.

O cálculo é realizado da seguinte forma:

São encontrados os valores médios dos dados para as duas características. Isso é igual a 1.2202 para o preço e 5.5 para o número da vela.
Na coluna Sign X, nós definimos '+' se o valor do Preço atual for maior que a média e '-' se o Preço estiver abaixo da média.
O mesmo é feito para os valores numéricos da velas.
Então, nós precisamos calcular os sinais correspondentes para as duas características (o preço e o número da vela).
Como pode ser visto na tabela, os valores correspondem apenas uma vez e assim Na = 1, enquanto Nb = 9.
Estes valores obtidos são substituídos na fórmula.

Como você pode ver, o método de cálculo do coeficiente de correlação de Fechner é bem simples. O valor resultante é -0,8. Novamente, essa é uma indicação de um forte relacionamento negativo entre o preço de fechamento e o número de velas.

Implementação dos indicadores

Agora, vamos implementar todos os métodos de cálculo de correlação usando a linguagem MQL5.

Coeficiente de correlação de Pearson

Como o coeficiente de Pearson é calculado usando uma fórmula grande, o cálculo é dividido em duas etapas, o cálculo do numerador e o denominador.

//+------------------------------------------------------------------+
//| Cálculo do numerador                                             |
//+------------------------------------------------------------------+
double Numerator(double &Ranks[],int N)
  {
//----
   double Y[],dx[],dy[],mx=0.0,my=0.0,sum=0.0,sm=0.0;
   ArrayResize(Y,N);
   ArrayResize(dx,N);
   ArrayResize(dy,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0;j<N;j++)
     {
      dx[j]=Y[j]-mx;
      dy[j]=Ranks[j]-my;
      sm+=dx[j]*dy[j];
     }
   return sm;
  }
//+------------------------------------------------------------------+
//| Cálculo do denominador                                           |
//+------------------------------------------------------------------+
double Denominator(double &Ranks[],int N)
  {
//----
   double Y[],dx2[],dy2[],mx=0.0,my=0.0,sum=0.0,smx2=0.0,smy2=0.0;
   ArrayResize(Y,N);
   ArrayResize(dx2,N);
   ArrayResize(dy2,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0;j<N;j++)
     {
      dx2[j]=MathPow(Y[j]-mx,2);
      dy2[j]=MathPow(Ranks[j]-my,2);
      smx2+=dx2[j];
      smy2+=dy2[j];
     }
   return(MathSqrt(smx2*smy2));
  }

O método de cálculo final e a lógica de cálculo para a visualização do indicador são os seguintes:

//+------------------------------------------------------------------+
//| Função de iteração do indicador personalizado                    |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // número de barras no histórico no tick atual
                const int prev_calculated,// número de barras calculadas na chamada anterior
                const int begin,          // índice do início da contagem de barras confiáveis
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=PearsonCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }

//+------------------------------------------------------------------+
//| Cálculo do coeficiente de correlação de Pearson                  |
//+------------------------------------------------------------------+
double PearsonCalc(double &Ranks[],int N)
  {
   double ch,zn;
   ch=Numerator(Ranks,N);
   zn=Denominator(Ranks,N);
   return (ch/zn);
  }

Coeficiente de correlação de postos de Spearman

Para um indicador baseado nesses métodos de cálculo, eu usei algumas das soluções existentes disponíveis aqui.

//+------------------------------------------------------------------+
//| Função de iteração do indicador personalizado                    |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // número de barras no histórico no tick atual
                const int prev_calculated,// número de barras calculadas na chamada anterior
                const int begin,          // índice do início da contagem de barras confiáveis
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=limit; i>=0; i--)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=int(price[i+k]*multiply);

      RankPrices(TrueRanks,PriceInt);
      ExtLineBuffer[i]=SpearmanCalc(R2,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Cálculo do coeficiente de correlação de Spearman                 |
//+------------------------------------------------------------------+
double SpearmanCalc(double &Ranks[],int N)
  {
//----
   double sumd2=0.0;

   for(int i=0; i<N; i++)
      sumd2+=MathPow(Ranks[i]-i-1,2);

   return(1-6*sumd2/(N*(MathPow(N,2)-1)));
  }

Coeficiente de correlação por postos de Kendall

Para o cálculo deste método, vamos usar as reservas internas do próprio MQL5. Ou seja, nós usaremos a biblioteca de estatísticas matemáticas embutidas.

//+------------------------------------------------------------------+
//| Função de iteração do indicador personalizado                    |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // número de barras no histórico no tick atual
                const int prev_calculated,// número de barras calculadas na chamada anterior
                const int begin,          // índice do início da contagem de barras confiáveis
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;

      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);

   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=KendallCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Cálculo do coeficiente de correlação de Kendall                  |
//+------------------------------------------------------------------+
double KendallCalc(double &Ranks[],int N)
  {
   double Y[],t;
   ArrayResize(Y,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }
   MathCorrelationKendall(Ranks,Y,t);
   return (t);
  }
//+------------------------------------------------------------------+

O coeficiente de correlação dos sinais de Fechner

Este método baseia-se no cálculo de sinais dos desvios correspondentes ao valor médio. Além disso, os sinais correspondentes são contados.

//+------------------------------------------------------------------+
//| Função de iteração do indicador personalizado                    |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,    // número de barras no histórico no tick atual
                const int prev_calculated,// número de barras calculadas na chamada anterior
                const int begin,          // índice do início da contagem de barras confiáveis
                const double &price[]
                )

  {
   if(rates_total<rangeN+begin)
      return(0);
   int limit;

   if(prev_calculated>rates_total || prev_calculated<=0)
     {
      limit=rates_total-2-rangeN-begin;
      if(begin>0)
         PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin);
     }
   else
      limit=rates_total-prev_calculated;

   ArraySetAsSeries(price,true);
   for(int i=0; i<=limit; i++)
     {
      for(int k=0; k<rangeN; k++)
         PriceInt[k]=price[k+i];
      ExtLineBuffer[i]=FechnerCalc(PriceInt,rangeN);
     }

   return(rates_total);
  }
//+------------------------------------------------------------------+
//| Cálculo do coeficiente de correlação de Fechner                  |
//+------------------------------------------------------------------+
double FechnerCalc(double &Ranks[],int N)
  {
   double Y[],res,mx,my,sum=0.0,markx[],marky[];
   double Na=0.0,Nb=0.0;
   ArrayResize(Y,N);
   ArrayResize(markx,N);
   ArrayResize(marky,N);

   int n=N;
   for(int i=0; i<N; i++)
     {
      Y[i]=n;
      n--;
     }

   mx=Average(Y);
   my=Average(Ranks);

   for(int j=0; j<N; j++)
     {
      markx[j]=(Y[j]>mx)?1:-1;
      marky[j]=(Ranks[j]>my)?1:-1;
      if(markx[j]==marky[j])
         Na++;
      else
         Nb++;
     }

   res=(Na-Nb)/(Na+Nb);
   return (res);
  }

A Figura 6 demonstra todos os quatro métodos de cálculo de correlação entre o preço de fechamento e o horário da vela. O período de 10 é definido para todos os indicadores e, portanto, você pode avaliar sua operação em condições semelhantes.

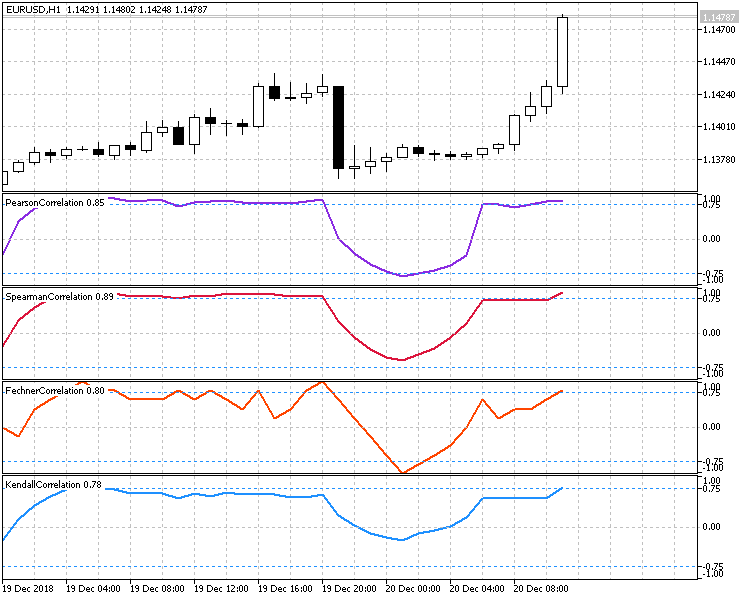
Fig.6 Comparação dos diferentes métodos de cálculo.

Sistema de negociação baseado em correlação

Ao criar uma estratégia de negociação baseada em correlações, você deve analisar cuidadosamente as especificidades do indicador e métodos de cálculo, bem como identificar possíveis riscos e condições desfavoráveis de entrada no mercado.

O uso de períodos grandes não é recomendado para quase todos os indicadores, pois o indicador estará mais atrasado. Eles também podem mostrar correlações fracas em caso de reversões acentuadas, porque eles serão responsáveis pelos valores dos movimentos opostos já concluídos.

Como os indicadores não analisam o preço atual, mas o agregado de vários valores ao longo de um período de tempo, o valor da correlação atual não deve ser tratado como uma estimativa absoluta. A dinâmica da correlação deve ser analisada. Isso pode ser feito usando osciladores que utilizam os valores atuais e anteriores do coeficiente de correlação.

Portanto, nossa estratégia analisará o comportamento do oscilador baseado no coeficiente de correlação e irá buscar por um rompimento dos níveis predefinidos. As duas opções a seguir são possíveis:

A queda do coeficiente. Vender, quando o coeficiente positivo cai e rompe o nível predefinido. Comprar, quando o coeficiente negativo cresce e rompe um nível simétrico definido em uma área positiva.
O crescimento do coeficiente. Vender, quando o coeficiente cai na área negativa e rompe um nível predefinido. Comprar, quando o coeficiente cresce e rompe um nível positivo simétrico.

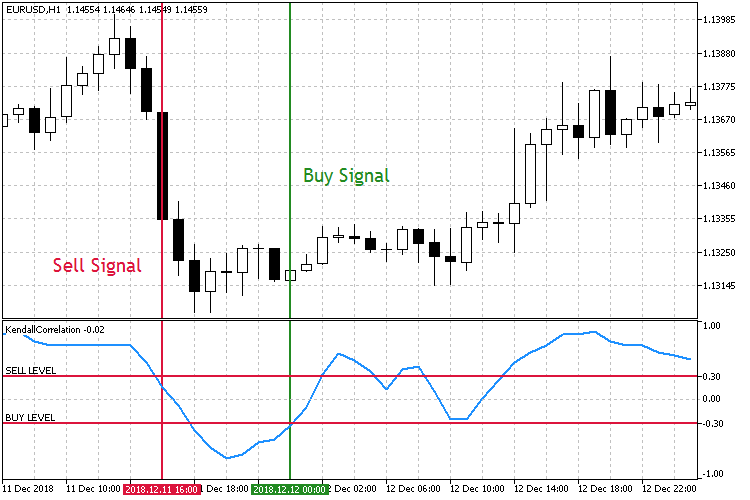
Os potenciais pontos de entrada são apresentados nas capturas de tela abaixo.

Fig.7 Negociando através da queda do coeficiente de correlação.

Como pode ser visto nas capturas de tela, há dois níveis de coeficientes de correlação simétricos, o Nível de Venda em 0.3 e o Nível de Compra em -0.3. Quando o Nível de Venda é rompido para baixo, abre-se uma ordem de Venda. Uma ordem de Compra é colocada quando o Nível de Compra for rompido para cima.

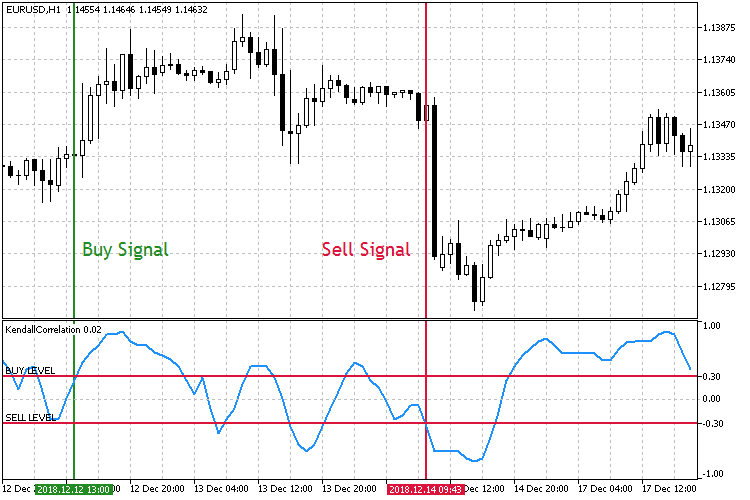
Fig.8 Negociando através do crescimento do coeficiente de correlação.

No segundo modo de negociação mostrado na Fig. 8, os principais níveis de entrada no mercado são os opostos. Desta vez, quando o Nível de Compra é rompido para cima, uma ordem de Compra é aberta. Uma ordem de Venda é aberta quando o Nível de Venda é rompido para baixo.

Para implementar o Expert Advisor, nós precisamos fornecer as estratégias acima e escolher um método de cálculo de correlação apropriado.

//+------------------------------------------------------------------+
//| Enumeração dos modos de operação                                 |
//+------------------------------------------------------------------+
enum Strategy_type
  {
   DECREASE = 1,           //Na queda       
   INCREASE                //No crescimento
  };
//+------------------------------------------------------------------+
//| Enumeração dos métodos de cálculo da correlação                  |
//+------------------------------------------------------------------+
enum Corr_method
  {
   PEARSON = 1,            //Pearson       
   SPEARMAN,               //Spearman
   KENDALL,                //Kendall
   FECHNER                 //Fechner
  };

Além dos parâmetros do EA, vamos adicionar as seguintes entradas: seleção do método de cálculo, a estratégia, o nível principal e o período gráfico operacional ajustável.

//+------------------------------------------------------------------+
//| Parâmetros de entrada do Expert Advisor                          |
//+------------------------------------------------------------------+
input    string               Inp_EaComment="Correlation Strategy";        //Comentário do EA
input    double               Inp_Lot=0.01;                                //Lote
input    MarginMode           Inp_MMode=LOT;                               //MM

//--- Seleção do método de cálculo da correlação e o tipo da estratégia
input    Corr_method          Inp_Corr_method=1;                           //Método de Correlação
input    Strategy_type        Inp_Strategy_type=1;                         //Tipo da Estratégia

//--- Parâmetros do EA
input    string               Inp_Str_label="===EA parameters===";         //Rótulo
input    int                  Inp_MagicNum=1111;                           //Magic number
input    int                  Inp_StopLoss=40;                             //Stop Loss(pontos)
input    int                  Inp_TakeProfit=60;                           //Take Profit(pontos)
//--- Parâmetros do indicador 
input    int                  Inp_RangeN=10;                               //Cálculo do intervalo
input    double               Inp_KeyLevel=0.2;                            //Nível principal    
input    ENUM_TIMEFRAMES      Inp_Timeframe=PERIOD_CURRENT;                //Período gráfico operacional

A exatidão do nível principal será verificado na etapa de inicialização do EA: o nível deve estar localizado entre 0 e 1, porque um valor absoluto será usado para o nível.

//--- Verificação da exatidão do nível principal
   if(Inp_KeyLevel>1 || Inp_KeyLevel<0)
     {
      Print(Inp_EaComment,": Incorrect key level!");
      return(INIT_FAILED);
     }

Em seguida, defina o método de cálculo da correlação selecionada nos parâmetros de entrada:

//--- 
   switch(Inp_Corr_method)
     {
      case 1:
         ind_type="Correlation\\PearsonCorrelation";
         break;
      case 2:
         ind_type="Correlation\\SpearmanCorrelation";
         break;
      case 3:
         ind_type="Correlation\\KendallCorrelation";
         break;
      case 4:
         ind_type="Correlation\\FechnerCorrelation";
         break;
      default:
         break;
     }
//--- Obtendo o manipulador do indicador 
   InpInd_Handle=iCustom(Symbol(),Inp_Timeframe,ind_type,Inp_RangeN);
   if(InpInd_Handle==INVALID_HANDLE)
     {
      Print(Inp_EaComment,": Failed to get indicator handle");
      Print("Handle = ",InpInd_Handle,"  error = ",GetLastError());
      return(INIT_FAILED);
     }

Depois disso, nós podemos configurar as condições de entrada e a lógica operacional do EA.

//+------------------------------------------------------------------+
//| Função Tick do Expert                                            |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Obtendo os dados para cálculo

   if(!GetIndValue())
      return;

   if(!Trade.IsOpenedByMagic(Inp_MagicNum))
     {
      //--- Abrindo uma ordem se houver um sinal de compra
      if(BuySignal())
         Trade.BuyPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment);
      //--- Abrindo uma ordem se houver um sinal de venda
      if(SellSignal())
         Trade.SellPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment);
     }
  }
//+------------------------------------------------------------------+
//| Condições de Compra                                              |
//+------------------------------------------------------------------+
bool BuySignal()
  {
   bool res=false;
   if(Inp_Strategy_type==1)
      res=(corr[1]>Inp_KeyLevel && corr[0]<Inp_KeyLevel)?true:false;
   else if(Inp_Strategy_type==2)
      res=(corr[0]>Inp_KeyLevel && corr[1]<Inp_KeyLevel)?true:false;
   return res;
  }
//+------------------------------------------------------------------+
//| Condições de Venda                                               |
//+------------------------------------------------------------------+
bool SellSignal()
  {
   bool res=false;
   if(Inp_Strategy_type==1)
      res=(corr[1]<-Inp_KeyLevel && corr[0]>-Inp_KeyLevel)?true:false;
   else if(Inp_Strategy_type==2)
      res=(corr[0]<-Inp_KeyLevel && corr[1]>-Inp_KeyLevel)?true:false;
   return res;
  }

Testando o sistema de negociação

O Expert Advisor será testado com os seguintes parâmetros:

Intervalo: para o modo de tendência de alta 01.01.2015 — 01.12.2018.
Par de moeda: EURUSD.
Modo de negociação: Sem atraso. Estas não são estratégias de negociação de alta frequência, portanto o efeito dos atrasos seria pequeno.
Teste:M1 OHLC. O pré-teste em ticks reais exibe quase que os mesmos resultados.
Depósito inicial: 1000 USD.
Alavancagem: 1:500.
Servidor: MetaQuotes-Demo.
Cotação: 5-digit.

Parâmetros de teste e otimização.

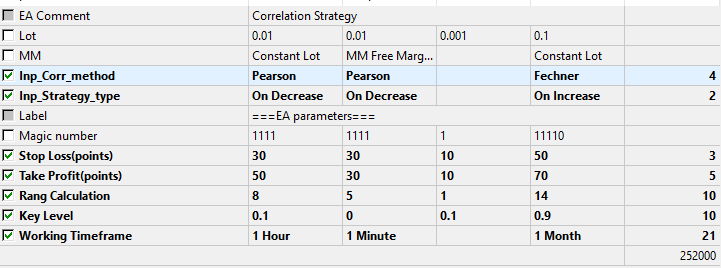
Fig.9 O conjunto de parâmetros a serem otimizados.

A otimização ajudará a determinar quais métodos de cálculo e tipos de estratégia são preferíveis. O teste e a otimização produziram os seguintes resultados.

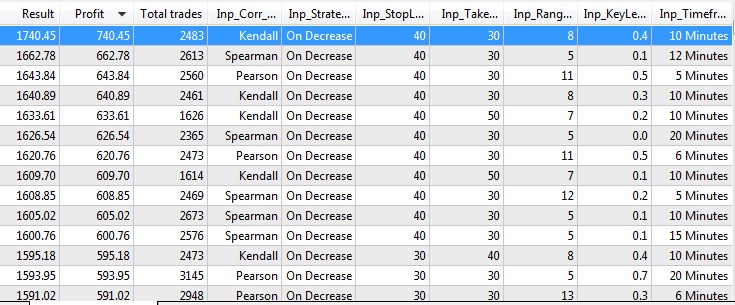
Fig.10 Resultados do teste e otimização.

Agora vamos testar o EA usando os melhores parâmetros de otimização.

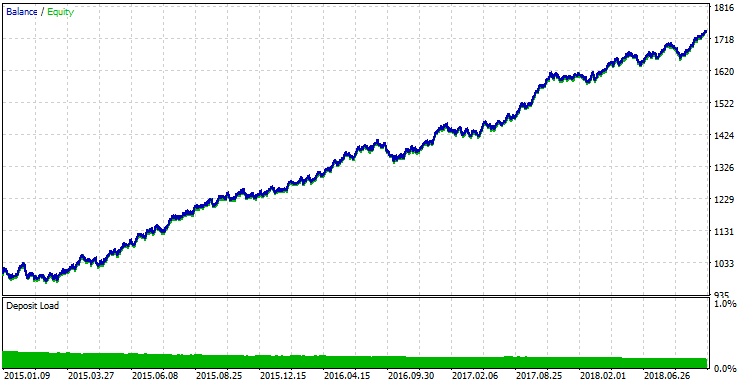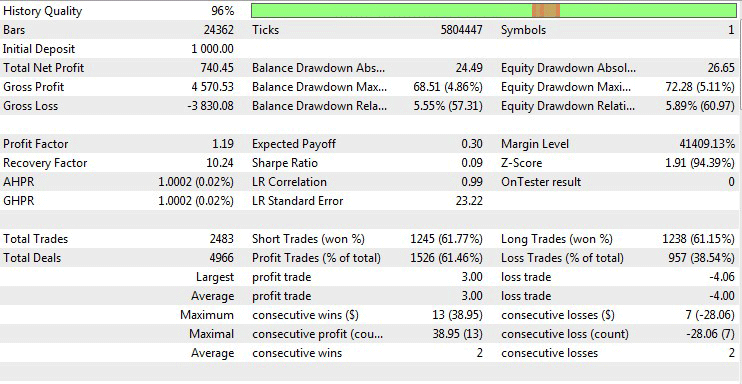
Fig.11 Testando os resultados com os melhores parâmetros da otimização.

Resultados

Com base nos resultados obtidos, as seguintes observações podem ser feitas:

Os melhores resultados são obtidos com a estratégia de queda do coeficiente de correlação, no modo On Decrease. Esse resultado só pode ser explicado pelo fato de que, quando os coeficientes caem, o oscilador responde mais rapidamente aos movimentos do mercado. Como mencionado acima, os osciladores baseados nos coeficientes de correlação (especialmente aqueles com grandes períodos) apresentam atrasos significativos.
O método de cálculo mais simples (coeficiente de Fechner) não é encontrado entre os 20 melhores resultados. O melhor resultado com este método está localizado apenas no 99º lugar.
Os melhores resultados foram obtidos em pequenos períodos gráficos com o take profit e stop loss apertados.
Não foram encontradas nenhuma dependência do montante do lucro no período selecionado e o nível principal. No entanto, os períodos menores prevalecem e o limite inferior do intervalo de otimização com o período de 5 é constantemente encontrado entre os melhores resultados. Esta é outra confirmação de que os indicadores baseados em correlação têm um grande atraso nos período maiores, exibindo resultados piores.

Conclusões

O arquivo anexado contém todos os arquivos listados, localizados nas pastas apropriadas. Para o seu bom funcionamento, você só precisa salvar a pasta MQL5 na pasta do terminal.

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Correlation.mq5	EA	O Expert Advisor, que inclui 4 métodos de cálculo de correlação e 2 estratégias baseadas nos mesmos.
2	Trade.mqh	Código Base	Uma classe de funções de negociação
3	FechnerCorrelation.mq5	Indicador	Indicador de cálculo do coeficiente de correlação de Fechner
4	KendallCorrelation.mq5	Indicador	Indicador de cálculo do coeficiente de correlação de Kendall
5	PearsonCorrelation.mq5	Indicador	Indicador de cálculo do coeficiente de correlação de Pearson
6	SpearmanCorrelation.mq5	Indicador	Indicador de cálculo do coeficiente de correlação de Spearman

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/5481

Arquivos anexados |

Baixar como ZIP

MQL5.zip (807.75 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

O poder do ZigZag (parte I). Desenvolvimento da classe base do indicador

Muitos pesquisadores não prestam atenção o suficiente para determinar o comportamento dos preços. Ao mesmo tempo, são usados métodos complexos, que muitas vezes são “caixas pretas”, como aprendizado de máquina ou redes neurais. A questão mais importante que surge nesse caso é quais dados enviar para o treinamento de um determinado modelo.

Utilitário de seleção e navegação em MQL5 e MQL4: Adição da busca automática de padrões e exibição dos símbolos detectados

Neste artigo, nós continuamos expandindo os recursos do utilitário para coleta e navegação através dos símbolos. Desta vez, nós criaremos novas guias exibindo apenas os símbolos que satisfazem alguns dos parâmetros necessários e descobriremos como adicionar facilmente guias personalizadas com as regras de classificação necessárias.

Estudo de técnicas de análise de velas (parte I): Verificação de padrões existentes

Neste artigo, nós vamos considerar os padrões populares de velas e tentaremos descobrir se eles ainda são relevantes e eficazes nos mercados atuais. A análise de velas ou candlestick apareceu há mais de 20 anos e desde então se tornou bem popular. Muitos traders consideram as velas japoneses a forma de visualização de preços de ativos mais conveniente e fácil de compreender.

Uso Prático das Redes Neurais de Kohonen na Negociação Algorítmica. Parte II. Otimização e previsão

Com base nas ferramentas universais projetadas para trabalhar com as redes de Kohonen, nós construímos o sistema de análise e seleção dos parâmetros ótimos do EA e consideramos a previsão das séries temporais. Na Parte I, nós corrigimos e melhoramos as classes das redes neurais publicamente disponíveis, adicionando os algoritmos necessários. Agora é hora de colocá-los em prática.