
Aplicación práctica de las correlaciones en el trading
Contenido
- Introducción
- El concepto de correlación
- Tipos de correlación
- Implementación de indicadores
- Sistema comercial basado en la correlación
- Simulando el sistema comercial
- Resumiendo
- Conclusión
Introducción
La esencia de cualquier comercio se reduce de una u otra forma a la necesidad de pronosticar el posterior desarrollo de eventos en el mercado. Del éxito de dicho pronóstico depende enormemente el beneficio potencial. Al inicio de nuestro artículo Estrategia de trading basada en la dirección y velocidad del movimiento de los precios describimos la idea siguiente: cada movimiento tiene características tales como dirección, aceleración y velocidad. Esto también se refiere a los movimientos de precio de otros mercados.
Cualquier movimiento tiene sus características de comienzo de movimiento, velocidad definida, inercia y finalización. Se consideran estrategias exitosas aquellas que determinan el inicio del movimiento y entran en el mercado lo más pronto posible, identificando asismismo su finalización. No obstante, ni una solo estrategia puede determinar con un cien por cien de fiabilidad los puntos de entrada y salida. Aquí solo podemos hablar de oportunidad favorable, de posibilidades. Por eso, en este artículo vamos a analizar una de las herramientas de la teoría de la probabilidad, la correlación, que usaremos en el marco de los mercados financieros.
El concepto de correlación
La correlación es la interacción estadística de dos o más magnitudes aleatorias (o bien magnitudes que se pueden considerar tales con cierto nivel de precisión permisible). En este caso, además, el cambio de los valores de una o varias de estas magnitudes acompaña al cambio sistemático de los valores de otra u otras magnitudes. La medida matemática de la correlación entre dos magnitudes aleatorias es el coeficiente de correlación. Cuando el cambio en una magnitud aleatoria no produce un cambio razonable en otra magnitud aleatoria, pero provoca el cambio de otra característica estadística de dicha magnitud aleatoria, esta relación no se considerará correlativa, aunque sí que será estadística.
El coeficiente de correlación puede adoptar un valor que va de -1 a +1. Cuando más cerca se encuentre la correlación a 1, mayor será la interrelación de las magnitudes investigadas. Además, si el valor tiende a 1, la relación se considerará positiva, y si tiende a -1, negativa. Es decir, en el caso de la interrelación positiva, normalmente, el aumento de una de las magnitudes investigadas conlleva el aumento de la segunda, mientras que en el caso de la negativa se produce al contrario, el aumento de una reduce el valor de la segunda.
Dicho de otra forma, la correlación ayuda a identificar la dependencia de una magnitud con respecto a otra con la ayuda de los datos disponibles. ¿Y cómo nos puede ayudar la correlación en los mercados financieros?
Vamos a echar un vistazo a la fig.1 y a la zona marcada de tendencia descendente.
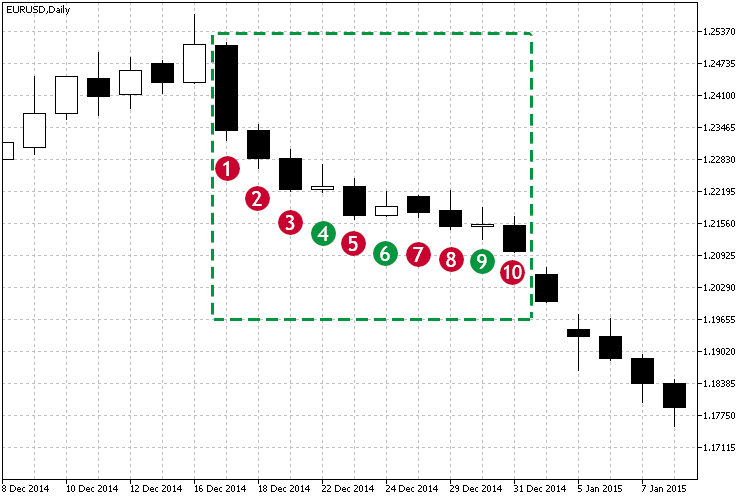
Fig.1 Ejemplo de tendencia descendente.
Como podemos ver en la zona marcada, a partir de la vela №1, el precio de cierre en una inmensa mayoría de los casos es inferior al precio de apertura, o dicho de otra forma: cada precio de cierre es inferior al anterior. Por consiguiente, con el paso del tiempo, el precio cae. En este caso, podemos ver que la tendencia es descendente, pero, ¿cómo entender la intensidad de la dependencia? Tanto más que la tendencia no es ideal, y según las velas 4,6,9, podemos ver que ha habido pequeños intentos de movimiento ascendente. ¿Cómo puede ayudarnos la correlación? En este caso, su coeficiente nos servirá como indicador de la fuerza del movimiento actual. Observando el coeficiente de correlación a lo largo del tiempo, podemos sacar varias conclusiones a la vez:
- La fuerza de la tendencia actual. El valor de correlación actual propiamente dicho.
- La duración de la tendencia. Observaciones a lo largo del tiempo del valor umbral elegido. Por ejemplo, el valor umbral es superior a 0,75 y no desciende durante 3-4 velas.
Tipos de correlación
Para determinar la relación, entre los tipos variables de correlaciones estudiadas pueden encontrarse los siguientes:
- Lineales y no lineales. Entendemos por lineal la correlación en la que la magnitud aumenta o disminuye, y la segunda cambia de forma correspondiente. En el caso de la dependencia no lineal, el cambio de una no provoca el cambio directo de la otra, y puede describirse con otras funciones.
- Entendemos por correlación positiva o negativa precisamente el carácter de la dependencia. Así, en el caso de la correlación positiva, el aumento de una de las magnitudes conlleva el crecimiento de la otra.
Podemos tomar como ejemplo la fig.1, donde se representa una correlación negativa lineal. A continuación, analizaremos varios tipos de cálculo y diversos métodos para aclarar la interrelación entre dos magnitudes.
Coeficiente de correlación lineal (coeficiente de correlación de Pearson)
Este método de cálculo permite establecer una relación directa entre magnitudes variables según sus valores absolutos. El cálculo se construye de forma que si la interrelación entre magnitudes tiene un carácter lineal, el coeficiente de Pearson lo muestre. En el contexto de los mercados financieros, esta relación conllevaría la presencia de un movimiento en tal o cual dirección en el tiempo. Para calcular el coeficiente de correlación de Pearson se aplica la siguiente fórmula:
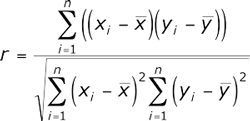
A modo de ejemplo, ahora vamos a calcular el coeficiente de correlación de Pearson para los datos mostrados en la fig.1, midiendo así de manera cuantitativa la dependencia de los precios de cierre a lo largo del tiempo. Para ello, introduciremos los datos en un recuadro:
| Precios de cierre | Número de vela |
|---|---|
| 1,23406 | 1 |
| 1,22856 | 2 |
| 1,22224 | 3 |
| 1,22285 | 4 |
| 1,21721 | 5 |
| 1,21891 | 6 |
| 1,21773 | 7 |
| 1,21500 | 8 |
| 1,21546 | 9 |
| 1,20995 | 10 |
Los cálculos completos se muestran en la siguiente figura.
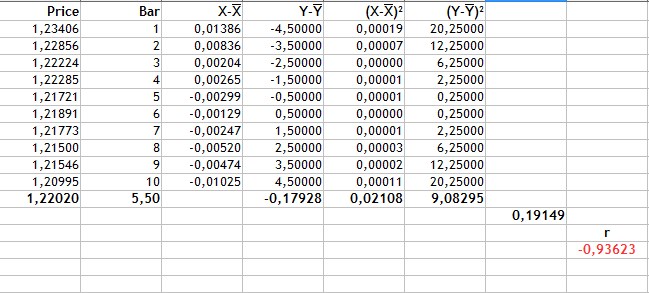
Fig.2 Cálculo del coeficiente de correlación de Pearson.
La secuencia del cálculo tiene el aspecto que sigue:
- Encontramos el valor medio del precio(Price) y el número de vela. Son 1,22020 y 5,5, respectivamente.
- Encontramos para cada tipo de variables la desviación respecto a la media(columnas 3-4).
- El valor -0,17928 es la suma de los productos de las desviaciones de precio y el número de vela. Es el numerador de la fórmula.
- Las columnas 5 y 6 son la desviación al cuadrado. Los valores 0,02108 y 9,08295 son las raíces cuadradas de la suma de los cuadrados de las desviaciones.
- El denominador de la fórmula o producto de las raíces cuadradas de las sumas de los cuadrados de las desviaciones es igual a 0,19149.
- El coeficiente de correlación de Pearson es -0,93623.
Coeficiente de correlación de puestos de Spearman
Este método de cálculo permite establecer una relación lineal entre magnitudes aleatorias. Para valorar la interrelación, se usan no los valores numéricos de las características investigadas, sino los puestos que les corresponden. Al igual que el coeficiente de Spearman, su magnitud se encuentra en el intervalo que va desde -1 hasta 1. El valor absoluto caracteriza la proximidad de la interconexión, mientras que la característica denota la dirección de la conexión entre los dos elementos. Se calcula según la fórmula:
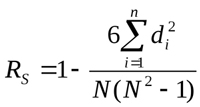
Donde Di es la diferencia entre las características estudiadas. Vamos a ver un ejemplo de cálculo de la correlación de puestos en la misma fig.1 e introducir los valores en un nuevo recuadro:
| Precios de cierre | Número de vela | Precio de cierre | Número de vela |
|---|---|---|---|
| 1,23406 | 1 | 10 | 1 |
| 1,22856 | 2 | 9 | 2 |
| 1,22224 | 3 | 7 | 3 |
| 1,22285 | 4 | 8 | 4 |
| 1,21721 | 5 | 4 | 5 |
| 1,21891 | 6 | 6 | 6 |
| 1,21773 | 7 | 5 | 7 |
| 1,21500 | 8 | 2 | 8 |
| 1,21546 | 9 | 3 | 9 |
| 1,20995 | 10 | 1 | 10 |
Como podemos ver por el recuadro, hemos clasificado los valores de precio asignando el puesto 1 al menor valor, y así sucesivamente. De acuerdo con la fórmula, calculamos la diferencia de los puestos D de las características investigadas y sustituimos los valores en la fórmula.
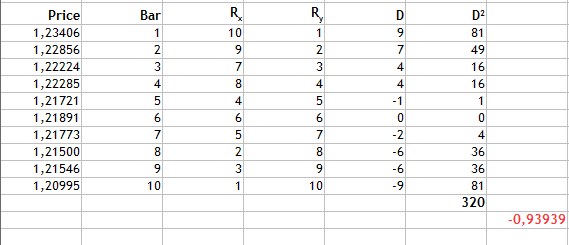
Fig.3 Cálculo del coeficiente de correlación de puestos de Spearman.
Como podemos ver por la fig.3, encontramos la diferencia de los puestos, a continuación, los cuadrados de las diferencias obtenidas, y luego sumamos, obteniendo 320. Sustituimos los valores obtenidos en la fórmula y nos da el resultado -0,93939.
Partiendo del valor obtenido del coeficiente de correlación, la conclusión sigue siendo la misma: existe una fuerte interrelación negativa lineal. En este caso, la proximidad de la interconexión es comparable al coeficiente de correlación de Pearson, pero debemos tener en cuenta que existe una desventaja en el cálculo de este método. Valores de diferencias incomparables pueden corresponder a los mismos valores de diferencias de puesto. Por ejemplo, los puestos de las barras son comparables, mientras que los valores de los niveles de precio carecen de uniformidad; sin embargo, la dispersión de la característica es pequeña y se diferencia en milésimas. Por eso, en este caso, el método de cálculo es apropiado.
Coeficiente de correlación de puestos de Kendall
Al igual que el coeficiente de Spearman, el coeficiente de correlación de puestos de Kendall ofrece una medición de la interrelación lineal entre magnitudes aleatorias. La clasificación de los valores comprobados sobre la interrelación de características es semejante, sin embargo, el método de cálculo se diferencia un tanto. La fórmula de cálculo del coeficiente es la siguiente:
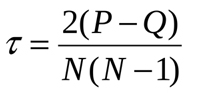
Donde P es la suma de las coincidencias, y Q es la suma de las inversiones. Para comprender qué significa esto, vamos a recurrir de nuevo al ejemplo investigado en la fig.1. Para comenzar, haremos la siguiente clasificación en el recuadro de datos:
| Precios de cierre | Número de vela | Precio de cierre | Número de vela |
|---|---|---|---|
| 1,20995 | 10 | 1 | 10 |
| 1,21500 | 8 | 2 | 8 |
| 1,21546 | 9 | 3 | 9 |
| 1,21721 | 5 | 4 | 5 |
| 1,21773 | 7 | 5 | 7 |
| 1,21891 | 6 | 6 | 6 |
| 1,22224 | 3 | 7 | 3 |
| 1,22285 | 4 | 8 | 4 |
| 1,22856 | 2 | 9 | 2 |
| 1,23406 | 1 | 10 | 1 |
Como podemos ver, el recuadro ha sido clasificado según la columna del precio de cierre. A continuación, determinamos los puestos por encima del actual, comenzando por la primera línea en la columna de número de vela. Es decir, tomamos el 10 y miramos si hay puestos por encima: no los hay. Después tomamos el 8 y encontramos solo un puesto, el 9. Etc. Estos serán los valores coincidentes de P.
De esta misma forma, calculamos el número de puestos por debajo. Así, para 10, habrá 9 por debajo, ya que se trata del mayor puesto, para 8, serán 7: 5,7,6,3,4,2,1. Estas serán las inversiones de Q. Introducimos los datos obtenidos en el recuadro y calculamos el coeficiente:
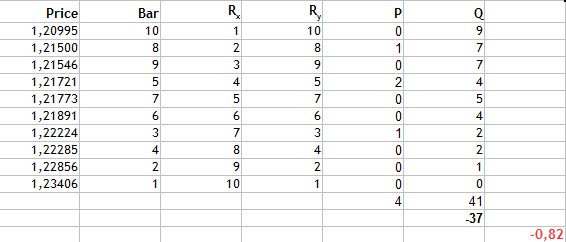
Fig.4 Cálculo del coeficiente de correlación de puestos de Kendall.
Sumamos los valores obtenidos de las coincidencias y los valores de las inversiones. Encontramos su diferencia -37, y tras insertarla en la fórmula, obtenemos el siguiente valor del coeficiente de correlación de Kendall -0,82. De nuevo vemos una fuerte correlación negativa lineal, no obstante, el resultado indica que este método de cálculo es más selectivo que los dos anteriores, puesto que el propio valor absoluto ha resultado menor.
Coeficiente de correlación de señales de Fechner
Este método se basa en la valoración del grado de consistencia de la dirección de las desviaciones de los valores con respecto al valor medio y el cálculo de las señales de desviación correspondientes a los valores. La fórmula de cálculo es muy sencilla:
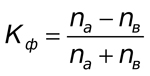
Donde Na es el número de coincidencias por la señal, y Nb es el número de disparidades por la misma. Para que resulte más fácil de entender, vamos a calcular de la misma forma el coeficiente de correlación para nuestro ejemplo de la fig.1.
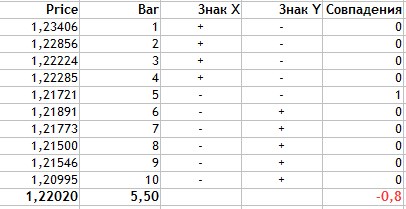
Fig.5 Cálculo del coeficiente de correlación de señales de Fechner.
Vamos a analizar el cálculo con mayor detalle:
- Enontramos los valores medios de los datos según las dos características. Para el precio, es 1,2202, para la vela, es 5,5.
- En la columna Sign Х, ponemos + si el valor actual de Precio es superior al valor medio, y - si es menor.
- Hacemos lo mismo con los valores de los números de vela.
- Calculamos el número de coincidencias de las señales para los valores comparados de las dos características.
- Como podemos ver, los valores coinciden solo una vez, esto significa que Na = 1, а Nb = 9.
- Insertamos los valores obtenidos en la fórmula.
Como podemos ver, el método de cálculo del coeficiente de correlación de Fechner es bastante sencillo, y su valor es igual a -0,8. Lo que, al igual que en los métodos anteriores, indica una fuerte dependencia negativa lineal del Precio de cierre con respecto al número de vela, o temporal.
Implementación de indicadores
Bien, vamos a implementar con los recursos MQL5 todos los métodos de cálculo de las correlaciones.
Coeficiente de correlación de Pearson
Ya que el cálculo de este método contiene una fórmula voluminosa, para visualizar y comprender las etapas de cálculo de forma más cómoda, vamos a dividirla en dos etapas: el cálculo del numerador y el cálculo del denominador.
//+------------------------------------------------------------------+ //| Cálculo del numerador de la fórmula | //+------------------------------------------------------------------+ double Numerator(double &Ranks[],int N) { //---- double Y[],dx[],dy[],mx=0.0,my=0.0,sum=0.0,sm=0.0; ArrayResize(Y,N); ArrayResize(dx,N); ArrayResize(dy,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0;j<N;j++) { dx[j]=Y[j]-mx; dy[j]=Ranks[j]-my; sm+=dx[j]*dy[j]; } return sm; } //+------------------------------------------------------------------+ //| Cálculo del denominador de la fórmula | //+------------------------------------------------------------------+ double Denominator(double &Ranks[],int N) { //---- double Y[],dx2[],dy2[],mx=0.0,my=0.0,sum=0.0,smx2=0.0,smy2=0.0; ArrayResize(Y,N); ArrayResize(dx2,N); ArrayResize(dy2,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0;j<N;j++) { dx2[j]=MathPow(Y[j]-mx,2); dy2[j]=MathPow(Ranks[j]-my,2); smx2+=dx2[j]; smy2+=dy2[j]; } return(MathSqrt(smx2*smy2)); }
El método final de cálculo y la lógica de cálculo de la visualización del indicador tienen el aspecto que se muestra en la lista:
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=PearsonCalc(PriceInt,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Cálculo del coeficiente de correlación de Pearson | //+------------------------------------------------------------------+ double PearsonCalc(double &Ranks[],int N) { double ch,zn; ch=Numerator(Ranks,N); zn=Denominator(Ranks,N); return (ch/zn); }
Coeficiente de correlación de puestos de Spearman
Para crear un indicador basado en este método, hemos decidido no inventar de nuevo la rueda, por eso, algunos métodos de cálculo se han tomado de aquí.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=limit; i>=0; i--) { for(int k=0; k<rangeN; k++) PriceInt[k]=int(price[i+k]*multiply); RankPrices(TrueRanks,PriceInt); ExtLineBuffer[i]=SpearmanCalc(R2,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Cálculo del coeficiente de correlación de Spearman | //+------------------------------------------------------------------+ double SpearmanCalc(double &Ranks[],int N) { //---- double sumd2=0.0; for(int i=0; i<N; i++) sumd2+=MathPow(Ranks[i]-i-1,2); return(1-6*sumd2/(N*(MathPow(N,2)-1))); }
Coeficiente de correlación de puestos de Kendall
Al calcular este método, actuaremos de otra forma: vamos a usar las reservas internas del propio mql5. Para ser más concretos, usaremos la biblioteca incorporada de estadística matemática, que aplicaremos a nuestros cálculos.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=KendallCalc(PriceInt,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Cálculo del coeficiente de correlación de Kendall | //+------------------------------------------------------------------+ double KendallCalc(double &Ranks[],int N) { double Y[],t; ArrayResize(Y,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } MathCorrelationKendall(Ranks,Y,t); return (t); } //+------------------------------------------------------------------+
Coeficiente de correlación de señales de Fechner
Este método de cálculo, como podemos recordar, se basa en el cálculo de las señales coincidentes de las desviaciones con respecto al valor medio. Y la posterior comparación de coincidencias.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=FechnerCalc(PriceInt,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Cálculo del coeficiente de correlación de Fechner | //+------------------------------------------------------------------+ double FechnerCalc(double &Ranks[],int N) { double Y[],res,mx,my,sum=0.0,markx[],marky[]; double Na=0.0,Nb=0.0; ArrayResize(Y,N); ArrayResize(markx,N); ArrayResize(marky,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0; j<N; j++) { markx[j]=(Y[j]>mx)?1:-1; marky[j]=(Ranks[j]>my)?1:-1; if(markx[j]==marky[j]) Na++; else Nb++; } res=(Na-Nb)/(Na+Nb); return (res); }
En la fig.6 se muestra el funcionamiento de los cuatro métodos de cálculo de correlación del Precio de cierre y la hora de la vela. En todos los indicadores se ha establecido un periodo de 10, por eso podemos ver claramente su funcionamiento en iguales condiciones.
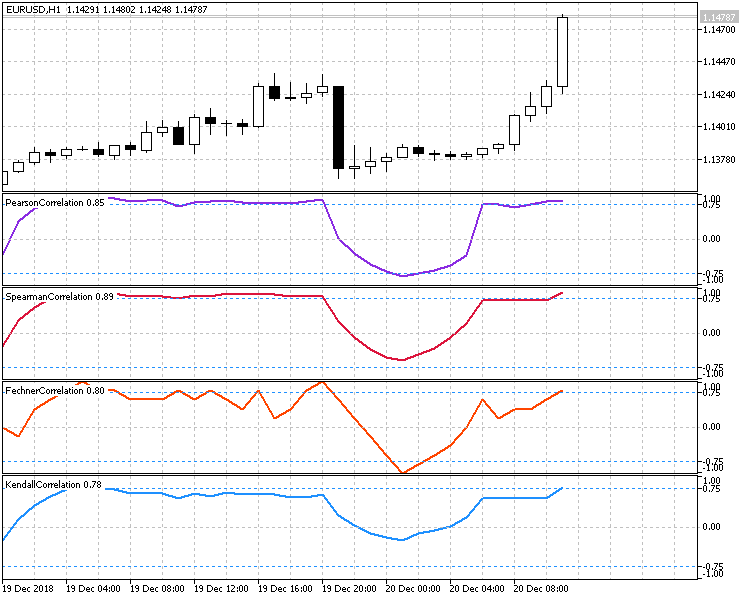
Fig.6 Demostración comparativa del funcionamiento de todos los métodos de trabajo.
Sistema comercial basado en la correlación
A la hora de crear una estrategia comercial basada en la correlación, debemos estudiar escrupulosamente las características específicas del funcionamiento de los indicadores y los métodos de cálculo, y también detectar las condiciones desfavorables o arriesgadas de entrada en el mercado.
Aplicar un gran periodo de cálculo en tiempo real no resulta adecuado para prácticamente todos los indicadores, porque el indicador se retrasará mucho, o bien veremos solo una correlación débil al darse un viraje brusco. Esto se debe a que los indicadores siguen teniendo en cuenta los valores del movimiento opuesto finalizado.
Puesto que con frecuencia el precio se analiza, no en el momento actual, sino como un conjunto de valores en un periodo de tiempo, no tiene mucho sentido analizar el valor de correlación actual como una evaluación total. Debemos analizarlo dentro de su dinámica. Para ello, contamos con la ayuda de los osciladores, construidos con los valores de los coeficientes de correlación actuales y anteriores.
Por eso, hemos decidido construir la estrategia partiendo del carácter del comportamiento del oscilador de los coeficientes de correlación. Concretamente, en el momento de ruptura de ciertos niveles preestablecidos. Aquí podemos ir por dos caminos:
- La caída del coeficiente. Vender cuando el coeficiente positivo desciende y rompe un nivel clave preestablecido, y comprar cuando el coeficiente negativo aumenta y rompe un nivel simétrico definido en un área positiva.
- El aumento del coeficiente. Vender cuando el coeficiente desciende en la zona negativa y rompe un nivel preestablecido, y comprar cuando el coeficiente aumenta y rompe un nivel positivo simétrico.
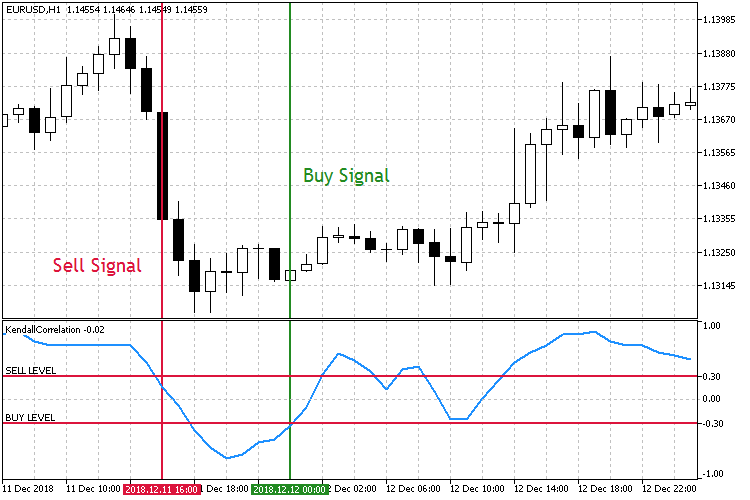
Fig.7 Comercio con la caída del coeficiente de correlación.
Como podemos ver por las capturas de pantalla, hay dos niveles simétricos establecidos del coeficiente de correlación, Sell Level 0,3 y Buy Level -0,3. Al darse la ruptura de Sell Level de arriba hacia abajo, abrimos una orden de venta, y al darse la ruptura de Buy Level de abajo hacia arriba, abrimos una orden de compra.
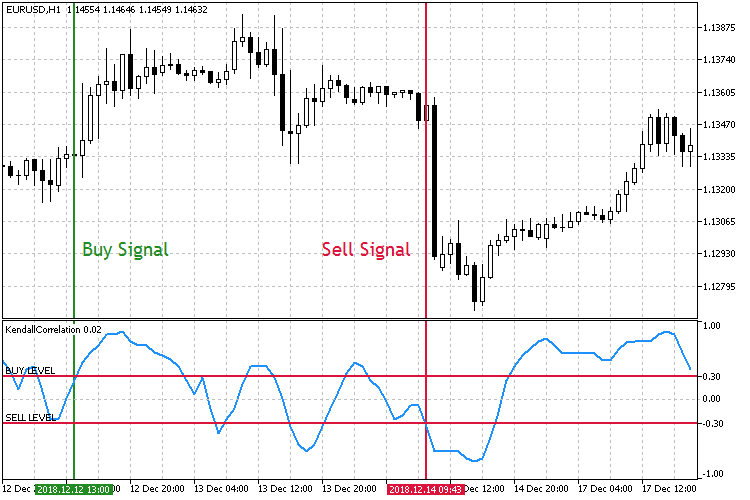
Fig.8 Comercio con el aumento del coeficiente de correlación.
En el segundo método de comercio, mostrado en la fig. 8, los niveles clave para entrar en el mercado son opuestos. Ahora, al darse la ruptura de Buy Level de abajo hacia arriba, abrimos una orden de compra, y al darse la ruptura de Sell Level de arriba hacia abajo, abrimos una orden de venta.
Bien, al implementar el experto comercial, conviene tener en cuenta el uso de una de las estrategias ofrecidas, así como la selección del método de cálculo de la correlación.
//+------------------------------------------------------------------+ //| Enumeración de los modos de trabajo | //+------------------------------------------------------------------+ enum Strategy_type { DECREASE = 1, //On Decrease INCREASE //On Increase }; //+------------------------------------------------------------------+ //| Enumeración de los métodos de medición de la correlación | //+------------------------------------------------------------------+ enum Corr_method { PEARSON = 1, //Pearson SPEARMAN, //Spearman KENDALL, //Kendall FECHNER //Fechner };
En los parámetros de entrada, aparte de los parámetros del asesor, añadiremos la selección del método de cálculo, el nivel clave y la selección ajustable del marco temporal.
//+------------------------------------------------------------------+ //| Parámetros de entrada del experto | //+------------------------------------------------------------------+ input string Inp_EaComment="Correlation Strategy"; //EA Comment input double Inp_Lot=0.01; //Lot input MarginMode Inp_MMode=LOT; //MM //--- Eligiendo el método de cálculo de la correlación y el tipo de estrategia input Corr_method Inp_Corr_method=1; //Correlation Method input Strategy_type Inp_Strategy_type=1; //Strategy type //--- Parámetros del experto input string Inp_Str_label="===EA parameters==="; //Label input int Inp_MagicNum=1111; //Magic number input int Inp_StopLoss=40; //Stop Loss(points) input int Inp_TakeProfit=60; //Take Profit(points) //--- Parámetros del indicador input int Inp_RangeN=10; //Rang Calculation input double Inp_KeyLevel=0.2; //Key Level input ENUM_TIMEFRAMES Inp_Timeframe=PERIOD_CURRENT; //Working Timeframe
Al inicializar el experto comercial, añadiremos la comprobación de la corrección del nivel clave, en concreto, debemos asegurarnos de que se encuentre entre 0 y 1. Ya que usaremos como nivel clave un valor absoluto.
//--- Comprobando que el nivel clave sea correcto if(Inp_KeyLevel>1 || Inp_KeyLevel<0) { Print(Inp_EaComment,": Incorrect key level!"); return(INIT_FAILED); }
A continuación, seleccionamos el método de cálculo de la correlación elegido en los ajustes:
//--- switch(Inp_Corr_method) { case 1: ind_type="Correlation\\PearsonCorrelation"; break; case 2: ind_type="Correlation\\SpearmanCorrelation"; break; case 3: ind_type="Correlation\\KendallCorrelation"; break; case 4: ind_type="Correlation\\FechnerCorrelation"; break; default: break; } //--- Obteniendo el manejador del indicador InpInd_Handle=iCustom(Symbol(),Inp_Timeframe,ind_type,Inp_RangeN); if(InpInd_Handle==INVALID_HANDLE) { Print(Inp_EaComment,": Failed to get indicator handle"); Print("Handle = ",InpInd_Handle," error = ",GetLastError()); return(INIT_FAILED); }
Después de ello, ajustamos las condciones de entrada y la lógica de funcionamiento del experto comercial.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Obteniendo los datos para el cálculo if(!GetIndValue()) return; if(!Trade.IsOpenedByMagic(Inp_MagicNum)) { //--- Abriendo orden al darse la señal de compra if(BuySignal()) Trade.BuyPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment); //--- Abriendo orden al darse la señal de venta if(SellSignal()) Trade.SellPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment); } } //+------------------------------------------------------------------+ //| Condiciones de compra | //+------------------------------------------------------------------+ bool BuySignal() { bool res=false; if(Inp_Strategy_type==1) res=(corr[1]>Inp_KeyLevel && corr[0]<Inp_KeyLevel)?true:false; else if(Inp_Strategy_type==2) res=(corr[0]>Inp_KeyLevel && corr[1]<Inp_KeyLevel)?true:false; return res; } //+------------------------------------------------------------------+ //| Condiciones de venta | //+------------------------------------------------------------------+ bool SellSignal() { bool res=false; if(Inp_Strategy_type==1) res=(corr[1]<-Inp_KeyLevel && corr[0]>-Inp_KeyLevel)?true:false; else if(Inp_Strategy_type==2) res=(corr[0]<-Inp_KeyLevel && corr[1]>-Inp_KeyLevel)?true:false; return res; }
Simulación
Para la simulación del experto comercial obtenido, seleccionaremos los parámetros iniciales:
- Intervalo: Para el modo Uptrend 01.01.2015 — 01.12.2018.
- Pareja de divisas: EURUSD.
- Modo de comercio: Sin retrasos. Las estaretegias no se relacionan con las de alta precisión, por eso la influencia de los retrasos sería muy pequeña.
- Simulación: OHLC en М1. La simulación preliminar con ticks reales ha resultado casi indistinguible de este modo.
- Depósito inicial: 1000 USD.
- Apalancamiento: 1:500.
- Servidor: MetaQuotes-Demo.
- Cotizaciones: de 5 dígitos.
Asimismo, elegimos los parámetros que serán simulados y optimizados.
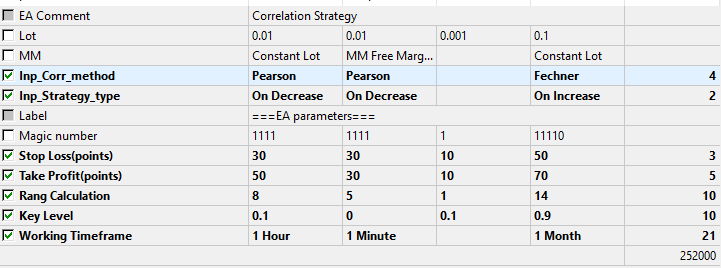
Fig.9 Conjunto de parámetros optimizados.
Según los resultados de la optimización, podemos dilucidar cuál de los métodos de cálculo y qué tipos de estrategia resultan preferibles. Bien, según los resultados de la simulación y optimización, obtenemos lo siguiente.
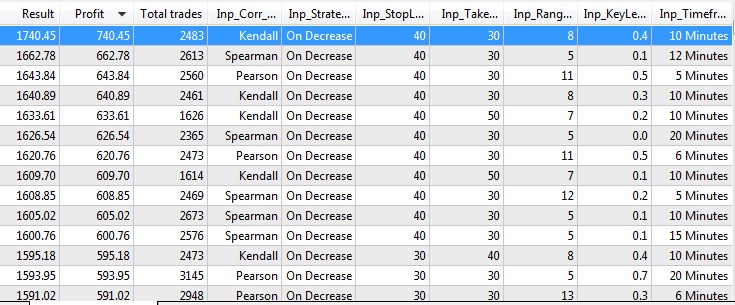
Fig.10 Resultados de simulación y optimización.
Asimismo, realizaremos la simulación de los mejores parámetros de optimización.
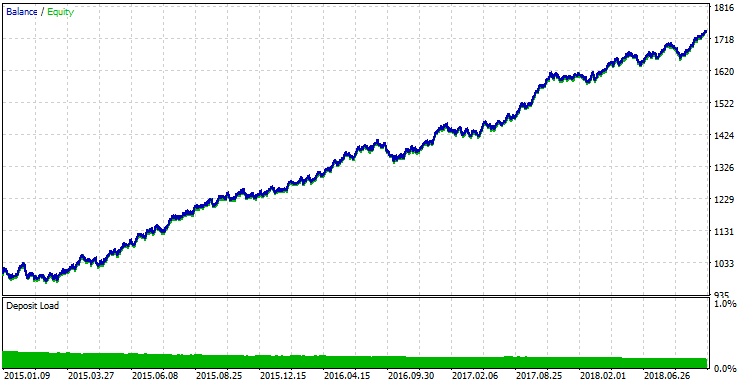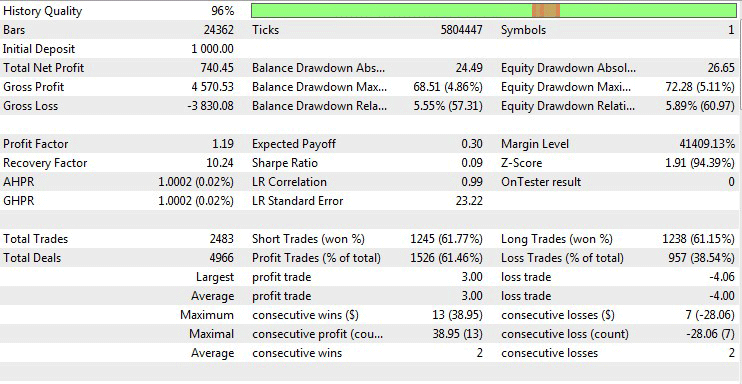
Fig.11 Resultados de la simulación de los mejores parámetros.
Resumiendo
Basándonos en los resultados obtenidos, podemos hacer las siguientes observaciones:
- Los mejores resultados de las simulaciones pertenecen a la estrategia de caída del coeficiente de correlación, con el modo On Decrease. Este resultado solo se puede explicar de una forma: en la caída de los coeficientes tiene lugar una reacción más temprana al movimiento del mercado. Como ya hemos comentado antes, los osciladores basados en los coeficientes de correlación, especialmente con grandes periodos, se retrasan notablemente.
- Salta a la vista que el cálculo más simple del coeficiente de correlación de Fechner no entra en los 20 primeros. El mejor con este método se encuentra en el puesto 99.
- Los mejores resultados se han dado en los marcos temporales pequeños, con un take profit y un stop loss también pequeño.
- No se ha encontrado ninguna dependencia de la magnitud del beneficio con respecto al periodo elegido y el nivel clave preestablecido. No obstante, prevalecen los periodos pequeños, en concreto, el límite inferior del intervalo de optimización con periodo 5 se encuentra constantemente entre los mejores resultados. Esto nos indica de nuevo que los indicadores basados en la correlación se retrasan mucho con la entrada en los periodos grandes, dando peores resultados.
Conclusión
Al final del artículo se adjunta un fichero con todos los archivos enumerados, clasificados por carpetas. Por eso, para que funcione correctamente, basta con colocar la carpeta MQL5 en la carpeta raíz del terminal.
Programas usados en el artículo:
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Correlation.mq5 | Experto | Experto comercial que incluye los 4 métodos de cálculo de la correlación y las 2 estrategias basadas en ellos. |
| 2 | Trade.mqh | Biblioteca | Clase de funciones comerciales. |
| 3 | FechnerCorrelation.mq5 | Indicador | Indicador de cálculo del coeficiente de correlación de Fechner |
| 4 | KendallCorrelation.mq5 | Indicador | Indicador de cálculo del coeficiente de correlación de Kendall |
| 5 | PearsonCorrelation.mq5 | Indicador | Indicador de cálculo del coeficiente de correlación de Pearson |
| 6 | SpearmanCorrelation.mq5 | Indicador | Indicador de cálculo del coeficiente de correlación de Spearman |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/5481
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Analizando resultados comerciales con la ayuda de informes HTML
Analizando resultados comerciales con la ayuda de informes HTML
 Uso práctico de las redes neuronales de Kohonen en el trading algorítmico (Parte II) Optimización y previsión
Uso práctico de las redes neuronales de Kohonen en el trading algorítmico (Parte II) Optimización y previsión
 Utilidad para la selección y navegación en MQL5 y MQL4: añadiendo las pestañas de "recordatorios" y guardando objetos gráficos
Utilidad para la selección y navegación en MQL5 y MQL4: añadiendo las pestañas de "recordatorios" y guardando objetos gráficos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
...
¿Qué tiene de especial y digno de mención?
Hola,
He intentado compilar esto, pero devuelve 7 errores, con los identificadores no declarados, paréntesis izquierda desequilibrada, etc.
¿podrías echarle un vistazo si tienes algo de tiempo? gracias