
Практическое применение корреляций в торговле
Содержание
- Введение
- Понятие корреляции
- Виды корреляций
- Реализация индикаторов
- Торговая система на основе корреляций
- Тестирование торговой системы
- Выводы
- Заключение
Введение
Суть любой торговли, так или иначе сводится к тому, что приходится прогнозировать дальнейшее развитие событий на рынке и потенциальная прибыль сильно зависит от успешности прогноза. В начале своей статьи Торговые идеи на основе направления и скорости движения цен я описывал такую идею — каждое движение имеет такие характеристики как направление, ускорение и скорость. Это и касается движений цен на валютных и других рынках.
Любое движение имеет свои признаки начала движения, определенную скорость, инерционность и окончание. Успешными являются те торговые стратегии, которые максимально рано определяют начавшее движение и входят в рынок, а также четко идентифицируют его окончание. Тем не менее ни одна стратегия не может со стопроцентной вероятностью определить точки входа и выхода. Здесь мы может только говорить о благоприятном шансе, возможности. Поэтому в данной статье мы рассмотрим один из инструментов теории вероятности — корреляцию, которую будем применять в рамках финансовых рынков.
Понятие корреляции
Корреляция — это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин является коэффициент корреляции. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Коэффициент корреляции может принимать значения от -1 до +1. Чем ближе значение корреляции к 1, тем выше взаимосвязь исследуемых величин. Причем если значение стремится к 1, то связь считается положительной, а к -1 отрицательной. То есть при положительной, как правило, увеличение одной из исследованных величин влечет увеличение второй, а в случае отрицательной наоборот — увеличение одной снижает значение второй.
Иными словами, корреляция помогает идентифицировать зависимость одной величины от другой на основе имеющихся данных. Чем же может помочь корреляция на финансовых рынках?
Давайте рассмотрим рис.1 и отмеченную зону нисходящего тренда.
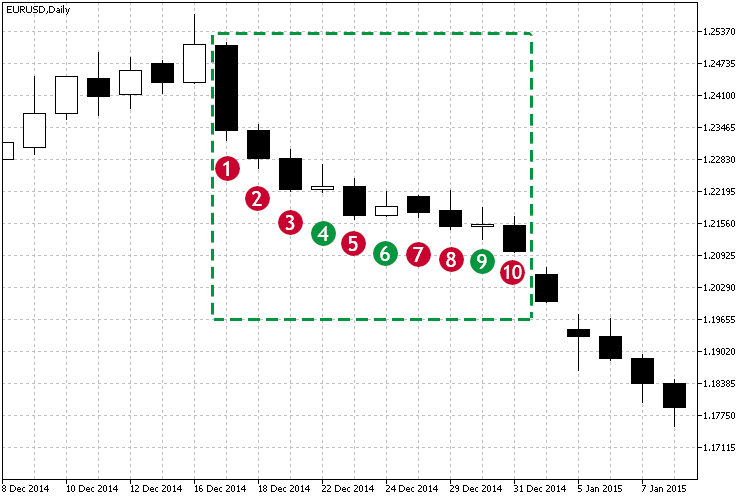
Рис.1 Пример нисходящего тренда.
Как видно на отмеченной области, начиная со свечи №1, цена закрытия в подавляющем случае ниже, нежели цена открытия, или говоря по-другому — каждая следующая цена закрытия ниже предыдущей. Соответственно, с течением времени цена падает. В данном случае визуально видно, что происходит нисходящий тренд, но как же понять, насколько сильна зависимость? Тем более что тренд неидеален, и по свечам №№4,6,9 видно что небольшие попытки движения вверх были. Как же нам поможет корреляция? В данном случае ее коэффициент будет служить показателем силы текущего движения. Исходя из наблюдения за коэффициентом корреляции во времени можно делать сразу несколько выводов:
- Сила текущего тренда. Непосредственно по текущему значению корреляции.
- Длительность тренда. По наблюдениям во времени выбранного порогового значения. Например, порог более 0,75 и не спадает в течение 3-4 свечей.
Виды корреляций
Для определения связи между исследуемыми переменными виды корреляций могут быть следующими:
- Линейные и нелинейные. Линейной называется корреляция, при которой одна величина увеличивается или убывает, при этом вторая также соответственно изменяется. При нелинейной зависимости изменение одной не приводит к прямому изменению другой и может описываться другими функциями.
- Положительной и отрицательной корреляцией называется как раз характер зависимости. Так, при положительной рост одной из взаимосвязанных величин приводит к росту другой.
Примером может служить рис.1 где изображения линейная, отрицательная корреляция. Далее мы рассмотрим несколько видов расчета и выяснения взаимосвязи между двумя величинами.
Линейный коэффициент корреляции (коэффициент корреляции Пирсона)
Данный метод расчета позволяет установить прямую связь между переменными величинами по их абсолютным значениям. Расчет построен таким образом, что если взаимосвязь между величинами имеет линейный характер, то коэффициент Пирсона это покажет. В контексте финансовых рынков эта связь означала бы наличие движения в ту или иную сторону во времени. Для расчета коэффициента корреляции Пирсона применяется следующая формула:
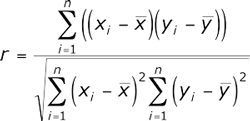
А теперь в качестве примера рассчитаем коэффициент корреляции Пирсона для данных, представленных на рис.1, чтобы уже количественно измерить зависимость цен закрытия с течением времени. Для этого занесем данные в таблицу:
| Цена закрытия | Номер свечи |
|---|---|
| 1,23406 | 1 |
| 1,22856 | 2 |
| 1,22224 | 3 |
| 1,22285 | 4 |
| 1,21721 | 5 |
| 1,21891 | 6 |
| 1,21773 | 7 |
| 1,21500 | 8 |
| 1,21546 | 9 |
| 1,20995 | 10 |
Весь расчет приведен на следующем рисунке.
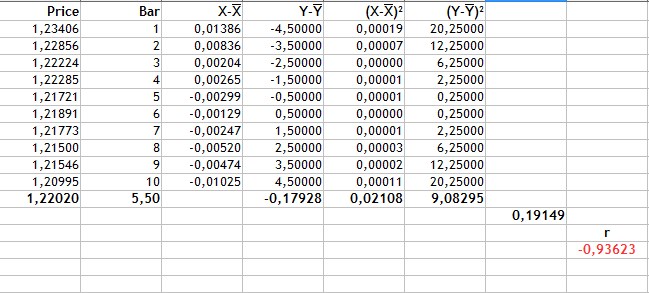
Рис.2 Расчет коэффициента корреляции Пирсона.
Очередность расчета выглядит следующим образом:
- Находим среднее значение цены(Price) и номера свечи. Это 1,22020 и 5,5 соответственно.
- Находим для каждого вида переменных отклонение от среднего(столбцы 3-4).
- Значение -0,17928 сумма произведений отклонений цены и номера свечи. Это числитель формулы.
- Столбцы 5 и 6 квадраты отклонений. Значения 0,02108 и 9,08295 это корни из суммы квадратов отклонений.
- Знаменатель формулы или произведение корней сумм квадратов отклонений равен 0,19149.
- Коэффициент корреляции Пирсона получается -0,93623.
Коэффициент ранговой корреляции Спирмена
Этот метод расчета позволяет устанавливать линейную связь между случайными величинами. Для оценки взаимосвязи используются не числовые значения исследуемых признаков, а соответствующие им ранги. Также как и коэффициент Спирмена, его величина лежит в пределах от -1 до 1. Абсолютное значение характеризует тесноту связи, а знак — направленность связи между двумя признаками. Рассчитывается он по формуле:
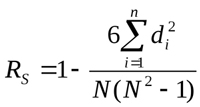
Где Di — разница рангов между исследуемыми признаками. Рассмотрим пример расчета ранговой корреляции на всё том же рис.1 и занесем показания в новую таблицу:
| Цена закрытия | Номер свечи | Ранг цены закрытия | Ранг номера свечи |
|---|---|---|---|
| 1,23406 | 1 | 10 | 1 |
| 1,22856 | 2 | 9 | 2 |
| 1,22224 | 3 | 7 | 3 |
| 1,22285 | 4 | 8 | 4 |
| 1,21721 | 5 | 4 | 5 |
| 1,21891 | 6 | 6 | 6 |
| 1,21773 | 7 | 5 | 7 |
| 1,21500 | 8 | 2 | 8 |
| 1,21546 | 9 | 3 | 9 |
| 1,20995 | 10 | 1 | 10 |
Как видно из таблицы, мы проранжировали значения цены закрытия, присвоив ранг 1 наименьшему значению и так далее. Согласно формуле рассчитаем разность рангов D исследуемых признаков и подставим полученные значения в формулу.
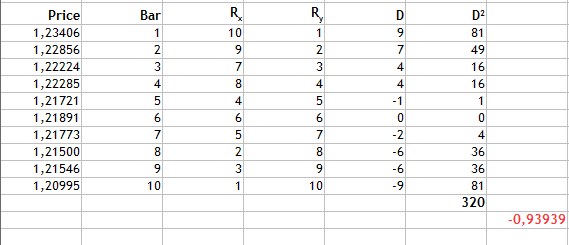
Рис.3 Расчет коэффициента ранговой корреляции Спирмена.
Как видно из рис.3, мы находим разности рангов, затем квадраты полученных разностей и суммируем, получаем 320. Подставляем полученные значения в формулу и получаем результат -0,93939.
Исходя из полученного значения коэффициента корреляции, вывод всё тот же — сильная линейная, отрицательная взаимосвязь. В данном случае теснота связи получилась сопоставима коэффициенту корреляции Пирсона, но следует учитывать тот факт, что существует один недостаток расчета данного метода. Это то, что одинаковым разностям рангов могут соответствовать несопоставимые значения разностей значений. К примеру ранжирование баров сопоставимо, а вот значения рангов цены не равномерно, но разброс признака цена у нас небольшой и отличается на тысячные доли. Потому в данном случае метод расчета уместен.
Коэффициент ранговой корреляции Кенделла
Также как и у Спирмена, коэффициент ранговой корреляции Кенделла есть мера линейной связи между случайными величинами. Аналогично происходит ранжирования значений проверяемых на взаимосвязь признаков, однако метод расчет несколько иной. Формула для расчета коэффициента такова:
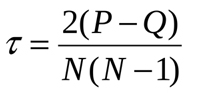
Где P — сумма совпадений, а Q — сумма инверсий. Чтобы понять что это означает, вновь обратимся к исследуемому нами примеру из рис.1 и для начала сделаем следующую сортировку в таблице данных:
| Цена закрытия | Номер свечи | Ранг цены закрытия | Ранг номера свечи |
|---|---|---|---|
| 1,20995 | 10 | 1 | 10 |
| 1,21500 | 8 | 2 | 8 |
| 1,21546 | 9 | 3 | 9 |
| 1,21721 | 5 | 4 | 5 |
| 1,21773 | 7 | 5 | 7 |
| 1,21891 | 6 | 6 | 6 |
| 1,22224 | 3 | 7 | 3 |
| 1,22285 | 4 | 8 | 4 |
| 1,22856 | 2 | 9 | 2 |
| 1,23406 | 1 | 10 | 1 |
Как видно, таблица была отсортирована по столбцу Ранга цены закрытия. Далее определяем количество рангов выше текущего, начиная с первой строки в столбце Ранг номера свечи. То есть берем 10 и смотрим, есть ли ранги выше — их нет. Далее берем 8 и находим всего один ранг, это 9. И так далее. Это будут совпадения P.
Таким же образом считаем количество рангов ниже. Так для 10 рангов ниже будет 9, так как это самый большой ранг, для 8 будут семь — 5,7,6,3,4,2,1. Это будут инверсии Q. Заносим получившиеся данные в таблицу и рассчитываем коэффициент:
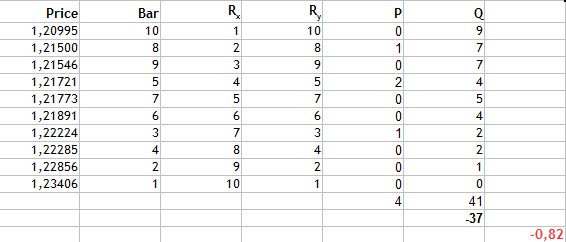
Рис.4 Расчет коэффициента ранговой корреляции Кенделла.
Суммируем получившиеся значения совпадений и значения инверсий. Находим их разницу -37 и подставив в формулу получаем следующее значение коэффициента корреляции Кенделла -0,82. Снова прослеживается сильная линейная отрицательная связь, тем не менее результат говорит о том, что данный метод расчета более избирателен, нежели два предыдущих, так как само абсолютное значение оказалось меньше.
Коэффициент корреляции знаков Фехнера
Данный метод основывается на оценке степени согласованности направления отклонений значений признаков от среднего значения и подсчете знаков отклонений, соответствующим значениям признаков. Формула для расчета очень проста:
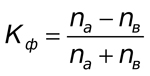
Где Na — количество совпадений по знаку, а Nb — количество несовпадений по знаку. Для более ясного понимания, также рассчитаем коэффициент корреляции для нашего примера из рис.1.
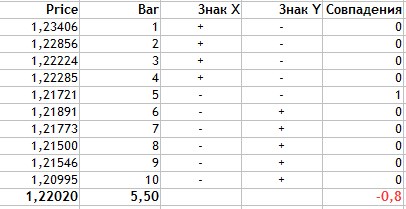
Рис.5 Расчет коэффициента корреляции знаков Фехнера.
Давайте рассмотрим более подробно расчет:
- Находим средние значения данных по двум признакам. Для Цены это 1,2202, для свечи 5,5.
- В столбце Знак Х ставим + если текущее значение признака Цена больше среднего значения и минус, если меньше.
- Аналогично поступаем со значениями номеров свечей.
- Подсчитываем количество совпадений знаков для сопоставленных значений двух признаков.
- Как видно, что совпадение знаков произошло лишь однажды, значит Na = 1, а Nb = 9.
- Подставляем полученные значения в формулу.
Как видно, метод расчета коэффициента корреляции Фехнера достаточно прост и его значение равно -0,8. Что, как и в предыдущих методах, говорит о сильной линейной, отрицательной зависимости Цены закрытия от номера свеча или во времени.
Реализация индикаторов
Итак давайте реализуем средствами MQL5 все методы расчета корреляций.
Коэффициент корреляции Пирсона
Так как расчет данного метода имеет большую формулу, то для лучшей визуализации и понимания этапов расчета она была разбита на два этапа расчета — расчет числителя и знаменателя.
//+------------------------------------------------------------------+ //| Расчет числителя формулы | //+------------------------------------------------------------------+ double Numerator(double &Ranks[],int N) { //---- double Y[],dx[],dy[],mx=0.0,my=0.0,sum=0.0,sm=0.0; ArrayResize(Y,N); ArrayResize(dx,N); ArrayResize(dy,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0;j<N;j++) { dx[j]=Y[j]-mx; dy[j]=Ranks[j]-my; sm+=dx[j]*dy[j]; } return sm; } //+------------------------------------------------------------------+ //| Расчет знаменателя формулы | //+------------------------------------------------------------------+ double Denominator(double &Ranks[],int N) { //---- double Y[],dx2[],dy2[],mx=0.0,my=0.0,sum=0.0,smx2=0.0,smy2=0.0; ArrayResize(Y,N); ArrayResize(dx2,N); ArrayResize(dy2,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0;j<N;j++) { dx2[j]=MathPow(Y[j]-mx,2); dy2[j]=MathPow(Ranks[j]-my,2); smx2+=dx2[j]; smy2+=dy2[j]; } return(MathSqrt(smx2*smy2)); }
Финальный метод расчета и логика расчета визуализации индикатора выглядит следующим образом на листинге ниже:
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=PearsonCalc(PriceInt,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Расчет коэффициента корреляции Пирсона | //+------------------------------------------------------------------+ double PearsonCalc(double &Ranks[],int N) { double ch,zn; ch=Numerator(Ranks,N); zn=Denominator(Ranks,N); return (ch/zn); }
Коэффициент ранговой корреляции Спирмена
Для создания индикатора на основе данного метода было решено не изобретать заново велосипед, поэтому некоторые методы расчета были взяты отсюда.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=limit; i>=0; i--) { for(int k=0; k<rangeN; k++) PriceInt[k]=int(price[i+k]*multiply); RankPrices(TrueRanks,PriceInt); ExtLineBuffer[i]=SpearmanCalc(R2,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Расчет коэффициента корреляции Спирмена | //+------------------------------------------------------------------+ double SpearmanCalc(double &Ranks[],int N) { //---- double sumd2=0.0; for(int i=0; i<N; i++) sumd2+=MathPow(Ranks[i]-i-1,2); return(1-6*sumd2/(N*(MathPow(N,2)-1))); }
Коэффициент ранговой корреляции Кенделла
При расчете данного метода поступим вариативно и используем внутренние резервы самого mql5. А именно используем встроенную библиотеку матстатистики и применим ее к нашим расчетам.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=KendallCalc(PriceInt,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Расчет коэффициента корреляции Кенделла | //+------------------------------------------------------------------+ double KendallCalc(double &Ranks[],int N) { double Y[],t; ArrayResize(Y,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } MathCorrelationKendall(Ranks,Y,t); return (t); } //+------------------------------------------------------------------+
Коэффициент корреляции знаков Фехнера
Данный метода расчета, как мы помним, основан на подсчете совпадающих знаков отклонений от среднего значения. И последующее сравнение на совпадение.
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // number of bars in history at the current tick const int prev_calculated,// number of bars calculated at previous call const int begin, // bars reliable counting beginning index const double &price[] ) { if(rates_total<rangeN+begin) return(0); int limit; if(prev_calculated>rates_total || prev_calculated<=0) { limit=rates_total-2-rangeN-begin; if(begin>0) PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rangeN+begin); } else limit=rates_total-prev_calculated; ArraySetAsSeries(price,true); for(int i=0; i<=limit; i++) { for(int k=0; k<rangeN; k++) PriceInt[k]=price[k+i]; ExtLineBuffer[i]=FechnerCalc(PriceInt,rangeN); } return(rates_total); } //+------------------------------------------------------------------+ //| Расчет коэффициента корреляции Фехнера | //+------------------------------------------------------------------+ double FechnerCalc(double &Ranks[],int N) { double Y[],res,mx,my,sum=0.0,markx[],marky[]; double Na=0.0,Nb=0.0; ArrayResize(Y,N); ArrayResize(markx,N); ArrayResize(marky,N); int n=N; for(int i=0; i<N; i++) { Y[i]=n; n--; } mx=Average(Y); my=Average(Ranks); for(int j=0; j<N; j++) { markx[j]=(Y[j]>mx)?1:-1; marky[j]=(Ranks[j]>my)?1:-1; if(markx[j]==marky[j]) Na++; else Nb++; } res=(Na-Nb)/(Na+Nb); return (res); }
На рис.6 продемонстрирована работа всех четырех методов расчета корреляции Цены закрытия свечи и времени. На всех индикаторах установлен период 10, поэтому можно наглядно увидеть их работу в одинаковых условиях.
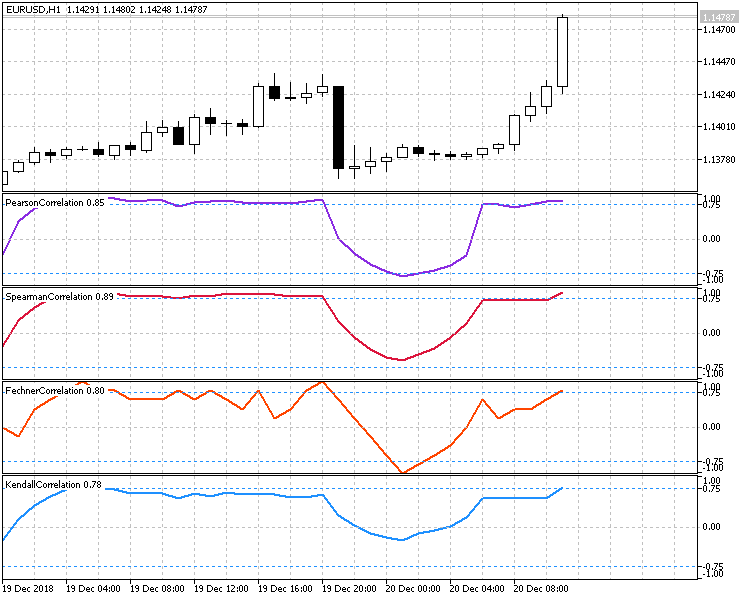
Рис.6 Сравнительная демонстрация работы всех методов работы.
Торговая система на основе корреляций
При создании торговой стратегии на основе корреляций нужно тщательно изучить специфику работы индикаторов и методов расчета, и выявить возможные неблагоприятные или рискованные условия входа в рынок.
Практически для всех индикаторов в реальном времени брать большой период расчета нецелесообразно, потому что индикатор будет сильно запаздывать, либо при резком развороте мы увидим лишь слабую корреляцию. Из-за того, что индикаторы все еще учитывают значения завершившегося противоположного движения.
Так как очень часто анализируют цену не в текущий момент, а в совокупности нескольких значений за период времени, то и нет большого смысла рассматривать текущее значение корреляции, как абсолютную оценку. Нужно рассматривать в динамике, в чем нам, собственно и помогают осцилляторы, построенные на значениях текущего и всех предыдущих коэффициентов корреляции.
Поэтому было решено строить стратегию исходя из характера поведения осциллятора коэффициентов корреляции. А именно в момент пробития неких предустановленных уровней. И тут можно пойти двумя путями:
- На падении коэффициента. Продавать при падении положительного коэффициента и пробитии ключевого предустановленного уровня, и покупать при росте отрицательного с пробитием уровня симметричного установленного в положительной области.
- На росте коэффициента. Продавать при падении коэффициента в отрицательной области и пробитии уровня, и покупать при росте коэффициента с пробитием положительного симметричного уровня.
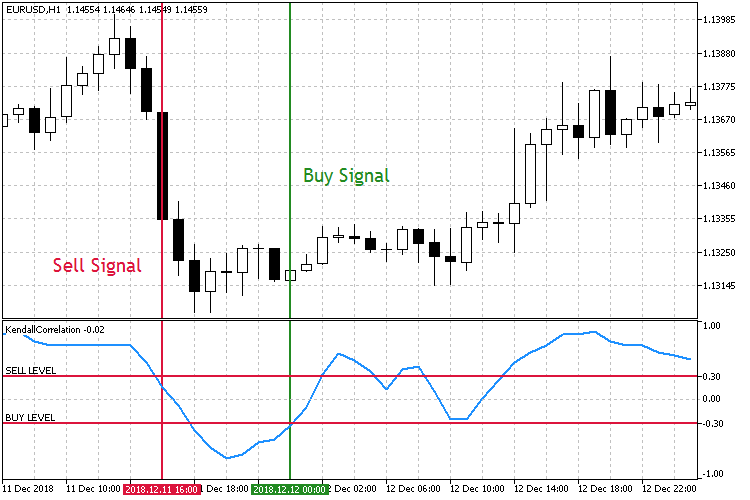
Рис.7 Торговля на падении коэффициента корреляции.
Как видно на скриншотах, есть два установленных симметричных уровня коэффициента корреляции Sell Level 0,3 и Buy Level -0,3. При пробитии Sell Level сверху вниз открываем ордер на продажу, а при пробитии Buy Level снизу вверх на покупку.
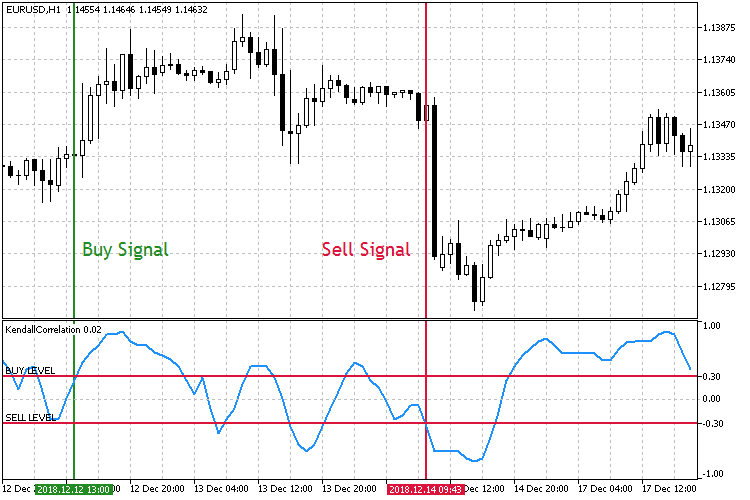
Рис.8 Торговля на росте коэффициента корреляции.
При другом режиме торговли, как показано на рис. 8, ключевые уровни для входа в рынок меняются местами. Теперь при пробитии Buy Level снизу вверх открывается ордер на покупку, а при пробитии Sell Level сверху вниз на продажу.
Итак, при реализации торгового эксперта следует учесть выбор использования одной из предложенных стратегий, а также выбор метода расчета корреляции.
//+------------------------------------------------------------------+ //| Перечисление режимов работы | //+------------------------------------------------------------------+ enum Strategy_type { DECREASE = 1, //On Decrease INCREASE //On Increase }; //+------------------------------------------------------------------+ //| Перечисление методов измерения корреляции | //+------------------------------------------------------------------+ enum Corr_method { PEARSON = 1, //Pearson SPEARMAN, //Spearman KENDALL, //Kendall FECHNER //Fechner };
Во входных параметрах помимо параметров советника добавим выбор метода расчет, тип стратегии, ключевой уровень и настраиваемый выбор рабочего таймфрейма.
//+------------------------------------------------------------------+ //| Входные параметры эксперта | //+------------------------------------------------------------------+ input string Inp_EaComment="Correlation Strategy"; //EA Comment input double Inp_Lot=0.01; //Lot input MarginMode Inp_MMode=LOT; //MM //--- Выбор метода расчета корреляции и тип стратегии input Corr_method Inp_Corr_method=1; //Correlation Method input Strategy_type Inp_Strategy_type=1; //Strategy type //--- Параметры эксперта input string Inp_Str_label="===EA parameters==="; //Label input int Inp_MagicNum=1111; //Magic number input int Inp_StopLoss=40; //Stop Loss(points) input int Inp_TakeProfit=60; //Take Profit(points) //--- Параметры индикатора input int Inp_RangeN=10; //Rang Calculation input double Inp_KeyLevel=0.2; //Key Level input ENUM_TIMEFRAMES Inp_Timeframe=PERIOD_CURRENT; //Working Timeframe
При инициализации торгового эксперта добавим проверку ключевого уровня на корректность, а именно нахождение его в диапазоне от 0 до 1. Так как для ключевого уровня мы будем использовать абсолютное значение.
//--- Проверка на правильность ключевого уровня if(Inp_KeyLevel>1 || Inp_KeyLevel<0) { Print(Inp_EaComment,": Incorrect key level!"); return(INIT_FAILED); }
Далее выбираем выбранный в настройках метод расчета корреляции:
//--- switch(Inp_Corr_method) { case 1: ind_type="Correlation\\PearsonCorrelation"; break; case 2: ind_type="Correlation\\SpearmanCorrelation"; break; case 3: ind_type="Correlation\\KendallCorrelation"; break; case 4: ind_type="Correlation\\FechnerCorrelation"; break; default: break; } //--- Получение хэндла индикатора InpInd_Handle=iCustom(Symbol(),Inp_Timeframe,ind_type,Inp_RangeN); if(InpInd_Handle==INVALID_HANDLE) { Print(Inp_EaComment,": Failed to get indicator handle"); Print("Handle = ",InpInd_Handle," error = ",GetLastError()); return(INIT_FAILED); }
После этого уже настраиваем условия входа и логику работы торгового эксперта.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Получение данных для расчета if(!GetIndValue()) return; if(!Trade.IsOpenedByMagic(Inp_MagicNum)) { //--- Открытие ордера при наличии сигнала на покупку if(BuySignal()) Trade.BuyPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment); //--- Открытие ордера при наличии сигнала на продажу if(SellSignal()) Trade.SellPositionOpen(Symbol(),Inp_Lot,Inp_StopLoss,Inp_TakeProfit,Inp_MagicNum,Inp_EaComment); } } //+------------------------------------------------------------------+ //| Условия на покупку | //+------------------------------------------------------------------+ bool BuySignal() { bool res=false; if(Inp_Strategy_type==1) res=(corr[1]>Inp_KeyLevel && corr[0]<Inp_KeyLevel)?true:false; else if(Inp_Strategy_type==2) res=(corr[0]>Inp_KeyLevel && corr[1]<Inp_KeyLevel)?true:false; return res; } //+------------------------------------------------------------------+ //| Условия на продажу | //+------------------------------------------------------------------+ bool SellSignal() { bool res=false; if(Inp_Strategy_type==1) res=(corr[1]<-Inp_KeyLevel && corr[0]>-Inp_KeyLevel)?true:false; else if(Inp_Strategy_type==2) res=(corr[0]<-Inp_KeyLevel && corr[1]>-Inp_KeyLevel)?true:false; return res; }
Тестирование
Для тестировании получившегося торгового эксперта выберем начальные предустановки:
- Интервал: Для режима Uptrend 01.01.2015 — 01.12.2018.
- Валютная пара: EURUSD.
- Режим торговли: Без задержки. Представленные стратегии не относятся к высокочастотным, поэтому влияние задержек было бы очень мало.
- Тестирование: OHLC на М1. Предварительное тестирование на реальных тиках оказалось почти неотличимо от этого режима.
- Начальный депозит: 1000 USD.
- Плечо: 1:500.
- Сервер: MetaQuotes-Demo.
- Котировки: 5-значные.
Также определимся с параметрами, которые будут тестироваться и оптимизироваться.
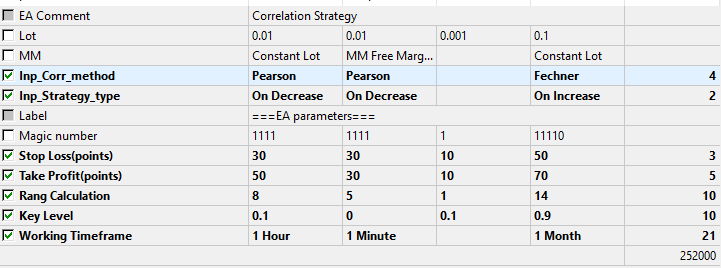
Рис.9 Набор оптимизируемых параметров.
По результатам оптимизации можно выяснить какой из методов расчета и типов стратегии оказался более предпочтителен. Итак, по результатам тестирования и оптимизации получились следующие результаты.
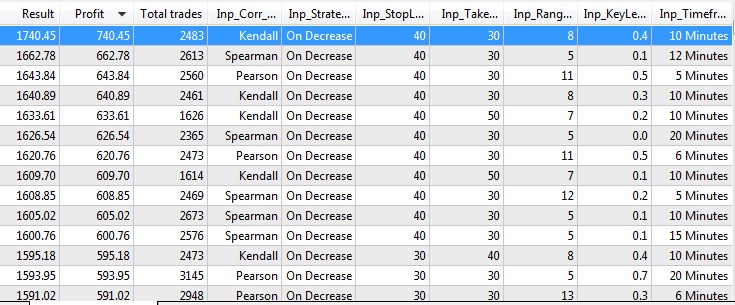
Рис.10 Результаты тестирования и оптимизации.
Также проведем тестирование лучших параметров оптимизации.
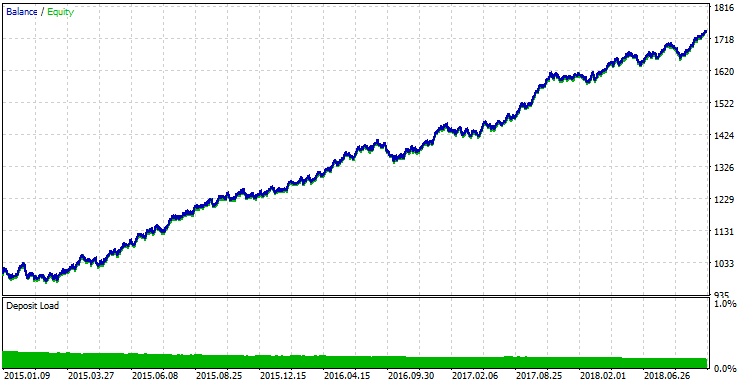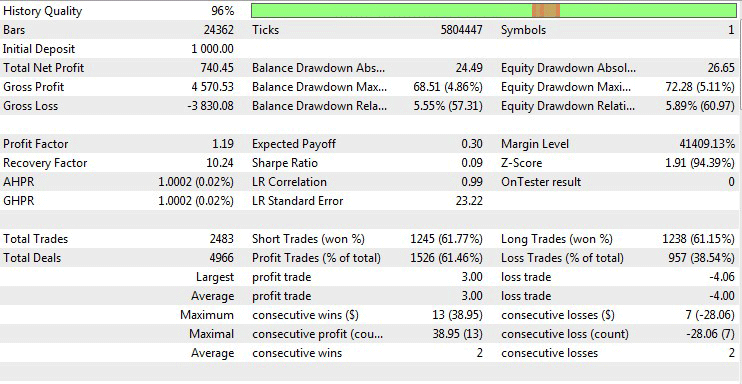
Рис.11 Результаты тестирования лучших параметров.
Выводы
На основе полученных результатов можно сделать следующие наблюдения:
- Лучшие результаты тестов показывает стратегия на падении коэффициента корреляции, режим On Decrease. Такой результат можно объяснить лишь тем, что на падении коэффициентов происходит более раннее реагирование на движения рынка. Как уже говорилось выше, осцилляторы на основе коэффициентов корреляции, особенно с большими периодами, заметно запаздывают.
- Бросается в глаза, что самый простой расчет коэффициента корреляции по Фехнеру в первой двадцатке не присутствует. Лучший по данному методу находится на 99-м месте.
- Наилучшие результаты получились на мелких таймфреймах с небольшими тейк-профита и стоп-лоссами.
- Какой-либо зависимости величины прибыли от выбранного периода и предустановленного ключевого уровня не найдены, тем не менее превалируют небольшие периоды, в частности — нижняя граница диапазона оптимизации с периодом 5 в лучших результатах встречается постоянно. Это еще раз говорит о том, что при больших периодах индикаторы на основе корреляции сильно запаздывают со входом и дают слабые результаты.
Заключение
В конце статьи приложен архив со всеми перечисленными файлами, отсортированными по папкам. Поэтому для корректной работы достаточно положить папку MQL5 в корень терминала.
Программы, используемые в статье:
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Correlation.mq5 | Эксперт | Торговый эксперт, включающий в себя 4 метода расчета корреляции и 2 стратегии на их основе. |
| 2 | Trade.mqh | Библиотека | Класс торговых функций. |
| 3 | FechnerCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Фехнера |
| 4 | KendallCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Кенделла |
| 5 | PearsonCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Пирсона |
| 6 | SpearmanCorrelation.mq5 | Индикатор | Индикатор расчета коэффициента корреляции Спирмена |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Анализ торговли по HTML-отчетам
Анализ торговли по HTML-отчетам
 Практическое использование нейросетей Кохонена в алгоритмическом трейдинге (Часть II): Оптимизация и прогнозирование
Практическое использование нейросетей Кохонена в алгоритмическом трейдинге (Часть II): Оптимизация и прогнозирование
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
...
Что там такого особенного и заслуживающего внимания?
Привет,
Я попытался скомпилировать это, но он возвращает 7 ошибок, с необъявленными идентификаторами, несбалансированной левой парантезой и т.д.
Не могли бы вы взглянуть, если у вас есть немного времени? Спасибо.