Otimização Controlada: Recozimento Simulado
1 862
0
Introdução
O Testador de Estratégia da plataforma de negociação MetaTrader 5 fornece apenas duas opções de otimização: otimização completa dos parâmetros e o algoritmo genético. Este artigo propõe um novo método para otimizar as estratégias de negociação — Recozimento Simulado (Simulated Annealing). Será introduzido neste artigo o algoritmo do método, sua implementação e integração em qualquer Expert Advisor. Em seguida, seu desempenho é testado utilizando o EA MovingAverage, e os resultados obtidos pelo método Recozimento Simulado são comparados com os do algoritmo genético.
Algoritmo de Recozimento Simulado
O Recozimento Simulado é um dos métodos de otimização estocástica. Ele é uma busca aleatória ordenada para a otimalidade da função objetivo.
O algoritmo de recozimento simulado é baseado na simulação da formação de uma estrutura cristalina em uma substância. Os átomos em uma rede cristalina de uma substância (por exemplo, um metal) podem tanto entrar em um estado com um nível de energia mais baixo quanto permanecer inalterado à medida que a temperatura diminui. A probabilidade de entrar em um novo estado diminui em proporção à temperatura. A mínima ou o máxima da função objetivo será encontrada através da simulação de tal processo.
O processo de busca pela função objetivo ótima pode ser representada da seguinte maneira:
Fig. 1. Busca pela função objetivo ótima
Na figura 1, os valores da função objetivo são representados como uma bola que rola ao longo de uma superfície irregular. A bola azul mostra o valor inicial da função objetivo, a verde mostra o valor final (mínimo global). As bolas vermelhas são os valores da função em seus mínimos locais. O algoritmo de recozimento simulado tenta encontrar o extremo global da função objetivo e evitar "ficar preso" em seus extremos locais. A probabilidade de cair em um extremo local diminui conforme ele se aproxima do extremo global.
Vamos considerar as etapas do algoritmo de recozimento simulado. Para maior clareza, será considerada a busca pelo mínimo global da função objetivo. Existem 3 variantes principais de implementação para o recozimento simulado: baseado na Distribuição de Boltzmann, Distribuição de Cauchy (recozimento rápido), recozimento ultra-rápido. A diferença entre eles está no método de geração de um novo ponto x(i) e na lei de decréscimo da temperatura.
Aqui estão as variáveis usadas no algoritmo:
- Fopt — valor ótimo da função objetivo;
- Fbegin — valor inicial da função objetivo;
- x(i) — valor do ponto atual (o valor da função objetivo depende desse parâmetro);
- F(x(i)) — valor da função objetivo para o ponto x(i);
- i — contador de iterações;
- T0 — temperatura inicial;
- T — temperatura atual;
- Xopt — valor do parâmetro, na qual a função objetivo ótima é alcançada;
- Tmin — o valor mínimo da temperatura;
- Imax — o número máximo de iterações.
O algoritmo de recozimento consiste nas seguintes etapas:
- Etapa 0. Inicialização do algoritmo: Fopt = Fbegin, i=0, T=T0, Xopt = 0.
- Etapa 1. Seleção aleatória do ponto atual x(0) e o cálculo da função objetivo F(x(0)) para o ponto dado. Se F(x(0))<Fbegin, então Fopt=F(x(0)).
- Etapa 2. Geração do novo ponto x(i).
- Etapa 3. Cálculo da função objetivo F(x(i)).
- Etapa 4. Verifica a transição para um novo estado. Em seguida, dois algoritmos de modificação são considerados:
- a). Se houve a transição para um novo estado, diminua a temperatura atual e vá para a etapa 5, caso contrário, vá para a etapa 2.
- b). Independentemente do resultado da verificação da transição para um novo estado, diminua a temperatura atual e vá para a etapa 5.
- Etapa 5. Verifique o critério de parada do algoritmo (a temperatura atingiu o valor mínimo de Tmin ou o número de iterações especificado por Imax foi alcançado). Se o critério de parada do algoritmo não foi atendido: aumente o contador de iteração (i=i+1) e vá para a etapa 2.
Vamos considerar cada uma das etapas com mais detalhes para o caso de encontrar o mínimo da função objetivo.
Etapa 0. Os valores iniciais são atribuídos às variáveis que têm seus valores modificados durante a operação do algoritmo.
Etapa 1. O ponto atual é um valor do parâmetro do EA que precisa ser otimizado. Pode haver vários desses parâmetros. Cada parâmetro recebe um valor aleatório, uniformemente distribuído no intervalo entre Pmin para Pmax com o passo especificado Step (Pmin, Pmax são os valores mínimos e máximos do parâmetro otimizado). O EA é executado uma única vez com os parâmetros gerados no testador e é calculado o valor da função objetivo F(x(0)), que é o resultado da otimização do parâmetro do EA (o valor do critério de otimização especificado). Se F(x(0))<Fbegin, Fopt=F(x(0)).
Etapa 2. A geração de um novo ponto, dependendo da variante de implementação do algoritmo, é realizada de acordo com as fórmulas da Tabela 1.
Tabela 1
| Variante de implementação do algoritmo | Fórmula para calcular o novo ponto inicial |
|---|---|
| Distribuição de Boltzmann |  , onde N(0,1) é a distribuição normal padrão |
| Distribuição de Cauchy (recozimento rápido) |  , onde C(0,1) é a distribuição de Cauchy |
| Recozimento ultra-rápido |  , onde Pmax, Pmin são os valores mínimos e máximos do parâmetro otimizado, a variável  é calculada usando a seguinte fórmula: , onde a é uma variável aleatória distribuída uniformemente no intervalo de [0,1), |
Etapa 3. É realizado um teste do EA com os parâmetros gerados na etapa 2. É atribuído o valor do critério de otimização selecionado na função objetivo F(x(i)).
Etapa 4. A verificação da transição para um novo estado é executada da seguinte maneira:
- Etapa 1. Se F(x(i))<Fopt, muda para um novo estado Xopt =x(i), Fopt=F(x(i)), caso contrário, vá para a etapa 2.
- Etapa 2. Gere uma variável aleatória a, uniformemente distribuído no intervalo de [0,1].
- Etapa 3. Calcula a probabilidade de transição para um novo estado:
- Etapa 4. Se P>a, muda para um novo estado Xopt =x(i), Fopt=F(x(i)); se a modificação a) do algoritmo for selecionada, vá para a etapa 2.
- Etapa 5. Diminuí a temperatura atual usando as fórmulas da Tabela 2.
Tabela 2
| Variante de implementação do algoritmo | Fórmula para diminuir a temperatura |
|---|---|
| Distribuição de Boltzmann | 
|
| Distribuição de Cauchy (recozimento rápido) |  , onde n é o número de parâmetros com valores sendo otimizados |
| Recozimento ultra-rápido |  , onde c(i)>0 e é calculado pela seguinte fórmula:  , onde m(i), p(i) são parâmetros adicionais do algoritmo.Por questões de simplicidade da configuração do algoritmo, os valores de m(i) e p(i) não se alteram enquanto o algoritmo estiver em execução: m(i)=const, p(i) = const |
Etapa 5. O algoritmo é encerrado quando as seguintes condições são atendidas: T(i)<=Tmin ou i=Imax.
- Se você selecionar a lei de mudança de temperatura onde a temperatura está diminuindo rapidamente, é preferível terminar o algoritmo quando T(i)<=Tmin, sem esperar que todas as iterações sejam concluídas.
- Se a temperatura diminuir muito lentamente, o algoritmo será encerrado assim que o número máximo de iterações for atingido. Neste caso, provavelmente será necessário alterar os parâmetros da lei de redução de temperatura.
Tendo considerado todos as etapas do algoritmo em detalhe, vamos prosseguir para sua implementação em MQL5.
Implementação do algoritmo
Vamos considerar a implementação e o procedimento de integrar o algoritmo em um EA com os parâmetros a serem otimizados.
A implementação do algoritmo exigirá duas novas classes, que devem ser incluídas no Expert Advisor otimizado:
- Classe AnnealingMethod.mqh — contém um conjunto de métodos que implementam etapas separadas do algoritmo;
- Classe FrameAnnealingMethod.mqh — contém métodos para operação da interface gráfica exibida no gráfico da plataforma.
Além disso, a operação do algoritmo requer um código adicional para ser incluído na função OnInit e deve-se adicionar as funções OnTester, OnTesterInit, OnTesterDeInit, OnTesterPass ao código do EA. O processo de integração do algoritmo em um EA é exibido na Fig. 2.
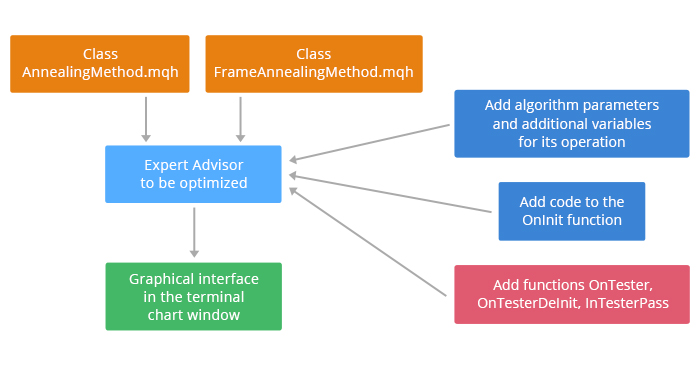
Fig. 2. Incluindo o algoritmo no Expert Advisor
Vamos agora descrever as classes AnnealingMethod e FrameAnnealingMethod.
A classe AnnealingMethod
Aqui está a descrição da classe AnnealingMethod e mais detalhes sobre os seus métodos.
#include "Math/Alglib/alglib.mqh" //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class AnnealingMethod { private: CAlglib Alg; // instância da classe para trabalhar com os métodos da biblioteca Alglib CHighQualityRandStateShell state; // instância da classe para geração de números aleatórios public: AnnealingMethod(); ~AnnealingMethod(); struct Input // estrutura para trabalhar com os parâmetros do EA { int num; double Value; double BestValue; double Start; double Stop; double Step; double Temp; }; uint RunOptimization(string &InputParams[],int count,double F0,double T); uint WriteData(Input &InpMass[],double F,int it); uint ReadData(Input &Mass[],double &F,int &it); bool GetParams(int Method,Input &Mass[]); double FindValue(double val,double step); double GetFunction(int Criterion); bool Probability(double E,double T); double GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2); double UniformValue(double min,double max,double step); bool VerificationOfVal(double start,double end,double val); double Distance(double a,double b); };
As funções da biblioteca ALGLIB destinadas a trabalhar com as variáveis aleatórias são usadas na operação dos métodos da classe AnnealingMethod. Esta biblioteca é parte do pacote padrão da MetaTrader 5 e está localizada na pasta "Include/Math/Alglib", como mostrado abaixo:
Fig. 3. Biblioteca ALGLIB
O bloco Privado contém as declarações das instâncias da classe CAlglib e CHighQualityRandStateShell para trabalhar com as funções da ALGLIB.
Para trabalhar com os parâmetros otimizados do EA, a estrutura Input foi criada, que armazena:
- número do parâmetro, num;
- valor atual do parâmetro, Value;
- o melhor valor do parâmetro, BestValue;
- valor inicial, Start;
- valor final, Stop;
- passo para alterar o valor do parâmetro, Step;
- temperatura atual para o parâmetro fornecido, Temp.
Vamos considerar os métodos da classe AnnealingMethod.mqh.
O método RunOptimization
Projetado para inicializar o algoritmo de recozimento simulado. Código do método:
uint AnnealingMethod::RunOptimization(string &InputParams[],int count,double F0,double T) { Input Mass[]; ResetLastError(); bool Enable=false; double Start= 0; double Stop = 0; double Step = 0; double Value= 0; int j=0; Alg.HQRndRandomize(&state); // inicialização for(int i=0;i<ArraySize(InputParams);i++) { if(!ParameterGetRange(InputParams[i],Enable,Value,Start,Step,Stop)) return GetLastError(); if(Enable) { ArrayResize(Mass,ArraySize(Mass)+1); Mass[j].num=i; Mass[j].Value=UniformValue(Start,Stop,Step); Mass[j].BestValue=Mass[j].Value; Mass[j].Start=Start; Mass[j].Stop=Stop; Mass[j].Step=Step; Mass[j].Temp=T*Distance(Start,Stop); j++; if(!ParameterSetRange(InputParams[i],false,Value,Start,Stop,count)) return GetLastError(); } else InputParams[i]=""; } if(j!=0) { if(!ParameterSetRange("iteration",true,1,1,1,count)) return GetLastError(); else return WriteData(Mass,F0,1); } return 0; }
Parâmetros de entrada do método:
- array de strings contendo os nomes de todos os parâmetros do Expert Advisor, InputParams[];
- o número de iterações do algoritmo, count;
- valor inicial da função objetivo, F0;
- temperatura inicial, T.
O método RunOptimization funciona da seguinte maneira:
- Ele procura os parâmetros do EA a serem otimizados. Esses parâmetros devem estar "marcados" na guia "Parâmetros" do Testador de estratégia:
- Os valores de cada parâmetro encontrado são armazenados no array Mass[] de estrutura do tipo Input, e o parâmetro é excluído da otimização. O array de estruturas Mass[] armazena:
- número do parâmetro;
- valor do parâmetro gerado pelo método UniformValue (considerado abaixo);
- os valores máximos dos parâmetros de Start e Stop;
- passo para alterar o valor do parâmetro, (Step);
- temperatura inicial calculada pela fórmula: T*Distance(Start,Stop); o método Distance será discutido abaixo.
- após a conclusão da busca, todos os parâmetros serão desativados e o parâmetro iteration é ativado, o que determina o número de iterações do algoritmo;
- valores do array Mass[], a função objetivo e o número da iteração são gravados em um arquivo binário usando o método WriteData.
O método WriteData
Projetado para a escrita do array de parâmetros, valores da função objetivo e o número da iteração em um arquivo.
Código do método WriteData:
uint AnnealingMethod::WriteData(Input &Mass[],double F,int it) { ResetLastError(); int file_handle=0; int i=0; do { file_handle=FileOpen("data.bin",FILE_WRITE|FILE_BIN); if(file_handle!=INVALID_HANDLE) break; else { Sleep(MathRand()%10); i++; if(i>100) break; } } while(file_handle==INVALID_HANDLE); if(file_handle!=INVALID_HANDLE) { if(FileWriteArray(file_handle,Mass)<=0) {FileClose(file_handle); return GetLastError();} if(FileWriteDouble(file_handle,F)<=0) {FileClose(file_handle); return GetLastError();} if(FileWriteInteger(file_handle,it)<=0) {FileClose(file_handle); return GetLastError();} } else return GetLastError(); FileClose(file_handle); return 0; }
Os dados são gravados no arquivo data.bin usando as funções FileWriteArray, FileWriteDouble e FileWriteInteger. O método implementa a capacidade de haver múltiplos acessos ao arquivo data.bin. Isso é feito para evitar erros ao acessar o arquivo, se o arquivo estiver ocupado por outro processo.
O método ReadData
Projetado para ler o array de parâmetros, valores da função objetivo e o número da iteração de um arquivo. Código do método ReadData:
uint AnnealingMethod::ReadData(Input &Mass[],double &F,int &it) { ResetLastError(); int file_handle=0; int i=0; do { file_handle=FileOpen("data.bin",FILE_READ|FILE_BIN); if(file_handle!=INVALID_HANDLE) break; else { Sleep(MathRand()%10); i++; if(i>100) break; } } while(file_handle==INVALID_HANDLE); if(file_handle!=INVALID_HANDLE) { if(FileReadArray(file_handle,Mass)<=0) {FileClose(file_handle); return GetLastError();} F=FileReadDouble(file_handle); it=FileReadInteger(file_handle); } else return GetLastError(); FileClose(file_handle); return 0; }
Os dados são lidos do arquivo usando as funções FileReadArray, FileReadDouble, FileReadInteger na mesma sequência em que foram escritos pelo método WriteData.
O método GetParams
O método GetParams é projetado para calcular os novos valores dos parâmetros otimizados do EA a serem usados na próxima execução do EA. As fórmulas para calcular os novos valores dos parâmetros otimizados do EA são fornecidas na Tabela 1.
Parâmetros de entrada do método:
- variante de implementação do algoritmo (Distribuição de Boltzmann, Distribuição de Cauchy ou recozimento ultra-rápido);
- array dos parâmetros otimizados do tipo Input;
- coeficiente CoeffTmin para calcular a temperatura mínima para terminar o algoritmo.
Código do método GetParams:
bool AnnealingMethod::GetParams(int Method,Input &Mass[],double CoeffTmin) { double delta=0; double x1=0,x2=0; double count=0; Alg.HQRndRandomize(&state); // inicialização switch(Method) { case(0): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count= 0; break; } count++; delta=Mass[i].Temp*Alg.HQRndNormal(&state); delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } // enquanto((delta<Mass[i].Start) || (delta>Mass[i].Stop)); while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } case(1): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count=0; break; } count++; Alg.HQRndNormal2(&state,x1,x2); delta=Mass[i].Temp*x1/x2; delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } case(2): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count=0; break; } count++; x1=Alg.HQRndUniformR(&state); if(x1-0.5>0) delta=Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop); else { if(x1==0.5) delta=0; else delta=-Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop); } delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } default: { Print("Annealing method was chosen incorrectly"); return false; } } return true; }
Vamos considerar o código desse método em mais detalhes.
Este método possui um operador switch para iniciar o cálculo dos novos valores dos parâmetros, dependendo da variante de implementação do algoritmo selecionada. Os novos valores dos parâmetros são calculados somente se a temperatura atual estiver acima do mínimo. A temperatura mínima é calculada pela fórmula: CoeffTmin*Distance(Start, Stop), onde Start e Stop são os valores mínimos e máximos do parâmetro. O método Distance será considerado abaixo.
O método HQRndRandomize da classe CAlglib é chamado para inicializar os métodos para trabalhar com os números aleatórios.
Alg.HQRndRandomize(&state);
A função HQRndNormal da classe CAlglib é usado para calcular o valor da distribuição normal padrão:
Alg.HQRndNormal(&state);
As distribuições de Cauchy podem ser modeladas de várias maneiras, por exemplo, através da distribuição normal ou funções inversas. A seguinte proporção será usada:
C(0,1)=X1/X2, onde X1 e X2 são variáveis independentes distribuídas normalmente, X1,X2 = N(0,1). A função HQRndNormal2 da classe CAlglib é usado para gerar duas variáveis distribuídas normalmente:
Alg.HQRndNormal2(&state,x1,x2);
Os valores das variáveis independentes normalmente distribuídas são armazenadas em x1, x2.
O método HQRndUniformR(&state) da classe CAlglib era um número aleatório, uniformemente distribuído no intervalo de 0 a 1:
Alg.HQRndUniformR(&state);
Usando o método FindValue (descrito abaixo), o valor do parâmetro calculado é arredondado para o passo especificado para alterar o parâmetro. Se o valor do parâmetro calculado exceder o intervalo de alteração do parâmetro (verificado pelo método VerificationOfVal), ele é recalculado.
O método FindValue
O valor de cada parâmetro otimizado deve ser alterado com o passo especificado. Um novo valor gerado em GetParams pode não atender a essa condição e precisará ser arredondado para um múltiplo do passo especificado. Isso é feito pelo método FindValue. Parâmetros de entrada do método: o valor a ser arredondado (val) e o passo para alterar o parâmetro (step).
Aqui está o código do método FindValue:
double AnnealingMethod::FindValue(double val,double step) { double buf=0; if(val==step) return val; if(step==1) return round(val); else { buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step); if(MathAbs(val)-buf*MathAbs(step)>=MathAbs(step)/2) { if(val<0) return -(buf + 1)*MathAbs(step); else return (buf + 1)*MathAbs(step); } else { if(val<0) return -buf*MathAbs(step); else return buf*MathAbs(step); } } }
Vamos considerar o código desse método em mais detalhes.
Se o passo for igual ao valor de entrada do parâmetro, a função retornará esse valor:
if(val==step) return val;
Se o passo for igual a 1, o valor de entrada do parâmetro só precisa ser arredondado para um inteiro:
if(step==1) return round(val);
Caso contrário, encontra-se o número de etapas no valor de entrada do parâmetro:
buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);
e calcule um novo valor, que é um múltiplo da etapa.
O método GetFunction
O método GetFunction é projetado para obter o novo valor da função objetivo. O parâmetro de entrada do método é o critério de otimização definido pelo usuário.
Dependendo do modo de cálculo selecionado, a função objetivo leva o valor de um ou vários parâmetros estatísticos calculados a partir dos resultados do teste. Código do método:
double AnnealingMethod::GetFunction(int Criterion) { double Fc=0; switch(Criterion) { case(0): return TesterStatistics(STAT_PROFIT); case(1): return TesterStatistics(STAT_PROFIT_FACTOR); case(2): return TesterStatistics(STAT_RECOVERY_FACTOR); case(3): return TesterStatistics(STAT_SHARPE_RATIO); case(4): return TesterStatistics(STAT_EXPECTED_PAYOFF); case(5): return TesterStatistics(STAT_EQUITY_DD);//min case(6): return TesterStatistics(STAT_BALANCE_DD);//min case(7): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_PROFIT_FACTOR); case(8): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_RECOVERY_FACTOR); case(9): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_SHARPE_RATIO); case(10): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_EXPECTED_PAYOFF); case(11): { if(TesterStatistics(STAT_BALANCE_DD)>0) return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_BALANCE_DD); else return TesterStatistics(STAT_PROFIT); } case(12): { if(TesterStatistics(STAT_EQUITY_DD)>0) return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_EQUITY_DD); else return TesterStatistics(STAT_PROFIT); } case(13): { // especifica o critério personalizado, por exemplo return TesterStatistics(STAT_TRADES)*TesterStatistics(STAT_PROFIT); } default: return -10000; } }
Como você pode ver no código, são implementadas no método 14 maneiras de calcular a função objetivo. Ou seja, os usuários podem otimizar um EA por vários parâmetros estatísticos. A descrição detalhada dos parâmetros estatísticos está disponível na documentação.
O método Probability
O método Probability foi desenvolvido para identificar uma transição para um novo estado. Os parâmetros de entrada do método: diferença entre os valores anteriores e atuais da função objetivo (E) e a temperatura atual (T). Código do método:
bool AnnealingMethod::Probability(double E,double T) { double a=Alg.HQRndUniformR(&state); double res=exp(-E/T); if(res<=a) return false; else return true; }
O método gera uma variável aleatória a, distribuída uniformemente no intervalo de 0 a 1:
a=Alg.HQRndUniformR(&state);
O valor obtido é comparado com a expressão exp(-E/T). Se a>exp(-E/T), então o método retorna true (a transição para um novo estado é executada).
O método GetT
O método GetT calcula o novo valor da temperatura. Parâmetros de entrada do método:
- variante de implementação do algoritmo (Distribuição de Boltzmann, Distribuição de Cauchy ou recozimento ultra-rápido);
- valor inicial da temperatura, T0;
- valor anterior da temperatura, Tlast;
- número da iteração, it;
- o número de parâmetros otimizados, D;
- parâmetros auxiliares p1 e p2 para o recozimento ultra-rápido.
Código do método:
double AnnealingMethod::GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2) { int Iteration=0; double T=0; switch(Method) { case(0): { if(Tlast!=T0) Iteration=(int)MathRound(exp(T0/Tlast)-1)+1; else Iteration=1; if(Iteration>0) T=T0/log(Iteration+1); else T=T0; break; } case(1): { if(it!=1) Iteration=(int)MathRound(pow(T0/Tlast,D))+1; else Iteration=1; if(Iteration>0) T=T0/pow(Iteration,1/D); else T=T0; break; } case(2): { if((T0!=Tlast) && (-p1*exp(-p2/D)!=0)) Iteration=(int)MathRound(pow(log(Tlast/T0)/(-p1*exp(-p2/D)),D))+1; else Iteration=1; if(Iteration>0) T=T0*exp(-p1*exp(-p2/D)*pow(Iteration,1/D)); else T=T0; break; } } return T; }
O método calcula o novo valor da temperatura dependendo da variante da implementação do algoritmo de acordo com as fórmulas na Tabela 2. Para levar em consideração a implementação do algoritmo que aumenta a temperatura somente quando ocorre uma transição para um novo estado, a iteração atual é calculada usando o valor da temperatura anterior Tlast. Assim, a temperatura atual é reduzida quando o método é chamado, independente da iteração atual do algoritmo.
O método UniformValue
O método UniformValue gera um valor aleatório do parâmetro otimizado, considerando seus valores mínimos, máximos e de step. O método é usado somente durante a inicialização do algoritmo, para gerar os valores iniciais dos parâmetros otimizados. Parâmetros de entrada do método:
- o valor máximo do parâmetro, max;
- o valor mínimo do parâmetro, min;
- passo para alterar o parâmetro, step.
Código do método:
double AnnealingMethod::UniformValue(double min,double max,double step) { Alg.HQRndRandomize(&state); //inicialização if(max>min) return FindValue(Alg.HQRndUniformR(&state)*(max-min)+min,step); else return FindValue(Alg.HQRndUniformR(&state)*(min-max)+max,step); }
O método VerificationOfVal
O VerificationOfVal verifica se o valor especificado da variável (val) está fora do intervalo (start, end). Este método é usado no método GetParams.
Código do método:
bool AnnealingMethod::VerificationOfVal(double start,double end,double val) { if(start<end) { if((val>=start) && (val<=end)) return true; else return false; } else { if((val>=end) && (val<=start)) return true; else return false; } }
O método leva em conta que o passo de alteração do parâmetro pode ser negativo, portanto, ele verifica a condição "start<end".
O método Distance
O método Distance calcula a distância entre dois parâmetros (a e b) e é usado no algoritmo para calcular o intervalo de mudança do parâmetro com o valor inicial de a e o valor final de b.
Código do método:
double AnnealingMethod::Distance(double a,double b) { if(a<b) return MathAbs(b-a); else return MathAbs(a-b); }
A classe FrameAnnealingMethod
A classe FrameAnnealingMethod é projetada para exibir o processo de execução do algoritmo na janela da plataforma. Aqui está a descrição da classe FrameAnnealingMethod:
#include <SimpleTable.mqh> #include <Controls\BmpButton.mqh> #include <Controls\Label.mqh> #include <Controls\Edit.mqh> #include <AnnealingMethod.mqh> //+------------------------------------------------------------------+ //| Classe para a saída dos resultados da otimização | //+------------------------------------------------------------------+ class FrameAnnealingMethod { private: CSimpleTable t_value; CSimpleTable t_inputs; CSimpleTable t_stat; CBmpButton b_playbutton; CBmpButton b_backbutton; CBmpButton b_forwardbutton; CBmpButton b_stopbutton; CLabel l_speed; CLabel l_stat; CLabel l_value; CLabel l_opt_value; CLabel l_temp; CLabel l_text; CLabel n_frame; CEdit e_speed; long frame_counter; public: //--- Construtor/destrutor FrameAnnealingMethod(); ~FrameAnnealingMethod(); //--- Eventos do testador de estratégia void FrameTester(double F,double Fbest,Input &Mass[],int num,int it); void FrameInit(string &SMass[]); void FrameTesterPass(int cr); void FrameDeinit(void); void FrameOnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam,int cr); uint FrameToFile(int count); };
A classe FrameAnnealingMethod contém os seguintes métodos:
- FrameInit — cria uma interface gráfica na janela do terminal;
- FrameTester — adiciona o quadro de dados atual;
- FrameTesterPass — exibe o quadro de dados atual para a janela do terminal;
- FrameDeInit — exibe as informações de texto sobre a conclusão da otimização do EA;
- FrameOnChartEvent — manipula os eventos de pressionamento do botão;
- FrameToFile — salva os resultados do teste em um arquivo de texto.
O código dos métodos é fornecido no arquivo FrameAnnealingMethod.mqh (anexado ao artigo). Observe que o arquivo SimpleTable.mqh (anexado ao artigo) é necessário para que os métodos da classe FrameAnnealingMethod funcionem. Coloque-o em MQL5/Include. O arquivo foi adotado deste projeto e é complementado com o método GetValue, que permite ler um valor de uma célula da tabela.
Aqui está uma interface gráfica da amostra criada na janela da plataforma usando a classe FrameAnnealingMethod.
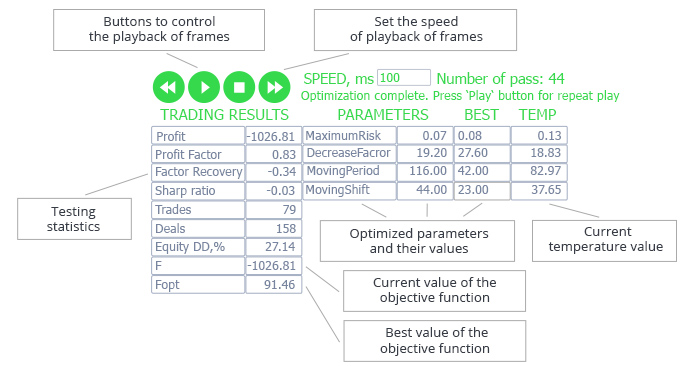
Fig. 4. Interface gráfica para demonstrar o funcionamento do algoritmo
O lado esquerdo da tabela contém parâmetros estatísticos gerados pelo testador de estratégia com base nos resultados da execução atual, bem como os valores atuais e os melhores da função objetivo (neste exemplo, o lucro líquido é escolhido como a função objetivo).
Os parâmetros otimizados estão localizados no lado direito da tabela: nome do parâmetro, valor atual, melhor valor, temperatura atual.
Acima da tabela, existem botões para controlar a reprodução dos quadros após a conclusão da execução do algoritmo. Assim, após a conclusão da otimização do EA, você poderá reproduzi-la na velocidade especificada. Os botões permitem interromper a reprodução de quadros e iniciá-lo novamente a partir do quadro, onde a reprodução foi interrompida. A velocidade de reprodução pode ser ajustada usando os botões ou pode ser ajustada manualmente. O número da execução atual é exibido à direita do valor de velocidade. Informações auxiliares sobre a operação do algoritmo são exibidas abaixo.
As classes AnnealingMethod e FrameAnnealingMethod foram consideradas. Agora vamos continuar testando o algoritmo usando de exemplo um Expert Advisor baseado na Média Móvel.
Testando o algoritmo no EA com base na Média Móvel
Preparando o EA para testar o algoritmo
O código do EA deve ser modificado para executar o algoritmo:
- inclua as classes AnnealingMethod e FrameAnnealingMethod, e declare as variáveis auxiliares para a operação do algoritmo;
- adicione o código à função OnInit, adicione as funções OnTester, OnTesterInit, OnTesterDeInit, OnTesterPass, OnChartEvent.
O código adicionado não afeta a operação do EA e ele é executado somente quando o EA é otimizado no testador de estratégia.
Então, vamos começar.
Inclua o arquivo com os parâmetros iniciais, gerados pela função OnTesterInit:
#property tester_file "data.bin"
Inclua as classes AnnealingMethod e FrameAnnealingMethod:
// inclusão das classes #include <AnnealingMethod.mqh> #include <FrameAnnealingMethod.mqh>
Declare as instâncias das classes incluídas:
AnnealingMethod Optim; FrameAnnealingMethod Frame;
Declare as variáveis auxiliares para o funcionamento do algoritmo:
Input InputMass[]; // array dos parâmetros de entrada string SParams[]; // array dos nomes dos parâmetros de entrada double Fopt=0; // o melhor valor da função int it_agent=0; // número da iteração do algoritmo para o agente de teste uint alg_err=0; // número do erro
O algoritmo de recozimento simulado modificará os valores dos parâmetros otimizados ao longo de seu trabalho. Para este propósito, os parâmetros de entrada do EA serão renomeados:
double MaximumRisk_Optim=MaximumRisk; double DecreaseFactor_Optim=DecreaseFactor; int MovingPeriod_Optim=MovingPeriod; int MovingShift_Optim=MovingShift;
Em todas as funções do EA, substitua os parâmetros: MaximumRisk com MaximumRisk_Optim, DecreaseFactor com DecreaseFactor_Optim, MovingPeriod com MovingPeriod_Optim, MovingShift com MovingShift_Optim.
Aqui estão as variáveis para configurar a operação do algoritmo:
sinput int iteration=50; // Número de iterações sinput int method=0; // 0 - Distribuição de Boltzmann, 1 - Distribuição de Cauchy, 2 - recozimento ultra-rápido sinput double CoeffOfTemp=1; // Coeficiente de escala para a temperatura inicial sinput double CoeffOfMinTemp=0; // Coeficiente para a temperatura mínima sinput double Func0=-10000; // Valor inicial da função objetivo sinput double P1=1; // Parâmetro adicional para o recozimento ultra-rápido, p1 sinput double P2=1; // Parâmetro adicional para o recozimento ultra-rápido, p2 sinput int Crit=0; // Método de cálculo da função objetivo sinput int ModOfAlg=0; // Tipo de modificação do algoritmo sinput bool ManyPoint=false; // Otimização de múltiplos pontos
Os parâmetros do algoritmo não devem mudar durante sua operação; portanto, todas as variáveis são declaradas com o identificador sinput.
A Tabela 3 explica o objetivo das variáveis declaradas.
Tabela 3
| Nome da variável | Propósito |
|---|---|
| iteration | Define o número de iterações do algoritmo |
| method | Define a variante de implementação do algoritmo: 0 — Distribuição de Boltzmann, 1 — Distribuição de Cauchy, 2 — recozimento ultra-rápido); |
| CoeffOfTemp | Define o coeficiente para ajuste da temperatura inicial calculada pela fórmula: T0=CoeffOfTemp*Distance(Start,Stop), onde Start, Stop são os valores mínimos e máximos do parâmetro, Distance é um método da classe AnnealingMethod (descrito acima) |
| CoeffOfMinTemp | Define o coeficiente para definir a temperatura mínima para finalizar o algoritmo. A temperatura máxima é calculada de forma similar à temperatura inicial: Tmin=CoeffOfMinTemp*Distance(Start,Stop), onde Start, Stop são os valores mínimos e máximos do parâmetro, Distance é um método da classe AnnealingMethod (descrito acima) |
| Func0 | Valor inicial da função objetivo |
| P1,P2 | Parâmetros utilizados para o cálculo da temperatura atual no recozimento ultra-rápido (ver Tabela 2) |
| Crit | Critério de otimização: 0 — Lucro Líquido Total; 1 — Fator de Lucro; 2 — Fator de Recuperação; 3 — Sharpe Ratio; 4 — Retorno Esperado; 5 — Rebaixamento Máximo do Capital; 6 — Rebaixamento Máximo do Saldo; 7 — Lucro Líquido Total + Fator de Lucro; 8 — Lucro Líquido Total + Fator de Recuperação; 9 — Lucro Líquido Total + Sharpe Ratio; 10 — Lucro Líquido Total + Retorno Esperado; 11 — Lucro Líquido Total + Rebaixamento Máximo do Saldo; 12 — Lucro Líquido Total + Rebaixamento Máximo do Capital; 13 — Critério personalizado. A função objetivo é calculada na função GetFunction da classe AnnealingMethod |
| ModOfAlg | Tipo de modificação do algoritmo: 0 - se ocorreu uma transição para um novo estado, diminua a temperatura atual e prossiga para a verificação da conclusão do algoritmo, caso contrário, calcule os novos valores dos parâmetros otimizados; 1 - independentemente do resultado da verificação da transição para um novo estado, diminua a temperatura atual e prossiga para a verificação da conclusão do algoritmo |
| ManyPoint | true — diferentes valores iniciais dos parâmetros otimizados serão gerados para cada agente de teste, false — os mesmos valores iniciais dos parâmetros otimizados serão gerados para cada agente de teste |
Adicione o código ao início da função OnInit:
//+------------------------------------------------------------------+ //| Recozimento simulado | //+------------------------------------------------------------------+ if(MQL5InfoInteger(MQL5_OPTIMIZATION)) { // abre o arquivo e lê os dados // if(FileGetInteger("data.bin",FILE_EXISTS,false)) // { alg_err=Optim.ReadData(InputMass,Fopt,it_agent); if(alg_err==0) { // Se for a primeira execução, gere os parâmetros aleatoriamente, se a busca for realizada a partir dos pontos diferentes if(Fopt==Func0) { if(ManyPoint) for(int i=0;i<ArraySize(InputMass);i++) { InputMass[i].Value=Optim.UniformValue(InputMass[i].Start,InputMass[i].Stop,InputMass[i].Step); InputMass[i].BestValue=InputMass[i].Value; } } else Optim.GetParams(method,InputMass,CoeffOfMinTemp); // gera novos parâmetros // preenche os parâmetros do Expert Advisor for(int i=0;i<ArraySize(InputMass);i++) switch(InputMass[i].num) { case (0): {MaximumRisk_Optim=InputMass[i].Value; break;} case (1): {DecreaseFactor_Optim=InputMass[i].Value; break;} case (2): {MovingPeriod_Optim=(int)InputMass[i].Value; break;} case (3): {MovingShift_Optim=(int)InputMass[i].Value; break;} } } else { Print("Error reading file"); return(INIT_FAILED); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
Vamos examinar o código em detalhes. O código adicionado é executado apenas no modo de otimização do testador de estratégia:
if(MQL5InfoInteger(MQL5_OPTIMIZATION))
Em seguida, os dados são lidos do arquivo data.bin, gerado pelo método RunOptimization da classe AnnealingMethod. Este método é chamado na função OnTesterInit, o código da função será exibido abaixo.
alg_err=Optim.ReadData(InputMass,Fopt,it_agent);
Se os dados foram lidos sem erros (alg_err=0), uma verificação é executada para ver se o algoritmo está na primeira iteração (Fopt==Func0), caso contrário, a inicialização do EA falhará com um erro. Se for a primeira iteração, e se ManyPoint = true, os valores iniciais dos parâmetros otimizados são gerados e armazenados na InputMass - estrutura do tipo Input (descrito na classe AnnealingMethod), caso contrário, o método GetParams é chamado
Optim.GetParams(method,InputMass,CoeffOfMinTemp);// gera novos parâmetros
e os valores dos parâmetros MaximumRisk_Optim, DecreaseFactor_Optim, MovingPeriod_Optim, MovingShift_Optim são preenchidos.
Agora vamos considerar o código da função OnTesterInit:
void OnTesterInit() { // preenche o array de nomes de todos os parâmetros do EA ArrayResize(SParams,4); SParams[0]="MaximumRisk"; SParams[1]="DecreaseFactor"; SParams[2]="MovingPeriod"; SParams[3]="MovingShift"; // inicia a otimização Optim.RunOptimization(SParams,iteration,Func0,CoeffOfTemp); // cria a interface gráfica Frame.FrameInit(SParams); }
Primeiro, preenche o array de string que contém os nomes de todos os parâmetros do EA. Em seguida, executa o método RunOptimization e cria uma interface gráfica usando o método FrameInit.
Depois de executar o EA no intervalo de tempo especificado, o controle será transferido para a função OnTester. Aqui está o seu código:
double OnTester() { int i=0; // contador do ciclo int count=0; // variável auxiliar // verifica a conclusão do algoritmo quando a temperatura mínima é atingida for(i=0;i<ArraySize(InputMass);i++) if(InputMass[i].Temp<CoeffOfMinTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop)) count++; if(count==ArraySize(InputMass)) Frame.FrameTester(0,0,InputMass,-1,it_agent); // adiciona um novo quadro com zero parâmetros e id=-1 else { double Fnew=Optim.GetFunction(Crit); // calcula o valor atual da função if((Crit!=5) && (Crit!=6) && (Crit!=11) && (Crit!=12)) // se for necessário maximizar a função objetivo { if(Fnew>Fopt) Fopt=Fnew; else { if(Optim.Probability(Fopt-Fnew,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop))) Fopt=Fnew; } } else // se for necessário minimizar a função objetivo { if(Fnew<Fopt) Fopt=Fnew; else { if(Optim.Probability(Fnew-Fopt,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop))) Fopt=Fnew; } } // sobrescreve os melhores valores dos parâmetros if(Fopt==Fnew) for(i=0;i<ArraySize(InputMass);i++) InputMass[i].BestValue=InputMass[i].Value; // diminui a temperatura if(((ModOfAlg==0) && (Fnew==Fopt)) || (ModOfAlg==1)) { for(i=0;i<ArraySize(InputMass);i++) InputMass[i].Temp=Optim.GetT(method,CoeffOfTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop),InputMass[i].Temp,it_agent,ArraySize(InputMass),P1,P2); } Frame.FrameTester(Fnew,Fopt,InputMass,iteration,it_agent); // adiciona um novo quadro it_agent++; // aumenta o contador de iteração alg_err=Optim.WriteData(InputMass,Fopt,it_agent); // escreve os novos valores no arquivo if(alg_err!=0) return alg_err; } return Fopt; }
Vamos considerar o código desta função em mais detalhes.
- Ele verifica a conclusão do algoritmo quando a temperatura mínima é atingida. Se a temperatura de cada parâmetro atingiu o valor mínimo, um quadro com id=-1 é adicionado, os valores dos parâmetros não mudam mais. A interface gráfica na janela da plataforma solicita ao usuário que conclua a otimização pressionando o botão "Stop" no testador de estratégia.
- O método GetFunction calcula o novo valor da função objetivo Fnew, usando os resultados do teste do Expert Advisor.
- Dependendo do critério de otimização (veja a Tabela 3), o valor de Fnew é comparado com o melhor valor de Fopt e a transição para um novo estado é verificada.
- Se ocorreu uma transição para um novo estado, os valores atuais dos parâmetros otimizados são definidos como os melhores:
for(i=0;i<ArraySize(InputMass);i++) InputMass[i].BestValue = InputMass[i].Value;
- A condição para diminuir a temperatura atual é verificada. Se for atendida, a nova temperatura é calculada usando o método GetT da classe AnnealingMethod.
- Um novo quadro é adicionado, os valores dos parâmetros otimizados são escritos no arquivo.
A função OnTester adiciona os quadros para serem processados posteriormente na função OnTesterPass. Aqui está o seu código:
void OnTesterPass() { Frame.FrameTesterPass(Crit);// método para exibir os quadros na interface gráfica }
A função OnTesterPass chama o método FrameTesterPass da classe FrameAnnealingMethod para exibir o processo de otimização na janela da plataforma.
Quando a otimização estiver concluída, a função OnTesterDeInit é chamada:
void OnTesterDeinit() { Frame.FrameToFile(4); Frame.FrameDeinit(); }
Essa função chama dois métodos da classe FrameAnnealingMethod: FrameToFile e FrameDeinit. O método FrameToFile grava os resultados da otimização em um arquivo de texto. Este método leva o número de parâmetros do EA a serem otimizados como entrada. O método FrameDeinit exibe uma mensagem sobre a conclusão da otimização para a janela da plataforma.
Depois que a otimização é concluída, a interface gráfica criada usando os métodos da classe FrameAnnealingMethod permite reproduzir os quadros em uma velocidade especificada. A reprodução dos quadros pode ser interrompida e reiniciada. Isso é feito pelos botões correspondentes da interface gráfica (veja a Fig. 4). Para manipular os eventos na janela do terminal, o método OnChartEvent foi adicionado ao código do EA:
void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { Frame.FrameOnChartEvent(id,lparam,dparam,sparam,Crit); // método para trabalhar com a interface gráfica }
O método OnChartEvent chama o método FrameOnChartEvent da classe FrameAnnealingMethod, que gerencia a reprodução dos quadros na janela da plataforma.
Isso conclui a modificação do código do EA MovingAverage. Vamos começar a testar o algoritmo.
Testando o algoritmo
O método de recozimento simulado proposto tem uma natureza estocástica (contém funções para calcular as variáveis aleatórias), portanto, cada execução do algoritmo produzirá um resultado diferente. Para testar a operação do algoritmo e identificar suas vantagens e desvantagens, é necessário executar a otimização do EA muitas vezes. Isso levaria uma quantidade considerável de tempo, então será feito o seguinte: executar a otimização no modo "Algoritmo completo lento", salvar os resultados obtidos e, em seguida, testar o algoritmo usando esses dados.
O algoritmo será testado usando o Expert Advisor TestAnnealing.mq5 (localizado no arquivo test.zip anexado ao artigo). Ele carrega uma tabela de resultados da otimização obtida pelo método de busca completa a partir de um arquivo de texto contendo 5 colunas com dados: as colunas 1-4 representam os valores das variáveis, a coluna 5 mostra os valores da função objetivo. O algoritmo implementado em TestAnnealing usa o método de recozimento simulado para percorrer a tabela e localizar os valores da função objetivo. Essa abordagem de teste permite verificar o desempenho do recozimento simulado em vários dados obtidos pela busca completa.
Então, vamos começar. Primeiro, teste o desempenho do algoritmo otimizando uma variável do EA — Moving Average period.
Execute a otimização do EA no modo de busca completa com os seguintes parâmetros iniciais:
- Maximum Risk in percentage — 0.02; Decrease factor — 3; Moving Average period: 1 - 120, step: 1; Moving Average shift — 6.
- Período: 01.01.2017 — 31.12.2017, modo de execução: sem latência, ticks: 1 minuto OHLC, depósito inicial: 10000, alavancagem: 1:100, par de moeda: EURUSD.
- A otimização será realizada usando o critério Balance máx.
Salve o resultado e crie um arquivo de teste com os dados obtidos. Os dados no arquivo de texto serão classificados em ordem crescente do valor do parâmetro "Average Average period", como mostrado na Fig. 5.
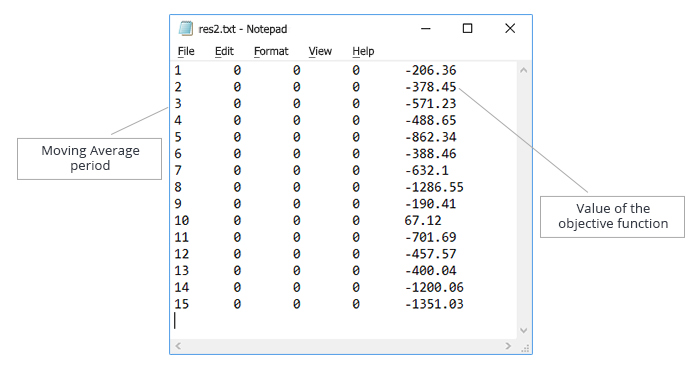
Fig. 5. Otimização do parâmetro "Moving Average period". Arquivo de texto com os dados para testar o funcionamento do algoritmo
120 iterações foram realizadas no modo de busca completa. O algoritmo de recozimento simulado será testado com o seguinte número de iterações: 30 (variante 1), 60 (variante 2), 90 (variante 3). O objetivo aqui é testar o desempenho do algoritmo enquanto é reduzido o número de iterações.
Para cada variante, 10000 execuções de otimização usando recozimento simulado foram realizadas nos dados obtidos pela busca completa. O algoritmo implementado no Expert Advisor TestAnnealing.mq5 conta quantas vezes o melhor valor da função objetivo foi encontrado, bem como quantas vezes os valores da função objetivo diferem do melhor em 5%, 10%, 15%, 20 %, 25% que foram encontrados.
Os seguintes resultados do teste foram obtidos.
Para 30 iterações do algoritmo, os melhores valores foram obtidos pelo recozimento ultra-rápido com redução de temperatura em cada iteração:
| Desvio do melhor valor da função objetivo, % | Resultado, % |
|---|---|
| 0 | 33 |
| 5 | 44 |
| 10 | 61 |
| 15 | 61 |
| 20 | 72 |
| 25 | 86 |
Os dados desta tabela são interpretados como: o melhor valor da função objetivo foi obtido em 33% das execuções (em 3.300 de 10.000 execuções), o desvio de 5% do melhor valor foi obtido em 44% das execuções, e assim por diante.
Por 60 iterações do algoritmo, o recozimento utilizando a distribuição de Cauchy está liderando, mas a melhor variante aqui foi a redução de temperatura durante a transição para um novo estado. Os resultados são os seguintes:
| Desvio do melhor valor da função objetivo, % | Resultado, % |
|---|---|
| 0 | 47 |
| 5 | 61 |
| 10 | 83 |
| 15 | 83 |
| 20 | 87 |
| 25 | 96 |
Assim, com a contagem de iteração reduzido a metade em comparação com a busca completa, o método de recozimento simulado encontra o melhor valor da função objetivo em 47% dos casos.
Para 90 iterações do algoritmo, o recozimento utilizando a distribuição de Boltzmann e a de Cauchy com redução de temperatura durante a transição para um novo estado tiveram aproximadamente o mesmo resultado. Aqui estão os resultados para o recozimento utilizando a distribuição de Cauchy:
| Desvio do melhor valor da função objetivo, % | Resultado, % |
|---|---|
| 0 | 62 |
| 5 | 71 |
| 10 | 93 |
| 15 | 93 |
| 20 | 95 |
| 25 | 99 |
Assim, com a contagem de iteração reduzida em um terço em comparação com a busca completa, o método de recozimento simulado encontrou o melhor valor da função objetivo em 62% dos casos. No entanto, é possível obter resultados bastante aceitáveis com um desvio de 10-15%.
O método de recozimento ultra-rápido foi testado com os parâmetros p1=1, p2=1. O aumento do número de iterações teve um impacto negativo maior no resultado obtido do que no recozimento utilizando a distribuição de Boltzmann e de Cauchy. No entanto, o algoritmo de recozimento ultra-rápido tem uma peculiaridade: mudando os coeficientes p1 e p2 permite o ajuste da velocidade de redução da temperatura.
Vamos considerar o gráfico de mudança de temperatura para o recozimento ultra-rápido (Fig. 6):
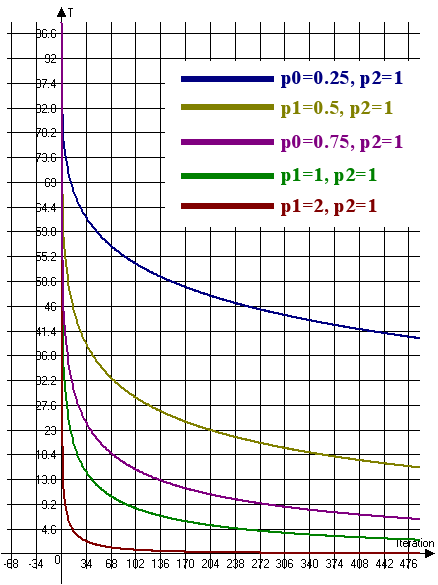
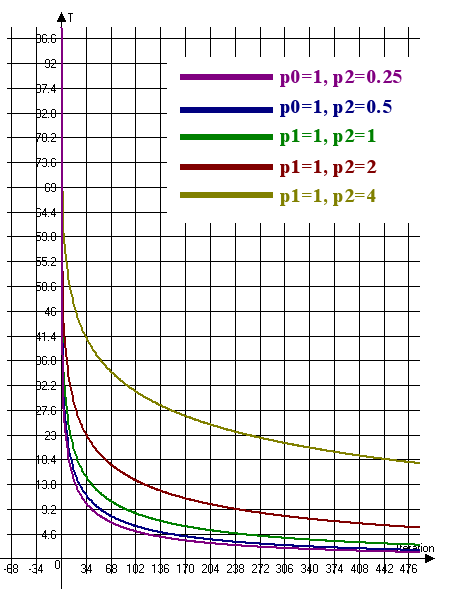
Fig. 6. O gráfico de mudança de temperatura para o recozimento ultra-rápido (T0 = 100, n = 4)
A fig. 6 implica que é necessário aumentar o coeficiente p1 e diminuir o coeficiente p2 para reduzir a taxa de mudança de temperatura. Assim, para aumentar a taxa de variação da temperatura, é necessário reduzir o coeficiente p1 e aumentar o coeficiente p2.
Nas iterações de 60 e 90, o recozimento ultra-rápido mostrou os piores resultados, porque a temperatura estava caindo muito rápido. Depois de diminuir o coeficiente p1, os seguintes resultados foram obtidos:
| Número de iterações | p1 | p2 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|---|---|
| 60 | 0.5 | 1 | 57 | 65 | 85 | 85 | 91 | 98 |
| 90 | 0.25 | 1 | 63 | 78 | 93 | 93 | 96 | 99 |
A tabela mostra que o melhor valor da função objetivo foi obtido em 57% das execuções em 60 iterações e em 63% das rodadas em 90 iterações.
Assim, o melhor resultado ao otimizar um parâmetro foi alcançado pelo recozimento ultra-rápido. No entanto, é necessário selecionar os coeficientes p1 e p2 dependendo do número de iterações.
Como mencionado acima, o algoritmo de recozimento simulado é estocástico, portanto, sua operação será comparada com uma busca aleatória. Para fazer isso, é gerado em cada iteração um valor aleatório de um parâmetro com um determinado passo e em um dado intervalo. Neste caso, os valores do parâmetro "Moving Average period" serão gerados com um passo de 1, no intervalo de 1 a 120.
A busca aleatória foi realizada com as mesmas condições do recozimento simulado:
- número de iterações: 30, 60, 90
- número de execuções em cada variante: 10000
Os resultados da pesquisa aleatória são apresentados na tabela abaixo:
| Número de iterações | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 30 | 22 | 40 | 54 | 54 | 64 | 84 |
| 60 | 40 | 64 | 78 | 78 | 87 | 97 |
| 90 | 52 | 78 | 90 | 90 | 95 | 99 |
Vamos comparar os resultados da busca aleatória e do recozimento ultra-rápido. A tabela mostra um aumento percentual entre os valores correspondentes da busca aleatória e do recozimento ultra-rápido. Por exemplo, em 30 iterações, o algoritmo de recozimento ultra-rápido é 50% melhor em encontrar o melhor valor da função do que a busca aleatória.
| Número de iterações | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 30 | 50 | 10 | 12.963 | 12.963 | 12.5 | 2.381 |
| 60 | 42.5 | 1.563 | 8.974 | 8.974 | 4.6 | 1.031 |
| 90 | 21.154 | 0 | 3.333 | 3.333 | 1.053 | 0 |
A tabela mostra que aumentar o número de iterações reduz a vantagem do algoritmo de recozimento ultra-rápido.
Agora vamos continuar testando o algoritmo na otimização de dois parâmetros do Expert Advisor, "Moving Average period" e "Moving Average Shift". Primeiro, gere os dados de entrada executando o algoritmo completo lento no testador de estratégia com os seguintes parâmetros:
- Maximum Risk in percentage — 0.02; Decrease factor — 3; Moving Average period: 1-120; Moving Average shift - 6-60.
- Período: 01.01.2017 - 31.12.2017, modo de execução: sem latência, ticks: 1 minuto OHLC, depósito inicial: 10000, alavancagem: 1:100, par de moeda: EURUSD
- A otimização será realizada usando o critério Balance máx.
Salve o resultado e crie um arquivo de teste com os dados obtidos. Os dados no arquivo de texto são classificados em ordem crescente do parâmetro "Moving Average period". O arquivo gerado é mostrado na Fig. 7.
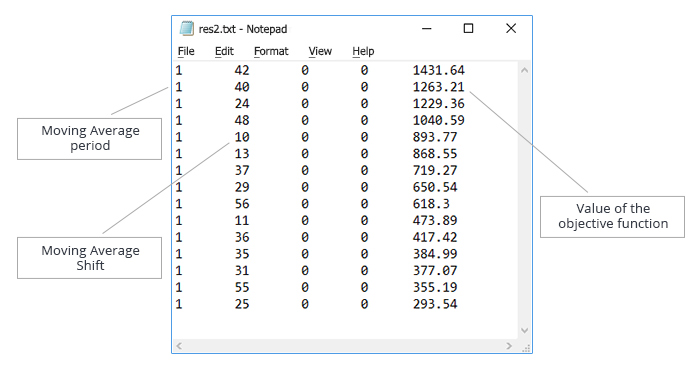
Fig. 7. Otimização dos parâmetros "Moving Average period" e "Moving Average shift". Arquivo de texto com os dados para testar o funcionamento do algoritmo
O algoritmo completo lento por duas variáveis realizou 6.600 iterações. Vamos tentar reduzir esse número usando o recozimento simulado. Teste o algoritmo com o seguinte número de iterações: 330, 660, 1665, 3300, 4950. O número de execuções em cada variante: 10000.
Os resultados do teste são os seguintes.
330 iterações: O recozimento utilizando a distribuição de Cauchy apresentou bons resultados, mas o melhor resultado foi obtido pelo recozimento ultra-rápido com redução de temperatura em cada iteração e coeficientes p1=1, p2=1.
660 iterações: resultados do recozimento utilizando a distribuição de Cauchy e do recozimento ultra rápido com redução de temperatura em cada iteração e coeficientes p1=1, p2=1 apresentaram aproximadamente os mesmos resultados.
Nas iterações 1665, 3300 e 4950, o melhor resultado foi obtido pelo recozimento ultra-rápido com redução de temperatura em cada iteração e os seguintes valores dos coeficientes p1 e p2:
- 1665 iterações: p1= 0.5, p2=1
- 3300 iterações: p1= 0.25, p2=1
- 4950 iterações: p1= 0.5, p2= 3
Os melhores resultados estão resumidos na tabela:
| Número de iterações | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 11 | 11 | 18 | 40 | 66 | 71 |
| 660 | 17 | 17 | 27 | 54 | 83 | 88 |
| 1665 | 31 | 31 | 41 | 80 | 95 | 98 |
| 3300 | 51 | 51 | 62 | 92 | 99 | 99 |
| 4950 | 65 | 65 | 75 | 97 | 99 | 100 |
As seguintes conclusões podem ser tiradas da tabela:
- quando o número de iterações é reduzido em 10 vezes, o algoritmo de recozimento ultra-rápido encontra o melhor valor da função objetivo em 11% dos casos; mas em 71% dos casos, produz um valor da função objetivo que é apenas 25% pior do que o melhor.
- quando o número de iterações é reduzido em 2 vezes, o algoritmo de recozimento ultra-rápido encontra o melhor valor da função objetivo em 51% dos casos; mas tem quase 100% de probabilidade de encontrar um valor da função objetivo que é apenas 20% pior do que o melhor.
Assim, o algoritmo de recozimento ultra-rápido pode ser usado para avaliar rapidamente a rentabilidade das estratégias quando um pequeno desvio do melhor valor é perfeitamente aceitável.
Agora vamos comparar o algoritmo de recozimento ultra-rápido com busca aleatória. Os resultados da pesquisa aleatória são apresentados na tabela abaixo:
| Número de iterações | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 5 | 5 | 10 | 14 | 33 | 42 |
| 660 | 10 | 10 | 19 | 27 | 55 | 67 |
| 1665 | 22 | 22 | 41 | 53 | 87 | 94 |
| 3300 | 40 | 40 | 64 | 79 | 98 | 99 |
| 4950 | 55 | 55 | 79 | 90 | 99 | 99 |
Vamos comparar os resultados da busca aleatória e do recozimento ultra-rápido. Os resultados serão representados na forma de uma tabela que mostra o aumento percentual entre os valores correspondentes da busca aleatória e do recozimento ultra-rápido.
| Número de iterações | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 120 | 120 | 80 | 185.714 | 100 | 69 |
| 660 | 70 | 70 | 42.105 | 100 | 50.909 | 31.343 |
| 1665 | 40.909 | 40.909 | 0 | 50.9434 | 9.195 | 4.255 |
| 3300 | 27.5 | 27.5 | -3.125 | 16.456 | 1.021 | 0 |
| 4950 | 18.182 | 18.182 | -5.064 | 7.778 | 0 | 1.01 |
Assim, observa-se uma vantagem significativa do algoritmo de recozimento ultra-rápido em um pequeno número de iterações. Quando ele aumenta, a vantagem diminui e às vezes até se torna negativa. Observe que uma situação semelhante ocorreu ao testar o algoritmo ao otimizar um parâmetro.
Agora, para o ponto principal: comparar o algoritmo de recozimento ultra-rápido e o algoritmo genético (AG), integrado ao testador de estratégia.
Comparação do AG e do recozimento ultra-rápido na otimização de duas variáveis: Moving Average period" e "Moving Average shift"
Os algoritmos começarão com os seguintes parâmetros iniciais:
- Maximum Risk in percentage — 0.02; Decrease factor — 3; Moving Average period: 1 — 120, step: 1; Moving Average shift — 6-60, step: 1
- Período: 01.01.2017 - 31.12.2017, modo de execução: sem latência, ticks: 1 minuto OHLC, depósito inicial: 10000, alavancagem: 1:100, par de moeda: EURUSD
- A otimização será realizada usando o critério Balance máx
Execute o algoritmo genético 20 vezes, salve os resultados e o número médio de iterações necessárias para concluir o algoritmo.
Após 20 execuções do AG, os seguintes valores foram obtidos: 1392.29; 1481.32; 2284.46; 1665.44; 1435.16; 1786.78; 1431.64; 1782.34; 1520.58; 1229.36; 1482.23; 1441.36; 1763.11; 2286.46; 1476.54; 1263.21; 1491.09; 1076.9; 913.42; 1391.72.
Número médio de iterações: 175; valor médio da função objetivo: 1529.771.
Dado que o melhor valor da função objetivo é de 2446.33, o AG não produziu um bom resultado, com o valor médio da função objetivo sendo apenas 62.53% do melhor valor.
Agora rode 20 execuções do algoritmo de recozimento ultra rápido em 175 iterações com os parâmetros: p1=1, p2=1.
O recozimento ultra-rápido foi lançado em 4 agentes de teste, enquanto a busca pela função objetivo foi realizada de forma autônoma em cada agente, de modo que cada agente realizou 43-44 iterações. Os seguintes resultados foram obtidos: 1996.83; 1421.87; 1391.72; 1727.38; 1330.07; 2486.46; 1687.51; 1840.69; 1687.51; 1472.19; 1665.44; 1607.19; 1496.9; 1388.37; 1496.9; 1491.09; 1552.02; 1467.08; 2446.33; 1421.15.
O valor médio da função objetivo: 1653.735, 67,6% da função objetivo de melhor valor, ligeiramente superior à obtida pelo AG.
Execute o algoritmo de recozimento ultra-rápido em um único agente de teste, executando 175 iterações. Como resultado, o valor médio da função objetivo foi de 1731.244 (70,8% do melhor valor).
Comparação do AG e do recozimento ultra-rápido na otimização de quatro variáveis: "Moving Average period", "Moving Average shift", "Decrease factor" e "Maximum Risk in percentage".
Os algoritmos começarão com os seguintes parâmetros iniciais:
- Moving Average period: 1 — 120, step: 1; Moving Average shift — 6-60, step: 1; Decrease factor: 0.02 — 0.2, step: 0,002; Maximum Risk in percentage: 3-30, step: 0.3.
- Período: 01.01.2017 - 31.12.2017, modo de execução: sem latência, ticks: 1 minuto OHLC, depósito inicial: 10000, alavancagem: 1:100, par de moeda: EURUSD
- A otimização será realizada usando o critério Balance máx
O AG foi concluído em 4870 iterações, com o melhor resultado de 32782.91. O algoritmo completo não pôde ser iniciada devido ao grande número de combinações possíveis; portanto, simplesmente compararemos os resultados dos algoritmos GA e do recozimento ultra-rápido.
O algoritmo de recozimento ultra-rápido foi iniciado com os parâmetros p1=0.75 e p2=1 em 4 agentes de teste e foi concluído com um resultado de 26676.22. O algoritmo não foi muito bem com essas configurações. Vamos tentar acelerar a redução de temperatura configurando p1=2, p2=1. Observe também que a temperatura calculada pela fórmula:
T0*exp(-p1*exp(-p2/4)*n^0.25), onde n é o número da iteração,
diminui acentuadamente na primeira iteração (em n=1, T=T0*0.558). Portanto, aumente o coeficiente na temperatura inicial definindo CoeffOfTemp=4. A execução do algoritmo com essas configurações melhorou significativamente o resultado: 39145.25. A operação do algoritmo é demonstrada no seguinte vídeo:
Demonstração do recozimento ultra-rápido com os parâmetros p1=2, p2=1
Assim, o algoritmo de recozimento ultra-rápido é um rival valioso para o GA e é capaz de superá-lo com as configurações corretas.
Conclusão
O artigo considera o algoritmo de recozimento simulado, sua implementação e integração no EA Moving Average. Foi realizado testes de desempenho em um número diferente de parâmetros do EA Moving Average. Além disso, o desempenho do recozimento simulado foi comparado com o do algoritmo genético.
Várias implementações de recozimento simulado foram testadas: baseado na Distribuição de Boltzmann, Distribuição de Cauchy e recozimento ultra-rápido. Os melhores resultados foram demonstrados pelo recozimento ultra-rápido.
Aqui estão as principais vantagens do recozimento simulado:
- otimização de diferentes números de parâmetros;
- os parâmetros do algoritmo podem ser personalizados, o que permite seu uso efetivo para várias tarefas de otimização;
- número selecionável de iterações para o algoritmo;
- interface gráfica para monitorar a operação do algoritmo, exibindo o melhor resultado e repetindo os resultados da operação do algoritmo.
Apesar das vantagens significativas, o algoritmo de recozimento simulado tem as seguintes desvantagens de implementação:
- o algoritmo não pode ser executado no teste em nuvem;
- a integração em um EA é complicada, e é necessário selecionar os parâmetros para obter os melhores resultados.
Essas desvantagens podem ser eliminadas através do desenvolvimento de um módulo universal, que incluiria vários algoritmos para otimizar os parâmetros do EA. Como ele recebe os valores da função objetivo após um teste, este módulo gerará novos valores dos parâmetros otimizados para a próxima execução.
Os seguintes arquivos estão anexados ao artigo:
| Nome do arquivo | Comentário |
|---|---|
| AnnealingMethod.mqh | Classe necessária para a operação do algoritmo de recozimento simulado, deve ser colocada em /MQL5/Include |
| FrameAnnealingMethod.mqh | Classe para exibir o processo de execução do algoritmo na janela do terminal, deve ser colocada em /MQL5/Include |
| SimpleTable.mqh | Classe auxiliar para trabalhar com tabelas da interface gráfica, deve ser colocada em /MQL5/Include |
| Moving Average_optim.mq5 | Versão modificada do EA Moving Average |
| test.zip | Arquivo contendo o EA TestAnnealing.mq5 para testar o algoritmo de recozimento simulado em dados de entrada carregados do arquivo de teste, bem como arquivos auxiliares |
| AnnealingMethod.zip | Arquivo zip com imagens para criar a interface do usuário. O arquivo deve ser colocado em MQL5/Images/AnnealingMethod |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/4150
Como criar uma Especificação de Requisitos para solicitar um indicador
Criando um feed de notícias personalizado para o MetaTrader 5
Comparamos a velocidade de indicadores de armazenamento automático em cache
ZUP - ZigZag universal com padrões Pesavento. Pesquisa de padrões
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso