
Kontrollierte Optimierung: Simuliertes Abkühlen
Einführung
Der Strategy Tester in der Handelsplattform MetaTrader 5 bietet nur zwei Optimierungsoptionen: Die vollständige Suche nach Parametern oder den genetischen Algorithmus. Dieser Artikel schlägt eine neue Methode zur Optimierung von Handelsstrategien vor — Simuliertes Abkühlen (simulated annealing). Dabei werden der Algorithmus der Methode, ihre Implementierung und die Integration in jeden Expert Advisor besprochen. Als nächstes wird seine Eignung mit dem MovingAverage EA getestet, und die Ergebnisse der simulierten Abkühlung werden mit denen des genetischen Algorithmus verglichen.
Der Algorithmus der simulierten Abkühlung
Die simulierte Abkühlung ist eine der Methoden der stochastischen Optimierung. Es ist eine geordnete Zufallssuche nach dem Optimum der Zielfunktion.
Die simulierte Abkühlung basiert auf der Simulation der Bildung einer Kristallstruktur in einer Substanz. Atome in einem Kristallgitter einer Substanz (z.B. eines Metalls) können entweder in einen Zustand mit einem niedrigeren Energieniveau eintreten oder bei abnehmender Temperatur an Ort und Stelle bleiben. Die Wahrscheinlichkeit, in einen neuen Zustand zu wechseln, sinkt proportional zur Temperatur. Das Minimum oder das Maximum der Zielfunktion wird durch die Simulation eines solchen Prozesses ermittelt.
Der Prozess der Suche nach dem Optimum der Zielfunktion kann wie folgt dargestellt werden:

Abb. 1. Suche nach dem Optimum der Zielfunktion
In Abbildung 1 sind die Werte der Zielfunktion als Kugel, die auf einer unebenen Oberfläche rollt, dargestellt. Die blaue Kugel zeigt den Anfangswert der Zielfunktion, die grüne den Endwert (globales Minimum). Rote Kugeln sind die Funktionswerte der lokalen Minima. Die simulierte Abkühlung versucht, das globale Extremum der Zielfunktion zu finden und zu vermeiden, dass es in einem lokalen Extremum "hängenbleibt". Die Wahrscheinlichkeit, dem lokalen Extremum zu entkommen, nimmt ab, wenn man sich dem globalen Extremum nähert.
Betrachten wir die Schritte der simulierten Abkühlung. Der Übersichtlichkeit halber wird die Suche nach dem globalen Minimum der Zielfunktion berücksichtigt. Für die simulierte Abkühlung gibt es 3 Hauptanwendungsoptionen: Boltzmannsches Abkühlen, Cauchysches Abkühlen (schnelles Abkühlen), Ultraschnelles Abkühlen. Der Unterschied zwischen ihnen liegt in der Berechnung des eines neuen Punktes x(i) und dem Temperaturabsenkungsgesetz.
Hier sind die Variablen, die im Algorithmus verwendet werden:
- Fopt — optimaler Wert der Zielfunktion;
- Fbegin — Anfangswert der Zielfunktion;
- x(i) — Wert des aktuellen Punktes (der Wert der Zielfunktion hängt von diesem Parameter ab);
- F(x(i)) — Wert der Zielfunktion für den Punkt x(i);
- i — Iterationszähler;
- T0 — Anfangstemperatur;
- T — aktuelle Temperatur;
- Xopt — Wert des Parameters, bei dem das Optimum der Zielfunktion erreicht wird;
- Tmin — der minimale Temperaturwert;
- Imax — die maximale Anzahl der Iterationen.
Der Algorithmus der Abkühlung besteht aus den folgenden Schritten:
- Schritt 0. Initialisierung des Algorithmus: Fopt = Fbegin, i=0, T=T0, Xopt = 0.
- Schritt 1. Zufallsauswahl des aktuellen Punktes x(0) und Berechnung der Zielfunktion F(x(0)) für den gegebenen Punkt. Wenn F(x(0))<Fbegin, dann Fopt=F(x(0)).
- Schritt 2. Generierung des neuen Punktes x(i).
- Schritt 3. Berechnung der Zielfunktion F(x(i)).
- Schritt 4. Überprüfen wir den Übergang in einen neuen Zustand. Als nächstes werden zwei Modifikationsalgorithmen betrachtet:
- a). Wenn ein Übergang in einen neuen Zustand stattgefunden hat, verringern wir die aktuelle Temperatur und fahren mit Schritt 5 fort, andernfalls mit Schritt 2.
- b). Unabhängig vom Ergebnis der Überprüfung des Übergangs in einen neuen Zustand, verringern wir die aktuelle Temperatur und fahren mit Schritt 5 fort.
- Schritt 5. Überprüfen wir, ob das Ausgangskriterium des Algorithmus erfüllt ist (die Temperatur hat den Minimalwert von Tmin oder die angegebene Anzahl von Iterationen Imax erreicht). Wenn das Ausgangskriterium des Algorithmus nicht erfüllt ist: Erhöhen wir den Iterationszähler (i=i+1) und fahren wir mit Schritt 2 fort.
Betrachten wir jeden einzelnen Schritt genauer, um das Minimum der Zielfunktion zu finden.
Schritt 0. Den Variablen, deren Werte während des Betriebs des Algorithmus geändert werden, werden Initialwerte zugewiesen.
Schritt 1. Der aktuelle Punkt ist ein Wert des EA-Parameters, der optimiert werden muss. Es kann mehrere solcher Parameter geben. Jedem Parameter wird ein Zufallswert zugewiesen, der gleichmäßig über das Intervall von Pmin bis Pmax mit dem angegebenen Step verteilt ist (Pmin, Pmax sind die Minimal- und Maximalwerte des optimierten Parameters). Im Tester wird ein einziger Durchlauf des EA mit den generierten Parametern durchgeführt und der Wert der Zielfunktion F(x(0)) berechnet, der das Ergebnis der EA-Parameteroptimierung (der Wert des angegebenen Optimierungskriteriums) ist. Wenn F(x(0))<Fbegin, Fopt=F(x(0)).
Schritt 2. Die Generierung eines neuen Punktes in Abhängigkeit von der Implementierungsvariante des Algorithmus erfolgt nach den Formeln in Tabelle 1.
Tabelle 1
| Implementierung einer Variante des Algorithmus | Formeln zur Berechnung des neuen Anfangspunktes. |
|---|---|
| Boltzmannsches Abkühlen | |
| Cauchysches Abkühlen (schnelles Abkühlen) | |
| Ultraschnelles Abkühlen | die Variable  |
Step 3. Mit den in Schritt 2 generierten Parametern wird ein Testlauf des EA durchgeführt. Der Zielfunktion F(x(i)) wird der Wert des gewählten Optimierungskriteriums zugewiesen.
Schritt 4. Die Prüfung auf Übergang in einen neuen Zustand wird wie folgt durchgeführt:
- Schritt 1. Wenn F(x(i))<Fopt, wechseln wir in einen neuen Zustand Xopt =x(i), Fopt=F(x(i)), andernfalls fahren wir mit Schritt 2 fort.
- Schritt 2. Erzeugen wir eine Zufallsvariable a, die gleichmäßig über das Intervall von[0,1] verteilt ist.
- Schritt 3. Berechnen wir die Wahrscheinlichkeit des Übergangs in einen neuen Zustand:
- Schritt 4. Wenn P>a, wechseln wir in einen neuen Zustand Xopt =x(i), Fopt=F(x(i)); andernfalls, wenn die Modifikation а) des Algorithmus ausgewählt ist, fahren wir mit Schritt 2 fort.
- Schritt 5. Verringern wir die aktuelle Temperatur mit Hilfe der Formeln in Tabelle 2.
Tabelle 2
| Implementierung einer Variante des Algorithmus | Formel für das Absenken der Temperatur |
|---|---|
| Boltzmannsches Abkühlen |
|
| Cauchysches Abkühlen (schnelles Abkühlen) | |
| Ultraschnelles Abkühlen | wobei c(i)>0 nach folgender Formel berechnet wird: Der Einfachheit halber ändern sich die Werte von m(i) und p(i) nicht, während der Algorithmus läuft: m(i)=const, p(i) = const |
Schritt 5. Der Algorithmus wird beendet, wenn folgende Bedingungen erfüllt sind: T(i)<=Tmin oder i=Imax.
- Wenn wir das Temperaturänderungsgesetz wählen, bei dem die Temperatur rapide sinkt, ist es vorzuziehen, den Algorithmus zu beenden, wenn T(i)<=Tmin, ohne zu warten, bis alle Iterationen abgeschlossen sind.
- Sinkt die Temperatur sehr langsam ab, wird der Algorithmus verlassen, sobald die maximale Anzahl der Iterationen erreicht ist. In diesem Fall ist es wahrscheinlich notwendig, die Parameter des Temperaturabsenkungsgesetzes zu ändern.
Nachdem wir alle Schritte des Algorithmus im Detail betrachtet haben, lassen wir uns mit seiner Implementierung in MQL5 fortfahren.
Implementierung des Algorithmus
Betrachten wir die Implementierung und das Verfahren der Integration des Algorithmus in einen Experten mit den zu optimierenden Parametern.
Die Implementierung des Algorithmus erfordert zwei neue Klassen, die in den optimierten Expert Advisor aufgenommen werden sollten:
- Die Klasse AnnealingMethod.mqh — sie enthält eine Reihe von Methoden, die separate Schritte des Algorithmus implementieren;
- Die Klasse FrameAnnealingMethod.mqh — enthält Methoden zur Bedienung der grafischen Oberfläche, die im Chart des Terminals angezeigt werden.
Außerdem erfordert der Betrieb des Algorithmus, dass zusätzlicher Code in die OnInit-Funktion aufgenommen wird und die Funktionen OnTester, OnTesterInit, OnTesterDeInit, OnTesterDeInit, OnTesterPass zum EA-Code hinzugefügt werden. Der Prozess der Integration des Algorithmus in einen Experten ist in Abb. 2 dargestellt.
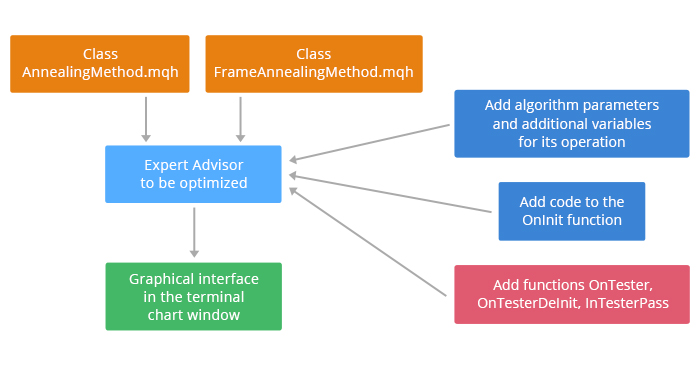
Abb. 2. Das Einbinden des Algorithmus in den Expert Advisor
Beschreiben wir nun die Klassen AnnealingMethod und FrameAnnealingMethod.
Die Klasse AnnealingMethod
Hier ist die Beschreibung der Klasse AnnealingMethod mit weiteren Details ihrer Methoden.
#include "Math/Alglib/alglib.mqh" //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class AnnealingMethod { private: CAlglib Alg; // Instanz der Klasse mit den Methoden aus Alglib CHighQualityRandStateShell state; // Instanz der Klasse für Zufallszahlen public: AnnealingMethod(); ~AnnealingMethod(); struct Input // Struktur für den EA { int num; double Value; double BestValue; double Start; double Stop; double Step; double Temp; }; uint RunOptimization(string &InputParams[],int count,double F0,double T); uint WriteData(Input &InpMass[],double F,int it); uint ReadData(Input &Mass[],double &F,int &it); bool GetParams(int Method,Input &Mass[]); double FindValue(double val,double step); double GetFunction(int Criterion); bool Probability(double E,double T); double GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2); double UniformValue(double min,double max,double step); bool VerificationOfVal(double start,double end,double val); double Distance(double a,double b); };
Funktionen aus der ALGLIB-Bibliothek, die für die Arbeit mit den Zufallsvariablen vorgesehen sind, werden im Betrieb der Methoden der Klasse AnnealingMethod verwendet. Diese Bibliothek ist Teil des Standardpakets MetaTrader 5 und befindet sich im Ordner "Include/Math/Alglib", wie unten gezeigt:
Abb. 3. Die Bibliothek ALGLIB
Der "private" Block enthält Deklarationen der Klasseninstanzen CAlglib und CHighQualityRandStateShell für die Arbeit mit den ALGLIB-Funktionen.
Um mit den optimierten Parametern des EA zu arbeiten, wurde die Struktur Input erstellt, die folgendes speichert:
- Parameter-Nummer, num;
- Aktueller Wert des Parameters, Value;
- Der beste Wert des Parameters, BestValue;
- Anfangswert, Start;
- Endwert, Stop;
- Schrittweite zum Ändern des Parameterwertes, Step;
- Aktuelle Temperatur für den angegebenen Parameter, Temp.
Betrachten wir die Methoden der Klasse AnnealingMethod.mqh.
Die RunOptimization-Methode
Entwickelt, um die simulierte Abkühlung zu initialisieren. Der Code dieser Methode:
uint AnnealingMethod::RunOptimization(string &InputParams[],int count,double F0,double T) { Input Mass[]; ResetLastError(); bool Enable=false; double Start= 0; double Stop = 0; double Step = 0; double Value= 0; int j=0; Alg.HQRndRandomize(&state); // Initialisierung for(int i=0;i<ArraySize(InputParams);i++) { if(!ParameterGetRange(InputParams[i],Enable,Value,Start,Step,Stop)) return GetLastError(); if(Enable) { ArrayResize(Mass,ArraySize(Mass)+1); Mass[j].num=i; Mass[j].Value=UniformValue(Start,Stop,Step); Mass[j].BestValue=Mass[j].Value; Mass[j].Start=Start; Mass[j].Stop=Stop; Mass[j].Step=Step; Mass[j].Temp=T*Distance(Start,Stop); j++; if(!ParameterSetRange(InputParams[i],false,Value,Start,Stop,count)) return GetLastError(); } else InputParams[i]=""; } if(j!=0) { if(!ParameterSetRange("iteration",true,1,1,1,count)) return GetLastError(); else return WriteData(Mass,F0,1); } return 0; }
Die Eingabeparameter der Methode:
- String-Array mit Namen aller Parameter des Expert Advisor, InputParams[];
- Die Anzahl der Iterationen des Algorithmus, count;
- Anfangswert der Zielfunktion, F0;
- Anfangstemperatur, T.
Die RunOptimization-Methode funktioniert wie folgt:
- Es sucht nach den zu optimierenden EA-Parametern. Solche Parameter sollten in der Registerkarte "Parameter" des Strategie-Testers "angekreuzt" werden:
- Die Werte von jedem gefundenen Parameter werden im Array Mass[] mit der Typstruktur von Input gespeichert, und der Parameter wird von der Optimierung ausgeschlossen. Die Strukturen Array Masse[] speichert:
- Parameter-Nummer
- Parameterwert, der durch die Methode UniformValue erzeugt wird (siehe unten);
- Die maximalen (Start) und maximalen (Stop) Werte des Parameters;
- Schrittweite zum Ändern des Parameterwertes, (Step);
- Die Anfangstemperatur wird nach der Formel: T*Distance(Start,Stop) berechnet; die Methode Distance wird weiter unten beschrieben.
- Nach Abschluss der Suche werden alle Parameter deaktiviert und der Parameter iteration aktiviert, der die Anzahl der Iterationen des Algorithmus bestimmt;
- Werte des Arrays Mass[], die Zielfunktion und die Iterationsnummer werden mit der Methode WriteData in eine Binärdatei geschrieben.
Die Methode WriteData
Entwickelt, um das Array von Parametern, Werten der Zielfunktion und der Iterationsnummer in eine Datei zu schreiben.
Der Code der Methode WriteData:
uint AnnealingMethod::WriteData(Input &Mass[],double F,int it) { ResetLastError(); int file_handle=0; int i=0; do { file_handle=FileOpen("data.bin",FILE_WRITE|FILE_BIN); if(file_handle!=INVALID_HANDLE) break; else { Sleep(MathRand()%10); i++; if(i>100) break; } } while(file_handle==INVALID_HANDLE); if(file_handle!=INVALID_HANDLE) { if(FileWriteArray(file_handle,Mass)<=0) {FileClose(file_handle); return GetLastError();} if(FileWriteDouble(file_handle,F)<=0) {FileClose(file_handle); return GetLastError();} if(FileWriteInteger(file_handle,it)<=0) {FileClose(file_handle); return GetLastError();} } else return GetLastError(); FileClose(file_handle); return 0; }
Die Daten werden mit den Funktionen FileWriteArray, FileWriteDouble und FileWriteInteger in die Datei data.bin geschrieben. Die Methode implementiert die Möglichkeit, mehrfach auf die Datei data.bin zuzugreifen. Dies geschieht, um Fehler beim Zugriff auf die Datei zu vermeiden, wenn die Datei von einem anderen Prozess belegt ist.
Die Methode ReadData
Entwickelt, um das Array von Parametern, Werten der Zielfunktion und der Iterationsnummer aus einer Datei zu lesen. Code der Methode ReadData:
uint AnnealingMethod::ReadData(Input &Mass[],double &F,int &it) { ResetLastError(); int file_handle=0; int i=0; do { file_handle=FileOpen("data.bin",FILE_READ|FILE_BIN); if(file_handle!=INVALID_HANDLE) break; else { Sleep(MathRand()%10); i++; if(i>100) break; } } while(file_handle==INVALID_HANDLE); if(file_handle!=INVALID_HANDLE) { if(FileReadArray(file_handle,Mass)<=0) {FileClose(file_handle); return GetLastError();} F=FileReadDouble(file_handle); it=FileReadInteger(file_handle); } else return GetLastError(); FileClose(file_handle); return 0; }
Die Daten werden mit den Funktionen FileReadArray, FileReadDouble, FileReadInteger in der gleichen Reihenfolge wie mit der Methode WriteData geschrieben.
Die Methode GetParams
Die Methode GetParams wurde entwickelt, um die neuen Werte der optimierten Parameter des Experten für den nächsten Lauf des EA zu berechnen. Formeln zur Berechnung der neuen Werte der optimierten Parameter des Experten finden wir in Tabelle 1.
Die Eingabeparameter der Methode:
- Variante der Algorithmus-Implementierung (Boltzmannsches Abkühlen, Cauchysches Abkühlen, Ultraschnelles Abkühlen);
- Array mit optimierten Parametern vom Typ Input;
- Koeffizient CoeffTmin für die Berechnung der Mindesttemperatur zum Beenden des Algorithmus.
Code der Methode GetParams:
bool AnnealingMethod::GetParams(int Method,Input &Mass[],double CoeffTmin) { double delta=0; double x1=0,x2=0; double count=0; Alg.HQRndRandomize(&state); // Initialisierung switch(Method) { case(0): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count= 0; break; } count++; delta=Mass[i].Temp*Alg.HQRndNormal(&state); delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } // while((delta<Mass[i].Start) || (delta>Mass[i].Stop)); while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } case(1): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count=0; break; } count++; Alg.HQRndNormal2(&state,x1,x2); delta=Mass[i].Temp*x1/x2; delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } case(2): { for(int i=0;i<ArraySize(Mass);i++) { if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop)) { do { if(count==100) { delta=Mass[i].Value; count=0; break; } count++; x1=Alg.HQRndUniformR(&state); if(x1-0.5>0) delta=Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop); else { if(x1==0.5) delta=0; else delta=-Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop); } delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step); } while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta)); Mass[i].Value=delta; } } break; } default: { Print("Annealing method was chosen incorrectly"); return false; } } return true; }
Betrachten wir den Code dieser Methode genauer.
Diese Methode verfügt über einen Umschalter zum Starten der Berechnung neuer Parameterwerte in Abhängigkeit von der gewählten Algorithmus-Implementierungsvariante. Die neuen Parameterwerte werden nur berechnet, wenn die aktuelle Temperatur über dem Minimum liegt. Die minimale Temperatur wird nach der Formel: CoeffTmin*Distance(Start,Stop) berechnet, wobei Start und Stop die minimalen und maximalen Werte des Parameters sind. Die Methode Distanz ird weiter unten beschrieben.
Die Methode HQRndRandomize der Klasse CAlglib wird aufgerufen, um die Methoden zum Arbeiten mit Zufallszahlen zu initialisieren.
Alg.HQRndRandomize(&state);
Die Funktion HQRndNormal der Klasse CAlglib wird zur Berechnung des Wertes der Standardnormalverteilung verwendet:
Alg.HQRndNormal(&state);
Die Cauchy-Verteilungen können auf verschiedene Weise modelliert werden, z.B. durch Normalverteilung oder inverse Funktionen. Das folgende Verhältnis wird verwendet:
C(0,1)=X1/X2, wobei X1 und X2 normalverteilte unabhängige Variablen sind, X1,X2 = N(0,1). Die Funktion HQRndNormal2 der Klasse CAlglib wird verwendet, um zwei normalverteilte Variablen zu erzeugen:
Alg.HQRndNormal2(&state,x1,x2);
Werte von normalverteilten unabhängigen Variablen werden in x1, x2 gespeichert.
Die Methode HQRndUniformR(&state) der Klasse CAlglib erzeugt eine Zufallszahl, gleichmäßig verteilt im Intervall von 0 bis 1:
Alg.HQRndUniformR(&state);
Mit der Methode FindValue (siehe unten) wird der berechnete Parameterwert auf den angegebenen Schritt zur Änderung des Parameters gerundet. Überschreitet der berechnete Parameterwert den Änderungsbereich der Parameter (geprüft durch die Methode VerificationOfVal), wird er neu berechnet.
Die Methode FindValue
Der Wert jedes optimierten Parameters sollte mit dem angegebenen Schritt geändert werden. Ein neuer Wert, der in GetParams erzeugt wurde, könnte diese Bedingung nicht erfüllen und muss dann auf ein Vielfaches der angegebenen Schrittweite gerundet werden. Dies geschieht mit der Methode FindValue. Eingabeparameter der Methode: der zu rundende Wert (val) und der Schrittweite zum Ändern des Parameters (step).
Hier ist der Code der Methode FindValue:
double AnnealingMethod::FindValue(double val,double step) { double buf=0; if(val==step) return val; if(step==1) return round(val); else { buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step); if(MathAbs(val)-buf*MathAbs(step)>=MathAbs(step)/2) { if(val<0) return -(buf + 1)*MathAbs(step); else return (buf + 1)*MathAbs(step); } else { if(val<0) return -buf*MathAbs(step); else return buf*MathAbs(step); } } }
Betrachten wir den Code dieser Methode genauer.
Wenn der Schritt gleich dem Eingabewert des Parameters ist, gibt die Funktion diesen Wert zurück:
if(val==step) return val;
Ist der Schritt 1, muss der Eingabewert des Parameters nur auf die ganze Zahl gerundet werden:
if(step==1) return round(val);
Ansonsten finden wir die Anzahl der Schritte im Eingabewert des Parameters:
buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);
und berechnen wir einen neuen Wert, der ein Vielfaches des Schrittes ist.
Die Methode GetFunction
Die Methode GetFunction wurde entwickelt, um den neuen Wert der Zielfunktion zu erhalten. Der Eingabeparameter der Methode ist das benutzerdefinierte Optimierungskriterium.
Abhängig vom gewählten Berechnungsmodus übernimmt die Zielfunktion den Wert eines oder mehrerer statistischer Parameter, die aus den Testergebnissen berechnet werden. Der Code dieser Methode:
double AnnealingMethod::GetFunction(int Criterion) { double Fc=0; switch(Criterion) { case(0): return TesterStatistics(STAT_PROFIT); case(1): return TesterStatistics(STAT_PROFIT_FACTOR); case(2): return TesterStatistics(STAT_RECOVERY_FACTOR); case(3): return TesterStatistics(STAT_SHARPE_RATIO); case(4): return TesterStatistics(STAT_EXPECTED_PAYOFF); case(5): return TesterStatistics(STAT_EQUITY_DD);//min case(6): return TesterStatistics(STAT_BALANCE_DD);//min case(7): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_PROFIT_FACTOR); case(8): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_RECOVERY_FACTOR); case(9): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_SHARPE_RATIO); case(10): return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_EXPECTED_PAYOFF); case(11): { if(TesterStatistics(STAT_BALANCE_DD)>0) return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_BALANCE_DD); else return TesterStatistics(STAT_PROFIT); } case(12): { if(TesterStatistics(STAT_EQUITY_DD)>0) return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_EQUITY_DD); else return TesterStatistics(STAT_PROFIT); } case(13): { // Angabe eines nutzerspezifischen Kriteriums, zum Beispiel return TesterStatistics(STAT_TRADES)*TesterStatistics(STAT_PROFIT); } default: return -10000; } }
Wie wir dem Code entnehmen können, sind 14 Möglichkeiten zur Berechnung der Zielfunktion in der Methode implementiert. Das heißt, der Anwender kann einen Experten durch verschiedene statistische Parameter optimieren. Die detaillierte Beschreibung der statistischen Parameter finden wir in der Dokumentation.
Die Methode Probability
Die Methode Probability wurde entwickelt, um einen Übergang in einen neuen Zustand zu identifizieren. Eingabeparameter der Methode: Differenz zwischen dem vorherigen und dem aktuellen Wert der Zielfunktion (E) und der aktuellen Temperatur (T). Der Code dieser Methode:
bool AnnealingMethod::Probability(double E,double T) { double a=Alg.HQRndUniformR(&state); double res=exp(-E/T); if(res<=a) return false; else return true; }
Die Methode erzeugt eine Zufallsvariable а, die gleichmäßig über das Intervall von 0 bis 1:<Segment 0594> verteilt ist.
a=Alg.HQRndUniformR(&state);
Der erhaltene Wert wird mit dem Ausdruck exp(-E/T) verglichen. Wenn a>exp(-E/T), dann gibt die Methode true zurück (Übergang in einen neuen Zustand wird durchgeführt).
Die Methode GetT
Die Methode GetT berechnet den neuen Temperaturwert. Die Eingabeparameter der Methode:
- Variante der Algorithmus-Implementierung (Boltzmannsches Abkühlen, Cauchysches Abkühlen, Ultraschnelles Abkühlen);
- Anfangswert der Temperatur, T0;
- Vorheriger Wert der Temperatur, Tlast;
- Iterationszahl, it;
- Die Anzahl der optimierten Parameter, D;
- Hilfsparameter p1 und p2 für das Ultraschnelle Abkühlen.
Der Code dieser Methode:
double AnnealingMethod::GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2) { int Iteration=0; double T=0; switch(Method) { case(0): { if(Tlast!=T0) Iteration=(int)MathRound(exp(T0/Tlast)-1)+1; else Iteration=1; if(Iteration>0) T=T0/log(Iteration+1); else T=T0; break; } case(1): { if(it!=1) Iteration=(int)MathRound(pow(T0/Tlast,D))+1; else Iteration=1; if(Iteration>0) T=T0/pow(Iteration,1/D); else T=T0; break; } case(2): { if((T0!=Tlast) && (-p1*exp(-p2/D)!=0)) Iteration=(int)MathRound(pow(log(Tlast/T0)/(-p1*exp(-p2/D)),D))+1; else Iteration=1; if(Iteration>0) T=T0*exp(-p1*exp(-p2/D)*pow(Iteration,1/D)); else T=T0; break; } } return T; }
Die Methode berechnet den neuen Temperaturwert abhängig von der Variante des nach den Formeln in Tabelle 2 implementierten Algorithmen. Um die Implementierung des Algorithmus zu berücksichtigen, der die Temperatur nur beim Übergang in einen neuen Zustand erhöht, wird die aktuelle Iteration mit dem vorherigen Temperaturwert Tlast berechnet. Dadurch wird die aktuelle Temperatur beim Aufruf der Methode verringert, unabhängig von der aktuellen Iteration des Algorithmus.
Die Methode UniformValue
Die Methode UniformValue erzeugt einen Zufallswert des optimierten Parameters unter Berücksichtigung seiner Minimal-, Maximalwerte und der Schrittweite. Die Methode wird nur während der Initialisierung des Algorithmus verwendet, um die Anfangswerte der optimierten Parameter zu erzeugen. Die Eingabeparameter der Methode:
- Der maximale Parameterwert, max;
- Der minimale Parameterwert, min;
- Schrittweite zum Ändern des Parameters, step.
Der Code dieser Methode:
double AnnealingMethod::UniformValue(double min,double max,double step) { Alg.HQRndRandomize(&state); //Initialisierung if(max>min) return FindValue(Alg.HQRndUniformR(&state)*(max-min)+min,step); else return FindValue(Alg.HQRndUniformR(&state)*(min-max)+max,step); }
Die Methode VerificationOfVal
VerificationOfVal prüft, ob der angegebene Wert der Variablen (val) außerhalb des Bereichs (Anfang, Ende) liegt. Diese Methode wird in der Methode GetParams verwendet.
Der Code dieser Methode:
bool AnnealingMethod::VerificationOfVal(double start,double end,double val) { if(start<end) { if((val>=start) && (val<=end)) return true; else return false; } else { if((val>=end) && (val<=start)) return true; else return false; } }
Die Methode berücksichtigt, dass die Schrittweite Parameteränderung negativ sein kann und prüft daher die Bedingung "start<end".
Die Methode Distance
Die Methode Distance berechnet den Abstand zwischen zwei Parametern (a und b) und wird im Algorithmus zur Berechnung des Bereiches der Parameteränderungen mit dem Anfangswert von a und dem Endwert von b verwendet.
Der Code dieser Methode:
double AnnealingMethod::Distance(double a,double b) { if(a<b) return MathAbs(b-a); else return MathAbs(a-b); }
Die Klasse FrameAnnealingMethod
Die Klasse FrameAnnealingMethod wurde entwickelt, um den Ausführungsprozess des Algorithmus im Terminalfenster anzuzeigen. Hier ist die Beschreibung der Klasse FrameAnnealingMethod:
#include <SimpleTable.mqh> #include <Controls\BmpButton.mqh> #include <Controls\Label.mqh> #include <Controls\Edit.mqh> #include <AnnealingMethod.mqh> //+------------------------------------------------------------------+ //| Klasse zur Ausgabe der Ergebnisse der Optimierungen | //+------------------------------------------------------------------+ class FrameAnnealingMethod { private: CSimpleTable t_value; CSimpleTable t_inputs; CSimpleTable t_stat; CBmpButton b_playbutton; CBmpButton b_backbutton; CBmpButton b_forwardbutton; CBmpButton b_stopbutton; CLabel l_speed; CLabel l_stat; CLabel l_value; CLabel l_opt_value; CLabel l_temp; CLabel l_text; CLabel n_frame; CEdit e_speed; long frame_counter; public: //--- Constructor/Destructor FrameAnnealingMethod(); ~FrameAnnealingMethod(); //--- Events of the strategy tester void FrameTester(double F,double Fbest,Input &Mass[],int num,int it); void FrameInit(string &SMass[]); void FrameTesterPass(int cr); void FrameDeinit(void); void FrameOnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam,int cr); uint FrameToFile(int count); };
Die Klasse FrameAnnealingMethod enthält die folgenden Methoden:
- FrameInit — erstellt eine grafische Oberfläche im Terminalfenster;
- FrameTester — fügt den aktuellen Datenrahmen hinzu;
- FrameTesterPass — gibt den aktuellen Datenrahmen im Terminalfenster aus;
- FrameDeInit — zeigt die Textinformationen über die Beendigung der Optimierung des Experten an;
- FrameOnChartEvent — behandelt die Ereignisse eines Tastendrucks;
- FrameToFile — speichert die Testergebnisse in eine Textdatei.
Der Code der Methoden ist in der Datei FrameAnnealingMethod.mqh (dem Artikel beigefügt) enthalten. Bitte beachten Sie, dass die SimpleTable.mqh-Datei (im Anhang des Artikels) erforderlich ist, damit die Methoden der Klasse FrameAnnealingMethod funktionieren. Kopieren wir sie in MQL5/Include. Die Datei wurde aus diesem Projekt übernommen und mit der GetValue-Methode ergänzt, die das Lesen eines Wertes aus einer Tabellenzelle ermöglicht.
Hier ist ein Beispiel für eine grafische Oberfläche, die im Terminalfenster mit der Klasse FrameAnnealingMethod erstellt wurde.
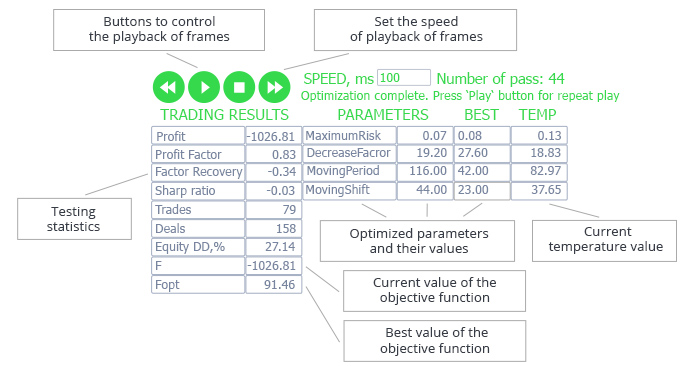
Abb. 4. Grafische Oberfläche zur Demonstration der Funktionsweise des Algorithmus
Die linke Seite der Tabelle enthält statistische Parameter, die vom Strategie-Tester auf der Grundlage der Ergebnisse des aktuellen Laufs generiert werden, sowie die aktuellen und die besten Werte der Zielfunktion (in diesem Beispiel wird der Nettogewinn als Zielfunktion gewählt).
Optimierte Parameter befinden sich auf der rechten Seite der Tabelle: Parametername, aktueller Wert, bester Wert, aktuelle Temperatur.
Über der Tabelle befinden sich Schaltflächen zur Steuerung der Wiedergabe von Frames nach der Ausführung des Algorithmus. So können wir nach Beendigung der Optimierung eines Experten diese mit der angegebenen Geschwindigkeit wiederholen. Mit den Schaltflächen können wir die Wiedergabe von Frames stoppen und wieder von dem Frame aus starten, in dem die Wiedergabe unterbrochen wurde. Die Wiedergabegeschwindigkeit kann mit den Tasten oder manuell eingestellt werden. Die Nummer des aktuellen Laufs wird rechts neben dem Geschwindigkeitswert angezeigt. Nachfolgend werden Zusatzinformationen zum Betrieb des Algorithmus angezeigt.
Die Klassen AnnealingMethod und FrameAnnealingMethod wurden beschrieben. Lassen wir uns nun den Algorithmus am Beispiel eines Expert Advisors anhand des gleitenden Mittelwerts testen.
Testen des Algorithmus auf dem EA basierend auf dem gleitenden Durchschnitt
Vorbereitung des EA zum Testen des Algorithmus
Der Code des Experten sollte geändert werden, um den Algorithmus auszuführen:
- Einbinden der Klassen AnnealingMethod und FrameAnnealingMethod und Deklarieren der Hilfsvariablen für das Funktionieren des Algorithmus;
- Einfügen des Codes in die Funktion OnInit, und der Funktionen OnTester, OnTesterInit, OnTesterDeInit, OnTesterPass, OnChartEvent.
Der hinzugefügte Code hat keinen Einfluss auf den EA und wird nur ausgeführt, wenn der EA im Strategie-Tester optimiert ist.
Fangen wir also an.
Binden wir die Datei mit den von der Funktion OnTesterInit erzeugten Anfangsparametern ein:
#property tester_file "data.bin"
Einbinden der Klassen AnnealingMethod und FrameAnnealingMethod auf:
// Einbinden der Klassen #include <AnnealingMethod.mqh> #include <FrameAnnealingMethod.mqh>
Deklarieren der Instanzen der eingebundenen Klassen:
AnnealingMethod Optim; FrameAnnealingMethod Frame;
Deklarieren der Hilfsvariablen für das Funktionieren des Algorithmus:
Input InputMass[]; // Array der Eingabeparameter string SParams[]; // Array der Namen der Eingabeparameter double Fopt=0; // Bestwert der Funktion int it_agent=0; // Iterationsnummer des Algorithmus des Testagenten uint alg_err=0; // Fehlernummer
Der Algorithmus der simulierte Abkühlung verändert die Variablen der zu optimierenden Parameter so lange er läuft. Dafür werden die Parameter des EAs umbenannt:
double MaximumRisk_Optim=MaximumRisk; double DecreaseFactor_Optim=DecreaseFactor; int MovingPeriod_Optim=MovingPeriod; int MovingShift_Optim=MovingShift;
Ersetzen wir in allen Funktionen des EA die Parameter: MaximumRisk mit MaximumRisk_Optim, DecreaseFactor mit DecreaseFactor_Optim, MovingPeriod mit MovingPeriod_Optim, MovingShift mit MovingShift_Optim.
Hier sind die Variablen für die Konfiguration der Funktionsweise des Algorithmus:
sinput int iteration=50; // Nummer de Iteration sinput int method=0; // 0 — Boltzmannsches Abkühlen, 1 — Cauchysches Abkühlen, 2 — Ultraschnelles Abkühlen sinput double CoeffOfTemp=1; // Koeffizient der Anfangstemperatur sinput double CoeffOfMinTemp=0; // Koeffizient der kleinsten Temperatur sinput double Func0=-10000; // Anfangswert der Zielfunktion sinput double P1=1; // zusätzliche Parameter für das Ultraschnelle Abkühlen, p1 sinput double P2=1; // zusätzliche Parameter für das Ultraschnelle Abkühlen, p2 sinput int Crit=0; // Methode der Zielfunktion sinput int ModOfAlg=0; // Typ der Algorithmusänderung sinput bool ManyPoint=false; // Optimierung mehrerer Punkte
Die Parameter des Algorithmus sollten sich während seines Betriebs nicht ändern; daher werden alle Variablen mit dem Identifikator sinput deklariert.
Tabelle 3 erläutert den Zweck der deklarierten Variablen.
Tabelle 3
| Variablenname | Zweck |
|---|---|
| iteration | Legt die Anzahl der Iterationen des Algorithmus fest. |
| method | Definiert die Variante der Algorithmus-Implementierung: 0 — Boltzmannsches Abkühlen, 1 — Cauchysches Abkühlen, 2 — Ultraschnelles Abkühlen |
| CoeffOfTemp | Definiert den Koeffizienten für die Einstellung der Anfangstemperatur, berechnet durch die Formel: T0=CoeffOfTemp*Distance(Start,Stop), wobei Start, Stop die minimalen und maximalen Werte des Parameters sind, Distance ist eine Methode der Klasse AnnealingMethod (siehe oben). |
| CoeffOfMinTemp | Definiert den Koeffizienten für die Einstellung der Mindesttemperatur zum Beenden des Algorithmus. Die maximale Temperatur wird ähnlich wie die Anfangstemperatur berechnet: Tmin=CoeffOfMinTemp*Distance(Start,Stop), wobei Start, Stop die minimalen und maximalen Werte des Parameters, Distance eine Methode der AnnealingMethod-Klasse ist (siehe oben). |
| Func0 | Anfangswert der Zielfunktion |
| P1,P2 | Parameter zur Berechnung der aktuellen Temperatur beim Ultraschnelles Abkühlen (siehe Tabelle 2) |
| Crit | Optimierungskriterium: 0 — Gesamter Jahresüberschuss; 1 — Profit Factor; 2 — Recovery Factor; 3 — Sharpe Ratio; 4 — Expected Payoff; 5 — Equity Drawdown Maximal; 6 — Balance Drawdown Maximal; 7 — Total Net Profit + Profit Factor; 8 — Total Net Profit + Recovery Factor; 9 — Total Net Profit + Sharpe Ratio; 10 — Total Net Profit + Expected Payoff; 11 — Total Net Profit + Balance Drawdown Maximal; 12 — Total Net Profit + Equity Drawdown Maximal; 13 — Custom criterion. Die Zielfunktion wird in der Methode GetFunction der Klasse AnnealingMethod berechnet. |
| ModOfAlg | Art der Algorithmusmodifikation: 0 — wenn ein Übergang in einen neuen Zustand stattgefunden hat, verringern wir die aktuelle Temperatur und fahren mit der Überprüfung des Algorithmus fort, andernfalls berechnen wir neuen Werte der optimierten Parameter. 1 — unabhängig vom Ergebnis der Prüfung des Übergangs in einen neuen Zustand, verringern wir die aktuelle Temperatur und fahren wir mit der Prüfung der Fertigstellung des Algorithmus fort. |
| ManyPoint | true — für jeden Testagenten werden unterschiedliche Anfangswerte der optimierten Parameter generiert, false — für jeden Testagenten werden dieselben Anfangswerte der optimierten Parameter generiert |
Fügen wir den Code zu Beginn der Funktion OnInit hinzu:
//+------------------------------------------------------------------+ //| Simuliertes Abkühlen | //+------------------------------------------------------------------+ if(MQL5InfoInteger(MQL5_OPTIMIZATION)) { // Datei öffnen und lesen // if(FileGetInteger("data.bin",FILE_EXISTS,false)) // { alg_err=Optim.ReadData(InputMass,Fopt,it_agent); if(alg_err==0) { // Wenn es der erste Lauf ist, zufälliges Generieren der Parameter, wenn die Suche von verschiedenen Stellen aus durchgeführt wird. if(Fopt==Func0) { if(ManyPoint) for(int i=0;i<ArraySize(InputMass);i++) { InputMass[i].Value=Optim.UniformValue(InputMass[i].Start,InputMass[i].Stop,InputMass[i].Step); InputMass[i].BestValue=InputMass[i].Value; } } else Optim.GetParams(method,InputMass,CoeffOfMinTemp); // Generieren neuer Parameter // Zuweisen der Parameter des Expert Advisors for(int i=0;i<ArraySize(InputMass);i++) switch(InputMass[i].num) { case (0): {MaximumRisk_Optim=InputMass[i].Value; break;} case (1): {DecreaseFactor_Optim=InputMass[i].Value; break;} case (2): {MovingPeriod_Optim=(int)InputMass[i].Value; break;} case (3): {MovingShift_Optim=(int)InputMass[i].Value; break;} } } else { Print("Error reading file"); return(INIT_FAILED); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
Betrachten wir den Code im Detail. Der hinzugefügte Code wird nur im Optimierungsmodus des Strategie-Testers ausgeführt:
if(MQL5InfoInteger(MQL5_OPTIMIZATION))
Anschließend werden die Daten aus der Datei data.bin gelesen, die von der RunOptimization-Methode der Klasse AnnealingMethod erzeugt wird. Diese Methode wird in der OnTesterInit-Funktion aufgerufen, der Funktionscode wird unten angezeigt.
alg_err=Optim.ReadData(InputMass,Fopt,it_agent);
Wurden die Daten fehlerfrei gelesen (alg_err=0), wird geprüft, ob sich der Algorithmus bei der ersten Iteration befindet (Fopt===Func0), ansonsten schlägt die EA-Initialisierung mit einem Fehler fehl. Wenn es die erste Iteration ist, und wenn ManyPoint = true, werden die Anfangswerte der optimierten Parameter erzeugt und in der Struktur InputMass des Typs Input (beschrieben in der Klasse AnnealingMethod) gespeichert, ansonsten wird die Methode GetParams aufgerufen.
Optim.GetParams(method,InputMass,CoeffOfMinTemp);// Generieren neuer Parameter
und die Werte der Parameter MaximumRisk_Optim, DecreaseFactor_Optim, MovingPeriod_Optim, MovingShift_Optim werden zugewiesen.
Betrachten wir nun den Code der Funktion OnTesterInit:
void OnTesterInit() { // Füllen des Arrays der Namen aller Parameter des EAs ArrayResize(SParams,4); SParams[0]="MaximumRisk"; SParams[1]="DecreaseFactor"; SParams[2]="MovingPeriod"; SParams[3]="MovingShift"; // Beginn der Optimierung Optim.RunOptimization(SParams,iteration,Func0,CoeffOfTemp); // Erstellen des grafischen Interfaces Frame.FrameInit(SParams); }
Wir Füllen zunächst das String-Array, das die Namen aller EA-Parameter enthält. Dann führen wir die Methode RunOptimization aus und erstellen wir eine grafische Oberfläche mit der Methode FrameInit.
Nach der Ausführung des EA im angegebenen Zeitintervall wird die Steuerung an die OnTester-Funktion übergeben. Das ist deren Code:
double OnTester() { int i=0; // Schleifenzähler int count=0; // Hilfsvariable // Prüfung auf Vollständigkeit des Algorithmus bei Erreichen der Mindesttemperatur for(i=0;i<ArraySize(InputMass);i++) if(InputMass[i].Temp<CoeffOfMinTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop)) count++; if(count==ArraySize(InputMass)) Frame.FrameTester(0,0,InputMass,-1,it_agent); // Hinzufügen eines neuen Frames ohne Parameter und id=-1 else { double Fnew=Optim.GetFunction(Crit); // Berechnen des aktuellen Wertes der Funktion if((Crit!=5) && (Crit!=6) && (Crit!=11) && (Crit!=12)) // Falls nötig, maximiere die Zielfunktion { if(Fnew>Fopt) Fopt=Fnew; else { if(Optim.Probability(Fopt-Fnew,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop))) Fopt=Fnew; } } else // Falls nötig, Minimieren der Zielfunktion { if(Fnew<Fopt) Fopt=Fnew; else { if(Optim.Probability(Fnew-Fopt,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop))) Fopt=Fnew; } } // Überschreiben der Bestwerte der Parameter if(Fopt==Fnew) for(i=0;i<ArraySize(InputMass);i++) InputMass[i].BestValue=InputMass[i].Value; // Absenken der Temperatur if(((ModOfAlg==0) && (Fnew==Fopt)) || (ModOfAlg==1)) { for(i=0;i<ArraySize(InputMass);i++) InputMass[i].Temp=Optim.GetT(method,CoeffOfTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop),InputMass[i].Temp,it_agent,ArraySize(InputMass),P1,P2); } Frame.FrameTester(Fnew,Fopt,InputMass,iteration,it_agent); // neuer Frame it_agent++; // Erhöhen des Iterationszählers alg_err=Optim.WriteData(InputMass,Fopt,it_agent); // Schreiben der neuen Werte in die Datei if(alg_err!=0) return alg_err; } return Fopt; }
Betrachten wir den Code dieser Funktion genauer.
- Er prüft, ob der Algorithmus abgeschlossen ist, wenn die Mindesttemperatur erreicht ist. Wenn die Temperatur jedes Parameters den Minimalwert erreicht hat, wird ein Frame mit id=-1 hinzugefügt, die Parameterwerte ändern sich nicht mehr. Die grafische Oberfläche im Terminalfenster fordert den Benutzer auf, die Optimierung durch Drücken der Schaltfläche "Stop" im Strategie-Tester abzuschließen.
- Die Methode GetFunction berechnet den neuen Wert der Zielfunktion Fnew anhand der Testergebnisse des Expert Advisor.
- Je nach Optimierungskriterium (siehe Tabelle 3) wird der Wert von Fnew mit dem besten Wert von Fopt verglichen und der Übergang in einen neuen Zustand geprüft.
- Ist ein Übergang in einen neuen Zustand erfolgt, werden die aktuellen Werte der optimierten Parameter als die besten eingestellt:
for(i=0;i<ArraySize(InputMass);i++) InputMass[i].BestValue = InputMass[i].Value;
- Die Bedingung für die Absenkung der aktuellen Temperatur wird überprüft. Ist sie erfüllt, wird die neue Temperatur mit der Methode GetT der Klasse AnnealingMethod berechnet.
- Ein neuer Rahmen wird hinzugefügt, die Werte der optimierten Parameter werden in die Datei geschrieben.
Die Funktion OnTester fügt Frames hinzu, die in der Funktion OnTesterPass weiterverarbeitet werden sollen. Das ist deren Code:
void OnTesterPass() { Frame.FrameTesterPass(Crit);// Methode zur Anzeige des Frames im grafischen Interface }
Die Funktion OnTesterPass ruft die Methode FrameTesterPass der Klasse FrameAnnealingMethod auf, um den Optimierungsprozess im Terminalfenster anzuzeigen.
Nach Abschluss der Optimierung wird die Funktion OnTesterDeInit aufgerufen:
void OnTesterDeinit() { Frame.FrameToFile(4); Frame.FrameDeinit(); }
Diese Funktion ruft zwei Methoden der Klasse FrameAnnealingMethod auf: FrameToFile und FrameDeinit. Die Methode FrameToFile schreibt die Optimierungsergebnisse in eine Textdatei. Diese Methode nimmt die Anzahl der zu optimierenden EA-Parameter als Eingabe. Die Methode FrameDeinit gibt eine Meldung über den Abschluss der Optimierung an das Terminalfenster aus.
Sobald die Optimierung abgeschlossen ist, ermöglicht die mit den Methoden der Klasse FrameAnnealingMethod erstellte grafische Oberfläche das Abspielen der Frames mit einer bestimmten Geschwindigkeit. Die Wiedergabe der Frames kann gestoppt und neu gestartet werden. Dies geschieht über die entsprechenden Schaltflächen der grafischen Oberfläche (siehe Abb. 4). Um die Ereignisse im Terminalfenster zu behandeln, wurde dem EA-Code die Methode OnChartEvent hinzugefügt:
void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam) { Frame.FrameOnChartEvent(id,lparam,dparam,sparam,Crit); // Methode für das Arbeiten mit dem grafischen Interface }
Die Methode OnChartEvent ruft die Methode FrameOnChartEvent der Klasse FrameAnnealingMethod auf, die die Wiedergabe von Frames im Terminalfenster verwaltet.
Damit ist die Änderung des MovingAverage EA-Codes abgeschlossen. Fangen wir an, den Algorithmus zu testen.
Testen des Algorithmus
Die vorgeschlagene simulierte Abkühlung hat einen stochastischen Charakter (sie enthält Funktionen zur Berechnung von Zufallsvariablen), daher wird jeder Durchlauf des Algorithmus zu einem anderen Ergebnis führen. Um das Funktionieren des Algorithmus zu testen und seine Vor- und Nachteile zu erkennen, ist es notwendig, die Experten-Optimierung mehrfach durchzuführen. Dies würde sehr viel Zeit in Anspruch nehmen, so dass folgende Schritte durchgeführt werden: Optimierung im Modus "Langsamer vollständiger Algorithmus" ausführen, die erhaltenen Ergebnisse speichern und den Algorithmus anhand dieser Daten testen.
Der Algorithmus wird mit dem TestAnnealing.mq5 Expert Advisor (in der Datei test.zip im Anhang des Artikels) getestet. Es lädt eine Tabelle der Optimierungsergebnisse aus einer Textdatei, die 5 Spalten mit Daten enthält: Die Spalten 1-4 stellen die Werte der Variablen dar, die Spalte 5 zeigt die Werte der Zielfunktion. Der in TestAnnealing implementierte Algorithmus verwendet die simulierte Abkühlung, um sich durch die Tabelle zu bewegen und die Werte der Zielfunktion zu finden. Dieser Testansatz ermöglicht es, die Leistung des simulierten Abkühlens an verschiedenen Daten zu überprüfen, die durch die vollständige Suche gewonnen wurden.
Also, fangen wir an. Testen wir zunächst die Leistung des Algorithmus, indem wir eine Variable des Experten — "Moving Average period" — optimieren.
Führen wir die Optimierung des Experten im kompletten Suchmodus mit den folgenden Anfangswerten der Parameter aus:
- Maximum Risk in percentage — 0.02; Decrease factor — 3; Moving Average period: 1 - 120, step: 1; Moving Average shift — 6.
- Zeitraum: 01.01.2017 — 31.12.2017, Handelsmodus: keine Verzögerung, Ticks: 1 Minute OHLC, Ersteinlage: 10000, Hebel: 1:100, Währung: EURUSD.
- Die Optimierung erfolgt nach dem Kriterium: Balance max.
Speichern wir das Ergebnis und erstellen wir eine Testdatei mit den erhaltenen Daten. Die Daten in der Textdatei werden aufsteigend nach dem Parameterwert "Moving Average period" sortiert, wie in Abb. 5 dargestellt.
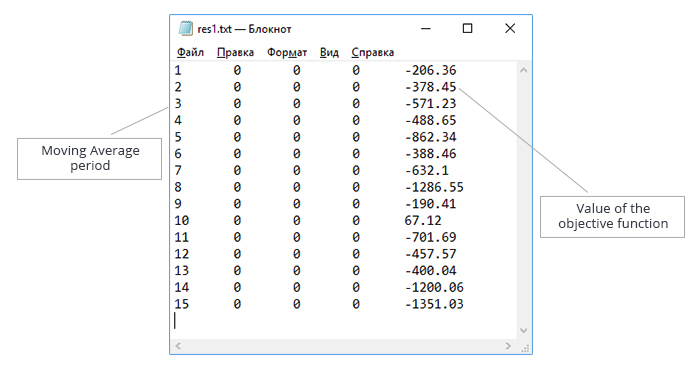
Abb. 5. Optimierung des Parameters "Moving Average period". Textdatei mit den Daten zum Testen des Algorithmus
120 Iterationen wurden im kompletten Suchmodus durchgeführt. Der Algorithmus der simulierten Abkühlung wird mit folgender Anzahl von Iterationen getestet: 30 (Variante 1), 60 (Variante 2), 90 (Variante 3). Hier geht es darum, die Performance des Algorithmus zu testen und gleichzeitig die Anzahl der Iterationen zu reduzieren.
Für jede Variante wurden 10000 Optimierungsläufe mit der simulierten Abkühlung auf den durch die vollständige Suche gewonnenen Daten durchgeführt. Der im Expert Advisor TestAnnealing.mq5 implementierte Algorithmus zählt, wie oft der beste Wert der Zielfunktion gefunden wurde und wie oft die Zielfunktionswerte um 5%, 10%, 15%, 20%, 25% von den besten abweichen.
Die folgenden Testergebnisse wurden erzielt.
Für 30 Iterationen des Algorithmus wurden die besten Werte durch das Ultraschnelle Abkühlen mit Temperaturabsenkung bei jeder Iteration erzielt:
| Abweichung vom Bestwert der Zielfunktion, % | Ergebnis, % |
|---|---|
| 0 | 33 |
| 5 | 44 |
| 10 | 61 |
| 15 | 61 |
| 20 | 72 |
| 25 | 86 |
Die Daten dieser Tabelle werden wie folgt interpretiert: der beste Wert der Zielfunktion wurde in 33% der Läufe erreicht (in 3.300 von 10.000 Läufen), 5% Abweichung vom besten Wert wurde in 44% der Läufe erreicht, und so weiter.
Für 60 Iterationen des Algorithmus ist das Cauchysches Abkühlen führend, aber die beste Variante war hier die Temperaturabsenkung beim Übergang in einen neuen Zustand. Die Ergebnisse sind wie folgt: Die Ergebnisse sind wie folgt:
| Abweichung vom Bestwert der Zielfunktion, % | Ergebnis, % |
|---|---|
| 0 | 47 |
| 5 | 61 |
| 10 | 83 |
| 15 | 83 |
| 20 | 87 |
| 25 | 96 |
So findet die simulierte Abkühlung bei halbierter Iterationszahl im Vergleich zur vollständigen Suche in 47% der Fälle den besten Wert der Zielfunktion.
Für 90 Iterationen oder den Algorithmus hatten Boltzmannsches Abkühlen und das Cauchysches Abkühlen mit Temperaturabsenkung beim Übergang in einen neuen Zustand ungefähr das gleiche Ergebnis. Hier sind die Ergebnisse für des Cauchyschen Abkühlens:
| Abweichung vom Bestwert der Zielfunktion, % | Ergebnis, % |
|---|---|
| 0 | 62 |
| 5 | 71 |
| 10 | 93 |
| 15 | 93 |
| 20 | 95 |
| 25 | 99 |
Bei einer um ein Drittel geringeren Iterationszahl im Vergleich zur vollständigen Suche findet das simulierte Abkühlen in 62% der Fälle den besten Wert der Zielfunktion. Es ist jedoch möglich, mit einer Abweichung von 10-15% durchaus akzeptable Ergebnisse zu erzielen.
Das Ultraschnelle Abkühlen wurde mit den Parametern p1=1, p2=1 getestet. Die Erhöhung der Anzahl der Iterationen hatte einen größeren negativen Einfluss auf das erzielte Ergebnis als das Boltzmannsche Abkühlen und das Cauchy abkühlen. Der Algorithmus des Ultraschnellen Abkühlens hat jedoch eine Besonderheit: Änderung der Koeffizienten p1, p2 erlaubt die Einstellung der Geschwindigkeit der Temperaturabsenkung.
Betrachten wir die Kurve der Temperaturänderung für das Ultraschnelle Abkühlen (Abb. 6):
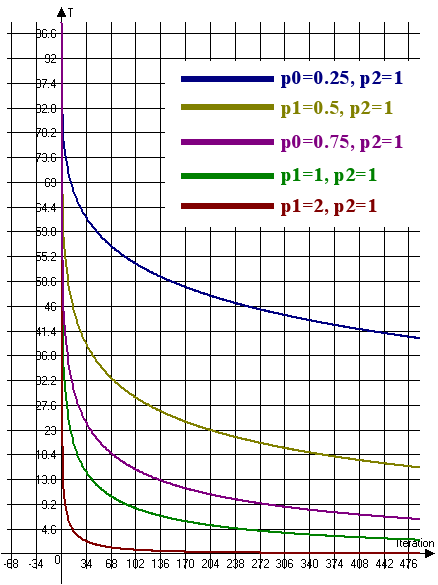
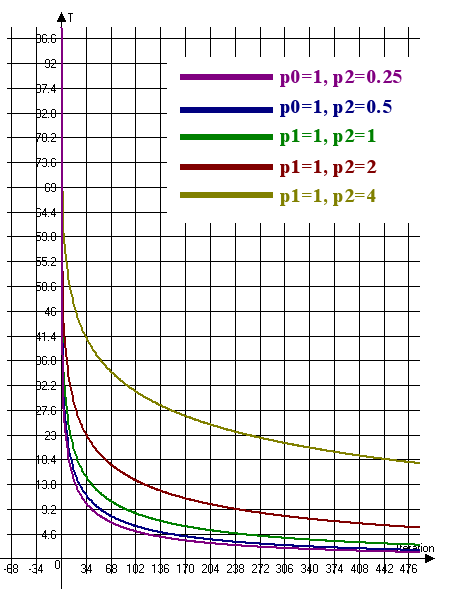
Abb. 6. Die Kurve der Temperaturänderung für das Ultraschnelle Abkühlen (T0=100, n=4)
Abb. 6 zeigt, dass es notwendig ist, den Koeffizienten p1 zu erhöhen und den Koeffizienten p2 zu verringern, um die Geschwindigkeit der Temperaturänderung zu verringern. Um die Geschwindigkeit der Temperaturänderung zu erhöhen, ist es daher notwendig, den Koeffizienten p1 zu verringern und den Koeffizienten p2 zu erhöhen.
Bei 60 und 90 Iterationen zeigte das Ultraschnelle Abkühlen die schlechtesten Ergebnisse, weil die Temperatur zu schnell fiel. Nach Verringerung des Koeffizienten p1 wurden folgende Ergebnisse erzielt:
| Anzahl der Iterationen | p1 | p2 | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|---|---|
| 60 | 0.5 | 1 | 57 | 65 | 85 | 85 | 91 | 98 |
| 90 | 0.25 | 1 | 63 | 78 | 93 | 93 | 96 | 99 |
Die Tabelle zeigt, dass der beste Wert der Zielfunktion in 57% der Läufe bei 60 Iterationen und in 63% der Läufe bei 90 Iterationen erreicht wurde.
So wurde das beste Ergebnis bei der Optimierung eines Parameters durch das Ultraschnelle Abkühlen erzielt. Es ist jedoch notwendig, die Koeffizienten p1 und p2 in Abhängigkeit von der Anzahl der Iterationen zu wählen.
Wie bereits erwähnt, ist das simulierte Abkühlen stochastisch, so dass es mit der Zufallssuche verglichen wird. Dazu wird bei jeder Iteration ein Zufallswert eines Parameters mit einem bestimmten Schritt und in einem bestimmten Bereich erzeugt. In diesem Fall werden die Werte des Parameters "Gleitender Durchschnitt" mit einem Schritt von 1 im Bereich von 1 bis 120 erzeugt.
Die Zufallssuche wurde unter den gleichen Bedingungen wie das simulierte Abkühlen durchgeführt:
- Anzahl der Iterationen: 30, 60, 90
- Anzahl der Durchläufe in jeder Variante: 10000
Die Ergebnisse der Zufallssuche sind in der folgenden Tabelle dargestellt:
| Anzahl der Iterationen | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 30 | 22 | 40 | 54 | 54 | 64 | 84 |
| 60 | 40 | 64 | 78 | 78 | 87 | 97 |
| 90 | 52 | 78 | 90 | 90 | 95 | 99 |
Vergleichen wir die Ergebnisse der Zufallssuche und des Ultraschnellen Abkühlens. Die Tabelle zeigt den prozentualen Anstieg zwischen den entsprechenden Werten der Zufallssuche und des Ultraschnellen Abkühlens. Zum Beispiel, bei 30 Iterationen, ist das Ultraschnelle Abkühlen 50% besser, um den besten Wert der Funktion zu finden, als die zufällige Suche.
| Anzahl der Iterationen | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 30 | 50 | 10 | 12.963 | 12.963 | 12.5 | 2.381 |
| 60 | 42.5 | 1.563 | 8.974 | 8.974 | 4.6 | 1.031 |
| 90 | 21.154 | 0 | 3.333 | 3.333 | 1.053 | 0 |
Die Tabelle zeigt, dass die Erhöhung der Anzahl der Iterationen den Vorteil des Ultraschnellen Abkühlens reduziert.
Lassen wir uns nun den Algorithmus zur Optimierung von zwei Parametern des Expert Advisors, "Moving Average period" und "Moving Average shift", testen. Erzeugen wir zunächst die Eingabedaten, indem wir die langsame, komplette Suche im Strategie-Tester mit den folgenden Parametern durchführen:
- Maximum Risk in percentage — 0.02; Decrease factor — 3; Moving Average period: 1-120; Moving Average shift - 6-60.
- Zeitraum: 01.01.2017 — 31.12.2017, Handelsmodus: keine Verzögerung, Ticks: 1 Minute OHLC, Ersteinlage: 10000, Hebel: 1:100, Währung: EURUSD
- Die Optimierung erfolgt nach dem Kriterium: Balance max.
Speichern wir das Ergebnis und erstellen wir eine Testdatei mit den erhaltenen Daten. Die Daten in der Textdatei werden in aufsteigender Reihenfolge des Parameters "Moving Average period" sortiert. Die erzeugte Datei ist in Abb. 7 dargestellt.
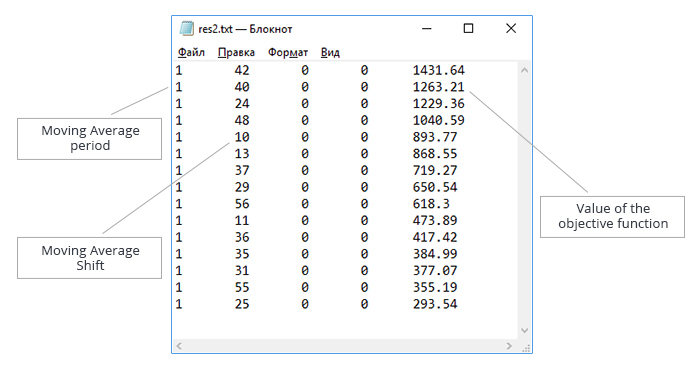
Abb. 7. Optimierung der Parameter von "Moving Average period" und "Moving Average shift". Textdatei mit den Daten zum Testen des Algorithmus
Die langsame vollständige Suche nach zwei Variablen erfolgt in 6.600 Iterationen. Wir werden versuchen, diese Zahl durch simuliertes Abkühlen zu reduzieren. Testen wir den Algorithmus mit folgender Anzahl von Iterationen: 330, 660, 1665, 3300, 4950. Die Anzahl der Läufe in jeder Variante: 10000.
Die Testergebnisse sind wie folgt.
330 Iterationen: Cauchysches Abkühlen zeigte gute Ergebnisse, aber das beste Ergebnis wurde durch Ultraschnelles Abkühlen mit Temperaturabsenkung bei jeder Iteration und Koeffizienten p1=1, p2=1 erreicht.
660 Iterationen: Die Ergebnisse des Cauchyschens Abkühlen mit Temperaturabsenkung bei jeder Iteration und den Koeffizienten p1=1, p2=1 zeigten ungefähr die gleichen Ergebnisse.
Bei den Iterationen 1665, 3300 und 4950 wurde das beste Ergebnis durch Ultraschnelles Abkühlen mit Temperaturabsenkung bei jeder Iteration und den folgenden Werten der Koeffizienten p1 und p2 erzielt:
- 1665 Iterationen: p1= 0.5, p2=1
- 3300 Iterationen: p1= 0,25, p2=1
- 4950 Iterationen: p1= 0,5, p2=3
Die besten Ergebnisse sind in der Tabelle zusammengefasst:
| Anzahl der Iterationen | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 11 | 11 | 18 | 40 | 66 | 71 |
| 660 | 17 | 17 | 27 | 54 | 83 | 88 |
| 1665 | 31 | 31 | 41 | 80 | 95 | 98 |
| 3300 | 51 | 51 | 62 | 92 | 99 | 99 |
| 4950 | 65 | 65 | 75 | 97 | 99 | 100 |
Die folgenden Schlussfolgerungen lassen sich aus der Tabelle ziehen:
- Wenn die Anzahl der Iterationen um das Zehnfache reduziert wird, findet das Ultraschnelle Abkühlen in 11% der Fälle den besten Wert der Zielfunktion; in 71% der Fälle erzeugt er jedoch einen Wert der Zielfunktion, der nur 25% schlechter ist als der beste.
- Wenn die Anzahl der Iterationen um das Zweifache reduziert wird, findet das Ultraschnelle Abkühlen in 51% der Fälle den besten Wert der Zielfunktion; aber es gibt eine fast 100% Wahrscheinlichkeit, einen Wert der Zielfunktion zu finden, der nur 20% schlechter ist als der beste.
So kann das Ultraschnelle Abkühlen verwendet werden, um die Rentabilität von Strategien schnell zu beurteilen, wenn eine kleine Abweichung vom besten Wert durchaus akzeptabel ist.
Vergleichen wir nun das Ultraschnelle Abkühlen mit der Zufallssuche. Die Ergebnisse der Zufallssuche sind in der folgenden Tabelle dargestellt:
| Anzahl der Iterationen | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 5 | 5 | 10 | 14 | 33 | 42 |
| 660 | 10 | 10 | 19 | 27 | 55 | 67 |
| 1665 | 22 | 22 | 41 | 53 | 87 | 94 |
| 3300 | 40 | 40 | 64 | 79 | 98 | 99 |
| 4950 | 55 | 55 | 79 | 90 | 99 | 99 |
Vergleichen wir die Ergebnisse der Zufallssuche und des Ultraschnellen Abkühlens. Die Ergebnisse werden in Form einer Tabelle dargestellt, die den prozentualen Anstieg zwischen den entsprechenden Werten der Zufallssuche und dem Ultraschnellen Abkühlen zeigt.
| Anzahl der Iterationen | 0% | 5% | 10% | 15% | 20% | 25% |
|---|---|---|---|---|---|---|
| 330 | 120 | 120 | 80 | 185.714 | 100 | 69 |
| 660 | 70 | 70 | 42.105 | 100 | 50.909 | 31.343 |
| 1665 | 40.909 | 40.909 | 0 | 50.9434 | 9.195 | 4.255 |
| 3300 | 27.5 | 27.5 | -3.125 | 16.456 | 1.021 | 0 |
| 4950 | 18.182 | 18.182 | -5.064 | 7.778 | 0 | 1.01 |
So wird ein signifikanter Vorteil des Ultraschnellen Abkühlens bei einer kleinen Anzahl von Iterationen beobachtet. Wenn sie erhöht werden, nimmt der Vorteil ab und wird manchmal sogar negativ. Beachten Sie, dass eine ähnliche Situation beim Testen des Algorithmus durch Optimierung eines Parameters auftrat.
Nun zum Hauptpunkt: Vergleich des Ultraschnellen Abkühlens und des genetischen Algorithmus (GA), integriert in den Strategie-Tester.
Vergleich von GA und Ultraschnellem Abkühlen bei der Optimierung von zwei Variablen: "Moving Average period" und "Moving Average shift".
Die Algorithmen beginnen mit den folgenden Anfangsparametern:
- Maximum Risk in percentage — 0.02; Decrease factor — 3; Moving Average period: 1 — 120, step: 1; Moving Average shift — 6-60, step: 1
- Zeitraum: 01.01.2017 — 31.12.2017, Handelsmodus: keine Verzögerung, Ticks: 1 Minute OHLC, Ersteinlage: 10000, Hebel: 1:100, Währung: EURUSD
- Die Optimierung erfolgt nach dem Kriterium Balance max
Führen wir den genetischen Algorithmus 20 Mal aus, speichern wir die Ergebnisse und die durchschnittliche Anzahl der Iterationen, die zur Vervollständigung des Algorithmus erforderlich sind.
Nach 20 Durchläufen der GA wurden folgende Werte ermittelt: 1392.29; 1481.32; 2284.46; 1665.44; 1435.16; 1786.78; 1431.64; 1782.34; 1520.58; 1229.36; 1482.23; 1441.36; 1763.11; 2286.46; 1476.54; 1263.21; 1491.09; 1076.9; 913.42; 1391.72.
Durchschnittliche Anzahl der Iterationen: 175; Durchschnittswert der Zielfunktion: 1529.771.
Da der beste Wert der Zielfunktion 2446,33 ist, liefert GA kein gutes Ergebnis, wobei der Durchschnittswert der Zielfunktion nur 62,53% des besten Wertes beträgt.
Führen wir nun 20 Durchläufe des Ultraschnellen Abkühlens bei 175 Iterationen mit den Parametern: p1=1, p2=1 durch.
Das Ultraschnelle Abkühlen wurde auf 4 Testagenten gestartet, während die Suche nach der Zielfunktion autonom auf jedem Mittel durchgeführt wurde, so dass jedes Mittel 43-44 Iterationen durchführte. Folgende Ergebnisse wurden erzielt: 1996.83; 1421.87; 1391.72; 1727.38; 1330.07; 2486.46; 1687.51; 1840.69; 1687.51; 1472.19; 1665.44; 1607.19; 1496.9; 1388.37; 1496.9; 1491.09; 1552.02; 1467.08; 2446.33; 1421.15.
Mittelwert der Zielfunktion: 1653.735, 67,6% der besten Zielfunktion, etwas höher als der von GA.
Führen wir das Ultraschnelle Abkühlen auf einem einzigen Testagenten aus und führen wir 175 Iterationen durch. Der Mittelwert der Zielfunktion lag somit bei 1731,244 (70,8% des besten Wertes).
Vergleich von GA und dem Ultraschnellen Abkühlen bei der Optimierung von vier Variablen: "Moving Average period", "Moving Average shift", "Decrease factor" und "Maximum Risk in percentage".
Die Algorithmen beginnen mit den folgenden Anfangsparametern:
- Moving Average period: 1 — 120, step: 1; Moving Average shift — 6-60, step: 1; Decrease factor: 0.02 — 0.2, step: 0,002; Maximum Risk in percentage: 3-30, step: 0.3.
- Zeitraum: 01.01.2017 — 31.12.2017, Handelsmodus: keine Verzögerung, Ticks: 1 Minute OHLC, Ersteinlage: 10000, Hebel: 1:100, Währung: EURUSD
- Die Optimierung erfolgt nach dem Kriterium Balance max
GA endete nach 4870 Iterationen, mit dem besten Ergebnis von 32782.91. Die komplette Suche konnte wegen der großen Anzahl möglicher Kombinationen nicht gestartet werden, daher werden wir die Ergebnisse von GA und Ultraschnellem Abkühlen einfach vergleichen.
Das Ultraschnelle Abkühlen wurde mit den Parametern p1=0,75 und p2=1 auf 4 Testagenten gestartet und mit einem Ergebnis von 26676,22 beendet. Der Algorithmus funktioniert mit diesen Einstellungen nicht sehr gut. Versuchen wir, die Temperaturabsenkung zu beschleunigen, indem wir p1=2, p2=1 einstellen. Beachten wir auch die Temperatur, berechnet durch die Formel:
T0*exp(-p1*exp(-p2/4)*n^0.25), wobei n die Iterationszahl ist,
bei der ersten Iteration stark abnimmt (bei n=1, T=T0*0,558). Erhöhen wir daher den Koeffizienten bei der Anfangstemperatur durch Setzen von CoeffOfTemp=4. Die Ausführung des Algorithmus mit diesen Einstellungen hat das Ergebnis deutlich verbessert: 39145.25. Die Funktionsweise des Algorithmus wird im folgenden Video demonstriert:
Demonstration des Ultraschnellen Abkühlens mit den Parametern p1=2, p2=1
Damit ist das Ultraschnelle Abkühlen ein würdiger Konkurrent für GA und kann ihn mit den richtigen Einstellungen übertreffen.
Schlussfolgerung
Der Artikel beschreibt den Algorithmus des simulierten Abkühlens, seine Implementierung und Integration in den Moving Average EA. Seine Leistung bei der Prüfung einer anderen Anzahl von Parametern des Moving Average EA wurde getestet. Auch die Leistung des simulierten Abkühlens wurde mit der des genetischen Algorithmus verglichen.
Verschiedene Implementierungen des simulierten Abkühlens wurden getestet: Boltzmannsches Abkühlen, Cauchysches Abkühlen, Ultraschnelles Abkühlen. Die besten Ergebnisse zeigten sich beim Ultraschnellen Abkühlen.
Hier sind die wichtigsten Vorteile des simulierten Abkühlens:
- Optimierung verschiedener Parameter;
- Anpassung der Parameter des Algorithmus, was eine effektive Nutzung für verschiedene Optimierungsaufgaben ermöglicht;
- Wählbare Anzahl von Iterationen für den Algorithmus;
- Grafische Oberfläche, um die Funktion des Algorithmus zu überwachen, das beste Ergebnis anzuzeigen und die Ergebnisse des Algorithmus wiederzugeben.
Trotz signifikanter Vorteile hat das simulierte Abkühlen folgende Implementierungsnachteile:
- Der Algorithmus kann nicht im Cloud-Test ausgeführt werden;
- Die Integration in einen Experten ist kompliziert, und es ist notwendig, die Parameter auszuwählen, um die besten Ergebnisse zu erzielen.
Diese Nachteile können durch die Entwicklung eines universellen Moduls beseitigt werden, das verschiedene Algorithmen zur Optimierung der Expertenparameter enthält. Da es nach einem Testlauf die Zielfunktionswerte erhält, generiert dieses Modul neue Werte der optimierten Parameter für den nächsten Lauf.
Die folgenden Dateien sind dem Artikel beigefügt:
| Dateiname | Kommentar |
|---|---|
| AnnealingMethod.mqh | Klasse, die für das Funktionieren des simulierten Abkühlens benötigt wird, sie sollte in /MQL5/Include platziert werden. |
| FrameAnnealingMethod.mqh | Klasse zur Anzeige des Ausführungsprozesses des Algorithmus im Terminalfenster, sie sollte in /MQL5/Include platziert werden. |
| SimpleTable.mqh | Hilfsklasse für die Arbeit mit Tabellen der grafischen Oberfläche, sie sollte in /MQL5/Include platziert werden. |
| Moving Average_optim.mq5 | Modifizierte Version des Moving Average EA |
| test.zip | Archiv mit dem ES TestAnnealing.mq5 zum Testen des simulierten Abkühlens mit den Eingangsdaten, die aus der Testdatei oder Hilfsdateien geladen werden. |
| AnnealingMethod.zip | Zip-Datei mit Bildern zur Erstellung der Oberfläche des Players. Die Datei sollte in MQL5/Images/AnnealingMethod platziert werden. |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/4150
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Erstellen eines eigenen Newsfeeds für MetaTrader 5
Erstellen eines eigenen Newsfeeds für MetaTrader 5
 LifeHack für Händler: ForEach mit #define zubereiten
LifeHack für Händler: ForEach mit #define zubereiten
 Wie man eine Anforderungsspezifikation bei der Bestellung eines Indikators erstellt
Wie man eine Anforderungsspezifikation bei der Bestellung eines Indikators erstellt
 LifeHack für Händler: Fast-Food aus Indikatoren
LifeHack für Händler: Fast-Food aus Indikatoren
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Kontrollierte Optimierung: Simuliertes Glühen ist veröffentlicht worden:
Autor: Aleksey Zinovik
Ich habe noch nicht begonnen, mit mt5 zu arbeiten, aber ich denke, dass ich (vielleicht mit einigen Änderungen und/oder bedingter Kompilierung) in der Lage sein werde, dies auch im Strategietester von mt4 zu verwenden.
Die genetische Optimierung von mt4 hat ein kleines Problem, das vielleicht auch für mt5 existiert und vielleicht auch für Ihren Ansatz.
Wenn ich in OnInit() den Parametersatz prüfe und feststelle, dass ein aktueller Satz nicht prüfenswert ist, komme ich aus OnInit() mit INIT_PARAMETERS_INCORRECT zurück. Die Optimierung wird nicht durchgeführt, was Zeit spart, ok - aber:
Haben Sie sich um diese Situation gekümmert: Rückkehr von OnInit(), obwohl es keinen Fehler gibt (wie: Datei nicht gefunden,..), nur weil die Parametereinstellung nicht getestet werden sollte, was in diesem Fall die Anzahl nicht erhöhen und die Temperatur senken sollte?
Auf jeden Fall vielen Dank für diesen interessanten Artikel!
Gooly
Ich habe noch nicht begonnen, mit mt5 zu arbeiten, aber ich denke, dass ich (vielleicht mit einigen Änderungen und/oder bedingter Kompilierung) in der Lage sein werde, dies auch im Strategietester von mt4 zu verwenden.
Die genetische Optimierung von mt4 hat ein kleines Problem, das auch für mt5 besteht und vielleicht auch für Ihren Ansatz gilt.
Wenn ich in OnInit() den Parametersatz prüfe und feststelle, dass ein aktueller Satz nicht prüfenswert ist, komme ich aus OnInit() mit INIT_PARAMETERS_INCORRECT zurück. Die Optimierung wird nicht durchgeführt, was Zeit spart, ok - aber:
Haben Sie sich um diese Situation gekümmert: Rückkehr von OnInit(), obwohl kein Fehler vorliegt (z.B.: Datei nicht gefunden,..), nur weil die Parametereinstellung nicht getestet werden sollte, was in diesem Fall die Anzahl nicht erhöhen und die Temperatur nicht verringern sollte?
Auf jeden Fall danke ich Ihnen für diesen interessanten Artikel!
Gooly
Ich überprüfe nicht die Korrektheit der Parameter und unterbreche die OnInit()-Funktion nicht, wenn die Parameter nicht korrekt sind. In der Funktion OnTesterInit() werden Parameter, deren Werte mit dem Strategietester optimiert werden müssen, von der Optimierung ausgeschlossen. Bei jeder neuen Iteration werden die Parameter aus der Datei gelesen, in der OnTester()-Funktion werden neue Parameterwerte in die Datei geschrieben. Damit ist es möglich, die vom Strategietester generierten Parameterwerte nicht zu verwenden, um die notwendigen Parameter selbständig an die OnInit()-Funktion auszugeben.
Ich verstehe jetzt - danke! Ich muss nur die Plausibilität des Parametersetups der nächsten Iteration überprüfen, bevor dieses Setup in die Datei für den nächsten Lauf geschrieben wird. Auf diese Weise lässt sich "mein Problem" vermeiden!
Vielen Dank für diese Idee und den Artikel!
Hallo ,
Sie sagten: "Die Nachteile können durch die Entwicklung eines universellen Moduls beseitigt werden, das verschiedene Algorithmen zur Optimierung der Expertenparameter enthält".
Können Sie das universelle Modul genauer beschreiben? Welche anderen Algorithmen zur Optimierung der Expertenparameter gibt es?
Hallo ,
Sie sagten: "Die Nachteile können durch die Entwicklung eines universellen Moduls beseitigt werden, das verschiedene Algorithmen zur Optimierung der Expertenparameter enthält".
Können Sie das universelle Modul genauer beschreiben? Welche anderen Algorithmen zur Optimierung der Expertenparameter gibt es?
Der Artikel zeigt, wie man einen neuen Optimierungsalgorithmus mit dem Strategietester verbindet. In ähnlicher Weise kann man durch Hinzufügen neuer Methoden zur Klasse AnnealingMethod.mqh oder durch Erstellen einer neuen Klasse andere Algorithmen anschließen, zum Beispiel Ameisenalgorithmen (Ant colony optimization). Ich plane, die Arbeit solcher Algorithmen zu testen und das Ergebnis zu teilen.