Optimización controlable: el método del recocido

Introducción

En el simulador de estrategias de la plataforma comercial MetaTrader 5 solo existen dos variantes de optimización: la iteración completa de parámetros y el algoritmo genético. En este artículo proponemos una nueva variante de optimización de estrategias comerciales: el método del recocido. Aquí se muestra el algoritmo del método del recocido, analizando su implementación y su método de inclusión en cualquier asesor. A continuación, simulamos su funcionamiento en el asesor MovingAverage y comparamos los resultados obtenidos con el método del recocido con el algoritmo genético.

Algoritmo del método de recocido

El método de recocido es uno de los métodos de optimización estocástica. Supone la búsqueda aleatoria ordenada del valor óptimo de la función objetivo.

El algoritmo del método del recocido se basa en la imitación del proceso de formación de una estructura cristálica en la sustancia. Los átomos de la red cristalina de una sustancia - por ejemplo, del metal - al reducir la temperatura pueden o bien pasar a un estado con menor nivel de energía, o bien permanecer inalterados. La probilidad del paso a un nuevo estado se reduce de forma proporcional a la temperatura. Si importamos este proceso, podremos encontrar el mínimo o el máximo de la función objetivo.

El proceso de búsqueda del valor óptimo de la función objetivo se puede imaginar como la figura siguiente:

Fig. 1 Búsqueda del valor óptimo de la función objetivo.

En la figura 1, los valores de la función objetivo se muestran en forma de bola que rueda sobre una superficie irregular. Con una bola azul se muestra el valor inicial de la función objetivo, en verde, el valor final (mínimo global). Las bolas rojas indican la función en mínimos locales. El algoritmo del método de recocido trata de encontrar el valor extremo global de la función objetivo y evitar "atascarse" en los locales. La probabilidad de salida del extremo local disminuye conforme se acerca al global.

Vamos a pasar directamente al análisis de las etapas del algoritmo del método de recocido. Para concretar, analizaremos la búsqueda del mínimo global de la función objetivo. Existen 3 variantes principales de implementación del algoritmo de recocido: el recocido de Boltzmann, el recocido de Cauchy (recocido rápido) y el recocido ultra-rápido. Estos se diferencian entre sí en el método de generación del nuevo punto x(i) y la ley de disminución de la temperatura.

Vamos a introducir las variables usadas en el algoritmo:

• Fopt — valor óptimo de la función objetivo;
• Fbegin — valor inicial de la función objetivo;
• x(i) — valor del punto actual (parámetro del que depende la función objetivo);
• F(x(i)) — valor de la función objetivo para el punto x(i);
• i — contador de iteraciones;
• T0 — tempratura inicial;
• T — temperatura actual;
• Xopt — valor del parámetro con el que se alcanza el valor óptimo de la función objetivo;
• Tmin — valor mínimo de la temperatura;
• Imax — valor máximo de la temperatura.

El algoritmo del método de recocido consta de las siguientes etapas:

• Etapa 0. Inicialización del algoritmo: Fopt = Fbegin, i=0, T=T0, Xopt = 0.
• Etapa 1. Elección aleatoria del punto actual x(0) y cálculo de la función objetivo F(x(0)) para el punto dado. SiF(x(0))<Fbegin, entonces Fopt=F(x(0)).
• Etapa 2. Generación de un nuevo punto x(i).
• Etapa 3. Cálculo de la función objetivo F(x(i)).
• Etapa 4. Comprobación del paso al nuevo estado. A continuación, se analizan dos modificaciones del algoritmo: 
• a). Si el paso al nuevo estado se ha ejecutado, reducimos la temperatura actual y pasamos a la etapa 5, de lo contrario, pasamos a la etapa 2.
• b). Independientemente del resultado de la comprobación del paso al nuevo estado, reducimos la temperatura actual y pasamos a la etapa 5.
• Etapa 5. La comprobación del criterio salida del algoritmo (la temperatura ha alcanzado el valor mínimo tmín o ha alcanzado el número predeterminado de iteraciones Imax). Si no se cumple el criterio de salida del algoritmo: aumentamos el contador de iteraciones (i = i + 1) y pasamos a la etapa 2.

Analizamos cada una de estas etapas para encontrar el mínimo de la función objetivo.

Etapa 0.  A las variables cuyos valores cambian durante el funcionamiento del algoritmo se les asignan los valores iniciales.

Etapa 1. Entendemos el punto actual como el valor del parámetro del asesor que necesitamos optimizar. Estos parámetros pueden ser varios. A cada parámetro se le asigna un valor aleatorio, distribuido de forma homogénea en el intervalo de Pmin a  Pmax con el salto establecido Step (Pmin, Pmax — valor mínimo y máximo del parámetro optimizado). Se ejecuta una pasada del asesor en el simulador con los parámetros generados y se calcula el valor de la función objetivo F(x(0)) : el resultado de la optimización de los parámetros del asesor (valor del criterio de optimización indicado). Si F(x(0))<Fbegin, Fopt=F(x(0)).

Etapa 2. La generación de un nuevo punto, dependiendo de la variante de implementación del algoritmo según las fórmulas dadas en la Recuadro 1.

Recuadro 1.

Variante de implementación del algoritmo	Fórmula para el cálculo de un nuevo punto
Recocido de Boltzmann	, donde N(0,1) es la distribución normal estándar
Recocido de Cauchy (recocido rápido)	, donde C(0,1) es la distribución de Cauchy
Recocido ultra-rápido	, donde Pmax, Pmin es el valor mínimo y máximo del parámetro optimizado, la magnitud se calcula según la fórmula siguiente: , donde a es una magnitud aleatoria, distribuida de forma homogénea en el intervalo [0,1),

Etapa 3. Se realiza la pasada del asesor en el simulador con los parámetros generados en la etapa 2. A la función objetivo F(x(i)) se le asigna el valor del criterio de optimización elegido. 

Etapa 4. La comprobación del paso a un nuevo estado se ejecuta de la siguiente forma:

• Paso 1. Si F(x(i))<Fopt, pasamos al nuevo estado Xopt =x(i), Fopt=F(x(i)), de lo contrario, nos trasladamos al paso 2.
• Paso 2. Generamos la magnitud aleatoria a, distribuida homogéneamente en el intervalo [0,1).
• Paso 3. Calculamos la probabilidad del paso a un nuevo estado: 
• Paso 4. Si P>a, entonces pasamos al nuevo estado Xopt =x(i), Fopt=F(x(i)), de lo contrario, si se elige la modificación del algoritmo а), pasamos a la etapa 2.
• Paso 5. Reducimos la temperatura actual según las fórmulas mostradas en el recuadro 2.

Recuadro 2

Variante de implementación del algoritmo	Fórmula para reducir la temperatura
Recocido de Boltzmann
Recocido de Cauchy (recocido rápido)	, donde n es el número de parámetros cuyos valores se optimizan
Recocido ultra-rápido	, donde c(i)>0 y se calcula precisamente según la fórmula siguiente: , donde m(i), p(i) son los parámetros adicionales del algoritmo. Normalmente, para que resulte más sencillo configurar el algoritmo, los valores de los parámetros m(i) y p(i) no se cambian durante el funcionamiento del algoritmo: m(i)=const, p(i) = const

Etapa 5. La salida del algoritmo tiene lugar al cumplirse las siguientes condiciones: T(i)<=Tmin o i=Imax.

• Si elegimos una ley de cambio de tempratura en la que la temperatura se reduce muy rápido, entonces será más conveniente finalizar el funcionamiento del algoritmo con T(i)<=Tmin, sin esperar la finalización de todas las iteraciones.
• Si la temperatura disminuye muy lentamente, la salida del algoritmo se ejecutará al alcanzar el número máximo de iteraciones. Lo más probable en este caso es que haya que cambiar los parámetros de la ley de disminución de temperatura.

Ya hemos visto detalladamente todas las etapas del funcionamiento del algoritmo, vamos a pasar ahora a la implmentación en el lenguaje MQL5.

Implementación del algoritmo

Vamos a examinar la implementación y el orden de conexión del algoritmo al asesor cuyos parámetros deben ser optimizados.

Para implementar el algoritmo, escribiremos dos clases que se deben incluir en el asesor optimizado:

• la clase AnnealingMethod.mqh contiene el conjunto de métodos que implementan las diferentes etapas del algoritmo;
• la clase FrameAnnealingMethod.mqh contiene los métodos para trabajar con la interfaz gráfica representada en la ventana del gráfico del terminal.

Asimismo, para que el algoritmo funcione, se necesita incluir un código adicional en la función OnInit y añadir al código del asesor las funciones OnTester, OnTesterInit, OnTesterDeInit,  OnTesterPass. El proceso de conexión del algoritmo al asesor se muestra en la fig. 2.

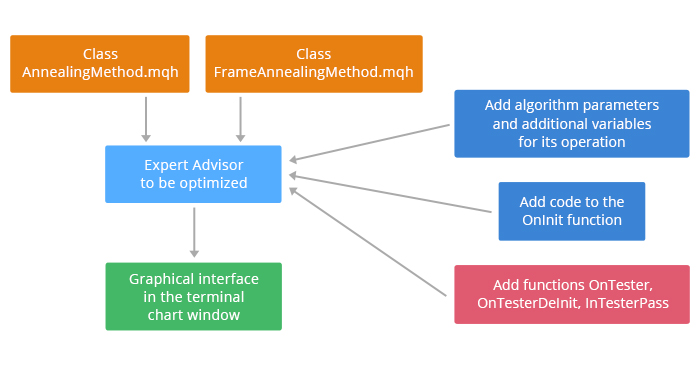
Fig. 2. Inclusión del algoritmo en el asesor

Vamos a pasar a la descripción de las clases AnnealingMethod y FrameAnnealingMethod.

La clase AnnealingMethod

Vamos a mostrar la descripción de la clase AnnealingMethod y a analizar con más detalle sus métodos.

#include "Math/Alglib/alglib.mqh"
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class AnnealingMethod
  {
private:
   CAlglib           Alg;                   //ejemplar de la clase para trabajar con los métodos de la biblioteca Alglib
   CHighQualityRandStateShell state;        //ejemplar de la clase para la generación de números aleatorios
public:
                     AnnealingMethod();
                    ~AnnealingMethod();
   struct Input                             //estructura para trabajar con los parámetros del asesor
     {
      int               num;
      double            Value;
      double            BestValue;
      double            Start;
      double            Stop;
      double            Step;
      double            Temp;
     };
   uint              RunOptimization(string &InputParams[],int count,double F0,double T);
   uint              WriteData(Input &InpMass[],double F,int it);
   uint              ReadData(Input &Mass[],double &F,int &it);
   bool              GetParams(int Method,Input &Mass[]);
   double            FindValue(double val,double step);
   double            GetFunction(int Criterion);
   bool              Probability(double E,double T);
   double            GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2);
   double            UniformValue(double min,double max,double step);
   bool              VerificationOfVal(double start,double end,double val);
   double            Distance(double a,double b);
  };

Para que funcionen los métodos de la clase AnnealingMethod, usamos las funciones para el trabajo con magnitudes aleatorias de la biblioteca ALGLIB. Esta biblioteca entra en el paquete estándar del terminal MetaTrader 5 y se encuentra en la carpeta Include/Math/Alglib, como se muestra en la figura:

Fig. 3. Biblioteca  ALGLIB

En el bloque Private se declaran los ejemplares de las clases CAlglib y CHighQualityRandStateShell para trabajar con las funciones de la biblioteca ALGLIB.

Para trabajar con los parámetros optimizables del asesor se ha creado la estructura Input, en la que se guardan:

• número del parámetro num;
• valor actual del parámetro Value;
• mejor valor del parámetro BestValue;
• valor inicial Start;
• valor final Stop;
• salto de cambio del valor del parámetro Step;
• temperatura actual para el parámetro Temp. dado

Vamos a analizar los métodos de la clase AnnealingMethod.mqh.

Método RunOptimization

Está diseñado para inicializar el algoritmo del método de recocido. Código del método:

uint AnnealingMethod::RunOptimization(string &InputParams[],int count,double F0,double T)
  {
   Input Mass[];
   ResetLastError();
   bool Enable=false;
   double Start= 0;
   double Stop = 0;
   double Step = 0;
   double Value= 0;
   int j=0;
   Alg.HQRndRandomize(&state);                //inicialización
   for(int i=0;i<ArraySize(InputParams);i++)
     {
      if(!ParameterGetRange(InputParams[i],Enable,Value,Start,Step,Stop))
         return GetLastError();
      if(Enable)
        {
         ArrayResize(Mass,ArraySize(Mass)+1);
         Mass[j].num=i;
         Mass[j].Value=UniformValue(Start,Stop,Step);
         Mass[j].BestValue=Mass[j].Value;
         Mass[j].Start=Start;
         Mass[j].Stop=Stop;
         Mass[j].Step=Step;
         Mass[j].Temp=T*Distance(Start,Stop);
         j++;
         if(!ParameterSetRange(InputParams[i],false,Value,Start,Stop,count))
            return GetLastError();
        }
      else
         InputParams[i]="";
     }
   if(j!=0)
     {
      if(!ParameterSetRange("iteration",true,1,1,1,count))
         return GetLastError();
      else
         return WriteData(Mass,F0,1);
     }
   return 0;
  }

Parámetros de entrada del método:

• matriz de líneas de los nombres de todos los parámetros del asesor InputParams[] ;
• número de iteraciones del algoritmo count ;
• valor inicial de la función objetivo F0 ;
• temperatura inicial T.

El método RunOptimization funciona de la forma siguiente:

• se ejecuta la búsqueda de los parámetros del asesor que se deben optimizar. Estos parámetros deberán ser marcados con un "tick" en la pestaña "parámetros" del simulador de estrategias;
• los valores de cada parámetro localizado se guardan en la matriz de estructuras Mass[] del tipoInput, y el parámetro se excluye de la optimización. En la matriz de estructuras Mass[] se guardan:
• el número del parámetro;
• el valor del parámetro generado por el método UniformValue (se verá más abajo);
• el valor máximo (Start) y máximo (Stop) del parámetro;
• el salto de cambio del valor del parámetro (Step);
• la temperatura inicial calculada según la fórmula: T*Distance(Start,Stop), el método Distance se analizará más abajo.
• después de finalizar la búsqueda, todos los parámetros resultan desactivados y se activa el parámetro iteration, que define el número de iteraciones del algoritmo;
• los valores de la matriz Mass[], la función objetivo y el número de iteración se anotan en un archivo binario con la ayuda del método WriteData. 

Método WriteData

Ha sido diseñado para grabar la matriz de parámetros, el valor de la función objetivo y el número de iteración en el archivo.

Código del método WriteData:

uint AnnealingMethod::WriteData(Input &Mass[],double F,int it)
  {
   ResetLastError();
   int file_handle=0;
   int i=0;
   do
     {
      file_handle=FileOpen("data.bin",FILE_WRITE|FILE_BIN);
      if(file_handle!=INVALID_HANDLE) break;
      else
        {
         Sleep(MathRand()%10);
         i++;
         if(i>100) break;
        }
     }
   while(file_handle==INVALID_HANDLE);
   if(file_handle!=INVALID_HANDLE)
     {
      if(FileWriteArray(file_handle,Mass)<=0)
        {FileClose(file_handle); return GetLastError();}
      if(FileWriteDouble(file_handle,F)<=0)
        {FileClose(file_handle); return GetLastError();}
      if(FileWriteInteger(file_handle,it)<=0)
        {FileClose(file_handle); return GetLastError();}
     }
   else
      return GetLastError();
   FileClose(file_handle);
   return 0;
  }

Los datos se anotan en el archivo data.bin con la ayuda de las funciones FileWriteArray, FileWriteDouble y FileWriteInteger. En el método se implementado la posibilidad de intentar acceder al archivo data.bin de forma múltiple. Esto se ha hecho para evitar errores al acceder al archivo, si el archivo está ocupado en otro proceso.

Método ReadData

Se ha diseñado para leer desde el archivo data.bin la matriz de parámetros, los valores de la función objetivo y los números de iteración. Código del método ReadData:

uint AnnealingMethod::ReadData(Input &Mass[],double &F,int &it)
  {
   ResetLastError();
   int file_handle=0;
   int i=0;
   do
     {
      file_handle=FileOpen("data.bin",FILE_READ|FILE_BIN);
      if(file_handle!=INVALID_HANDLE) break;
      else
        {
         Sleep(MathRand()%10);
         i++;
         if(i>100) break;
        }
     }
   while(file_handle==INVALID_HANDLE);
   if(file_handle!=INVALID_HANDLE)
     {
      if(FileReadArray(file_handle,Mass)<=0)
        {FileClose(file_handle); return GetLastError();}
      F=FileReadDouble(file_handle);
      it=FileReadInteger(file_handle);
     }
   else
      return GetLastError();
   FileClose(file_handle);
   return 0;
  }

Los datos se leen desde el archivo con la ayuda de las funciones FileReadArray,FileReadDouble,FileReadInteger en la misma secuencia que se anotaron con el método WriteData. 

Método GetParams

El método GetParams se ha pensado para calcular los nuevos valores de los parámetros optimizables del asesor, para los que se ejecutará la pasada del asesor. Las fórmulas de cálculo de los nuevos valores de los parámetros optimizables del asesor se muestran en el recuadro 1.

Parámetros de entrada del método:

• variante de implementación del algoritmo (recocido de Boltzmann, recocido de Cauchy o recocido ultra-rápido);
• matriz de parámetros optimizables del tipo Input;
• coeficiente CoeffTmin para el cálculo de la temperatura mínima, al alcanzar la cual el algoritmo finaliza el trabajo.

Código del método GetParams:

bool AnnealingMethod::GetParams(int Method,Input &Mass[],double CoeffTmin)
  {
   double delta=0;
   double x1=0,x2=0;
   double count=0;

   Alg.HQRndRandomize(&state);         //inicialización
   switch(Method)
     {
      case(0):
        {
         for(int i=0;i<ArraySize(Mass);i++)
           {
            if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop))
              {
               do
                 {
                  if(count==100)
                    {
                     delta=Mass[i].Value;
                     count= 0;
                     break;
                    }
                  count++;
                  delta=Mass[i].Temp*Alg.HQRndNormal(&state);
                  delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step);
                 }
               //  while((delta<Mass[i].Start) || (delta>Mass[i].Stop));
               while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta));
               Mass[i].Value=delta;
              }
           }
         break;
        }
      case(1):
        {
         for(int i=0;i<ArraySize(Mass);i++)
           {
            if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop))
              {
               do
                 {
                  if(count==100)
                    {
                     delta=Mass[i].Value;
                     count=0;
                     break;
                    }
                  count++;
                  Alg.HQRndNormal2(&state,x1,x2);
                  delta=Mass[i].Temp*x1/x2;
                  delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step);
                 }
               while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta));
               Mass[i].Value=delta;
              }
           }
         break;
        }
      case(2):
        {
         for(int i=0;i<ArraySize(Mass);i++)
           {
            if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop))
              {
               do
                 {
                  if(count==100)
                    {
                     delta=Mass[i].Value;
                     count=0;
                     break;
                    }
                  count++;
                  x1=Alg.HQRndUniformR(&state);
                  if(x1-0.5>0)
                     delta=Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop);
                  else
                    {
                     if(x1==0.5)
                        delta=0;
                     else
                        delta=-Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop);
                    }
                  delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step);
                 }
               while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta));
               Mass[i].Value=delta;
              }
           }
         break;
        }
      default:
        {
         Print("Annealing method was chosen incorrectly");
         return false;
        }
     }
   return true;
  }

Vamos a analizar el código de este método con más detalle.

En el método se organiza el operador Switсh, que inicia el cálculo de los nuevos valores de los parámetros dependiendo de la variante del algoritmo elegida. El cálculo de los nuevos valores se ejecuta solo si la temperatura está por encima de la mínima. La temperatura mínima se calcula según la fórmula: CoeffTmin*Distance(Start,Stop), donde Start, Stop son los valores máximo y mínimo del parámetro. El método Distance se analizará más abajo.

Para inicializar los métodos de trabajo con números aleatorios se llama el método HQRndRandomize de la clase CAlglib:

 Alg.HQRndRandomize(&state);

Para calcular el valor de la distribución normal estándar se usa la función HQRndNormal de la clase CAlglib:

Alg.HQRndNormal(&state);

Las distribuciones de Cauchy se pueden modelar de formas diferentes, por ejemplo, con una distribución normal o funciones inversas. Usaremos la siguiente proporción:

C(0,1)=X1/X2, donde X1 y X2 son las magnitudes normales independientes, X1,X2 = N(0,1). Para generar dos magnitudes distribuidas normales independientes, se usa la función HQRndNormal2 de la clase CAlglib:

 Alg.HQRndNormal2(&state,x1,x2);

Los valores de las magnitudes distribuidas normales independientes se guardan en las variables x1,x2.

Con la ayuda del método HQRndUniformR(&state) de la clase CAlglibse genera un número aleatorio, distribuido uniformemente en un intervalo de 0 a 1:

Alg.HQRndUniformR(&state);

Con la ayuda del método FindValue (se describirá abajo), el valor calculado del parámetro se redondea para el salto de cambio del parámetro indicado. Si el valor calculado del parámetro se sale de los límites del rango de cambio del parámetro (esto se comprueba con el método VerificationOfVal), se calcula de nuevo.

Método FindValue

El valor de cada parámetro optimizado se puede cambiar con el salto establecido. El valor nuevo del parámetro, formado en el método GetParams, podría no corresponderse con la condición: deberemos redondearlo hasta un valor múltiplo del salto indicado. Para ello se usa el método FindValue. Parámetros de entrada del método: valor que se necesitará redondear (val), y salto de cambio del parámetro (step).

Vamos a mostrar el código del método FindValue:

double AnnealingMethod::FindValue(double val,double step)
  {
   double buf=0;
   if(val==step)
      return val;
   if(step==1)
      return round(val);
   else
     {

      buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);
      if(MathAbs(val)-buf*MathAbs(step)>=MathAbs(step)/2)
        {
         if(val<0)
            return -(buf + 1)*MathAbs(step);
         else
            return (buf + 1)*MathAbs(step);
        }
      else
        {
         if(val<0)
            return -buf*MathAbs(step);
         else
            return buf*MathAbs(step);
        }
     }
  }

Vamos a analizar el código con más detalle.

Si el salto es igual al valor del parámetro de entrada, la función retorna el valor:

   if(val==step)
      return val;

Si el sato es igual a 1, será necesario redondear hasta el valor entero de entrada del parámetro:

   if(step==1)
      return round(val);

De lo contrario, encontramos el número de saltos en el valor de entrada del parámetro:

buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);

y calculamos el nuevo valor múltiple del salto step.

Método GetFunction

El método GetFunction se ha pensado para obtener un nuevo valor de la función objetivo. El valor de entrada del método es el criterio de optimización elegido por el usuario.

La función objetivo, dependiendo del método de cálculo elegido, adopta el valor de uno o varios índices estadísticos calculados según los resultados de la simulación. Código del método:

double AnnealingMethod::GetFunction(int Criterion)
  {
   double Fc=0;
   switch(Criterion)
     {
      case(0):
         return TesterStatistics(STAT_PROFIT);
      case(1):
         return TesterStatistics(STAT_PROFIT_FACTOR);
      case(2):
         return TesterStatistics(STAT_RECOVERY_FACTOR);
      case(3):
         return TesterStatistics(STAT_SHARPE_RATIO);
      case(4):
         return TesterStatistics(STAT_EXPECTED_PAYOFF);
      case(5):
         return TesterStatistics(STAT_EQUITY_DD);//min
      case(6):
         return TesterStatistics(STAT_BALANCE_DD);//min
      case(7):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_PROFIT_FACTOR);
      case(8):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_RECOVERY_FACTOR);
      case(9):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_SHARPE_RATIO);
      case(10):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_EXPECTED_PAYOFF);
      case(11):
        {
         if(TesterStatistics(STAT_BALANCE_DD)>0)
            return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_BALANCE_DD);
         else
            return TesterStatistics(STAT_PROFIT);
        }
      case(12):
        {
         if(TesterStatistics(STAT_EQUITY_DD)>0)
            return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_EQUITY_DD);
         else
            return TesterStatistics(STAT_PROFIT);
        }
      case(13):
        {
         //indique el criterio personalizado, por ejemplo
         return TesterStatistics(STAT_TRADES)*TesterStatistics(STAT_PROFIT);
        }
      default: return -10000;
     }
  }

Como se puede ver por el código, en el método se han implementado 14 formas de cálculo de la función objetivo. Es decir, el usuario puede optimizar el asesor según los diferentes índices estadísticos. Podrá ver una descripción detallada de los índices estadísticos en la documentación.

Método Probability

El método Probability se ha pensado para definir el paso a un nuevo estado. Parámetros de entrada del método: diferencia entre el valor actual y el anterior de la función objetivo (E) y la tempratura actual (T). Código del método:

bool AnnealingMethod::Probability(double E,double T)
  {
   double a=Alg.HQRndUniformR(&state);
   double res=exp(-E/T);
   if(res<=a)
      return false;
   else
      return true;
  }

En el método se genera el valor aleatorio а, distribuido uniformemente en el intervalo de 0 a 1:

a=Alg.HQRndUniformR(&state);

El valor obtenido se compara con la expresión exp(-E/T). Si a>exp(-E/T), el método retorna true (el paso al nuevo estado ha finalizado).

Método GetT

El método GetT calcula el nuevo valor de la temperatura. Parámetros de entrada del método:

• variante de implementación del algoritmo (recocido de Boltzmann, recocido de Cauchy o recocido ultra-rápido);
• valor inicial de la temperatura T0;
• valor anterior de la temperatura Tlast;
• número de iteración it;
  
• número de parámetros optimizables D;
• parámetros auxiliares p1 y p2 para el recocido ultra-rápido.

Código del método:

double AnnealingMethod::GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2)
  {
   int Iteration=0;
   double T=0;
   switch(Method)
     {
      case(0):
        {
         if(Tlast!=T0)
            Iteration=(int)MathRound(exp(T0/Tlast)-1)+1;
         else
            Iteration=1;
         if(Iteration>0)
            T=T0/log(Iteration+1);
         else
            T=T0;
         break;
        }
      case(1):
        {
         if(it!=1)
            Iteration=(int)MathRound(pow(T0/Tlast,D))+1;
         else
            Iteration=1;
         if(Iteration>0)
            T=T0/pow(Iteration,1/D);
         else
            T=T0;
         break;
        }
      case(2):
        {
         if((T0!=Tlast) && (-p1*exp(-p2/D)!=0))
            Iteration=(int)MathRound(pow(log(Tlast/T0)/(-p1*exp(-p2/D)),D))+1;
         else
            Iteration=1;
         if(Iteration>0)
            T=T0*exp(-p1*exp(-p2/D)*pow(Iteration,1/D));
         else
            T=T0;
         break;
        }
     }
   return T;
  }

El método calcula el nuevo valor de la temperatura dependiendo de la variante de implementación del algortimo, según las fórmulas indicadas en el recuadro 2. Para tener en cuenta la variable de implementación del algoritmo según la cual la disminución de la temperatura se ejecuta solo al pasar a un nuevo estado, la iteración actual se calcula usando el valor anterior de la temperatura Tlast. De esta forma, la temperatura disminuye al llamar al método, independientemente de la iteración actual del algoritmo.

Método UniformValue

El método UniformValue genera un valor aleatorio del parámetro optimizado teniendo en cuenta sus valores máximo, mínimo y su salto. El método se usa solo al inicializar el algoritmo, para generar los valores iniciales de los parámetros optimizables. Parámetros de entrada del método:

• valor máximo del parámetro max;
• valor mínimo del parámetro min;
• salto de cambio del parámetro step.

Código del método:

double AnnealingMethod::UniformValue(double min,double max,double step)
  {
   Alg.HQRndRandomize(&state);       //inicialización
   if(max>min)
      return FindValue(Alg.HQRndUniformR(&state)*(max-min)+min,step);
   else
      return FindValue(Alg.HQRndUniformR(&state)*(min-max)+max,step);
  }

Método VerificationOfVal

El método VerificationOfVal comprueba si el valor indicado de la variable (val) no se sale de los límites del rango (start,end). Este método se usa en el método GetParams.

Código del método:

bool AnnealingMethod::VerificationOfVal(double start,double end,double val)
  {
   if(start<end)
     {
      if((val>=start) && (val<=end))
         return true;
      else
         return false;
     }
   else
     {
      if((val>=end) && (val<=start))
         return true;
      else
         return false;
     }
  }

El método tiene en cuenta que el salto de cambio del parámetro puede ser negativo, por eso se ejecuta la comprobación de la condición start<end.

Método Distance

El método Distance calcula la distancia entre los dos parámetros (a y b) y se usa en el algoritmo para calcular el tamaño del rango de cambio del parámetro con el valor inicial a y el valor final b.

>Código del método:

double AnnealingMethod::Distance(double a,double b)
  {
   if(a<b)
      return MathAbs(b-a);
   else
      return MathAbs(a-b);
  }

Clase FrameAnnealingMethod

La clase FrameAnnealingMethod se ha pensado para representar en la ventana del terminal el proceso de ejecución del algoritmo. Vamos a mostrar la descripción de la clase FrameAnnealingMethod:

#include <SimpleTable.mqh>
#include <Controls\BmpButton.mqh>
#include <Controls\Label.mqh>
#include <Controls\Edit.mqh>
#include <AnnealingMethod.mqh>
//+------------------------------------------------------------------+
//|  Clase para mostrar los resultados de optimización                        |
//+------------------------------------------------------------------+
class FrameAnnealingMethod
  {
private:
   CSimpleTable      t_value;
   CSimpleTable      t_inputs;
   CSimpleTable      t_stat;
   CBmpButton        b_playbutton;
   CBmpButton        b_backbutton;
   CBmpButton        b_forwardbutton;
   CBmpButton        b_stopbutton;
   CLabel            l_speed;
   CLabel            l_stat;
   CLabel            l_value;
   CLabel            l_opt_value;
   CLabel            l_temp;
   CLabel            l_text;
   CLabel            n_frame;
   CEdit             e_speed;
   long              frame_counter;

public:
   //--- constructor/destructor
                     FrameAnnealingMethod();
                    ~FrameAnnealingMethod();
   //--- evento del simulador de estrategias
   void              FrameTester(double F,double Fbest,Input &Mass[],int num,int it);
   void              FrameInit(string &SMass[]);
   void              FrameTesterPass(int cr);
   void              FrameDeinit(void);
   void              FrameOnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam,int cr);
   uint              FrameToFile(int count);
  };

La clase FrameAnnealingMethod contiene los siguientes métodos:

• FrameInit — pensado para crear la interfaz gráfica en la ventana del terminal;
• FrameTester — pensado para añadir el frame de datos actual;
• FrameTesterPass — muestra en la ventana del terminal el frame de datos actual;
• FrameDeInit — pensado para representar información textual sobre la finalización de la optimización del asesor;
• FrameOnChartEvent — pensado para procesar los eventos de pulsación de botones;
• FrameToFile — pensado para guardar los resultados de la simulación en un archivo de texto.

El código de los métodos se muestra en el archivo FrameAnnealingMethod.mqh (se adjunta al artículo). Destacaremos que para el funcionamiento de los métodos de la clase FrameAnnealingMethod se necesita el archivo SimpleTable.mqh (adjunto al artículo), que se debe ubicar en la carpeta MQL5/Include. El archivo se ha tomado prestado del proyecto y se complementa con el método GetValue, que permite leer el valor desde una celda del recuadro.

Vamos a mostrar un ejemplo de interfaz gráfica creada en la ventana del terminal con la ayuda de la clase FrameAnnealingMethod.

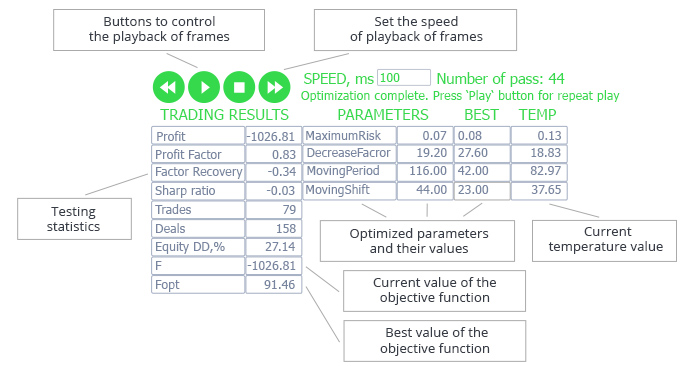
Fig. 4. Interfaz gráfica para demostrar el funcionamiento del algoritmo

A la izquierda en el recuadro se representan los índices estadísticos formados por el simulador de estrategias según los resultados de la pasada actual y el mejor valor de la función objetivo (en este ejemplo, como función objetivo se ha elegido el beneficio neto).

A la derecha en el recuadro se encuentran los parámetros optimizables: el nombre del parámetro, el valor actual, el mejor valor, la temperatura actual.

En la parte superior del recuadro se ubican los botones de control de la reproducción de frames tras la finalización del funcionamiento del algoritmo. De esta forma, al terminar la optimización del asesor, usted podrá reproducirla de nuevo con la velocidad indicada. Con ayuda de los botones, se puede detener la reproducción de frames e iniciarla de nuevo desde el mismo frame en el que se ha interrumpido la reproducción. Podemos regular la velocidad de reproducción con la ayuda de los botones, o introducirla manualmente. A la derecha del valor de la velocidad, se representa el número de la pasada actual del asesor. Más abajo, se representa la información auxiliar sobre el funcionamiento del algoritmo.

Hemos analizado las clases AnnealingMethod y FrameAnnealingMethod. Ahora vamos a simular el algoritmo usando como ejemplo el asesor Moving Average.

Simulación del algoritmo con el asesor Moving Average

Preparación del asesor para la simulación del algoritmo

Para que el algoritmo funcione, es necesario modificar el código del asesor:

• conectar las clases AnnealingMethod y FrameAnnealingMethod y declarar las variables auxiliares para el funcionamiento del algoritmo;
• añadir el código a la función OnInit, añadir las funciones OnTester, OnTesterInit, OnTesterDeInit,  OnTesterPass, OnChartEvent.

El código añadido no influye en el funcionamiento del algoritmo del asesor, y se inicia al optimizar el asesor en el simulador de estrategias.

Bien, vamos a comenzar.

Incluimos el archivo con los parámetros iniciales, formado por la función OnTesterInit:

#property tester_file "data.bin"

Incluimos las clases AnnealingMethod y FrameAnnealingMethod:

//incluimos las clases
#include <AnnealingMethod.mqh>
#include <FrameAnnealingMethod.mqh>

Declaramos los ejemplares de las clases incluidas:

AnnealingMethod Optim;
FrameAnnealingMethod Frame;

Declaramos las variables auxiliares para el funcionamiento del algoritmo:

Input InputMass[];            //matriz de los parámetros de entrada
string SParams[];             //matriz de los nombres de los parámetros de entrada
double Fopt=0;                //mejores valores de la función
int it_agent=0;               //número de iteración del algoritmo para el agente de simulación
uint alg_err=0;               //número de error

Durante el proceso de funcionamiento, el algoritmo del método de recocido cambiará el valor de los parámetros optimizables, para ello, redesignaremos los parámetros de entrada del asesor:

double MaximumRisk_Optim=MaximumRisk;
double DecreaseFactor_Optim=DecreaseFactor;
int MovingPeriod_Optim=MovingPeriod;
int MovingShift_Optim=MovingShift;

En todas las funciones del asesor, sustituimos los parámetros: MaximumRisk porMaximumRisk_Optim, DecreaseFactor por DecreaseFactor_Optim, MovingPeriod por MovingPeriod_Optim,  MovingShift porMovingShift_Optim

Introducimos las variables para ajustar el funcionamiento del algoritmo:

sinput int iteration=50;         //Número de iteraciones
sinput int method=0;             //0 - recocido de Boltzmann, 1 - recocido de Cauchy, 2 - recocido ultra-rápido 
sinput double CoeffOfTemp=1;     //Coeficiente a escala para la temperatura inicial
sinput double CoeffOfMinTemp=0;  //Coeficiente para la temperatura mínima
sinput double Func0=-10000;      //Valor inicial de la función objetivo
sinput double P1=1;              //Parámetro adicional para el recocido ultra-rápido p1
sinput double P2=1;              //Parámetro adicional para el recocido ultra-rápido p2
sinput int Crit=0;               //Método de cálculo de la función objetivo
sinput int ModOfAlg=0;           //Tipo de modificación del algoritmo
sinput bool ManyPoint=false;     //Optimización de varios puntos

Los parámetros del algoritmo no deberán modificarse durante su funcionamiento, por eso todas las variables se declaran con el identificador sinput.

En el recuadro 3 aclararemos el significado de las variables declaradas.

Recuadro 3

Nombre de la variable	Utilidad
iteration	Establece el número de iteración del algoritmo
method	Establece la variante de implementación del algoritmo: 0 — recocido de Boltzmann, 1 — recocido de Cauchy, 2 — recocido ultra-rápido
CoeffOfTemp	Establece el coeficiente para ajustar la temperatura inicial, que se calcula según la fórmula: T0=CoeffOfTemp*Distance(Start,Stop), donde Start, Stop son el valor máximo y mínimo del parámetro, Distance es el método de la clase AnnealingMethod (descrita mñas arriba)
CoeffOfMinTemp	Establece el coeficiente para el cálculo de la temperatura mínima, al alcanzar la cual el algoritmo finaliza el trabajo. La temperatura mínima se calcula de forma análoga a la temperatura inicial: Tmin=CoeffOfMinTemp*Distance(Start,Stop), donde Start, Stop son el valor máximo y mínimo del parámetro, Distance es el método de la clase AnnealingMethod (descrita más arriba)
Func0	Valor inicial de la función objetivo
P1,P2	Parámetros usados en el cálculo de la temperatura inicial para el recocido ultra-rápido (ver Recuadro 2)
Crit	Criterios de optimización: 0 — beneficio neto; 1 — rentabilidad; 2 — factor de recuperación; 3 — coeficiente de Sharpe; 4 —esperanza matemática de las ganancias; 5 — reducción máxima de los fondos; 6 — reducción máxima del balance; 7 — beneficio neto + rentabilidad; 8 — beneficio neto + factor de recuperación; 9 — beneficio neto + coeficiente de Sharpe; 10 — beneficio neto + esperanza matemática de las ganancias; 11 — benefico neto + reducción máxima del balance; 12 — beneficio neto + reucción máxima de los fondos; 13 — criterio personalizado. El cálculo de la función objetivo se ejecuta en el método GetFunction de la clase AnnealingMethod
ModOfAlg	Tipo de modificación del algoritmo: 0 - Si el paso al nuevo estado se ha ejecutado, reducimos la temperatura actual y pasamos a la comprobación de la finalización del funcionamiento del algoritmo, de lo contrario, calculamos los nuevos valores de los parámetros optimizables; 1 - independientemente del resultado de la comprobación del paso al nuevo estado, reducimos la temperatura actual y pasamos a la comprobación de la finalización del funcionamiento del algoritmo
ManyPoint	true — para cada agente de simulación se formarán diferentes valores iniciales de los parámetros optimizables, false — para cada agente de simulación se formarán idénticos valores iniciales de los parámetros optimizables

Añadimos el código al inicio de la función OnInit:

//+------------------------------------------------------------------+
//|Método de recocido                                                |
//+------------------------------------------------------------------+
 if(MQL5InfoInteger(MQL5_OPTIMIZATION))
    {
     //abrimos el archivo y cotejamos los datos
     //  if(FileGetInteger("data.bin",FILE_EXISTS,false))
     //  {
         alg_err=Optim.ReadData(InputMass,Fopt,it_agent);
         if(alg_err==0)
           {
            //Si se trata del primer inicio, generamos los parámetros aleatoriamente, si la búsqueda se ejecuta desde diferentes puntos
            if(Fopt==Func0)
              {
               if(ManyPoint)
                  for(int i=0;i<ArraySize(InputMass);i++)
                    {
                     InputMass[i].Value=Optim.UniformValue(InputMass[i].Start,InputMass[i].Stop,InputMass[i].Step);
                     InputMass[i].BestValue=InputMass[i].Value;
                    }
              }
            else
               Optim.GetParams(method,InputMass,CoeffOfMinTemp);    //generamos los nuevos parámetros
            //rellenamos los parámetros del asesor
            for(int i=0;i<ArraySize(InputMass);i++)
               switch(InputMass[i].num)
                 {
                  case (0): {MaximumRisk_Optim=InputMass[i].Value; break;}
                  case (1): {DecreaseFactor_Optim=InputMass[i].Value; break;}
                  case (2): {MovingPeriod_Optim=(int)InputMass[i].Value; break;}
                  case (3): {MovingShift_Optim=(int)InputMass[i].Value; break;}
                 }
           }
         else
           {
            Print("Error reading file");
            return(INIT_FAILED);
           }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+

Vamos a analizar el código con más detalle. El código añadido se ejecuta solo en el modo de optimización del simulador de estrategias:

if(MQL5InfoInteger(MQL5_OPTIMIZATION))

A continuación se cotejan los datos desde el archivo data.bin, formado con el método RunOptimization de la clase AnnealingMethod. Este método se llama en la función OnTesterInit, el código de la función se mostrará más abajo.

alg_err=Optim.ReadData(InputMass,Fopt,it_agent);

Si los datos se han cotejado sin errores (alg_err=0), se comprueba la presencia del algoritmo en la primera iteración (Fopt==Func0), de lo contrario, la inicialización del asesor se finalizará con error. Si la iteración es la primera, al darse ManyPoint = true formaremos los valores iniciales de los parámetros optimizables y los anotaremos en InputMass de la estructura Input (descrita en la clase AnnealingMethod), de lo contrario, se llamará al método GetParams

 Optim.GetParams(method,InputMass,CoeffOfMinTemp);//generamos los nuevos parámetros

y se rellenan los valores de los parámetros  MaximumRisk_Optim, DecreaseFactor_Optim, MovingPeriod_Optim, MovingShift_Optim.

Ahora vamos a analizar el código de la función OnTesterInit:

void OnTesterInit()
  {
  //rellenamos la matriz de los nombres de todos los parámetros del asesor
   ArrayResize(SParams,4);
   SParams[0]="MaximumRisk";
   SParams[1]="DecreaseFactor";
   SParams[2]="MovingPeriod";
   SParams[3]="MovingShift";
   //iniciamos la optimización
   Optim.RunOptimization(SParams,iteration,Func0,CoeffOfTemp);
   //creamos la interfaz gráfica
   Frame.FrameInit(SParams);
  }

Primero, rellenamos la matriz de línea que contiene los nombres de todos los parámetros del asesor. A continuación, iniciamos el método RunOptimization y creamos la interfaz gráfica con el método FrameInit.

Después de realizar la pasada en el intervalo temporal indicado, el control será transmitido a la función OnTester. Vamos a echar un vistazo a su código:

double OnTester()
  {
   int i=0;                                                       //contador del ciclo
   int count=0;                                                   //variable auxiliar
  //comprobación de la finalización del algoritmo al alcanzar la temperatura mínima
   for(i=0;i<ArraySize(InputMass);i++)
      if(InputMass[i].Temp<CoeffOfMinTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop))
         count++;
   if(count==ArraySize(InputMass))
      Frame.FrameTester(0,0,InputMass,-1,it_agent);               //añadimos un nuevo frame con parámetros cero id=-1 
   else
     {
      double Fnew=Optim.GetFunction(Crit);                        //calculamos el valor actual de la función
      if((Crit!=5) && (Crit!=6) && (Crit!=11) && (Crit!=12))      //si se necesita maximizar la función objetivo
        {
         if(Fnew>Fopt)
            Fopt=Fnew;
         else
           {
            if(Optim.Probability(Fopt-Fnew,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop)))
               Fopt=Fnew;
           }
        }
      else                                                        //si se necesita minimizar la función objetivo
        {
         if(Fnew<Fopt)
            Fopt=Fnew;
         else
           {
            if(Optim.Probability(Fnew-Fopt,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop)))
               Fopt=Fnew;
           }
        }
      //reescribimos los mejores valores de los parámetros
      if(Fopt==Fnew)
         for(i=0;i<ArraySize(InputMass);i++)
            InputMass[i].BestValue=InputMass[i].Value;
      //reducimos la temperatura
      if(((ModOfAlg==0) && (Fnew==Fopt)) || (ModOfAlg==1))
        {
         for(i=0;i<ArraySize(InputMass);i++)
            InputMass[i].Temp=Optim.GetT(method,CoeffOfTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop),InputMass[i].Temp,it_agent,ArraySize(InputMass),P1,P2);
        }
      Frame.FrameTester(Fnew,Fopt,InputMass,iteration,it_agent);          //añadimos el nuevo frame
      it_agent++;                                                         //aumentamos el contador de iteraciones    
      alg_err=Optim.WriteData(InputMass,Fopt,it_agent);                   //anotamos los nuevos valores en un archivo
      if(alg_err!=0)
         return alg_err;
     }
   return Fopt;
  }

Vamos a analizar el código de la función con más detalle.

• Se comprueba la finalización del algoritmo al alcanzar la temperatura mínima. Si la temperatura de cada parámetro ha alcanzado el valor mínimo, se añade el frame id=-1, los valores de los parámetros no se cambian más. En la interfaz gráfica de la ventana del terminal, al usuario se le propone finalizar la optimización con el botón "Stop" en el simulador de estrategias. 
• Con la ayuda del método GetFunction, se calcula el nuevo valor de la función objetivo Fnew, usando los resultados de la pasada del asesor.
• Dependiendo del criterio de optimización (ver el recuadro 3), el valor de Fnew se compara con el mejor resultado de Fopt, y se ejecuta la comprobación del paso a un nuevo estado.
• Si el paso a un nuevo estado se ha ejecutado, los valores actuales de los parámetros optimizables se convierte en los mejores:

 for(i=0;i<ArraySize(InputMass);i++)
         InputMass[i].BestValue = InputMass[i].Value;

• Se comprueban las condiciones de la reducción de la temperatura actual, de darse su cumplimiento, la nueva temperatura se calcula con la ayuda del método GetT de la clase AnnealingMethod.
• Se añade un nuevo frame, los valores de los parámetros optimizables se anotan en un archivo.

En la función OnTester añadimos frames para su posterior procesamiento en la función OnTesterPass. Vamos a echar un vistazo a su código:

void OnTesterPass()
  {
      Frame.FrameTesterPass(Crit);//método de representación de frames en la interfaz gráfica
  }

En la función OnTesterPass se llama al método FrameTesterPass de la clase FrameAnnealingMethod para representar el proceso de optimización en la ventana del terminal.

Después de finalizar la optimización, se llama la función OnTesterDeInit:

void OnTesterDeinit()
  {
   Frame.FrameToFile(4);
   Frame.FrameDeinit();
  }

En esta función se llaman dos métodos de la clase FrameAnnealingMethod: FrameToFile y FrameDeinit. En el método FrameToFile se anotan los resultados de la optimización en un archivo de texto. El parámetro de entrada de este método es el número de parámetros optimizables del asesor. El método FrameDeinit en la ventana del terminal muestra al usuario un mensaje sobre la finalización de la optimización.

Después de finalizar la optimización, la interfaz gráfica creada con la ayuda de los métodos de la clase FrameAnnealingMethod, permite representar los frames con la velocidad establecida. Podemos detener la representación de frames e iniciarla de nuevo. Para ello se han previsto los botones correspondientes en la interfaz gráfica (ver la fig. 4). Para procesar los eventos en la ventana del terminal, se ha añadido al código del asesor el método OnChartEvent:

void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam)
  {
   Frame.FrameOnChartEvent(id,lparam,dparam,sparam,Crit); //método de trabajo con la interfaz gráfica 
  }

En el método OnChartEvent se llama al método FrameOnChartEvent de la clase FrameAnnealingMethod, que gestiona la representación de los frames en la ventana del terminal.

Con esto hemos finalizado la modificación del código del asesor MovingAverage. Vamos a poner a prueba el algoritmo.

Simulación del algoritmo

El algoritmo desarrollado del método de recocido es estocástico (dispone de funciones para calcular magnitudes aleatorias), por eso cada inicio del algoritmo mostrará un resultado distinto. Para comprobar el funcionamiento del algoritmo y descubrir sus ventajas y desventajas, es necesario iniciar la optimización del asesor muchas veces. Esto ocupará un tiempo considerable, por eso haremos lo siguiente: inciamos la optimización en el modo "Lento (iteración de parámetros completa", guardamos los resultados obtenidos y después simulamos el algoritmo con estos datos.

Para poner a prueba el algoritmo, se usará el asesor TestAnnealing.mq5 (se adjunta al artículo en el directorio test.zip). Este carga el recuadro con los resultados de optimización obtenidos con el método de iteración completa desde un archivo de texto: las columnas 1-4 son los valores de las variables, la columna 5 representa los valores de la función objetivo. El algoritmo implementado en el asesor TestAnnealing con la ayuda del método de recocido se desplazará por el recuadro y encontrará los valores de la función objetivo. Este método de simulación permitirá comprobar el funcionamiento del método de recocido con diferentes datos obtenidos con el método de iteración completa.

Bien, vamos a comenzar. Primero comprobamos el funcionamiento del algoritmo usando como ejemplo la optimización de un asesor moderno: Moving Average period.

Iniciamos la optimización del asesor en el modo de iteración completa con los siguientes parámetros originales:

• Maximum Risk in percentage — 0,02; Descrease factor — 3;Moving Average period: 1 - 120, salto: 1; Moving Average shift — 6.
• Periodo: 01.01.2017 — 31.12.2017, modo comercial - sin retrasos, ticks: OHLC en M1, depósito inicial 10000, apalancamiento — 1:100, divisa — EURUSD.
• La optimizaicón se ejecutará según el criterio Balance max.

Guardamos el resultado y creamos un archivo de texto con los datos obtenidos. Los datos en el archivo de texto los clasificamos en orden creciente según el valor del parámetro Moving Average period, como se muestra en la fig.5.

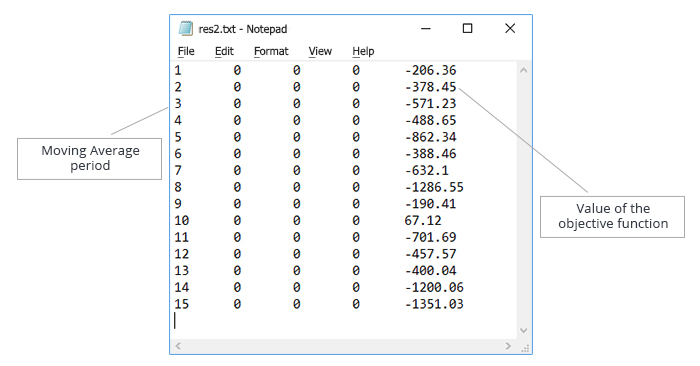
Fig. 5. Optimización del parámetro Moving Average period. Archivo de texto con los datos para la simulación del funcionamiento del algoritmo

En el modo de iteración completa se han ejecutado 120 iteraciones. Simularemos el algoritmo del método de recocido con el siguiente número de iteraciones: 30 (variante 1), 60 (variante 2), 90 (variante 3). Nuestro objetivo es comprobar el funcionamiento del algoritmo al reducir el número de iteraciones.

Para cada variante se han realizado 10000 inicios de optimización con el método de recocido, usando los datos obtenidos con el método de iteración completa. El algoritmo implementado en el asesor TestAnnealing.mq5 calcula cuántas veces se ha encontrado el mejor valor de la función objetivo y cuántas veces se han encontrado valores de la función objetivo diferentes al mejor en un 5%, 10%, 15%, 20%, 25%. 

Se han obtenido los siguientes resultados de optimización.

Para 30 iteraciones del algoritmo, los índices obtenidos con el recocido ultra-rápido con la variante de disminución de temperatura en cada iteración son:

Desviciación con respecto al mejor valor de la función objetivo, %	Resultado, %
0	33
5	44
10	61
15	61
20	72
25	86

Los datos de este recuadro se integran de la forma siguiente: el mejor valor de la función objetivo se ha obtenido en el 33% de los inicios (en 3 300 inicios de 10 000), se ha obtenido una desviación con respecto al mejor valor en un 5% en el 44% e los inicios, etcétera.

Para 60 iteraciones del algoritmo, lidera el recocido de Cauchy, pero la mejor variante ha sido la opción con reducción de temperatura al pasar a un nuevo estado. Los resultados son los siguientes:

Desviciación con respecto al mejor valor de la función objetivo, %	Resultado, %
0	47
5	61
10	83
15	83
20	87
25	96

De esta forma, al reducir las iteraciones 2 veces en comparación con la iteración completa, el algoritmo del método de recocido encuentra el mejor valor de la función objetivo en el 47% de los casos.

Para 90 iteraciones del algoritmo, el recocido de Boltzmann y el recocido de Cauchy con la variante de reducción de temperatura en el paso a un nuevo estado han mostrado un resultado aproximadamente igual. Vamos a exponer los resultados para el recocido de Cauchy

Desviciación con respecto al mejor valor de la función objetivo, %	Resultado, %
0	62
5	71
10	93
15	93
20	95
25	99

De esta forma, al reducir las iteraciones 1/3 veces en comparación con la iteración completa, el algoritmo del método de recocido encuentra el mejor valor de la función objetivo en el 62% de los casos. Pero ya con una desviación del 10-15% pueden obtenerse resultados bastante aceptables.

El método de recocido ultra-rápido se probó con los parámetros p1 = 1, p2 = 1, y al aumentar el número de iteraciones, el resultado obtenido fue peor que el recocido de Boltzmann y el recocido de Cauchy. Sin embargo, en el algoritmo de recocido ultra-rápido existe una peculiaridad: cambiando el coeficiente p1, p2 podemos ajustar la velocidad de disminución de la temperatura.

Vamos a ver el gráfico de cambio de temperatura para el recocido ultra-rápido (ver 6):

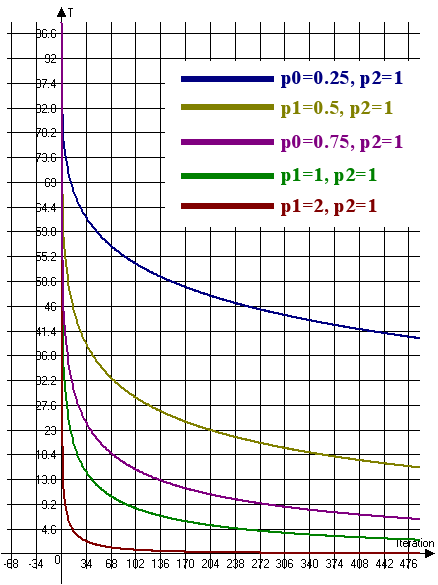
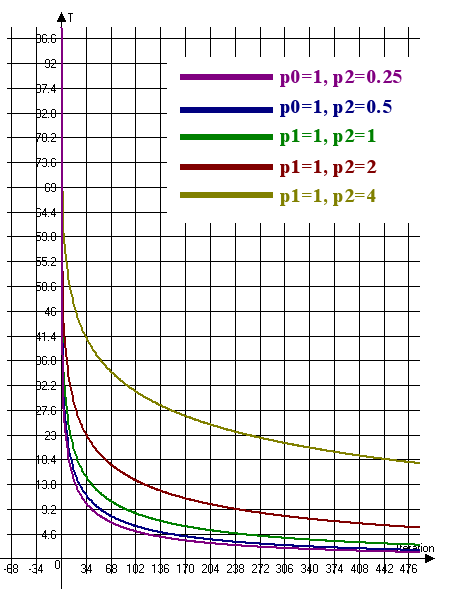
Fig. 6. Gráfico de cambio de temperatura para el recocido ultra-rápido (T0=100, n=4)

En la fig. 6 se comprende que para reducir la velocidad de cambio de la temperatura es necesario aumentar el coeficiente p1 y reducir el coeficiente p2. Por consiguiente, para aumentar la velocidad de cambio de la temperatura es necesario disminuir el coeficiente p1 y aumentar el coeficiente p2.

Con 60 y 90 iteraciones, el recocido ultra-rápido ha mostrado los peores resultados, porque la temperatura ha descendido demasiado rápido. Tras el descenso del coeficiente p1 se han obtenido los siguientes resultados:

Número de iteraciones	p1	p2	0%	5%	10%	15%	20%	25%
60	0,5	1	57	65	85	85	91	98
90	0,25	1	63	78	93	93	96	99

Gracias al recuadro, podemos entender que el mejor valor de la función objetivo se ha obtenido con un 57% de inicios a 60 iteraciones y con un 63% de inicios a 90 iteraciones.

De esta manera, al optimizar un parámetro, el mejor resultado lo ha mostrado el algoritmo de recocido ultra-rápido; sin embargo, es necesario elegir los coeficientes p1 y p2 dependiendo del número de iteraciones.

Como hemos dicho más arriba, el algoritmo del método de recocido es estocástico, por eso comparamos su funcionamiento con la búsqueda aleatoria. Para ello, en cada iteración generaremos un valor aleatorio para el parámetro con un salto y rango establecidos. En nuestro caso, los valores del parámetro Moving Average period se generarán con un salto de 1, en un rango de 1 a 120.

La búsqueda aleatoria se realiza en las mismas condiciones que con el algoritmo del método de recocido:

• número de iteraciones: 30, 60, 90
• número de inicios en cada variante: 10000

Los resultados de la búsqueda aleatoria se muestran en el recuadro:

Número de iteraciones	0%	5%	10%	15%	20%	25%
30	22	40	54	54	64	84
60	40	64	78	78	87	97
90	52	78	90	90	95	99

Comparamos los resultados del la búsqueda aleatoria y del recocido ultra-rápido. El siguiente recuadro muestra el incremento en tanto por ciento entre los valores de la búsqueda aleatoria y el recocido ultra-rápido. Por ejemplo, con 30 iteraciones, el algoritmo de recocido ultra-rápido encuentra con un 50% más de eficacia el mejor valor de la función, en comparación con la búsqueda aleatoria.

Número de iteraciones	0%	5%	10%	15%	20%	25%
30	50	10	12,963	12,963	12,5	2,381
60	42,5	1,563	8,974	8,974	4,6	1,031
90	21,154	0	3,333	3,333	1,053	0

En el recuadro podemos ver que, al aumentar el número de iteraciones, disminuye la ventaja del algoritmo de recocido ultra-rápido.

Ahora vamos a pasar a la simulación del algoritmo para optimizar dos variables del asesor: Moving Average period y Moving Average shift. Primero formamos los datos de entrada, iniciando el método de iteración completa en el simulador de estrategias con los siguientes parámetros:

• Maximum Risk in percentage — 0,02; Descrease factor — 3; Moving Average period: 1-120; Moving Average shift - 6-60.
  
• Periodo: 01.01.2017 — 31.12.2017, modo comercial - sin retrasos, ticks: OHLC en M1, depósito inicial 10000, apalancamiento — 1:100, divisa — EURUSD
• La optimizaicón se ejecutará según el criterio Balance max.

Guardamos el resultado y creamos un archivo de texto con los datos obtenidos. Los datos en el archivo de texto los clasificamos en orden creciente según el parámetro Moving Average period. El archivo formado se muestra en la fig. 7.

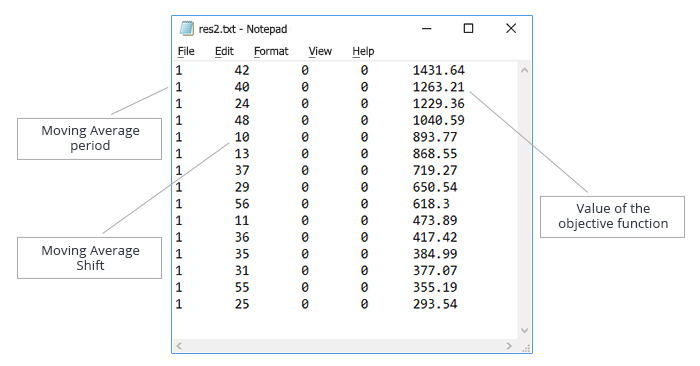
Fig. 7. Optimización de los parámetros Moving Average period y Moving Average shift.Archivo de texto con los datos para la optimización del funcionamiento del algoritmo

El método de iteración completa para las dos variables se ejecuta en 6600 iteraciones. Vamos a tratar de reducir su número usando el método de recocido. Ponemos a prueba el algoritmo con el siguiente número de iteraciones: 330, 660, 1665, 3300, 4950. Número de inicios en cada variante: 10000.   

Los resultados de la simulación son los siguientes.

330 iteraciones: el recocido de Cauchy no ha mostrado malos resultados, pero los mejores pertenecen al algoritmo de recocido ultra-rápido con la variante de reducción de la temperatura en cada iteración y los coeficientes p1= 1, p2=1.

660 iteraciones: el recocido de Cauchy y el recocido ultra-rápido con la variante de reducción de la temperatura en cada iteración y los coeficientes p1= 1, p2=2 han mostrado unos resultados más o menos iguales.

Con 1665, 3300 y 4950 iteraciones, el mejor resultado lo ha mostrado el recocido ultra-rápido con la variante de reducción de la temperatura en cada iteración y los siguientes valores de los coeficientes p1 y p2:

• 1665 iteraciones: p1= 0,5, p2=1
• 3300 iteraciones: p1= 0,25, p2=1
• 4950 iteraciones: p1= 0,5, p2=3

Reunimos los resultados en un recuadro:

Número de iteraciones	0%	5%	10%	15%	20%	25%
330	11	11	18	40	66	71
660	17	17	27	54	83	88
1665	31	31	41	80	95	98
3300	51	51	62	92	99	99
4950	65	65	75	97	99	100

Del recuadro podemos sacar las siguientes conclusiones:

• al acortar las iteraciones 10 veces, el algoritmo de recocido ultra-rápido encuentra el mejor resultado de la función objetivo el 11% de las ocasiones, pero en un 71% de los casos obtenemos un valor de la función objetivo que es solo un 25% peor que el mejor resultado.
• al acortar las iteraciones 2 veces, el algoritmo de recocido ultra-rápido encuentra el mejor resultado de la función objetivo el 51% de las ocasiones, pero casi con un 100% de probabilidad el algoritmo encuentra un valor de la función objetivo que sea solo un 20% peor que el mejor resultado.

Por lo tanto, el algoritmo de recocido ultra-rápido se puede utilizar para evaluar rápidamente la rentabilidad de las estrategias donde es aceptable una pequeña desviación con respecto al mejor valor.

Ahora vamos a comparar el algoritmo de recocido ultra-rápido con la búsqueda aleatoria. Los resultados de la búsqueda aleatoria se muestran en el recuadro:

Número de iteraciones	0%	5%	10%	15%	20%	25%
330	5	5	10	14	33	42
660	10	10	19	27	55	67
1665	22	22	41	53	87	94
3300	40	40	64	79	98	99
4950	55	55	79	90	99	99

Comparamos los resultados del la búsqueda aleatoria y del recocido ultra-rápido. Presentamos los resultados en forma de recuadro. En este se muestra el incremento en tanto por ciento entre los valores de la búsqueda aleatoria y el recocido ultra-rápido.

Número de iteraciones	0%	5%	10%	15%	20%	25%
330	120	120	80	185.714	100	69
660	70	70	42.105	100	50,909	31,343
1665	40,909	40,909	0	50,9434	9,195	4,255
3300	27,5	27,5	-3,125	16,456	1,021	0
4950	18,182	18,182	-5,064	7,778	0	1,01

De esta forma, observamos una ventaja significativa del algoritmo de recocido ultra-rápido con una pequeña cantidad de iteraciones. Al aumentarla, la ventaja se ve reducida, e incluso a veces se hace negativa. Debemos tener en cuenta que se observó una situación similar al probar el algoritmo en la optimización de un parámetro.

Ahora pasemos a lo importante: vamos a comparar el algoritmo de recocido ultra-rápido y el algoritmo genético (AG), incorporado en el simulador de estrategias.

Comparamos el AG y el recocido ultra-rápido en la optimización de dos variables: Moving Average period y Moving Average shift

Podemos iniciar los algoritmos con los siguientes parámetros de entrada:

• Maximum Risk in percentage — 0,02; Descrease factor — 3; Moving Average period: 1 — 120, salto: 1; Moving Average shift — 6-60, salto: 1
• Periodo: 01.01.2017 — 31.12.2017, modo comercial - sin retrasos, ticks: OHLC en M1, depósito inicial 10000, apalancamiento — 1:100, divisa — EURUSD
• La optimización se ejecuta según el criterio Balance max

Realizamos 20 inicios del algoritmo genético, guardamos los resultados y el número medio de iteraciones en el que se ejecuta el algoritmo.

Después de 20 inicios del AG, se han obtenido los siguientes valores de la función objetivo: 1392.29; 1481.32; 2284.46; 1665.44; 1435.16; 1786.78; 1431.64; 1782.34; 1520.58; 1229.36; 1482.23; 1441.36; 1763.11; 2286.46; 1476.54; 1263.21; 1491.09; 1076.9; 913.42; 1391.72.

Número medio de iteraciones: 175, valor medio de las iteraciones: 1529.771.

Teniendo en cuenta que el mejor valor de la función objetivo es 2446.33, el AG da un resultado muy bueno, pues el valor medio de la función objetivo es de solo el 62,53% del mejor valor.

Ahora realizamos 20 inicios del algoritmo de recocido ultra-rápido en 175 iteraciones con los parámetros: p1=1, p2=1.

El algoritmo de recocido ultra-rápido ha sido iniciado en 4 agentes de simulación, en este caso, además, la búsqueda del valor de la función objetivo se ha ejecutado en cada agente de forma autónoma, de tal forma que en cada agente de simulación se ejecuten 43-44 iteraciones. Se han obtenido los siguientes resultados: 1996.83; 1421.87; 1391.72; 1727.38; 1330.07; 2486.46; 1687.51; 1840.69; 1687.51; 1472.19; 1665.44; 1607.19; 1496.9; 1388.37; 1496.9; 1491.09; 1552.02; 1467.08; 2446.33; 1421.15.

Valor medio de la función objetivo: 1653.735, un 67.6% del mejor valor de la función objetivo, y ligeramente superior al obtenido por el AG.

Iniciamos el algoritmo de recocido ultra-rápido en un agente de simulación, ejecutando en él 175 iteraciones: como resultado, el valor medio de la función objetivo es de 1731.244 (70.8% del mejor valor).

Comparamos el AG y el recocido ultra-rápido en la optimización de cuatro variables: Moving Average period, Moving Average shift, Descrease factor y Maximum Risk in percentage.

Podemos iniciar los algoritmos con los siguientes parámetros de entrada:

• Moving Average period: 1 — 120, salto 1; Moving Average shift — 6-60, шаг 1; Descrease factor: 0.02 — 0.2, salto: 0,002; Maximum Risk in percentage: 3-30, salto: 0.3.
• Periodo: 01.01.2017 — 31.12.2017, modo comercial - sin retrasos, ticks: OHLC en M1, depósito inicial 10000, apalancamiento — 1:100, divisa — EURUSD
• La optimización se ejecuta según el criterio Balance max

El AG se ejecuta en 4870 iteraciones con un mejor valor de 32782.91. La iteración completa no se ha iniciado debido al gran número de variantes, por eso, vamos a comparar simplemente los resultados obtenidos por el AG y el algoritmo de recocido ultra-rápido.

El algoritmo de recocido ultra-rápido se ha iniciado con los parámetros p1=0.75, p2=1 en 4 agentes de simulación y ha finalizado con el resultado 26676.22. Con estos ajustes, el algoritmo no funciona muy bien. Vamos a acelerar el descenso de la temperatura, estableciendo p1=2, p2=1. También debemos destacar que la temperatura calculada según la fórmula:
T0*exp(-p1*exp(-p2/4)*n^0.25), donde n - es el número de iteración,

desciende bruscamente ya en la primera iteración (con n=1, T=T0*0.558). Por eso, vamos a aumentar el coeficiente con la temperatura inicial, indicando el parámetro CoeffOfTemp=4. Al iniciar el algoritmo con estos ajustes, el resultado mejora notablemente: 39145.25. El funcionamioento del algoritmo se muestra en el siguiente vídeo:

 

Demostración del funcionamiento del recocido ultra-rápido con los parámetros 1=2, p2=1

De esta forma, el algoritmo de recocido ultra-rápido es un competidor digno del AG, y con los ajustes correctos, puede mostrar un resultado mejor.

Conclusión

En el artíclo se han analizado el algoritmo de recocido, su implementación y la inclusión en el asesor Moving Average. Se ha simulado su funcionamiento al optimizar diferentes números de parámetros en el asesor Moving Average. Asimismo, hemos comparado el funcionamiento del método de recocido con el funcionamiento del algoritmo genético.

Hemos puesto a prueba diferentes implementaciones del método de recocido: el recocido de Boltzmann, el recocido de Cauchy (recocido rápido) y el recocido ultra-rápido. Los mejores resultados los ha mostrado el método de recocido ultra-rápido.

Podemos destacar las principales ventajas del método de recocido:

• optimización de diferentes números de parámetros;
• los parámetros del algoritmo se pueden ajustar, lo cual permite usarlo de forma efectiva en distintas tareas de optimización;
• elección del número de iteraciones del algoritmo;
• la interfaz gráfica permite monitorear el funcionamiento del algoritmo, representar el mejor resultado y representar de nuevo los resultados del funcionamiento del algoritmo.

A pesar de sus considerables ventajas, el algoritmo del método de recocido tiene las siguientes desventajas:

• no es posible iniciar el algoritmo en la simulación en la nube;
• resulta complejo de conectar al asesor y requiere que se elijan los parámetros para obtener los mejores resultados.

Las desventajas indicadas se pueden eliminar desarrollando un módulo universal en el que ir incluyendo diferentes algoritmos para optimizar los parámetros del asesor. El módulo, tras recibir los valores de la función objetivo después de la pasada del asesor, dará los nuevos valores de los parámetros optimizados para la siguiente pasada.

Adjuntamos al artículo los siguientes archivos:

Nombre del archivo	Comentarios
AnnealingMethod.mqh	Clase para trabajar con el método de recocido, es necesario ubicarla en la carpeta /MQL5/Include
FrameAnnealingMethod.mqh	Clase para representar en la ventana del terminal el proceso de ejecución del algoritmo, es necesario ubicarla en la carpeta /MQL5/Include
SimpleTable.mqh	Clase auxiliar para trabajar con los recuadros de la interfaz gráfica, es necesario ubicarla en la carpeta /MQL5/Include
Moving Average_optim.mq5	Asesor Moving Average modificado
test.zip	Directorio que contiene TestAnnealing.mq5 para simular el algoritmo del método de recocido con los datos de entrada cargados desde un archivo de texto, y los archivos auxiliares
AnnealingMethod.zip	Archivo Zip con imágenes para crear la interfaz del reproductor. Los archivos se deben ubicar en MQL5/Images/AnnealingMethod