制御された最適化: シミュレーティットアニーリング

イントロダクション

MetaTrader5トレーディングプラットフォームのストラテジーテスターは、パラメータと遺伝的アルゴリズムの完全な検索、つまり、2 つの最適化オプションのみを提供します。 この記事では、トレーディング戦略を最適化するための新しいメソッドを提案します (シミュレーティットアニーリング)。 このメソッドのアルゴリズムは、その実装と任意のEAに統合します。 次に, その性能をMovingAverage EA を用いてテストし、 シミュレーティットアニーリング法により得られた結果を遺伝的アルゴリズムと比較します。

シミュレーティットアニーリングアルゴリズム

シミュレーティットアニーリングは、確率最適化のメソッドの1つです。 目的関数の最適なオーダーランダム検索です。

シミュレーティットアニーリングアルゴリズムは、物質中の結晶構造の形成をシミュレートすることに基づいています。 物質の結晶格子内の原子 (例えば、金属) は、低いエネルギー準位の状態か、温度が下がるにつれて所定の位置にとどまることができます。 新しい状態に入る確率は、温度に比例して減少します。 このようなプロセスをシミュレートすることで、目的関数の最小値または最大値が検出されます。

目的関数の最適な検索のプロセスは、次のメソッドで表すことができます。

図1. 目的関数の最適な検索

図1において、目的関数の値は、凹凸面に沿ったボールローリングとして表されます。 青色のボールは、目標関数の初期値を示し、緑の1つは最終的な値 (グローバルミニマム) を示しています。 赤のボールは、ローカルの最小値での関数を指定します。 シミュレートされたアニーリングアルゴリズムは、目的関数のグローバル極値を検索し、ローカルの極端に "行き詰まる " ことを回避するために試みます。 グローバル極値に近づくと、ローカルの極値を超える確率が下がります。

シミュレーティットアニーリングアルゴリズムのステップを考えてみましょう。 わかりやすくするために、目的関数のグローバルな最小値の検索が考慮されます。 シミュレーティットアニーリングには、ボルツマンアニール、コーシーアニール (高速アニーリング)、超高速アニーリングの3つの主な実装オプションがあります。 違いは、新しい点x (i)と温度デクリメント法の生成メソッドにあります。

このアルゴリズムで使用される変数は次のとおりです。

• Fopt —目的関数の最適な値。
• Fbegin —目的関数の初期値。
• x (i) —現在のポイントの値 (目的関数の値はこのパラメータに依存します)。
• F (x (i )) —ポイントx (i)の目的関数の値。
• i — 反復カウンター;
• T0 — 初期温度;
• T — 現在の温度;
• Xopt —目的の関数の最適な値に到達するパラメータを指定します。
• Tmin -最小温度値。
• Imax —反復の最大数。

アニーリングアルゴリズムは、次の手順で構成されます。

• ステップ0。 アルゴリズムの初期化: Fopt = Fbegin、i = 0、T = T0、Xopt = 0。
• ステップ 1. 現在のポイントx (0)のランダムな選択と、指定されたポイントの目的関数F (x (0))の計算。 f (x (0<>))の場合は、 Fopt = f (x (0)) をクリックします。
• ステップ 2. 新しいポイントx (i)の生成。
• ステップ 3. 目的関数F (x (i))の計算。
• ステップ 4. 新しい状態への移行を確認します。 次に、2つの変更アルゴリズムを検討します。
• a). 新しい状態への遷移が発生した場合は、現在の温度を下げて手順5に進み、以外の場合は手順2に進みます。
• b). 新しい状態への移行を確認した結果に関係なく、現在の温度を下げて手順5に進みます。
• ステップ 5. アルゴリズムの終了基準を確認します (温度がTminの最小値に達したか、指定された回数の反復Imaxに到達)。 アルゴリズムの終了条件が満たされていない場合: 反復カウンター (i = i + 1) を増やし、ステップ2に進みます。

目的関数の最小値を見つける場合、より詳細に各手順を検討してみましょう。

手順 0。 初期値は、アルゴリズムの操作中に値が変更された変数に割り当てられます。

手順 1. 現在のポイントは、最適化する必要がある EA パラメータの値です。 このようなパラメータはいくつかあります。 各パラメータにはランダムな値が割り当てられ、指定したステップ(Pmin、Pmaxは最適化されたパラメータの最小および最大値) を使用して、 PminからPmaxまでの間隔で一様に分散されます。 生成されたパラメータを持つ EA はテスターで実行され、目標関数F (x (0))の値が計算され、EAパラメータの最適化 (指定された最適化基準の値) の結果となります。 f (x (0))<>の場合は、 Fopt = f (x (0)) となります。

手順 2. アルゴリズム実装バリアントに依存する新しい点の生成は、表1の式に従って行われます。

表1

アルゴリズムの実装のバリアント	新しい初期ポイントを計算するための式
ボルツマンアニール	ただし、N (0, 1) は標準正規分布です。
コーシーアニーリング (高速アニーリング)	ただし、C (0, 1) がコーシー分布
超高速アニーリング	ただし、 Pmax, Pminが最適化されたパラメータの最小値と最大数を指定します。 変数は、次の数式を使用して計算されます。 、ただし aが [0, 1] の間隔で一様に分布するランダム変数である場合、

手順 3. EA のテスト実行は、ステップ2で生成されたパラメータで実行されます。 目的関数F (x (i))には、選択した最適化基準の値が割り当てられます。

手順 4. 新しい状態への移行のチェックは、次のように実行されます。

• ステップ 1. f (x (i)<Fopt) の場合は、新しい状態Xopt = x (i)、Fopt = F (x (i)) に移動し、それ以外の場合はステップ2に進みます。
• ステップ 2. ランダム変数aを生成し、[0, 1] の間隔で一様に分散します。
• ステップ 3. 新しい状態への移行の確率を計算します。 
• ステップ 4. P > a の場合は、新しい状態Xopt = x (i)、Fopt = F (x (i)) に移動します。それ以外の場合は、アルゴリズムの変更а) が選択されている場合は、手順2に進みます。
• ステップ 5. 表2の数式を使用して、現在の温度を下げます。

表2

アルゴリズムの実装のバリアント	温度を下げるための式
ボルツマンアニール
コーシーアニーリング (高速アニーリング)	nは、値が最適化されるパラメータの数です。
超高速アニーリング	, ここで、 c (i) > 0と、次の数式によって計算されます。 ただし、 m (i)、 p (i)はアルゴリズムの追加パラメータです。 このアルゴリズムの構成を簡潔にするために、アルゴリズムの実行中にm (i) とp (i)の値は変更されません: m (i ) = const, p (i) = const

手順 5. このアルゴリズムは、次の条件が満たされたときに終了します。 T(i)<=Tminまたはi = Imax。

• 温度が急激に減少している温度変化法則を選択した場合は、すべての反復が完了するのを待たずに、 T(i)<=Tminを実行するときにアルゴリズムを終了します。
• 温度が非常にゆっくりと減少した場合は、繰り返しの最大数に達すると、アルゴリズムが終了します。 この場合、温度低減法のパラメータを変更する必要があるでしょう。

アルゴリズムのすべての手順を詳細に考慮したうえで、MQL5 の実装に進むことができます。

アルゴリズムの実装

最適化するパラメータを持つエキスパートにアルゴリズムを統合する実装と手順を考えてみましょう。

アルゴリズムの実装は、最適化されたEAに含める必要があり、2つの新しいクラスが必要になります。

• AnnealingMethod.mqh クラス-アルゴリズムの個別のステップを実装するメソッドのセットです。
• FrameAnnealingMethod.mqh クラス-ターミナルチャートに表示されるグラフィカルインターフェイスの操作メソッドです。

また、このアルゴリズムの操作には、OnTester、OnTesterInit、OnTesterDeInit、OnTesterPass 関数を EA コードに追加するための追加のコードがあります。 このアルゴリズムをエキスパートに統合するプロセスを図2に示します。

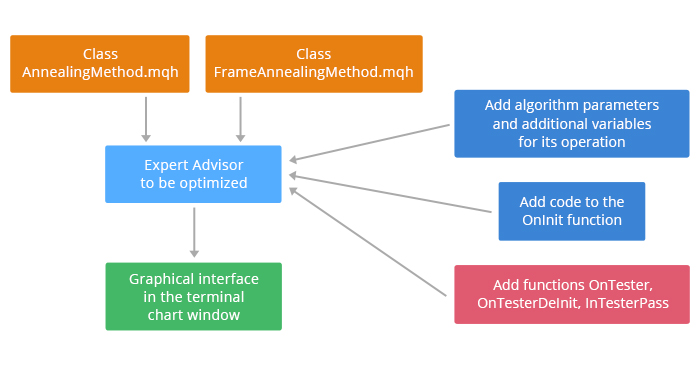
図2. EAのアルゴリズムを含む

AnnealingMethod と FrameAnnealingMethod クラスについて説明しましょう。

AnnealingMethod クラス

ここでは、AnnealingMethod クラスの説明とそのメソッドの詳細を示します。

#include "Math/Alglib/alglib.mqh"
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class AnnealingMethod
  {
private:
   CAlglib           Alg;                   //Alglib ライブラリのメソッドを操作するためのクラスのインスタンス
   CHighQualityRandStateShell state;        //乱数の生成クラスのインスタンス
public:
                     AnnealingMethod();
                    ~AnnealingMethod();
   struct Input                             //EA パラメータを使用するための構造
     {
      int               num;
      double            Value;
      double            BestValue;
      double            Start;
      double            Stop;
      double            Step;
      double            Temp;
     };
   uint              RunOptimization(string &InputParams[],int count,double F0,double T);
   uint              WriteData(Input &InpMass[],double F,int it);
   uint              ReadData(Input &Mass[],double &F,int &it);
   bool              GetParams(int Method,Input &Mass[]);
   double            FindValue(double val,double step);
   double            GetFunction(int Criterion);
   bool              Probability(double E,double T);
   double            GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2);
   double            UniformValue(double min,double max,double step);
   bool              VerificationOfVal(double start,double end,double val);
   double            Distance(double a,double b);
  };

ランダム変数を操作するための ALGLIB ライブラリの関数は、AnnealingMethod クラスメソッドの演算で使用されます。 このライブラリは、標準的なMetaTrader5パッケージの一部であり、 "Include/Math/Alglib" フォルダに位置しています。

図3. ALGLIB ライブラリ

プライベートブロックには、ALGLIB 関数を操作するためのCAlglibクラスとCHighQualityRandStateShellのインスタンスの宣言があります。

EA の最適化されたパラメータを使用するには、 Input構造体が作成されています。

• parameter number, num;
• パラメータの現在の値、 Value;
• パラメータの最適な値は、 BestValueです。
• 初期値, Start;
• 最終値, Stop;
• パラメータ値を変更するステップ、 Step;
• 指定されたパラメータの現在の温度 ( Temp)。

AnnealingMethod mqh クラスのメソッドについて考えてみましょう。

RunOptimization メソッド

シミュレートされたアニーリングアルゴリズムを初期化するように設計。 このメソッドのコード:

uint AnnealingMethod::RunOptimization(string &InputParams[],int count,double F0,double T)
  {
   Input Mass[];
   ResetLastError();
   bool Enable=false;
   double Start= 0;
   double Stop = 0;
   double Step = 0;
   double Value= 0;
   int j=0;
   Alg.HQRndRandomize(&state);                //初期化
   for(int i=0;i<ArraySize(InputParams);i++)
     {
      if(!ParameterGetRange(InputParams[i],Enable,Value,Start,Step,Stop))
         return GetLastError();
      if(Enable)
        {
         ArrayResize(Mass,ArraySize(Mass)+1);
         Mass[j].num=i;
         Mass[j].Value=UniformValue(Start,Stop,Step);
         Mass[j].BestValue=Mass[j].Value;
         Mass[j].Start=Start;
         Mass[j].Stop=Stop;
         Mass[j].Step=Step;
         Mass[j].Temp=T*Distance(Start,Stop);
         j++;
         if(!ParameterSetRange(InputParams[i],false,Value,Start,Stop,count))
            return GetLastError();
        }
      else
         InputParams[i]="";
     }
   if(j!=0)
     {
      if(!ParameterSetRange("iteration",true,1,1,1,count))
         return GetLastError();
      else
         return WriteData(Mass,F0,1);
     }
   return 0;
  }

このメソッドのインプットパラメータ:

• エキスパートアドバイザのすべてのパラメータの名前を含む文字列配列、 InputParams [];
• アルゴリズムの繰り返しの数、 count。
• 目的関数の初期値、 F0;
• 初期温度、 T。

RunOptimization メソッドは次のように動作します。

• 最適化する EA パラメータを検索します。 このようなパラメータは、ストラテジーテスタの "パラメータ " タブが "チィック " である必要があります。
• 見つかった各パラメータの値は、 Input型構造体の配列Mass[] に格納され、パラメータは最適化から除外されます。 ストラクチャー配列Mass[] :
• パラメータ数;
• UniformValue メソッドによって生成されるパラメータ値 (後述)。
• パラメータの最大 (開始) 値と最大 (ストップ) 数。
• パラメータ値を変更する手順 (ステップ);
• 式で計算された初期温度: T*Distance(Start,Stop);Distanceメソッドについては、以下で説明します。
• 検索が完了すると、すべてのパラメータが無効になり、反復パラメータがアクティブになり、アルゴリズムの繰り返し回数が決まります。
• Mass[] 配列の値、目的関数、および反復番号は、WriteData メソッドを使用してバイナリファイルに書き込まれます。 

WriteData メソッド

パラメータの配列、目的関数の値、および反復番号をファイルに書き込むように設計されています。

WriteData メソッドのコード:

uint AnnealingMethod::WriteData(Input &Mass[],double F,int it)
  {
   ResetLastError();
   int file_handle=0;
   int i=0;
   do
     {
      file_handle=FileOpen("data.bin",FILE_WRITE|FILE_BIN);
      if(file_handle!=INVALID_HANDLE) break;
      else
        {
         Sleep(MathRand()%10);
         i++;
         if(i>100) break;
        }
     }
   while(file_handle==INVALID_HANDLE);
   if(file_handle!=INVALID_HANDLE)
     {
      if(FileWriteArray(file_handle,Mass)<=0)
        {FileClose(file_handle); return GetLastError();}
      if(FileWriteDouble(file_handle,F)<=0)
        {FileClose(file_handle); return GetLastError();}
      if(FileWriteInteger(file_handle,it)<=0)
        {FileClose(file_handle); return GetLastError();}
     }
   else
      return GetLastError();
   FileClose(file_handle);
   return 0;
  }

このデータは、関数FileWriteArray、 FileWriteDouble 、および FileWriteIntegerを使用して、data.bin ファイルに書き込まれます。 このメソッドは、data.bin ファイルへのアクセスを複数回試行する関数を実装します。 これは、ファイルが別のプロセスによって占有されている場合のエラーを避けるために行われます。

ReadData メソッド

パラメータの配列、目的関数の値、およびファイルからの反復番号を読み取るように設計されています。 ReadData メソッドのコード:

uint AnnealingMethod::ReadData(Input &Mass[],double &F,int &it)
  {
   ResetLastError();
   int file_handle=0;
   int i=0;
   do
     {
      file_handle=FileOpen("data.bin",FILE_READ|FILE_BIN);
      if(file_handle!=INVALID_HANDLE) break;
      else
        {
         Sleep(MathRand()%10);
         i++;
         if(i>100) break;
        }
     }
   while(file_handle==INVALID_HANDLE);
   if(file_handle!=INVALID_HANDLE)
     {
      if(FileReadArray(file_handle,Mass)<=0)
        {FileClose(file_handle); return GetLastError();}
      F=FileReadDouble(file_handle);
      it=FileReadInteger(file_handle);
     }
   else
      return GetLastError();
   FileClose(file_handle);
   return 0;
  }

このデータは、 WriteDataメソッドによって書き込まれたのと同じ順番で、関数 FileReadArray、 FileReadDouble、 FileReadInteger を使用してファイルから読み込まれます。

GetParams メソッド

GetParamsメソッドは、EA の次の実行で使用されるエキスパートの最適化されたパラメータの新しい値を計算するために設計されています。 エキスパートの最適化されたパラメータの新しい値を計算するための式を表1に示します。

このメソッドのインプットパラメータ:

• アルゴリズムの実装のバリアント (ボルツマンアニーリング、コーシーアニーリングまたは超高速アニーリング);
• エントリーの最適化されたパラメータの配列;
• アルゴリズムを終了する最小温度を計算するための係数 CoeffTmin。

GetParamsメソッドのコード:

bool AnnealingMethod::GetParams(int Method,Input &Mass[],double CoeffTmin)
  {
   double delta=0;
   double x1=0,x2=0;
   double count=0;

   Alg.HQRndRandomize(&state);         //初期化
   switch(Method)
     {
      case(0):
        {
         for(int i=0;i<ArraySize(Mass);i++)
           {
            if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop))
              {
               do
                 {
                  if(count==100)
                    {
                     delta=Mass[i].Value;
                     count= 0;
                     break;
                    }
                  count++;
                  delta=Mass[i].Temp*Alg.HQRndNormal(&state);
                  delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step);
                 }
               //  while((delta<Mass[i].Start) || (delta>Mass[i].Stop));
               while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta));
               Mass[i].Value=delta;
              }
           }
         break;
        }
      case(1):
        {
         for(int i=0;i<ArraySize(Mass);i++)
           {
            if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop))
              {
               do
                 {
                  if(count==100)
                    {
                     delta=Mass[i].Value;
                     count=0;
                     break;
                    }
                  count++;
                  Alg.HQRndNormal2(&state,x1,x2);
                  delta=Mass[i].Temp*x1/x2;
                  delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step);
                 }
               while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta));
               Mass[i].Value=delta;
              }
           }
         break;
        }
      case(2):
        {
         for(int i=0;i<ArraySize(Mass);i++)
           {
            if(Mass[i].Temp>=CoeffTmin*Distance(Mass[i].Start,Mass[i].Stop))
              {
               do
                 {
                  if(count==100)
                    {
                     delta=Mass[i].Value;
                     count=0;
                     break;
                    }
                  count++;
                  x1=Alg.HQRndUniformR(&state);
                  if(x1-0.5>0)
                     delta=Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop);
                  else
                    {
                     if(x1==0.5)
                        delta=0;
                     else
                        delta=-Mass[i].Temp*(MathPow(1+1/Mass[i].Temp,MathAbs(2*x1-1))-1)*Distance(Mass[i].Start,Mass[i].Stop);
                    }
                  delta=FindValue(Mass[i].BestValue+delta,Mass[i].Step);
                 }
               while(!VerificationOfVal(Mass[i].Start,Mass[i].Stop,delta));
               Mass[i].Value=delta;
              }
           }
         break;
        }
      default:
        {
         Print("Annealing method was chosen incorrectly");
         return false;
        }
     }
   return true;
  }

このメソッドのコードについて詳しく考えてみましょう。

このメソッドには、選択したアルゴリズムの実装バリアントに応じて、新しいパラメータ値の計算を開始するための switch 演算子があります。 新しいパラメータ値は、現在の温度が最小よりも上にある場合にのみ計算されます。 最小温度は、式: CoeffTmin*Distance(Start,Stop)で計算され、ここで、開始とストップは、パラメータの最小値と最大数です。 Distanceメソッドは以下のように考えられます。

CAlglib クラスのHQRndRandomizeメソッドは、乱数を処理するためのメソッドを初期化するために呼び出されます。

 Alg.HQRndRandomize(&state);

標準正規分布の値の計算には、 CAlglib クラスのHQRndNormal関数が使用されます。

Alg.HQRndNormal(&state);

コーシー分布は、通常の分布や逆関数など、さまざまなメソッドでモデル化できます。 次の比率が使用されます。

C (0, 1) = x1/x2、ただし x1, x2 は, 通常, 独立変数, X1, X2 = N (0, 1) を分散している. CAlglib クラスのHQRndNormal2関数は、2つの通常の分散変数を生成するために使用されます。

 Alg.HQRndNormal2(&state,x1,x2);

通常、分散独立変数の値は x1, x2 に格納されます。

CAlglib クラスのHQRndUniformR (& state)メソッドは、0から1までの間隔で一様に分布する乱数を生成します。

Alg.HQRndUniformR(&state);

FindValueメソッド (後述) を使用すると、計算されるパラメータの値は、パラメータを変更するために指定したステップに丸められます。 計算されるパラメータの値がパラメータの変更範囲 ( VerificationOfValメソッドによってチェックされます) を超えた場合は、再計算が行われます。

FindValue メソッド

最適化された各パラメータの値は、指定したステップで変更する必要があります。 GetParamsで生成された新しい値は、この条件を満たしていない可能性があり、指定されたステップの倍数に丸められる必要があります。 FindValueメソッドによって行われます。 メソッドのインプットパラメータ: 丸められる値 (val)、およびパラメータを変更するためのステップ (ステップ)。

FindValueメソッドのコードを次に示します。

double AnnealingMethod::FindValue(double val,double step)
  {
   double buf=0;
   if(val==step)
      return val;
   if(step==1)
      return round(val);
   else
     {

      buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);
      if(MathAbs(val)-buf*MathAbs(step)>=MathAbs(step)/2)
        {
         if(val<0)
            return -(buf + 1)*MathAbs(step);
         else
            return (buf + 1)*MathAbs(step);
        }
      else
        {
         if(val<0)
            return -buf*MathAbs(step);
         else
            return buf*MathAbs(step);
        }
     }
  }

このメソッドのコードについて詳しく考えてみましょう。

ステップがパラメータのエントリー値と等しい場合、関数はその値を返します。

   if(val==step)
      return val;

ステップが1の場合、パラメータのエントリー値は、整数に丸められるだけである必要があります。

   if(step==1)
      return round(val);

それ以外の場合は、パラメータのエントリー値のステップ数を検索します。

buf=(MathAbs(val)-MathMod(MathAbs(val),MathAbs(step)))/MathAbs(step);

ステップの倍数である新しい値を計算します。

GetFunction メソッド

GetFunctionメソッドは、目的関数の新しい値を取得するように設計されています。 このメソッドのインプットパラメータは、ユーザー定義の最適化条件です。

選択した計算モードに応じて、目標関数は、テスト結果から計算された1つまたは複数の統計パラメータの値を取得します。 このメソッドのコード:

double AnnealingMethod::GetFunction(int Criterion)
  {
   double Fc=0;
   switch(Criterion)
     {
      case(0):
         return TesterStatistics(STAT_PROFIT);
      case(1):
         return TesterStatistics(STAT_PROFIT_FACTOR);
      case(2):
         return TesterStatistics(STAT_RECOVERY_FACTOR);
      case(3):
         return TesterStatistics(STAT_SHARPE_RATIO);
      case(4):
         return TesterStatistics(STAT_EXPECTED_PAYOFF);
      case(5):
         return TesterStatistics(STAT_EQUITY_DD);//min
      case(6):
         return TesterStatistics(STAT_BALANCE_DD);//min
      case(7):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_PROFIT_FACTOR);
      case(8):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_RECOVERY_FACTOR);
      case(9):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_SHARPE_RATIO);
      case(10):
         return TesterStatistics(STAT_PROFIT)*TesterStatistics(STAT_EXPECTED_PAYOFF);
      case(11):
        {
         if(TesterStatistics(STAT_BALANCE_DD)>0)
            return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_BALANCE_DD);
         else
            return TesterStatistics(STAT_PROFIT);
        }
      case(12):
        {
         if(TesterStatistics(STAT_EQUITY_DD)>0)
            return TesterStatistics(STAT_PROFIT)/TesterStatistics(STAT_EQUITY_DD);
         else
            return TesterStatistics(STAT_PROFIT);
        }
      case(13):
        {
         //カスタム条件を指定します。
         return TesterStatistics(STAT_TRADES)*TesterStatistics(STAT_PROFIT);
        }
      default: return -10000;
     }
  }

コードからわかるように、目的関数を計算する14の方法がメソッドに実装されています。 つまり、ユーザーはさまざまな統計パラメータによってエキスパートを最適化できます。 統計パラメータの詳細な説明は、ドキュメントを参照してください。

確率メソッド

確率メソッドは、新しい状態への遷移を識別するために設計されています。 メソッドのインプットパラメータ: 目標関数 (E) と現在の温度 (T) の前と現在の値の差。 このメソッドのコード:

bool AnnealingMethod::Probability(double E,double T)
  {
   double a=Alg.HQRndUniformR(&state);
   double res=exp(-E/T);
   if(res<=a)
      return false;
   else
      return true;
  }

このメソッドは、0から1までの間隔で一様に分散されたランダム変数аを生成します。

a=Alg.HQRndUniformR(&state);

得られた値は、式 exp (-E/T) と比較されます。 a > exp (-E/T) の場合、このメソッドは true を返します (新しい状態への遷移が実行されます)。

GetTメソッド

GetTメソッドは、新しい温度値を計算します。 このメソッドのインプットパラメータ:

• アルゴリズムの実装のバリアント (ボルツマンアニーリング、コーシーアニーリングまたは超高速アニーリング);
• 温度の初期値、T0;
• 温度の前の価値、Tlast;
• 反復番号、it;
  
• 最適化されたパラメータの数、D;
• 超高速アニーリング用の補助パラメータ p1 と p2。

このメソッドのコード:

double AnnealingMethod::GetT(int Method,double T0,double Tlast,int it,double D,double p1,double p2)
  {
   int Iteration=0;
   double T=0;
   switch(Method)
     {
      case(0):
        {
         if(Tlast!=T0)
            Iteration=(int)MathRound(exp(T0/Tlast)-1)+1;
         else
            Iteration=1;
         if(Iteration>0)
            T=T0/log(Iteration+1);
         else
            T=T0;
         break;
        }
      case(1):
        {
         if(it!=1)
            Iteration=(int)MathRound(pow(T0/Tlast,D))+1;
         else
            Iteration=1;
         if(Iteration>0)
            T=T0/pow(Iteration,1/D);
         else
            T=T0;
         break;
        }
      case(2):
        {
         if((T0!=Tlast) && (-p1*exp(-p2/D)!=0))
            Iteration=(int)MathRound(pow(log(Tlast/T0)/(-p1*exp(-p2/D)),D))+1;
         else
            Iteration=1;
         if(Iteration>0)
            T=T0*exp(-p1*exp(-p2/D)*pow(Iteration,1/D));
         else
            T=T0;
         break;
        }
     }
   return T;
  }

このメソッドは、表2の数式に従って、アルゴリズムの実装のバリアントに応じて新しい温度値を計算します。 新しい状態への遷移が発生した場合にのみ温度を増加させるアルゴリズムの実装を考慮に入れるために、現在の反復は、前の温度値 Tlast を使用して計算します。 したがって、現在の温度は、アルゴリズムの現在の反復に関係なく、メソッドが呼び出されたときに減少します。

UniformValue メソッド

UniformValue メソッドは、最小、最大値、およびステップを考慮して、最適化されたパラメータのランダムな値を生成します。 このメソッドは、最適化されたパラメータの初期値を生成するために、アルゴリズムの初期化中にのみ使用します。 このメソッドのインプットパラメータ:

• 最大パラメータ値、 max;
• 最小パラメータ値、 min;
• パラメータを変更する手順については、stepを実行します。

このメソッドのコード:

double AnnealingMethod::UniformValue(double min,double max,double step)
  {
   Alg.HQRndRandomize(&state);       //初期化
   if(max>min)
      return FindValue(Alg.HQRndUniformR(&state)*(max-min)+min,step);
   else
      return FindValue(Alg.HQRndUniformR(&state)*(min-max)+max,step);
  }

VerificationOfVal メソッド

VerificationOfVal は、(val) 変数の指定された値が範囲外であるかどうかをチェックします (start、end)。 このメソッドは、 GetParamsメソッドで使用されます。

このメソッドのコード:

bool AnnealingMethod::VerificationOfVal(double start,double end,double val)
  {
   if(start<end)
     {
      if((val>=start) && (val<=end))
         return true;
      else
         return false;
     }
   else
     {
      if((val>=end) && (val<=start))
         return true;
      else
         return false;
     }
  }

このメソッドは、パラメータの変更ステップが負の値であることを考慮して、条件 "start<end" をチェックします。

Distanceメソッド

Distanceメソッドは、2つのパラメータ (a と b) の間の距離を計算し、a の初期値と b の最終的な値のパラメータ変更範囲を計算するアルゴリズムで使用されます。

このメソッドのコード:

double AnnealingMethod::Distance(double a,double b)
  {
   if(a<b)
      return MathAbs(b-a);
   else
      return MathAbs(a-b);
  }

FrameAnnealingMethod クラス

FrameAnnealingMethod クラスは、アルゴリズムの実行プロセスをターミナルウィンドウに表示するように設計されています。 FrameAnnealingMethod クラスの説明を次に示します。

#include<SimpleTable.mqh></SimpleTable.mqh>
#include<ControlsBmpButton.mqh></ControlsBmpButton.mqh>
#include<ControlsLabel.mqh></ControlsLabel.mqh>
#include<ControlsEdit.mqh></ControlsEdit.mqh>
#include<AnnealingMethod.mqh></AnnealingMethod.mqh>
//+------------------------------------------------------------------+
//| Class for the output of the optimization results                 |
//+------------------------------------------------------------------+
class FrameAnnealingMethod
  {
private:
   CSimpleTable      t_value;
   CSimpleTable      t_inputs;
   CSimpleTable      t_stat;
   CBmpButton        b_playbutton;
   CBmpButton        b_backbutton;
   CBmpButton        b_forwardbutton;
   CBmpButton        b_stopbutton;
   CLabel            l_speed;
   CLabel            l_stat;
   CLabel            l_value;
   CLabel            l_opt_value;
   CLabel            l_temp;
   CLabel            l_text;
   CLabel            n_frame;
   CEdit             e_speed;
   long              frame_counter;

public:
   //---コンストラクタ/デストラクタ
                     FrameAnnealingMethod();
                    ~FrameAnnealingMethod();
   //ストラテジーテスターの---イベント
   void              FrameTester(double F,double Fbest,Input &Mass[],int num,int it);
   void              FrameInit(string &SMass[]);
   void              FrameTesterPass(int cr);
   void              FrameDeinit(void);
   void              FrameOnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam,int cr);
   uint              FrameToFile(int count);
  };

FrameAnnealingMethod クラスには、次のメソッドが含まれます。

• FrameInit —ターミナルウィンドウにグラフィカルインターフェイスを作成します。
• FrameTester —現在のデータフレームを追加します。
• FrameTesterPass —現在のデータフレームをターミナルウィンドウに出力します。
• FrameDeInit —エキスパート最適化の完了に関するテキスト情報を表示します。
• FrameOnChartEvent —ボタンのイベントを処理します。
• FrameToFile —テスト結果をテキストファイルに保存します。

このメソッドのコードは、FrameAnnealingMethod.mqh ファイル (アーティクルに添付) に用意されています。 FrameAnnealingMethod クラスのメソッドが動作するには、SimpleTable.mqh ファイル (アーティクルに添付) が必要です。 MQL5/Include に配置します。 ファイルはこのプロジェクトから採用されており、テーブルセルから値を読み取ることができるメソッドを使用して補足されています。

FrameAnnealingMethod クラスを使用して、ターミナルウィンドウで作成されたサンプルのグラフィカルインターフェイスを次に示します。

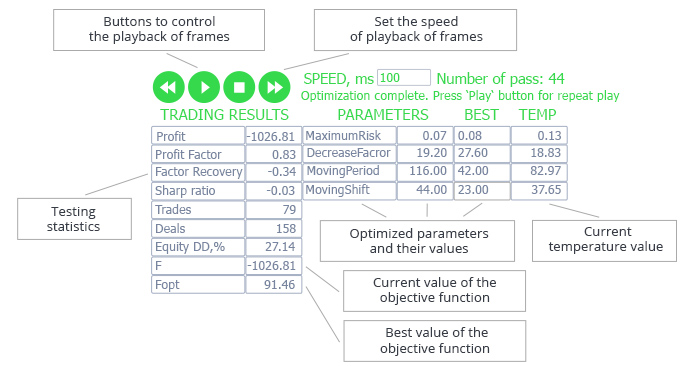
図4. アルゴリズムの動作を示すグラフィカルインタフェース

テーブルの左側には、現在の実行の結果に基づいてストラテジーテスターによって生成された統計パラメータと、目的関数の現在および最適な値 (この例では、純利益が目的関数として選択されます) があります。

最適化されたパラメータは、テーブルの右側にあります: パラメータ名、現在の値、最適値、現在の温度。

このテーブル上には、アルゴリズムの実行が完了した後にフレームの再生を制御するボタンがあります。 したがって、エキスパートの最適化が完了したら、指定した速度で再生することができます。 ボタンを使用すると、フレームの再生をストップし、再生が中断されたフレームからもう一度開始できます。 再生速度は、ボタンを使用して調整することも、手動で設定することもできます。 現在の実行数は、速度の値の右側に表示されます。 アルゴリズム操作に関する補助情報は以下に表示されます。

AnnealingMethod と FrameAnnealingMethod のクラスが検討されています。 次に、移動平均に基づくエキスパートアドバイザを使用したアルゴリズムのテストに進みます。

移動平均に基づく EA のアルゴリズムのテスト

アルゴリズムをテストするための EA の準備

エキスパートのコードは、アルゴリズムを実行するように変更する必要があります。

• クラス AnnealingMethod と FrameAnnealingMethod を含め、アルゴリズムの操作の補助変数を宣言します。
• OnTester、OnTesterInit、OnTesterDeInit、OnTesterPass、OnChartEvent 関数を追加するには、コードを追加します。

追加されたコードは 操作には影響せず、ストラテジーテスタで最適化された場合にのみ実行されます。

さて、始めましょう。

OnTesterInit 関数によって生成された初期パラメータでファイルをインクルードします。

#property tester_file "data.bin"

クラス AnnealingMethod と FrameAnnealingMethod をインクルード:

// including classes
#include<AnnealingMethod.mqh></AnnealingMethod.mqh>
#include<FrameAnnealingMethod.mqh></FrameAnnealingMethod.mqh>

インクルードされたクラスのインスタンスを宣言

AnnealingMethod Optim;
FrameAnnealingMethod Frame;

アルゴリズムの操作の補助変数を宣言します。

Input InputMass[];            //インプットパラメータの配列
string SParams[];             //インプットパラメータ名の配列
double Fopt=0;                //関数の最適な値
int it_agent=0;               //テストエージェントのアルゴリズム反復番号
uint alg_err=0;               //エラー番号

シミュレートされたアニーリングアルゴリズムは、タスクの過程で、最適化したパラメータの値を変更します。 この目的に、EA のインプットパラメータは次のように変更されます。

double MaximumRisk_Optim=MaximumRisk;
double DecreaseFactor_Optim=DecreaseFactor;
int MovingPeriod_Optim=MovingPeriod;
int MovingShift_Optim=MovingShift;

EA のすべての関数では、パラメータを置き換えます: MaximumRisk 、 MaximumRisk_Optim、 DecreaseFactor 、 DecreaseFactor_Optim、MovingPeriod、 MovingPeriod_Optim、 MovingShiftMovingShift_Optimを使用します。

アルゴリズムの動作を設定するための変数を次に示します。

sinput int iteration=50;         //繰り返し回数
sinput int method=0;             //0-ボルツマンアニール、1-コーシーアニーリング、2-超高速アニーリング
sinput double CoeffOfTemp=1;     //初期温度の尺度係数
sinput double CoeffOfMinTemp=0;  //最小温度係数
sinput double Func0=-10000;      //目的関数の初期値
sinput double P1=1;              //超高速アニーリングの追加パラメータ p1
sinput double P2=1;              //超高速アニーリングの追加パラメータ, p2
sinput int Crit=0;               //目的関数計算法
sinput int ModOfAlg=0;           //アルゴリズム修正タイプ
sinput bool ManyPoint=false;     //複数ポイントの最適化

アルゴリズムのパラメータは、その操作中に変更しないでください。したがって、すべての変数はsinput識別子で宣言されます。

表3は、宣言された変数の目的について説明します。

表3

変数名	目的
繰り返し	アルゴリズムの繰り返し回数を定義します。
メソッド	アルゴリズムの実装のバリアントを定義します: 0 —ボルツマンアニーリング, 1 —コーシーアニーリング, 2 —超高速アニーリング
CoeffOfTemp	式によって計算される初期温度を設定する係数を定義します: T0=CoeffOfTemp*Distance(Start,Stop)、ただし、開始ポジション、ストップがパラメータの最小値と最大数、距離は AnnealingMethod クラスのメソッド (説明上記)
CoeffOfMinTemp	アルゴリズムを終了する最小温度を設定する係数を定義します。 最大温度は、初期温度と同様に計算されます: Tmin=CoeffOfMinTemp*Distance(Start,Stop)、ここで、開始、パラメータの最小値と最大数をストップすると、距離は AnnealingMethod クラスのメソッドです (前述)
Func0	目的関数の初期値
P1,P2	超高速アニーリングにおける現在の温度の計算に使用されるパラメータ (表2参照)
Crit	最適化基準: 0—純利益合計; 1—利益率; 2—回復係数; 3-シャープレシオ; 4—期待されるペイオフ; 5-エクイティドローダウン最大; 6-バランスドローダウン最大; 7—純利益合計 + 利益率 8—総純利益 + 回収率 9—総純利益 + シャープレシオ; 10—総純利益 + 期待ペイオフ; 11—総純利益 + 残高のドローダウン最大; 12—総純利益 + 自己資本ドローダウン最大; 13-カスタム基準。 目的関数は、AnnealingMethod クラスの GetFunction 関数で計算されます。
ModOfAlg	アルゴリズムの変更の種類: 0-新しい状態への遷移が発生した場合は、現在の温度を下げて、アルゴリズムの完了のチェックに進み、それ以外の場合は、最適化されたパラメータの新しい値を計算します。 1-新しい状態への移行を確認した結果に関係なく、現在の温度を下げて、アルゴリズム完了のチェックに進みます。
ManyPoint	true —各テストエージェントに対して、最適化されたパラメータの異なる初期値が生成されます。 false —各テストエージェントに対して、最適化されたパラメータの同じ初期値が生成されます。

コードを、次のように、関数の先頭に追加します。

//+------------------------------------------------------------------+
//| Simulated annealing                                              |
//+------------------------------------------------------------------+
 if(MQL5InfoInteger(MQL5_OPTIMIZATION))
    {
     //ファイルを開き、データを読み取る
     //FileGetInteger ( "data bin "、FILE_EXISTS、false)
     //{
         alg_err=Optim.ReadData(InputMass,Fopt,it_agent);
         if(alg_err==0)
           {
            //最初の実行の場合、異なるポイントから検索を実行する場合は、パラメータをランダムに生成します。
            if(Fopt==Func0)
              {
               if(ManyPoint)
                  for(int i=0;i<ArraySize(InputMass);i++)
                    {
                     InputMass[i].Value=Optim.UniformValue(InputMass[i].Start,InputMass[i].Stop,InputMass[i].Step);
                     InputMass[i].BestValue=InputMass[i].Value;
                    }
              }
            else
               Optim.GetParams(method,InputMass,CoeffOfMinTemp);    //新しいパラメータの生成
            // fill the parameters of the Expert Advisor
            for(int i=0;i<ArraySize(InputMass);i++)
               switch(InputMass[i].num)
                 {
                  case (0): {MaximumRisk_Optim=InputMass[i].Value; break;}
                  case (1): {DecreaseFactor_Optim=InputMass[i].Value; break;}
                  case (2): {MovingPeriod_Optim=(int)InputMass[i].Value; break;}
                  case (3): {MovingShift_Optim=(int)InputMass[i].Value; break;}
                 }
           }
         else
           {
            Print("Error reading file");
            return(INIT_FAILED);
           }
//+------------------------------------------------------------------+
//|                                                                |
//+------------------------------------------------------------------+

詳細については、コードを調べてみましょう。 追加されたコードは、ストラテジーテスタの最適化モードでのみ実行されます。

if(MQL5InfoInteger(MQL5_OPTIMIZATION))

次に、このデータは AnnealingMethod クラスの RunOptimization メソッドによって生成されたデータの bin ファイルから読み込まれます。 このメソッドは OnTesterInit 関数で呼び出され、関数コードは次のようになります。

alg_err=Optim.ReadData(InputMass,Fopt,it_agent);

データがエラーなしで読み取られた場合 (alg_err = 0)、アルゴリズムが最初の反復 (Fopt == Func0) にあるかどうかを確認するためにチェックが実行され、それ以外の場合は EA の初期化はエラーで失敗します。 最初の反復で、 ManyPoint = trueの場合、最適化されたパラメータの初期値が生成され、 Input型のInputMass構造体に格納されます (AnnealingMethod クラスで説明します)、それ以外の場合はGetParamsメソッドが呼び出されます。

 Optim.GetParams(method,InputMass,CoeffOfMinTemp);//新しいパラメータの生成

そして、パラメータの値MaximumRisk_Optim、 DecreaseFactor_Optim、 MovingPeriod_Optim、 MovingShift_Optimが満たされています。

次に、OnTesterInit 関数のコードについて考えてみましょう。

void OnTesterInit()
  {
  //すべての EA パラメータの名前の配列を埋める
   ArrayResize(SParams,4);
   SParams[0]="MaximumRisk";
   SParams[1]="DecreaseFactor";
   SParams[2]="MovingPeriod";
   SParams[3]="MovingShift";
   //最適化を開始する
   Optim.RunOptimization(SParams,iteration,Func0,CoeffOfTemp);
   //グラフィカルインターフェイスを作成する
   Frame.FrameInit(SParams);
  }

最初に、すべての EA パラメータの名前を含む文字列配列をエントリーします。 次に、RunOptimization メソッドを実行し、FrameInit メソッドを使用してグラフィカルインターフェイスを作成します。

指定された時間間隔で EA を実行した後、制御は OnTester 関数に移されます。 そのコードです:

double OnTester()
  {
   int i=0;                                                       //サイクルカウンタ
   int count=0;                                                   //補助変数
  //最小温度に達すると、アルゴリズムの完了を確認します。
   for(i=0;i<ArraySize(InputMass);i++)
      if(InputMass[i].Temp<CoeffOfMinTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop))
         count++;
   if(count==ArraySize(InputMass))
      Frame.FrameTester(0,0,InputMass,-1,it_agent);               //ゼロパラメータと id =-1 で新しいフレームを追加します。
   else
     {
      double Fnew=Optim.GetFunction(Crit);                        //関数の現在の値を計算します。
      if((Crit!=5) && (Crit!=6) && (Crit!=11) && (Crit!=12))      //目的関数を最大化する必要がある場合
        {
         if(Fnew>Fopt)
            Fopt=Fnew;
         else
           {
            if(Optim.Probability(Fopt-Fnew,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop)))
               Fopt=Fnew;
           }
        }
      else                                                        //目的関数を最小化する必要がある場合
        {
         if(Fnew<Fopt)
            Fopt=Fnew;
         else
           {
            if(Optim.Probability(Fnew-Fopt,CoeffOfTemp*InputMass[0].Temp/Optim.Distance(InputMass[0].Start,InputMass[0].Stop)))
               Fopt=Fnew;
           }
        }
      //最適なパラメータ値を上書きする
      if(Fopt==Fnew)
         for(i=0;i<ArraySize(InputMass);i++)
            InputMass[i].BestValue=InputMass[i].Value;
      //温度を下げる
      if(((ModOfAlg==0) && (Fnew==Fopt)) || (ModOfAlg==1))
        {
         for(i=0;i<ArraySize(InputMass);i++)
            InputMass[i].Temp=Optim.GetT(method,CoeffOfTemp*Optim.Distance(InputMass[i].Start,InputMass[i].Stop),InputMass[i].Temp,it_agent,ArraySize(InputMass),P1,P2);
        }
      Frame.FrameTester(Fnew,Fopt,InputMass,iteration,it_agent);          //新しいフレームを追加する
      it_agent++;                                                         //反復カウンターを増やす
      alg_err=Optim.WriteData(InputMass,Fopt,it_agent);                   //新しい値をファイルに書き込む
      if(alg_err!=0)
         return alg_err;
     }
   return Fopt;
  }

この関数のコードについて詳しく考えてみましょう。

• 最小温度に達すると、アルゴリズムの完了をチェックします。 各パラメータの温度が最小値に達した場合、id =-1 のフレームが追加され、パラメータ値はもう変わりません。 ターミナルウィンドウのグラフィカルインターフェイスは、ストラテジーテスターの "Stop " ボタンを押して、最適化を完了するようユーザーにリクエストします。 
• GetFunction メソッドは、EAのテスト結果を使用して、目的関数 Fnew の新しい値を計算します。
• 最適化基準 (表3参照) によっては、Fnew の値が Fopt の最適値と比較され、新しい状態への遷移がチェックされます。
• 新しい状態への遷移が発生した場合は、最適化されたパラメータの現在の値が最適な設定になります。

 for(i=0;i<ArraySize(InputMass);i++)
         InputMass[i].BestValue = InputMass[i].Value;

• 現在の温度を下げるための条件がチェックされます。 これが満たされている場合、新しい温度は AnnealingMethod クラスのゲットメソッドを使用して計算されます。
• 新しいフレームが追加され、最適化されたパラメータの値がファイルに書き込まれます。

OnTester 関数は、OnTesterPass 関数でさらに処理されるフレームを追加します。 そのコードです:

void OnTesterPass()
  {
      Frame.FrameTesterPass(Crit);//メソッドを使用して、フレームをグラフィカルインターフェイスに表示します。
  }

OnTesterPass 関数は、FrameAnnealingMethod クラスの FrameTesterPass メソッドを呼び出して、ターミナルウィンドウに最適化処理を表示します。

最適化が完了すると、OnTesterDeInit 関数が呼び出されます。

void OnTesterDeinit()
  {
   Frame.FrameToFile(4);
   Frame.FrameDeinit();
  }

この関数は、FrameAnnealingMethod クラスの2つのメソッド (FrameToFile と FrameDeinit) を呼び出します。 FrameToFile メソッドは、最適化結果をテキストファイルに書き込みます。 このメソッドは、EA のパラメータの数をインプットとして最適化するために使用します。 FrameDeinit メソッドは、最適化の完了に関するメッセージをターミナルウィンドウに出力します。

最適化が完了すると、FrameAnnealingMethod クラスメソッドを使用して作成されたグラフィカルインターフェイスは、指定された速度でフレームを再生できます。 フレームの再生をストップして再起動することができます。 グラフィカルインタフェースの対応するボタンによって行われます (図4参照)。 ターミナルウィンドウでイベントを処理するために、OnChartEvent メソッドが EA コードに追加されました。

void OnChartEvent(const int id,const long &lparam,const double &dparam,const string &sparam)
  {
   Frame.FrameOnChartEvent(id,lparam,dparam,sparam,Crit); //グラフィカルインターフェイスを使用するメソッド
  }

OnChartEvent メソッドは、ターミナルウィンドウのフレームの再生を管理する FrameAnnealingMethod クラスの FrameOnChartEvent メソッドを呼び出します。

MovingAverage EA コードの修正を終了します。 アルゴリズムのテストを開始しましょう。

アルゴリズムのテスト

提案するシミュレーティットアニーリング法には確率的性質がある (ランダム変数を計算する関数が含まれている) ため, アルゴリズムの各実行は異なる結果を生成します。 アルゴリズムの動作をテストし、その長所と短所を特定するには、エキスパートの最適化を何度も実行する必要があります。 これにはかなりの時間がかかるので、次の処理が行われます: "低速完全アルゴリズム " モードで最適化を実行し、取得した結果を保存してから、データを使用してアルゴリズムをテストします。

このアルゴリズムは、TestAnnealing.mq5 EA (記事に添付されているtest.zip ファイルにあります) を使用してテストされます。 完全な検索メソッドによって得られた最適化結果のテーブルを読み込む5列のデータを含むテキストファイルから: 列1-4 は、変数の値を表し、列5は、目的関数の値を示しています。 TestAnnealing で実装されたアルゴリズムは、シミュレートされたアニーリング法を使用してテーブル内を移動し、目的関数の値を割り出します。 この手法により、完全検索で得られた各種データに対して、シミュレーティットアニーリングの性能を確認することができます。

さて、始めましょう。 まず、エキスパートの1つの変数 (移動平均期間) を最適化して、アルゴリズムのパフォーマンスをテストします。

完全検索モードでエキスパートの最適化を実行し、次の初期パラメータを指定します。

• パーセンテージの最大リスク-0.02;ファクターの減少— 3;移動平均期間: 1-120、ステップ: 1;移動平均シフト-6.
• 期間: 01.01.2017-31.12.2017、トレードモード: 遅延なし、ティック: 1 分 OHLC、デポジット: 1万、レバレッジ: 1:100、通貨: EURUSD。
• 最適化は、基準残高 max を使用して実行されます。

その結果を保存し、取得したデータを使用してテストファイルを作成します。 図5に示すように、テキストファイル内のデータは、 "移動平均期間 " パラメータ値の昇順でソートされます。

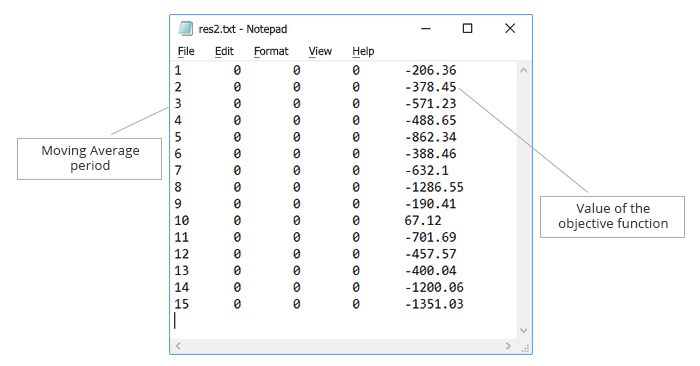
図5. "移動平均期間 " パラメータの最適化。 アルゴリズム操作をテストするためのデータを含むテキストファイル

120の反復は、完全な検索モードで実行されました。 シミュレートされたアニーリングのアルゴリズムは、次の繰り返し回数でテストされます:30 (バリアント 1)、60 (バリアント 2)、90 (バリアント 3)。 ここでの目的は、繰り返し回数を減らしながらアルゴリズムのパフォーマンスをテストすることです。

各バリアントについて、完全検索によって得られたデータに対してシミュレーティットアニールを用いて1万の最適化を実行しました。 TestAnnealing.mq5 EAで実装されたアルゴリズムは、最適な値が何回発見されたかだけでなく、目標関数の値が最も良いものと異なる回数を 5%、10%、15%、20%、25% と数えていた。 

以下のテスト結果が得られました。

アルゴリズムの30の繰り返しに、最もよい値は各繰り返しの温度の減少の超高速アニーリングによって得られました:

目的関数の最も良い値からの偏差、%	結果、%
0	33
5	44
10	61
15	61
20	72
25	86

このテーブルのデータは次のように解釈されます。目的関数の最適値は、実行の 33% で取得されました (1万の実行のうち3300で)、最適値からの 5% の偏差は、実行の 44% で得られました。

アルゴリズムの60の繰り返しに、コーシーアニーリングは導くが、最もよいバリアントは新しい状態への転移の間に温度低下した。 結果は次のとおりです。

目的関数の最も良い値からの偏差、%	結果、%
0	47
5	61
10	83
15	83
20	87
25	96

したがって、繰り返し回数が完全な検索に比べて半減したので、シミュレートされたアニーリング法は、47パーセントで目的関数の最もよい値を割り出します。

90の繰り返しまたはアルゴリズムに、新しい状態への転移の間の温度低下のボルツマンのアニーリングそしてコーシーのアニーリングはほぼ同じ結果を持っていた。 コーシーのアニーリングの結果は次のとおりです:

目的関数の最も良い値からの偏差、%	結果、%
0	62
5	71
10	93
15	93
20	95
25	99

したがって、繰り返し回数は完全な検索に比べて3分の1減少し、シミュレートされたアニーリング法は、このケースの 62% で目的関数の最適な値を検出します。 しかし、10-15% の偏差で許容可能な結果を得ることができます。

超高速アニーリング法をパラメータ p1 = 1, p2 = 1 でテストしました。 繰り返し回数を増やすと、ボルツマンアニールとコーシーアニーリングよりも、得られた結果に対する悪影響が大きくなりました。 しかし、超高速アニーリングアルゴリズムは1つの特異性を持っています: 係数 p1 を変更すると、 p2 は温度の減速速度を調整することができます。

超高速アニーリングの温度変化チャートを考えてみましょう (図6)。

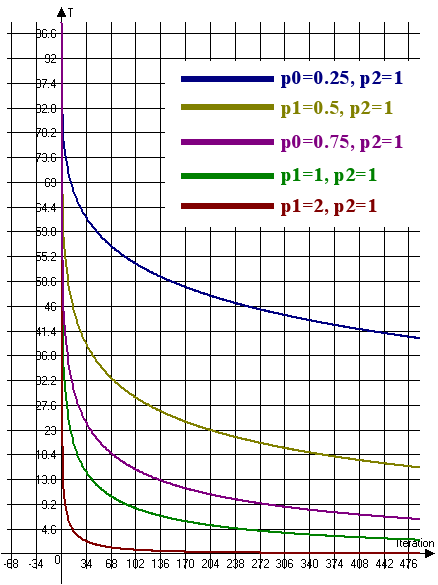
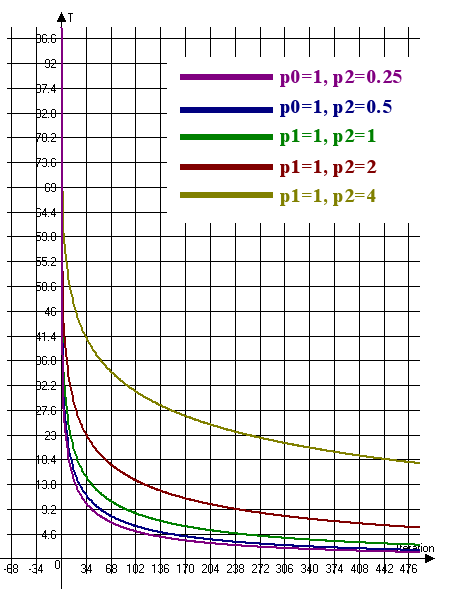
図6. 超高速アニールの温度変化チャート (T0 = 100, n = 4)

図6は、温度変化率を低下させるために係数 p1 を大きくして係数 p2 を小さくする必要があることを意味します。 したがって、温度変化率を高めるためには、係数 p1 を小さくして係数 p2 を大きくする必要があります。

60および90の繰り返しでは、超高速アニーリングは、温度が速すぎて落下したため、最悪の結果を示しました。 係数 p1 を減少させた後、以下の結果が得られた。

繰り返し回数	p1	p2	0%	5%	10%	15%	20%	25%
60	0.5	1	57	65	85	85	91	98
90	0.25	1	63	78	93	93	96	99

この表は、目標関数の最適値を60の繰り返しで実行し、90の繰り返しでの実行の 63% で 57% で取得したことを示しています。

したがって、1つのパラメータを最適化するときの最良の結果は、超高速アニーリングによって達成された。 ただし、繰り返し回数に応じて係数 p1 と p2 を選択する必要があります。

前述のように、シミュレーティットアニーリングアルゴリズムは確率的なので、その操作はランダムサーチと比較されます。 これを行うには、特定のステップと指定された範囲内のパラメータのランダムな値が各反復で生成されます。 この場合、 "移動平均期間 " パラメータの値は、1 ~ 120 の範囲のステップ1で生成されます。

ランダムサーチは、シミュレートされたアニーリングと同じ条件で実行されました。

• 反復の数:30、60、90
• 各バリアントの実行回数: 1万

ランダム検索の結果は、以下の表に示されています。

繰り返し回数	0%	5%	10%	15%	20%	25%
30	22	40	54	54	64	84
60	40	64	78	78	87	97
90	52	78	90	90	95	99

ランダムサーチと超高速アニーリングの結果を比較してみましょう。 ランダムサーチと超高速アニーリングの対応する値の増加率を表に示します。 たとえば、30回の繰り返しでは、超高速アニーリングアルゴリズムは、ランダム検索よりも関数の最適な値を見つけることに 50% 優れています。

繰り返し回数	0%	5%	10%	15%	20%	25%
30	50	10	12.963	12.963	12.5	2.381
60	42.5	1.563	8.974	8.974	4.6	1.031
90	21.154	0	3.333	3.333	1.053	0

この表は、繰り返し回数を増やすことで、超高速アニーリングアルゴリズムの利点を減らすことを示しています。

次に、EAの2つのパラメータの最適化に関するアルゴリズムのテストに進み、 "移動平均期間 " と "移動平均シフト " を確認してください。 まず、ストラテジーテスタで低速で完全検索を実行し、次のパラメータを指定してインプットデータを生成します。

• パーセンテージの最大リスク-0.02;ファクターの減少— 3;移動平均期間: 1-120;移動平均シフト-6-60。
  
• 期間: 01.01.2017-31.12.2017、トレードモード: 遅延なし、ティック: 1 分 OHLC、デポジット: 1万、レバレッジ: 1:100、通貨: EURUSD
• 最適化は、基準残高 max を使用して実行されます。

その結果を保存し、取得したデータを使用してテストファイルを作成します。 テキストファイル内のデータは、 "移動平均期間 " パラメータの昇順で並べ替えられます。 生成されたファイルを図7に示します。

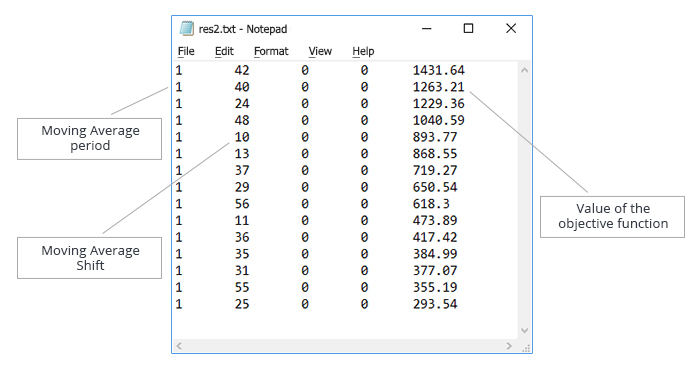
図7. "移動平均期間 " および "移動平均シフト " パラメータの最適化。 アルゴリズム操作をテストするためのデータを含むテキストファイル

2つの変数のスロー完全検索は、6600繰り返しで実行されます。 シミュレーティットアニーリングを用いて減します。 次の繰り返し回数を使用してアルゴリズムをテストします。 330, 660, 1665, 3300, 4950. 各バリアントの実行数: 1万。   

テスト結果は以下の通りです。

330繰り返し: コーシーアニールは良好な結果を示したが、各繰り返しの温度低下と係数 p1 = 1, p2 = 1 の超高速アニールによって最良の結果が得られた。

660繰り返し: 各繰り返しと係数 p1 = 1, p2 = 1 の温度低下によるコーシーアニール超高速アニーリングの結果はほぼ同じ結果を示した。

1665、3300および4950の繰り返しでは、各繰り返しの温度低下と p1 および p2 係数の次の値を持つ超高速アニーリングによって最良の結果が得られました。

• 1665繰り返し: p1 = 0.5、p2 = 1
• 3300繰り返し: p1 = 0.25、p2 = 1
• 4950繰り返し: p1 = 0.5、p2 = 3

最良の結果は、テーブルに要約されます:

繰り返し回数	0%	5%	10%	15%	20%	25%
330	11	11	18	40	66	71
660	17	17	27	54	83	88
1665	31	31	41	80	95	98
3300	51	51	62	92	99	99
4950	65	65	75	97	99	100

次の結論は、テーブルから導くことができます:

• 繰り返し回数が10回に減少すると、超高速アニーリングアルゴリズムは、ケースの 11% で目的関数の最適な値を検出します。しかし、このケースの 71% で、最高よりも悪い 25% である目的関数の値を生成します。
• 繰り返し回数が2回減少すると, 超高速アニーリング法は, 51% において目的関数の最適値を検出する。しかし、最高よりもわずか 20% 悪い目的関数の値を見つけるほぼ 100% の確率があります。

したがって、超高速アニーリングアルゴリズムは、最適な値からの小さな偏差が完全に許容される場合に、戦略の収益性を迅速に評価するために使用することができます。

ここでは、ランダム検索で超高速アニーリングアルゴリズムを比較してみましょう。 ランダム検索の結果は、以下の表に示されています。

繰り返し回数	0%	5%	10%	15%	20%	25%
330	5	5	10	14	33	42
660	10	10	19	27	55	67
1665	22	22	41	53	87	94
3300	40	40	64	79	98	99
4950	55	55	79	90	99	99

ランダムサーチと超高速アニーリングの結果を比較してみましょう。 この結果は、ランダム検索と超高速アニーリングの対応する値の間の割合の増加を示す表の形で表されます。

繰り返し回数	0%	5%	10%	15%	20%	25%
330	120	120	80	185.714	100	69
660	70	70	42.105	100	50.909	31.343
1665	40.909	40.909	0	50.9434	9.195	4.255
3300	27.5	27.5	-3.125	16.456	1.021	0
4950	18.182	18.182	-5.064	7.778	0	1.01

このように、超高速アニーリングアルゴリズムの大きな利点は、少数の繰り返しで観察されます。 増加すると、利点が減少し、時にはマイナスになります。 1つのパラメータを最適化してアルゴリズムをテストするとき、同様の状況が起こったことに注意してください。

さて、メインポイントですが、超高速アニーリングアルゴリズムと遺伝的アルゴリズム (GA) を比較して、ストラテジーテスターに統合しました。

GA と超高速アニールの2つの変数の最適化における比較: "移動平均期間 " と "移動平均シフト "

このアルゴリズムは、次の初期パラメータで開始されます。

• パーセンテージの最大リスク-0.02;ファクターの減少— 3;移動平均期間: 1 — 120, ステップ: 1;移動平均シフト-6-60、ステップ: 1
• 期間: 01.01.2017-31.12.2017、トレードモード: 遅延なし、ティック: 1 分 OHLC、デポジット: 1万、レバレッジ: 1:100、通貨: EURUSD
• 最適化は、基準残高 max を使用して実行されます

遺伝的アルゴリズムを20回実行し、結果を保存し、アルゴリズムを完了するために必要な反復の平均数を指定します。

GA の20の後で、次の値が得られた: 1392.29;1481.32;2284.46;1665.44;1435.16;1786.78;1431.64;1782.34;1520.58;1229.36;1482.23;1441.36;1763.11;2286.46;1476.54;1263.21;1491.09;1076.9;913.42;1391.72.

平均繰り返し回数: 175;目的関数の平均値: 1529.771。

目的関数の最高の値は2446.33 であることを考えると、GA は、目的関数の平均値は、最高の値の 62.53% であると良い結果を生成しません。

ここで、パラメータ: p1 = 1、p2 = 1 の175繰り返しで、超高速アニーリングアルゴリズムを20回実行します。

この超高速アニールは4つのテストに対して開始されたが、各エージェントに対して目的関数の探索が自律的に行われ、43-44 繰り返しを行いました。 以下の結果が得られました: 1996.83;1421.87;1391.72;1727.38;1330.07;2486.46;1687.51;1840.69;1687.51;1472.19;1665.44;1607.19;1496.9;1388.37;1496.9;1491.09;1552.02;1467.08;2446.33;1421.15.

目的関数の平均値: 1653.735, 67.6% 最適値の目的関数, わずかに GA によって得られたものよりも高い結果です。

1つのテストエージェントで超高速アニーリングアルゴリズムを実行し、175の繰り返し処理を行います。 その結果、目的関数の平均値は 1731.244 (最適値の 70.8%) でした。

4つの変数の最適化における GA と超高速アニーリングの比較: "移動平均期間 ", "移動平均シフト ", "ファクターを減少 " と "パーセントの最大のリスク".

このアルゴリズムは、次の初期パラメータで開始されます。

• 移動平均期間: 1 — 120, ステップ: 1;移動平均シフト-6-60、ステップ: 1;減少率: 0.02 — 0.2, ステップ: 0002;パーセンテージの最大リスク: 3-30、ステップ: 0.3。
• 期間: 01.01.2017-31.12.2017、トレードモード: 遅延なし、ティック: 1 分 OHLC、デポジット: 1万、レバレッジ: 1:100、通貨: EURUSD
• 最適化は、基準残高 max を使用して実行されます

GA は、32782.91 の最良の結果で、4870の繰り返しで完了しました。 可能な組み合わせが多数あるため、完全検索を開始できませんでした。したがって、 GAと超高速アニーリングアルゴリズムの結果を比較します。

超高速アニーリングアルゴリズムは、パラメータ p1 = 0.75 および p2 = 1 で4つのテストエージェントで開始され、26676.22 の結果で完成しました。 このアルゴリズムは、この設定ではよく実行されません。 p1 = 2, p2 = 1 を設定することにより、温度の低下を加速させてみましょう。 また、式で計算された温度に注意してください。
T0 * exp (-p1 * exp (-p2/4) * n ^ 0.25)、n は反復番号、

最初の繰り返し (n = 1, T = T0 * 0.558) で急激に減少します。 したがって、CoeffOfTemp = 4 を設定することにより、初期温度での係数を大きくします。 この設定を使用してアルゴリズムを実行すると、結果が大幅に改善されました: 39145.25。 アルゴリズムの操作は、次のビデオで示されています。

 

パラメータ p1 = 2, p2 = 1 の超高速アニーリングのデモンストレーション

したがって、超高速アニーリングアルゴリズムは、GA の価値のあるライバルであり、適切な設定でを勝るすることができます。

結論

この記事では、シミュレートされたアニーリングアルゴリズム、その実装と移動平均 EA への統合を考察しました。 移動平均 EA のパラメータの異なる数をテストし、その性能がテストされています。 また、シミュレーティットアニーリングの性能を遺伝的アルゴリズムと比較しています。

ボルツマンアニール、コーシーアニーリング、超高速アニーリングなどの様々な実装がテストされています。 最高の結果は、超高速アニーリングによって示されました。

ここでは、シミュレートされたアニーリングの主な利点を上げます。

• パラメータの異なる数の最適化;
• アルゴリズムパラメータはカスタマイズ可能で、さまざまな最適化タスクに有効な使用が可能です。
• アルゴリズムの繰り返しの選択可能な数。
• アルゴリズムの操作を監視し、最良の結果を表示し、アルゴリズムの操作結果を再生するグラフィカルインターフェイス。

大きな利点にもかかわらず、シミュレートされたアニーリングアルゴリズムには、次の欠点があります。

• このアルゴリズムはクラウドテストでは実行できません。
• エキスパートへの統合は複雑であり、最良の結果を得るためにパラメータを選択する必要があります。

これらの欠点は、エキスパートパラメータを最適化するための様々なアルゴリズムを含む汎用モジュールを開発することによって排除することができます。 テストの実行後に目的の関数の値を受け取ると、このモジュールは次の実行に最適化されたパラメータの新しい値を生成します。

次のファイルがこの記事に添付されています。

ファイル名	コメント
AnnealingMethod.mqh	シミュレーティットアニーリングアルゴリズムの動作に必要なクラスは、/MQL5/Include に配置する必要があります。
FrameAnnealingMethod.mqh	ターミナルウィンドウのアルゴリズム実行プロセスを表示するクラスは、/MQL5/Include に配置する必要があります。
SimpleTable.mqh	グラフィカルインターフェイスのテーブルを操作するための補助クラスは、/MQL5/Include に配置する必要があります
Moving Average_optim.mq5	移動平均 EA の修正版
test.zip	TestAnnealing.mq5 を含むアーカイブ、テストファイルから読み込んだエントリーデータに対するシミュレートされたアニーリングアルゴリズム、および補助ファイルをテストするためのファイル
AnnealingMethod.zip	プレーヤーのインターフェイスを作成するための画像と Zip ファイル。 このファイルは MQL5/Images/AnnealingMethod に配置する必要があります。