
Métodos de ordenação e sua visualização usando a MQL5
Conteúdo
- Introdução
- Aplicando a biblioteca Graphics\Graphic.mqh
- Troca, comparação e funções de limite
- Métodos de ordenação
- Ordenação por Seleção (Selection Sort)
- Ordenação por Inserção (Insertion Sort)
- Ordenação por Flutuação (Bubble Sort)
- Ordenação por Troca de Partição (Quick Sort)
- Ordenação por Intercalação (Merge Sort)
- Ordenação por Heap (Heap Sort)
- Ordenação de Raízes MSD/LSD (Radix Sort MSD/LSD)
- Outros métodos de ordenação
- Tabela de velocidade dos métodos
- Todos os métodos em uma única tela
- Testes em multi-threading
- Notas do autor
Introdução
Na web, você pode encontrar uma série de vídeos que mostram vários tipos de ordenação. Por exemplo, aqui você pode encontrar a visualização de 24 algoritmos de ordenação. Eu tomei esse vídeo como base, juntamente com uma lista de algoritmos de ordenação.
A biblioteca Graphic.mqh é responsável por trabalhar com gráficos na MQL5. Ela já foi descrita em vários artigos. Por exemplo, os recursos da biblioteca são mostrados em detalhes aqui. Meu objetivo é descrever suas áreas de aplicação e considerar o processo de ordenação em detalhes. O conceito geral de ordenação é descrito aqui, pois cada tipo de ordenação já possui pelo menos um artigo separado, enquanto que alguns tipos de ordenação são objetos de estudos detalhados.
Aplicando a biblioteca Graphics\Graphic.mqh
Primeiro, nós precisamos incluir a biblioteca.
#include <Graphics\Graphic.mqh>
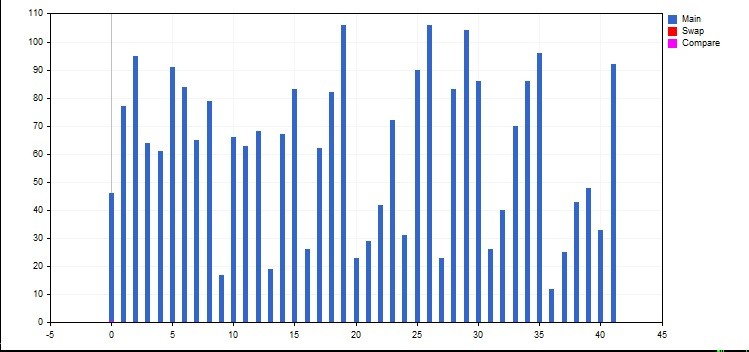
Vamos classificar as colunas do histograma através da aplicação das funções de troca e comparação Gswap() e GBool(), respectivamente. Os elementos a serem processados (comparação, substituição, etc.) são realçados em cores. Para conseguir isso, um objeto separado do tipo CCurve é atribuído a cada cor. Crie objetos globais para não compartimentá-los pelas funções Gswap (int i, int j, CGraphic &G, CCurve &A, CCurve &B e CCurve &C). A classe CCurve não possui um construtor padrão, por isso ela não pode ser simplesmente declarada globalmente. Portanto, declare globalmente os ponteiros do tipo CCurve — *CMain.
A cor pode ser definida de três maneiras diferentes. A mais visível delas é C'0x00,0x00,0xFF' ou C'Blue, Green, Red'. A curva é criada usando o CurveAdd() da classe CGraphic, que possui várias implementações. Para a maioria dos elementos, é conveniente selecionar o CurveAdd(arr, CURVE_HISTOGRAM, "Main") com um único array de valores, enquanto que para os auxiliares — CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap") com o array X de argumentos e o array Y de valores, uma vez que haverá apenas dois elementos. É conveniente criar arrays para linhas auxiliares globais.
#include <Graphics\Graphic.mqh> #property script_show_inputs input int N =42; CGraphic Graphic; CCurve *CMain; CCurve *CGreen; CCurve *CBlue; CCurve *CRed; CCurve *CViolet; double X[2],Y[2],XZ[2],YZ[2]; //+------------------------------------------------------------------+ //| Script da função de início do programa | //+------------------------------------------------------------------+ void OnStart() { //arrays------------------------------ double arr[]; FillArr(arr,N); X[0]=0;X[1]=0; Y[0] =0;Y[1]=0; //------------------------------------- Graphic.Create(0,"G",0,30,30,780,380); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //índice 0 CMain.HistogramWidth(4*50/N); CBlue =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); //índice 1 CBlue.Color(C'0xFF,0x00,0x00'); CBlue.HistogramWidth(4*50/N); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //índice 2 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(4*50/N); CGreen =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); //índice 3 CGreen.Color(C'0x00,0xFF,0x00'); CGreen.HistogramWidth(4*50/N); CViolet =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); //índice 4 CViolet.Color(C'0xFF,0x00,0xFF'); CViolet.HistogramWidth(4*50/N); Graphic.XAxis().Min(-0.5); Graphic.CurvePlot(4); Graphic.CurvePlot(2); Graphic.CurvePlot(0); //Graphic.CurvePlotAll(); Exibe todas as curvas disponíveis Graphic.Update(); Sleep(5000); int f =ObjectsDeleteAll(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void FillArr(double &arr[],int num) { int x =ArrayResize(arr,num); for(int i=0;i<num;i++) arr[i]=rand()/328+10; }
Graphic.XAxis().Min(-5) Define o recuo a partir do eixo Y, de modo que o elemento zero não se intercala com ele. Histogramwidth() é a largura da coluna.
A função FillArr() preenche o array com números aleatórios de 10 (não para mesclar com o eixo X) a 110. O array 'arr' é criado localmente para que as funções de troca tenham a aparência padrão swap(arr, i, j). O último comando ObjectDeleteAll remove todos os objetos desenhados. Caso contrário, teríamos que excluir o objeto através da Lista de Objetos do Menu - Ctrl + B.
Nossos preparativos estão completos. É hora de começar a ordenar.
Troca, comparação e funções de limite
Vamos escrever as funções para visualizar a troca, comparações e alocação de limites para a ordenação por divisão. A primeira função de troca void Gswap() é padrão, embora tenha a curva CRed para alocar os elementos comparados
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void Gswap(double &arr[],int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CRed.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmS); double sw = arr[i]; arr[i]=arr[j]; arr[j]=sw; //------------------------- Y[0] =0; Y[1] =0; CRed.Update(X,Y); CMain.Update(arr); Graphic.Redraw(); Graphic.Update(); //------------------------- }
Primeiro, aloque as colunas. Em seguida, retorne ao estado inicial após um tempo Sleep(TmS) definindo a velocidade de demonstração. Escreva as funções de comparação para "<" e "<=" como bool GBool(double arr, int i, int j) e GBoolEq(double arr, int i, int j) de forma semelhante. Adicione as colunas de outra cor CViole a elas.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool GBool(double &arr[], int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmC); Y[0]=0; Y[1]=0; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); return arr[i]<arr[j]; }
A função para alocar as extremidades, cujas colunas não devem ser apagadas.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i];YZ[1]=a[j]; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); }
Agora, vamos concentrar nossa atenção na ordenação.
Métodos de ordenação
Antes de proceder à análise dos métodos, eu recomendo iniciar o aplicativo VisualSort anexado abaixo (VisualSort.ex5). Ele permite visualizar visualmente como cada tipo funciona separadamente. O código de ordenação completo está no arquivo de inclusão GSort.mqh. O arquivo é bem grande, portanto, eu esbocei aqui apenas as principais ideias.
- A primeira ordenação, que geralmente começa o estudo é a Ordenação por Seleção. Primeiro, encontramos o número do valor mínimo na lista atual e substituímos pelo valor da primeira posição não ordenada.
template <typename T> void Select(T &arr[]) { int n = ArraySize(arr); for(int j=0;j<n;j++) { int mid=j; for(int i=j+1;i<n;i++) { if(arr[i]<arr[mid]) { mid=i; } } if(arr[j]>arr[mid]){swap(arr,j,mid);} } }
Aqui e mais abaixo, a função de troca é a Gswap() que foi descrita anteriormente, enquanto que a comparação dos elementos do array é então substituída por GBool(). Por exemplo, if(Arr[i]<arr[mid]) => if(GBool(arr,i,mid).
- O próximo tipo de ordenação (usado frequentemente quando jogamos cartas) é a Ordenação de Inserção. Neste método, os elementos da seqüência de entrada são analisados um de cada vez. Cada elemento recém chegado é colocado em um local adequado junto daqueles que foram ordenados anteriormente. Método básico:
template<typename T> void Insert(T &arr[]) { int n= ArraySize(arr); for(int i=1;i<n;i++) { int j=i; while(j>0) { if(arr[j]<arr[j-1]) { swap(arr,j,j-1); j--; } else j=0; } } }
Os derivados do método são Ordenação de Shell e Ordenação por Inserção Binária. O primeiro compara não apenas os elementos adjacentes, mas também aqueles localizados a uma certa distância um do outro. Em outras palavras, esta é a Ordenação de Inserção com passes preliminares "brutos".A Inserção Binária aplica a pesquisa binária para encontrar o local de inserção. Na demonstração acima mencionada (VisualSort.ex5), podemos ver claramente que o Shell procura a o array usando um "pente" gradualmente decrescente. A este respeito, há muita similaridade com o método Comb, descrito abaixo.
- Ordenação por Flutuação e seus derivados — Ordenação Shake, Gnom, Comb e Odd-Even. A ideia por trás da Ordenação por flutuação é simples: nós passamos por toda o array desde o início até o final, comparando dois elementos vizinhos. Se eles não estão ordenados, nós trocamos suas posições. Como resultado de cada iteração, o maior elemento será localizado no final do array. O processo é então repetido. No final, nós recebemos um array ordenado. O algoritmo básico de Ordenação por Flutuação:
template<typename T> void BubbleSort(T &a[]) { int n =ArraySize(a); for (int i = 0; i < n - 1; i++) { bool swapped = false; for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a,j,j+1); swapped = true; } } if (!swapped) break; } }
Na Ordenação de Shake ou método da coqueteleira, as passagens são feitas em ambas as direções, permitindo detectar elementos grandes e pequenos. A Odenação de Gnome é interessante porque é implementado em um único ciclo. Vamos dar uma olhada em seu código:
void GGnomeSort(double &a[]) { int n =ArraySize(a); int i=0; while(i<n) { if(i==0||GBoolEq(a,i-1,i)) i++; //if(i==0||a[i-1]<a[i]) else { Gswap(a,i,i-1); //Troca a[i] e a[i-1] i--; } } }
Se nós marcarmos o local dos elementos já ordenados, nós obteremos a Ordenação de Inserção. Comb usa a mesma ideia que o Shell: ele vai ao longo do array com pentes tendo etapas diferentes. O fator de redução ótimo = 1.247 ≈ ( 1 / ( 1-е^(-φ) ) ), onde "е" é um expoente e "φ" é o número de "ouro". Quando aplicados em pequenos arrays, a Ordenação de Comb e Shell são semelhantes aos métodos de ordenação rápidos em termos de velocidade. Ordenação de Odd-Even passa elementos ímpares/pares em turnos. Uma vez que ele foi desenvolvido para implementação multi-thread, ele não tem utilidade para o nosso caso.
- Métodos mais complexos são baseados no princípio de "divisão e conquista". Os exemplos padrão são Ordenação de Hoare ou QuickSort
A ideia geral do algoritmo é o seguinte: selecionamos o elemento pivô do array. Qualquer elemento do array pode ser selecionado como um pivô. Todos os outros elementos são comparados com o pivô e rearranjados dentro do array para que o array seja dividido em dois segmentos contínuos: "menor" do que o pivô e "maior" que ele. Se o comprimento do segmento for superior a um, a mesma seqüência de operações é realizada para segmentos "menores" e "maiores" de forma recursiva. A ideia básica pode ser encontrada no pseudocódigo:
algorithm quicksort(A, lo, hi) is if (lo < hi) { p = partition(A, lo, hi); quicksort(A, lo, p – 1); quicksort(A, p, hi);}
A diferença nas opções de ordenação neste caso é reduzida a diferentes maneiras de particionar o array. Na versão original, os ponteiros se movem um para o outro dos lados opostos. O ponteiro esquerdo encontra o elemento que excede o pivô, enquanto o direito procura o menor, e eles são trocados. Em outra versão, ambos os ponteiros se movem da esquerda para a direita. Quando o primeiro ponteiro encontra o elemento "menor", ele move esse elemento para a localização do segundo ponteiro. Se o array contiver muitos elementos idênticos, o particionamento aloca espaço para elementos iguais ao pivô. Tal arranjo é aplicado, por exemplo, quando é necessário categorizar funcionários apenas por duas chaves — "M" (masculino) e "F" (feminino). O particionamento apropriado é exibido abaixo:
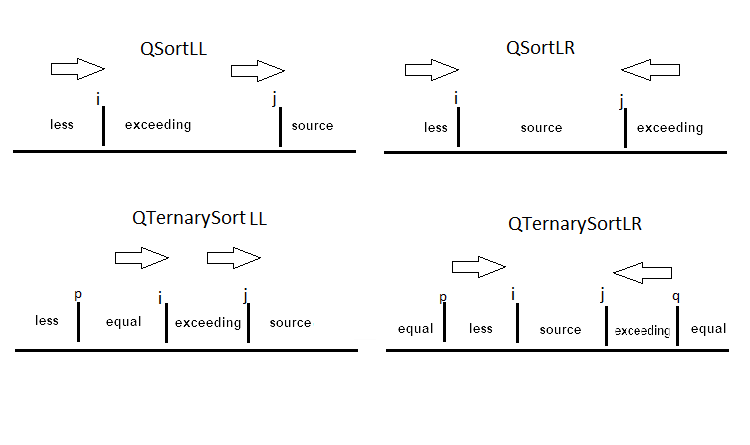
Vamos dar uma olhada no exemplo do QSortLR com particionamento de Hoare:
//----------------------QsortLR----------------------------------------+ void GQsortLR(double &arr[],int l,int r) { if(l<r) { GBorders(arr,l,r); int mid =PartitionLR(arr,l,r); GQsortLR(arr,l,mid-1); GQsortLR(arr,mid+1,r); } } int PartitionLR(double &arr[],int l,int r) { int i =l-1; int j =r; for(;;) { while(GBool(arr,++i,r)); j--; while(GBool(arr,r,j)){if(j==l) break;j--;} if(i>=j) break; Gswap(arr,i,j); } //--------------------------------------------- Gswap(arr,i,r); YZ[0]=0;YZ[1]=0; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); return i; }
O array pode ser dividido em 3, 4, 5... partes com vários elementos de pivô. A ordenação DualPivot com dois elementos de pivô também pode ser usada.
- Outros métodos baseados no princípio de "divisão e conquista" usam a intercalação das partes do array já ordenadas. Eles dividem o array até seu comprimento se tornar igual a 1 (ordenado), então eles aplicam a função de intercalação que também ordena os elementos ao longo do caminho. Princípio geral:
void GMergesort (double &a[], int l, int r) { int m = (r+l)/2; GMergesort(a, l, m); GMergesort(a, m+1, r) ; Merge(a, l, m, r); }
BitonicSort() faz a metade do array ascendente, enquanto que a outra decrescente seja combinada depois.
- Ordenação por Heap (Heap Sort)
O princípio geral é o seguinte. Forme um "heap" por "peneirar" o array. Remova o elemento antigo na parte superior do "heap". Mova-o para o final do array de origem como o mais antigo, substituindo-o pelo último elemento da parte não ordenada. Crie o novo "heap" com o tamanho de n-1, etc. Os "heaps" podem ser baseados em princípios diferentes. Por exemplo, a ordenação Smooth() aplica "heaps" tendo o número de elementos iguais aos números de Leonardo L(x+2) = L(x+1) +L(x) +1.
- Ordenação de Raízes. Ordenação por Contagem e Ordenação de Raízes MSD/LSD
A Ordenação por Contagem (Counting Sort) é um algoritmo de ordenação aplicando uma faixa de números do array (lista) para calcular os elementos correspondentes. A aplicação da Ordenação por Contagem é razoável apenas quando os números ordenados possuem um intervalo de valores possíveis, que é pequeno o suficiente em comparação com o conjunto ordenado, por exemplo, um milhão de números naturais inferiores a 1000. Seu princípio também é aplicado na Ordenação por Raízes. Aqui está o algoritmo:
void CountSort(double &a[]) { int count[]; double aux[]; int k =int(a[int(ArrayMaximum(a))]+1); int n =ArraySize(a); ArrayResize(count,k); ArrayResize(aux,n); for (int i=0;i<k;i++) count[i] = 0; for (int i=0;i<n;i++) count[int(a[i])]++; // número de elementos igual a i for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; // número de elementos que não excedem a i for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // preenche o array intermediário for(int i=0;i<n;i++)a[i]=aux[i]; }
As ideias da Ordenação por Contagem são aplicadas nas Ordenações MSD e LSD em tempo linear. Este é o tempo N*R, onde N é uma série de elementos, enquanto que R é um número de dígitos na representação numérica dentro do sistema de números selecionado. O MSD (dígito mais significativo) ordena pelo dígito superior, enquanto que o LSD (dígito menos significativo) — pelo menor. Por exemplo, no sistema binário, o LSD calcula quantos números terminam em 0 e 1 colocando os números pares (0) na primeira metade e, posteriormente, os números ímpares (1) para a segunda metade. Já o MSD, inicia com o maior dígito. No sistema decimal, ele coloca os números < 100 no início e os números > 100 mais adiante. Então, o array é novamente ordenado em segmentos 0-19, 10-19, ..., 100-109 etc. Esse método de ordenação é aplicado a números inteiros. No entanto, a cotação 1.12307 pode ser do tipo inteiro 1.12307*100 000.
A Ordenação por Troca de Partição - QuicksortB() é obtida combinando as ordenações Quick e de Raízes. A ordenação QSortLR é aplicada aqui, embora a seleção seja realizada pelo dígito superior em vez do elemento do array de pivô. Para fazer isso, é aplicado a função de busca do enésimo dígito do número e em LSD/MSD:
int digit(double x,int rdx,int pos) // Número x aqui, sitema de números rdx { // em nosso caso 2, índice pós dígito int mid =int(x/pow(rdx,pos)); return mid%rdx; }Primeiro, a classificação pelo maior dígito é executada int d =int(log(a[ArrayMaximum(a)])/log(2)), então as partes são ordenadas pelos menores dígitos recursivamente. Visualmente, ele parece semelhante ao QuickSortLR.
- Algumas ordenações específicas
A Ordenação de Ciclo (Cycle Sort) destina-se a sistemas onde a substituição de dados leva ao desgaste de recurso. Portanto, a tarefa aqui é encontrar a ordenação com a menor quantidade de trocas (Gswap). Ordenações de Ciclo são usadas para isso. A grosso modo, 1 é rearranjado para 3, 3 para 2, 2 para 1. Cada elemento é reorganizado tanto 0 ou 1 vez. Tudo isso demora muito tempo: O(n^2). Os detalhes sobre a ideia e o método podem ser encontrados aqui.
A Ordenação "Fantoche" (Stooge sort) é mais um exemplo de uma ordenação rebuscada e muito lenta. O algoritmo é o seguinte. Se o valor do elemento no final da lista for menor que o valor do elemento no início, eles devem trocar de lugares. Se o subconjunto atual da lista contiver 3 ou mais elementos, então: chame o Stoodge() de forma recursiva para os primeiros 2/3 da lista, chame recursivamente Stooda() para os últimos 2/3, chame Stooda() recursivamente para os primeiros 2/3 novamente, etc.
Tabela de velocidade dos métodos
| Métodos de ordenação | Tempo médio |
|---|---|
| Ordenação por Seleção (Selection Sort) | O(n^2) |
| Ordenação por Inserção (Insertion Sort) | O(n^2) |
| Ordenação de Seleção Binária | O(n^2) |
| Ordenação de Shell (Shell Sort) | O(n*log(n)) |
| Ordenação por Flutuação (Bubble Sort) | O(n^2) |
| Ordenação de Shaker/Cocktail | O(n^2) |
| Ordenação de Gnom (Gnom Sort) | O(n^2) |
| Ordenação de Comb (Comb Sort) | O(n*log(n)) |
| Ordenação por Intercalação (Merge Sort) | O(n*log(n)) |
| Ordenação Bitônica (Bitonic Sort) | O(n*log(n)) |
| Ordenação por Heap (Heap Sort) | O(n*log(n)) |
| Ordenação SmoothSort | O(n*log(n)) |
| Quick Sort LR | O(n*log(n)) |
| Quick Sort LL | O(n*log(n)) |
| Quick Sort (ternary, LR ptrs) | O(n*log(n)) |
| Quick Sort (ternary, LL ptrs) | O(n*log(n)) |
| Quick Sort (dual pivot) | O(n*log(n)) |
| Ordenação por Contagem | O(n+k) |
| Ordenação de Raízes (Radix LSD) | O(n*k) |
| Ordenação de Raízes (Radix MSD) | O(n*k) |
| Ordenação Binária Rápida (Quick Binary Sort) | O(n*log(n)) |
| Ordenação de Ciclo (Cycle Sort) | O(n^2) |
| Ordenação "Fantoche" (Stoodge Sort) | O(n^2.7) |
Todos os métodos em uma única tela
Vamos desenhar todos os tipos descritos em uma única tela simultaneamente. No vídeo, as ordenações descritas são executadas uma por vez. Os resultados foram editados no editor de vídeo. A plataforma de negociação não possui recursos internos de edição de vídeo. Existem várias soluções.
Opção 1
Simular ao multi-threading. Paralelizar os tipos para que seja possível sair da função após cada comparação e troca, passando a fila para outro tipo e depois voltar a inseri-lo novamente no mesmo local. A ausência do operador GOTO complica a tarefa. Por exemplo, é assim que a Ordenação de Seleção mais simples, descrita no início, se parece:
void CSelect(double &arr[]) { static bool ch; static int i,j,mid; int n =ArraySize(arr); switch(mark) { case 0: j=0; mid=j; i=j+1; ch =arr[i]<arr[mid]; if(ch) mid =i; mark =1; return; break; case 1: for(i++;i<n;i++) { ch =arr[i]<arr[mid]; mark =1; if(ch) mid=i; return; } ch =arr[j]>arr[mid]; mark=2; return; break; case 2: if(ch) { swap(arr,j,mid); mark=3; return; } for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark =2; return; } break; case 3: for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark=2; return; } break; } mark=10; }
A solução é bem viável. Em tal lançamento, o array está ordenado:
while(mark !=10) { CSelectSort(arr); count++; }
A variável 'count' mostra o número total de comparações e trocas. Ao mesmo tempo, o código tornou-se maior de três a quatro vezes, e essa é a ordenação mais simples. Existem também tipos consistindo de várias funções, recursivas, etc.
Opção 2
Existe uma solução mais simples. O terminal MQL5 suporta o conceito de multi-threading. Para implementá-lo, um indicador personalizado deve ser chamado para cada tipo. O indicador deve pertencer a um par de moedas separado para cada thread. A janela Observador do Mercado deve ter ferramentas suficientes para cada ordenação.
n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);
Aqui, SymbolName (n,0) é uma ferramenta separada para cada fluxo criado e os parâmetros passados para o indicador. O nome do objeto gráfico pode ser convenientemente atribuído por SymbolName (n,0). Um gráfico só pode ter um objeto da classe CGraphic com este nome. O método de ordenação, o número de elementos no array e o tamanho do próprio CGraphic não são exibidos aqui.
A seleção da função de ordenação e outras ações adicionais relacionadas à exibição visual (por exemplo, adicionando o nome de classificação aos eixos) ocorrem no próprio indicador.
switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");Select(arr); break; case 1: Graphic.XAxis().Name("Insertion"); CMain.Name("Insertion");Insert(arr);break; etc............................................. }
A criação de objetos gráficos leva uma certa quantidade de tempo. Portanto, as variáveis globais foram adicionadas para que os tipos funcionem simultaneamente. NAME é uma variável global com o nome do instrumento de valor inicial igual a 0. Depois de criar todos os objetos necessários, ele obtém o valor de 1, enquanto o valor de 2 é atribuído após a conclusão da ordenação. Desta forma, você pode acompanhar o início e o fim da ordenação. Para fazer isso, o timer é iniciado no EA:
void OnTimer() { double x =1.0; double y=0.0; static int start =0; for(int i=0;i<4;i++) { string str; str = SymbolName(i,0); x =x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } if(x&&start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } if(y==8) {PlaySound("success.wav"); EventKillTimer();} }
Aqui a variável de Х Pega o começo, enquanto У — o fim do processo.
No início do processo, é tocado som do vídeo original. Para trabalhar com os arquivos de som, ele deve estar localizado na pasta MetaTrader/Sound juntamente com outros sons do sistema *.wav. Se ele estiver localizado em outro lugar, especifique o caminho da pasta MQL5. Para conclusão, o arquivo success.wav é usado.
Então, vamos criar o EA e o indicador do seguinte tipo. EA:
enum SortMethod { Selection, Insertion, ..........Métodos de ordenação......... }; input int Xscale =475; //Escala do gráfico input int N=64; //Número de elementos input SortMethod Sort1; //Método ..........Várias entradas................. int OnInit() { //--- Define as variáveis globais, inicia o timer, etc. for(int i=0;i<4;i++) { SymbolSelect(SymbolName(i,0),1); GlobalVariableSet(SymbolName(i,0),0);} ChartSetInteger(0,CHART_SHOW,0); EventSetTimer(1); GlobalVariableSet("ALL",0); //.......................Abre uma thread do indicador separado para cada ordenação......... x=0*Xscale-Xscale*2*(0/2);//linha de comprimento igual a 2 y=(0/2)*Yscale+1; SymbolSelect(SymbolName(0,0),1); // Sem ele, um erro pode ocorrer em alguns instrumentos S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N); return(0); } //+------------------------------------------------------------------+ //| Função de desinicialização do Expert | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ChartSetInteger(0,CHART_SHOW,1); EventKillTimer(); int i =ObjectsDeleteAll(0); PlaySound("ok.wav"); GlobalVariableSet("ALL",0); IndicatorRelease(Sort1); .......Tudo isso deve ser removido...... //+------------------------------------------------------------------+ //| Função tick do Expert | //+------------------------------------------------------------------+ void OnTick() { ...Empty... } //+------------------------------------------------------------------+ void OnTimer() { ....Descrito acima.... }
O indicador apropriado:
#include <GSort.mqh> //Incluí todas as ordenações escritas anteriormente //+------------------------------------------------------------------+ //| Função de inicialização do indicador personalizado | //+------------------------------------------------------------------+ ..........Blocos de entrada..................................... input int SortName; //método int N=30; //número ...................................................................... int OnInit() { double arr[]; FillArr(arr,N); //preenche o array com um número aleatório GlobalVariableSet(NAME,0); //define as variáveis globais Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2); //NOME — par de moeda Graphic.IndentLeft(-30); Graphic.HistoryNameWidth(0); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //índice 0 CMain.HistogramWidth(2); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //índice 1 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(width); ......Vários parâmetros gráficos.......................... Graphic.CurvePlotAll(); Graphic.Update(); GlobalVariableSet(NAME,1); while(!GlobalVariableGet("ALL")); //Aguarda ate que todos os objetos gráficos sejam criados switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");GSelect(arr); break; .....Lista de ordenação.......................................... ... } GlobalVariableSet(NAME,2); return INIT_SUCCEEDED; } //+------------------------------------------------------------------+ //| Função de iteração do indicador personalizado | //+------------------------------------------------------------------+ int OnCalculate(...) { ..............Vazio........................ } //+------------------------------------------------------------------+ void OnDeinit(const int reason) { Graphic.Destroy(); delete CMain; delete CRed; delete CViolet; delete CGreen; ObjectDelete(0,NAME); }
Testes em multi-threading
Light.ex5 e Sort24.ex5 são programas prontos para uso. Eles foram copiados através dos recursos e não exigem mais nada. Ao trabalhar com códigos fonte, eles devem ser instalados nas pastas correspondentes dos indicadores e dos sons.
Sort24.ex5 com 24 tipos de ordenação é instável e funciona de forma irregular no meu PC de núcleo único. Portanto, eu deveria fechar todos os programas desnecessários e não tocar em nada. Cada ordenação contém cinco objetos gráficos — quatro curvas e uma tela. Todos eles são redesenhados continuamente. Vinte e quatro threads criam 120 (!) objetos gráficos alterando de forma contínua e individual em 24 threads. Esta é uma mera demonstração. Eu não trabalhei mais com isso.
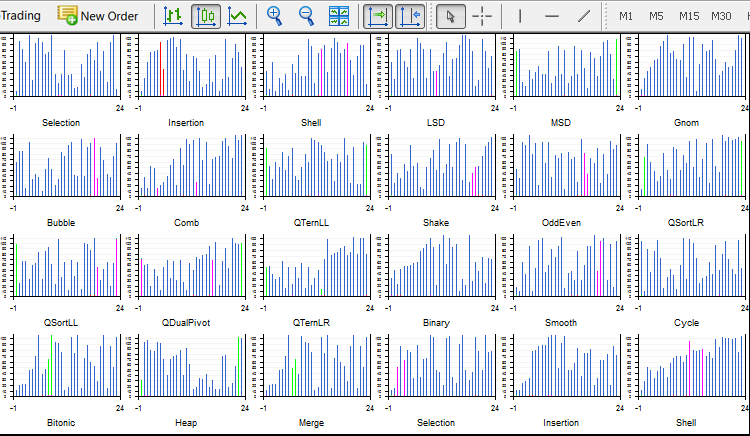
A versão funcional e estável do Light.ex5 exibe 4 ordenações simultaneamente. Aqui você pode selecionar o número de elementos e métodos de ordenação em cada janela. Além disso, é possível selecionar o método de embaralhar o array: aleatório, para cima (já ordenado), para baixo (ordenado em ordem inversa) e um array com muitos elementos idênticos (array de etapas). Por exemplo, o Quick Sort degrada-se para O(n^2) em um array ordenado na ordem inversa, enquanto que o Heap sempre ordena para n*log(n). Infelizmente, a função Sleep() não é suportada nos indicadores, portanto, a velocidade depende apenas do sistema. Além disso, a quantidade de recursos alocados para cada thread também é arbitrária. Se a mesma ordenação for iniciada em cada janela, todas elas terminam de diferentes maneiras.
Resumo:
- VisualSort de thread único está funcionando 100%
- O programa Light de 4 threads é estável
- O programa Sort24 de 24 threads é instável
Nós podemos seguir a primeira opção simulando multi-threading. Nesse caso, poderemos controlar o processo. As funções Sleep() deveriam funcionar, cada ordenação receberia um tempo estritamente igual, etc. Mas o próprio conceito de programação MQL5 multi-thread seria uma perda nesse caso.
Versão final:
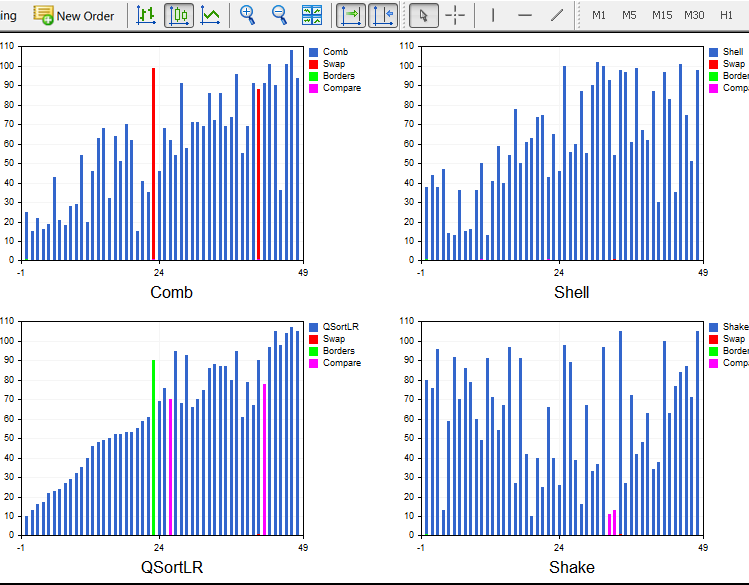
....................................................................................................................................................................
A lista de arquivos anexados
- VisaulSort.ex5 - cada tipo apresentado individualmente
- Programas (Sort24.ex5, Light.ex5) - aplicações prontas
- Arquivos de áudio
- Códigos. Código fonte do programa - tipos, indicadores, arquivos de inclusão, EAs.
Notas do autor
O autor do artigo implementou uma versão interessante versão de ordenação multi-thread usando o a execução simultânea de múltiplos indicadores. Esta arquitetura carrega pesadamente o PC, então modificamos um pouco os códigos-fonte do autor, a saber:
- Chamada desativada para desenho de gráfico de cada indicador no arquivo auxiliar.mqh
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i]+2;YZ[1]=a[j]+5; CGreen.Update(XZ,YZ); Graphic.Redraw(false); Graphic.Update(false); }
- Adicionado a função randomize() que prepara os mesmos dados aleatórios no array para todos os indicadores
- Adicionado os parâmetros externos ao arquivo IndSort2.mq5 para definir o tamanho do array com valores aleatórios (ele foi rigorosamente igual ao 24 na versão do autor) e o número 'sid' de inicialização para geração de dados
input uint sid=0; //inicialização do randomizer int N=64; //número de barras no histograma
- Adicionado o timer para desenhar o gráfico usando ChartRedraw() ao arquivo Sort24.mq5
//+------------------------------------------------------------------+ //| Funçao timer | //+------------------------------------------------------------------+ void OnTimer() { double x=1.0; double y=0.0; static int start=0; //--- Verifica o sinalizador de inicialização de cada indicador no loop for(int i=0;i<methods;i++) { string str; str=SymbolName(i,0); x=x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } //--- todos os indicadores são inicializados com sucesso if(x && start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } //--- todos as ordenações terminaram if(y==methods*2) { PlaySound("success.wav"); EventKillTimer(); } //--- atualiza os gráficos de ordenação ChartRedraw(); }
- Movido os arquivos de áudio para as pastas <>\MQL5\Sounds, para que eles possam ser incluídos como um recurso - resource
#resource "\\Sounds\\Sort.wav"; #resource "\\Sounds\\success.wav"; #resource "\\Indicators\\Sort\\IndSort2.ex5"
A estrutura pronta para compilação está anexada no arquivo moderators_edition.zip. Basta descompactá-lo e copiar para o seu terminal. Se o seu PC não for muito potente, nós recomendamos definir methods=6 ou methods=12 nos parâmetros de entrada.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/3118
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Expert Advisor multiplataforma: Controle de capital
Expert Advisor multiplataforma: Controle de capital
 Interfaces Gráficas XI: Controles renderizados (build 14.2)
Interfaces Gráficas XI: Controles renderizados (build 14.2)
 Indicadores personalizados e infográficos no CCanvas
Indicadores personalizados e infográficos no CCanvas
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
A propósito, no youtube original, toda a classificação é feita individualmente e depois editada em um editor de vídeo. Há um link para um programa C++ lá. Mas eles também são escritos um de cada vez em C++, embora o C++ tenha mais possibilidades.
Eu li sobre isso no artigo. E de forma alguma eu queria censurá-lo por trabalho injusto.
Mas seria interessante descobrir isso.
Eu li sobre isso no artigo. E de forma alguma eu quis censurá-lo por trabalho injusto.
Mas seria interessante dar uma olhada no assunto.
Eu sei qual é o problema. A MQL5 foi escrita para Windows, e não podemos controlar threads... Os indicadores têm multi-threading, mas sem interrupções.
Você participará da discussão?