
Sortierverfahren und deren Visualisierung mit MQL5
Inhaltsverzeichnis
- Einleitung
- Anwendung der Bibliothek Graphics\Graphic.mqh
- Funktionen der Vertauschung, des Vergleichs und der Begrenzung
- Sortierverfahren
- Selection Sort
- Insertion Sort
- Bubble-Sort
- Quick-Sort
- Merge-Sort
- Heap-Sort
- Sortieren in linearer Zeit MSD und LSD
- Weitere Sortierverfahren
- Tabelle der durchschnittlichen Laufzeit der Sortierverfahren
- Alle Methoden auf einem Bildschirm
- Testen der Mehrsträngigkeit
- Anmerkungen der Lektoren
Einleitung
Im Netz kann man viele Videos mit der Demonstration verschiedener Sortierverfahren finden. Hier werden zum Beispiel 24 Sortierverfahren visualisiert. Dieses Video haben ich neben der Liste der Sortieralgorithmen als Grundlage genommen.
Für das Arbeiten mit Grafiken wurde in MQL5 eine spezielle Bibliothek Graphic.mqh entwickelt. Sie ist bereits in Artikeln beschrieben worden: die Möglichkeiten der Bibliothek werden zum Beispiel hier ausführlich geschildert. Meine Aufgabe ist, über Anwendungsmöglichkeiten der Bibliothek sowie über Sortierverfahren zu erzählen. Zu jedem Sortierverfahren gibt es mindestens einen Artikel, zu einigen wurden bereits ganze Untersuchungen veröffentlicht, deswegen wird in dem Artikel nur die Grundidee beschrieben.
Anwendung der Bibliothek Graphics\Graphic.mqh
Die Arbeit mit der Bibliothek beginnt mit deren Miteinbeziehung.
#include <Graphics\Graphic.mqh>
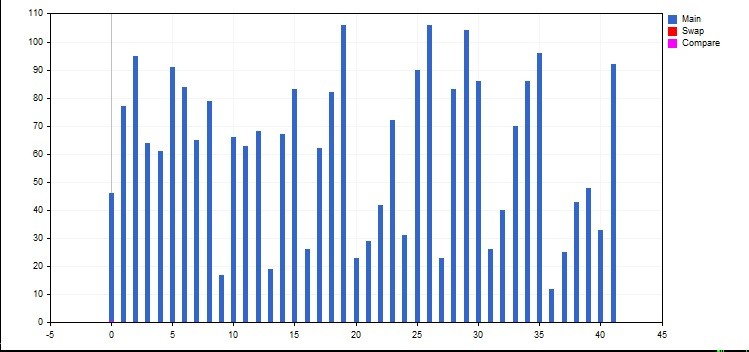
Wir werden die Spalten eines Histogramms sortieren, dafür verwenden wir die Funktionen Gswap() (Vertauschung) und GBool() (Vergleich). Die Elemente, mit welchen verschiedene Operationen (Vergleich, Vertauschung usw.) durchgeführt werden, werden mit Farbe markiert. Dafür wurde jeder Farbe ein separates Objekt vom Typ CCurve (eine Kurve) zugewiesen. Um diese Objekte nicht in einzelne Gswap-Funktionen (int i, int j, CGraphic &G, CCurve &A, CCurve &B, CCurve &C) aufzuspalten, machen wir diese global. Die Klasse CCurve verfügt standardmäßig über keinen Konstruktor, deswegen können wir ihn nicht als Global deklarieren. Deswegen deklarieren wir globale Pointer vom Typ CCurve *CMain.
Die Farbe kann auf drei verschiedene Arten zugewiesen werden. Besonders anschaulich ist zum Beispiel C'0x00,0x00,0xFF', oder C'Blue, Green, Red'. Die Kurve wird durch die Methode der Klasse CGraphic CurveAdd() erstellt, die mehrere Implementierungen hat. Für die meisten Elemente ist es praktisch, CurveAdd(arr, CURVE_HISTOGRAM, "Main") mit einem Array für Werte auszuwählen, für Hilfselemente — CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap") mit einem Array von X-Argumenten und einem Array von Y-Werten, denn es wird nur zwei Elemente geben. Die Arrays für Hilfslinien macht man am besten Global.
#include <Graphics\Graphic.mqh> #property script_show_inputs input int N =42; CGraphic Graphic; CCurve *CMain; CCurve *CGreen; CCurve *CBlue; CCurve *CRed; CCurve *CViolet; double X[2],Y[2],XZ[2],YZ[2]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //arrays------------------------------ double arr[]; FillArr(arr,N); X[0]=0;X[1]=0; Y[0] =0;Y[1]=0; //------------------------------------- Graphic.Create(0,"G",0,30,30,780,380); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0 CMain.HistogramWidth(4*50/N); CBlue =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); //index 1 CBlue.Color(C'0xFF,0x00,0x00'); CBlue.HistogramWidth(4*50/N); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 2 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(4*50/N); CGreen =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); //index 3 CGreen.Color(C'0x00,0xFF,0x00'); CGreen.HistogramWidth(4*50/N); CViolet =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); //index 4 CViolet.Color(C'0xFF,0x00,0xFF'); CViolet.HistogramWidth(4*50/N); Graphic.XAxis().Min(-0.5); Graphic.CurvePlot(4); Graphic.CurvePlot(2); Graphic.CurvePlot(0); //Graphic.CurvePlotAll(); einfach alle vorhandenen Kurven anzeigen Graphic.Update(); Sleep(5000); int f =ObjectsDeleteAll(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void FillArr(double &arr[],int num) { int x =ArrayResize(arr,num); for(int i=0;i<num;i++) arr[i]=rand()/328+10; }
Graphic.XAxis().Min(-5) legt den Abstand von der Y-Achse fest, damit das Nullelement sich nicht mit der Achse zusammenfällt. Histogramwidth() — die Breite einer Spalte.
Die Funktion FillArr() füllt das Array mit zufälligen Zahlen von 10 (um das Zusammenzufallen mit der X-Achse zu vermeiden) bis 110 aus. Das Array arr ist lokal, damit die Funktionen des Vergleichs standardmäßig als swap(arr, i, j) dargestellt werden. Der letzte Befehl ObjectDeleteAll löscht das, was wir gezeichnet haben. Sonst müssen wir das Objekt über das Menü "Objektliste" - Ctrl+B löschen.
Die Vorbereitung ist abgeschlossen, man kann mit dem Sortieren anfangen.
Funktionen der Vertauschung, des Vergleichs und der Begrenzung
Schreiben wir Funktionen für die Visualisierung von Vertauschung, Vergleich und Begrenzung für Sortieren durch Teilen. Die erste Funktion der Vertauschung void Gswap() ist eine Standardfunktion, ihr wird aber die Kurve CRed für die Markierung der zu vergleichenden Elemente hinzugefügt.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void Gswap(double &arr[],int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CRed.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmS); double sw = arr[i]; arr[i]=arr[j]; arr[j]=sw; //------------------------- Y[0] =0; Y[1] =0; CRed.Update(X,Y); CMain.Update(arr); Graphic.Redraw(); Graphic.Update(); //------------------------- }
Zuerst wählen wir die Spalten aus; nach einiger Zeit, Sleep(TmS), die die Geschwindigkeit der Demonstration bestimmt, setzen wir zurück. Auf die gleiche Weise schreiben wir die Vergleichsfunktionen für "<" und "<=" als bool GBool(double arr, int i, int j) und GBoolEq(double arr, int i, int j). Fügen wir ihnen Spalten von der Farbe CViolet hinzu.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool GBool(double &arr[], int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmC); Y[0]=0; Y[1]=0; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); return arr[i]<arr[j]; }
Die Funktion für die Auswahl der Grenzen, in denen die Spalten nicht gelöscht werden müssen.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i];YZ[1]=a[j]; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); }
Nun gehen wir auf Sortierverfahren ein.
Sortierverfahren
Bevor wir auf die Erläuterung von Algorithmen eingehen, empfehle ich, das Programm VisualSort zu starten, das in der angehängten Datei VisualSort.ex5 befindet. Es veranschaulicht, wie jedes Sortierverfahren einzeln funktioniert. Die Include-Datei GSort.mqh beinhaltet den vollständigen Code der Sortierungen. Sie ist relativ groß, deswegen habe ich hier nur Hauptideen geschildert.
- Das erste Sortierverfahren, mit welchem man gewöhnlich beginnt, ist das Sortieren durch Auswählen (Selection Sort). Finden wir das kleinste Element in der aktuellen Liste und vertauschen wir es mit dem ersten Element im unsortierten Teil der Liste.
template <typename T> void Select(T &arr[]) { int n = ArraySize(arr); for(int j=0;j<n;j++) { int mid=j; for(int i=j+1;i<n;i++) { if(arr[i]<arr[mid]) { mid=i; } } if(arr[j]>arr[mid]){swap(arr,j,mid);} } }
Hier und weiter wird als Funktion der Vertauschung die von uns vorher geschriebenen Gswap() verwendet, der Vergleich der Elemente des Arrays wird durch GBool() ersetzt. Zum Beispiel, if(arr[i]<arr[mid]) => if(GBool(arr,i,mid).
- Ein weiteres Sortierverfahren (das eigentlich häufig beim Kartenspielen verwendet wird) stellt das Sortieren durch Einfügen dar. In dieser Methode werden die Elemente der Eingabefolge einzeln durchlaufen und in den bereits sortierten Teil des Arrays an passender Stelle eingefügt. Die Basismethode:
template<typename T> void Insert(T &arr[]) { int n= ArraySize(arr); for(int i=1;i<n;i++) { int j=i; while(j>0) { if(arr[j]<arr[j-1]) { swap(arr,j,j-1); j--; } else j=0; } } }
Als Varianten von Insertion Sort können Shell Sort und Binary Insertion Sort betrachtet werden. Die Idee der Shell-Methode besteht darin, nicht nur benachbarte Elemente, sondern auch voneinander entfernte Elemente zu vergleichen. Mit anderen Worten ist das das Insertion Sort Verfahren mit vorläufigen groben Durchläufen. Binary Insertion verwendet eine binäre Suche für die Festlegung der Einfügeposition. In der oben erwähnten Demonstration (VisualSort.ex5) sieht man, wie Shell das Array Schritt für Schritt "durchkämmt", dabei wird der Abstand zwischen den Zinken dieses Kamms immer kleiner. In diesem Sinne ist es dem oben beschriebenen Comb Verfahren ähnlich.
- Bubble-Sort und seine Varianten — Shake Sort, Gnome-Sort Comb-Sort und Odd-Even Sort. Die Idee des Bubble-Sort Verfahrens ist ganz einfach: wir durchlaufen das ganze Array und vergleichen zwei benachbarte Elemente miteinander. Wenn sie nicht sortiert wurden, vertauschen wir sie. Am Ende jeder Iteration befindet sich das größte Element am Ende des Arrays. Danach wird der Vorgang wiederholt, und als Ergebnis erhalten wir ein Array, das geordnet und sortiert wurde. Der Bubblesort-Basisalgorithmus:
template<typename T> void BubbleSort(T &a[]) { int n =ArraySize(a); for (int i = 0; i < n - 1; i++) { bool swapped = false; for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a,j,j+1); swapped = true; } } if (!swapped) break; } }
Im Shake-Sort Verfahren wird das zu sortierende Feld in beide Richtungen durchlaufen, deswegen werden nicht nur große sondern auch kleine Elemente abgesetzt. Gnome-Sort kommt mit einer einzigen Schleife aus. Hier ist der Code dieses Sortierverfahrens angeführt:
void GGnomeSort(double &a[]) { int n =ArraySize(a); int i=0; while(i<n) { if(i==0||GBoolEq(a,i-1,i)) i++; //if(i==0||a[i-1]<a[i]) else { Gswap(a,i,i-1); //Austausch von a[i] und a[i-1] i--; } } }
Wenn man die Position der bereits sortierten Elemente findet, erhalten wir Insertion Sort. Comb basiert auf der gleichen Idee, wie Shell: das Array wird in mehreren Schritten mit unterschiedlichen Schrittweiten durchlaufen. Für dieses Verfahren wurde sogar der optimale Reduktionsfaktor berechnet = 1,247 ≈ ( 1 / ( 1-e^(-φ) ) ), wobei e — Exponent; φ — die "goldene" Zahl sind. In Schnelligkeit stehen Comb und Shell schnellen Sortierverfahren nicht nach. Odd-Even Sort durchläuft gerade/ungerade Elemente. Da diese als Sortierung für eine Multithread-Implementierung gedacht wurde, ist sie in unserem Fall sinnlos.
- Kompliziertere Verfahren basieren auf dem Grundsatz "Teile und herrsche". Zu den klassischen Beispielen gehört das Sortierverfahren von Hoare, oder Quick-Sort.
Die Grundidee des Algorithmus besteht darin, ein Pivot-Element aus dem Array auszuwählen. Das kann jedes der Elemente des Arrays sein. Wir vergleichen alle anderen Elemente mit dem Pivot-Element und ordnen diese im Array so ein, dass das Array in zwei Teile zerlegt wird: "kleiner" als das Pivot-Element und "größer" als das Pivot-Element. Für die Segmente der kleineren und größeren Werte führen wir gleiche Operationen rekursiv durch, wenn das Segment länger als 1 ist. Die Grundidee ist im Pseudocode enthalten:
algorithm quicksort(A, lo, hi) is if (lo < hi) { p = partition(A, lo, hi); quicksort(A, lo, p – 1); quicksort(A, p, hi);}
Der Unterschied zwischen den Varianten des Sortierverfahrens läuft auf verschiedene Weisen des Aufteilens des Arrays hinaus. In der ursprünglichen Variante laufen die Pointer von zwei Seiten einander entgegen. Der linke Pointer findet ein Element, das größer als das Pivot-Element ist, und der rechte — das kleinere Element, und diese werden vertauscht. In einer anderen Variante laufen beide Pointer von links nach rechts. Wenn der Erste ein "kleineres" Element findet, fügt er es an die Position des zweiten Pointers ein. Für die Fälle, wenn es viele gleiche Elemente im Array gibt, wird Platz für Elemente zugewiesen, die gleich dem Pivot-Element sind. Dieses Schema wird verwendet, wenn man z.B. Mitarbeiter nach nur zwei Schlüssel sortieren muss — "männlich" und "weiblich". Das Schema der Aufteilung ist auf dem Bild dargestellt:
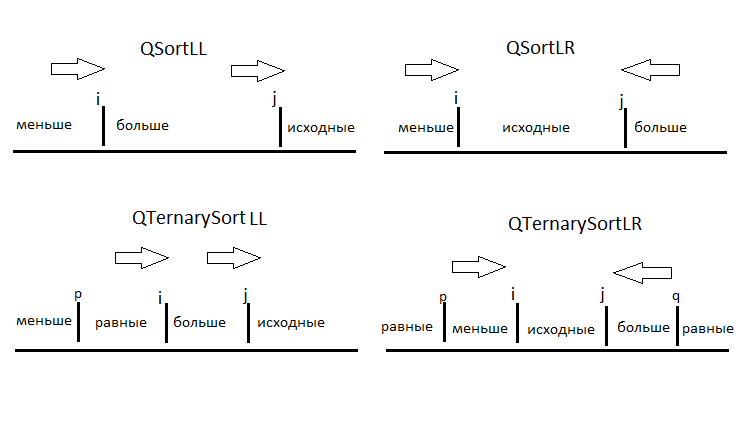
Als Beispiel führe ich hier nur QSortLR mit der Variante von Hoare an:
//----------------------QsortLR----------------------------------------+ void GQsortLR(double &arr[],int l,int r) { if(l<r) { GBorders(arr,l,r); int mid =PartitionLR(arr,l,r); GQsortLR(arr,l,mid-1); GQsortLR(arr,mid+1,r); } } int PartitionLR(double &arr[],int l,int r) { int i =l-1; int j =r; for(;;) { while(GBool(arr,++i,r)); j--; while(GBool(arr,r,j)){if(j==l) break;j--;} if(i>=j) break; Gswap(arr,i,j); } //--------------------------------------------- Gswap(arr,i,r); YZ[0]=0;YZ[1]=0; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); return i; }
Ein Array kann nicht nur in zwei Teile, sondern in drei, vier, fünf ... mit mehreren Pivot-Elementen aufgeteilt werden. Als eine Variante wird das Sortierverfahren DualPivot mit zwei Pivot-Elementen verwendet.
- Andere Methoden, die auf dem Prinzip "Teile und herrsche" basieren, verwenden das Zusammenfügen bereits sortierter Teile des Arrays. Sie teilen das Array, bis es die Länge 1 hat, d.h. bis es sortiert ist, und verwenden anschließend die Merge-Funktion, die gleichzeitig auch die Elemente sortiert. Das Grundprinzip:
void GMergesort (double &a[], int l, int r) { int m = (r+l)/2; GMergesort(a, l, m); GMergesort(a, m+1, r) ; Merge(a, l, m, r); }
BitonicSort() sortiert einen Teil des Arrays aufsteigend, den anderen absteigend und dann vereint diese Teile.
- Treesort (Heap-Sort)
Das Grundprinzip ist wie folgt. Zuerst machen wir aus dem Array einen "Haufen". Dann löschen wir das ältere Element an der Spitze des Haufens. Platzieren wir es am Ende des Quellarrays als ältestes Element, an seine Stelle platzieren wir das letzte Element aus dem nicht sortierten Teil. Dann bilden wir einen neuen Haufen von der Größe n-1 usw. Die "Haufen" können nach zwei verschiedenen Grundsätzen gebildet werden. Zum Beispiel verwendet das Sortierverfahren Smooth() die Haufen, deren Elementenanzahl den Leonardo-Zahlen gleich ist L(x+2) = L(x+1) +L(x) +1.
- Sortieren in linearer Zeit. Counting-Sort und Radix-Sort MSD und LSD
Counting sort ist ein Sortierverfahren, welches den Wertebereich des zu sortierenden Arrays (Liste) für die Zählung der zusammenfallenden Elemente verwendet. Die Anwendung der Counting-Sort ist nur dann sinnvoll, wenn die zu sortierende Zahlen einen Wertebereich haben, der im Vergleich zur zu sortierenden Menge relativ klein ist. Zum Beispiel, eine Million natürlicher Zahlen kleiner als 1000. Das Prinzip wird auch in Radix-Sort verwendet. Der Algorithmus:
void CountSort(double &a[]) { int count[]; double aux[]; int k =int(a[int(ArrayMaximum(a))]+1); int n =ArraySize(a); ArrayResize(count,k); ArrayResize(aux,n); for (int i=0;i<k;i++) count[i] = 0; for (int i=0;i<n;i++) count[int(a[i])]++; // Anzahl der Elemente die gleich i sind for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; // Anzahl der Elemente, die nicht größer als i sind for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // füllen wir das Zwischenarray aus for(int i=0;i<n;i++)a[i]=aux[i]; }
Die Idee des Sortierens durch Zählen wird in den Sortierverfahren in linearer Zeit MSD und LSD verwendet. Gemeint ist die Zeit N*R, wobei N — Anzahl der Elemente, und R — Anzahl der Stellen als Zahl in der ausgewählten Zahlensystem sind. MSD (most significant digit) sortiert nach der höchstwertigen Stelle, LSD (least significant digit) — nach der niedrigsten. Im Binärsystem, zum Beispiel, berechnet LSD, wie viele Zahlen mit Null enden, und wie viele mit 1, und platziert gerade Zahlen (0) in die erste Hälfte, und ungerade Zahlen (1) — in die zweite. MSD geht umgekehrt vor und beginnt mit der höchstwertigen Stelle. Im Dezimalsystem werden zuerst die Zahlen kleiner als 100, und dann größer als 100 platziert. Danach wird das Array wieder in Strecken 0-19, 10-19,..., 100-109 usw. sortiert. Nach diesem Algorithmus werden ganze Zahlen sortiert. Aber der Kurs 1.12307 kann ganzzahlig werden: 1.12307*100 000.
Durch das Kombinieren von Quick-Sort und Radix-Sort erhalten wir ein schnelles binäres Sortierverfahren - QuicksortB(). Hier wird die Aufteilung von QSortLR verwendet, aber die Sortierung erfolgt nicht nach einem Pivot-Element, sondern nach der höchstwertigen Stelle. Dafür wird hier sowie in LSD und MSD die Funktion der Ermittlung der Ziffer der n-Stelle angewandt.
int digit(double x,int rdx,int pos) // Wobei x - die Zahl, rdx - das Zahlensystem { // in unserem Fall 2, pos Nummer der Stelle int mid =int(x/pow(rdx,pos)); return mid%rdx; }Zuerst wird nach der höchstwertigen Stelle aufgeteilt int d =int(log(a[ArrayMaximum(a)])/log(2)), danach werden die Teile nach den niedrigsten Stellen rekursiv sortiert. Sieht ähnlich dem QuickSortLR Verfahren aus.
- Einige spezifische Sortierverfahren
Cycle Sort ist für Systeme vorgesehen, in welchen das Umschreiben von Daten zum Verschleiß von Ressourcen führt. Daraus folgt die Aufgabe, ein Sortierverfahren mit der kleinsten Anzahl von Vertauschungen (Gswap) zu finden. Dafür werden zyklische Vertauschungen verwendet. Grob gesagt wird 1 mit 3 vertauscht, 3 mit 2, 2 mit 1. Jedes Element wird entweder 0 Mal oder einmal vertauscht. Dies nimmt relativ viel Zeit in Anspruch, Zeit O(n^2). Mehr Informationen über die Idee und das Verfahren finden Sie hier.
Stooge sort. Ein weiteres Beispiel für ein sehr langsames Sortierverfahren. Der Algorithmus besteht im Folgenden. Wenn der Wert des Elements am Ende der Liste kleiner als der Wert des Elements am Anfang der Liste ist, müssen sie vertauscht werden. Wenn es drei oder mehr Elemente in der aktuellen Teilmenge der Liste gibt, dann: rufen wir Stoodge() für die ersten zwei Drittel der Liste rekursiv auf, rufen wir Stoodge() für die letzten zwei Drittel der Liste rekursiv auf, rufen wir wieder Stoodge() für die ersten zwei Drittel der Liste rekursiv auf usw.
Tabelle der durchschnittlichen Laufzeit der Sortierverfahren
| Sortierverfahren | Durchschnittliche Laufzeit |
|---|---|
| Selection Sort | O(n^2) |
| Insertion Sort | O(n^2) |
| Binary Selection Sort | O(n^2) |
| Shell Sort | O(n*log(n)) |
| Bubble Sort | O(n^2) |
| Shaker/Cocktail Sort | O(n^2) |
| Gnome Sort | O(n^2) |
| Comb Sort | O(n*log(n)) |
| Merge Sort | O(n*log(n)) |
| Bitonic sort | O(n*log(n)) |
| Heap Sort | O(n*log(n)) |
| Smooth Sort | O(n*log(n)) |
| Quick Sort LR | O(n*log(n)) |
| Quick Sort LL | O(n*log(n)) |
| Quick Sort (ternary, LR ptrs) | O(n*log(n)) |
| Quick Sort (ternary, LL ptrs) | O(n*log(n)) |
| Quick Sort (dual pivot) | O(n*log(n)) |
| Counting-Sort | O(n+k) |
| Radix Sort LSD | O(n*k) |
| Radix Sort MSD | O(n*k) |
| Binäres Quick Sort | O(n*log(n)) |
| Cycle sort | O(n^2) |
| Stoodge sort | O(n^2.7) |
Alle Methoden auf einem Bildschirm
Geben wir alle beschriebenen Sortierungen auf ein Bildschirm gleichzeitig aus. Im Video werden die Sortierungen einzeln gestartet, danach wird das Ganze im Videoeditor zusammengeschnitten. Das Handelsterminal verfügt aber über keinen Videoeditor. Dieses Problem kann man auf verschiedene Weisen gelöscht werden.
Variante 1.
Mehrsträngigkeit imitieren. Parallelisieren wir die Sortierungen so, dass man nach jedem Vergleich und Austausch die Funktion verlassen und eine andere Sortierung laufen lassen kann, und dann wieder an derselben Stelle in die Funktion eingehen. Da der Operator GOTO nicht vorhanden ist, wird die Aufgabe kompliziert. So wird, zum Beispiel, die einfachste Selection Sort aussehen, die ganz am Anfang angeführt wurde:
void CSelect(double &arr[]) { static bool ch; static int i,j,mid; int n =ArraySize(arr); switch(mark) { case 0: j=0; mid=j; i=j+1; ch =arr[i]<arr[mid]; if(ch) mid =i; mark =1; return; break; case 1: for(i++;i<n;i++) { ch =arr[i]<arr[mid]; mark =1; if(ch) mid=i; return; } ch =arr[j]>arr[mid]; mark=2; return; break; case 2: if(ch) { swap(arr,j,mid); mark=3; return; } for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark =2; return; } break; case 3: for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark=2; return; } break; } mark=10; }
Diese Variante ist funktionsfähig. Bei solchem Start wird das Array sortiert:
while(mark !=10) { CSelectSort(arr); count++; }
Die Variable count zeigt die Gesamtanzahl der Vergleiche und Vertauschungen. Dabei ist der Code drei- bis viermal so groß, obwohl es um ein einfaches Sortierverfahren geht. Darüber hinaus gibt es Sortierungen, die aus mehreren Funktionen bestehen, rekursive Sortierverfahren...
Variante 2.
Es gibt eine einfachere Variante. Die MQL5 Terminals unterstützen die Mehrsträngigkeit. Um diese zu implementieren, muss ein benutzerdefinierter Indikator für jede Sortierung aus einem Expert Advisor aufgerufen werden. Für jeden Thread aber muss der Indikator nach einem separaten Währungspaar sein. Im Marktübersicht-Fenster (Market Watch) muss es ausreichend Werkzeuge für jede Sortierung geben.
n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);
Hier ist SymbolName (n,0) ein separates Werkzeug für jeden Thread sowie Parameter, die in den Indikator übergeben werden. Für die Festlegung des Namens eines grafischen Objekts verwendet man am einfachsten SymbolName (n,0). Auf einem Chart kann nur ein Objekt der Klasse CGraphic mit diesem Namen sein. Der Typ des Sortierverfahrens, die Anzahl der Elemente im Array sowie die Größe der Leinwand CGraphic sind hier nicht angezeigt.
Im Indikator erfolgt die Auswahl einer Sortierfunktion und weitere zusätzliche Aktionen, die mit der Gestaltung verbunden sind (zum Beispiel, die Beschriftung der Achsen mit dem Namen der Sortierung).
switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");Select(arr); break; case 1: Graphic.XAxis().Name("Insertion"); CMain.Name("Insertion");Insert(arr);break; etc............................................. }
Die Erstellung der grafischen Objekte nimmt eine gewisse Zeit in Anspruch. Aus diesem Grund wurden globale Variablen hinzgefügt, damit die Sortierungen gleichzeitig arbeiten. NAME — eine globale Variable mit dem Symbolname, der am Anfang 0 zugewiesen wird. Nach der Erstellung aller benötigten Objekte bekommt sie den Wert 1, und nach dem Abschluss der Sortierung 2. So kann man den Anfang und das Ende eines Sortierverfahrens verfolgen. Dafür wird Timer im Expert Advisor gestartet:
void OnTimer() { double x =1.0; double y=0.0; static int start =0; for(int i=0;i<4;i++) { string str; str = SymbolName(i,0); x =x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } if(x&&start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } if(y==8) {PlaySound("success.wav"); EventKillTimer();} }
Die Variable х fängt hier den Anfang auf, und y — das Ende des Vorgangs.
Am Anfang der Aktionen wird der Ton wiedergegeben, der dem originellen Video entnommen wurde. Für die Arbeit mit Quellcodes muss er zusammen mit den anderen Systemtönen im Format *.wav im Ordner MetaTrader/Sound sein, oder wenn er sich an einer anderen Stelle befindet, muss man den Pfad vom MQL5 Ordner angeben. Am Ende wird die Datei success.wav verwendet.
Erstellen wir den folgenden Expert Advisor und Indikator. Expert Advisor:
enum SortMethod { Selection, Insertion, ..........Sortierverfahren......... }; input int Xscale =475; //Maßstab input int N=64; //Anzahl der Elemente input SortMethod Sort1; //Verfahren ..........Verschiedene Input-Parameter................. int OnInit() { //--- Globale Variablen setzen, Timer starten usw. for(int i=0;i<4;i++) { SymbolSelect(SymbolName(i,0),1); GlobalVariableSet(SymbolName(i,0),0);} ChartSetInteger(0,CHART_SHOW,0); EventSetTimer(1); GlobalVariableSet("ALL",0); //.......................Öffnen wir den separaten Thread-Indikator für jede Sortierung......... x=0*Xscale-Xscale*2*(0/2);// eine Reihe mit der Länge 2 y=(0/2)*Yscale+1; SymbolSelect(SymbolName(0,0),1); // ohne sind Fehler auf einigen Symbolen möglich S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N); return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ChartSetInteger(0,CHART_SHOW,1); EventKillTimer(); int i =ObjectsDeleteAll(0); PlaySound("ok.wav"); GlobalVariableSet("ALL",0); IndicatorRelease(Sort1); .......Alles was gelöscht werden muss...... //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { ...Leer... } //+------------------------------------------------------------------+ void OnTimer() { ....Oben beschrieben.... }
Und einen Indikator dazu:
#include <GSort.mqh> //Beziehen wir alle geschriebenen Sortierverfahren mitein //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ ..........Block der Input-Parameter..................................... input int SortName; //method int N=30; //number ...................................................................... int OnInit() { double arr[]; FillArr(arr,N); //füllen wir das Array mit zufälligen Zahlen GlobalVariableSet(NAME,0); //setzen wir globale Variablen Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2); //NAME — Währungspaar Graphic.IndentLeft(-30); Graphic.HistoryNameWidth(0); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0 CMain.HistogramWidth(2); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 1 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(width); ......Verschiedene grafische Parameter.......................... Graphic.CurvePlotAll(); Graphic.Update(); GlobalVariableSet(NAME,1); while(!GlobalVariableGet("ALL")); //Warten, bis alle grafischen Objekte erstellt sind switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");GSelect(arr); break; .....Sortierliste.............................................. } GlobalVariableSet(NAME,2); return INIT_SUCCEEDED; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(...) { ..............Leer........................ } //+------------------------------------------------------------------+ void OnDeinit(const int reason) { Graphic.Destroy(); delete CMain; delete CRed; delete CViolet; delete CGreen; ObjectDelete(0,NAME); }
Testen der Mehrsträngigkeit
Light.ex5 und Sort24.ex5 sind fertige funktionsfähige Programme. Sie wurden über Ressourcen kompiliert und benötigen nichts mehr. Bei der Arbeit mit Quellcodes müssen sie in den entsprechenden Ordnern für Indikatoren und Töne gespeichert werden.
Die Version Sort24.ex5 mit 24 Sortierverfahren erwies sich auf meinem Einkernprozessor-Rechner als instabil. Man muss alles Unnötige schließen und darf nichts anfassen. In jeder Sortierung gibt es fünf grafische Objekte — vier Kurven und eine Leinwand. Sie werden ununterbrochen neu gezeichnet. Die 24 Threads erstellen 120 (!) separate sich ständig ändernde grafische Objekte in 24 Threads. Ich habe dies gemacht um zu zeigt, dass das möglich ist. Mehr habe ich damit nicht gearbeitet.
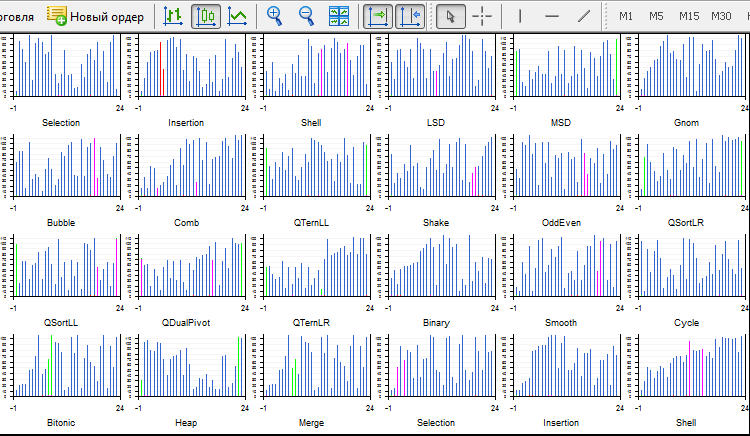
Die einsatzfähige und relativ stabile Version Light.ex5 kann gleichzeitig 4 Sortierungen ausgeben. Es wurde die Möglichkeit hinzugefügt, die Anzahl der Elemente und ein Sortierverfahren in jedem Fenster auszuwählen. Darüber hinaus gibt es die Möglichkeit, eine Permutationsmethode für das Arrays auszuwählen: zufällig, aufsteigend (bereits sortiert), absteigend (rückwärts sortiert) und ein Array, in welchem es viele gleiche Elemente gibt (step array). Quicksort verzögert sich, zum Beispiel, auf einem Array, das rückwärts sortiert wurde, bis auf O(n^2), und das Heap Sort Verfahren braucht immer n*log(n). Leider wird die Funktion Sleep() nicht in Indikatoren unterstützt, die Schnelligkeit hängt nur vom System ab. Darüber hinaus ist die Anzahl der Ressourcen, die jedem Thread zugeteilt werden, auch zufällig. Wenn man den gleichen Sortieralgorithmus in jedem Fenster startet, wird er verschiedene Ergebnisse am Ende liefern.
Fassen wir zusammen:
- Einsträngige VisualSort — 100% funktionsfähig
- Viersträngige Light — stabil
- 24-strängige Sort24 — instabil
Man könnte die erste Variante nehmen und die Mehrsträngigkeit imitieren. In diesem Fall hätten wir den Vorgang kontrolliert. Hätten die Funktionen Sleep() gearbeitet, hätte jede Sortierung gleiche Zeit bekommen usw. Dabei wäre die Konzeption eines mehrsträngigen Programmierens auf MQL5 verloren gegangen.
Die endgültige Variante:
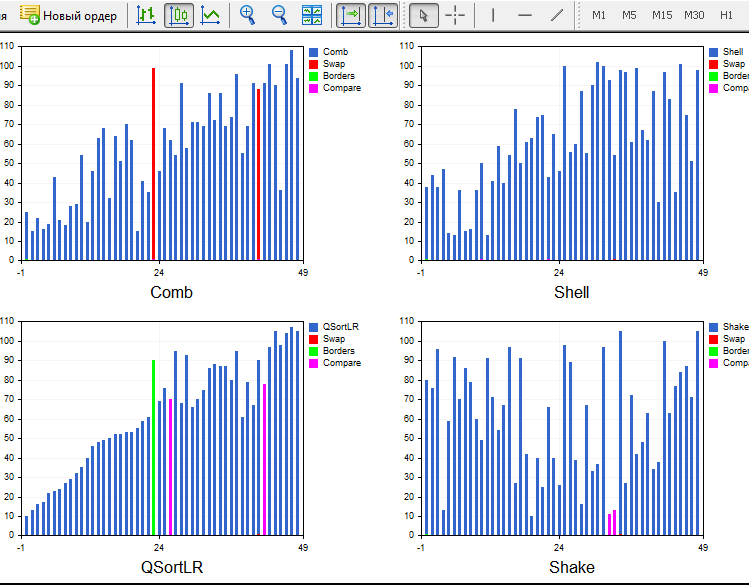
....................................................................................................................................................................
Liste der angehängten Dateien
- VisaulSort.ex5 - jede Sortierung einzeln
- Programs(Sort24.ex5, Light.ex5) - fertige Programme
- Audiodateien
- Codes. Quellcodes - Sortierverfahren, Indiakatoren, Include-Dateien und Expert Advisors.
Anmerkungen der Lektoren
Der Autor des Artikels implementierte eine interessante Variante einer mehrsträngigen Sortierung durch einen gleichzeitigen Start vieler Indikatoren. Diese Architektur belastet das PC, deswegen haben wie die Quellcodes des Autors ein bisschen verfeinert, und zwar:
- in der Datei auxiliary.mq wurde der Aufruf der Neuzeichnung des Charts aus jedem Indikator verboten
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i]+2;YZ[1]=a[j]+5; CGreen.Update(XZ,YZ); Graphic.Redraw(false); Graphic.Update(false); }
- es wurde die Funktion randomize() hinzugefügt, die die gleichen zufälligen Daten im Array für alle Indikatoren vorbereitet
- der Datei IndSort2.mq5 wurden externe Parameter hinzugefügt, die die Größe des Arrays mit zufälligen Werten setzen (bei dem Autor ist sie strikt gleich 24) und die initialisierende Zahl seed für die Generierung von Daten
input uint sid=0; //initialization of randomizer int N=64; //number of bars on histogramm
- der Datei Sort24.mq5 wurde ein Timer für das Zeichnen der Grafik mithilfe von ChartRedraw() hinzugefügt
//+------------------------------------------------------------------+ //| Timer function | //+------------------------------------------------------------------+ void OnTimer() { double x=1.0; double y=0.0; static int start=0; //--- überprüfen wir das Flag der Initialisierung für jeden Indikator in der Schleife for(int i=0;i<methods;i++) { string str; str=SymbolName(i,0); x=x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } //--- alle Indikatoren sind erfolgreich initialisiert if(x && start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } //--- alle Sortierungen abgeschlossen if(y==methods*2) { PlaySound("success.wav"); EventKillTimer(); } //--- Grafiken aktualisieren ChartRedraw(); }
- die Audiodateien wurden in den Ordner <>\MQL5\Sounds übertragen, damit man diese als Ressource miteinbeziehen kann
#resource "\\Sounds\\Sort.wav"; #resource "\\Sounds\\success.wav"; #resource "\\Indicators\\Sort\\IndSort2.ex5"
Die zur Kompilierung bereite Struktur ist in der Zip-Datei moderators_edition.zip zu finden, die man einfach entpacken und ins Terminal kopieren muss. Wenn Ihr PC nicht besonders leistungsstark ist, ist es empfehlenswert, methods=6 oder methods=12 in den Inputparametern zu setzen.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3118
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Universeller Expert Advisor: Zugang zu Symboleigenschaften (Teil 8)
Universeller Expert Advisor: Zugang zu Symboleigenschaften (Teil 8)
 Muster, die beim Handeln mit Währungskörben verfügbar sind. Teil III
Muster, die beim Handeln mit Währungskörben verfügbar sind. Teil III
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Im Original-Youtube werden übrigens alle Sortierungen einzeln vorgenommen und dann in einem Video-Editor bearbeitet. Dort gibt es einen Link zu einem C++-Programm. Aber sie sind auch einzeln in C++ geschrieben, obwohl C++ mehr Möglichkeiten hat.
Das habe ich in dem Artikel gelesen. Und keineswegs wollte ich Ihnen unlautere Arbeit vorwerfen.
Aber es wäre interessant, es herauszufinden.
Das habe ich in dem Artikel gelesen. Und ich wollte Ihnen keineswegs unfaire Arbeit vorwerfen.
Aber es wäre interessant, der Sache nachzugehen.
Ich weiß, was das Problem ist. MQL5 ist für Windows geschrieben, und wir können keine Threads kontrollieren... Die Indikatoren haben Multi-Threading, aber ohne Unterbrechungen... Wir hätten über den Expert Advisor schreiben sollen...
Werden Sie sich an der Diskussion beteiligen?