
Методы сортировки и их визуализация с помощью MQL5
Содержание
- Введение
- Применение библиотеки Graphics\Graphic.mqh
- Функции обмена, сравнения и границ
- Методы сортировки
- Сортировка выбором
- Сортировки вставками
- Сортировки пузырьком
- Быстрые сортировки
- Сортировки слиянием
- Пирамидальная сортировка
- Сортировки за линейное время MSD и LSD
- Другие сортировки
- Сводная таблица скорости методов
- Все методы на одном экране
- Тестируем многопоточность
- Примечание редакторов статьи
Введение
В Сети можно найти ряд видеороликов с демонстрацией различных видов сортировок. Например, здесь представлена визуализация 24 алгоритмов сортировки. Это видео я и взял за основу, наряду со списком алгоритмов сортировки.
Для работы с графиками в MQL5 разработана специальная библиотека Graphic.mqh. Она уже описана в статьях: в частности, здесь подробно рассказывается о возможностях библиотеки. Моя задача — описать ее точки приложения, практическое применение, а также подробно рассказать о самих сортировках. По каждой сортировке существует как минимум отдельная статья, а по ряду из них — целые исследования, поэтому опишу лишь общую идею.
Применение библиотеки Graphics\Graphic.mqh
Работа с библиотекой начинается с ее подключения.
#include <Graphics\Graphic.mqh>
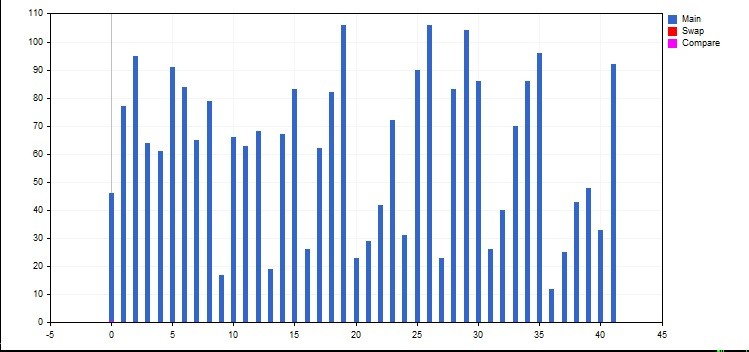
Сортировать будем столбики гистограммы, применим для этого функции обмена Gswap() и сравнения GBool(). Элементы, над которыми будут производиться операции (сравнение, замена и т.д.), выделяются цветом. Для этого каждому цвету выделен отдельный объект типа CCurve (кривая). Чтобы не разносить эти объекты по функциям Gswap (int i, int j, CGraphic &G, CCurve &A, CCurve &B, CCurve &C), сделаем их глобальными. Класс CCurve не имеет конструктора по умолчанию, поэтому просто объявить его глобальным не получится. Поэтому объявим глобальные указатели типа CCurve *CMain.
Цвет можно задавать тремя разными способами. Наиболее наглядный из них имеет вид C'0x00,0x00,0xFF', или C'Blue, Green, Red'. Кривая создаётся методом класса CGraphic CurveAdd(), который имеет несколько реализаций. Для основной массы элементов удобно выбрать CurveAdd(arr, CURVE_HISTOGRAM, "Main") с одним массивом значений, для вспомогательных — CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap") с массивом аргументов X и массивом значений Y, так как элементов будет всего два. Массивы для вспомогательных линий удобно сделать глобальными.
#include <Graphics\Graphic.mqh> #property script_show_inputs input int N =42; CGraphic Graphic; CCurve *CMain; CCurve *CGreen; CCurve *CBlue; CCurve *CRed; CCurve *CViolet; double X[2],Y[2],XZ[2],YZ[2]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //arrays------------------------------ double arr[]; FillArr(arr,N); X[0]=0;X[1]=0; Y[0] =0;Y[1]=0; //------------------------------------- Graphic.Create(0,"G",0,30,30,780,380); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0 CMain.HistogramWidth(4*50/N); CBlue =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); //index 1 CBlue.Color(C'0xFF,0x00,0x00'); CBlue.HistogramWidth(4*50/N); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 2 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(4*50/N); CGreen =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); //index 3 CGreen.Color(C'0x00,0xFF,0x00'); CGreen.HistogramWidth(4*50/N); CViolet =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); //index 4 CViolet.Color(C'0xFF,0x00,0xFF'); CViolet.HistogramWidth(4*50/N); Graphic.XAxis().Min(-0.5); Graphic.CurvePlot(4); Graphic.CurvePlot(2); Graphic.CurvePlot(0); //Graphic.CurvePlotAll(); просто отобразить все имеющиеся кривые Graphic.Update(); Sleep(5000); int f =ObjectsDeleteAll(0); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void FillArr(double &arr[],int num) { int x =ArrayResize(arr,num); for(int i=0;i<num;i++) arr[i]=rand()/328+10; }
Graphic.XAxis().Min(-5) задаёт отступ от оси ординат, чтобы нулевой элемент не сливался с ней. Histogramwidth() — ширина столбца.
Функция FillArr() заполняет массив случайными числами от 10 (чтобы не сливаться с осью абсцисс) до 110. Массив arr cделан локальным, чтобы функции обмена имели стандартный вид swap(arr, i, j). Последняя команда ObjectDeleteAll стирает то, что мы нарисовали. Иначе придется удалять объект через Меню "Список объектов" Ctrl+B.
Наша заготовка завершена, можно приступать к сортировке.
Функции обмена, сравнения и границ
Напишем функции для визуализации обмена, сравнений и выделения границ для сортировок делением. Первая функция обмена void Gswap() стандартная, но с добавлением кривой CRed для выделения сравниваемых элементов
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void Gswap(double &arr[],int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CRed.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmS); double sw = arr[i]; arr[i]=arr[j]; arr[j]=sw; //------------------------- Y[0] =0; Y[1] =0; CRed.Update(X,Y); CMain.Update(arr); Graphic.Redraw(); Graphic.Update(); //------------------------- }
Сначала выделяем столбцы, потом через некоторое время Sleep(TmS), определяющее скорость демонстрации, возвращаем в исходное состояние. Аналогично пишем функции сравнения для "<" и "<=" в виде bool GBool(double arr, int i, int j) и GBoolEq(double arr, int i, int j). В них добавляем столбцы другого цвета CViole.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool GBool(double &arr[], int i, int j) { X[0]=i;X[1]=j; Y[0] =arr[i];Y[1] =arr[j]; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); Sleep(TmC); Y[0]=0; Y[1]=0; CViolet.Update(X,Y); Graphic.Redraw(); Graphic.Update(); return arr[i]<arr[j]; }
Функция для выделения границ, столбцы которой стирать не нужно.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i];YZ[1]=a[j]; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); }
Теперь перейдём непосредственно к самим сортировкам.
Методы сортировки
Прежде чем перейти к разбору методов, хочу посоветовать запустить программу VisualSort, которая находится в прикреплённом файле VisualSort.ex5. Она позволит наглядно посмотреть, как работает каждая сортировка по отдельности. Полный код сортировок находится во включаемом файле GSort.mqh. Он получился довольно большой, поэтому здесь я обрисовал только основные идеи.
- Первая сортировка, с которой обычно начинают изучение — сортировка выбором (Selection sort). Находим номер минимального значения в текущем списке и меняем его на значение первой неотсортированной позиции.
template <typename T> void Select(T &arr[]) { int n = ArraySize(arr); for(int j=0;j<n;j++) { int mid=j; for(int i=j+1;i<n;i++) { if(arr[i]<arr[mid]) { mid=i; } } if(arr[j]>arr[mid]){swap(arr,j,mid);} } }
Здесь и далее функция обмена — это ранее написанные нами Gswap(), а сравнение элементов массива затем заменяется на GBool(). Например, if(arr[i]<arr[mid]) => if(GBool(arr,i,mid).
- Следующая сортировка (которая, кстати, часто используется при игре в карты) — сортировка вставками. В этом методе элементы входной последовательности просматриваются по одному, и каждый новый поступивший элемент размещается в подходящее место среди уже упорядоченных ранее. Базовый метод:
template<typename T> void Insert(T &arr[]) { int n= ArraySize(arr); for(int i=1;i<n;i++) { int j=i; while(j>0) { if(arr[j]<arr[j-1]) { swap(arr,j,j-1); j--; } else j=0; } } }
Производные от неё — сортировка Шелла (Shell Sort) и Вставка с двоичным поиском (Binary Insertion Sort). Идея метода Шелла состоит в сравнении элементов, стоящих не просто рядом, но и на определённом расстоянии друг от друга. Иными словами, это сортировка вставками с предварительными «грубыми» проходами. Binary Insertion использует для поиска места вставки двоичный поиск. На уже упомянутой выше демонстрации (VisualSort.ex5) хорошо видно, как Shell постепенно "расчёсывает" массив всё более мелкой гребёнкой. В этом плане он схож с методом Comb, описанным ниже.
- Пузырьковая сортировка и производные от неё — Шейкерная (Shake Sort), Гномья (Gnom), Расчёской (Comb) и Odd-Even Sort. Суть пузырьковой сортировки проста: проходимся по массиву от начала до конца и сравниваем между собой два соседних элемента. Если они неотсортированы, меняем их местами. В итоге каждой итерации наибольший элемент будет находиться в конце массива. Затем процедура повторяется, и в итоге мы получаем упорядоченный, отсортированный массив. Базовый алгоритм пузырьковой сортировки:
template<typename T> void BubbleSort(T &a[]) { int n =ArraySize(a); for (int i = 0; i < n - 1; i++) { bool swapped = false; for (int j = 0; j < n - i - 1; j++) { if (a[j] > a[j + 1]) { swap(a,j,j+1); swapped = true; } } if (!swapped) break; } }
При шейкерной сортировке проходы совершаются в обе стороны, поэтому "всплывают" не только большие элементы, но и "осаждаются" маленькие. Гномья интересна тем, что она реализована всего одним циклом. Приведу ее код:
void GGnomeSort(double &a[]) { int n =ArraySize(a); int i=0; while(i<n) { if(i==0||GBoolEq(a,i-1,i)) i++; //if(i==0||a[i-1]<a[i]) else { Gswap(a,i,i-1); //Обмен a[i] и a[i-1] i--; } } }
Если засечь место уже отсортированных элементов, получим сортировку вставками. Comb использует туже идею, что и Shell: проходится по массиву гребешками с разным шагом. Для него даже высчитали оптимальный коэффициент уменьшения = 1,247 ≈ ( 1 / ( 1-е^(-φ) ) ), где е — экспонента; φ — "золотое" число. По скорости на небольших массивах Comb и Shell не уступают быстрым сортировкам. Odd-Even Sort проходит по очереди по чётным/нечётным элементам. Поскольку она задумывалась как сортировка для многопоточной реализации, то в нашем случае совершенно бессмысленна.
- Более сложные методы основаны на принципе "разделяй и властвуй". Классические примеры — сортировка Хоара или быстрая сортировка
Общая идея алгоритма состоит в следующем: выбираем из массива элемент, называемый опорным (pivot). Это может быть любой из элементов массива. Сравниваем все остальные элементы с опорным и переставляем их в массиве так, чтобы разбить массив на два непрерывных отрезка: "меньше" опорного и "больше". Для отрезков "меньших" и "больших" значений выполняем рекурсивно ту же последовательность операций, если длина отрезка больше единицы. Основная идея содержится в псевдокоде:
algorithm quicksort(A, lo, hi) is if (lo < hi) { p = partition(A, lo, hi); quicksort(A, lo, p – 1); quicksort(A, p, hi);}
Различие вариантов сортировки в этом случае сводится к различным способам разбиений массива. В первоначальном варианте указатели бегут с разных сторон навстречу друг другу. Левый указатель находит элемент больше эталонного, а правый — меньше, и они обмениваются. В другом варианте оба указателя бегут слева направо. Когда первый находит "меньший" элемент, он переставляет его в позицию второго указателя. Для случаев, когда в массиве много одинаковых элементов, разбиение выделяет место для элементов, равных опорному. Такая схема применяется, когда нужно, например, отсортировать сотрудников всего по двум ключам — "М" и "Ж". Схема разбиения на рисунке:
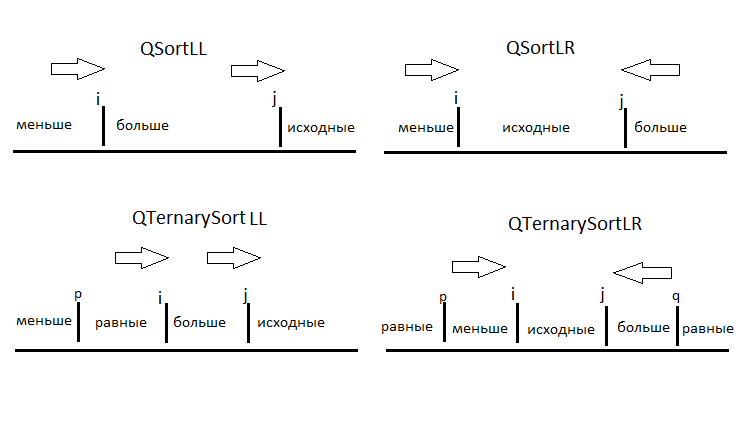
Для примера приведу лишь QSortLR с вариантом разбиения Хоара:
//----------------------QsortLR----------------------------------------+ void GQsortLR(double &arr[],int l,int r) { if(l<r) { GBorders(arr,l,r); int mid =PartitionLR(arr,l,r); GQsortLR(arr,l,mid-1); GQsortLR(arr,mid+1,r); } } int PartitionLR(double &arr[],int l,int r) { int i =l-1; int j =r; for(;;) { while(GBool(arr,++i,r)); j--; while(GBool(arr,r,j)){if(j==l) break;j--;} if(i>=j) break; Gswap(arr,i,j); } //--------------------------------------------- Gswap(arr,i,r); YZ[0]=0;YZ[1]=0; CGreen.Update(XZ,YZ); Graphic.Redraw(); Graphic.Update(); return i; }
Делить массив можно не на две части, а на 3, 4, 5 ... с несколькими эталонными элементами. Как вариант используется сортировка DualPivot, с двумя опорными элементами.
- Другие методы, основанные на принципе "разделяй и властвуй", используют слияние уже отсортированных частей массива. Они делят массив до тех пор пока он не станет длины 1, т.е. отсортированным, затем используют функцию слияния, которая заодно и сортирует элементы. Общий принцип:
void GMergesort (double &a[], int l, int r) { int m = (r+l)/2; GMergesort(a, l, m); GMergesort(a, m+1, r) ; Merge(a, l, m, r); }
Сортировка BitonicSort() делает одну половину массива возрастающей, другую убывающей, затем их соединяет.
- Сортировки с помощью деревьев (пирамидальная сортировка)
Общий принцип следующий. Сначала с помощью метода "просеивания" из массива образуем "кучу". Затем удаляем старший элемент, который находится в вершине кучи. Его помещаем в конец исходного массива как самый старший, и на его место ставим последний элемент из неотсортированной части. Строим новую кучу размера n-1 и т.д. "Кучи" могут быть построены по различным принципам. Например, сортировка Smooth() использует кучи, число элементов в которых равно числам Леонардо L(x+2) = L(x+1) +L(x) +1.
- Сортировки за линейное время. Сортировка подсчётом и поразрядные сортировки MSD и LSD
Сортировка подсчётом (Counting sort) — алгоритм сортировки, в котором используется диапазон чисел сортируемого массива (списка) для подсчёта совпадающих элементов. Применение сортировки подсчётом целесообразно лишь тогда, когда сортируемые числа имеют диапазон возможных значений, который достаточно мал по сравнению с сортируемым множеством, например, миллион натуральных чисел, меньших 1000. Её принцип применяется и в поразрядных сортировках. Приведу алгоритм:
void CountSort(double &a[]) { int count[]; double aux[]; int k =int(a[int(ArrayMaximum(a))]+1); int n =ArraySize(a); ArrayResize(count,k); ArrayResize(aux,n); for (int i=0;i<k;i++) count[i] = 0; for (int i=0;i<n;i++) count[int(a[i])]++; // количество элементов равных i for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; // количество элементов не превышающих i for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // заполняем промежуточный массив for(int i=0;i<n;i++)a[i]=aux[i]; }
Идея сортировки подсчетом применяются в MSD- и LSD-сортировках за линейное время. Имеется в виду время время N*R, где N — число элементов, а R — число разрядов в представлении числа в выбранной системе счисления. MSD (most significant digit) сортирует по старшему разряду, LSD (least significant digit) — по младшему. Например, в двоичной системе LSD подсчитает, сколько чисел оканчивается на 0, а сколько — на 1, и затем в первую половину поместит чётные числа (0), а во вторую нечётные (1). MSD — наоборот, начинает со старшего разряда. Если взять десятичную систему то в начале она поместит числа < 100, а дальше >100. Затем массив будет снова отсортирован на отрезки 0-19, 10-19,..., 100-109 и т.д. Сортировке по этому методу подвергаются целые числа. Но котировку 1.12307 можно сделать целой 1.12307*100 000.
Комбинацией быстрой сортировки и поразрядной получаем двоичную быструю сортировку QuicksortB(). Здесь применяется разбиение сортировки QSortLR, только отбор происходит не по эталонному элементу (pivot) массива, а по старшему разряду. Для этого здесь и в LSD c MSD применяется функция нахождения цифры n-го разряда
int digit(double x,int rdx,int pos) // Здесь x число, rdx систем счисления { // в нашем случае 2, pos номер разряда int mid =int(x/pow(rdx,pos)); return mid%rdx; }Сначала происходит разделение по старшему разряду int d =int(log(a[ArrayMaximum(a)])/log(2)), затем рекурсивно сортируются части по младшим разрядам. Внешне похожа на QuickSortLR.
- Некоторые специфические сортировки
Циклическая сортировка (Cycle Sort) предназначалась для систем, где перезапись данных ведёт к износу ресурсов. Следовательно, задача здесь — найти сортировку с наименьшим количеством обменов (Gswap). Для этого и используются циклические перестановки. Грубо говоря, 1 переставляется в 3, 3 в 2, 2 в 1. Каждый элемент переставляется либо 0, либо 1 раз. Всё это происходит довольно долго, время O(n^2). Подробнее с идеей и методом можно познакомиться здесь.
Блуждающая сортировка (Stooge sort). Это еще один пример надуманной и очень медленной сортировки. Алгоритм состоит в следующем. Если значение элемента в конце списка меньше, чем значение элемента в начале, то нужно поменять их местами. Если есть 3 или более элементов в текущем подмножестве списка, то: рекурсивно вызываем Stoodge() для первых 2/3 списка, рекурсивно вызываем Stoodge() для последних 2/3, снова рекурсивно вызываем Stoodge() для первых 2/3 и т.д.
Сводная таблица скорости методов
| Методы сортировки | Среднее время |
|---|---|
| Сортировка выбором (Selection sort) | O(n^2) |
| Сортировка вставками (Insertion sort) | O(n^2) |
| Вставками с двоичным поиском (Binary Selection Sort) | O(n^2) |
| Сортировка Шелла (Shell sort) | O(n*log(n)) |
| Пузырьковая сортировка (Bubble sort) | O(n^2) |
| Шейкерная сортировка (Shaker/Cocktail sort) | O(n^2) |
| Гномья сортировка (Gnom Sort) | O(n^2) |
| Сортировка расчёской (Comb Sort) | O(n*log(n)) |
| Сортировка слиянием (Merge Sort) | O(n*log(n)) |
| Битонная сортировка (Bitonic sort) | O(n*log(n)) |
| Пирамидальная сортировка (Heap sort) | O(n*log(n)) |
| Плавная сортировка (Smooth sort) | O(n*log(n)) |
| Быстрая сортировка(LR) (Quick sort LR) | O(n*log(n)) |
| Быстрая сортировка(LL) (Quick sort LL) | O(n*log(n)) |
| Quick Sort (ternary, LR ptrs) | O(n*log(n)) |
| Quick Sort (ternary, LL ptrs) | O(n*log(n)) |
| Quick Sort (dual pivot) | O(n*log(n)) |
| Сортировка подсчётом (Counting sort) | O(n+k) |
| Поразрядная сортировка LSD (Radix LSD) | O(n*k) |
| Поразрядная сортировка MSD (Radix MSD) | O(n*k) |
| Двоичная быстрая сортировка (Quick Binary sort) | O(n*log(n)) |
| Циклическая сортировка (Cycle sort) | O(n^2) |
| Stoodge sort | O(n^2.7) |
Все методы на одном экране
Выведем все описанные сортировки одновременно на один экран. В исходном видео разобранные сортировки запущены по одной, затем всё это смонтировано в видеоредакторе. Но в торговый терминал не встроены возможности видеостудии. Выйти из положения можно несколькими способами.
Вариант №1.
Имитировать многопоточность. Распараллелим сортировки так, чтобы после каждого сравнения и обмена можно было бы выйти из функции и передать очередь другой сортировке, а затем снова войти в неё на том же месте. Учитывая, что оператора GOTO нет, задача усложняется. Вот, например, как будет выглядеть в этом варианте простейшая сортировка выбором, которая приводилась в самом начале:
void CSelect(double &arr[]) { static bool ch; static int i,j,mid; int n =ArraySize(arr); switch(mark) { case 0: j=0; mid=j; i=j+1; ch =arr[i]<arr[mid]; if(ch) mid =i; mark =1; return; break; case 1: for(i++;i<n;i++) { ch =arr[i]<arr[mid]; mark =1; if(ch) mid=i; return; } ch =arr[j]>arr[mid]; mark=2; return; break; case 2: if(ch) { swap(arr,j,mid); mark=3; return; } for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark =2; return; } break; case 3: for(j++;j<n;j++) { mid=j; for(i=j;i<n;i++) { ch =arr[i]<arr[mid]; if(ch) mid=i; mark =1; return; } ch =arr[j]>arr[mid]; mark=2; return; } break; } mark=10; }
Это вполне рабочий вариант. При таком запуске массив будет отсортирован:
while(mark !=10) { CSelectSort(arr); count++; }
Переменная count покажет общее количество сравнений и перестановок. При этом код разросся в три-четыре раза, а ведь это простейшая сортировка. Есть ещё сортировки состоящие из нескольких функций, рекурсивные...
Вариант №2
Есть более простой вариант. В терминале MQL5 поддерживается концепция многопоточности. Чтобы ее реализовать, для каждой сортировки нужно из эксперта вызвать пользовательский индикатор. Но для каждого потока индикатор должен быть по отдельной валютной паре. В окне Обзор Рынка (Market Watch) должно быть достаточно инструментов для каждой сортировки.
n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);
Здесь SymbolName (n,0) — отдельный инструмент для каждого создаваемого потока и параметры, передаваемые в индикатор. Для назначения имени графического объекта удобно использовать SymbolName (n,0). На одном графике может быть только один объект класса CGraphic с данным именем. Вид сортировки и количество элементов в массиве, а также размеры самого холста CGraphic здесь не показаны.
В самом индикаторе происходит выбор функции сортировки и другие дополнительные действия, связанные с оформлением (например, подпись осей именем сортировки).
switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");Select(arr); break; case 1: Graphic.XAxis().Name("Insertion"); CMain.Name("Insertion");Insert(arr);break; etc............................................. }
На создание графических объектов уходит определённое время. Поэтому, чтобы сортировки начали работать одновременно, были добавлены глобальные переменные. NAME — глобальная переменная с именем инструмента, которой вначале присваивается значение 0. После создания всех необходимых объектов она получает значение 1, а после завершения сортировки 2. Так можно отслеживать моменты начала и окончания сортировок. Для этого в эксперте запускается таймер:
void OnTimer() { double x =1.0; double y=0.0; static int start =0; for(int i=0;i<4;i++) { string str; str = SymbolName(i,0); x =x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } if(x&&start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } if(y==8) {PlaySound("success.wav"); EventKillTimer();} }
Здесь переменная х отлавливает начало, а у — конец процесса.
В начале действия включается звук, снятый с оригинального видео. Для работы с исходниками он должен находиться в папке MetaTrader/Sound вместе с другими системными звуками формата *.wav или, если он находится в другом месте, необходимо указать путь от папки MQL5. Для завершения используется другой файл success.wav.
Итак, создаём эксперт и индикатор следующего вида. Эксперт:
enum SortMethod { Selection, Insertion, ..........Методы сортировки......... }; input int Xscale =475; //Масштаб графики input int N=64; //Количество элементов input SortMethod Sort1; //Метод ..........Различные входные параметры................. int OnInit() { //--- Устанавливаем глобальные переменные, запускаем таймер и т.п. for(int i=0;i<4;i++) { SymbolSelect(SymbolName(i,0),1); GlobalVariableSet(SymbolName(i,0),0);} ChartSetInteger(0,CHART_SHOW,0); EventSetTimer(1); GlobalVariableSet("ALL",0); //.......................Открываем отдельный поток-индикатор для каждой сортировки......... x=0*Xscale-Xscale*2*(0/2);//ряд длиной 2 y=(0/2)*Yscale+1; SymbolSelect(SymbolName(0,0),1); // Без неё на некоторых инструментах возможна ошибка S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N); return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ChartSetInteger(0,CHART_SHOW,1); EventKillTimer(); int i =ObjectsDeleteAll(0); PlaySound("ok.wav"); GlobalVariableSet("ALL",0); IndicatorRelease(Sort1); .......Всё что нужно удалить...... //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { ...Пусто... } //+------------------------------------------------------------------+ void OnTimer() { ....Описана выше.... }
И к нему индикатор:
#include <GSort.mqh> //Включаем все предварительно написанные сортировки //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ ..........Блок входных параметров..................................... input int SortName; //method int N=30; //number ...................................................................... int OnInit() { double arr[]; FillArr(arr,N); //заполняем массив случайными числами GlobalVariableSet(NAME,0); //устанавливаем глобальные переменные Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2); //NAME — валютная пара Graphic.IndentLeft(-30); Graphic.HistoryNameWidth(0); CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); //index 0 CMain.HistogramWidth(2); CRed =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); //index 1 CRed.Color(C'0x00,0x00,0xFF'); CRed.HistogramWidth(width); ......Различны графические параметры.......................... Graphic.CurvePlotAll(); Graphic.Update(); GlobalVariableSet(NAME,1); while(!GlobalVariableGet("ALL")); //Ожидание, пока все графические объекты не созданы switch(SortName) { case 0: Graphic.XAxis().Name("Selection"); CMain.Name("Selection");GSelect(arr); break; .....Список сортировок.............................................. } GlobalVariableSet(NAME,2); return INIT_SUCCEEDED; } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(...) { ..............Пусто........................ } //+------------------------------------------------------------------+ void OnDeinit(const int reason) { Graphic.Destroy(); delete CMain; delete CRed; delete CViolet; delete CGreen; ObjectDelete(0,NAME); }
Тестируем многопоточность
Light.ex5 и Sort24.ex5 — готовые к работе программы. Они скомпилированы через ресурсы и ничего больше не требуют. При работе с исходниками они должны быть установлены в соответствующие папки индикаторов и звуков.
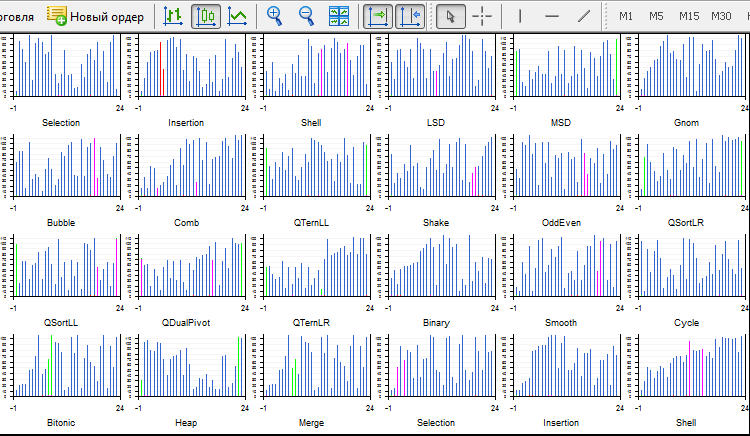
Версия Sort24.ex5 с 24 сортировками на моём обычном одноядерном компьютере нестабильная, дорабатывает через раз. Надо закрыть всё лишнее и ничего не трогать. В каждой сортировке пять графических объектов — четыре кривые и холст. Все они непрерывно перерисовываются. Двадцать четыре потока создают 120 (!) отдельных непрерывно меняющихся графических объекта в 24 потоках. Её я сделал просто как демонстрацию, что такое в принципе возможно и больше с ней не работал.
Рабочая, довольно стабильная версия Light.ex5 одновременно выводит 4 сортировки. Здесь добавлены возможности выбора количества элементов и методов сортировки в каждом окне. Кроме того, есть возможность выбрать способ перетасовки массива: случайный, по восходящей (т.е. уже отсортированный), по нисходящей (отсортированный в обратном порядке) и массив, где много одинаковых элементов (step array). Например, быстрая сортировка деградирует до O(n^2) на массиве, отсортированном в обратном порядке, а пирамидальная всегда сортирует за n*log(n). К сожалению, в индикаторах функция Sleep() не поддерживается, так что скорость зависит только от системы. Кроме того, количество ресурсов, выделяемых каждому потоку, также произвольно. Если в каждом окне запустить одну и ту же сортировку, то они придут к финишу все по-разному.
Подводя итоги:
- Однопоточная VisualSort — на 100% рабочая
- Четырёхпоточная Light — стабильная
- Двадцатичетырёхпоточная Sort24 — нестабильная
Можно было бы пойти по первому варианту, имитируя многопоточность. Тогда бы мы полностью контролировали процесс. Работали бы функции Sleep(), каждая сортировка получала бы строго равное время и т.д. Но при этом терялась бы сама концепция многопоточного программирования на MQL5.
Окончательный вариант:
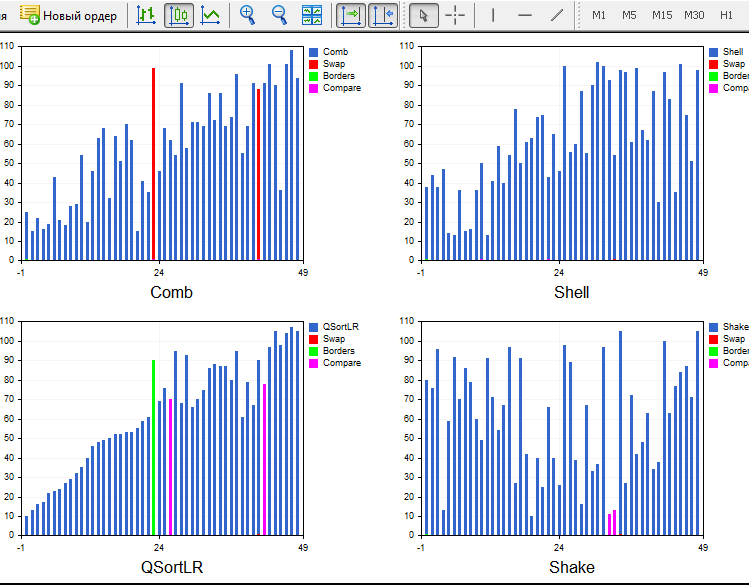
....................................................................................................................................................................
Список прилагаемых файлов
- VisaulSort.ex5 - каждая сортировка отдельно
- Programs(Sort24.ex5, Light.ex5) - готовые программы
- Звуковые файлы
- Codes. Исходники программ - сами сортировки, индикаторы, включаемые файлы, эксперты.
Примечание от редакторов статьи
Автор статьи реализовал интересный вариант многопоточной сортировки с помощью одновременного запуска множества индикаторов. Данная архитектура очень сильно нагружает компьютер, поэтому мы немного доработали исходные коды автора, а именно:
- в файле auxiliary.mq запретили вызов перерисовки графика из каждого индикатора
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void GBorders(double &a[],int i,int j) { XZ[0]=i;XZ[1]=j; YZ[0]=a[i]+2;YZ[1]=a[j]+5; CGreen.Update(XZ,YZ); Graphic.Redraw(false); Graphic.Update(false); }
- добавили функцию randomize(), которая подготавливает для всех индикаторов одни и те же случайные данные в массиве
- в файл IndSort2.mq5 добавили внешние параметры, которые задают размер массива со случайными значениями (у автора оно жестко равно 24) и инициализирующее число sid для генерации данных
input uint sid=0; //initialization of randomizer int N=64; //number of bars on histogramm
- в файл Sort24.mq5 добавили таймер для отрисовки графика с помощью ChartRedraw()
//+------------------------------------------------------------------+ //| Timer function | //+------------------------------------------------------------------+ void OnTimer() { double x=1.0; double y=0.0; static int start=0; //--- проверим в цикле флаг инициализации каждого индикатора for(int i=0;i<methods;i++) { string str; str=SymbolName(i,0); x=x*GlobalVariableGet(str); y=y+GlobalVariableGet(str); } //--- все индикаторы успешно инициализировались if(x && start==0) { start=1; GlobalVariableSet("ALL",1); PlaySound("Sort.wav"); } //--- все сортировки завершились if(y==methods*2) { PlaySound("success.wav"); EventKillTimer(); } //--- обновить графики сортировок ChartRedraw(); }
- звуковые файлы перенесли в папку <>\MQL5\Sounds чтобы можно было включить их в качестве ресурса
#resource "\\Sounds\\Sort.wav"; #resource "\\Sounds\\success.wav"; #resource "\\Indicators\\Sort\\IndSort2.ex5"
Готовая для компиляции структура приложена в архиве moderators_edition.zip, которую достаточно распаковать и скопировать в свой терминал. Если у вас не слишком мощный компьютер, рекомендуем во входных параметрах установить methods=6 или methods=12.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Универсальный торговый эксперт: Доступ к свойствам инструмента (часть 8)
Универсальный торговый эксперт: Доступ к свойствам инструмента (часть 8)
 Паттерны, доступные при торговле корзинами валют. Часть III
Паттерны, доступные при торговле корзинами валют. Часть III
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Между прочим, в оригинале, на youtube все сортировки сделаны по отдельности, а потом смонтированы в видеоредакторе. Там есть ссылка на программу на С++. Но и на С++ они написаны по одной, хотя возможностей у С++ побольше.
Я прочел об этом в статье. И ни в коем случае не хотел упрекнуть вас в недобросовестной работе.
Но разобраться было бы интересно.
Я прочел об этом в статье. И ни в коем случае не хотел упрекнуть вас в недобросовестной работе.
Но разобраться было бы интересно.
Я знаю в чём проблема. MQL5 написан под винду, и мы не можем контролировать потоки...В индикаторах заложена многопоточность, но без прерывания.Надо было писать через эксперт...
Присоединитесь к обсуждению?