MQL5を使用した整列法とその可視化

内容

• はじめに
• Graphics\Graphic.mqh librライブラリの適応
• 交換、比較、境界関数
• 整列法
•   選択ソート
•   挿入ソート
•   バブルソート
•   クイックソート
•   マージソート
•   ヒープソート
•   基数MSDとLSDソート
•   他のソート
• 整列法速度表のサマリー
• 1つの画面上のすべての整列法
• マルチスレッドのテスト
• 編集者のメモ
  

はじめに

ウェブ上では、さまざまな整列タイプを示す多数のビデオを見つけることができます。例としてここでは24の整列法の視覚化がみられます。私は整列アルゴリズムの一覧と共にこのビデオを基礎としました。

Graphic.mqhライブラリには、MQL5のグラフィックスを扱う責任があり、すでに多くの記事に記載されています。たとえば、ライブラリの機能はここでみられます。私の目的は、アプリケーション分野を記述し、整列プロセスを詳しく検討することです。ソートタイプには既に少なくとも1つの別個の記事が書かれておりソートタイプのいくつかは詳細な調査の対象なので、ここではソートの一般的な概念が説明されます。

Graphics\Graphic.mqh librライブラリの適応

初めにライブラリをインクルードします。

#include <Graphics\Graphic.mqh>

ヒストグラムの列は、Gswap() とGBool() の交換関数と比較関数を適用してソートします。処理される要素（比較、置換など）は色で強調表示されます。これを達成するために、各色に別々のCCurve型オブジェクトが割り当てられます。Gswap関数 (int i, int j, CGraphic &G, CCurve &A, CCurve &B and CCurve &C)によってこれらのオブジェクトを区画化しないために、それらをグローバルにします。CCurveクラスにはデフォルトコンストラクタがないので、単にグローバル宣言することはできません。よってCCurve型グローバルポインタの *CMainを宣言します。

色は3つの異なる方法で設定できます。最も目立つのは C'0x00,0x00,0xFF'または C'Blue, Green, Red'です。曲線は、いくつかの実装を持つCGraphicクラスのCurveAdd() 関数を使用して作成されます。大部分の要素では2要素のみがあるので、値が1つの配列でCurveAdd(arr, CURVE_HISTOGRAM, "Main") を選択すると便利です。補助配列の場合、引数のX配列と値のY配列CurveAdd(X, Y, CURVE_HISTOGRAM, "Swap") 。補助線の配列をグローバルにすると便利です。

#include <Graphics\Graphic.mqh> 
                               
#property script_show_inputs
input int N  =42;

CGraphic Graphic;
CCurve *CMain;
CCurve *CGreen;
CCurve *CBlue;
CCurve *CRed;
CCurve *CViolet;

double X[2],Y[2],XZ[2],YZ[2];

//+------------------------------------------------------------------+
//| スクリプトプログラム開始関数                                         |
//+------------------------------------------------------------------+
void OnStart()
  {
   // 配列------------------------------  
   double arr[];
   FillArr(arr,N);
   X[0]=0;X[1]=0;
   Y[0] =0;Y[1]=0;
   //-------------------------------------
   Graphic.Create(0,"G",0,30,30,780,380);

   CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); // インデックス0
   CMain.HistogramWidth(4*50/N);

   CBlue  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Pivot"); // インデックス1
   CBlue.Color(C'0xFF,0x00,0x00');
   CBlue.HistogramWidth(4*50/N);

   CRed  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); // インデックス2
   CRed.Color(C'0x00,0x00,0xFF');
   CRed.HistogramWidth(4*50/N);

   CGreen  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Borders"); // インデックス3
   CGreen.Color(C'0x00,0xFF,0x00');
   CGreen.HistogramWidth(4*50/N);

   CViolet  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Compare"); // インデックス4
   CViolet.Color(C'0xFF,0x00,0xFF');
   CViolet.HistogramWidth(4*50/N);

   Graphic.XAxis().Min(-0.5);

   Graphic.CurvePlot(4);
   Graphic.CurvePlot(2);
   Graphic.CurvePlot(0);
  //Graphic.CurvePlotAll(); 使用可能なすべての曲線を表示するだけ
   Graphic.Update();

   Sleep(5000);
   int f =ObjectsDeleteAll(0);
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void FillArr(double &arr[],int num)
  {
   int x =ArrayResize(arr,num);
   for(int i=0;i<num;i++)
     arr[i]=rand()/328+10; 
  }

Graphic.XAxis().Min(-5) は、ゼロ要素がマージしないように、Y軸からインデントを設定します。Histogramwidth()は列の幅です。

FillArr() 関数は、10から（X軸とマージしない）110までの乱数で配列を塗りつぶします。'arr' 配列は、交換関数が標準のルックswap(arr, i, j).を持つようにローカルになります。最後のObjectDeleteAllコマンドは、プロットしたものを消去します。それ以外の場合は、メニューのオブジェクトリストCtrl+Bでオブジェクトを削除する必要があります。  

準備が完了です。ソートを始めます。

交換、比較、境界関数

区画ごとのソートのための交換、比較、境界の割り当てを視覚化するための関数を記述しましょう。最初の交換関数であるvoid Gswap() は標準ですが、比較要素を割り当てるためのCRed曲線をもちます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void Gswap(double &arr[],int i, int j)
  {
   X[0]=i;X[1]=j;
   Y[0] =arr[i];Y[1] =arr[j];
   CRed.Update(X,Y);
   Graphic.Redraw();
   Graphic.Update();
   Sleep(TmS);

   double sw = arr[i];
   arr[i]=arr[j];
   arr[j]=sw;

   //-------------------------
   Y[0] =0;
   Y[1] =0;
   CRed.Update(X,Y);
   CMain.Update(arr);
   Graphic.Redraw();
   Graphic.Update();
  //-------------------------
  }

まず、列を割り当てます。その後、デモ速度を定義するSleep(TmS) 時間後に初期状態に戻ります。同様の方法で、"<"と "<="の比較関数のbool GBool(double arr, int i, int j) とGBoolEq(double arr, int i, int j) を記述し、別の色のCVioleの列を追加します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool GBool(double &arr[], int i, int j)
  {
   X[0]=i;X[1]=j;
   Y[0] =arr[i];Y[1] =arr[j];
   CViolet.Update(X,Y);
   Graphic.Redraw();
   Graphic.Update();
   Sleep(TmC);
   Y[0]=0;
   Y[1]=0;
   CViolet.Update(X,Y);
   Graphic.Redraw();
   Graphic.Update();
   return arr[i]<arr[j];
  }

境界を割り当てるための関数。列は消去してはいけません。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void GBorders(double &a[],int i,int j)
  {
   XZ[0]=i;XZ[1]=j;
   YZ[0]=a[i];YZ[1]=a[j];
   CGreen.Update(XZ,YZ);
   Graphic.Redraw();
   Graphic.Update();
  }

では、並べ替えに注目してみましょう。

整列法

メソッドの分析に進む前に、下記のVisualSortアプリケーション（VisualSort.ex5）を起動することをお勧めします。各ソートが個別にどのように動作するかを視覚的に確認することができます。完全なソートコードはGSort.mqhインクルードファイルにあります。ファイルはかなり大きいので、ここでは主なアイデアのみを概説しました。

• 調査を開始する最初の並べ替えは選択ソートです。まず、現在のリスト内の最小値の番号を見つけ、それを最初のソートされていない位置の値に置き換えます。 

template <typename T>
void Select(T &arr[])
  {
   int n = ArraySize(arr);
   for(int j=0;j<n;j++)
     {
      int mid=j;
      for(int i=j+1;i<n;i++)
        {   
         if(arr[i]<arr[mid])
          {
           mid=i;
          }   
        }
      if(arr[j]>arr[mid]){swap(arr,j,mid);}
     }
  }

交換関数はここでも下記でも前述のGswap()のままですが、配列要素の比較関数はGBool()に置き換えられています。例はif(arr[i]<arr[mid]) => if(GBool(arr,i,mid)です。

• 次のソートタイプ（カードをプレイするときによく使用される）は挿入ソートです。この方法では、入力シーケンスの要素が一度に1つずつ分析されます。新しく到着した各要素は、以前に配置された要素の中の適切な場所に配置されます。下記は基本メソッドです。

template<typename T>
void Insert(T &arr[])
  {
   int n= ArraySize(arr);
   for(int i=1;i<n;i++)
     {
      int j=i;
      while(j>0)
        {
         if(arr[j]<arr[j-1])
           {
            swap(arr,j,j-1);
            j--;
           }
         else j=0;   
        }
      }
  }

この整列法の派生物は、シェルソートおよびバイナリ挿入ソートです。 前者は、隣接する要素だけでなく、互いから特定の距離にある要素も比較します。言い換えれば、これは予備的な「粗い」パスを伴う挿入ソートです。 バイナリ挿入での挿入場所の検索にはバイナリ検索が適用されます。上記の実証（VisualSort.ex5）では、「シェルソート」が徐々に減少する「コム」 を使用して配列を検索していることが明確です。この点に関しては、以下に説明するComb法との共通点が多いです。

• バブルソートとその派生物 - シェイクソート、ノームソート、コムソート、奇偶転置ソートバブルソートの背後にあるアイデアは簡単です。つまり、配列全体を最初から最後まで調べて、2つの隣接要素を比較し、順番でなければ、それらの位置を交換します。各反復の結果、最大要素は配列の最後に配置されます。その後、この過程が繰り返されます。配列は最終的にソートされます。基本的なバブルソートアルゴリズムは下記です。

template<typename T>
void BubbleSort(T &a[])
  {
   int n =ArraySize(a);  
   for (int i = 0; i < n - 1; i++)
     {
      bool swapped = false;
      for (int j = 0; j < n - i - 1; j++)
        {
         if (a[j] > a[j + 1])
          {
           swap(a,j,j+1);
           swapped = true;                                        
          }
        }
     if (!swapped)
       break;
    }
 }

シェイクソートでは、両方向にパスして大小両方の要素を検出できます。ノーむソートは、1つのサイクルで実装されているという点で面白いので、そのコードを見てみましょう。

void GGnomeSort(double &a[])
  {
   int n =ArraySize(a);
   int i=0;
   while(i<n)
     {
      if(i==0||GBoolEq(a,i-1,i))
        i++; //if(i==0||a[i-1]<a[i])
      else
        {
         Gswap(a,i,i-1); // a[i]とa[i-1]を交換する
         i--;
        }      
     }
   }

すでにソートされた要素の場所をマークすると、これは挿入ソートになります。コムソートはシェルソートと同じアイデアを使用し、異なるステップを持つコムで配列に沿って移動します。最適縮小係数 = 1.247  ≈ ( 1 / ( 1-е^(-φ) ) )で、ここでеは指数で、φは「金色」の数です。小さな配列に適用されると、コムソートとシェルソートは高速の整列法に似ています。奇偶転置ソートは奇数/偶数の要素を交互にパスしますが、マルチスレッド実装のために開発されているので、ここでは役に立ちません。 

• より複雑な方法は「分割による征服」原則に基づいており、標準的な例はクイックソート（ホーアソート）です。

このアルゴリズムの一般的な考え方は次のとおりです。配列からピボット要素を選択します。任意の配列要素をピボットとして選択できます。他のすべての要素は、ピボット1と比較され、配列が、それぞれピボット1より「小さい」要素とピボット1より「大きい」要素からなる2つの連続したセグメントに分割されるように、配列内で再配置されます。セグメントの長さが1より大きい場合、再帰的に「小さい」および「大きい」セグメントに対して同じ一連の操作が実行されます。基本的な考え方は擬似コードでみられます。

 quicksort(A, lo, hi) のアルゴリズム
 if (lo < hi)
   { 
    p = partition(A, lo, hi);
    quicksort(A, lo, p – 1);
    quicksort(A, p, hi);
   }

この場合の並べ替えオプションの違いは、配列を分割するさまざまな方法によって異なります。元のバージョンでは、ポインタは反対側からお互いに向かって移動します。左のポインタはピボット1より大きい要素を探し、右のポインタはピボット1より小さい要素を探し、それらは入れ替えられます。別のバージョンでは、両方のポインタが左から右に移動します。第1のポインタが「より小さい」要素を見つけると、その要素を第2のポインタの位置に移動させます。配列に多数の同一要素が含まれている場合、分割によってピボット1と等しい要素の領域が割り当てられます。このような配置は、例えば、"M"（男性）と "F"（女性）の2つのキーのみで従業員を分類する必要がある場合に適用されます。適切な分割が以下に表示されます。

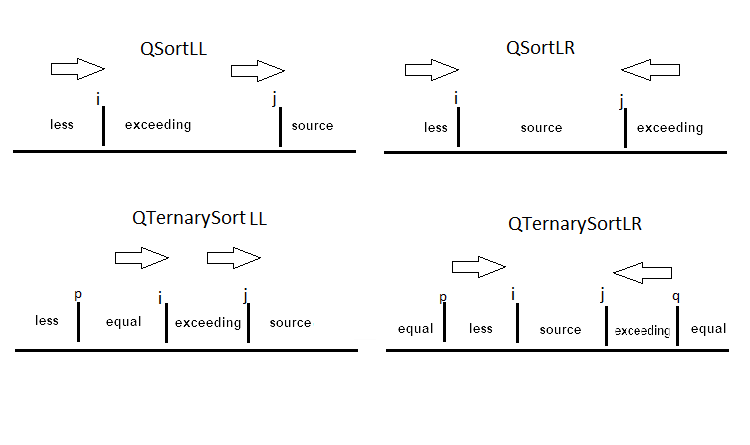
ホーアの分割法を例にしてQSortLRを見てみましょう。

//----------------------QsortLR----------------------------------------+
void GQsortLR(double &arr[],int l,int r)
  {
   if(l<r)
     {
      GBorders(arr,l,r);
      int mid =PartitionLR(arr,l,r);
      GQsortLR(arr,l,mid-1);
      GQsortLR(arr,mid+1,r);   
     }
  }

int PartitionLR(double &arr[],int l,int r)
  {
   int i =l-1;
   int j =r;
   for(;;)
     {
      while(GBool(arr,++i,r));
      j--; 
      while(GBool(arr,r,j)){if(j==l) break;j--;}
      if(i>=j) 
        break;
      Gswap(arr,i,j);
     }
//---------------------------------------------
 Gswap(arr,i,r);
 YZ[0]=0;YZ[1]=0;
 CGreen.Update(XZ,YZ);
 Graphic.Redraw();    
 Graphic.Update();
  
 return i;
}

配列は、いくつかのピボット要素で3,4,5 ...の部分に分割できます。2つのピボット要素によるデュアルピボットソートも使用できます。 

• 「分割による征服」原理に基づく他の方法は、既にソートされた配列部分のマージを使用します、。長さが1に等しくなるまで配列を分割した（ソート済み）後、途中で要素をソートするマージ関数を適用します。一般原則：

void GMergesort (double &a[], int l, int r)
  {
   int m = (r+l)/2;
   GMergesort(a, l, m); 
   GMergesort(a, m+1, r) ; 
   Merge(a, l, m, r);
  }

BitonicSort() は、配列の半分を昇順にし、もう一方は降順に後でそれらを組み合わせます。

• ヒープソート

一般原則は次の通りです。配列を「シフト」することによって「ヒープ」を形成します。「ヒープ」の上部にある古い要素を削除します。ソース配列の最後に移動して、ソートされていない部分の最後の要素と置き換えます。n-1などのサイズの新しい「ヒープ」を構築します。「ヒープ」はさまざまな原則に基づいています。たとえば、Smooth() ソートでは、レオナルド数 L(x+2) = L(x+1) +L(x) +1.に等しい要素数を持つ「ヒープ」が適用されます。

• 基数ソート分布数え上げソートと基数MSD/LSDソート

分布数え上げソートは、一致する要素の計算にソートされた配列（リスト）の数の範囲を適用する整列法です。 分布数え上げソートの適用は、ソートされた数値が、ソートされたセットと比較して十分小さい可能な値の範囲を持つ場合、たとえば1000未満の100万の自然数などの場合にのみ合理的です。その原理は基数ソートにも適用されます。下記がそのアルゴリズムです。

void CountSort(double &a[])
  { 
   int count[];
   double aux[];
   int k =int(a[int(ArrayMaximum(a))]+1);
   int n =ArraySize(a);
   ArrayResize(count,k);
   ArrayResize(aux,n);  
   for (int i=0;i<k;i++) count[i] = 0; 
   for (int i=0;i<n;i++) count[int(a[i])]++;             // 要素数がiに等しい
   for (int i=1;i<k;i++) count[i] = count[i]+count[i-1]; //  i以下の要素の数
   for(int j=n-1;j>=0;j--) aux[--count[int(a[j])]]=a[j]; // 中間的な配列に書き入れる 
   for(int i=0;i<n;i++)a[i]=aux[i];
  }

分布数え上げソートのアイデアは、MSDとLSDソートで線形時間で適用されます。これはN * R時間で、ここでNは要素の数、Rは選択された番号システム内の数字表現の桁数です。 MSD（最上位桁）は最上位桁でソートし、LSD（最下位桁）は最下位桁でソートします。たとえば、二進数では、LSDは、0と1で終わる数字の数を計算して、前半に偶数 (0) 、後半に奇数 (1) を配置します。 逆に、MSDは先頭桁から始まります。十真数では、最初の数値は100未満、後の数値は100になります。次に、配列は再び0-19,10-19、...、100-109などのセグメントにソートされます。この整列法は整数に適用されます。しかし、1.12307のクオーツは整数1.12307 * 100 000にすることができます。

QuicksortB() バイナリクイックソートは、クイックソートと基数ソートを組み合わせたものです。ここではQSortLRソートが適用されますが、選択はピボット配列要素ではなく、最上位桁で実行されます。これを行うために、ここでn番目の桁数を検索する機能がLSD/MSDに適用されます。

int digit(double x,int rdx,int pos) // xが数、rdxは記数法 
  {				    // でここでは2、 posは桁のインデックス 
   int mid =int(x/pow(rdx,pos));
   return mid%rdx;
  }

最初に、上の桁によるソートが int d =int(log(a[ArrayMaximum(a)])/log(2))で実行され、次に桁順に行われます。視覚的にはこれはQuickSortLRと似ています。

• いくつかの特定のソート

サイクルソートは、データの上書きがリソースの消耗につながるシステム向けです。したがって、タスクは最小限の交換をするソートを見つけることです (Gswap).。サイクルソートはこのためのものです。大まかに言えば、1は3、3は2、2は1に再配置されます。各要素は、0回または1回のいずれか再配置されます。これにはO(n^2)の時間がかかります。概念と方法の詳細はここにあります。

ストゥージソートこれは、あと一つの不自然な、非常に遅いソートの例です。アルゴリズムは下記の通りです。リストの終わりにある要素の値が最初の要素の値よりも小さい場合、要素の値を交換します。リストの現在のサブセットに3つ以上の要素が含まれている場合、リストの最初の2/3に対してStoodge()を再帰的に呼び出し、最後の2/3に対してStoodge() を再帰的に呼び出し、再び最初のの2/3に対して再帰的にStoodge() を呼び出すなどです。

整列法速度表のサマリー

整列法	平均時間
選択ソート	O(n^2)
挿入ソート	O(n^2)
バイナリ選択ソート	O(n^2)
シェルソート	O(n*log(n))
バブルソート	O(n^2)
シェーカー/カクテルソート	O(n^2)
ノームソート	O(n^2)
コムソート	O(n*log(n))
マージソート	O(n*log(n))
バイトニックソート	O(n*log(n))
ヒープソート	O(n*log(n))
スムースソート	O(n*log(n))
クイックソートLR	O(n*log(n))
クイックソートLL	O(n*log(n))
クイックソート（3進、LRポインター）	O(n*log(n))
クイックソート（3進、LLポインター）	O(n*log(n))
クイックソート（デュアルピボット）	O(n*log(n))
分布数え上げソート	O(n+k)
基数LSDソート	O(n*k)
基数MSDソート	O(n*k)
クイックバイナリソート	O(n*log(n))
サイクルソート	O(n^2)
ストゥージソート	O(n^2.7)

1つの画面上のすべての整列法

記述されたすべての種類を同時に1つの画面にプロットしましょう。ソースビデオでは、記述されたソートが1つずつ起動されます。結果はビデオエディタで編集されました。ビデオ編集機能は取引プラットフォームには組み込まれていません。解決策がいくつかあります。

オプション1

マルチスレッドのシミュレーション各比較の後に関数を終了し、キューを別のソートに渡して交換し、同じ場所にもう一度入力し直すことができるように、ソートを並列化します。このタスクはGOTO演算子がないと複雑になります。たとえば、下記は、そのような場合の、最初の例で説明した最も単純な選択ソートです。

void CSelect(double &arr[])
  {
   static bool ch;
   static int i,j,mid;
   int n =ArraySize(arr);

   switch(mark)
     {
      case 0:
        j=0;
        mid=j;
        i=j+1;
        ch =arr[i]<arr[mid];     
        if(ch)
          mid =i;
        mark =1; 
        return;     
        break;
  
      case 1:
        for(i++;i<n;i++)
          {   
          ch =arr[i]<arr[mid];
          mark =1;
          if(ch)
            mid=i;
          return;     
         }
       ch =arr[j]>arr[mid];
       mark=2;
       return;
       break;
          
     case 2:
       if(ch)
         {
          swap(arr,j,mid);
          mark=3;
          return;
         }
       for(j++;j<n;j++)
         { 
          mid=j;
          for(i=j;i<n;i++)
            {   
             ch =arr[i]<arr[mid];     
             if(ch)
               mid=i;
             mark =1;
             return;     
            }
         ch =arr[j]>arr[mid];
         mark =2;
         return;                               
        }
       break;
  
   case 3:
     for(j++;j<n;j++)
       { 
        mid=j;
        for(i=j;i<n;i++)
          {   
           ch =arr[i]<arr[mid];     
           if(ch)
             mid=i;
             mark =1;
           return;     
          }
        ch =arr[j]>arr[mid];
        mark=2;
        return;
       }
     break;   
    } 
   mark=10;
 }

この解決策はかなり実行可能です。このような起動時に、配列がソートされます。

while(mark !=10)
  {
   CSelectSort(arr);
   count++;
  }

'count'変数は、比較と交換の総数を示します。同時に、コードは3〜4倍大きくなり、これは最も簡単なソートです。いくつかの関数、再帰的な関数などからなるソートもあります。

オプション2

よりシンプルな解決法があります。MQL5端末は、マルチスレッドの概念をサポートしています。それを実装するには、ソートごとにカスタム指標を呼び出します。指標は、各スレッドに対して 別々の通貨ペア に属している必要があります。気配値表示ウィンドウには、それぞれのソートのツールが必要です。

n = iCustom(SymbolName(n,0),0,"IndcatorSort",...,SymbolName(n,0),Sort1,N);

ここで、SymbolName (n,0) は、生成されたそれぞれのフローに対するツールと指標に渡されるパラメータです。図形オブジェクト名は便利にSymbolName (n,0)で割り当てられます。1つのチャートには、指定された名前のCGraphicクラスオブジェクトが1つしかありません。ここでは整列法、配列内の要素数、CGraphic自体のサイズは表示されません。

ソート関数の選択と、ビジュアル表示に関連するその他の追加アクション（たとえば、ソート名の軸への追加）は、指標自体で行われます。

switch(SortName)
  {
   case 0:
     Graphic.XAxis().Name("Selection");   
     CMain.Name("Selection");Select(arr); break;
   case 1:
     Graphic.XAxis().Name("Insertion");
     CMain.Name("Insertion");Insert(arr);break;
   など.............................................
  }

グラフィカルオブジェクトの作成には一定の時間がかかるため、ソートを同時に行うためにグローバル変数が追加されました。NAMEは、製品名を表すグローバル変数で初期値は0です。必要なオブジェクトがすべて作成されると1の値が取得され、ソートの完了後には2の値が割り当てられます。このようにして、ソートの開始と終了を追跡できます。これを行うには、EAでタイマーが起動されます。

void OnTimer()
  {
   double x =1.0;
   double y=0.0;
   static int start =0;
   for(int i=0;i<4;i++)
     {
      string str;
      str = SymbolName(i,0);
      x =x*GlobalVariableGet(str);
      y=y+GlobalVariableGet(str);
     }
  if(x&&start==0)
    {
     start=1;
     GlobalVariableSet("ALL",1);
     PlaySound("Sort.wav");
    }
  if(y==8) {PlaySound("success.wav"); EventKillTimer();}   
 }

ここでは変数 хがプロセスの開始、у がその終了を示します。

プロセスの開始時には、元のビデオの音声が再生されます。ソースファイルを操作するには、他の* .wavシステムサウンドと一緒にMetaTrader/Soundフォルダに配置します。他の場所にある場合は、MQL5フォルダからパスを指定します。完了時には、success.wavファイルが使用されます。

以下のタイプのEAと指標を作成しましょう。EA：

enum SortMethod
  {
   Selection,
   Insertion,
   ..........整列法.........
  };

input int Xscale =475;          // チャートスケール
input int N=64;                 // 要素数
input SortMethod Sort1;         // 整列法
..........様々な入力.................

int OnInit()
  {
   //--- グローバル変数の設定、タイマーの起動など
   for(int i=0;i<4;i++)
     {
      SymbolSelect(SymbolName(i,0),1);
      GlobalVariableSet(SymbolName(i,0),0);}
      ChartSetInteger(0,CHART_SHOW,0);
      EventSetTimer(1);  
      GlobalVariableSet("ALL",0);
//.......................ソートごとに個別の指標スレッドを開く.........
   x=0*Xscale-Xscale*2*(0/2);// 長さ2の行
   y=(0/2)*Yscale+1;
   SymbolSelect(SymbolName(0,0),1); // これなしでは、製品によってエラーが発生する
   S1 = iCustom(SymbolName(0,0),0,"Sort1",0,0,x,y,x+Xscale,y+Yscale,SymbolName(0,0),Sort1,N);

   return(0);
  }
//+------------------------------------------------------------------+
//| エキスパート初期化解除関数                                          |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ChartSetInteger(0,CHART_SHOW,1);
   EventKillTimer();
   int i =ObjectsDeleteAll(0);
   PlaySound("ok.wav");
   GlobalVariableSet("ALL",0);
   IndicatorRelease(Sort1);
   .......すべてを削除する......
//+------------------------------------------------------------------+
//| エキスパートティック関数                                            |
//+------------------------------------------------------------------+
void OnTick()
  {
   ...空... 
  }
//+------------------------------------------------------------------+
void OnTimer()
  {
   ....前述.... 
   }

適切な指標は下記の通りです

#include <GSort.mqh>  // 以前に書かれたすべてのソートを含める
//+------------------------------------------------------------------+
//| カスタム指標初期化関数                                              |
//+------------------------------------------------------------------+

..........入力ブロック.....................................
input int SortName;         // 整列法
int N=30;                   // 数
......................................................................
int OnInit()
  {
   double arr[];
   FillArr(arr,N);                 // 配列に乱数を書き込む  
   GlobalVariableSet(NAME,0);      // グローバル変数を設定する  
  
   Graphic.Create(0,NAME,0,XX1,YY1,XX2,YY2);      //NAME — 現在の対
   Graphic.IndentLeft(-30);
   Graphic.HistoryNameWidth(0);
   CMain =Graphic.CurveAdd(arr,CURVE_HISTOGRAM,"Main"); // インデックス0
   CMain.HistogramWidth(2);

   CRed  =Graphic.CurveAdd(X,Y,CURVE_HISTOGRAM,"Swap"); // インデックス1
   CRed.Color(C'0x00,0x00,0xFF');
   CRed.HistogramWidth(width);
   ......さまざまなグラフィックパラメータ..........................
   Graphic.CurvePlotAll();
   Graphic.Update();
   GlobalVariableSet(NAME,1);

   while(!GlobalVariableGet("ALL")); // すべてのグラフィックオブジェクトが作成されるまで待つ

   switch(SortName)
     {
      case 0:
        Graphic.XAxis().Name("Selection");   
        CMain.Name("Selection");GSelect(arr); break;
      .....ソートの一覧..............................................
     }

   GlobalVariableSet(NAME,2);
   return INIT_SUCCEEDED;
  }
//+------------------------------------------------------------------+
//| カスタム指標反復関数                                               |
//+------------------------------------------------------------------+
int OnCalculate(...)
  {
   ..............空........................
  }
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   Graphic.Destroy();
   delete CMain;
   delete CRed;
   delete CViolet;
   delete CGreen;
   ObjectDelete(0,NAME);
  }

マルチスレッドのテスト

Light.ex5とSort24.ex5はすぐに使えるプログラムです。これらはリソースを介してコピーされており、他には何も必要ありません。ソースコードを使って作業するときは、指標と音声を対応するフォルダにインストールする必要があります。

私のごく普通のシングルコアPCでは24のソートを持つSort24.ex5は不安定で、不均等 に動作するので、不要なプログラムはすべて終了し、何にも手を触れないようにします。各ソートには、4つの曲線とキャンバスの5つのグラフィックオブジェクトが含まれており、それらのすべてが再描画され続きます。24スレッドは、それぞれで連続的に変化するグラフィカルオブジェクトを120個 (!) 作成します。これは単なる実証で、使うのはもうやめました。

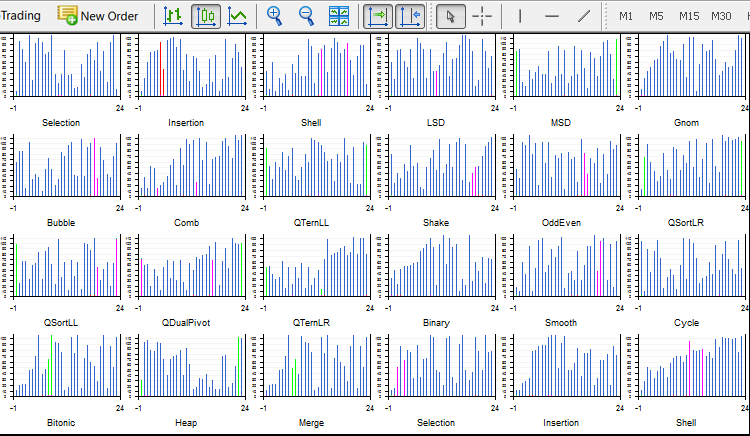
Light.ex5の作業版とかなり安定版は同時に4種類表示されます。ここでは、各ウィンドウの要素数と整列法を選択できます。さらに、ランダム、上向き（ソート済み）、下向き（逆順ソート済み）、および多数の同一要素を持つ配列（ステップ配列）を使用して、配列をシャッフルする方法を選択することができます。たとえば、クイックソートは、逆順にソートされた配列ではO(n^2) まで悪化する一方、ヒープは常にn*log(n)でソートされます。残念ながら、 Sleep() 関数は指標ではサポートされていないため、速度はシステムにのみ依存します。また、スレッドごとに割り当てられるリソースの量も任意です。同じソートが各ウィンドウで開始された場合、それらはすべて異なる方法で完成します。

まとめ

• シングルスレッドVisualSortは100％動作
• 4スレッドのライト版は安定
• 24スレッドのSort24は不安定

マルチスレッドをシミュレートする最初のオプションに従うことも可能で、その場合、プロセスを制御することができます。Sleep()関数は機能し、各ソートは厳密に等しい時間などを受け取ることになりますが、そのような場合には、MQL5マルチスレッドプログラミングの概念は失われます。

最終版：

....................................................................................................................................................................

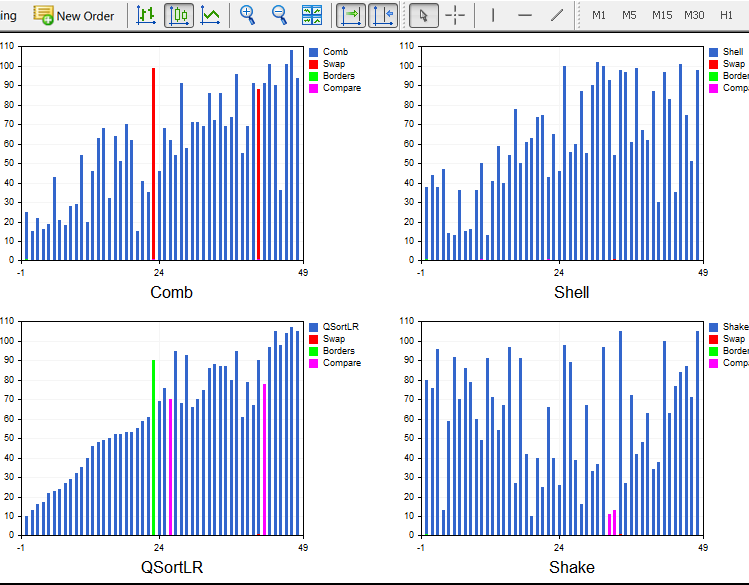
添付ファイルの一覧

• VisaulSort.ex5 - 個別に提示されたソート
• プログラム(Sort24.ex5, Light.ex5)  - 既製のアプリケーション
• 音声ファイル
• コードプログラムソースコード - ソート、指標、インクルードファイル、EA

編集者のメモ

本稿の著者は、複数の指標を同時に起動して、興味深いバージョンのマルチスレッドソートを実装しました。このアーキテクチャーはPCにかなりの負担を与えるので、著者のソースコードを少し変更しました。

• auxiliary.mqファイル内の各指標からのチャート再描画の無効化
  

  //+------------------------------------------------------------------+
  //|                                                                  |
  //+------------------------------------------------------------------+
  void GBorders(double &a[],int i,int j)
    {
     XZ[0]=i;XZ[1]=j;
     YZ[0]=a[i]+2;YZ[1]=a[j]+5;
     CGreen.Update(XZ,YZ);
     Graphic.Redraw(false);
     Graphic.Update(false);
    }
  

• すべての指標に対して同じランダムデータを配列内に準備するrandomize()関数を追加
• IndSort2.mq5ファイルに、乱数で配列サイズを定義（著者のバージョンでは24に厳密に等しくなっています）してデータ生成のために 'sid'を初期化するための外部パラメータを追加
  

  input uint sid=0;             // 乱数生成器の初期化 
  int   N=64;                   // ヒストグラムのバーの数
  

• Sort24.mq5ファイルにChartRedraw()を使ったチャート描画タイマーを追加
  

  //+------------------------------------------------------------------+
  //| タイマー関数                                                      |
  //+------------------------------------------------------------------+
  void OnTimer()
    {
     double x=1.0;
     double y=0.0;
     static int start=0;
  //--- 各指標の初期化フラグをループで確認する
     for(int i=0;i<methods;i++)
       {
        string str;
        str=SymbolName(i,0);
        x=x*GlobalVariableGet(str);
        y=y+GlobalVariableGet(str);
       }
  //--- すべての指標が正常に初期化された
     if(x && start==0)
       {
        start=1;
        GlobalVariableSet("ALL",1);
        PlaySound("Sort.wav");
       }
  //--- すべてのソートが完了
     if(y==methods*2)
       {
        PlaySound("success.wav");
        EventKillTimer();
       }
  //--- ソートのチャートを更新する
     ChartRedraw();
    }
  

• リソースとして含めることができるように音声ファイルを<>\MQL5\Soundsフォルダに移動
  

  #resource "\\Sounds\\Sort.wav";
  #resource "\\Sounds\\success.wav";
  #resource "\\Indicators\\Sort\\IndSort2.ex5"
  

コンパイルできる構造がmoderators_edition.zipにアーカイブにされているので、単に解凍して端末にコピーしてください。お使いのPCがあまり強力でない場合は、入力にmethods=6またはmethods=12を設定することをお勧めします。