
Receitas MQL5 - Criamos um buffer circular para calcular rapidamente indicadores numa janela deslizante
Tabela de conteúdos
- Introdução
- Problema do cálculo de média móvel
- Teoria do buffer circular
- Protótipo de trabalho
- Exemplo de cálculo da média móvel simples no buffer circular
- Exemplo de cálculo da média móvel exponencial no buffer circular
- Cálculo de máximos/mínimos no buffer circular
- Integração do buffer circular com a biblioteca AlgLib
- Construção do MACD com base em primitivas circulares
- Construção do indicador Stochastic com base em primitivas circulares
- Otimizando o uso da memória operativa
- Otimizando o tempo de teste do Expert Advisor
- Conclusões e sugestões para melhorar o desempenho
- Conclusão
Introdução
Não é nenhum segredo que a maioria dos cálculos que tem de executar o trader está associada com cálculos numa janela deslizante. Esta é uma característica específica dos dados financeiros que quase sempre andam num fluxo contínuo em forma de informações de preços, ordens colocadas ou volumes de negociação. Como regra geral, o trader precisa calcular um valor para um determinado período. Por exemplo, o cálculo da média móvel refere-se ao preço médio para as últimas N barras, onde N é o período da média móvel. Obviamente, neste caso, o tempo necessário para o cálculo da média, não deve depender do período da média. No entanto, na prática, nem sempre é fácil implementar o algoritmo com esta propriedade. Do ponto de vista algorítmico, é muito mais fácil recalcular o valor da média quando aparece uma nova barra. O algoritmo de buffer circular resolve o problema do cálculo eficaz, proporcionando um bloco de cálculo à janela deslizante, de modo que seus cálculos internos sejam eficazes e ainda simples.
Problema do cálculo de média móvel
Vamos considerar um exemplo específico: o cálculo da média móvel. No exemplo deste algoritmo simples, mostraremos que tipo de problemas se podem encontrar durante sua construção. O valor médio é calculado de acordo com a bem conhecida fórmula:
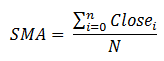
Implementamos este cálculo escrevendo um script simples em linguagem MQL5:
//+------------------------------------------------------------------+ //| SMA.mq5 | //| Copyright 2015, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2015, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" input int N = 10; // Período de média //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double closes[]; if(CopyClose(Symbol(), Period(), 0, N, closes)!= N) { printf("Need more data"); return; } double sum = 0.0; for(int i = 0; i < N; i++) sum += closes[i]; sum /= N; printf("SMA: " + DoubleToString(sum, Digits())); } //+------------------------------------------------------------------+
Do ponto de vista do cálculo tudo tem sido feito corretamente: o resultado do script é o valor da média móvel exibido numa janela do terminal. Mas que se deve fazer quando trabalhamos numa janela deslizante? Na prática, o último valor da cotação mudará constantemente e serão adicionadas novas barras. O algoritmo sempre recalculará o valor da média móvel, aproveitando duas operações com uso intensivo de recursos:
- Copiar e colar N elementos no receptor de matriz;
- Pesquisa detalhada do receptor de matriz no ciclo for.
A última ação usa mais intensivamente recursos. Para o período 10 serão implementadas dez iterações, e para o período 500, quinhentas. Assim, verifica-se que a complexidade do algoritmo depende do período de média e pode ser registrada como O(n), onde O é função de complexidade.
No entanto, há um algoritmo de cálculo de média muito mais rápido na janela deslizante. Para fazer isso, basta saber a soma de todos os valores no cálculo anterior:
SMA = (Soma de todos os valores - primeiro valor da janela deslizante + novo valor)/Período de média
A função de complexidade deste algoritmo é a constante O(1), que é independente do período de média. O desempenho deste algoritmo é mais elevado, mas é mais difícil de ser implementado. Cada vez que se adiciona uma nova barra devem ser realizados os seguintes passos:
- subtrair da soma atual o valor que foi adicionado em primeiro lugar e, em seguida, removê-lo na série;
- adicionar à soma atual o valor que foi adicionado por último e, em seguida, adicioná-lo na série;
- dividir a soma atual no período de média e retorná-lo como uma média móvel.
Se o último valor não é adicionado, e só é atualizado, o algoritmo torna-se ainda mais complicado:
- determinar o valor que é atualizado e lembrar seu estado atual;
- subtrair da soma atual o valor que foi lembrado na etapa anterior;
- substituir o valor por um novo;
- adicionar à soma atual o novo valor;
- dividir a soma atual no período de média e retorná-lo como uma média móvel.
O fato de a MQL5, como a maioria das linguagens de programação, ter recursos embutidos para trabalhar apenas com tipos básicos de dados, por exemplo, com matrizes, representa mais uma complexidade. No entanto, matrizes sem a devida modificação não são adequadas para este papel, porque, no caso mais óbvio, é necessário organizar uma fila FIFO (First In - First Out), ou seja, fazer uma lista, cujo primeiro elemento é removido ao adicionar um novo elemento. As matrizes permitem excluir e adicionar elementos. Mas estes procedimentos consomem muitos recursos, porque, na verdade, cada vez que realizada uma operação deste tipo há uma redistribuição da matriz.
Para evitar esse tipo de dificuldades e, ao mesmo tempo, implementar um algoritmo realmente eficiente, voltamos para o buffer circular.
Teoria do buffer circular
Uma característica chave no trabalho do buffer circular é a possibilidade de adicionar ou remover elementos sem redistribuição da matriz. De fato, se assumirmos que o número de elementos na matriz é sempre constante (que é o caso para os cálculos na janela deslizante), a adição de um novo elemento é acompanhada pela remoção do antigo. Assim, o número total de elementos não é alterado, mas sua indexação muda após adicionado cada novo elemento. O último elemento torna-se o penúltimo, o segundo elemento assume o lugar do primeiro e, desse modo, o primeiro deixa permanentemente a fila.
Graças a esta possibilidade, o buffer circular pode ser baseado numa matriz convencional. Criamos uma classe cuja base é uma matriz convencional:
class CRingBuffer { private: double m_array[]; };
Assumimos que nosso buffer será composto de apenas três elementos. Então, o primeiro elemento é adicionado à célula da matriz com o índice de 0, o segundo elemento, à célula com o índice de 1 e, finalmente, o terceiro, à célula com o índice de 2. O que acontece se adicionamos um quarto elemento? Obviamente, ao ser adicionado, o primeiro elemento deve ser removido. Assim, o local mais apropriado para o quarto elemento será o primeiro lugar, isto é, seu índice será novamente zero. Como se pode calcular este índice? Para isso, usamos a operação especial 'resto da divisão inteira'. Em linguagem MQL5, esta operação é indicada pelo especial símbolo de porcentagem %. Como a numeração começa com zero, nosso quarto elemento será o terceiro na fila e, além disso, seu índice de alojamento será calculado usando a fórmula:
Aqui 'total' é o tamanho total do buffer. No nosso exemplo, três é dividido por três, sem um resto. Assim, o índice conterá um resto igual a zero. Os subsequentes elementos serão localizados sob as mesmas regras: o número do elemento adicionado será dividido pelo número de elementos na matriz. O resto desta divisão será o índice real no buffer circular. Realizemos a imputação de índices dos 8 primeiros elementos a serem adicionados ao buffer circular com uma dimensão de 3:
0 % 3 = [0] 1 % 3 = [1] 2 % 3 = [2] 3 % 3 = [0] 4 % 3 = [1] 5 % 3 = [2] 6 % 3 = [0] 7 % 3 = [1]...
Protótipo de trabalho
Já temos uma boa ideia sobre a teoria do buffer circular. Chegou a hora de criar um protótipo funcional. Nosso buffer circular terá três recursos principais:
- adicionar um novo valor;
- excluir o último valor;
- alterar o valor de um índice arbitrário.
Precisamos da última função para trabalhar em tempo real, quando a última barra se encontra em estado de formação e o preço de fechamento está constantemente mudando.
Também nosso buffer terá duas propriedades básicas, isto é: conter o tamanho máximo de buffer e o número atual de elementos. Na maioria das vezes, estes valores serão os mesmos, porque quando os elementos preenchem toda a dimensão do buffer, cada elemento posterior substitui o mais antigo. Assim, o número total de elementos permanecerá inalterado. Mas durante o preenchimento inicial do buffer, os valores destas propriedades variará. O número máximo de elementos será alterado pela propriedade. O usuário pode tanto aumentá-lo como diminui-lo.
A exclusão do elemento mais antigo ocorrerá automaticamente, sem interação explícita do usuário. Isso é feito deliberadamente, porque na prática a remoção manual de elementos antigos complica o cálculo das estatísticas de apoio.
Neste algoritmo, maior dificuldade é o cálculo dos índices reais do buffer interno em que ambos conterão valores reais. Por exemplo, se o utilizador pedir um elemento com um índice de 0, o valor real, onde localizado o elemento, pode ser diferente. Por exemplo, quando se adiciona o elemento 17 ao buffer circular com uma dimensão 10, o elemento de zero será localizado no índice de 8, e o último, isto é, o nono elemento, no índice de 7.
Para ver como trabalham as operações principais do buffer circular, apresentamos seu arquivo de cabeçalho e o conteúdo dos principais métodos:
//+------------------------------------------------------------------+ //| Buffer circular Double | //+------------------------------------------------------------------+ class CRiBuffDbl { private: bool m_full_buff; int m_max_total; int m_head_index; protected: double m_buffer[]; //Buffer circular para acesso direto. Atenção: os índices não correspondem ao seu número de ordem! ... int ToRealInd(int index); public: CRiBuffDbl(void); void AddValue(double value); void ChangeValue(int index, double new_value); double GetValue(int index); int GetTotal(void); int GetMaxTotal(void); void SetMaxTotal(int max_total); void ToArray(double& array[]); }; //+------------------------------------------------------------------+ //| Construtor | //+------------------------------------------------------------------+ CRiBuffDbl::CRiBuffDbl(void) : m_full_buff(false), m_head_index(-1), m_max_total(0) { SetMaxTotal(3); } //+------------------------------------------------------------------+ //| Define o novo tamanho do buffer circular | //+------------------------------------------------------------------+ void CRiBuffDbl::SetMaxTotal(int max_total) { if(ArraySize(m_buffer) == max_total) return; m_max_total = ArrayResize(m_buffer, max_total); } //+------------------------------------------------------------------+ //| Retorna o tamanho real do buffer circular | //+------------------------------------------------------------------+ int CRiBuffDbl::GetMaxTotal(void) { return m_max_total; } //+------------------------------------------------------------------+ //| Retorna o valor segundo o índice | //+------------------------------------------------------------------+ double CRiBuffDbl::GetValue(int index) { return m_buffer[ToRealInd(index)]; } //+------------------------------------------------------------------+ //| Retorna o número total de elementos | //+------------------------------------------------------------------+ int CRiBuffDbl::GetTotal(void) { if(m_full_buff) return m_max_total; return m_head_index+1; } //+------------------------------------------------------------------+ //| Adiciona o novo numero ao buffer circular | //+------------------------------------------------------------------+ void CRiBuffDbl::AddValue(double value) { if(++m_head_index == m_max_total) { m_head_index = 0; m_full_buff = true; } //... m_buffer[m_head_index] = value; } //+------------------------------------------------------------------+ //| Substitui o valor previamente adicionado por um novo | //+------------------------------------------------------------------+ void CRiBuffDbl::ChangeValue(int index, double value) { int r_index = ToRealInd(index); double prev_value = m_buffer[r_index]; m_buffer[r_index] = value; } //+------------------------------------------------------------------+ //| Converte um índice virtual em real | //+------------------------------------------------------------------+ int CRiBuffDbl::ToRealInd(int index) { if(index >= GetTotal() || index < 0) return m_max_total; if(!m_full_buff) return index; int delta = (m_max_total-1) - m_head_index; if(index < delta) return m_max_total + (index - delta); return index - delta; }
A base desta classe é um ponteiro para o último elemento adicionado, m_head_index. Ao adicionar um novo elemento usando o método AddValue, ele é incrementado em 1. Se o valor começa a exceder o tamanho da matriz, ele zerar-se-ia.
A característica mais complexa do buffer circular é o método interno ToRealInd. Ele implementa - para entrada - o índice do buffer, a partir do ponto de vista do utilizador, e devolve o índice real da matriz, em que localizado o elemento desejado.
Como visto acima, em si o buffer circular é projetado muito simplesmente, isto é: sem ter em conta a aritmética de ponteiros, ele suporta os passos básicos para adicionar um novo elemento e fornece acesso ao elemento arbitrário usando GetValue(). No entanto, normalmente, esta funcionalidade é usada apenas para facilitar a organização do processo de cálculo da característica exigida, seja ela uma média móvel normal ou um algoritmo de pesquisa de máximos/mínimos. No buffer circular, podem ser calculados muitos objetos estatísticos. Trata-se de uma grande variedade de indicadores ou critérios estatísticos, como a dispersão e o desvio padrão. Portanto, é impossível fornecer uma classe de buffer circular a todos os algoritmos do cálculo. E não é necessário fazer isso. Em vez disso, pode-se criar uma solução mais flexível, isto é, fazer classes herdeiras que implementam um algoritmo para cálculo de indicadores ou estatísticas.
Para que estas classes herdeiras possam calcular facilmente os respectivos valores, é necessário proporcionar um buffer circular aos métodos adicionais, que passaremos a chamar de métodos-eventos. Trata-se de métodos convencionais colocados na seção protected. Todos estes métodos - a serem redefinidos - são prefixados com On:
//+------------------------------------------------------------------+ //| Buffer circular Double | //+------------------------------------------------------------------+ class CRiBuffDbl { private: ... protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double prev_value, double new_value); virtual void OnChangeArray(void); virtual void OnSetMaxTotal(int max_total); };
Toda vez que, no buffer circular, acontece alguma alteração, é chamado um método que indica isso. Por exemplo, se no buffer cair um novo valor, será chamado o método OnAddValue. Seu parâmetro contém o valor adicionado. Se, na classe herdeira, a partir do buffer circular, for redefinido este método, cada vez que for adicionado um novo valor, será chamado o bloco de cálculo apropriado da classe herdeira.
O buffer circular contém cinco eventos que podem ser monitorados numa classe herdeira (entre parênteses indicados os métodos com ajuda dos quais isto é feito):
- adição do novo elemento (OnAddValue);
- exclusão do antigo elemento (OnRemoveValue);
- alteração do elemento de acordo com o índice arbitrário (OnChangeValue);
- alteração de todo o conteúdo do buffer circular (OnChangeArray);
- alteração do número máximo de elementos no buffer circular (OnSetMaxTotal).
É preciso separadamente mencionar o evento OnChangeArray. Ele é chamado quando o recálculo do indicador requer acesso a toda a matriz de valores acumulados. Neste caso, na classe herdeira, basta redefinir esse método. No método, é preciso obter - usando a função ToArray - toda a matriz atual de valores e já nela fazer os cálculos adequados. Um exemplo desse tipo de cálculo será dado a seguir na secção de integração do buffer circular com a biblioteca AlgLib.
A classe de buffer circular é chamada CRiBuffDbl. Como o nome indica, ela funciona com valores do tipo double. Os números reais são o tipo de dados mais comum para algoritmos numéricos. No entanto, além dos números reais, pode ser preciso trabalhar com números inteiros, portanto, o conjunto de classes, além da classe CRiBuffDbl, contém uma classe semelhante CRiBuffInt que trabalha com números de tipo integer. Em processadores modernos, a aritmética de inteiro é realizada muito mais rápido do que os cálculos de ponto flutuante. Portanto, para os problemas inteiros específicos é melhor usar CRiBuffInt.
Na presente abordagem, não é usada a técnica de classes de modelo, que pode ser usada para descrever um tipo genérico <template T> e trabalhar com ele. Isso foi feito deliberadamente, porque se assume que os algoritmos específicos de cálculo são herdados diretamente a partir do buffer circular, e cada um desses algoritmos funciona com um tipo de dados bem definido.
Exemplo de cálculo da média móvel simples no buffer circular
Nós examinamos em detalhe as classes que implementam o princípio de buffer circular, e agora é hora de resolver vários problemas práticos com sua ajuda. Comecemos com o mais simples, isto é, criamos o bem conhecido indicador Simple Moving Average. Ele é uma média móvel comum, o que significa que, para seu cálculo, é necessário dividir a soma da série no período da média. Repetimos a fórmula de cálculo dada no início do artigo:
SMA = (Soma de todos os valores - primeiro valor da janela deslizante + novo valor)/Período de média
Para implementar nosso algoritmo, será necessário redefinir dois métodos na classe herdeira da CRiBuffDbl, isto é: OnAddValue e OnRemoveValue. O valor médio será calculado no método Sma. Aqui está o código de classe resultante:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Cálculo de média móvel no buffer circular | //+------------------------------------------------------------------+ class CRiSMA : public CRiBuffDbl { private: double m_sum; protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); public: CRiSMA(void); double SMA(void); }; CRiSMA::CRiSMA(void) : m_sum(0.0) { } //+------------------------------------------------------------------+ //| Aumentamos o valor total | //+------------------------------------------------------------------+ void CRiSMA::OnAddValue(double value) { m_sum += value; } //+------------------------------------------------------------------+ //| Reduzimos o valor total | //+------------------------------------------------------------------+ void CRiSMA::OnRemoveValue(double value) { m_sum -= value; } //+------------------------------------------------------------------+ //| Alteramos o valor total | //+------------------------------------------------------------------+ void CRiSMA::OnChangeValue(int index,double del_value,double new_value) { m_sum -= del_value; m_sum += new_value; } //+------------------------------------------------------------------+ //| Retorna uma média móvel simples | //+------------------------------------------------------------------+ double CRiSMA::SMA(void) { return m_sum/GetTotal(); }
Além dos métodos que reagem à adição e exclusão do elemento (OnAddValue e OnRemoveValue respectivamente), precisaremos predefinir mais um método que se chama ao alterar o elemento arbitrário (OnChangeValue). O buffer circular suporta a alteração arbitrária de qualquer elemento incluído em sua composição, por isso é necessário monitorar a mudança. Como regra geral, apenas o último elemento é sujeito a alteração no modo de formação de última barra. É neste caso, é previso o evento OnChangeValue, que é preciso redefinir.
Escrevemos um indicador personalizado que usa uma classe de buffer circular para o cálculo da média móvel:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_chart_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiSMA.mqh> input int MaPeriod = 13; double buff[]; CRiSMA Sma; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); Sma.SetMaxTotal(MaPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { Sma.AddValue(price[i]); buff[i] = Sma.SMA(); calc = true; } if(!calc) { Sma.ChangeValue(MaPeriod-1, price[rates_total-1]); buff[rates_total-1] = Sma.SMA(); } return(rates_total-1); } //+------------------------------------------------------------------+
No início do cálculo, o indicador simplesmente adiciona os novos valores no buffer circular de média móvel. Não é necessário controlar o número de valores adicionados. Todos os cálculos e remoção de elementos obsoletos ocorre no modo automático. Se a chamada do indicador acontecer ao alterar o preço da última barra, só será preciso mudar o último valor da média móvel para um novo, o método ChangeValue toma conta disso.
A exibição gráfica do indicador é equivalente ao indicador padrão MovingAverage:
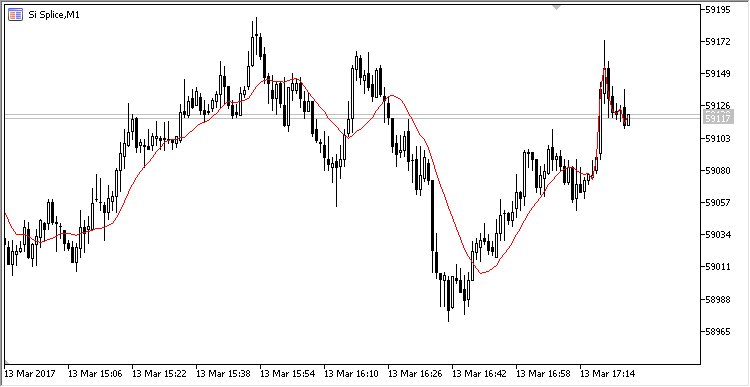
Fig. 1. Exibição da média móvel simples calculada num buffer circular.
Exemplo de cálculo da média móvel exponencial no buffer circular
Tomemos um exemplo de um pouco mais complicado, isto é, o cálculo da média móvel exponencial. Ao contrário a média móvel simples, a média móvel exponencial não responde à remoção do elemento mais antigo no buffer de valores, portanto, para calculá-lo, é preciso substituir apenas dois métodos, nomeadamente, OnAddValue e OnChangeValue. Como no exemplo anterior, criaremos a classe CRiEMA, o herdeiro de CRiBuffDbl e redefiniremos os métodos apropriados:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Cálculo de média móvel exponencial no buffer circular | //+------------------------------------------------------------------+ class CRiEMA : public CRiBuffDbl { private: double m_prev_ema; // Valor anterior da EMA double m_last_value; // Último valor do preço double m_smoth_factor; // Fator de suavização bool m_calc_first_v; // Sinalizador que indica o cálculo do primeiro valor double CalcEma(); // Cálculo direto da média protected: virtual void OnAddValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiEMA(void); double EMA(void); }; //+------------------------------------------------------------------+ //| Assinamos notificações de adição e alteração de valor | //+------------------------------------------------------------------+ CRiEMA::CRiEMA(void) : m_prev_ema(EMPTY_VALUE), m_last_value(EMPTY_VALUE), m_calc_first_v(false) { } //+--------------------------------------------------------------------------+ //| Cálculo de fator de suavização de acordo com a fórmula MetaQuotes EMA | //+--------------------------------------------------------------------------+ void CRiEMA::OnSetMaxTotal(int max_total) { m_smoth_factor = 2.0/(1.0+max_total); } //+------------------------------------------------------------------+ //| Aumentamos a soma total | //+------------------------------------------------------------------+ void CRiEMA::OnAddValue(double value) { //Calculamos o valor anterior da EMA if(m_prev_ema != EMPTY_VALUE) m_prev_ema = CalcEma(); //Lembramos o preço atual m_last_value = value; } //+------------------------------------------------------------------+ //| Corrigimos a EMA | //+------------------------------------------------------------------+ void CRiEMA::OnChangeValue(int index,double del_value,double new_value) { if(index != GetMaxTotal()-1) return; m_last_value = new_value; } //+------------------------------------------------------------------+ //| Cálculo direto da EMA | //+------------------------------------------------------------------+ double CRiEMA::CalcEma(void) { return m_last_value*m_smoth_factor+m_prev_ema*(1.0-m_smoth_factor); } //+------------------------------------------------------------------+ //| Retorna a média móvel simples | //+------------------------------------------------------------------+ double CRiEMA::EMA(void) { if(m_calc_first_v) return CalcEma(); else { m_prev_ema = m_last_value; m_calc_first_v = true; } return m_prev_ema; }
O método CalcEma trata do cálculo da média móvel. Na verdade, ele retorna a soma de dois produtos: o último valor conhecido anterior multiplicado pelo fator de suavização, mais o valor anterior do indicador, multiplicado pelo inverso do valor do fator de suavização. Se o valor anterior do indicador não foi calculado, em seguida, em vez dele, é tomado o primeiro valor colocado no buffer (no nosso caso, será o preço de fechamento da barra de zero).
Para exibir o cálculo no gráfico, escrevemos um indicador semelhante ao da seção anterior. Ele será parecido com este:
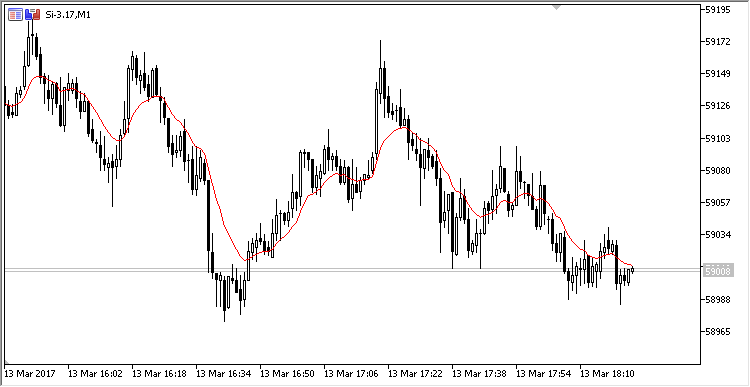
Fig. 2. Cálculo da média móvel exponencial calculada no buffer circular
Cálculo de máximos/mínimos no buffer circular
O problema mais complicado e interessante é o cálculo de máximos e mínimos na janela deslizante. Claro, isso pode ser feito muito simplesmente, referindo-se às funções padrão ArrayMaximum e ArrayMinimum, no entanto, os benefícios do cálculo numa janela deslizante, neste caso, desaparecem. Apesar de tudo, se os dados são excluídos do buffer, é possível calcular o máximo e mínimo sem executar uma busca exaustiva. Imaginemos que, para cada novo valor que vai cair dentro do buffer, serão calculados dois valores adicionais. O primeiro especificará o número de elementos anteriores abaixo do elemento atual, e o segundo, o número de elementos anteriores acima do elemento atual. O primeiro valor será usado para uma busca efetiva do máximo, o segundo, para busca do mínimo.
Agora imaginemos que estamos a lidar com as barras de preços habituais e precisamos calcular os extremos de preços segundo seus valores High para um determinado período. Para este efeito, em cada barra, escrevemos um número igual ao número de barras anteriores, cujos valores máximos estejam abaixo do valor máximo da barra de atual. A sequência de barras é apresentada na figura abaixo:
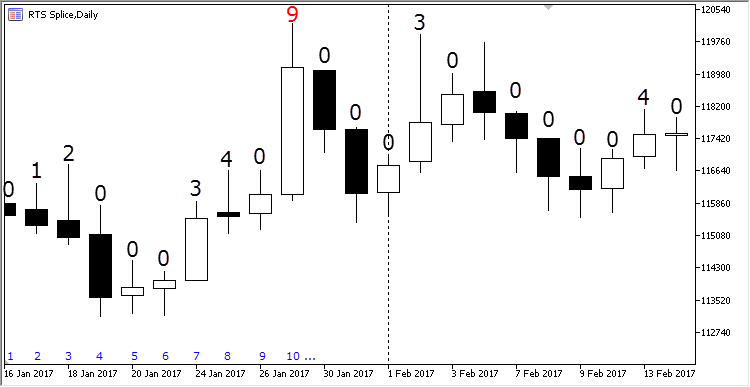
Fig. 3. Hierarquia dos extremos das barras
A primeira barra tem sempre um extremo zero, porque não há valores anteriores para verificação. A barra №2 está acima dela, porque seu índice de extremo será igual a um. A terceira barra está acima da barra anterior, o que significa que também está acima da primeira barra. Seu número de extremo é igual a dois. Atrás dele estão três barras, cada um das quais é menor do que a anterior. Todas elas estão abaixo da barra № 3, por isso seu número extremo é igual a zero. Em seguida aparece a sétima barra, que está acima das três anteriores, mas abaixo da quarta, por isso seu índice de extremo será igual a três. Da mesma forma, para cada nova barra é calculado seu índice de extremo imediatamente após a adição.
Quando todos os índices anteriores são calculados, é fácil calcular o valor extremo da barra atual. Para fazer isso, basta comparar o extremo da barra com os outros extremos. É possível acessar diretamente cada extremo subsequente, saltando algumas barras seguidas, uma vez que, graças aos números colocados, podemos saber seu índice. Ilustremos isso:
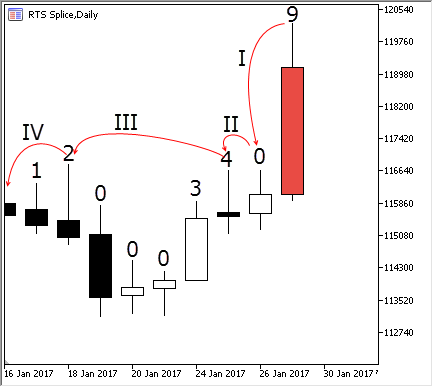
Fig. 4. Pesquisa de extremo de barra atual
Imaginemos que adicionamos uma barra destacada em vermelho. Esta barra tem o número 9, já que a numeração ocorre a partir do zero. Para determinar seu índice de extremo, comparamo-la com a barra №8, seguindo o passo I: ela estava acima dela, portanto, seu estremo, pelo menos, é igual a um. Comparamo-la com a barra №7, seguindo o passo II, ela novamente está acima desta barra. Como a barra №7 está acima das quatro anteriores, podemos comparar imediatamente nossa última barra com a barra №3, seguindo o passo III. A barra №9 está acima da barra №3 e, portanto, acima de todas as barras atualmente. Graças aos índices calculados anteriormente, evitamos a comparação com as quatro barras intermediárias, que são notoriamente inferiores à atual. Assim funciona a pesquisa rápida de extremo num buffer circular. De forma semelhante, funciona a busca de mínimo, com a única diferença de que é usado o índice adicional de mínimos.
Agora, descrito o algoritmo, mostramos seu código-fonte. A classe apresentada é interessante em que, como buffers auxiliares, também são utilizados dois buffers circulares do tipo CRiBuffInt. Cada um deles contém índices de extremos e mínimos, respectivamente.
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiBuffInt.mqh" //+------------------------------------------------------------------+ //| Cálculo de média móvel exponencial no buffer circular | //+------------------------------------------------------------------+ class CRiMaxMin : public CRiBuffDbl { private: CRiBuffInt m_max; CRiBuffInt m_min; bool m_full; int m_max_ind; int m_min_ind; protected: virtual void OnAddValue(double value); virtual void OnCalcValue(int index); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiMaxMin(void); int MaxIndex(int max_period = 0); int MinIndex(int min_period = 0); double MaxValue(int max_period = 0); double MinValue(int min_period = 0); void GetMaxIndexes(int& array[]); void GetMinIndexes(int& array[]); }; CRiMaxMin::CRiMaxMin(void) { m_full = false; m_max_ind = 0; m_min_ind = 0; } void CRiMaxMin::GetMaxIndexes(int& array[]) { m_max.ToArray(array); } void CRiMaxMin::GetMinIndexes(int& array[]) { m_min.ToArray(array); } //+------------------------------------------------------------------+ //| Mudamos o tamanho dos buffers internos de acordo ao novo tamanho | //| do buffer base | //+------------------------------------------------------------------+ void CRiMaxMin::OnSetMaxTotal(int max_total) { m_max.SetMaxTotal(max_total); m_min.SetMaxTotal(max_total); } //+------------------------------------------------------------------+ //| Cálculo de índices Max/Min | //+------------------------------------------------------------------+ void CRiMaxMin::OnAddValue(double value) { m_max_ind--; m_min_ind--; int last = GetTotal()-1; if(m_max_ind > 0 && value >= GetValue(m_max_ind)) m_max_ind = last; if(m_min_ind > 0 && value <= GetValue(m_min_ind)) m_min_ind = last; OnCalcValue(last); } //+------------------------------------------------------------------+ //| Cálculo de índices Max/Min | //+------------------------------------------------------------------+ void CRiMaxMin::OnCalcValue(int index) { int max = 0, min = 0; int offset = m_full ? 1 : 0; double value = GetValue(index); int p_ind = index-1; //Busca do máximo while(p_ind >= 0 && value >= GetValue(p_ind)) { int extr = m_max.GetValue(p_ind+offset); max += extr + 1; p_ind = GetTotal() - 1 - max - 1; } p_ind = GetTotal()-2; //Busca do mínimo while(p_ind >= 0 && value <= GetValue(p_ind)) { int extr = m_min.GetValue(p_ind+offset); min += extr + 1; p_ind = GetTotal() - 1 - min - 1; } m_max.AddValue(max); m_min.AddValue(min); if(!m_full && GetTotal() == GetMaxTotal()) m_full = true; } //+------------------------------------------------------------------+ //| Recalcula os índices máximos/mínimos após a mudança | //| o valor de qualquer índice | //+------------------------------------------------------------------+ void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value) { if(m_max_ind >= 0 && new_value >= GetValue(m_max_ind)) m_max_ind = index; if(m_min_ind >= 0 && new_value >= GetValue(m_min_ind)) m_min_ind = index; for(int i = index; i < GetTotal(); i++) OnCalcValue(i); } //+------------------------------------------------------------------+ //| Retorna o índice do elemento máximo | //+------------------------------------------------------------------+ int CRiMaxMin::MaxIndex(int max_period = 0) { int limit = 0; if(max_period > 0 && max_period <= m_max.GetTotal()) { m_max_ind = -1; limit = m_max.GetTotal() - max_period; } if(m_max_ind >=0) return m_max_ind; int c_max = m_max.GetTotal()-1; while(c_max > limit) { int ext = m_max.GetValue(c_max); if((c_max - ext) <= limit) return c_max; c_max = c_max - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Retorna o índice do elemento mínimo | //+------------------------------------------------------------------+ int CRiMaxMin::MinIndex(int min_period = 0) { int limit = 0; if(min_period > 0 && min_period <= m_min.GetTotal()) { limit = m_min.GetTotal() - min_period; m_min_ind = -1; } if(m_min_ind >=0) return m_min_ind; int c_min = m_min.GetTotal()-1; while(c_min > limit) { int ext = m_min.GetValue(c_min); if((c_min - ext) <= limit) return c_min; c_min = c_min - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Retorna o valor do elemento máximo | //+------------------------------------------------------------------+ double CRiMaxMin::MaxValue(int max_period = 0) { return GetValue(MaxIndex(max_period)); } //+------------------------------------------------------------------+ //| Retorna o valor do elemento mínimo | //+------------------------------------------------------------------+ double CRiMaxMin::MinValue(int min_period = 0) { return GetValue(MinIndex(min_period)); }
O algoritmo contém uma modificação adicional. Ele lembra os máximos e mínimos atuais, e se eles permanecem os mesmos, os métodos MaxValue e MinValue devolvem-nos sem cálculo adicional.
Aqui está a exibição de extremos e mínimos no gráfico:
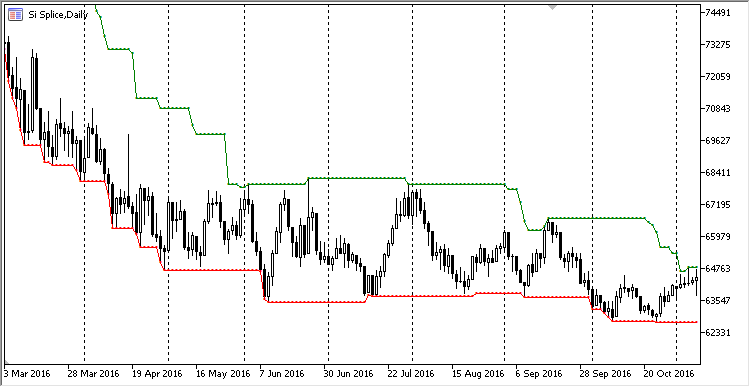
Fig. 5. Canal de extremos/mínimos sob a forma de indicador
Acrescentamos que a classe de definição do máximo/mínimo tem recursos avançados. Ela pode retornar o índice de extremo num buffer circular ou apenas seu valor. Também pode calcular o extremo para um período inferior ao período do buffer circular, basta especificar o período de limitação nos métodos MaxIndex/MinIndex e MaxValue/MinValue.
Integração do buffer circular com a biblioteca AlgLib
Um outro exemplo interessante no que diz respeito à utilização do buffer circular, isto é, cálculos matemáticos especializados. Normalmente, os algoritmos para calcular diferentes estatísticas são criados sem levar em conta o uso na janela deslizante. Este tipo de algoritmo nem sempre é fácil de usar. O buffer circular resolve este problema. Escreveremos um indicador que calcula as principais características da distribuição de Gauss:
- valor médio (Mean);
- desvio padrão (StdDev);
- distribuição assimétrica (Skewness);
- curtose (Kurtosis).
Para cálculo destas características, usamos o método estático AlgLib::SampleMoments. Tudo o que precisa fazer é criar a classe de buffer circular CRiGaussProperty e colocar o método dentro do manipulador OnChangeArray. Este é todo o código que inclui a classe:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiBuffDbl.mqh> #include <Math\AlgLib\AlgLib.mqh> //+------------------------------------------------------------------+ //| Cálculo de características básicas de uma distribuição de Gauss | //+------------------------------------------------------------------+ class CRiGaussProperty : public CRiBuffDbl { private: double m_mean; // Médio double m_variance; // Desvio double m_skewness; // Assimetria double m_kurtosis; // Curtose protected: virtual void OnChangeArray(void); public: double Mean(void){ return m_mean;} double StdDev(void){return MathSqrt(m_variance);} double Skewness(void){return m_skewness;} double Kurtosis(void){return m_kurtosis;} }; //+--------------------------------------------------------------------------+ //| O cálculo e realizado imediatamente após quaisquer alterações da matriz | //+--------------------------------------------------------------------------+ void CRiGaussProperty::OnChangeArray(void) { double array[]; ToArray(array); CAlglib::SampleMoments(array, m_mean, m_variance, m_skewness, m_kurtosis); } //+------------------------------------------------------------------+ //| Tipo de propriedade de distribuição de Gauss | //+------------------------------------------------------------------+ enum ENUM_GAUSS_PROPERTY { GAUSS_MEAN, // Médio GAUSS_STDDEV, // Desvio GAUSS_SKEWNESS, // Assimetria GAUSS_KURTOSIS // Curtose }; input int BPeriod = 13; //Period input ENUM_GAUSS_PROPERTY Property; double buff[]; CRiGaussProperty RiGauss; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); RiGauss.SetMaxTotal(BPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { RiGauss.AddValue(price[i]); buff[i] = GetGaussValue(Property); calc = true; } if(!calc) { RiGauss.ChangeValue(BPeriod-1, price[rates_total-1]); buff[rates_total-1] = GetGaussValue(Property); } return(rates_total-1); } //+------------------------------------------------------------------+ //| Retorna o valor de uma das propriedades da distribuição de Gauss | //+------------------------------------------------------------------+ double GetGaussValue(ENUM_GAUSS_PROPERTY property) { double value = EMPTY_VALUE; switch(Property) { case GAUSS_MEAN: value = RiGauss.Mean(); break; case GAUSS_STDDEV: value = RiGauss.StdDev(); break; case GAUSS_SKEWNESS: value = RiGauss.Skewness(); break; case GAUSS_KURTOSIS: value = RiGauss.Kurtosis(); break; } return value; }
Como pode ser visto a partir da lista acima, a classe CRiGaussProperty resultou básica. Mas por trás dessa simplicidade esconde-se uma grande funcionalidade. Agora para que a função CAlglib::SampleMoments funcione não é necessário preparar uma matriz deslizante a cada iteração, basta adicionar os novos valores no método AddValue. A figura abaixo mostra o resultado desse indicador. Nas configurações, selecionamos o cálculo do desvio padrão e exibimo-no na subjanela do gráfico:
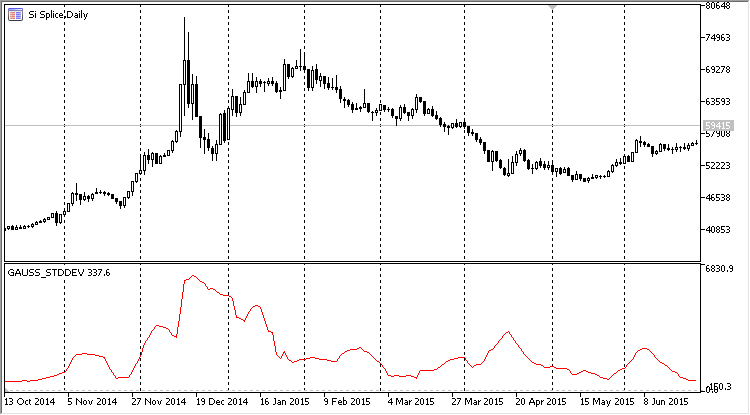
Fig. 6 Principais características da distribuição de Gauss como um indicador de deslizamento
Construção do MACD com base em primitivas circulares
Nós desenvolvemos três primitivas circulares: médias móveis simples e exponencial em movimento, indicador de máximos e mínimos. Isto é suficiente para a construção dos principais indicadores padrão, porque, como regra, são baseados num cálculo simples. Por exemplo, o indicador MACD é composto por duas médias móveis exponenciais e uma linha de sinal com base numa média simples. Vamos tentar construir este indicador com base nos códigos existentes.
No exemplo dos indicadores de máximos e mínimos, usamos dois buffers circulares adicionais contidos na classe CRiMaxMin. Faremos o mesmo no caso do MACD. Nossa classe, após adicionado um novo valor, simplesmente enviá-lo-á para seus buffers adicionais e, depois, calculará a diferença entre os dois. A diferença cairá no terceiro buffer circular, que calcula - com base nele - a SMA simples. Esta será a linha de sinal do MACD:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiEMA.mqh" //+------------------------------------------------------------------+ //| Cálculo de média móvel no buffer circular | //+------------------------------------------------------------------+ class CRiMACD { private: CRiEMA m_slow_macd; // Média móvel exponencial lenta CRiEMA m_fast_macd; // Média móvel exponencial rápida CRiSMA m_signal_macd; // Linha de sinal double m_delta; // Diferença entre as EMA rápida e lenta public: double Macd(void); double Signal(void); void ChangeLast(double new_value); void SetFastPeriod(int period); void SetSlowPeriod(int period); void SetSignalPeriod(int period); void AddValue(double value); }; //+------------------------------------------------------------------+ //| Recalcula a MACD | //+------------------------------------------------------------------+ void CRiMACD::AddValue(double value) { m_slow_macd.AddValue(value); m_fast_macd.AddValue(value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.AddValue(m_delta); } //+------------------------------------------------------------------+ //| Altera a MACD | //+------------------------------------------------------------------+ void CRiMACD::ChangeLast(double new_value) { m_slow_macd.ChangeValue(m_slow_macd.GetTotal()-1, new_value); m_fast_macd.ChangeValue(m_fast_macd.GetMaxTotal()-1, new_value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.ChangeValue(m_slow_macd.GetTotal()-1, m_delta); } //+------------------------------------------------------------------+ //| Retorna o histograma da MACD | //+------------------------------------------------------------------+ double CRiMACD::Macd(void) { return m_delta; } //+------------------------------------------------------------------+ //| Retorna a linha de sinal | //+------------------------------------------------------------------+ double CRiMACD::Signal(void) { return m_signal_macd.SMA(); } //+------------------------------------------------------------------+ //| Define o período rápido | //+------------------------------------------------------------------+ void CRiMACD::SetFastPeriod(int period) { m_slow_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Define o período lento | //+------------------------------------------------------------------+ void CRiMACD::SetSlowPeriod(int period) { m_fast_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Define o período da lina de sinal | //+------------------------------------------------------------------+ void CRiMACD::SetSignalPeriod(int period) { m_signal_macd.SetMaxTotal(period); }
Observe que a classe CRiMacd em si é uma classe independente e não é herdada da CRiBuffDbl. Na verdade, a classe CRiMacd não usa seus próprios buffers de cálculo. Em vez disso, na classe é aplicado o esquema de "inclusão", quando as classes primitivas circulares são colocadas como objetos independentes na seção private.
Os dois métodos básicos Macd() e Signal() retornam o valor do indicador MACD e sua linha de sinal. Este código resultou simples, além disso, cada buffer tem seu período deslizante. A classe CRiMacd não monitora as alterações do elemento arbitrário. Em vez disso, ela acompanha a alteração apenas do último elemento, proporcionando a mudança do indicador na barra de zero.
Visualmente o indicador MACD, calculado no buffer circular, tem a aparência do indicador clássico:
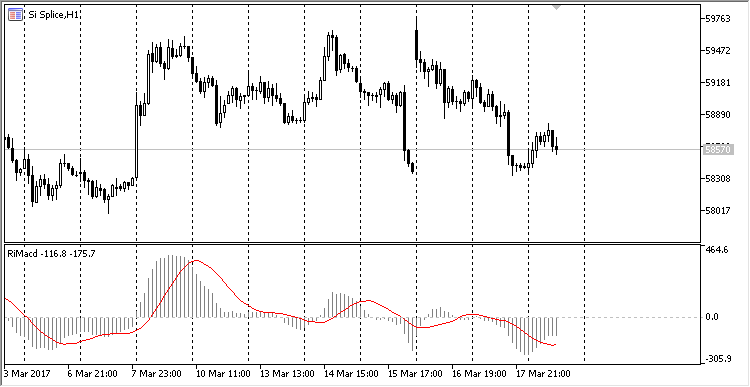
Fig. 7. Indicador MACD calculado no buffer circular
Construção do indicador Stochastic com base em primitivas circulares
Da mesma forma, construímos o indicador Stochastic. Esse indicador combina a busca de extremos e o cálculo de média móvel. Assim, neste caso, usamos os algoritmos que já calculamos anteriormente.
O Stochastic usa três séries de preço: preços máximos (barras High), preços de mínimos (barras Low) e preços de fechamento (barras Close). Seu cálculo é simples: primeiro, são procurados o máximo, para os preços High, e o mínimo, para o preço Low. Então, é calculada a relação entre o preço atual close e a faixa entre o máximo e o mínimo. Finalmente, com base nesta relação, é calculado o valor médio para N períodos (no indicador N é chamado "desaceleração K%"):
K% = SMA((close-min)/((max-min)*100.0%), N)
Em seguida, para o K% resultante, é calculada mais uma média com período %D, isto é, uma linha de sinal, como a linha de sinal do MACD:
Signal D% = SMA(K%, D%)
O dois valores resultantes - K% e seu D% de sinal - exibirão o indicador Stochastic.
Antes de escrever o código do Estocástico para o buffer circular, mostraremos seu código, executado em estilo clássico, para isso, usaremos o exemplo pronto Stochastic.mq5 a partir da pasta Indicators\Examples:
//+------------------------------------------------------------------+ //| Stochastic Oscillator | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,k,start; //--- check for bars count if(rates_total<=InpKPeriod+InpDPeriod+InpSlowing) return(0); //--- start=InpKPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) { ExtLowesBuffer[i]=0.0; ExtHighesBuffer[i]=0.0; } } //--- calculate HighesBuffer[] and ExtHighesBuffer[] for(i=start;i<rates_total && !IsStopped();i++) { double dmin=1000000.0; double dmax=-1000000.0; for(k=i-InpKPeriod+1;k<=i;k++) { if(dmin>low[k]) dmin=low[k]; if(dmax<high[k]) dmax=high[k]; } ExtLowesBuffer[i]=dmin; ExtHighesBuffer[i]=dmax; } //--- %K start=InpKPeriod-1+InpSlowing-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtMainBuffer[i]=0.0; } //--- main cycle for(i=start;i<rates_total && !IsStopped();i++) { double sumlow=0.0; double sumhigh=0.0; for(k=(i-InpSlowing+1);k<=i;k++) { sumlow +=(close[k]-ExtLowesBuffer[k]); sumhigh+=(ExtHighesBuffer[k]-ExtLowesBuffer[k]); } if(sumhigh==0.0) ExtMainBuffer[i]=100.0; else ExtMainBuffer[i]=sumlow/sumhigh*100; } //--- signal start=InpDPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtSignalBuffer[i]=0.0; } for(i=start;i<rates_total && !IsStopped();i++) { double sum=0.0; for(k=0;k<InpDPeriod;k++) sum+=ExtMainBuffer[i-k]; ExtSignalBuffer[i]=sum/InpDPeriod; } //--- OnCalculate done. Return new prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
Este código é escrito numa única unidade e compreende 8 ciclos for, três dos quais estão anexados. O cálculo é realizado em duas partes: primeiro, são calculados os máximos e mínimos cujos valores são armazenados em dois buffers adicionais. O cálculo dos máximos e mínimos requer dupla pesquisa detalhada: para cada barra são feitas N iterações adicionais no ciclo anexado for, em que N é o período K%.
Depois de calcular os máximos/mínimos, é calculado K%, para fazer isto, também é utilizado um ciclo duplo que faz em cada barra F iterações adicionais, onde F é o período a desaceleração K%.
Em seguida, é calculada a linha de sinal D%, e também com uma pesquisa detalhada for, em que para cada barra são necessárias T iterações adicionais (T é o período de médio D%).
O código resultante funciona bastante rápido. O principal problema aqui é que, sem o buffer circular, tem de se realizarem cálculos simples em vários passos independentes. Perde-se a visibilidade e a facilidade de entender o código.
Para demonstrar isso, apresentamos o conteúdo do método principal de cálculo na classe CRiStoch Ele executa exatamente o mesmo trabalho que o código postado acima:
//+------------------------------------------------------------------+ //| Adição de novos valores e cálculo do Stochastic | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Adição do novo valor do máximo m_min.AddValue(low); // Adição do novo valor do mínimo double c = close; double max = m_max.MaxValue() // Obtemos o máximo double min = m_min.MinValue(); // Obtemos o mínimo double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Encontramos K% segundo a formula do Stochastic m_slowed_k.AddValue(k); // Suavizamos K% (Desaceleração K%) m_slowed_d.AddValue(m_slowed_k.SMA()); // Encontramos %D a partir do K% suavizado }
Este método não está envolvido nos cálculos intermédios. Em vez disso, ele simplesmente aplica a fórmula do Stochastic para os valores existentes. A pesquisa de valores desejados é delegado a primitivas circulares: média móvel, pesquisa de máximos e mínimos.
Os outros métodos da classe CRiStoch são, além de triviais, métodos Get/Set de instalação de períodos e dos valores correspondentes do indicador. Aqui estão o código CRiStoch na íntegra:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiMaxMin.mqh" //+------------------------------------------------------------------+ // Classe do indicador Stochastic | //+------------------------------------------------------------------+ class CRiStoch { private: CRiMaxMin m_max; // Indicador de máximos/mínimos CRiMaxMin m_min; // Indicador de mínimos/máximos CRiSMA m_slowed_k; // Cálculos de média K% CRiSMA m_slowed_d; // Média móvel D% public: void ChangeLast(double new_value); void AddValue(double close, double high, double low); void AddHighValue(double value); void AddLowValue(double value); void AddCloseValue(double value); void SetPeriodK(int period); void SetPeriodD(int period); void SetSlowedPeriodK(int period); double GetStochK(void); double GetStochD(void); }; //+------------------------------------------------------------------+ //| Adição de novos valores e cálculo do Stochastic | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Adição do novo valor do máximo m_min.AddValue(low); // Adição do novo valor do mínimo double c = close; double max = m_max.MaxValue() double min = m_min.MinValue(); double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Encontramos K% segundo a fórmula m_slowed_k.AddValue(k); // Suavizamos K% (Desaceleração K%) m_slowed_d.AddValue(m_slowed_k.SMA()); // Encontramos %D a partir do K% suavizado } //+------------------------------------------------------------------+ //| Define o período rápido | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodK(int period) { m_max.SetMaxTotal(period); m_min.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Define o período lento | //+------------------------------------------------------------------+ void CRiStoch::SetSlowedPeriodK(int period) { m_slowed_k.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Define o período da linha de sinal | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodD(int period) { m_slowed_d.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Obtém o valor %K | //+------------------------------------------------------------------+ double CRiStoch::GetStochK(void) { return m_slowed_k.SMA(); } //+------------------------------------------------------------------+ //| Obtém o valor %D | //+------------------------------------------------------------------+ double CRiStoch::GetStochD(void) { return m_slowed_d.SMA(); }
O indicador Stochastic resultante é diferente de sua contraparte padrão. Você pode verificar isso construindo esse indicador em conjunto com o padrão (todos os arquivos auxiliares e de indicadores estão anexados a este artigo):
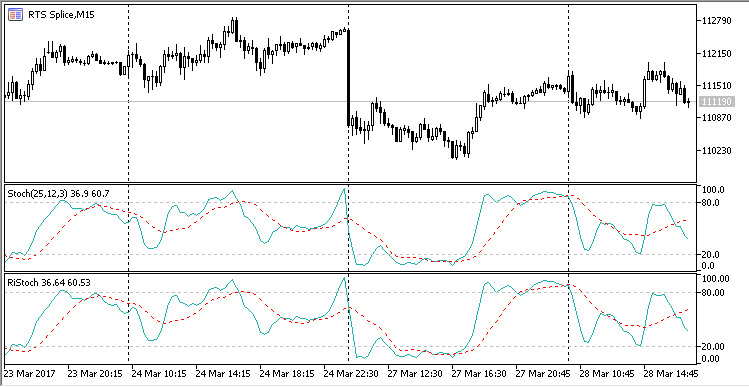
Fig. 8 Indicadores padrão e cíclico do Stochastic.
Otimizando o uso da memória operativa
O cálculo dos indicadores requer certos recursos. O trabalho de indicadores de sistema através dos identificadores não é a excepção. Na verdade, o identificador do indicador é um tipo especial de ponteiro para um bloco de cálculo interno do indicador e seus buffers de dados. Por si só, o identificador não ocupa muito lugar, apenas é um número de 64 bits. O tamanho básico está oculto "atrás dos bastidores" do MetaTrader, por isso, ao criar um novo identificador, é atribuída uma certa quantidade de memória maior do que o tamanho do identificador.
Além disso, a cópia de valores do indicador também requer um certo tempo, que é maior do que é necessário para o cálculo dos valores do indicador dentro do Expert Advisor. Portanto, os desenvolvedores recomendam oficialmente criar um bloco de cálculo de indicador diretamente no Expert Advisor e usá-lo. Claro, isso não significa que seja sempre necessário escrever o cálculo do indicador no código do Expert Advisor e não chamar os indicadores padrão. Não há nada de errado se você estiver usando um, dois ou até mesmo cinco indicadores em seu Expert Advisor. Só que para trabalhar com eles é preciso de um pouco mais de memória e um pouco mais tempo do que se estes cálculos fossem feitos diretamente no código interno do Expert Advisor.
No entanto, existem problemas onde é preciso otimizar o uso de memória e o tempo gasto. É por estes problemas que o uso de bufferes circulares é uma coisa preferível. Em primeiro lugar, isto é necessário ao utilizar vários indicadores. Por exemplo, os painéis informativos (também chamados de scanners de mercado), normalmente, fazem uma fatia de mercado incluindo vários instrumentos e timeframes, usando em seu arsenal, um conjunto de indicadores. Por exemplo, este é um dos painéis colocados no Mercado de aplicativos MetaTrader 5:
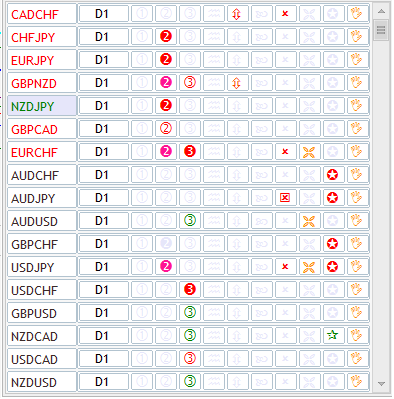
Fig. 8 Painel informativo, utilizando vários indicadores
Vemos que aqui são analisados 17 instrumentos diferentes para 9 indicadores diferentes. Cada componente é representado pelo seu indicador. É fácil calcular que levaria 117 * 9 = 153 indicadores só para mostrar "apenas alguns ícones." Para a análise de todos os 21 timeframes para cada símbolo já se precisa de 3213 indicadores. Para acomodá-los todos, é necessária uma enorme quantidade de memória.
Para entender como a memória é alocada, escreveremos um teste de carga especial na forma de um Expert Advisor. O Expert Advisor calculará o valor de um conjunto de indicadores, utilizando para tal fim duas opções:
- a chamada de um indicador padrão e cópia de seus valores através do identificador obtido;
- cálculo do indicador no buffer circular.
No segundo caso, não serão criados indicadores, e todos os cálculos serão feitos dentro do Expert Advisor, com a ajuda de dois indicadores circulares, nomeadamente, MACD e Stochastic. Cada um deles terá três configurações: rápido, padrão e lento. Os indicadores serão calculados com base em quatro instrumentos: EURUSD, GBPUSD, USDCHF e USDJPY no timeframe 21. É fácil contar o número total de valores calculados:
número total de valores = 2 indicadores * 3 conjuntos de parâmetros * 4 instrumentos * 21 timeframes = 504;
Para que, num Expert Advisor, seja possível utilizar abordagens diferentes na construção de indicadores, escreveremos classes recipientes auxiliares. Ao chamá-las, elas darão o último valor do indicador. Ele é calculado de maneiras diferentes, dependendo do tipo de indicador usado. Se for usado o indicador padrão, o último valor será tomado pela função CopyBuffer do identificador de sistema do indicador. No caso de se utilizar o buffer circular, o valor será calculado usando os respectivos indicadores circulares.
Aqui está o código-fonte para o protótipo do recipiente em forma de uma classe abstrata:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Arrays\ArrayObj.mqh> #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Tipo de indicador a ser usado | //+------------------------------------------------------------------+ enum ENUM_INDICATOR_TYPE { INDICATOR_SYSTEM, // Indicador de sistema INDICATOR_RIBUFF // Indicador de buffer circular }; //+------------------------------------------------------------------+ //| Recipiente do indicador | //+------------------------------------------------------------------+ class CIndBase : public CObject { protected: int m_handle; // Identificador do indicador string m_symbol; // Símbolo para cálculo do indicador ENUM_INDICATOR_TYPE m_ind_type; // Tipo de indicador ENUM_TIMEFRAMES m_period; // Período para cálculo do indicador CBarDetector m_bar_detect; // Detector da nova barra CIndBase(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type); public: string Symbol(void){return m_symbol;} ENUM_TIMEFRAMES Period(void){return m_period;} virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| Construtor protegido requer um símbolo, timeframe e tipo | //| de indicador | //+------------------------------------------------------------------+ CIndBase::CIndBase(string symbol,ENUM_TIMEFRAMES period,ENUM_INDICATOR_TYPE ind_type) { m_handle = INVALID_HANDLE; m_symbol = symbol; m_period = period; m_ind_type = ind_type; m_bar_detect.Symbol(symbol); m_bar_detect.Timeframe(period); } //+------------------------------------------------------------------+ //| Obtém o último valor do indicador | //+------------------------------------------------------------------+ double CIndBase::GetLastValue(int index_buffer) { return EMPTY_VALUE; }
Ele contém o método virtual GetLastValue. Este método toma o número de buffer do indicador e retorna o último valor do indicador para este buffer. Além disso, a classe fornece as propriedades básicas do indicador: seu timeframe, símbolo e tipo de cálculo (ENUM_INDICATOR_TYPE).
Nesta base, criaremos duas classes descendente CRiInMacd e CRiStoch. Ambos calcularão os valores dos respectivos indicadores e devolvê-los-ão através do método de substituição GetLastValue. Aqui está o código-fonte de uma dessas classes CRiIndMacd:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <RingBuffer\RiMACD.mqh> #include "RiIndBase.mqh" //+------------------------------------------------------------------+ //| Recipiente do indicador | //+------------------------------------------------------------------+ class CIndMacd : public CIndBase { private: CRiMACD m_macd; // Versão circular do indicador public: CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period, int slow_period, int signal_period); virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| Criamos o indicador MACD | //+------------------------------------------------------------------+ CIndMacd::CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period,int slow_period,int signal_period) : CIndBase(symbol, period, ind_type) { if(ind_type == INDICATOR_SYSTEM) { m_handle = iMACD(m_symbol, m_period, fast_period, slow_period, signal_period, PRICE_CLOSE); if(m_handle == INVALID_HANDLE) printf("Create iMACD handle failed. Symbol: " + symbol + " Period: " + EnumToString(period)); } else if(ind_type == INDICATOR_RIBUFF) { m_macd.SetFastPeriod(fast_period); m_macd.SetSlowPeriod(slow_period); m_macd.SetSignalPeriod(signal_period); } } //+------------------------------------------------------------------+ //| Obtém o último valor do indicador | //+------------------------------------------------------------------+ double CIndMacd::GetLastValue(int index_buffer) { if(m_handle != INVALID_HANDLE) { double array[]; if(CopyBuffer(m_handle, index_buffer, 1, 1, array) > 0) return array[0]; return EMPTY_VALUE; } else { if(m_bar_detect.IsNewBar()) { //printf("Obtida uma nova barra em " + m_symbol + " Período " + EnumToString(m_period)); double close[]; CopyClose(m_symbol, m_period, 1, 1, close); m_macd.AddValue(close[0]); } switch(index_buffer) { case 0: return m_macd.Macd(); case 1: return m_macd.Signal(); } return EMPTY_VALUE; } }
A classe-recipiente para o cálculo do Stochastic é organizada da mesma forma, por isso não vamos dar seu código-fonte aqui.
O cálculo dos valores do indicador ocorre apenas na abertura de uma nova barra. Isso facilita o teste. Para este fim, na classe base CRiIndBase é construído o módulo especial NewBarDetecter. Esta classe pode detectar a abertura de uma nova barra e sinalizar isso, retornando true usando o método IsNewBar.
Agora dar apresentamos o código do Expert de teste. É o chamado TestIndEA.mq5:
//+------------------------------------------------------------------+ //| TestIndEA.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Object.mqh> #include <Arrays\ArrayObj.mqh> #include "RiIndBase.mqh" #include "RiIndMacd.mqh" #include "RiIndStoch.mqh" #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Parâmetros MACD | //+------------------------------------------------------------------+ struct CMacdParams { int slow_period; int fast_period; int signal_period; }; //+------------------------------------------------------------------+ //| Parâmetros Stoch | //+------------------------------------------------------------------+ struct CStochParams { int k_period; int k_slowed; int d_period; }; input ENUM_INDICATOR_TYPE IndType = INDICATOR_SYSTEM; // Tipo de indicador string Symbols[] = {"EURUSD", "GBPUSD", "USDCHF", "USDJPY"}; CMacdParams MacdParams[3]; CStochParams StochParams[3]; CArrayObj ArrayInd; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MacdParams[0].fast_period = 3; MacdParams[0].slow_period = 13; MacdParams[0].signal_period = 6; MacdParams[1].fast_period = 9; MacdParams[1].slow_period = 26; MacdParams[1].signal_period = 12; MacdParams[2].fast_period = 18; MacdParams[2].slow_period = 52; MacdParams[2].signal_period = 24; StochParams[0].k_period = 6; StochParams[0].k_slowed = 3; StochParams[0].d_period = 3; StochParams[1].k_period = 12; StochParams[1].k_slowed = 5; StochParams[1].d_period = 6; StochParams[2].k_period = 24; StochParams[2].k_slowed = 7; StochParams[2].d_period = 12; // Aqui são criados 504 indicadores MACD e Stochastic for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PeriodByIndex(period), IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PeriodByIndex(period), IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } printf("Create " + (string)ArrayInd.Total() + " indicators sucessfully"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { for(int i = 0; i < ArrayInd.Total(); i++) { CIndBase* ind = ArrayInd.At(i); double value = ind.GetLastValue(0); double value_signal = ind.GetLastValue(1); } } //+------------------------------------------------------------------+ //| Retorna o timeframe segundo seu índice | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES PeriodByIndex(int index) { switch(index) { case 0: return PERIOD_CURRENT; case 1: return PERIOD_M1; case 2: return PERIOD_M2; case 3: return PERIOD_M3; case 4: return PERIOD_M4; case 5: return PERIOD_M5; case 6: return PERIOD_M6; case 7: return PERIOD_M10; case 8: return PERIOD_M12; case 9: return PERIOD_M15; case 10: return PERIOD_M20; case 11: return PERIOD_M30; case 12: return PERIOD_H1; case 13: return PERIOD_H2; case 14: return PERIOD_H3; case 15: return PERIOD_H4; case 16: return PERIOD_H6; case 17: return PERIOD_H8; case 18: return PERIOD_H12; case 19: return PERIOD_D1; case 20: return PERIOD_W1; case 21: return PERIOD_MN1; default: return PERIOD_CURRENT; } } //+------------------------------------------------------------------+
A funcionalidade base é realizada no bloco OnInit. Nele, são processados os símbolos, timeframes e conjuntos de parâmetros para indicadores. Os conjuntos de parâmetros dos indicadores são armazenados nas estruturas auxiliares CMacdParams e CStochParams.
O bloco de processamento de valores está colocado na função OnTick, ela consiste numa pesquisa detalhada de indicadores e seus últimos valores obtidos usando o método virtual GetLastalue. Como o número de buffers de cálculo é o mesmo para os dois indicadores, não é preciso fazer verificações neles, e é possível obter os valores dos dois através do método base GetLastValue.
A execução do Expert Advisor mostrou o seguinte: o modo de cálculo com base em chamadas de indicadores padrão requereu 11,9 GB de RAM, enquanto no modo de cálculo de indicadores baseado nas primitivas circulares foram necessários 2,9 GB. O teste foi realizado num computador com 16 GB de RAM.
No entanto, deve-se entender que a memória foi poupada em grande parte NÃO através do uso de buffers circulares, mas sim colocando os módulos de cálculo no código do Expert Advisor. O simples facto de fazer isso economiza memória.
Preservar a memória quatro vezes é mais do que um resultado decente. No entanto, ainda nos levou quase 3 GB de RAM. Será que é possível reduzir de alguma forma ainda mais esta cifra? É, mas só se for otimizado o número de timeframes. Tentaremos alterar um pouco o código de teste, e em vez de 21 timeframes só usaremos um, nomeadamente, PERIOD_M1. O número de indicadores permanecerá o mesmo, mas alguns deles serão duplicados:
... for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PERIOD_M1, IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PERIOD_M1, IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } ...
Agora, os mesmos 504 indicadores no modo de cálculo interno vem fazendo 548 MB de RAM. Se for usada uma formulação mais precisa, a memória é ocupada não só por indicadores, ou dados baixados para seu cálculo. O terminal em si ocupa cerca de 100 MB do total, portanto, os dados reais a serem baixados são menos. Nós novamente reduzimos significativamente o consumo de memória:
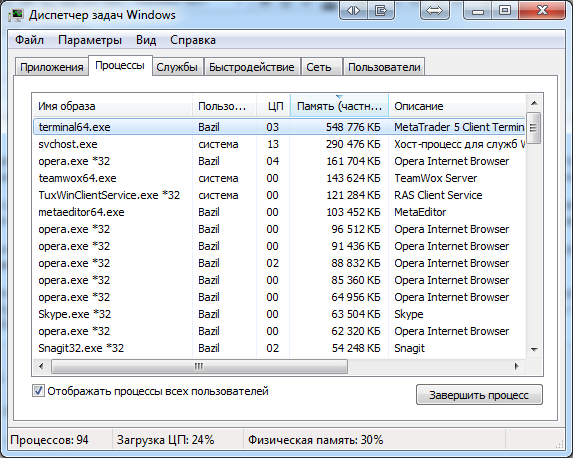
O cálculo com base nos indicadores de sistema nesta modalidade requer 1,9 GB de memória, que também é significativamente menos do que usar toda a lista de 21 timeframe.
Otimizando o tempo de teste do Expert Advisor
A plataforma MetaTrader 5 tem a capacidade de lidar - durante os testes - com vários instrumentos de negociação, bem como com o timeframe arbitrário de cada instrumento. Assim, é possível criar e testar multi-Experts, quando um deles opera em vários instrumentos. O acesso ao ambiente de negociação pode demorar algum tempo, especialmente se for preciso acessar os dados de quaisquer indicadores calculados sobre estes instrumentos. O tempo de acesso pode ser encurtado, se todos os cálculos são executados dentro de um único Expert Advisor. Ilustremos isso testando nosso exemplo anterior no testador de estratégias MetaTrader 5. Para começar, testaremos o Expert Advisor no último mês em EURUSD no modo "Somente Abertura de Preços" em M1. Para os cálculos usamos os indicadores de sistema. Este teste foi concluído em 58 segundos num computador com um processador Intel Core i7 870 2.9 Ghz:
2017.03.30 14:07:12.223 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:57.923.
Agora realizaremos o mesmo teste, mas no modo de cálculos internos:
2017.03.30 14:08:29.472 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:12.292.
Como pode ser visto, o tempo de cálculo é reduzido significativamente. Neste modo, levou 12 segundos.
Conclusões e sugestões para melhorar o desempenho
Nós testamos o uso de memória ao criar indicadores e medimos a velocidade dos testes em dois modos diferentes de operação. Ao utilizar os cálculos internos com base em buffers circulares, conseguimos reduzir o uso de memória e melhorar o desempenho em várias vezes. Naturalmente, os exemplos apresentados são artificiais em muitos aspectos. A maioria dos programadores nunca precisará criar 500 indicadores em simultâneo e testá-los em todos os timeframes possíveis. No entanto, um "teste de stress" ou teste de resistência ajuda a revelar os mecanismos mais dispendiosos e reduze sua utilização a um mínimo. Aqui estão algumas recomendações a partir dos resultados dos testes:
- Coloque a parte do cálculo dos indicadores dentro dos Expert Advisors. Isto ajudará a poupar tempo e espaço de RAM gastos no teste.
- Se possível, evite os pedidos para a obtenção de dados do conjunto de timeframes. Em vez disso, para os cálculos, use um timeframe (o menor). Por exemplo, se você precisa calcular dois indicadores em M1 e H1, obtenha os dados M1, convertê-los para H1 e, em seguida, envie esses dados para calcular o indicador em H1. Esta abordagem é mais complicada, mas permitirá economizar muita memória.
- Use com moderação o cálculo de indicadores em seus desenvolvimentos. Um excelente candidato para o cálculo econômico é os buffers circulares. Eles exigem mais memória do que é necessário para o cálculo de indicadores. Além disso, os buffers circulares permitem optimizar alguns algoritmos de cálculo, tais como, por exemplo, a pesquisa para máximos/mínimos.
- Crie uma interface universal para o trabalho com os indicadores e usá-la para obter seus valores. Se o cálculo do indicador for difícil de implementar no bloco interior, a interface chamará o indicador exterior MetaTrader. Se você criar um bloco interno de cálculo do indicador, basta conectá-lo à interface. O Expert Advisor, neste caso, será sujeito à alteração mínima.
- Avaliar com precisão a possibilidade de otimização. Se você estiver usando um indicador num único instrumento, o indicador pode ser deixado como ele é e não transferi-lo para um cálculo interno. O tempo gasto com essa transferência, pode exceder significativamente o ganho global no desempenho.
Conclusão
Consideramos a criação de buffers circulares e sua aplicação prática para a construção de indicadores econômicos. É difícil encontrar um uso mais corrente de buffers circulares do que na negociação. Ainda mais surpreendente é o fato de o algoritmo para construir os dados ainda não estar publicado na comunidade MQL.
Os buffers circulares e indicadores, com base neles, não consistem apenas numa poupança de memória e um cálculo rápido. A principal vantagem dos buffers circulares é a facilidade de implementação de indicadores com base neles. Verifica-se pelo fato de a esmagadora maioria dos indicadores estarem dispostos segundo o princípio FIFO (primeira entrada-primeira saída). Portanto, normalmente, as dificuldades surgem precisamente quando os indicadores estão tentando calcular não no buffer circular.
O apêndice a este documento contém todo o código-fonte considerado, incluindo os códigos dos próprios indicadores e os algoritmos simples em que se baseiam. Espero que este material seja útim como um bom ponto de partida para a criação de uma simples, rápida, versátil e completa biblioteca cheia de indicadores cíclicos.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/3047
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Excelente trabalho aqui, muito obrigado ao autor. Talvez o bug que você está vendo, Savio, esteja aqui:
int RingBuffer::iToRealInd(int iIndex)
{
if(iIndex >= iNumElements() || iIndex < 0)
return iBufferSize-1; //previous bug was caused by no -1 here
...
Eu adicionei o -1 na última linha citada; ele não estava lá antes e causaria o retorno de um índice inadequado. Observe que mudei os nomes das variáveis/métodos de acordo com meu estilo de programação, mas a ideia é a mesma
Tentei sua correção, mas a atualização ainda não está correta. Parece que está faltando alguma coisa e não consigo encontrar o problema ao tentar executar o buffer de anel na formação de uma nova barra. Quando o mercado está funcionando, as linhas Alto/Baixo ficam completamente misturadas. O código funciona muito bem e muito rápido ao processar dados antigos, mas com novos dados chegando durante a formação de uma nova barra, ele simplesmente não funciona para mim.
Se eu puder fazer alguns comentários:
1. Na classe void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value), no método " OnChangeValue" na linha
.
Figura: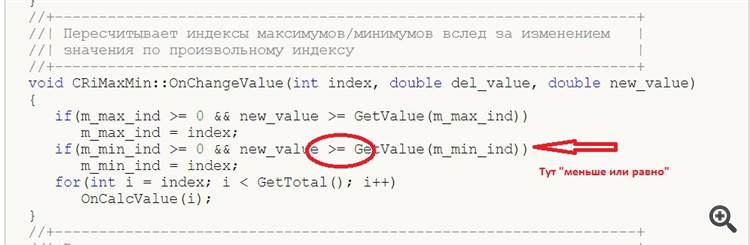
typo - sinal "less than or equal to".

2.Ao pesquisar os elementos Min e Max de uma matriz, se usados exatamente como um buffer em anel (quando novos elementos começam a ser gravados no início da matriz), min e mah são definidos incorretamente. O mínimo é maior que o máximo. Em uma matriz. Tudo funciona usando os métodos padrão (ArrayMinimum e ArrayMaximum).
Picture:
Em algum lugar, a indexação está se desviando. Não consigo consertar isso sozinho. Se alguém puder corrigi-lo, seria ótimo. Anexei um orientador de teste.
Você cometeu um erro em ToRealInd(int index).
Deveria ser: