MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
MQL5クックブック - スライディングウィンドウ内指標の高速計算のためのリングバッファの作成

MQL5クックブック - スライディングウィンドウ内指標の高速計算のためのリングバッファの作成

MetaTrader 5 — 例 | 14 6月 2017, 09:17
1 133 0
Vasiliy Sokolov
Vasiliy Sokolov

内容

はじめに

トレーダーによって実行される計算のほとんどはスライディングウィンドウで行われます。これは、価格、ビッド、取引量のいずれを扱っているかにかかわらず、市場データにはほとんど常に連続的に流れ入ってくるという性質があるからです。通常、トレーダーには一定期間の値を計算することが必要です。たとえば、移動平均を計算する場合に取り扱うのは最後のNバーの平均価格値です（Nは移動平均期間）。この場合、平均値の計算に費やされた時間は平均期間に依存すべきではありません。しかし、実際の状況で、このような性質を持つアルゴリズムを実装することは必ずしも容易ではありません。アルゴリズム的な観点からは、新しいバーが到着したときに平均値を一から再計算するほうがはるかに簡単です。リングバッファアルゴリズムは、計算の効率性の問題を解決し、計算ブロックにスライディングウインドウを提供し、その内部計算が簡単かつ効率的に行われるようにします。

移動平均計算の問題

移動平均の計算について考えてみましょう。単純なアルゴリズムで、プロットするときに直面する可能性のある問題を説明することができます。平均値は、下記のよく知られている式を使用して計算されます。

 

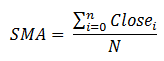
簡単なMQL5スクリプトで実装します。

//+------------------------------------------------------------------+
//|                                                          SMA.mq5 |
//|                        Copyright 2015, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2015, MetaQuotes Software Corp."
#property link      "http://www.mql5.com"
#property version   "1.00"
input int N = 10;       // 移動平均期間
//+------------------------------------------------------------------+
//| スクリプトプログラム開始関数                                        |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   double closes[];
   if(CopyClose(Symbol(), Period(), 0, N, closes)!= N)
   {
      printf("Need more data");
      return;
   }
   double sum = 0.0;
   for(int i = 0; i < N; i++)
      sum += closes[i];
   sum /= N;
   printf("SMA: " + DoubleToString(sum, Digits()));  
  }
    //+------------------------------------------------------------------+

一見すると、すべてがよさそうにみえます。スクリプトは移動平均値を取得して端末ウィンドウに表示します。しかし、スライディングウィンドウで作業するときはどうすればいいでしょうか。直近のクォートが変更して新しいバーが常に表示されます。アルゴリズムは、それごとに、非常にリソース集約的な操作を使用して移動平均値を再計算することになります。

  • N個の要素を出力先配列にコピーする
  • 出力先配列全体を'for'ループで検索する

2番目の操作は、最もリソース集中的です。10の期間は10回の反復を必要とし、500の期間は500の反復を必要とします。アルゴリズムの複雑さは平均期間に直接依存しO(n)として表すことができます。ここで、Oは複雑性関数です。

しかし、スライディングウインドウで移動平均を計算するはるかに高速なアルゴリズムがあります。その実装には、前の計算でのすべての値の合計を知る必要があります。

SMA = (すべての値の合計 - スライディングウインドウの最初の値 + 新しい値) / 移動平均期間

アルゴリズムの複雑性関数は、平均化期間に依存しないO(1) 定数です。このようなアルゴリズムは、性能はより高いですが、実装することはより困難です。新しいバーが表示されるたびに、次の手順が実行されなければなりません。

  • 最初に追加された値を現在の合計から減算するとともに系列から削除する
  • 最後に加算された値を現在の合計に加算するとともに系列に含める
  • 現在の合計を平均期間で除算して移動平均として返す

直近の値が追加されずに更新された場合、アルゴリズムはさらに複雑になります。

  • 更新された値を定義して現在の状態を記憶する
  • 前のステップで記憶された値を現在の合計から減算する
  • その値を新しいものと置き換える
  • 現在の合計に新しい値を追加する
  • 現在の合計を平均期間で除算して移動平均として返す

あと1つの課題は、他のほとんどのシステムプログラミング言語同様、MQL5の組み込みツールは基本的なデータ型（配列など）のみを扱うということです。ほとんどの場合、 FIFO（First In - First Out、先入れ先出し）キューを配置する（新しい要素が出現したときに 最初に追加された要素を削除する必要がある）ため、適切な修正を行わないかぎり配列はこの役割には適していません。配列では要素の削除と追加の両方が可能です。しかし、これらの操作は配列を再配布するのでかなりリソース集約的です。 

このような困難を避けて本当に効率的なアルゴリズムを実装するにはリングバッファを見てみましょう。

リングバッファ理論

リングバッファでは、操作中に配列を再配布することなく要素を追加したり削除したりすることができます。配列要素の数が常に一定であると仮定（スライディングウィンドウでの計算の場合）して、新しい要素を追加した後に古い要素を削除します。したがって、要素の総数は変更されませんが、新しい要素が追加されるたびにインデックスが変更されます。最後の要素は最後から2番目の要素になり、初めから2番目の要素が一番初めの要素になり、一番初めだった要素はキューから永久に削除されます。

この特徴によって、リングバッファは通常の配列に基づくことができます。通常の配列に基づいたクラスを作成しましょう。

class CRingBuffer
{
private:
   double      m_array[];
        };

バッファが3要素で構成されているとします。この場合、1番目の要素はインデックス0を持つ配列スロットに追加され、2番目の要素はインデックス1のスロット、3番目の要素はインデックス2のスロットを占めることになります。4番目の要素を追加するとどうなるでしょうか。明らかに、1番目の要素が削除されます。すると、4番目の要素の場所として最も適しているのは1番目の要素の場所で、そのインデックスが再びゼロになります。このインデックスはどのように計算できるでしょうか。「除算の余り」という特別な操作を適用しましょう。MQL5では、この操作は特別なパーセント記号%で示されます。数値が0から始まるので、4番目の要素はキューの3番目の要素になり、その配置インデックスは次の式を使用して計算されます。

int index = 3 % total;

ここで"total"はバッファサイズです。この例では、3の3による除算には余りがありません。したがって、indexは余りに等しくゼロです。後続の要素は同じ規則に従って配置されます。追加された要素の数は、配列内の要素の数で除算されます。この除算の余りは循環バッファ内の実際のインデックスになります。以下は、サイズ3のリングバッファに追加された最初の8つの要素のインデックスの条件付き計算です。

0 % 3 = [0]
1 % 3 = [1]
2 % 3 = [2]
3 % 3 = [0]
4 % 3 = [1]
5 % 3 = [2]
6 % 3 = [0]
7 % 3 = [1]

...

作業プロトタイプ

リングバッファーの理解が深まったので、実際のプロトタイプを開発することにします。ここでのリングバッファには3つの基本的な機能があります。

  • 新しい値を追加する
  • 最後の値を削除する
  • 任意のインデックスでの値を変更する

後者の機能は、最後のバーが形成中で終値が絶えず変化しているときにリアルタイムで作業するために必要です。 

また、バッファには2つの基本的な特性があります。最大バッファサイズと現在の要素数です。これらの値はほとんどの場合に一致します。これは、要素がバッファサイズ全体を満たすとき、後続の各要素が最も古い要素を上書きするため、要素の総数は変更されないからです。しかし、これらのプロパティの値はバッファが初めて書き入れられているときには異なります。要素の最大数は可変プロパティであり、ユーザによって増減されることができます。

最も古い要素は、明示的なユーザー要求がなくても自動的に削除されます。古い要素を手動で削除すると補助統計の計算が複雑になるため、この動作は意図的なものです。

アルゴリズムの最大の複雑さは、実際の値を格納するための内部バッファの実際のインデックスの計算にあります。たとえば、ユーザがインデックス0の要素を要求した場合、その要素が配置されている実際のインデックス値は異なる場合があります。17番目の要素をサイズ10のリングバッファに追加する場合、要素0はインデックス8に配置され、最後の（9番目の）要素はインデックス7に配置されます。 

リングバッファのヘッダファイルとメインメソッドの内容を見て、リングバッファのメイン操作がどのようなものかを見てみましょう。

//+------------------------------------------------------------------+
//| Double リングバッファ                                              |
//+------------------------------------------------------------------+
class CRiBuffDbl
{
private:
   bool           m_full_buff;
   int            m_max_total;
   int            m_head_index;
protected:
   double         m_buffer[];                // ダイレクトアクセス用リングバッファ。注：インデックスはカウント数と一致しない
   ...
   int            ToRealInd(int index);
public:
                  CRiBuffDbl(void);
   void           AddValue(double value);
   void           ChangeValue(int index, double new_value);
   double         GetValue(int index);
   int            GetTotal(void);
   int            GetMaxTotal(void);
   void           SetMaxTotal(int max_total);
   void           ToArray(double& array[]);
};
//+------------------------------------------------------------------+
//| コンストラクタ                                                     |
//+------------------------------------------------------------------+
CRiBuffDbl::CRiBuffDbl(void) : m_full_buff(false),
                                 m_head_index(-1),
                                 m_max_total(0)
{
   SetMaxTotal(3);
}
//+------------------------------------------------------------------+
//| リングバッファの新しいサイズを設定する                                |
//+------------------------------------------------------------------+
void CRiBuffDbl::SetMaxTotal(int max_total)
{
   if(ArraySize(m_buffer) == max_total)
      return;
   m_max_total = ArrayResize(m_buffer, max_total);
}
//+------------------------------------------------------------------+
//| 実際のリングバッファサイズを取得する                                 |
//+------------------------------------------------------------------+
int CRiBuffDbl::GetMaxTotal(void)
{
   return m_max_total;
}
//+------------------------------------------------------------------+
//| インデックス値を取得する                                            |
//+------------------------------------------------------------------+
double CRiBuffDbl::GetValue(int index)
{
   return m_buffer[ToRealInd(index)];
}
//+------------------------------------------------------------------+
//| 要素総数を取得する                                                 |
//+------------------------------------------------------------------+
int CRiBuffDbl::GetTotal(void)
{
   if(m_full_buff)
      return m_max_total;
   return m_head_index+1;
}
//+------------------------------------------------------------------+
//| リングバッファに新しい値を追加する                                   |
//+------------------------------------------------------------------+
void CRiBuffDbl::AddValue(double value)
{
   if(++m_head_index == m_max_total)
   {
      m_head_index = 0;
      m_full_buff = true;
   }  
   //...
   m_buffer[m_head_index] = value;
}
//+------------------------------------------------------------------+
//| 前に追加された値を新しい値に変える                                   |
//+------------------------------------------------------------------+
void CRiBuffDbl::ChangeValue(int index, double value)
{
   int r_index = ToRealInd(index);
   double prev_value = m_buffer[r_index];
   m_buffer[r_index] = value;
}
//+------------------------------------------------------------------+
//| 仮想インデックスを実際のインデックスに変換する                         |
//+------------------------------------------------------------------+
int CRiBuffDbl::ToRealInd(int index)
{
   if(index >= GetTotal() || index < 0)
      return m_max_total;
   if(!m_full_buff)
      return index;
   int delta = (m_max_total-1) - m_head_index;
   if(index < delta)
      return m_max_total + (index - delta);
   return index - delta;
}

このクラスの基盤は最後に追加された要素へのm_head_indexポインタです。AddValueメソッドを使用して新しい要素を追加すると、それは1で増えます。値は、配列サイズを超えはじめるとリセットされます。

リングバッファの最も複雑な関数は、内部のToRealIndメソッドです。このメソッドは、ユーザの視点からバッファインデックスを受け取り、必要な要素が配置されている配列の実際のインデックスを返します。

これでわかるように、リングバッファは非常に簡単です。ポインタ演算を除くと、サポートされているのは、新しい要素を追加し、GetValue()を使用して任意の要素へのアクセスを提供するという基本的なアクションです。しかし、通常、この機能は、通常の移動平均や高/低値検索アルゴリズムのように、必要なパラメータの計算を便利に配置するために適用されます。リングバッファーを使用すると、一連の統計オブジェクトを計算できます。これらは、分散と標準偏差のような、あらゆる種類の指標や統計的基準です。したがって、リングバッファクラスにすべての計算アルゴリズムを一度に与えることは不可能で、実際、必要ではありません。代わりに、特定の指標や統計計算アルゴリズムを実装する、より柔軟なソリューションである派生クラスを適用することができます。

これらの派生クラスがクラスを便利に計算できるようにするには、リングバッファに追加のメソッドを用意する必要があります。それらをイベントメソッドと呼ぶことにしましょう。これらは、"protected"セクションに配置された普通のメソッドです。これらのメソッドはすべて再定義できOnから始まります。

//+------------------------------------------------------------------+
//| Double リングバッファ                                              |
//+------------------------------------------------------------------+
class CRiBuffDbl
{
private:
   ...
protected:
   virtual void   OnAddValue(double value);
   virtual void   OnRemoveValue(double value);
   virtual void   OnChangeValue(int index, double prev_value, double new_value);
   virtual void   OnChangeArray(void);
   virtual void   OnSetMaxTotal(int max_total);
};

リングバッファに変更があるたびに、これを通知するメソッドが呼び出されます。たとえば、新しい値がバッファに出現する場合、OnAddValueメソッドが呼び出されます。そのパラメータには、追加する値が含まれています。リングバッファの派生クラスでこのメソッドを再定義すると、新しい値が追加されるたびに適切な派生クラスの計算ブロックが呼び出されます。 

リングバッファには、派生クラスで監視できる5つのイベントがあります（括弧内に適切なメソッドが指定されています）。

  1. 新しい要素の追加 (OnAddValue)
  2. 古い要素の削除 (OnRemoveValue)
  3. 任意のインデックスでの値の変更 (OnChangeValue)
  4. リングバッファの内容全体の変更 (OnChangeArray)
  5. リングバッファ内の要素の最大数の変更(OnSetMaxTotal)

OnChangeArrayイベントには特別な注意が必要です。これは、指標の再計算で累積値の配列全体にアクセスする必要がある場合に呼び出されます。この場合、派生クラスでメソッドを再定義すれば十分です。このメソッドではToArray関数を使用して値の配列全体を取得し、適切な計算を行う必要があります。そのような計算の例は、下記のリングバッファとAlgLibライブラリの統合についてのセクションで見つけることができます。

リングバッファクラスはCRiBuffDblと呼ばれ、その名が示すようにdouble値と動作します。実数は、計算アルゴリズムの最も一般的なデータ型です。しかし、実数とは別に、整数も必要かもしれません。よって、このクラスのセットにはCRiBuffIntクラスが含まれます。現代のPCでは、固定小数点演算は浮動小数点演算よりも高速に実行されます。これが、特定の整数タスクにはCRiBuffIntを使用する方が良い理由です。

ここに示したアプローチは、記述を可能にして普遍的な<template T>型で作業するテンプレートクラスを適用しません。これは、特定の計算アルゴリズムが循環バッファから直接継承され、この種のアルゴリズムのそれぞれが、明確に定義されたデータ型で動作することを前提としているため、意図的に行われます。

リングバッファでの単純移動平均の計算例

これまでは、リングバッファの原理を実装するクラスの内部配置について検討しました。次に、この知識を使っていくつかの実用的な問題を解決していきます。単純移動平均指標の開発という単純なタスクから始めましょう。これは一般的な移動平均で、系列の和を平均期間で除算する必要があります。前述した計算式を繰り返しましょう。

SMA = (すべての値の合計 - スライディングウインドウの最初の値 + 新しい値) / 移動平均期間

アルゴリズムを実装するには、CRiBuffDblから派生したクラスでOnAddValueとOnRemoveValueの2つのメソッドを再定義する必要があります。平均値はSmaメソッドで計算します。以下は結果のクラスのコードです。

//+------------------------------------------------------------------+
//|                                                   RingBuffer.mqh |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#include "RiBuffDbl.mqh"
//+------------------------------------------------------------------+
//| リングバッファで移動平均を計算する                                   |
//+------------------------------------------------------------------+
class CRiSMA : public CRiBuffDbl
{
private:
   double        m_sum;
protected:
   virtual void  OnAddValue(double value);
   virtual void  OnRemoveValue(double value);
   virtual void  OnChangeValue(int index, double del_value, double new_value);
public:
                 CRiSMA(void);
   
   double        SMA(void);
};

CRiSMA::CRiSMA(void) : m_sum(0.0)
{
}
//+------------------------------------------------------------------+
//| 合計の和を増やす                                                   |
//+------------------------------------------------------------------+
void CRiSMA::OnAddValue(double value)
{
   m_sum += value;
}
//+------------------------------------------------------------------+
//| 合計の和を減らす                                                   |
//+------------------------------------------------------------------+
void CRiSMA::OnRemoveValue(double value)
{
   m_sum -= value;
}
//+------------------------------------------------------------------+
//| 合計の和を変更する                                                 |
//+------------------------------------------------------------------+
void CRiSMA::OnChangeValue(int index,double del_value,double new_value)
{
   m_sum -= del_value;
   m_sum += new_value;
}
//+------------------------------------------------------------------+
//| 単純移動平均を計算する                                              |
//+------------------------------------------------------------------+
double CRiSMA::SMA(void)
{
   return m_sum/GetTotal();
}

要素の追加や削除（それぞれOnAddValueとOnRemoveValue）に反応するメソッドのほかに、任意の要素を変更するときに呼び出されるメソッド（OnChangeValue）を再定義する必要がありました。リングバッファは任意の要素の任意の変更をサポートするので、そのような変更は追跡されるべきです。通常、最後の要素のみが変更されます（最後のバー形成モードで）。これは、OnChangeValueイベントの再定義によって処理されます。

移動平均を計算するためにリングバッファクラスを使用してカスタム指標を作成しましょう。

//+------------------------------------------------------------------+
//|                                                        RiEma.mq5 |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#property version   "1.00"
#property indicator_chart_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#include <RingBuffer\RiSMA.mqh>

input int MaPeriod = 13;
double buff[];
CRiSMA Sma;
//+------------------------------------------------------------------+
//| カスタム指標初期化関数                                              |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- 指標バッファマッピング
   SetIndexBuffer(0, buff, INDICATOR_DATA);
   Sma.SetMaxTotal(MaPeriod);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| カスタム指標反復処理関数                                            |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const int begin,
                const double &price[])
{
//---
   bool calc = false;
   for(int i = prev_calculated; i < rates_total; i++)
   {
      Sma.AddValue(price[i]);
      buff[i] = Sma.SMA();
      calc = true;
   }
   if(!calc)
   {
      Sma.ChangeValue(MaPeriod-1, price[rates_total-1]);
      buff[rates_total-1] = Sma.SMA();
   }
   return(rates_total-1);
}
//+------------------------------------------------------------------+

計算の開始時に、指標は移動平均のリングバッファに単に新しい値を追加します。追加された値の数を制御する必要はありません。計算と不要な要素の削除はすべて自動的に行われます。指標が最後のバーの価格を変更するときに呼び出された場合は、最後の移動平均値を新しい値に置き換える必要があります。これはChangeValueメソッドが担当します。

指標のグラフィック表示は標準移動平均と同等です。

 

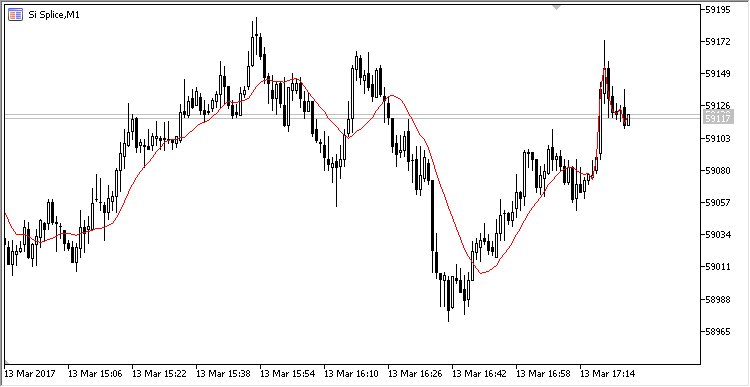
図1　リングバッファで計算された単純移動平均‌

リングバッファでの指数移動平均の計算例

より複雑なケースである指数移動平均の計算を試してみましょう。単純平均とは異なり、指数平均は値バッファから古い要素を削除しても影響を受けません。したがって、計算には2つのメソッド（OnAddValueとOnChangeValue）のみを再定義する必要があります。前の例と同様に、CRiBuffDblから派生したCRiMEAクラスを作成し、適切なメソッドを再定義しましょう。

//+------------------------------------------------------------------+
//|                                                   RingBuffer.mqh |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#include "RiBuffDbl.mqh"
//+------------------------------------------------------------------+
//| リングバッファの指数移動平均を計算する                                |
//+------------------------------------------------------------------+
class CRiEMA : public CRiBuffDbl
{
private:
   double        m_prev_ema;        // 1つ前のEMA値
   double        m_last_value;      // 直近価格
   double        m_smoth_factor;    // 平滑化係数
   bool          m_calc_first_v;    // 最初の値の計算を示すフラグ
   double        CalcEma();         // 直接平均計算
protected:
   virtual void  OnAddValue(double value);
   virtual void  OnChangeValue(int index, double del_value, double new_value);
   virtual void  OnSetMaxTotal(int max_total);
public:
                 CRiEMA(void);
   double        EMA(void);
};
//+------------------------------------------------------------------+
//| 値の追加/変更通知を購読する                                         |
//+------------------------------------------------------------------+
CRiEMA::CRiEMA(void) : m_prev_ema(EMPTY_VALUE), m_last_value(EMPTY_VALUE),
                                                m_calc_first_v(false)
{
}
//+------------------------------------------------------------------+
//| MetaQuotes EMAの式に従って平滑化係数を計算する                       |
//+------------------------------------------------------------------+
void CRiEMA::OnSetMaxTotal(int max_total)
{
   m_smoth_factor = 2.0/(1.0+max_total);
}
//+------------------------------------------------------------------+
//| 総数の和を増やす                                                   |
//+------------------------------------------------------------------+
void CRiEMA::OnAddValue(double value)
{
   // 1つ前のEMA値を計算する
   if(m_prev_ema != EMPTY_VALUE)
      m_prev_ema = CalcEma();
   // 現在価格を保存する
   m_last_value = value;
}
//+------------------------------------------------------------------+
//| EMAを修正する                                                     |
//+------------------------------------------------------------------+
void CRiEMA::OnChangeValue(int index,double del_value,double new_value)
{
   if(index != GetMaxTotal()-1)
      return;
   m_last_value = new_value;
}
//+------------------------------------------------------------------+
//| 直接的なEMA計算                                                   |
//+------------------------------------------------------------------+
double CRiEMA::CalcEma(void)
{
   return m_last_value*m_smoth_factor+m_prev_ema*(1.0-m_smoth_factor);
}
//+------------------------------------------------------------------+
//| EMAを取得する                                                     |
//+------------------------------------------------------------------+
double CRiEMA::EMA(void)
{
   if(m_calc_first_v)
      return CalcEma();
   else
   {
      m_prev_ema = m_last_value;
      m_calc_first_v = true;
   }
   return m_prev_ema;
}

CalcEmaメソッドは移動平均の計算を担当します。これは、最後に知られている前の値に平滑化係数を乗算したもの、前回の指標値に平滑化係数の逆数を乗算したものの2つの積の和を返します。指標の1つ前の値がまだ計算されていない場合は、バッファに入れられた最初の値が使われます（この場合、ゼロバーの終値です）。

前のセクションのような指標を作成して、チャートに計算を表示しましょう。これは下記のように見えます。

‌

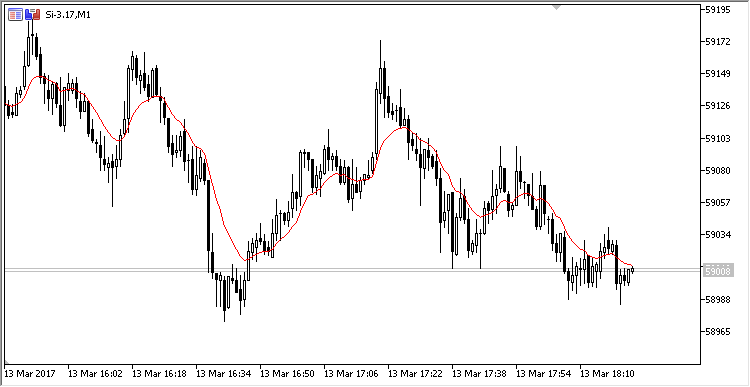
図2　リングバッファで計算された指数移動平均

リングバッファでの高値/安値の計算

最も挑戦的でエキサイティングなタスクは、スライディングウインドウでの高値と安値の計算です。もちろん、これはArrayMaximumとArrayMinimum標準関数を参照するだけで簡単に行うことができます。ただし、この場合、スライディングウインドウで計算することの利点はすべて消えます。高値と安値は、完全な検索を実行せずにバッファから順にデータを追加して削除することによって計算することができます。バッファに追加される新たな値のそれぞれに対して2つの追加の値が計算されると仮定します。最初の値は、現在の要素を下回る以前の要素の数を指定し、2番目の値は、現在の要素を上回る以前の要素の数を示します。最初の値は高値、2番目の値は安値を効率的に検索するために適用されます。 

さて、よくある値のバーがあって、ある期間の高値の極値を計算する必要があると仮定します。これを行うには、各バーの上に、現在のバーの高値より低い高値を持つ以前のバーの数を示すラベルを追加します。以下の図にバーのシーケンスを示します。

‌

図3　バーの極点階層

前の値が確認されていないため、最初のバーは常にゼロの極値を持ちます。2番目のバーはそれより高いので、 その極値インデックスは1です。3番目のバーは2番目のバーより高いので、1番目のバーよりも高いということになり、その極値は2です。その後3つのバーが続き、それぞれのバーは前のバーよりも低くなっています。それらはすべて3番目のバーよりも低いので、その極値はゼロです。7番目のバーは前の3つのバーより高いですが、4番目のバーよりは低いです。したがって、その極限インデックスは3です。同様に、新しいバーが追加されるたびに極値インデックスが計算されていきます。

以前のすべてのインデックスが計算されれば、現在のバーの極点は簡単に取得できます。これを行うには、単に、バーの極点を他のものと比較する必要があります。インデックスは表示された数字のおかげでわかるので、連続したいくつかのバーをスキップして後続の極点に直接アクセスすることができます。この過程全体を以下に示します。

‌

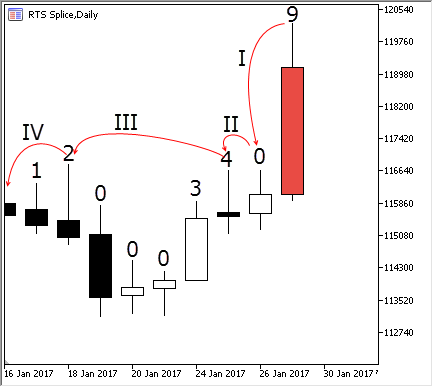
図4　現在のバーの極点の検索

赤でマークされたバーを追加したとします。番号付けはゼロから始まるので、このバーは9番目です。極限インデックスを定義するには、ステップIを実行してこれを8番目のバーと比較してみます。バー#9はより高いので極点は1になります。次にバー＃7と比較します（ステップ II） 。#9は同様に#7より高いことがわかります。バー＃7が前の4つのバーより高いので、すぐに最後のバーとバー＃3を比較することができます（ステップIII）。バー＃9はバー＃3より高いです。したがって、現時点ではすべてのバーよりも高くなります。インデックスが以前に計算されたため、現在のバーより低い4つの中間バーとの比較は避けました。以上が、リングバッファ内で極値がどのように高速検索されるかです。安値の検索は同じ方法で動作します。唯一の違いは、追加の安値インデックスの使用です。

アルゴリズムの説明が終わったので、そのソースコードを見てみましょう。このクラスは、CRiBuffInt型の2つのリングバッファが補助バッファとしても使用されているという点で興味深いものです。それぞれには高インデックスと低インデックスが含まれています。

//+------------------------------------------------------------------+
//|                                                   RingBuffer.mqh |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#include "RiBuffDbl.mqh"
#include "RiBuffInt.mqh"
//+------------------------------------------------------------------+
//| リングバッファで指数移動平均を計算する                                |
//+------------------------------------------------------------------+
class CRiMaxMin : public CRiBuffDbl
{
private:
   CRiBuffInt    m_max;
   CRiBuffInt    m_min;
   bool          m_full;
   int           m_max_ind;
   int           m_min_ind;
protected:
   virtual void  OnAddValue(double value);
   virtual void  OnCalcValue(int index);
   virtual void  OnChangeValue(int index, double del_value, double new_value);
   virtual void  OnSetMaxTotal(int max_total);
public:
                 CRiMaxMin(void);
   int           MaxIndex(int max_period = 0);
   int           MinIndex(int min_period = 0);
   double        MaxValue(int max_period = 0);
   double        MinValue(int min_period = 0);
   void          GetMaxIndexes(int& array[]);
   void          GetMinIndexes(int& array[]);
};

CRiMaxMin::CRiMaxMin(void)
{
   m_full = false;
   m_max_ind = 0;
   m_min_ind = 0;
}
void CRiMaxMin::GetMaxIndexes(int& array[])
{
   m_max.ToArray(array);
}
void CRiMaxMin::GetMinIndexes(int& array[])
{
   m_min.ToArray(array);
}
//+------------------------------------------------------------------+
//| メインバッファの新しいサイズに応じて   　　                         　 |
//| 内部バッファのサイズを変更する                                       |
//+------------------------------------------------------------------+
void CRiMaxMin::OnSetMaxTotal(int max_total)
{
   m_max.SetMaxTotal(max_total);
   m_min.SetMaxTotal(max_total);
}
//+------------------------------------------------------------------+
//| 最大/最小インデックスを計算する                                      |
//+------------------------------------------------------------------+
void CRiMaxMin::OnAddValue(double value)
{
   m_max_ind--;
   m_min_ind--;
   int last = GetTotal()-1;
   if(m_max_ind > 0 && value >= GetValue(m_max_ind))
      m_max_ind = last;
   if(m_min_ind > 0 && value <= GetValue(m_min_ind))
      m_min_ind = last;
   OnCalcValue(last);
}
//+------------------------------------------------------------------+
//| 最大/最小インデックスを計算する                                      |
//+------------------------------------------------------------------+
void CRiMaxMin::OnCalcValue(int index)
{
   int max = 0, min = 0;
   int offset = m_full ?1 : 0;
   double value = GetValue(index);
   int p_ind = index-1;
   // 最高を探す
   while(p_ind >= 0 && value >= GetValue(p_ind))
   {
      int extr = m_max.GetValue(p_ind+offset);
      max += extr + 1;
      p_ind = GetTotal() - 1 - max - 1;
   }
   p_ind = GetTotal()-2;
   // 最低を探す
   while(p_ind >= 0 && value <= GetValue(p_ind))
   {
      int extr = m_min.GetValue(p_ind+offset);
      min += extr + 1;
      p_ind = GetTotal() - 1 - min - 1;
   }
   m_max.AddValue(max);
   m_min.AddValue(min);
   if(!m_full && GetTotal() == GetMaxTotal())
      m_full = true;
}
//+------------------------------------------------------------------+
//| 任意のインデックスによる値の変更後に                                  |
//| 高/低インデックスを再計算する                                        |
//+------------------------------------------------------------------+
void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value)
{
   if(m_max_ind >= 0 && new_value >= GetValue(m_max_ind))
      m_max_ind = index;
   if(m_min_ind >= 0 && new_value >= GetValue(m_min_ind))
      m_min_ind = index;
   for(int i = index; i < GetTotal(); i++)
      OnCalcValue(i);
}
//+------------------------------------------------------------------+
//| 最大要素のインデックスを取得する                                     |
//+------------------------------------------------------------------+
int CRiMaxMin::MaxIndex(int max_period = 0)
{
   int limit = 0;
   if(max_period > 0 && max_period <= m_max.GetTotal())
   {
      m_max_ind = -1;
      limit = m_max.GetTotal() - max_period;
   }
   if(m_max_ind >=0)
      return m_max_ind;
   int c_max = m_max.GetTotal()-1;
   while(c_max > limit)
   {
      int ext = m_max.GetValue(c_max);
      if((c_max - ext) <= limit)
         return c_max;
      c_max = c_max - ext - 1;
   }
   return limit;
}
//+------------------------------------------------------------------+
//| 最小要素のインデックスを取得する                                     |
//+------------------------------------------------------------------+
int CRiMaxMin::MinIndex(int min_period = 0)
{
   int limit = 0;
   if(min_period > 0 && min_period <= m_min.GetTotal())
   {
      limit = m_min.GetTotal() - min_period;
      m_min_ind = -1;
   }
   if(m_min_ind >=0)
      return m_min_ind;
   int c_min = m_min.GetTotal()-1;
   while(c_min > limit)
   {
      int ext = m_min.GetValue(c_min);
      if((c_min - ext) <= limit)
         return c_min;
      c_min = c_min - ext - 1;
   }
   return limit;
}
//+------------------------------------------------------------------+
//| 最大要素の値を取得する                                              |
//+------------------------------------------------------------------+
double CRiMaxMin::MaxValue(int max_period = 0)
{
   return GetValue(MaxIndex(max_period));
}
//+------------------------------------------------------------------+
//| 最小要素の値を取得する                                              |
//+------------------------------------------------------------------+
double CRiMaxMin::MinValue(int min_period = 0)
{
   return GetValue(MinIndex(min_period));
}

このアルゴリズムの変更点はあと1つあります。現在の最高値と最低値が記憶され、変更がない場合は、MaxValueとMinValueメソッドは追加の計算をバイパスして単にそれらの値を返します。

チャート上で高値と安値がどのように見えるかは次のとおりです。

‌

図5　指標としての高/低チャネル

高/低定義クラスには高度な機能があります。リングバッファ内の極値インデックスまたはその値のみを返すことができます。また、リングバッファの周期より短い周期で極値を計算することができます。これを行うには、MaxIndex/MinIndexおよびMaxValue/MinValueメソッドで制限期間を指定します。

リングバッファとAlgLibライブラリの統合

リングバッファのあと一つの興味深い使用例は、特殊な数学計算の領域にあります。一般に、統計計算アルゴリズムの開発にはスライディングウィンドウが考慮されていません。これは不便を招くかもしれません。リングバッファはその問題を解決します。ガウス分布の主要パラメータを計算する指標を開発しましょう。

  • 平均値 (Mean)
  • 標準偏差 (StdDev)
  • ベル形の分布の非対称性 (Skewness)
  • 尖度

これらの特徴にAlgLib::SampleMoments統計メソッドを適用しましょう。それには、CRiGaussPropertyリングバッファクラスを作成し、OnChangeArrayハンドラの中にメソッドを配置するだけです。下記はクラスを含む指標の完全なコードです。

//+------------------------------------------------------------------+
//|                                                        RiEma.mq5 |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#property version   "1.00"
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_plots   1
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#include <RingBuffer\RiBuffDbl.mqh>
#include <Math\AlgLib\AlgLib.mqh>
 
//+------------------------------------------------------------------+
//| ガウス分布の主なパラメータを計算する                                  |
//+------------------------------------------------------------------+
class CRiGaussProperty : public CRiBuffDbl
{
private:
   double        m_mean;      // 平均
   double        m_variance;  // 分散
   double        m_skewness;  // 歪度
   double        m_kurtosis;  // 尖度
protected:
   virtual void  OnChangeArray(void);
public:
   double        Mean(void){ return m_mean;}
   double        StdDev(void){return MathSqrt(m_variance);}
   double        Skewness(void){return m_skewness;}
   double        Kurtosis(void){return m_kurtosis;}
};
//+------------------------------------------------------------------+
//| 任意の配列が変更された場合に計算が実行される                           |
//+------------------------------------------------------------------+
void CRiGaussProperty::OnChangeArray(void)
{
   double array[];
   ToArray(array);
   CAlglib::SampleMoments(array, m_mean, m_variance, m_skewness, m_kurtosis);
}
//+------------------------------------------------------------------+
//| ガウス分布プロパティ型                                              |
//+------------------------------------------------------------------+
enum ENUM_GAUSS_PROPERTY
{
   GAUSS_MEAN,       // 平均
   GAUSS_STDDEV,     // 分散
   GAUSS_SKEWNESS,   // 歪度
   GAUSS_KURTOSIS    // 尖度
};
 
input int                  BPeriod = 13;       // 期間
input ENUM_GAUSS_PROPERTY  Property;

double buff[];
CRiGaussProperty RiGauss;
//+------------------------------------------------------------------+
//| カスタム指標初期化関数                                              |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- 指標バッファマッピング
   SetIndexBuffer(0, buff, INDICATOR_DATA);
   RiGauss.SetMaxTotal(BPeriod);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| カスタム指標初期化関数                                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const int begin,
                const double &price[])
{
//---
   bool calc = false;
   for(int i = prev_calculated; i < rates_total; i++)
   {
      RiGauss.AddValue(price[i]);
      buff[i] = GetGaussValue(Property);
      calc = true;
   }
   if(!calc)
   {
      RiGauss.ChangeValue(BPeriod-1, price[rates_total-1]);
      buff[rates_total-1] = GetGaussValue(Property);
   }
   return(rates_total-1);
}
//+------------------------------------------------------------------+
//| ガウス分布のプロパティの値を取得する                                  |
//+------------------------------------------------------------------+
double GetGaussValue(ENUM_GAUSS_PROPERTY property)
{
   double value = EMPTY_VALUE;
   switch(Property)
   {
      case GAUSS_MEAN:
         value = RiGauss.Mean();
         break;
      case GAUSS_STDDEV:
         value = RiGauss.StdDev();
         break;
      case GAUSS_SKEWNESS:
         value = RiGauss.Skewness();
         break;
      case GAUSS_KURTOSIS:
         value = RiGauss.Kurtosis();
         break;    
   }
   return value;
}


上からわかるように、CRiGaussPropertyクラスは非常にシンプルですが、その中には豊富な機能が隠されています。CAlglib :: SampleMoments関数操作の各反復でスライディング配列を準備する必要はなくなり、代わりに、AddValueメソッドに新しい値を追加するだけとなります。下の図は、指標の操作結果を示しています。設定で標準偏差の計算を選択して、チャートのサブウィンドウにプロットしましょう。

‌

図6　スライディング指標の形でのガウス分布の主要パラメータ

 

リングプリミティブに基づいたMACDの構築

これまで、単純移動平均、指数移動平均、高/低指標の3つのリングプリミティブを開発してきました。これは、簡単な計算に基づいて主要な標準指標を構築するのには十分です。例えば、MACDは、2つの指数移動平均と、単純移動平均に基づく1つのシグナルラインからなります。すでに利用可能なコードを使用して指標を開発しましょう。

高/低指標を扱う場合、CRiMaxMinクラス内にはすでに2つの追加リングバッファが適用されています。MACDでも同じことをします。新しい値を追加するとき、クラスはそれを単に追加のバッファに転送し、それらの単純な差を計算します。差は第3のリングバッファに転送され、単純なSMAを計算するときに使用されます。これがMACDシグナルラインです。

//+------------------------------------------------------------------+
//|                                                   RingBuffer.mqh |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#include "RiBuffDbl.mqh"
#include "RiSMA.mqh"
#include "RiEMA.mqh"
//+------------------------------------------------------------------+
//| リングバッファで移動平均を計算する                                   |
//+------------------------------------------------------------------+
class CRiMACD
{
private:
   CRiEMA        m_slow_macd;    // 高速指数移動平均
   CRiEMA        m_fast_macd;    // 低速指数移動平均
   CRiSMA        m_signal_macd;  // シグナルライン
   double        m_delta;        // 高速EMAと低速EMAの差
public:
   double        Macd(void);
   double        Signal(void);
   void          ChangeLast(double new_value);
   void          SetFastPeriod(int period);
   void          SetSlowPeriod(int period);
   void          SetSignalPeriod(int period);
   void          AddValue(double value);
};
//+------------------------------------------------------------------+
//| MACDを再計算する                                                  |
//+------------------------------------------------------------------+
void CRiMACD::AddValue(double value)
{
   m_slow_macd.AddValue(value);
   m_fast_macd.AddValue(value);
   m_delta = m_slow_macd.EMA() - m_fast_macd.EMA();
   m_signal_macd.AddValue(m_delta);
}

//+------------------------------------------------------------------+
//| MACDを変更する                                                    |
//+------------------------------------------------------------------+
void CRiMACD::ChangeLast(double new_value)
{
   m_slow_macd.ChangeValue(m_slow_macd.GetTotal()-1, new_value);
   m_fast_macd.ChangeValue(m_fast_macd.GetMaxTotal()-1, new_value);
   m_delta = m_slow_macd.EMA() - m_fast_macd.EMA();
   m_signal_macd.ChangeValue(m_slow_macd.GetTotal()-1, m_delta);
}
//+------------------------------------------------------------------+
//| MACDヒストグラムを取得する                                          |
//+------------------------------------------------------------------+
double CRiMACD::Macd(void)
{
   return m_delta;
}
//+------------------------------------------------------------------+
//| シグナルラインを取得する                                            |
//+------------------------------------------------------------------+
double CRiMACD::Signal(void)
{
   return m_signal_macd.SMA();
}
//+------------------------------------------------------------------+
//| 高速期間を取得する                                                 |
//+------------------------------------------------------------------+
void CRiMACD::SetFastPeriod(int period)
{
   m_slow_macd.SetMaxTotal(period);
}
//+------------------------------------------------------------------+
//| 低速期間を取得する                                                 |
//+------------------------------------------------------------------+
void CRiMACD::SetSlowPeriod(int period)
{
   m_fast_macd.SetMaxTotal(period);
}
//+------------------------------------------------------------------+
//| シグナルライン期間を設定する                                        |
//+------------------------------------------------------------------+
void CRiMACD::SetSignalPeriod(int period)
{
   m_signal_macd.SetMaxTotal(period);
}

CRiMacdは独立したクラスなのでご注意ください。CRiBuffDblから派生したものではありません。実際、CRiMacdクラスは独自の計算バッファを使用しません。代わりに、リングプリミティブクラスは独立したオブジェクトとして"private"セクション（「包含」システム）に配置されます。

Macd()とSignal()の2つの主要メソッドは、MACDの値とシグナルラインの値を返します。結果のコードはシンプルで、各バッファにはスライド期間があります。CRiMacdクラスは、任意の要素の変更を追跡しません。代わりに、最後の要素の変化を追跡するだけで、ゼロバーで指標を変更します。

リングバッファで計算されたMACDは、標準指標と同じように見えます。

図7　リングバッファで計算されたMACD指標

リングプリミティブに基づいたストキャスティクスの構築

ストキャスティクスを同様の方法でプロットしましょう。この指標は、極値の検索と移動平均計算を組み合わせたものです。したがって、ここでは既に計算されたアルゴリズムを使用します。

ストキャスティクスには、高値（バーの高値）、安値（バーの低値）、終値（バーの終値）の3つの価格系列が適用されます。その計算は簡単です。まず、最高値と最低値の検索が実行されます。その後、現在の「終値」の高/低の範囲に対する比率が計算されます。最後に、この比率を使用してN個の期間の平均値を計算します（N指標は"K%減速"と呼ばれます）。

K% = SMA((close-min)/((max-min)*100.0%), N)

得られたK％について、%Dの期間（MACDと同様のシグナルライン）を有する別の平均が計算されます。

シグナルD% = SMA(K%, D%)

得られた2つの値（K％とそのシグナルD%）は、ストキャスティクスを表示します。

リングバッファ用のストキャスティクスのコードを書く前に、標準的な方法で実行されるコードを見てみましょう。このためには、Indicators\Examplesフォルダにある既成のStochastic.mq5を使用します。

//+------------------------------------------------------------------+
//| ストキャスティクス                                                 |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
   int i,k,start;
//--- バーの数を確認する
   if(rates_total<=InpKPeriod+InpDPeriod+InpSlowing)
      return(0);
//---
   start=InpKPeriod-1;
   if(start+1<prev_calculated) start=prev_calculated-2;
   else
     {
      for(i=0;i<start;i++)
        {
         ExtLowesBuffer[i]=0.0;
         ExtHighesBuffer[i]=0.0;
        }
     }
//--- HighesBuffer[]とExtHighesBuffer[]を計算する
   for(i=start;i<rates_total && !IsStopped();i++)
     {
      double dmin=1000000.0;
      double dmax=-1000000.0;
      for(k=i-InpKPeriod+1;k<=i;k++)
        {
         if(dmin>low[k])  dmin=low[k];
         if(dmax<high[k]) dmax=high[k];
        }
      ExtLowesBuffer[i]=dmin;
      ExtHighesBuffer[i]=dmax;
     }
//--- %K
   start=InpKPeriod-1+InpSlowing-1;
   if(start+1<prev_calculated) start=prev_calculated-2;
   else
     {
      for(i=0;i<start;i++) ExtMainBuffer[i]=0.0;
     }
//--- メインループ
   for(i=start;i<rates_total && !IsStopped();i++)
     {
      double sumlow=0.0;
      double sumhigh=0.0;
      for(k=(i-InpSlowing+1);k<=i;k++)
        {
         sumlow +=(close[k]-ExtLowesBuffer[k]);
         sumhigh+=(ExtHighesBuffer[k]-ExtLowesBuffer[k]);
        }
      if(sumhigh==0.0) ExtMainBuffer[i]=100.0;
      else             ExtMainBuffer[i]=sumlow/sumhigh*100;
     }
//--- シグナル
   start=InpDPeriod-1;
   if(start+1<prev_calculated) start=prev_calculated-2;
   else
     {
      for(i=0;i<start;i++) ExtSignalBuffer[i]=0.0;
     }
   for(i=start;i<rates_total && !IsStopped();i++)
     {
      double sum=0.0;
      for(k=0;k<InpDPeriod;k++) sum+=ExtMainBuffer[i-k];
      ExtSignalBuffer[i]=sum/InpDPeriod;
     }
//--- OnCalculate終了Get new prev_calculated.
   return(rates_total);
  }
//+------------------------------------------------------------------+

コードは単一のブロックに書かれており、8つの"for"ループ'を含んでいます。そのうち3つはネストされています。計算は2段階で実行されます。まず、高値と安値が計算され、2つの追加のバッファに配置されます。高値と安値の計算には二重の検索が必要です。Nの反復は各バーのネストされたforループで実行されます（NはK％の期間です）。

高値と安値の計算に続いてK％が計算されます。これにも二重ループが使用され、FがK％の減速期間である各バーで追加のF反復を実行します。 

これに続いて、D％シグナルラインが2回の 'for'検索を伴って計算され、各バーに対して追加のT繰り返し（T-D％平滑化期間）が必要とされます。

生成されたコードは十分に速く動作します。ここでの主な問題は、リングバッファがなければ、単純な計算をいくつかの独立した段階で実行する必要があるため、コードの可視性が低下し、コードがより複雑になるということです。

これを説明するために、CRiStochクラスの主要計算メソッドの内容を見てみましょう。これは上記のコードとまったく同じ機能を持っています。

//+------------------------------------------------------------------+
//| 新しい値を追加してストキャスティクスを計算する                         |
//+------------------------------------------------------------------+
void CRiStoch::AddValue(double close, double high, double low)
{
   m_max.AddValue(high);                     // 新しい最高値を追加する
   m_min.AddValue(low);                      // 新しい最低値を追加する
   double c = close;
   double max = m_max.MaxValue()             // 最高値を取得する
   double min = m_min.MinValue();            // 最低値を取得する
   double delta = max - min;
   double k = 0.0;
   if(delta != 0.0)
      k = (c-min)/delta*100.0;               // ストキャスティクス方程式を使ってK％を求める
   m_slowed_k.AddValue(k);                   // K%を平滑化する (K% 減速)
   m_slowed_d.AddValue(m_slowed_k.SMA());    // 平滑化されたK%から%Dを求める
}

このメソッドは中間計算には関係しません。代わりに、単にストキャスティクス方程式をすでに利用可能な値に適用します。移動平均と高/低という必要な値の検索は、リングプリミティブによって実行されます。

CRiStochメソッドの残りは、期間と適切な指標値を設定するGet/Setメソッドです。CRiStochのコード全体を以下に示します。

//+------------------------------------------------------------------+
//|                                                   RingBuffer.mqh |
//|                                 Copyright 2016, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#include "RiBuffDbl.mqh"
#include "RiSMA.mqh"
#include "RiMaxMin.mqh"
//+------------------------------------------------------------------+
//| ストキャスティクスクラス                                            |
//+------------------------------------------------------------------+
class CRiStoch
{
private:
   CRiMaxMin     m_max;          // 高/低指標
   CRiMaxMin     m_min;          // 高/低指標
   CRiSMA        m_slowed_k;     // K%平滑化
   CRiSMA        m_slowed_d;     // D%移動平均
public:
   void          ChangeLast(double new_value);
   void          AddValue(double close, double high, double low);
   void          AddHighValue(double value);
   void          AddLowValue(double value);
   void          AddCloseValue(double value);
   void          SetPeriodK(int period);
   void          SetPeriodD(int period);
   void          SetSlowedPeriodK(int period);
   double        GetStochK(void);
   double        GetStochD(void);
};
//+------------------------------------------------------------------+
//| 新しい値の追加とストキャスティクスの計算                              |
//+------------------------------------------------------------------+
void CRiStoch::AddValue(double close, double high, double low)
{
   m_max.AddValue(high);                     // 新しい最高値を追加する
   m_min.AddValue(low);                      // 新しい最低値を追加する
   double c = close;
   double max = m_max.MaxValue()
   double min = m_min.MinValue();
   double delta = max - min;
   double k = 0.0;
   if(delta != 0.0)
      k = (c-min)/delta*100.0;               // 方程式を使ってK％を求める
   m_slowed_k.AddValue(k);                   // K%を平滑化する (K%減速)
   m_slowed_d.AddValue(m_slowed_k.SMA());    // 平滑化されたK％から％Dを求める
}
//+------------------------------------------------------------------+
//| 高速期間を設定する                                                 |
//+------------------------------------------------------------------+
void CRiStoch::SetPeriodK(int period)
{
   m_max.SetMaxTotal(period);
   m_min.SetMaxTotal(period);
}
//+------------------------------------------------------------------+
//| 低速期間を設定する                                                 |
//+------------------------------------------------------------------+
void CRiStoch::SetSlowedPeriodK(int period)
{  
   m_slowed_k.SetMaxTotal(period);
}
//+------------------------------------------------------------------+
//| シグナルライン期間を設定する                                        |
//+------------------------------------------------------------------+
void CRiStoch::SetPeriodD(int period)
{  
   m_slowed_d.SetMaxTotal(period);
}
//+------------------------------------------------------------------+
//| %K値を取得する                                                     |
//+------------------------------------------------------------------+
double CRiStoch::GetStochK(void)
{
   return m_slowed_k.SMA();
}
//+------------------------------------------------------------------+
//| %D値を取得する                                                     |
//+------------------------------------------------------------------+
double CRiStoch::GetStochD(void)
{
   return m_slowed_d.SMA();
}

結果として生じるストキャスティクスは標準のものと変わりません。確認のために、対応する指標を標準のものと一緒にプロットします（指標と補助ファイルはすべて本稿に添付されています）。

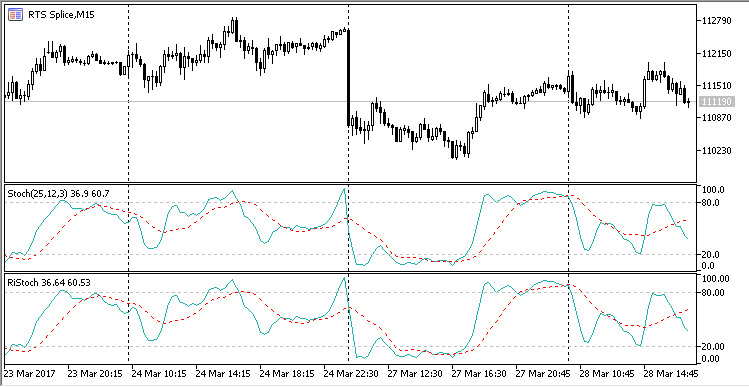
図8　標準およびリングストキャスティクス

メモリ使用量の最適化

指標を計算するには、特定の計算資源が必要です。いわゆるハンドルによるシステム指標の操作も例外ではありません。指標ハンドルとは、指標の内部計算ブロックおよびそのデータバッファへの特定のタイプのポインタです。ハンドルは単に64ビットの数なので、スペースをあまり占有しません。主なサイズはMetaTraderの「裏側」に隠されているので、新しいハンドルが作成されると、そのサイズよりも大きい一定量のメモリが割り当てられます。

また、指標値のコピーにも一定の時間がかかります。これは、EA内で指標値を計算するのに必要な時間を超えています。したがって、開発者は指標計算ブロックを直接EAで作成することを推奨しています。もちろん、常にEAコードに指標の計算を記述して標準指標を呼び出さないわけではありません。EAは指標の1つや2つ、5つも適用することがあります。ただし、EAの内部コードで直接計算を実行するのと比較して、その操作にはより多くのメモリと時間がかかることには留意されるべきです。

しかし、メモリと時間の最適化は避けられない場合もあります。これがリングバッファの出番です。初めの例は、複数の指標を適用するときでしょう。例えば、インフォメーションパネル（別名マーケットスキャナ）は、通常、一連の指標セットを適用するいくつかの銘柄と時間枠の市場の瞬間的な画像を提供します。これは、MetaTrader 5マーケットで見つかるパネルの1つです。

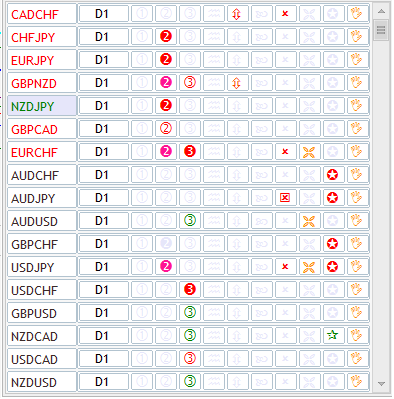
図8　複数の指標を適用するインフォメーションパネル


お分かりのように、ここでは17種類の製品が9種類のパラメータで分析されています。各パラメータはその指標によって表されます。つまり、「ほんの少数のアイコン」を表示するのにも17 * 9 = 153の指標が必要です。各銘柄の21時間枠をすべて分析するには、3213の指標が必要です。それらをすべて配置するには膨大なメモリが必要です。

メモリの割り当て方法を理解するために、特別な負荷テストをEAの形で作成しましょう。2つのオプションのみを使用して複数の指標値を計算します。

  1. 標準の指標を呼び出し、結果ハンドルを介してその値をコピーする
  2. リングバッファ内で指標を計算する

2番目の場合には指標は作成されません。すべての計算は、MACDとストキャスティクス2つのリング指標を使用してEA内部で実行されます。それぞれには、高速、標準、低速の3つの設定があります。指標は21時間枠で、EURUSD、GBPUSD、USDCHF、USDJPYの4つの銘柄で計算されます。計算された値の合計数を定義するのは簡単です。

合計値数 = 2指標 * 3パラメータセット * 4銘柄 * 21時間枠 = 504

このようなさまざまなアプローチを単一のEA内で使用できるように、補助コンテナクラスを作成してみましょう。アクセスされると、最後の指標値が表示されます。値は、使用される指標のタイプに応じて、さまざまな方法で計算されます。標準指標の場合、最後の値は指標のシステムハンドルであるCopyBuffer関数を使用して取得されます。リングバッファを適用する場合、値は対応するリング指標を使用して計算されます。

下記に、抽象クラスの形式のコンテナプロトタイプのソースコードを示します。

//+------------------------------------------------------------------+
//|                                                    RiIndLoad.mq5 |
//|                                 Copyright 2017, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#property version   "1.00"
#include <Arrays\ArrayObj.mqh>
#include "NewBarDetector.mqh"
//+------------------------------------------------------------------+
//| 作成された指標の型                                                 |
//+------------------------------------------------------------------+
enum ENUM_INDICATOR_TYPE
{
   INDICATOR_SYSTEM,       // システム指標
   INDICATOR_RIBUFF        // リングバッファ指標
};
//+------------------------------------------------------------------+
//| 指標コンテナ                                                       |
//+------------------------------------------------------------------+
class CIndBase : public CObject
{
protected:
   int         m_handle;               // 指標ハンドル
   string      m_symbol;               // 指標計算銘柄
   ENUM_INDICATOR_TYPE m_ind_type;     // 指標のタイプ
   ENUM_TIMEFRAMES m_period;           // 指標計算期間
   CBarDetector m_bar_detect;          // 新しいバーの検出
   CIndBase(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type);
public:
   string          Symbol(void){return m_symbol;}
   ENUM_TIMEFRAMES Period(void){return m_period;}
   virtual double  GetLastValue(int index_buffer);
};
//+------------------------------------------------------------------+
//| 保護されたコンストラクタでは、指標の銘柄、時間枠、時間を                |
//| 指定する必要があります                                              |
//+------------------------------------------------------------------+
CIndBase::CIndBase(string symbol,ENUM_TIMEFRAMES period,ENUM_INDICATOR_TYPE ind_type)
{
   m_handle = INVALID_HANDLE;
   m_symbol = symbol;
   m_period = period;
   m_ind_type = ind_type;
   m_bar_detect.Symbol(symbol);
   m_bar_detect.Timeframe(period);
}
//+------------------------------------------------------------------+
//| 指標の最終値を取得する                                              |
//+------------------------------------------------------------------+
double CIndBase::GetLastValue(int index_buffer)
{
   return EMPTY_VALUE;
}

これにはGetLastValue仮想メソッドが含まれます。このメソッドは、バッファ番号を受け取ってこのバッファの最後の指標値を返します。また、クラスには、基本的な指標プロパティ（ENUM_INDICATOR_TYPE）である時間枠、銘柄、計算タイプが含まれています。

CRiInMacdクラスとCRiStoch派生クラスを作成しましょう。両クラスは、適切な指標値を計算し、再定義されたGetLastValueメソッドを使用してそれらを返します。以下は、これらのクラスの1つであるCRiIndMacdのソースコードです。

//+------------------------------------------------------------------+
//|                                                    RiIndLoad.mq5 |
//|                                 Copyright 2017, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#property version   "1.00"
#include <RingBuffer\RiMACD.mqh>
#include "RiIndBase.mqh"
//+------------------------------------------------------------------+
//| 指標コンテナ                                                       |
//+------------------------------------------------------------------+
class CIndMacd : public CIndBase
{
private:
   CRiMACD        m_macd;                 // 指標リングバッファ
public:
                  CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period, int slow_period, int signal_period);
   virtual double GetLastValue(int index_buffer);
};
//+------------------------------------------------------------------+
//| MACD指標を作成する                                                 |
//+------------------------------------------------------------------+
CIndMacd::CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type,
                          int fast_period,int slow_period,int signal_period) : CIndBase(symbol, period, ind_type)
{
   if(ind_type == INDICATOR_SYSTEM)
   {
      m_handle = iMACD(m_symbol, m_period, fast_period, slow_period, signal_period, PRICE_CLOSE);
      if(m_handle == INVALID_HANDLE)
         printf("Create iMACD handle failed. Symbol: " + symbol + " Period: " + EnumToString(period));
   }
   else if(ind_type == INDICATOR_RIBUFF)
   {
      m_macd.SetFastPeriod(fast_period);
      m_macd.SetSlowPeriod(slow_period);
      m_macd.SetSignalPeriod(signal_period);
   }
} 
//+------------------------------------------------------------------+
//| 指標の最終値を取得する                                              |
//+------------------------------------------------------------------+
double CIndMacd::GetLastValue(int index_buffer)
{
   if(m_handle != INVALID_HANDLE)
   {
      double array[];
      if(CopyBuffer(m_handle, index_buffer, 1, 1, array) > 0)
         return array[0];
      return EMPTY_VALUE;
   }
   else
   {
      if(m_bar_detect.IsNewBar())
      {
         //printf("Received a new bar on " + m_symbol + " Period " + EnumToString(m_period));
         double close[];
         CopyClose(m_symbol, m_period, 1, 1, close);
         m_macd.AddValue(close[0]);
      }
      switch(index_buffer)
      {
         case 0: return m_macd.Macd();
         case 1: return m_macd.Signal();
      }
      return EMPTY_VALUE;
   }
}

ストキャスティクスを計算するためのコンテナクラスは同じ構造をしているので、ソースコードを表示するのは無意味です。 

テストを簡単にするために、指標値は新しいバーを開いたときにのみ計算されます。そのために、特殊なNewBarDetecterモジュールがCRiIndBase基本クラスに組み込まれています。このクラスは、新しいバーの開始を再定義し、IsNewBarメソッドによって"true"を返すことによってこれを通知します。

さて、テストEAコードを見てみましょう。これはTestIndEA.mq5と呼ばれます。

//+------------------------------------------------------------------+
//|                                                    TestIndEA.mq5 |
//|                                 Copyright 2017, Vasiliy Sokolov. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, Vasiliy Sokolov."
#property link      "http://www.mql5.com"
#property version   "1.00"
#include <Object.mqh>
#include <Arrays\ArrayObj.mqh>
#include "RiIndBase.mqh"
#include "RiIndMacd.mqh"
#include "RiIndStoch.mqh"
#include "NewBarDetector.mqh"
//+------------------------------------------------------------------+
//| MACDパラメータ                                                    |
//+------------------------------------------------------------------+
struct CMacdParams
{
   int slow_period;
   int fast_period;
   int signal_period;
};
//+------------------------------------------------------------------+
//| ストキャスティクスパラメータ                                         |
//+------------------------------------------------------------------+
struct CStochParams
{
   int k_period;
   int k_slowed;
   int d_period;
};

input ENUM_INDICATOR_TYPE IndType = INDICATOR_SYSTEM;    // 指標の種類

string         Symbols[] = {"EURUSD", "GBPUSD", "USDCHF", "USDJPY"};
CMacdParams    MacdParams[3];
CStochParams   StochParams[3];
CArrayObj      ArrayInd; 
//+------------------------------------------------------------------+
//| エクスパート初期化関数                                              |
//+------------------------------------------------------------------+
int OnInit()
{  
   MacdParams[0].fast_period = 3;
   MacdParams[0].slow_period = 13;
   MacdParams[0].signal_period = 6;
   
   MacdParams[1].fast_period = 9;
   MacdParams[1].slow_period = 26;
   MacdParams[1].signal_period = 12;
   
   MacdParams[2].fast_period = 18;
   MacdParams[2].slow_period = 52;
   MacdParams[2].signal_period = 24;
   
   StochParams[0].k_period = 6;
   StochParams[0].k_slowed = 3;
   StochParams[0].d_period = 3;
   
   StochParams[1].k_period = 12;
   StochParams[1].k_slowed = 5;
   StochParams[1].d_period = 6;
   
   StochParams[2].k_period = 24;
   StochParams[2].k_slowed = 7;
   StochParams[2].d_period = 12;
   // 504 MACDとストキャスティクスがここで作成される
   for(int symbol = 0; symbol < ArraySize(Symbols); symbol++)
   {
      for(int period = 1; period <=21; period++)
      {
         for(int i = 0; i < 3; i++)
         {
            CIndMacd* macd = new CIndMacd(Symbols[symbol], PeriodByIndex(period), IndType,
                                          MacdParams[i].fast_period, MacdParams[i].slow_period,
                                          MacdParams[i].signal_period);
            CIndStoch* stoch = new CIndStoch(Symbols[symbol], PeriodByIndex(period), IndType,
                                          StochParams[i].k_period, StochParams[i].k_slowed,
                                          StochParams[i].d_period);
            ArrayInd.Add(macd);
            ArrayInd.Add(stoch);
         }
      }
   }
   printf("Create " + (string)ArrayInd.Total() + " indicators sucessfully");
   return(INIT_SUCCEEDED);
}
//+------------------------------------------------------------------+
//| エクスパートティック関数                                            |
//+------------------------------------------------------------------+
void OnTick()
{
   for(int i = 0; i < ArrayInd.Total(); i++)
   {
      CIndBase* ind = ArrayInd.At(i);
      double value = ind.GetLastValue(0);
      double value_signal = ind.GetLastValue(1);
   }
}
//+------------------------------------------------------------------+
//| インデックスで時間枠を取得する                                       |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES PeriodByIndex(int index)
{
   switch(index)
   {
      case  0: return PERIOD_CURRENT;
      case  1: return PERIOD_M1;
      case  2: return PERIOD_M2;
      case  3: return PERIOD_M3;
      case  4: return PERIOD_M4;
      case  5: return PERIOD_M5;
      case  6: return PERIOD_M6;
      case  7: return PERIOD_M10;
      case  8: return PERIOD_M12;
      case  9: return PERIOD_M15;
      case 10: return PERIOD_M20;
      case 11: return PERIOD_M30;
      case 12: return PERIOD_H1;
      case 13: return PERIOD_H2;
      case 14: return PERIOD_H3;
      case 15: return PERIOD_H4;
      case 16: return PERIOD_H6;
      case 17: return PERIOD_H8;
      case 18: return PERIOD_H12;
      case 19: return PERIOD_D1;
      case 20: return PERIOD_W1;
      case 21: return PERIOD_MN1;
      default: return PERIOD_CURRENT;
   }
}
//+------------------------------------------------------------------+

主な機能はOnInitブロックにあります。そこでは、銘柄、時間枠、指標パラメータセットが並び替えられます。指標パラメータセットは、CMacdParamsおよびCStochParams補助構造に格納されます。 

値処理ブロックは、OnTick関数内にあって指標の共通の並び替えを表し、GetLastalue仮想メソッドを使用して最後の値を受け取ります。両指標には同じ量の計算バッファがあるため、追加のチェックは必要ありません。両指標値は、一般化されたGetLastValueメソッドを使用して取得できます。

EAの起動において、標準指標の呼び出しに基づく計算モードでは11.9GBのRAMが必要でしたが、リングプリミティブに基づく指標の計算モードでは必要なのは2.9GBでした。テストは、16 GBのRAMを搭載したPCで実行されました。

ただし、メモリは、リングバッファの使用によってではなく計算モジュールをEAコードに配置することによって節約されたことにご注意ください。このモジュールの配置によってすでに多量のメモリが節約されます。

メモリ消費量を四分の一に減らすということは、かなりいい結果です。とにかく、この上3GBのRAMを消費しなければなりません。消費量をさらに減らすことは可能でしょうか。可能です。時間枠の数を最適化するだけです。テストコードを少しだけ変更して、21時間枠（PERIOD_M1）の代わりに1時間枠（PERIOD_M1）を使用してみましょう。指標の数は変わりませんが、そのうちのいくつかは重複しています。

...
for(int symbol = 0; symbol < ArraySize(Symbols); symbol++)
   {
      for(int period = 1; period <=21; period++)
      {
         for(int i = 0; i < 3; i++)
         {
            CIndMacd* macd = new CIndMacd(Symbols[symbol], PERIOD_M1, IndType,
                                          MacdParams[i].fast_period, MacdParams[i].slow_period,
                                          MacdParams[i].signal_period);
            CIndStoch* stoch = new CIndStoch(Symbols[symbol], PERIOD_M1, IndType,
                                          StochParams[i].k_period, StochParams[i].k_slowed,
                                          StochParams[i].d_period);
            ArrayInd.Add(macd);
            ArrayInd.Add(stoch);
         }
      }
   }
...

この場合、504指標の内部計算モードは548MBのRAMを使用します。より正確に言えば、メモリは、指標自体ではなく、指標計算のためにダウンロードされたデータによって消費されます。端末自体の総容量は約100MBで、ダウンロードされるデータ量はさらに少なくなります。したがって、メモリ消費量を大幅に削減することができました。


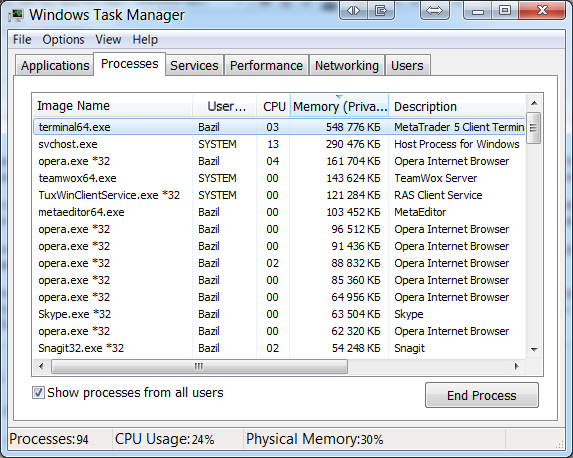
このモードでのシステム指標に基づく計算には、1.9GBのRAMが必要です。これは、21の時間枠のリスト全体を使用する場合に消費されるRAMの量に比べても大幅に少なくなります。

EAテスト時間の最適化

MetaTrader 5は、同時に複数の取引製品にアクセスすることができ、同時に各製品の任意の時間枠にアクセスすることもできます。これにより、マルチエキスパート（複数の銘柄で同時に取引する単一のEA）を作成してテストすることができます。取引環境へのアクセスには、特にこれらの商品に基づいて計算された指標のデータにアクセスする必要がある場合、時間がかかることがあります。アクセス時間は、すべての計算が1つのEA内で実行されると短縮できます。前の例をMetaTrader 5ストラテジーテスターでテストして説明しましょう。まず、「始値のみ」モードで、先月のEURUSD M1のEAをテストします。計算にはシステム指標を使用します。Intel Core i7 870 2.9GHzでのテストには58秒かかりました。

2017.03.30 14:07:12.223 Core 1EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:57.923.

さて、内部の計算モードで同じテストを実行しましょう。

2017.03.30 14:08:29.472Core 1EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:12.292.

お分かりのように、このモードでは計算は12秒しかかからず、計算時間が大幅に短縮されています。

パフォーマンス向上のための結論と示唆

指標を開発する際にメモリの使用をテストし、2つの動作モードでテスト速度を測定しました。リングバッファを使用した内部計算を使用すると、メモリ消費量を削減し、パフォーマンスを何度か向上させることができました。もちろん、提示された例は大部分人工的です。ほとんどのプログラマは、500指標を同時に作成してすべての可能な時間枠でテストする必要はありません。しかし、このような「ストレステスト」は、最もコストのかかるメカニズムを特定し、その使用を最小限に抑えるのに役立ちます。テスト結果に基づいたヒントをいくつか紹介します。

  • 指標計算ブロックをEAに配置する。これによって、テストに費やされた時間とRAMが節約される。
  • 可能であれば、複数の時間枠でデータを受信する要求は避ける。代わりに、計算に1つの（最低の）時間枠を使用する。たとえば、指標をM1とH1の2つで計算する必要がある場合は、M1データを受信してH1に変換し、H1での指標計算に適用する。このアプローチはより複雑であるが、メモリを大幅に節約する。
  • 計算資源を控えめに使用する。これにはリングバッファが適している。リングバッファは、指標を計算するために必要なだけのメモリを使用し、高値/安値の検索といったいくつかの計算アルゴリズムを最適化することができる。
  • 指標を操作するための汎用インタフェースを作成して、その値を受け取るのに使用する。指標計算を内部ブロックで実装することが困難な場合、インタフェースは外部MetaTrader指標を呼び出す。内部指標ブロックを作成する場合は、単に指標ブロックをそのインタフェースに接続する。その場合、EAの変更は最小限である。
  • 最適化機能を明確に評価する。1銘柄で1指標を使用する場合は、内部計算に変換せずにそのまま使用することができる。そのような変換に費やされた時間は、全体的なパフォーマンス向上を大幅に上回る可能性がある。

終わりに

本稿では、リングバッファーの開発と経済指標の構築への実用的な適用について述べてきました。リングバッファに最も直結した適用として、取引以外のものを考えることは困難です。これまでのところ、このデータ構築アルゴリズムはまだMQLコミュニティではカバーされていませんでした。

リングバッファとそれに基づいた指標はメモリを節約し、高速計算を提供します。リングバッファはほとんどがFIFO（先入れ先出し）の原則に従うため、その主な利点は、それらに基づく指標の実装が単純なことです。したがって、指標がリングバッファ内で計算されない i場合、問題が通常発生します。

説明されたソースコードのすべては、指標コード及び指標の基礎となる簡単なアルゴリズムとともに下記に提供されています。著者は、本稿がリング指標の完全、シンプル、高速、多用途なライブラリを開発するための出発点として役立つと確信しています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3047

添付されたファイル |
ZIPをダウンロード
RingBuffer.zip (22.88 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
クロスプラットフォームEA: シグナル クロスプラットフォームEA: シグナル
この記事では、クロスプラットフォームEAで使用される CSignal および CSignals クラスについて解説します。 MQL4 と MQL5 の違いについて、トレードシグナルの評価に必要なデータがどのようにアクセスされるかを調べ、記述されたコードが両方のコンパイラと互換性があることを確認します。
クロスプラットフォームEA: オーダーマネージャ クロスプラットフォームEA: オーダーマネージャ
この記事では、クロスプラットフォームEAのオーダーマネージャの作成について説明します。 オーダーマネージャは、EAによってエントリーされたオーダーと決済、および両方で独立した記録を保持します。
銘柄とEAのORDER_MAGICによるバランス/エクイティチャートの分析 銘柄とEAのORDER_MAGICによるバランス/エクイティチャートの分析
MetaTrader 5のヘッジ導入は、複数のエキスパートアドバイザーを1つの取引口座で同時に取引する絶好の機会を提供します。1つの戦略が利益を上げ、2番目の戦略が損失を生み出している場合、利益チャートはゼロに近い値を表示するかもしれません。この場合、各取引戦略のバランスチャートとエクイティチャートを別々に作成することが便利です。
ドンチャンチャネルを使った取引 ドンチャンチャネルを使った取引
本稿では、さまざまなフィルタを使用してドンチャンチャネルに基づいているいくつかの戦略を開発してテストします。それらの操作の比較分析も実行します。