
MQL5 酷宝典 - 创建的环形缓存用于快速计算滑动窗口中的指标
内容
- 概述
- 均线计算难题
- 环形缓存原理
- 工作原型
- 在环形缓存中计算简单均值的示例
- 在环形缓存中计算指数均值的示例
- 在环形缓存中计算最高价/最低价的示例
- 环形缓存与 AlgLib 函数库的集成
- 基于环形基元构建 MACD
- 基于环形基元构建随机振荡器
- 优化内存使用
- 优化专家交易系统测试时间
- 提高效能的结论和建议
- 结论
概述
交易者执行的大多数计算是在滑动窗口中进行的。这是由于行情数据的性质几乎总是连续流入, 无论我们是否处理价格、价格亦或交易量。典型地, 一位交易者需要计算某个时间段的数值。例如, 如果我们计算一条均线, 我们处理最后 N 根柱线的平均价格值, 其中 N 是移动平均周期。在此情况下, 计算平均值所花费的时间不应依赖于此平均周期。不过, 在真实条件中, 实现具有这种属性的算法并非总是容易的。从算法的角度来看, 当新的条到达时, 重新计算平均值要容易得多。环形缓存算法解决了计算的效率难题, 为计算模块提供一个滑动窗口, 使其内部计算保持简单且尽可能高效。
均线计算难题
我们来研究计算移动平均线。简单的算法可在绘制它的时候令我们能够描绘可能遇到的难题。均值的计算使用众所周知的方程:
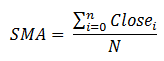
我们通过编写一个简单的 MQL5 脚本来实现它:
//+------------------------------------------------------------------+ //| SMA.mq5 | //| 版权所有 2015, MetaQuotes 软件公司 | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2015, MetaQuotes 软件公司" #property link "http://www.mql5.com" #property version "1.00" input int N = 10; // 移动均值周期 //+------------------------------------------------------------------+ //| 脚本程序的 start 函数 | //+------------------------------------------------------------------+ void OnStart() { //--- double closes[]; if(CopyClose(Symbol(), Period(), 0, N, closes)!= N) { printf("需要更多数据"); return; } double sum = 0.0; for(int i = 0; i < N; i++) sum += closes[i]; sum /= N; printf("SMA: " + DoubleToString(sum, Digits())); } //+------------------------------------------------------------------+
第一印象, 一切都看起来不错。脚本获取移动平均值, 并将其显示在终端窗口中。但在滑动窗口中工作时我们应如何做?最后的报价不断变化, 新的柱线不断出现。每次, 算法使用资源密集型的操作重新计算移动平均值:
- 将 N 个元素复制到目标数组;
- 在 'for' 循环中搜索全部目标数组。
最后的操作是最耗资源的。周期 10 需要 10 次迭代, 而周期 500 需要 500 次。这意味着算法的复杂性直接取决于平均周期, 并且可以写为 O(n), 此处 O 是复杂度函数。
然而, 在滑动窗口中计算移动平均值的算法要快得多。为了实现它, 我们需要知道上一次计算中所有数值的总和:
SMA = (所有数值总和 - 滑动窗口的第一个数值 + 新数值)/移动均线周期
算法复杂度函数是 O(1) 常量, 不依赖于平均周期。这种算法的性能更高, 但更难实现。每次新柱线出现时, 都应执行以下步骤:
- 减去当前总和中第一个添加的数值, 然后从序列中删除此数值;
- 将最后添加的数值计入当前总和中, 然后将此数值包含到该序列中;
- 将当前总和除以平均周期, 并将其作为移动平均值返回。
如果最后的数值没有被加入, 但只是被更新, 算法变得更加复杂:
- 定义更新的数值并记住其当前状态;
- 从当前总和中减去上一步记忆的数值;
- 用新的数替换值;
- 将新值添加到当前总和中;
- 将当前总和除以平均周期, 并将其作为移动平均值返回。
另一个挑战是 MQL5 (类似于大多数其它系统的编程语言) 已有的内置工具仅用于处理基本数据类型 (如数组)。未经适当修改的数组不适合这个角色, 因为在最明显的情况下, 我们需要排列一个 FIFO 队列 (先进先出), 即当出现新元素时, 从队列中删除第一个添加的元素。数组允许删除和添加元素。然而, 这些操作是相当资源密集型的, 因为每次均要为它们重新排布数组。
我们转到 环形缓存 以便避免这种困难, 实现真正有效的算法。
环形缓存原理
在使用环形缓存时, 您可以添加和删除元素, 而无需重新排布数组。如果我们假设数组中的元素数量总是维持常数 (这是滑动窗口中计算的情况), 则添加一个新元素之后则要删除一个旧的元素。因此, 元素的总数不会改变, 但是每次添加新元素时, 它们的索引都会发生变化。最后一个元素成为倒数第二个元素, 倒数第二个元素取代倒数第一个元素,而倒数第一个元素则永久离开队列。
此功能允许环形缓存基于常规数组。我们来创建一个基于常规数组的类:
class CRingBuffer { private: double m_array[]; };
假设我们的缓存只包含三个元素。在此情况下, 第一个元素将被添加到索引为 0 的数组单元中, 第二个元素将占用索引为 1 的单元, 而第三个元素将占用单元 2。如果我们添加第四个元素会发生什么?显然, 第一个元素将被删除。然后, 最适合第四个元素的位置就是第一个元素的地方, 它的索引将再次清零。如何计算这个索引?我们要应用特殊操作 '除法余数'。在 MQL5 中, 此操作由特殊百分比符号 % 表示。由于数字从零开始, 第四个元素将是队列中的第三个元素, 并且其位置索引将使用以下方程计算:
此处, 'total' 是缓存的大小总数。在我们的示例中, 三除以三没有余数。所以, 索引包含的余数等于零。后续元素将按照相同的规则进行放置: 添加元素的数量将除以数组中元素的数量。这个除法的余数将是回环缓存中的实际索引。以下是将前 8 个元素添加到维度为 3 的环形缓存时的索引条件计算:
0 % 3 = [0] 1 % 3 = [1] 2 % 3 = [2] 3 % 3 = [0] 4 % 3 = [1] 5 % 3 = [2] 6 % 3 = [0] 7 % 3 = [1]...
工作原型
现在, 我们对环形缓存有了很好的了解, 现在是开发工作原型的时候了。我们的环形缓存有三个基本功能:
- 添加一个新数值;
- 删除最后的数值;
- 修改任意索引处的数值。
后一种功能是实时操作时需要的, 比如当最后一根柱线处于正在形成状态, 且收盘价不断变化时。
另外, 我们的缓存有两个基本属性。它包含最大缓存大小和其内的当前元素数量。大部分时间里, 这些数值相匹配, 因为当元素填充整个缓存区时, 每个后续元素将覆盖最旧的元素。因此, 元素总数保持不变。然而, 在缓存区的初始填充期间, 这些属性的值将有所不同。元素的最大数量将是一个可变属性。用户能够增加或减少它。
最旧的元素将被自动删除而不需要用户明确的请求。这是一个有意的行为, 因为手动删除旧元素会使辅助统计的计算复杂化。
算法的最大复杂性在于计算内部缓存的实际索引, 内部缓存用于保存实际数值。例如, 如果用户请求索引为 0 的元素, 则元素所在的实际数值可能不同。当添加第 17 号元素到维度为 10 的环形存时, 零号元素可以位于索引 8 处, 而最后的 (第九号) 可以在索引 7 处。
我们来查看环形缓存的头文件和主要方法的内容, 看看环形缓存主要操作的工作:
//+------------------------------------------------------------------+ //| 双精度环形缓存 | //+------------------------------------------------------------------+ class CRiBuffDbl { private: bool m_full_buff; int m_max_total; int m_head_index; protected: double m_buffer[]; //用于直接访问的环形缓存。注意: 这些索引与它们的计数不匹配! ... int ToRealInd(int index); public: CRiBuffDbl(void); void AddValue(double value); void ChangeValue(int index, double new_value); double GetValue(int index); int GetTotal(void); int GetMaxTotal(void); void SetMaxTotal(int max_total); void ToArray(double& array[]); }; //+------------------------------------------------------------------+ //| 构造器 | //+------------------------------------------------------------------+ CRiBuffDbl::CRiBuffDbl(void) : m_full_buff(false), m_head_index(-1), m_max_total(0) { SetMaxTotal(3); } //+------------------------------------------------------------------+ //| 设置新的环形缓存大小 | //+------------------------------------------------------------------+ void CRiBuffDbl::SetMaxTotal(int max_total) { if(ArraySize(m_buffer) == max_total) return; m_max_total = ArrayResize(m_buffer, max_total); } //+------------------------------------------------------------------+ //| 获取环形缓存的实际大小 | //+------------------------------------------------------------------+ int CRiBuffDbl::GetMaxTotal(void) { return m_max_total; } //+------------------------------------------------------------------+ //| 获取索引值 | //+------------------------------------------------------------------+ double CRiBuffDbl::GetValue(int index) { return m_buffer[ToRealInd(index)]; } //+------------------------------------------------------------------+ //| 获取元素的总数 | //+------------------------------------------------------------------+ int CRiBuffDbl::GetTotal(void) { if(m_full_buff) return m_max_total; return m_head_index+1; } //+------------------------------------------------------------------+ //| 添加新元素至环形缓存 | //+------------------------------------------------------------------+ void CRiBuffDbl::AddValue(double value) { if(++m_head_index == m_max_total) { m_head_index = 0; m_full_buff = true; } //... m_buffer[m_head_index] = value; } //+------------------------------------------------------------------+ //| 用新的数值值替以前添加数值 | //+------------------------------------------------------------------+ void CRiBuffDbl::ChangeValue(int index, double value) { int r_index = ToRealInd(index); double prev_value = m_buffer[r_index]; m_buffer[r_index] = value; } //+------------------------------------------------------------------+ //| 将虚拟索引转换为真实索引 | //+------------------------------------------------------------------+ int CRiBuffDbl::ToRealInd(int index) { if(index >= GetTotal() || index < 0) return m_max_total; if(!m_full_buff) return index; int delta = (m_max_total-1) - m_head_index; if(index < delta) return m_max_total + (index - delta); return index - delta; }
这个类的基础是指向最后添加元素 m_head_index 的指针。当使用 AddValue 方法添加新元素时, 会递增一个。如果其值开始超过数组大小, 则会重置。
环形缓存最复杂的函数是内部的 ToRealInd 方法。它从用户的观点接收缓存索引, 并返回所需元素在数组的实际索引。
正如我们所见, 环形缓存非常简单。除了指针算术之外, 它支持添加新元素的基本动作, 并利用 GetValue() 提供对任意元素的访问。然而, 此功能通常用于方便地分配必要参数的计算, 如一般的移动平均, 或最高价/最低价的搜索算法。环形缓存允许您计算一组统计对象。这些都是各种指标或统计标准, 如方差和标准差。因此, 不可能一次向所有计算算法提供环形缓存类。实际上, 我们也不需要如此。代之, 我们可以应用更灵活的解决方案 –派生类 来实现特定的指标或统计计算算法。
为了让这些派生类便利地计算它们的类, 应该为环形缓存提供其它方法。我们称之为事件方法。 这些方法通常放在 'protected' 部分。所有这些方法都可以重新定义, 它们均以 On 开头:
//+------------------------------------------------------------------+ //| 双精度环形缓存 | //+------------------------------------------------------------------+ class CRiBuffDbl { private: ... protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double prev_value, double new_value); virtual void OnChangeArray(void); virtual void OnSetMaxTotal(int max_total); };
每次环形缓存有任何变化时, 都会调用一个方法来发出信号。例如, 如果缓存中出现一个新值, 则调用 OnAddValue 方法。其参数包含要添加的值。如果我们在环形缓存派生的类中重新定义此方法, 则每次添加新值时要调用适当的派生类计算模块。
环形缓存包含可以在派生类中监视的五个事件 (在括号中指定适当的方法):
- 添加一个新元素 (OnAddValue);
- 删除一个旧元素 (OnRemoveValue);
- 通过任意索引修改元素 (OnChangeValue);
- 修改整个环形缓存的内容 (OnChangeArray);
- 修改环形缓存内的最大元素数量 (OnSetMaxTotal).
应该特别注意 OnChangeArray 事件。当指标重新计算过程中需要访问整个累加值数组时调用它。在此情况下, 在派生类中重新定义方法就足够了。在此方法中, 我们需要使用 ToArray 函数获取整个数组的数值, 并进行适当的计算。这种计算的示例可在下面的环形缓存与 AlgLib 函数库的集成部分找到。
环形缓存类称为 CRiBuffDbl。顾名思义, 它适用于双精度数值。实数是计算算法中最常见的数据类型。然而, 除了实数之外, 我们也可能需要整数。因此, 类的集合里还包含 CRiBuffInt 类。在现今的 PC 上, 定点计算的执行速度比浮点数更快。这就是为什么对于特定的整数任务使用 CRiBuffInt 更好。
这里介绍的方法不适用于那些带有 <template T> 类型描述及操作的模板类。这样做是有意的, 因为假设特定的计算算法直接从回环缓存继承, 并且这种类型的每个算法都使用明确定义的数据类型。
在环形缓存中计算简单均值的示例
我们已研究了实现环形缓存原理的类的内部安排。现在是时候用我们的知识来解决一些实际问题。我们从一个简单的任务开始 - 开发一款著名的简单移动平均指标。这是一个常见的移动平均值, 意即我们需要将一个序列的合计除以平均周期。我们重复文章开头的计算公式:
SMA = (所有数值总和 - 滑动窗口的第一个数值 + 新数值)/移动均线周期
为了实现这个算法, 我们需要在派生自 CRiBuffDbl 的类中重新定义两个方法: OnAddValue 和 OnRemoveValue。平均值将在 Sma 方法中计算。以下是结果类的代码:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| 计算环形缓存中的移动平均值 | //+------------------------------------------------------------------+ class CRiSMA : public CRiBuffDbl { private: double m_sum; protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); public: CRiSMA(void); double SMA(void); }; CRiSMA::CRiSMA(void) : m_sum(0.0) { } //+------------------------------------------------------------------+ //| 递增总和 | //+------------------------------------------------------------------+ void CRiSMA::OnAddValue(double value) { m_sum += value; } //+------------------------------------------------------------------+ //| 递减总和 | //+------------------------------------------------------------------+ void CRiSMA::OnRemoveValue(double value) { m_sum -= value; } //+------------------------------------------------------------------+ //| 修改总和 | //+------------------------------------------------------------------+ void CRiSMA::OnChangeValue(int index,double del_value,double new_value) { m_sum -= del_value; m_sum += new_value; } //+------------------------------------------------------------------+ //| 返回简单移动均值 | //+------------------------------------------------------------------+ double CRiSMA::SMA(void) { return m_sum/GetTotal(); }
除了添加或删除元素 (分别为 OnAddValue 和 OnRemoveValue) 的方法之外, 我们还需要重新定义另一个在更改任意元素 (OnChangeValue) 时调用的方法。环形缓存支持所包含任何元素的任意修改, 因此这种修改应予以跟踪。通常, 只有最后一个元素被改变 (在最后一根柱线形成模式)。此情况由重新定义的 OnChangeValue 事件处理。
我们来利用环形缓存类编写一个自定义指标, 用于计算移动平均:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_chart_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiSMA.mqh> input int MaPeriod = 13; double buff[]; CRiSMA Sma; //+------------------------------------------------------------------+ //| 自定义指标初始化函数 | //+------------------------------------------------------------------+ int OnInit() { //--- 指标缓存映射 SetIndexBuffer(0, buff, INDICATOR_DATA); Sma.SetMaxTotal(MaPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| 自定义指标迭代函数 | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { Sma.AddValue(price[i]); buff[i] = Sma.SMA(); calc = true; } if(!calc) { Sma.ChangeValue(MaPeriod-1, price[rates_total-1]); buff[rates_total-1] = Sma.SMA(); } return(rates_total-1); } //+------------------------------------------------------------------+
在计算伊始, 指标只是将新的数值添加到移动平均的环形缓存当中。您不必控制添加值的数量。所有过时元素的计算和清除都会自动进行。如果在更改最后一根柱线的价格时调用此指标, 则最后一个移动平均值应由新数值替换。ChangeValue 方法为此负责。
指标的图形显示与标准版移动平均值等效:
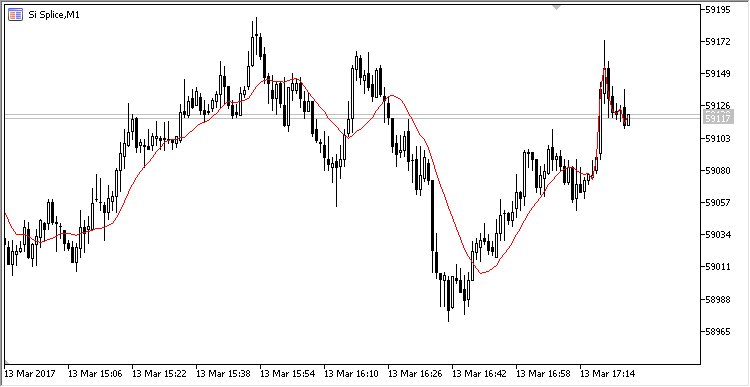
图例. 1. 在环形缓存中计算的简单移动平均值
在环形缓存中计算指数均值的示例
我们来尝试更复杂的情况 – 指数移动平均的计算。与简单平均值不同, 指数不受缓存中删除的旧元素的影响, 因此我们需要重新定义两个方法 (OnAddValue 和 OnChangeValue) 来计算它。与前面的例子类似, 我们来创建一个派生自 CRiBuffDbl 的 CRiMEA 类, 并重新定义适当的方法:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| 计算环形缓存中的指数移动平均值 | //+------------------------------------------------------------------+ class CRiEMA : public CRiBuffDbl { private: double m_prev_ema; // 前一个 EMA 数值 double m_last_value; // 最后的价格值 double m_smoth_factor; // 平滑因子 bool m_calc_first_v; // 计算第一个数值的指示标志 double CalcEma(); // 直接平均计算 protected: virtual void OnAddValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiEMA(void); double EMA(void); }; //+------------------------------------------------------------------+ //| 订阅数值增加/更改通知 | //+------------------------------------------------------------------+ CRiEMA::CRiEMA(void) : m_prev_ema(EMPTY_VALUE), m_last_value(EMPTY_VALUE), m_calc_first_v(false) { } //+------------------------------------------------------------------+ //| 根据 MetaQuotes EMA 方程计算平滑因子 | //+------------------------------------------------------------------+ void CRiEMA::OnSetMaxTotal(int max_total) { m_smoth_factor = 2.0/(1.0+max_total); } //+------------------------------------------------------------------+ //| 总和递加 | //+------------------------------------------------------------------+ void CRiEMA::OnAddValue(double value) { //计算前一个 EMA 值 if(m_prev_ema != EMPTY_VALUE) m_prev_ema = CalcEma(); //保存当前价格 m_last_value = value; } //+------------------------------------------------------------------+ //| 调整 EMA | //+------------------------------------------------------------------+ void CRiEMA::OnChangeValue(int index,double del_value,double new_value) { if(index != GetMaxTotal()-1) return; m_last_value = new_value; } //+------------------------------------------------------------------+ //| 直接 EMA 计算 | //+------------------------------------------------------------------+ double CRiEMA::CalcEma(void) { return m_last_value*m_smoth_factor+m_prev_ema*(1.0-m_smoth_factor); } //+------------------------------------------------------------------+ //| 获取简单移动均值 | //+------------------------------------------------------------------+ double CRiEMA::EMA(void) { if(m_calc_first_v) return CalcEma(); else { m_prev_ema = m_last_value; m_calc_first_v = true; } return m_prev_ema; }
CalcEma 方法负责计算移动平均值。它返回两个乘积之和: 最后已知的前一个值乘以平滑因子, 加上前一个指标值乘以平滑因子的倒数。如果指标的前值尚未计算, 则将取用缓存中放置的第一个数值 (在本例中为零号柱线的收盘价格)。
我们来开发一款类似于上一节的指标, 在图表上显示计算。它将如下所示:
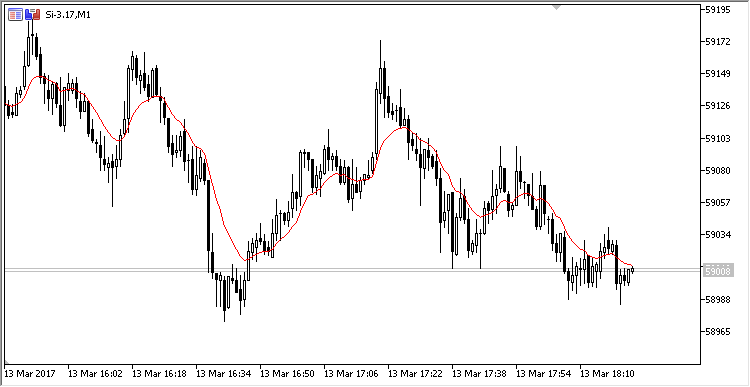
图例. 2. 在环形缓存中计算指数移动平均值
在环形缓存中计算最高价/最低价的示例
最具挑战性并令人兴奋的任务是在滑动窗口中计算最高价和最低价。当然, 这可以通过简单地引入 ArrayMaximum 和 ArrayMinimum 标准函数来轻松地完成。不过, 在此情况下, 在滑动窗口中进行计算的所有优点都消失了。如果在缓存中依次添加和删除数据, 则可以在不执行完整搜索的情况下计算出最高和最低价。假设在每次添加新数值到缓存时计算两个附加值。第一个指定有多少以前的元素低于当前元素, 而第二个元素则表示有多少以前的元素高于当前元素。第一个数值用于高效搜索最高价, 而第二个数值用于搜索最低价。
现在, 想象一下我们正在处理正常的价格柱线, 我们需要在某段时间内依据最高价来计算极值价格。为此, 让我们在每根柱线上面添加一个标签, 其中包含以前的最高价低于当前柱线最高价的柱线数量。柱线顺序如下图所示:
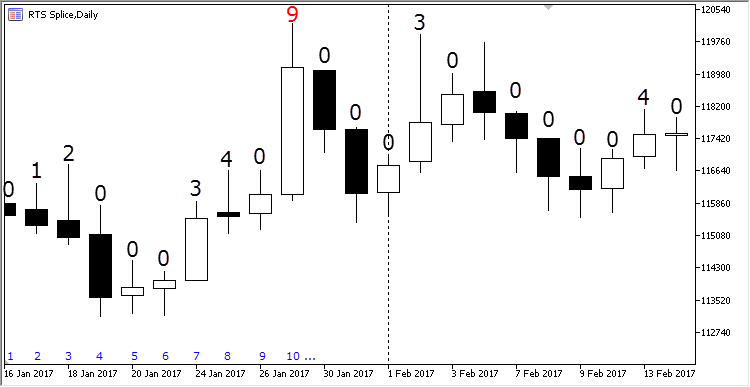
图例. 3. 柱线的极值点等级
第一根柱线总是具有零极值, 因为没有以前的数值来检查。柱线 #2 高于它。所以, 其极值指数是一。第三根柱线高于前一根, 意即它也在第一根柱线之上。其极值为二。它随后的三根柱线, 每根柱线都比前一根低。所有这些都低于柱线 #3, 因此它们的极值为零。第七根柱线高于前三根, 但低于第四根, 因此其极值指数为三。类似地, 当每次添加新柱线时, 为每根新的柱线计算极值指数。
当所有以前的指数都已计算完毕时, 我们可以很轻易地获得当前柱线的极值点。要做到这一点, 我们应简单地将柱线的极值点与其它点进行比较。我们可以连续跳过几根柱线, 直接访问每个后续的极值点, 因为我们知道它的索引, 感谢所显示的数字。整个过程如下所示:
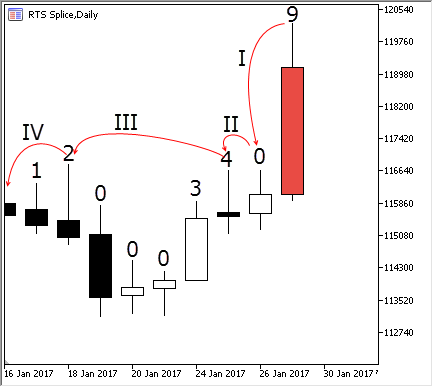
图例. 4. 寻找当前柱线的极值点
假设我们添加一根标记为红色的柱线。这根柱线带有数字 9, 因为编号从零开始。为了定义其极值指数, 我们通过执行步骤 I 将其与柱线 #8 进行比较: 这根柱线变得更高, 因此它的极值点等于 1。我们完成步骤 II 将它与 #7 号柱线进行比较 — 事实证明它也较高。由于柱线 #7 高于前四根, 我们可以在完成步骤 III 后, 立即将最后一根柱线与柱线 #3 进行比较。柱线 #9 高于柱线 #3, 所以高于目前所有的柱线。由于以前已计算的指数, 我们避免了与四个中间柱线的比较, 这些中间柱线肯定低于当前的。这就是在环形缓存中如何快速搜索极值。搜索最低价的工作方式与此相同。唯一的区别是附带的最低价指数的用法。
现在已经描述了算法, 我们来测验它的源代码。所呈现的类是很有趣的, 因为 CRiBuffInt 类型的两个缓存也用作辅助缓存。它们分别包含最高价和最低价指数。
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiBuffInt.mqh" //+------------------------------------------------------------------+ //| 计算环形存中的指数移动平均值 | //+------------------------------------------------------------------+ class CRiMaxMin : public CRiBuffDbl { private: CRiBuffInt m_max; CRiBuffInt m_min; bool m_full; int m_max_ind; int m_min_ind; protected: virtual void OnAddValue(double value); virtual void OnCalcValue(int index); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiMaxMin(void); int MaxIndex(int max_period = 0); int MinIndex(int min_period = 0); double MaxValue(int max_period = 0); double MinValue(int min_period = 0); void GetMaxIndexes(int& array[]); void GetMinIndexes(int& array[]); }; CRiMaxMin::CRiMaxMin(void) { m_full = false; m_max_ind = 0; m_min_ind = 0; } void CRiMaxMin::GetMaxIndexes(int& array[]) { m_max.ToArray(array); } void CRiMaxMin::GetMinIndexes(int& array[]) { m_min.ToArray(array); } //+------------------------------------------------------------------+ //| 依据主要缓存的新尺寸 | //| 修改内部缓存的尺寸 | //+------------------------------------------------------------------+ void CRiMaxMin::OnSetMaxTotal(int max_total) { m_max.SetMaxTotal(max_total); m_min.SetMaxTotal(max_total); } //+------------------------------------------------------------------+ //| 计算最大/最小指数 | //+------------------------------------------------------------------+ void CRiMaxMin::OnAddValue(double value) { m_max_ind--; m_min_ind--; int last = GetTotal()-1; if(m_max_ind > 0 && value >= GetValue(m_max_ind)) m_max_ind = last; if(m_min_ind > 0 && value <= GetValue(m_min_ind)) m_min_ind = last; OnCalcValue(last); } //+------------------------------------------------------------------+ //| 计算最大/最小指数 | //+------------------------------------------------------------------+ void CRiMaxMin::OnCalcValue(int index) { int max = 0, min = 0; int offset = m_full ?1 : 0; double value = GetValue(index); int p_ind = index-1; //搜索最高价 while(p_ind >= 0 && value >= GetValue(p_ind)) { int extr = m_max.GetValue(p_ind+offset); max += extr + 1; p_ind = GetTotal() - 1 - max - 1; } p_ind = GetTotal()-2; //搜索最低价 while(p_ind >= 0 && value <= GetValue(p_ind)) { int extr = m_min.GetValue(p_ind+offset); min += extr + 1; p_ind = GetTotal() - 1 - min - 1; } m_max.AddValue(max); m_min.AddValue(min); if(!m_full && GetTotal() == GetMaxTotal()) m_full = true; } //+------------------------------------------------------------------+ //| 修改任意位置的数值之后 | //| 重新计算最高价/最低价指数 | //+------------------------------------------------------------------+ void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value) { if(m_max_ind >= 0 && new_value >= GetValue(m_max_ind)) m_max_ind = index; if(m_min_ind >= 0 && new_value >= GetValue(m_min_ind)) m_min_ind = index; for(int i = index; i < GetTotal(); i++) OnCalcValue(i); } //+------------------------------------------------------------------+ //| 获取最大元素索引 | //+------------------------------------------------------------------+ int CRiMaxMin::MaxIndex(int max_period = 0) { int limit = 0; if(max_period > 0 && max_period <= m_max.GetTotal()) { m_max_ind = -1; limit = m_max.GetTotal() - max_period; } if(m_max_ind >=0) return m_max_ind; int c_max = m_max.GetTotal()-1; while(c_max > limit) { int ext = m_max.GetValue(c_max); if((c_max - ext) <= limit) return c_max; c_max = c_max - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| 获取最小元素索引 | //+------------------------------------------------------------------+ int CRiMaxMin::MinIndex(int min_period = 0) { int limit = 0; if(min_period > 0 && min_period <= m_min.GetTotal()) { limit = m_min.GetTotal() - min_period; m_min_ind = -1; } if(m_min_ind >=0) return m_min_ind; int c_min = m_min.GetTotal()-1; while(c_min > limit) { int ext = m_min.GetValue(c_min); if((c_min - ext) <= limit) return c_min; c_min = c_min - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| 获取最大元素值 | //+------------------------------------------------------------------+ double CRiMaxMin::MaxValue(int max_period = 0) { return GetValue(MaxIndex(max_period)); } //+------------------------------------------------------------------+ //| 获取最小元素值 | //+------------------------------------------------------------------+ double CRiMaxMin::MinValue(int min_period = 0) { return GetValue(MinIndex(min_period)); }
算法还包含一处修改。它记忆当前的最高价和最低价, 如果它们保持不变, MaxValue 和 MinValue 方法会将它们返回, 从而绕过额外的计算。
这是最高价和最低价在图表上的模样:
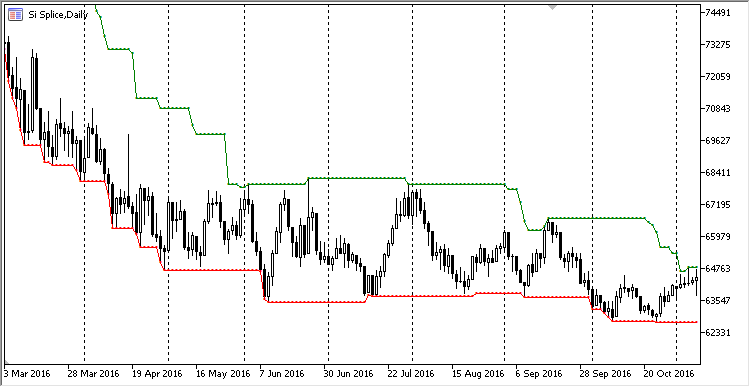
图例. 5. 最高价/最低价的通道作为指标
最高价/最低价所定义的类具有高级能力。它可以返回环形缓存中的极值索引或其值。此外, 能够计算小于环形缓存周期的区间极限值。为此, 请在 MaxIndex/MinIndex 和 MaxValue/MinValue 方法中指定限制周期。
环形缓存与 AlgLib 函数库的集成
另一个使用环形缓存的有趣的示例在于专门的数学计算领域。通常, 开发统计计算的算法不用考虑滑动窗口。这可能会造成不便。环形缓存解决了这个难题。我们来开发计算主要高斯分布参数的指标:
- 平均值 (Mean);
- 标准偏离 (StdDev);
- 钟形非对称分布 (Skewness);
- 峰度。
我们应用 AlgLib::SampleMoments 静态方法来计算这些特征。我们所要做的一切就是创建 CRIGaussProperty 环形缓存类, 并在 OnChangeArray 处理器中放置一个方法。包括在类中的完整指标代码:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiBuffDbl.mqh> #include <Math\AlgLib\AlgLib.mqh> //+------------------------------------------------------------------+ //| 计算高斯分布的主要参数 | //+------------------------------------------------------------------+ class CRiGaussProperty : public CRiBuffDbl { private: double m_mean; // 均值 double m_variance; // 方差 double m_skewness; // 偏态 double m_kurtosis; // 峰度 protected: virtual void OnChangeArray(void); public: double Mean(void){ return m_mean;} double StdDev(void){return MathSqrt(m_variance);} double Skewness(void){return m_skewness;} double Kurtosis(void){return m_kurtosis;} }; //+------------------------------------------------------------------+ //| 数组产生任何变化的情况下执行计算 | //+------------------------------------------------------------------+ void CRiGaussProperty::OnChangeArray(void) { double array[]; ToArray(array); CAlglib::SampleMoments(array, m_mean, m_variance, m_skewness, m_kurtosis); } //+------------------------------------------------------------------+ //| 高斯分布属性类型 | //+------------------------------------------------------------------+ enum ENUM_GAUSS_PROPERTY { GAUSS_MEAN, // 均值 GAUSS_STDDEV, // 方差 GAUSS_SKEWNESS, // 偏态 GAUSS_KURTOSIS // 峰度 }; input int BPeriod = 13; //周期 input ENUM_GAUSS_PROPERTY Property; double buff[]; CRiGaussProperty RiGauss; //+------------------------------------------------------------------+ //| 自定义指标初始化函数 | //+------------------------------------------------------------------+ int OnInit() { //--- 指标缓存映射 SetIndexBuffer(0, buff, INDICATOR_DATA); RiGauss.SetMaxTotal(BPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| 自定义指标迭代函数 | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { RiGauss.AddValue(price[i]); buff[i] = GetGaussValue(Property); calc = true; } if(!calc) { RiGauss.ChangeValue(BPeriod-1, price[rates_total-1]); buff[rates_total-1] = GetGaussValue(Property); } return(rates_total-1); } //+------------------------------------------------------------------+ //| 获取高斯分布属性之一的值 | //+------------------------------------------------------------------+ double GetGaussValue(ENUM_GAUSS_PROPERTY property) { double value = EMPTY_VALUE; switch(Property) { case GAUSS_MEAN: value = RiGauss.Mean(); break; case GAUSS_STDDEV: value = RiGauss.StdDev(); break; case GAUSS_SKEWNESS: value = RiGauss.Skewness(); break; case GAUSS_KURTOSIS: value = RiGauss.Kurtosis(); break; } return value; }
正如您从上面的列表中所见, CRiGaussProperty 类非常简单。然而, 这种简单性掩盖了丰富的功能。现在, 您不需要在 CAlglib::SampleMoments 函数操作的每次迭代中准备一个滑动数组。代之, 只需在 AddValue 方法中添加新值即可。下图显示了指标的操作结果。我们在设置中选择标准偏差的计算, 并将其绘制在图表子窗口中:
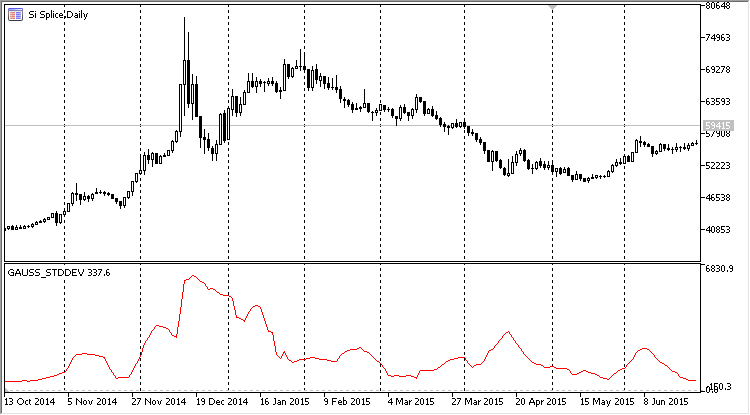
图例. 6. 滑动指标形式的主要高斯分布参数
基于环形基元构建 MACD
我们已经开发出三种环形基元: 简单和指数移动平均线以及最高价/最低价指标。它们足以根据简单的计算构建主要的标准指标。例如, MACD 由两条指数移动平均线和一条基于简单平均线的信号线组成。我们尝试使用已提供的代码开发此指标。
We have already applied two additional ring buffers within the CRiMaxMin class when dealing with the High/Low indicator. 在 MACD 的情况下我们要做的也一样。当添加新值时, 我们的类简单地将其转发到其附加的缓存中并简单计算它们之间的差值。差值转发到第三个环形缓存, 并在计算 SMA 时使用。这是 MACD 信号线:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiEMA.mqh" //+------------------------------------------------------------------+ //| 计算环形缓存中的移动平均值 | //+------------------------------------------------------------------+ class CRiMACD { private: CRiEMA m_slow_macd; // 快速指数均线 CRiEMA m_fast_macd; // 慢速指数均线 CRiSMA m_signal_macd; // 信号线 double m_delta; // 快速和慢速 EMA 之间的差值 public: double Macd(void); double Signal(void); void ChangeLast(double new_value); void SetFastPeriod(int period); void SetSlowPeriod(int period); void SetSignalPeriod(int period); void AddValue(double value); }; //+------------------------------------------------------------------+ //| 重新计算 MACD | //+------------------------------------------------------------------+ void CRiMACD::AddValue(double value) { m_slow_macd.AddValue(value); m_fast_macd.AddValue(value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.AddValue(m_delta); } //+------------------------------------------------------------------+ //| 修改 MACD | //+------------------------------------------------------------------+ void CRiMACD::ChangeLast(double new_value) { m_slow_macd.ChangeValue(m_slow_macd.GetTotal()-1, new_value); m_fast_macd.ChangeValue(m_fast_macd.GetMaxTotal()-1, new_value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.ChangeValue(m_slow_macd.GetTotal()-1, m_delta); } //+------------------------------------------------------------------+ //| 获取 MACD 直方图 | //+------------------------------------------------------------------+ double CRiMACD::Macd(void) { return m_delta; } //+------------------------------------------------------------------+ //| 获取信号线 | //+------------------------------------------------------------------+ double CRiMACD::Signal(void) { return m_signal_macd.SMA(); } //+------------------------------------------------------------------+ //| 设置快速周期 | //+------------------------------------------------------------------+ void CRiMACD::SetFastPeriod(int period) { m_slow_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| 设置慢速周期 | //+------------------------------------------------------------------+ void CRiMACD::SetSlowPeriod(int period) { m_fast_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| 设置信号线周期 | //+------------------------------------------------------------------+ void CRiMACD::SetSignalPeriod(int period) { m_signal_macd.SetMaxTotal(period); }
请注意, CRiMacd 是一个独立的类。它并非从 CRiBuffDbl 派生的。实际上, CRiMacd 类不会用到自身的计算缓存。取而代之, 环形基元类被放置在 "private" 部分 ("inclusion" 系统) 中的独立对象。
两个主要方法 Macd() 和 Signal() 返回 MACD 及其信号线数值。结果代码很简单, 每个缓存都有滑动周期。CRiMacd 类不会跟踪任何元素的变化。反而, 它仅在指标零号柱线上跟踪最后一个元素中的变化。
在环形缓存中计算出的 MACD 视觉上与标准版指标相同:
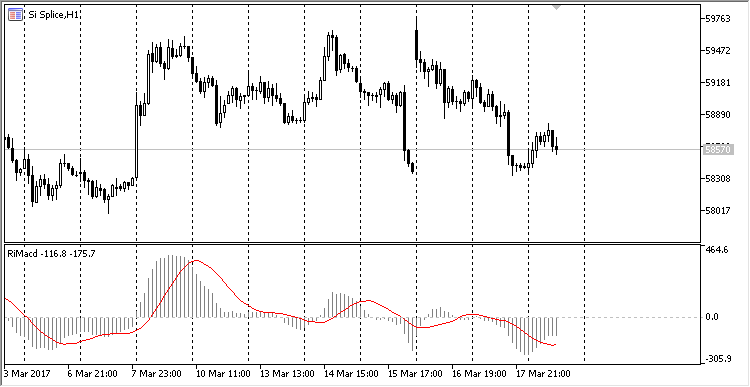
图例. 7. 在环形缓存中计算的 MACD 指标
基于环形基元构建随机振荡器
我们以类似的方式绘制随机振荡指标。指标将极值搜索与移动平均计算结合起来。因此, 我们在此使用已计算的算法。
随机振荡应用三个价格系列: 最高价 (柱线最高价), 最低价 (柱线最低价) 和收盘价 (柱线收盘价)。其计算很简单: 首先, 搜索最高价的最高值, 以及最低价的最低值。之后计算当前 "收盘" 价格与最高价/最低价的比率。最后, 此比率用于计算 N 个周期的平均值 (参数 N 称为 "K% 慢速"):
K% = SMA((收盘价-最小价)/((最大价-最小价)*100.0%), N)
对于所获得的 K%, 还要计算另一条 %D 周期的均线 (类似于 MACD 的信号线):
信号 D% = SMA(K%, D%)
两个结果值 — K% 和其信号 D% — 显示随机振荡指标。
在编写环形缓存的随机振荡代码之前, 我们来看看它的标准方式执行的代码。为此, 我们将使用来自 Indicators\Examples 文件夹的现成例程 Stochastic.mq5:
//+------------------------------------------------------------------+ //| 随机振荡器 | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,k,start; //--- 检查柱线计数 if(rates_total<=InpKPeriod+InpDPeriod+InpSlowing) return(0); //--- start=InpKPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) { ExtLowesBuffer[i]=0.0; ExtHighesBuffer[i]=0.0; } } //--- 计算 HighesBuffer[] 和 ExtHighesBuffer[] for(i=start;i<rates_total && !IsStopped();i++) { double dmin=1000000.0; double dmax=-1000000.0; for(k=i-InpKPeriod+1;k<=i;k++) { if(dmin>low[k]) dmin=low[k]; if(dmax<high[k]) dmax=high[k]; } ExtLowesBuffer[i]=dmin; ExtHighesBuffer[i]=dmax; } //--- %K start=InpKPeriod-1+InpSlowing-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtMainBuffer[i]=0.0; } //--- 主要循环 for(i=start;i<rates_total && !IsStopped();i++) { double sumlow=0.0; double sumhigh=0.0; for(k=(i-InpSlowing+1);k<=i;k++) { sumlow +=(close[k]-ExtLowesBuffer[k]); sumhigh+=(ExtHighesBuffer[k]-ExtLowesBuffer[k]); } if(sumhigh==0.0) ExtMainBuffer[i]=100.0; else ExtMainBuffer[i]=sumlow/sumhigh*100; } //--- 信号 start=InpDPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtSignalBuffer[i]=0.0; } for(i=start;i<rates_total && !IsStopped();i++) { double sum=0.0; for(k=0;k<InpDPeriod;k++) sum+=ExtMainBuffer[i-k]; ExtSignalBuffer[i]=sum/InpDPeriod; } //--- OnCalculate 完成。获得新的 prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
所编写的代码写在一个单独的模块中, 且包含 8 个 'for' 循环。它们当中的三个是嵌套的。计算分两个阶段执行: 首先, 计算最高价和最低价, 并将它们的数值放置到两个附加缓存区中。计算最高价和最低价需要双重搜索: 在每根柱线上的嵌套 'for' 循环中执行额外的 N 次迭代, 其中 N 是 K% 周期。
计算最高价和最低价之后是计算 K%, 在此期间再次使用双循环。它在每根柱线上执行额外的 F 次迭代, 其中 F 是 K% 慢速周期。
随后用双重 "搜索" 计算 D% 信号线, 其中每根柱线都需要额外的 T 次迭代 (T — D% 平滑周期)。
结果代码的工作速度足够快。这里的主要难题是, 没有环形缓存, 必须在几个独立的阶段执行简单的计算, 这会降低代码的可见性, 使其更加复杂。
为了描绘这一点, 我们来看看 CRiStoch 类中主要计算方法的内容。它与上面发布的代码具有完全相同的功能:
//+------------------------------------------------------------------+ //| 添加新值并计算随机振荡 | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // 添加新的最高价数值 m_min.AddValue(low); // 添加新的最低价数值 double c = close; double max = m_max.MaxValue() // 获取最高价 double min = m_min.MinValue(); // 获取最低价 double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // 使用随机振荡方程搜索 K% m_slowed_k.AddValue(k); // 平滑 K% (K% 慢速) m_slowed_d.AddValue(m_slowed_k.SMA()); // 从平滑的 K% 中搜索 %D }
此方法不涉及中间计算。取而代之, 它只是将随机振荡方程应用于已提供的数值。通过环形基元执行必要的数值搜索: 移动平均线并搜索最高价/最低价。
其余的 CRiStoch 方法是用于设置周期和相应指标值的 Get/Set 方法。完整的 CRiStoch 代码如下所示:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| 版权所有 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiMaxMin.mqh" //+------------------------------------------------------------------+ //| 随机振荡指标类 | //+------------------------------------------------------------------+ class CRiStoch { private: CRiMaxMin m_max; // 最高价指标 CRiMaxMin m_min; // 最低价指标 CRiSMA m_slowed_k; // K% 平滑 CRiSMA m_slowed_d; // D% 移动均线 public: void ChangeLast(double new_value); void AddValue(double close, double high, double low); void AddHighValue(double value); void AddLowValue(double value); void AddCloseValue(double value); void SetPeriodK(int period); void SetPeriodD(int period); void SetSlowedPeriodK(int period); double GetStochK(void); double GetStochD(void); }; //+------------------------------------------------------------------+ //| 添加新值并计算随机振荡 | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // 添加新的最高价 m_min.AddValue(low); // 添加新的最低价 double c = close; double max = m_max.MaxValue() double min = m_min.MinValue(); double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // 使用方程搜索 K% m_slowed_k.AddValue(k); // 平滑 K% (K% 慢速) m_slowed_d.AddValue(m_slowed_k.SMA()); // 从平滑的 K% 中搜索 %D } //+------------------------------------------------------------------+ //| 设置快速周期 | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodK(int period) { m_max.SetMaxTotal(period); m_min.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| 设置慢速周期 | //+------------------------------------------------------------------+ void CRiStoch::SetSlowedPeriodK(int period) { m_slowed_k.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| 设置信号线周期 | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodD(int period) { m_slowed_d.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| 获取 %K 数值 | //+------------------------------------------------------------------+ double CRiStoch::GetStochK(void) { return m_slowed_k.SMA(); } //+------------------------------------------------------------------+ //| 获取 %D 数值 | //+------------------------------------------------------------------+ double CRiStoch::GetStochD(void) { return m_slowed_d.SMA(); }
所得到的随机振荡指标与其标准版对照没有不同。您可以通过将相应的指标与标准版并排绘制 (所有指标和辅助文件都在本文中附带) 来检查:
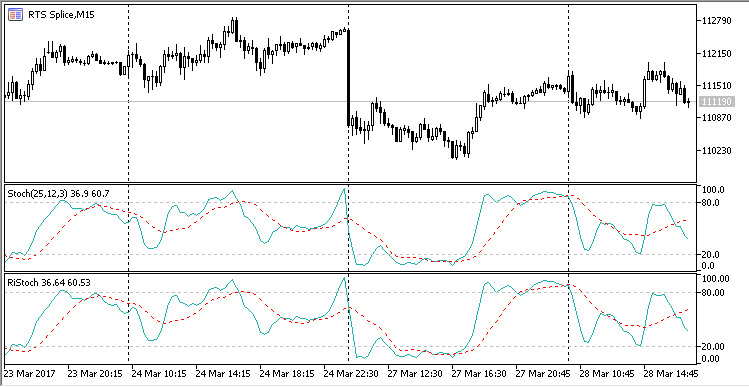
图例. 8. 标准版和环形随机振荡指标。
优化内存使用
计算指标需要一定的计算资源。通过所谓的句柄操纵系统指标也不例外。指标句柄是特定类型的指针, 指向指标内部计算模块和其数据缓存。句柄不会占用太多的空间, 因为它只是一个 64 位的数字。主要的大小隐藏在 MetaTrader 的 "幕后", 因此当创建新的句柄时, 会分配超过其大小的一定数量的内存。
另外, 复制指标值也需要一定的时间。它超过 EA 计算内部指标值所需的时间。因此, 开发人员建议直接在 EA 中创建指标计算块。当然, 这并不意味着您一定要在 EA 代码中编写指标的计算逻辑, 而不去调用标准指标。您的 EA 可能会应用一、两个甚至五个指标。请记住, 与 EA 在内部代码中直接执行计算相比, 它们的操作将占用更多的内存和时间。
不过, 在某些情况下, 内存和时间优化也许是无法避免的。逢此时刻, 环形缓存即可派上用场了。首先, 它们在应用多个指标时可能很有用处。例如, 信息面板 (也称为市场扫描仪) 通常为若干品种和时间帧所应用的整套指标提供行情的瞬时全貌。这是 MetaTrader 5 市场中可以找到的面板之一:
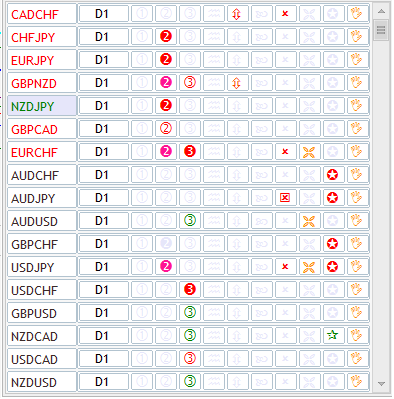
图例. 8. 信息面板会用到多个指标
正如我们所见, 在此分析了 17 种各类金融工具, 不同的参数有 9 套。每组参数由其指标呈现, 这意味着我们需要 17 * 9 = 153 个指标来显示 "只是几个图标"。为了分析每个品种的所有 21 个时间帧, 我们需要多达 3213 个指标。全盘安置它们需要大量的内存。
我们来以 EA 的形式写一个特殊的负载测试, 以便了解内存是如何分配的。它使用两个选项来计算多个指标的值:
- 调用标准指标并通过生成的句柄复制其值;
- 计算环形缓存中的指标。
在第二种情况下, 不会创建任何指标。所有计算都在 EA 内部使用两个环形指标执行 – MACD 和随机振荡指标。它们当中每一个都有三个设置: 快速, 标准和慢速。指标将计算四个品种: EURUSD, GBPUSD, USDCHF 和 USDJPY 在 21 个时间帧的数值。很容易定义数值计算的总数:
数值总数 = 2 个指标 * 3 个参数集 * 4 个品种 * 21 个时间帧 = 504;
我们来编写辅助容器类, 以便在单个 EA 中使用这些不同的方法。当访问时, 它们将提供最后一个指标值。此数值将以不同的方式计算, 具体取决于所用指标的类型。在标准指标的情况下, 使用 CopyBuffer 函数从指标的系统句柄中获取最后一个数值。应用环形缓存时, 使用相应的环形指标计算该值。
以抽象类形式实现的容器原型的源代码如下所示:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| 版权所有 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Arrays\ArrayObj.mqh> #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| 创建的指标类型 | //+------------------------------------------------------------------+ enum ENUM_INDICATOR_TYPE { INDICATOR_SYSTEM, // 系统指标 INDICATOR_RIBUFF // 环形缓存指标 }; //+------------------------------------------------------------------+ //| 指标容器 | //+------------------------------------------------------------------+ class CIndBase : public CObject { protected: int m_handle; // 指标句柄 string m_symbol; // 指标计算品种 ENUM_INDICATOR_TYPE m_ind_type; // 指标类型 ENUM_TIMEFRAMES m_period; // 指标计算周期 CBarDetector m_bar_detect; // 新柱线探测器 CIndBase(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type); public: string Symbol(void){return m_symbol;} ENUM_TIMEFRAMES Period(void){return m_period;} virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| 受保护构造器需要指定指标的 | //| 品种, 时间帧和时间 | //+------------------------------------------------------------------+ CIndBase::CIndBase(string symbol,ENUM_TIMEFRAMES period,ENUM_INDICATOR_TYPE ind_type) { m_handle = INVALID_HANDLE; m_symbol = symbol; m_period = period; m_ind_type = ind_type; m_bar_detect.Symbol(symbol); m_bar_detect.Timeframe(period); } //+------------------------------------------------------------------+ //| 获取最后的指标值 | //+------------------------------------------------------------------+ double CIndBase::GetLastValue(int index_buffer) { return EMPTY_VALUE; }
它包含 GetLastValue 虚方法, 它接受指标缓存编号并返回此缓存的最后一个指标值。此外, 该类还包含基本指标属性: 时间帧, 品种和计算类型 (ENUM_INDICATOR_TYPE)。
我们来创建基于它的 CRiInMacd 和 CRiStoch 派生类。两者都计算相应指标的值, 并通过重新定义的 GetLastValue 方法返回它们。以下是这些类之一 CRiIndMacd 的源代码:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| 版权所有 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <RingBuffer\RiMACD.mqh> #include "RiIndBase.mqh" //+------------------------------------------------------------------+ //| 指标容器 | //+------------------------------------------------------------------+ class CIndMacd : public CIndBase { private: CRiMACD m_macd; // 指标环形缓存 public: CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period, int slow_period, int signal_period); virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| 创建 MACD 指标 | //+------------------------------------------------------------------+ CIndMacd::CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period,int slow_period,int signal_period) : CIndBase(symbol, period, ind_type) { if(ind_type == INDICATOR_SYSTEM) { m_handle = iMACD(m_symbol, m_period, fast_period, slow_period, signal_period, PRICE_CLOSE); if(m_handle == INVALID_HANDLE) printf("创建 iMACD 句柄失败。品种: " + symbol + " 周期: " + EnumToString(period)); } else if(ind_type == INDICATOR_RIBUFF) { m_macd.SetFastPeriod(fast_period); m_macd.SetSlowPeriod(slow_period); m_macd.SetSignalPeriod(signal_period); } } //+------------------------------------------------------------------+ //| 获取最后的指标值 | //+------------------------------------------------------------------+ double CIndMacd::GetLastValue(int index_buffer) { if(m_handle != INVALID_HANDLE) { double array[]; if(CopyBuffer(m_handle, index_buffer, 1, 1, array) > 0) return array[0]; return EMPTY_VALUE; } else { if(m_bar_detect.IsNewBar()) { //printf("收到新柱线 " + m_symbol + " 周期 " + EnumToString(m_period)); double close[]; CopyClose(m_symbol, m_period, 1, 1, close); m_macd.AddValue(close[0]); } switch(index_buffer) { case 0: return m_macd.Macd(); case 1: return m_macd.Signal(); } return EMPTY_VALUE; } }
用于计算随机振荡的容器类具有相同的结构, 所以在此没有显示其源代码。
指标值仅在新柱线开始时进行计算, 以简化测试。为此, 在 CRiIndBase 基础类中内置特别的 NewBarDetecter 模块。这个类重新定义一根新柱线的开盘, 并通过 IsNewBar 方法返回 'true' 来通知它。
现在, 我们来看看 EA 代码的测试。它由 TestIndEA.mq5 调用:
//+------------------------------------------------------------------+ //| TestIndEA.mq5 | //| 版权所有 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2017, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Object.mqh> #include <Arrays\ArrayObj.mqh> #include "RiIndBase.mqh" #include "RiIndMacd.mqh" #include "RiIndStoch.mqh" #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| MACD 参数 | //+------------------------------------------------------------------+ struct CMacdParams { int slow_period; int fast_period; int signal_period; }; //+------------------------------------------------------------------+ //| 随机振荡参数 | //+------------------------------------------------------------------+ struct CStochParams { int k_period; int k_slowed; int d_period; }; input ENUM_INDICATOR_TYPE IndType = INDICATOR_SYSTEM; // 指标类型 string Symbols[] = {"EURUSD", "GBPUSD", "USDCHF", "USDJPY"}; CMacdParams MacdParams[3]; CStochParams StochParams[3]; CArrayObj ArrayInd; //+------------------------------------------------------------------+ //| 专家系统初始化函数 | //+------------------------------------------------------------------+ int OnInit() { MacdParams[0].fast_period = 3; MacdParams[0].slow_period = 13; MacdParams[0].signal_period = 6; MacdParams[1].fast_period = 9; MacdParams[1].slow_period = 26; MacdParams[1].signal_period = 12; MacdParams[2].fast_period = 18; MacdParams[2].slow_period = 52; MacdParams[2].signal_period = 24; StochParams[0].k_period = 6; StochParams[0].k_slowed = 3; StochParams[0].d_period = 3; StochParams[1].k_period = 12; StochParams[1].k_slowed = 5; StochParams[1].d_period = 6; StochParams[2].k_period = 24; StochParams[2].k_slowed = 7; StochParams[2].d_period = 12; // 504 MACD 和 随机振荡指标在此已被创建 for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PeriodByIndex(period), IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PeriodByIndex(period), IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } printf("创建 " + (string)ArrayInd.Total() + " 指标成功"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| 专家系统即时报价函数 | //+------------------------------------------------------------------+ void OnTick() { for(int i = 0; i < ArrayInd.Total(); i++) { CIndBase* ind = ArrayInd.At(i); double value = ind.GetLastValue(0); double value_signal = ind.GetLastValue(1); } } //+------------------------------------------------------------------+ //| 通过其索引获取时间帧 | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES PeriodByIndex(int index) { switch(index) { case 0: return PERIOD_CURRENT; case 1: return PERIOD_M1; case 2: return PERIOD_M2; case 3: return PERIOD_M3; case 4: return PERIOD_M4; case 5: return PERIOD_M5; case 6: return PERIOD_M6; case 7: return PERIOD_M10; case 8: return PERIOD_M12; case 9: return PERIOD_M15; case 10: return PERIOD_M20; case 11: return PERIOD_M30; case 12: return PERIOD_H1; case 13: return PERIOD_H2; case 14: return PERIOD_H3; case 15: return PERIOD_H4; case 16: return PERIOD_H6; case 17: return PERIOD_H8; case 18: return PERIOD_H12; case 19: return PERIOD_D1; case 20: return PERIOD_W1; case 21: return PERIOD_MN1; default: return PERIOD_CURRENT; } } //+------------------------------------------------------------------+
主要功能位于 OnInit 模块当中。在那里执行品种、时间帧排序, 以及设置指标参数集。指标参数集合保存在 CMacdParams 和 CStochParams 辅助结构中。
数值处理模块位于 OnTick 函数中, 体现指标的通用排序, 并使用 GetLastalue 虚方法接收其最后值。由于两个指标具有相同数量的计算缓存, 因此不需要额外的检查。两个指标的值均可以通过广义的 GetLastValue 方法获得。
启动 EA 显示如下: 在基于调用标准指标的计算模式下, 占用了 11.9 GB 的内存, 而在基于环形基元的指标计算模式下占用了 2.9 GB。执行测试的 PC 拥有16 GB 内存。
然而, 我们应该记住, 节省的内存并非主要来自使用环形缓存, 而是将计算模块放在 EA 代码中。模块的位置已经节省了大量的内存。
减少四倍内存消耗是非常体面的结果。无论如何, 我们仍然需要消耗几乎 3 GB 的内存。 是否可以进一步减少消耗?是的, 可以。我们只需要优化时间帧的数量。我们尝试略微修改测试代码, 只使用一个时间帧 (PERIOD_M1) 而非 21 个。指标数量仍然相同, 尽管其中一些将会重复:
... for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PERIOD_M1, IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PERIOD_M1, IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } ...
在此情况下, 内部计算模式中相同的 504 个指标占用了 548 MB 的内存。更确切地说, 内存消耗主体是下载指标计算所需的数据, 而非指标自身。终端本身需要大约 100 MB 的总量, 这意味着下载的数据量甚至更低。因此, 我们再次大大降低了内存消耗:
在此模式下基于系统指标计算需要 1.9 GB 的内存, 与整个列表使用 21 个时间帧所消耗的内存相比, 它也显著降低。
优化专家交易系统测试时间
MetaTrader 5 能够同时访问多个交易金融工具, 以及每个金融工具的任何时间帧。这允许创建和测试多专家系统 (一个 EA 同时交易多个品种)。访问交易环境可能需要时间, 尤其是如果我们需要访问的指标数据依据这些金融工具计算。如果在单个 EA 中执行所有计算, 则可以减少访问时间。我们通过在 MetaTrader 5 策略测试器中测试前一个例子来描绘这一点。首先, 我们的 EA 在 "仅开盘价" 模式下, EURUSD M1, 测试最后一个月。我们将使用系统指标进行计算。在 Intel Core i7 870 2.9 Ghz 上测试花费 58 秒:
2017.03.30 14:07:12.223 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:57.923.
现在, 我们在内部计算模式下执行相同的测试:
2017.03.30 14:08:29.472 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:12.292.
正如所见, 在这种模式下, 计算时间仅有 12 秒。
提高效能的结论和建议
我们在开发指标时测试了内存的使用情况, 并在两种操作模式下测量了测试速度。当使用基于环形缓存的内部计算时, 我们设法减少内存消耗并将性能提高多倍。当然, 所呈现的示例大都是人为造就的。大多数程序员将永远不需要同时创建 500 个指标, 并在所有可能的时间帧内进行测试。然而, 这种 "压力测试" 有助于确定开销最昂贵的机制并尽量减少其使用。以下是基于测试结果的几个提示:
- 将指标的计算模块放在 EA 内部。这在测试当中会节省时间和内存。
- 避免在多个时间帧内接收数据的请求 (如果可能)。使用单一 (最低) 时间帧进行计算。例如, 如果需要在 M1 和 H1 上计算两个指标, 则接收 M1 数据, 将其转换为 H1, 然后利用这些数据计算 H1 上的指标。这种方式比较复杂, 但却大大节省了内存。
- 在您的工作中谨慎使用计算资源。环形缓存对此很擅长。它们需要的内存与计算指标完全一样。此外, 环形缓存允许优化一些计算算法, 例如搜索最高价/最低价。
- 创建一个通用接口来操纵指标, 并用它来接收它们的数值。如果在内部模块中难以实现指标计算, 则通过接口调用外部 MetaTrader 指标。如果创建一个内部指标模块, 只需将其连接到此接口。在此情况下, EA 仅会经受最小的变化。
- 明确评估优化功能。如果您在一个品种上只使用一个指标, 则可将其维持原样, 而不必将其转换为内部计算。花费在这种转化上的时间可能显著地超过总体性能增益。
结论
我们已经描述了环形缓存的发展及其在构建财经指标方面的实际应用。在交易当中, 难以找到更多环形缓存相关的应用。更令人惊讶的是, 截至目前, 这种数据构建算法还没有被 MQL 社区所涵盖。
环形缓存以及基于它的指标可以节省内存并提供快速计算。环形缓存的主要优点是基于它们的指标实现简单, 因为它们大多遵循 FIFO (先进先出) 原理。因此, 不 在环形缓存中计算的指标通常会出现问题。
所有已描述的源代码附加于后, 包括指标代码, 以及指标所基于的简单算法。我相信, 本文将成为开发完善、简单、快速和多功能的环形指标库的良好起点。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/3047
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

非常感谢作者。萨维奥,也许你看到的错误就在这里:
int RingBuffer::iToRealInd(int iIndex)
{
if(iIndex >= iNumElements() || iIndex < 0)
return iBufferSize-1; //previous bug was caused by no -1 here
...
我在最后一行引号中加上了-1;之前没有,会导致返回不正确的索引。请注意,我根据自己的编程风格更改了变量/方法名称,但想法是一样的
我尝试了您的更正,但仍然无法正确更新。似乎缺少了什么,而且当我试图在形成新的条形图时运行环形缓冲区 时,我找不到问题所在。当市场运行时,高低线完全混淆。在处理旧数据时,代码运行得非常好、非常快,但在形成新的条形图时,新数据到达时,代码就无法运行了。
请允许我发表一些意见:
1.在 void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value) 类中,在方法 "OnChangeValue" 的第
行。
图片: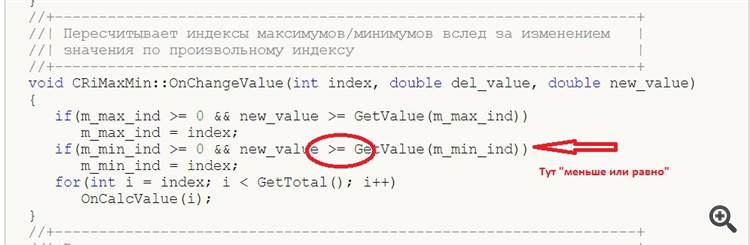
2.在搜索数组的最小和最大元素时,如果完全作为环形缓冲区使用(当新元素开始写入数组开头时),min 和 mah 的定义是错误的。最小值大于最大值。在一个数组中。使用标准方法(ArrayMinimum 和 ArrayMaximum)一切正常。
图片:
某个地方的索引出错了。我自己解决不了。如果有人能解决,那就太好了。我附上了一个测试顾问。
ToRealInd(int index) 中有一处错误。
应该是