
Die Rezepte MQL5 - Die Erstellung des Ringpuffers für eine schnelle Berechnung der Indikatoren im gleitenden Fenster
Inhaltsverzeichnis
- Einführung
- Der gleitende Durchschnitt als Berechnungsbeispiel
- Die Theorie des Ringpuffers
- Ein Arbeitsmuster
- Das Beispiel der Berechnung eines einfachen, gleitenden Durchschnitts mit dem Ringpuffer
- Das Beispiel der Berechnung eines exponentiellen, gleitenden Durchschnitts mit dem Ringpuffer
- Berechnen von Maxima und Minima mit dem Ringpuffer
- Anpassen des Ringpuffers aus der Bibliothek AlgLib
- Erstellen des MACD mittels einfacher Ringpuffer
- Erstellen der Stochastic mittels einfacher Ringpuffer
- Optimieren der Speicherauslastung
- Optimieren der Testszeit des Experten
- Schlussfolgerungen und Vorschläge zur Leistungssteigerung
- Fazit
Einführung
Es ist kein Geheimnis, dass die Mehrzahl der Berechnungen, die ein Händler machen muss, mit Berechnungen im gleitenden Fenster verbunden ist. Es ist eine Besonderheit des Handels, dass Daten in einem unterbrochen Strom eintreffen, seien es Preise oder Daten zu den Aufträgen. In der Regel muss ein Händler irgendwelche Werte eines bestimmten Zeitrahmens rechnen. Wenn zum Beispiel ein einfacher, gleitender Durchschnitt errechnet werden soll, wird ein Durchschnitt des Preises in letzten N Bars ermittelt, wobei N die Periodenlänge des gleitenden Durchschnitts bedeutet. Es wäre wünschenswert, wenn die benötigte Zeit für die Berechnung nicht von der Länge der Periodenzahl abhängig ist. Jedoch ist es in der Praxis nicht immer leicht, einen Algorithmus mit einer solchen Eigenschaft zu finden. Aus einer algorithmischen Sicht ist es viel einfacher, beim Empfang einer neuen Bar den Durchschnitt vollständig neu zu berechnen. Der Algorithmus des Ringpuffers löst das Problem einer effektive Weise. Er bietet ein gleitendes Fenster, in dem die Berechnungen korrekt und gleichzeitig sehr einfach werden.
Der gleitende Durchschnitt als Berechnungsbeispiel
Arbeiten wir mit einem konkreten Beispiel: Die Berechnung eines einfachen, gleitenden Durchschnitts. Mit diesem Beispiel zeigen wir, welche Probleme man bewältigen muss. Der Durchschnitt wird nach der bekannten Formel berechnet:
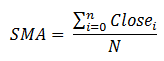
Das folgende Skript für MQL5 berechnet den einfachen, gleitenden Durchschnitt:
//+------------------------------------------------------------------+ //| SMA.mq5 | //| Copyright 2015, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2015, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" input int N = 10; // Die Periode des Durchschnitts //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double closes[]; if(CopyClose(Symbol(), Period(), 0, N, closes)!= N) { printf("Need more data"); return; } double sum = 0.0; for(int i = 0; i < N; i++) sum += closes[i]; sum /= N; printf("SMA: " + DoubleToString(sum, Digits())); } //+------------------------------------------------------------------+
Rein mathematisch ist alles richtig: Das Skript errechnet den gleitenden Durchschnitt, der im Fenster des Terminals ausgedruckt wird. Aber was soll man machen, wenn wir im gleitenden Fenster arbeiten? In diesem Fall ändert sich ständig der Wert der letzten Bar, und es werden neue Bars hinzugefügt. Dieser Algorithmus müsste jedes Mal den Wert des gleitenden Durchschnitts durch zwei sehr rechenintensiven Vorgängen neu berechnen:
- Das Kopieren der N Preise in den Empfänger-Array;
- Das Aufsummieren aller N Preise in der 'for'-Schleife.
Der zweite Vorgang dauert am längsten. Für die Periodenlänge 10 werden zehn Iterationen benötigt, für eine Periodenlänge 500 schon 500. Daraus ergibt sich, dass die Komplexität des Algorithmus direkt von der Periodenlänge der Durchschnittsbildung abhängig ist. Für sie gilt O(n), wobei O allgemein für die Funktion der Komplexität steht.
Jedoch gibt es einen schnelleren Algorithmus, um den Durchschnitt im gleitenden Fenster zu berechnen. Dazu muss man die Summe aller Werte auf der vorhergehenden Berechnungen zu wissen:
SMA = (die Summe aller Werte - der erste Wert des gleitenden Fensters + der neue Wert) / die Periodenlänge des Durchschnitts
Jetzt ist beträgt die Komplexität nur mehr O(1), und ist nicht mehr von der Periodenlänge abhängig. Die Produktivität eines solchen Algorithmus ist höher, aber ihn zu realisieren ist komplizierter. Bei jeder neuen Bar müssen folgenden Schritte ausgeführt werden:
- Den Wert von der laufenden Summe abziehen, der als letzter hinzugefügt wurde, und ihn dann aus der Liste entfernen;
- Den Wert zur laufenden Summe addieren, der zuletzt hinzugefügt wurde, und dann ihn der Liste hinzufügen;
- Die neue Summe durch die Periodenlänge des Durchschnitts teilen, und sie als neuer, gleitende Durchschnitt zurückgeben.
Wenn der neue Wert nicht hinzugefügt sondern nur geändert wird, wird der Algorithmus noch komplizierter:
- Den aktualisierten Wert erkennen und bereithalten;
- Den bisherigen Wert von der laufenden Summe abziehen, der zuletzt in der Liste gespeichert wurde;
- Den bisherigen Wert ersetzen;
- Den Wert zur laufenden Summe hinzufügen;
- Die laufende Summe durch die Periodenlänge teilen, und den erhaltenen Wert als gleitenden Durchschnitt zurückgeben.
Zusätzlich verkompliziert die Tatsache, dass nur grundlegende Datentypen in MQL5 wie auch in der Mehrheit der System-Programmiersprachen zu Verfügung stehen — zum Beispiel die Arrays. Sie müssen allerdings in der Art von FIFO (First In - First Out) organisiert werden, also eine Liste, dessen erstes Element als erstes wieder entfernt wird. Diese Arrays können alte Elemente löschen und neue aufnehmen, aber diese Vorgänge benötigen Zeit und Speicher, denn tatsächlich wird bei jeder dieser Operationen die Arrays neu beschrieben.
Mit dem Ringpuffer werden wir den Algorithmus verwirklichen und so diese Schwierigkeiten vermeiden.
Die Theorie des Ringpuffers
Das wichtigste Merkmal des Ringpuffers ist die Möglichkeit, neue Elemente hinzuzufügen ohne die anderen in dem Array hin und her zuschieben. Unter der Annahme, das die Anzahl der Elemente des Arrays konstant ist (das ja mit der Definition des gleitenden Fensters übereinstimmt), wird durch das Hinzufügen des neuen Elementes das alte automatisch entfernt bzw. überschrieben. Die Gesamtzahl der Elemente ändert sich nicht, es ändert sich nur der Index des neuesten Elementes. Das letzte Element wird zum vorletzten sein, das zweite wird zum ersten und das erste wurde entfernt.
Dank dieser Möglichkeit kann ein Ringpuffer mit einfachen Arrays erstellt werden. Wir erstellen eine Klasse mit so einem einfachen Array:
class CRingBuffer { private: double m_array[]; };
Der Einfachheit halber soll unser Puffer nur aus 3 Elementen bestehen. Das erste Element des Arrays hat den Index 0, das zweite 1 und das dritte den Index 2. Was passiert, wenn wir jetzt ein viertes Element hinzufügen? Offenbar muss beim Hinzufügen das erste Element entfernt werden und an diese Stelle wird das neue Element eingetragen. Und wie muss jetzt der Index berechnet werden? Dazu verwenden wir eine spezielle Operation den 'Rest einer Division'. In MQL5 wird diese Operation durch das spezielle Symbol % (Prozent) gekennzeichnet. Da die Indexierung mit Null beginnt, wäre unser viertes Element in dem Array an dritter Stelle zu platzieren, und dessen Index wird daher mit folgender Formel berechnet:
'total' ist der Größe des Puffers. In unserem Beispiel wird also der Rest von 3 dividiert durch 3 ermittelt und so erhalten wir den Index Null. Weitere Elemente werden nach denselben Regeln eingetragen: die Nummer des hinzuzufügenden Elementes wird durch die Anzahl der Elemente im Array geteilt und der Rest dieser Division wird zum Index unseres Ringpuffers. Im Folgenden sind die Indices der ersten 8 Elemente, die in den Ringpuffer der Länge 3 eingetragen werden, aufgelistet:
0 % 3 = [0] 1 % 3 = [1] 2 % 3 = [2] 3 % 3 = [0] 4 % 3 = [1] 5 % 3 = [2] 6 % 3 = [0] 7 % 3 = [1]...
Ein Arbeitsmuster
Wir wissen jetzt genug über die Theorie des Ringpuffers, um einmal ein Arbeitsmuster zu erstellen. Unser Ringpuffer wird drei Möglichkeiten anbieten:
- Einen neuen Werte eintragen;
- Den letzten Wert entfernen;
- Den Wert eines willkürlichen Index ändern.
Die letzte Funktion benötigen wir im online Betrieb, wenn sich die letzte Bar bildet und der einzutragende Wert sich ständig ändert.
Unser Puffer verfügt über zwei grundlegende Merkmale: die maximale Größe des Puffers und die aktuelle Zahl der Elemente. Die meiste Zeit werden beide Werte übereinstimmen, denn wenn die Elemente die ganze Dimension des Puffers belegen, wird jedes nachfolgende Element das Älteste überschreiben. So bleibt Gesamtzahl der Elemente unveränderlich. Nur beim ersten Auffüllung des Puffers unterscheiden sich beide Werte. Die maximale Anzahl der Elemente ist eine änderbare Eigenschaft. Der Benutzer kann sie vergrößern oder verringern.
Das Überschreiben des jeweils ältesten Elementes geschieht automatisch, ohne dass der Nutzer eingreifen muss. Das ist absichtlich so gemacht, da die manuelle Entfernung von Elemente in der Praxis die Verwaltung des Ringpuffers unnötig stark verkomplizieren würde.
Am Schwierigsten ist die Berechnung der wirklichen Index des Puffers mit den realen Werten. Wenn der Nutzer das Element mit dem Index 0 abfragt, kann der tatsächliche Wert diese Elementes wo anders liegen. Wurde zum Beispiel das 17. Element in den Ringpuffer mit der Größe 10 eingetragen, wurde es als letztes Element an der Stelle mit dem Index 7 eingetragen.
Um zu sehen wie unser Ringpuffer funktioniert, folgen die Headerdateien und die Hauptmethoden:
//+------------------------------------------------------------------+ //| Der Ringpuffer Double | //+------------------------------------------------------------------+ class CRiBuffDbl { private: bool m_full_buff; int m_max_total; int m_head_index; protected: double m_buffer[]; //Der Ringpuffer für einen direkten Zugriff. Achtung: Die Indices entsprechen nicht der Nummerierung! ... int ToRealInd(int index); public: CRiBuffDbl(void); void AddValue(double value); void ChangeValue(int index, double new_value); double GetValue(int index); int GetTotal(void); int GetMaxTotal(void); void SetMaxTotal(int max_total); void ToArray(double& array[]); }; //+------------------------------------------------------------------+ //| Der Konstruktor | //+------------------------------------------------------------------+ CRiBuffDbl::CRiBuffDbl(void) : m_full_buff(false), m_head_index(-1), m_max_total(0) { SetMaxTotal(3); } //+------------------------------------------------------------------+ //| Setzen der Größe des Ringpuffers | //+------------------------------------------------------------------+ void CRiBuffDbl::SetMaxTotal(int max_total) { if(ArraySize(m_buffer) == max_total) return; m_max_total = ArrayResize(m_buffer, max_total); } //+------------------------------------------------------------------+ //| Rückgabe der aktuellen Größe des Ringpuffers | //+------------------------------------------------------------------+ int CRiBuffDbl::GetMaxTotal(void) { return m_max_total; } //+------------------------------------------------------------------+ //| Rückgabe des Wertes an der Stelle des Index | //+------------------------------------------------------------------+ double CRiBuffDbl::GetValue(int index) { return m_buffer[ToRealInd(index)]; } //+------------------------------------------------------------------+ //| Rückgabe der gesamtzahl der Elemente | //+------------------------------------------------------------------+ int CRiBuffDbl::GetTotal(void) { if(m_full_buff) return m_max_total; return m_head_index+1; } //+------------------------------------------------------------------+ //| Eintragen eines neuen Wertes | //+------------------------------------------------------------------+ void CRiBuffDbl::AddValue(double value) { if(++m_head_index == m_max_total) { m_head_index = 0; m_full_buff = true; } //... m_buffer[m_head_index] = value; } //+------------------------------------------------------------------+ //| Ändern eines bestehenden Wertes an der Setelle des Index | //+------------------------------------------------------------------+ void CRiBuffDbl::ChangeValue(int index, double value) { int r_index = ToRealInd(index); double prev_value = m_buffer[r_index]; m_buffer[r_index] = value; } //+------------------------------------------------------------------+ //| Umwandeln des virtuellen Index in den realen Index | //+------------------------------------------------------------------+ int CRiBuffDbl::ToRealInd(int index) { if(index >= GetTotal() || index < 0) return m_max_total; if(!m_full_buff) return index; int delta = (m_max_total-1) - m_head_index; if(index < delta) return m_max_total + (index - delta); return index - delta; }
Die Basis dieser Klasse ist der Zeiger auf das zuletzt eingetragenen Element, m_head_index. Wir ein neues Element mit der Methode AddValue() eingetragen, wird er um 1 erhöht. Würde sein Wert die Größe des Arrays überschreiten, wird er wieder auf Null gesetzt.
Die komplexeste Funktion des Rundpuffers ist die interne Methode ToRealInd(). Ihr wird der von Nutzer gewünschte Index übergeben, und sie gibt den aktuellen Index des entsprechenden Elementes im Ringpuffer zurück.
Wie man es oben sehen kann, ist der Ringpuffer eigentlich ziemlich einfach: Mit Ausnahme der Adressarithmetik unterstützt er die elementare Aktion, um ein neues Element einzutragen und ermöglicht den Zugriff auf ein beliebiges Element mit GetValue(). Allerdings wird diese Funktion selbst in der Regel nur für die bequeme Abfrage für weitere Berechnungen benötigt, sei es ein herkömmlicher, gleitender Durchschnitt oder ein Algorithmus, um Maxima und Minima zu suchen. Mit Hilfe des Ringpuffers können Sie eine ganze Reihe statistischer Werte berechnen. Dies sind alle Arten von Indikatoren oder statistischen Kriterien, wie Varianz und Standardabweichung. Daher ist es unmöglich, die Klasse des Ringpuffers mit all den möglichen Algorithmen zu versehen. Aber das muss man gar nicht. Stattdessen bietet sich sich eine flexiblere Lösung an: Erstellen Sie abgeleitete Klassen mit den von Ihnen gewünschten Algorithmen der Indikatoren oder Statistik.
Damit diese abgeleiteten Klassen ihre Werte bequem berechnen können, wird der Ringpuffer mit zusätzlichen, virtuellen Methoden versehen. Es sind Methoden in der Sektion 'protected', die angepasst werden können, sie beginnen mit On:
//+------------------------------------------------------------------+ //| Der Ringpuffer Double | //+------------------------------------------------------------------+ class CRiBuffDbl { private: ... protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double prev_value, double new_value); virtual void OnChangeArray(void); virtual void OnSetMaxTotal(int max_total); };
Jedes Mal, wenn sich der Ringpuffer ändert, wird einer der Methoden aufgerufen. Wird ein neuer Wert eingetragen, wird die Methode OnAddValue() aufgerufen. Ihr Parameter enthält den einzutragenden Wert. Wird diese Methode in der abgeleiteten Klasse des Ringpuffers umdefiniert, wird der entsprechende Block der Berechnung der abgeleiteten Klasse jedes Mal beim Hinzufügen des neuen Wertes aufgerufen.
Der Ringpuffer enthält fünf Methoden, mit denen man in der abgeleiteten Klasse die Berechnungen kontrollieren kann (in den Klammern sind die Methoden angegeben):
- Eintragen eines neuen Elementes (OnAddValue);
- Entfernung des ältesten Elementes (OnRemoveValue);
- Änderung des Elementen an der Stelle eines willkürlichen Index (OnChangeValue);
- Änderung des ganzen Ringpuffers (OnChangeArray);
- Änderung der maximalen Anzahl der Elemente im Ringpuffer (OnSetMaxTotal).
Die Methode OnChangeArray() verdient ein paar extra Worte. Sie wird aufgerufen, wenn die Neuberechnung eines Indikators einen Zugriff auf den ganze Array erfordert. In diesem Fall genügt es, die vorliegende Methode in der abgeleiteten Klasse umzudefinieren. In der Methode muss mit Hilfe der Funktion ToArray() auf das ganze Array mit den aktuellen Werten für die Berechnungen zugegriffen werden. Das Beispiel einer Berechnung wird unten angeführt, im Abschnitt mit dem Titel "Anpassen des Ringpuffers aus der Bibliothek AlgLib".
Die Klasse des Ringpuffers heißt CRiBuffDbl. Wie man es aus dem Namen sehen kann, arbeitet er mit den reellen (double) Zahlen, dem verbreitetsten Zahlentyp für Berechnungen. Es könnte jedoch auch die Verwendung ganzen Zahlen notwendig sein. Deshalb gibt es außer der Klasse Klasse CRiBuffDbl die entsprechende Klasse CRiBuffInt für die Arbeit mit ganzen Zahlen. Auf den modernen Prozessoren ist die Arithmetik der ganzen Zahlen wesentlich schneller als die der Gleitkommazahlen. Deshalb ist es für spezialisierte, ganzzahlige Aufgaben besser, CRiBuffInt zu verwenden.
Auf die Verwendung vorgefertigter Schablonen vom universellen Typ <template T=""> wird hier bewusst verzichtet, da angenommen wird, dass die konkreten Algorithmen unmittelbar vom Ringpuffer ererbt werden, und jeder Algorithmus mit dem geeigneten Typ der Daten arbeitet.
Das Beispiel der Berechnung eines einfachen, gleitenden Durchschnitts mit dem Ringpuffer
Wir haben eingehend das Funktionieren und Erstellen eines Ringpuffers betrachtet. Jetzt ist es an der Zeit, mit seiner Hilfe eine praktische Aufgaben zu lösen. Fangen wir mit dem Einfachsten an, erstellen wir den bereits erwähnten Indikator des gleitenden Durchschnitts, den Simple Moving Average. Der einfache, gleitende Durchschnitt ergibt sich aus der Summe der der Einzelwerte, die durch ihre Anzahl dividiert wird. Wir wiederholen die Formel der Berechnung, die am Anfang des Artikels angeführt wurde:
SMA = (die Summe aller Werte - der erste Wert des gleitenden Fensters + der neue Wert) / die Periode des Durchschnitts
Für die Realisierung unseres Algorithmus ist es erforderlich, zwei Methoden in der abgeleiteten Klasse von CRiBuffDbl anders zu definieren: OnAddValue() und OnRemoveValue(). Der Durchschnitt wird dann in der Methode Sma() ermittelt. Der Code ist unten zu sehen:
//+------------------------------------------------------------------+ //| RingBufferDbl.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Die Berechnung des gleitenden Durchschnitts im Ringpuffer | //+------------------------------------------------------------------+ class CRiSMA : public CRiBuffDbl { private: double m_sum; protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); public: CRiSMA(void); double SMA(void); }; CRiSMA::CRiSMA(void) : m_sum(0.0) { } //+------------------------------------------------------------------+ //| Erhöhen der Summe | //+------------------------------------------------------------------+ void CRiSMA::OnAddValue(double value) { m_sum += value; } //+------------------------------------------------------------------+ //| Verringern der Summe | //+------------------------------------------------------------------+ void CRiSMA::OnRemoveValue(double value) { m_sum -= value; } //+------------------------------------------------------------------+ //| Ändern der Summe | //+------------------------------------------------------------------+ void CRiSMA::OnChangeValue(int index,double del_value,double new_value) { m_sum -= del_value; m_sum += new_value; } //+------------------------------------------------------------------+ //| Rückgabe des einfachen, gleitenden Durchschnitts | //+------------------------------------------------------------------+ double CRiSMA::SMA(void) { return m_sum/GetTotal(); }
Außer den Methoden, die auf das Eintragen und dem Entfernen eines Elementes reagieren (die Methoden OnAddValue() und OnRemoveValue()), müssten wir noch die Methode ändern, die bei der Veränderung eines willkürlichen Elements (OnChangeValue()) aufgerufen wird. Der Ringpuffer unterstützt die willkürliche Veränderung eines Elements, deshalb muss eine solche Veränderung berücksichtigt werden. In der Regel wird nur das letzte Element geändert, wenn sich die letzte Bar bildet. Gerade für diesen Fall ist die Methode OnChangeValue() vorgesehen, die aber angepasst werden muss.
Jetzt können wir unseren eigenen Indikator schreiben, der die Klasse des Ringpuffers zur Berechnung des gleitenden Durchschnitts verwendet:
//+------------------------------------------------------------------+ //| RiSma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #property version "1.00" #property indicator_chart_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiSMA.mqh> input int MaPeriod = 13; double buff[]; CRiSMA Sma; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); Sma.SetMaxTotal(MaPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { Sma.AddValue(price[i]); buff[i] = Sma.SMA(); calc = true; } if(!calc) { Sma.ChangeValue(MaPeriod-1, price[rates_total-1]); buff[rates_total-1] = Sma.SMA(); } return(rates_total-1); } //+------------------------------------------------------------------+
Zu Anfang trägt der Indikator einfach nur die neuen Werte in den Ringpuffer ein. Die Anzahl der eingetragenen Werte muss nicht kontrolliert werden. Alle Berechnungen und die Entfernung der alten Elemente werden automatischen ausgeführt. Wird der Indikator durch einen neuen Preis der letzten Bar aufgerufen wird, wird der letzte Wert des gleitenden Durchschnitts mittels der Methode ChangeValue() durch einen neuen ersetzt.
Die graphische Abbildung des Indikators ist äquivalent zu dem gleichnamigen Standardindikator MovingAverage:
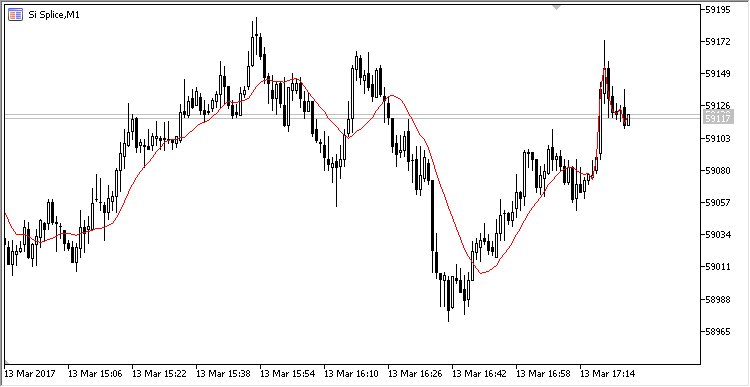
Abb. 1. Die Abbildung des einfachen, gleitenden Durchschnitts, der mit dem Ringpuffer berechnet wurde.
Das Beispiel der Berechnung eines exponentiellen, gleitenden Durchschnitts mit dem Ringpuffer
Wir betrachten ein etwas komplizierteres Beispiel: die Berechnung eines exponentiellen, gleitenden Durchschnitts. Im Unterschied zu dem einfachen, gleitenden Durchschnitt wird bei der Berechnung des exponentiellen, gleitenden Durchschnitts das älteste Element nicht entfernt bzw. von der Summe abgezogen. Deshalb müssen für seine Berechnung zwei Methoden umdefiniert werden: OnAddValue() und OnChangeValue(). Genauso wie im vorhergehenden Beispiel, erstellen wir die Klasse CRiEMA, abgeleitet von CRiBuffDbl und ändern die entsprechenden Methoden:
//+------------------------------------------------------------------+ //| RiEMA.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "RiBuffDbl.mqh" //+-----------------------------------------------------------------------------+ //| Berechnen eines exponentiellen, gleitenden Durchschnitts mit dem Ringpuffer | //+-----------------------------------------------------------------------------+ class CRiEMA : public CRiBuffDbl { private: double m_prev_ema; // Der vorherige Wert EMA double m_last_value; // Der letzte Wert double m_smoth_factor; // Der Faktor der Glättung bool m_calc_first_v; // Die Flagge, die auf die Berechnung des ersten Werts zeigt double CalcEma(); // Die direkte Berechnung des Durchschnitts protected: virtual void OnAddValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiEMA(void); double EMA(void); }; //+---------------------------------------------------------------------------+ //| Der Konstruktor | //+---------------------------------------------------------------------------+ CRiEMA::CRiEMA(void) : m_prev_ema(EMPTY_VALUE), m_last_value(EMPTY_VALUE), m_calc_first_v(false) { } //+---------------------------------------------------------------------------+ //| Die Berechnung des Faktors der Glättung nach der Formel MetaQuotes EMA | //+---------------------------------------------------------------------------+ void CRiEMA::OnSetMaxTotal(int max_total) { m_smoth_factor = 2.0/(1.0+max_total); } //+------------------------------------------------------------------+ //| Ändern der Summe | //+------------------------------------------------------------------+ void CRiEMA::OnAddValue(double value) { //wir berechnen den vorherigen Wert des EMA if(m_prev_ema != EMPTY_VALUE) m_prev_ema = CalcEma(); //Wir speichern die aktuelle Summe m_last_value = value; } //+------------------------------------------------------------------+ //| Korrigieren des EMA | //+------------------------------------------------------------------+ void CRiEMA::OnChangeValue(int index,double del_value,double new_value) { if(index != GetMaxTotal()-1) return; m_last_value = new_value; } //+------------------------------------------------------------------+ //| Berechnen des EMA | //+------------------------------------------------------------------+ double CRiEMA::CalcEma(void) { return m_last_value*m_smoth_factor+m_prev_ema*(1.0-m_smoth_factor); } //+------------------------------------------------------------------+ //| Rückgabe des EMA | //+------------------------------------------------------------------+ double CRiEMA::EMA(void) { if(m_calc_first_v) return CalcEma(); else { m_prev_ema = m_last_value; m_calc_first_v = true; } return m_prev_ema; }
Die Methode CalcEma() berechnet den EMA. Eigentlich liefert sie die Summe von zwei Produkten: dem neuesten Wert multipliziert mit dem Glättungsfaktor plus dem vorherigen Indikatorwert multipliziert mit 1 minus dem Glättungsfaktors. Wenn der vorherige Wert des Indikators noch nicht gerechnet wurde, so wird an seiner Statt der erste Wert im Puffer genommen (in unserem Fall der Schlusskurs der aktuellen Bar).
Um den EMA auf dem Chart zu zeichnen, schreiben wir einen Indikator ähnlich dem im vorherigen Abschnitt dargestellten. So schaut er aus:
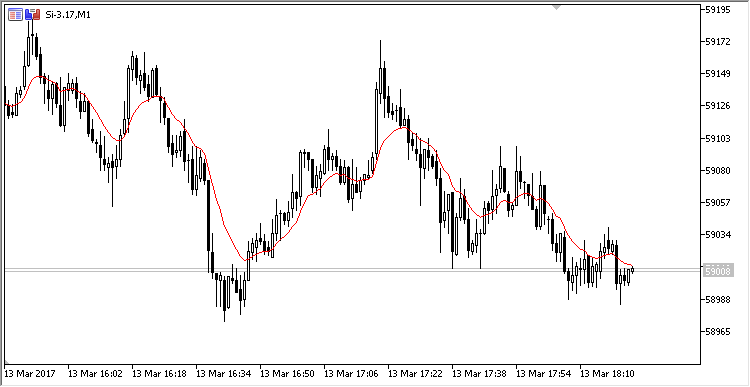
Abb. 2. Die Berechnung eines exponentiellen, gleitenden Durchschnitts, der mit dem Ringpuffer berechnet wurde.
Berechnen von Maxima und Minima mit dem Ringpuffer
Die komplizierteste und interessante Aufgabe — die Berechnung der Maxima und Minima im gleitenden Fenster. Natürlich kann man sich das durch die Verwendung der Standardfunktionen ArrayMaximum und ArrayMinimum ziemlich einfach machen, allerdings verliert man in diesem Fall alle Vorteile einer Berechnung mit dem gleitenden Fenster. Doch wenn Daten gelöscht und aus dem Puffer nacheinander entfernt werden, ist es möglich, das Maximum und Minimum zu berechnen, ohne eine vollständige Suche durchzuführen. Stellen wir uns vor, dass für jeden neuen Wert, der in den Puffer eingetragen wird, zwei zusätzliche Werte berechnet werden. Der Erste gibt an, wieviel vorhergehende Elemente größer als das aktuelle Element, und der Zweite, wieviel vorhergehende Elemente kleiner als das aktuelle Element sind. Der erste Wert wird für die effektive Suche des Maximums, der zweite Wert für die Suche des Minimums verwendet.
Jetzt stellen wir uns vor, dass wir es mit gewöhnlichen Preisbars zu tun haben, und wir den Höchstwert innerhalb einer bestimmten Periodenlänge bestimmen sollen. Dazu werden wir über alle neun Bars die Zahl schreiben, die die Anzahl der vorangehenden Bars angibt, deren Maxima unter dem Höchstpreis der aktuellen Bar liegen. Die Reihenfolge der Bars ist in der Abb. 3. unten gezeigt:
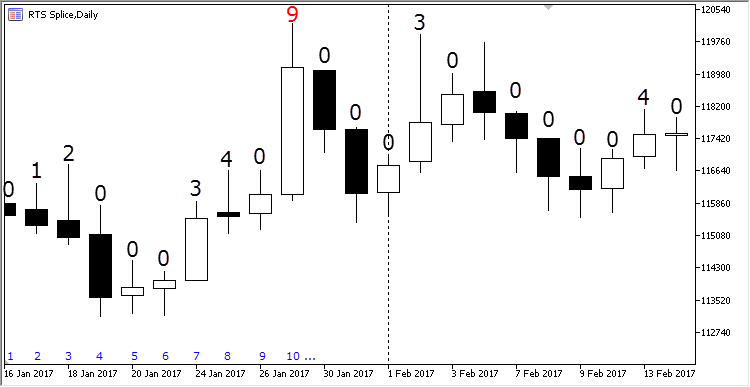
Abb. 3. Die Hierarchie der Extremums der Bars
Über der ersten Bar muss immer Null stehen, da es keinen vorhergehenden Wert. Die Bar №2 ist höher als die erste, deshalb erhält sie den Wert 1. Die dritte Bar ist wiederum höher als vorhergehende, damit auch höher als die erste Bar. Ihr Wert beträgt daher Zwei. Danach sind drei Bars kleiner als ihre jeweiligen Vorgänger. Sie sind alle kleiner als die Bar № 3, deshalb erhalten sie alle drei den Wert Null. Die siebte bar jetzt ist größer als ihre drei Vorgänger, aber niedriger als die vierte, daher erhält sie den Wert 3. In gleicher Weise wurde für jede weitere Bar der entsprechenden Wert zugewiesen.
Wenn alle vorhergehende Indices berechnet wurden, ist es sehr leicht, das höchste Hoch für die jeweilige Bar zu bestimmen. Dazu genügt es, den zugewiesenen Wert der Bar mit denen der anderen zu vergleichen. Jeden folgenden Wert kann man direkt aufrufen, und dabei einige Bars nacheinander überspringen, weil wir Dank den ermittelten Zahlen die Indices erkennen können. Wir stellen es dar:
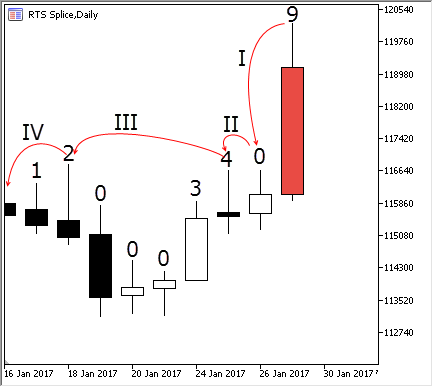
Abb. 4. Die Suche des Extremums der laufenden Bar
Nehemen wir an, das die rot gezeichnete Bar ausgewählt ist. Es ist die Bar mit dem Index 9, da die Indexierung bei Null beginnt. Für das Definieren ihres Index des Extremums vergleichen wir es mit der Bar №8, machen wir den Schritt I: sie ist höher als er geworden, deshalb ist ihr Extremum mindestens 1 gleich. Wir werden es mit der Bar №7 vergleichen, machen wir den Schritt II — sie ist wieder höher als diese Bar. Da die Bar №7 höher ist als vier Vorhergehende, so können wir unsere letzte Bar mit der Bar №3 direkt vergleichen, machen wir den Schritt III. Die Bar №9 ist höher als die Bar №3 und, folglich ist es höher als die alle Bars im laufenden Moment. Wegen der früher berechneten Indexen haben wir den Vergleich mit vier Zwischenbars vermieden, die geplant niedriger sind, als die laufende Bar. Gerade so arbeitet die schnelle Suche des Extremums im Ringpuffer. Auf die ähnliche Weise arbeitet auch die Suche des Minimums, nur mit dem Unterschied, dass ein zusätzlicher Index der Minimums verwendet wird.
Nun, da der Algorithmus bekannt ist, schreiben wir den Quellcode. Interessant an der vorgestellten Klasse ist die Verwendung von zwei hilfsweisen Ringpuffer des Typs CRiBuffInt. Jeder von diesen enthält die jeweiligen Indices der Maxima und Minima.
//+------------------------------------------------------------------+ //| RiMaxMin.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiBuffInt.mqh" //+--------------------------------------------------------------------------+ //| Ermitteln der Maxima und Minima | //+--------------------------------------------------------------------------+ class CRiMaxMin : public CRiBuffDbl { private: CRiBuffInt m_max; CRiBuffInt m_min; bool m_full; int m_max_ind; int m_min_ind; protected: virtual void OnAddValue(double value); virtual void OnCalcValue(int index); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiMaxMin(void); int MaxIndex(int max_period = 0); int MinIndex(int min_period = 0); double MaxValue(int max_period = 0); double MinValue(int min_period = 0); void GetMaxIndexes(int& array[]); void GetMinIndexes(int& array[]); }; CRiMaxMin::CRiMaxMin(void) { m_full = false; m_max_ind = 0; m_min_ind = 0; } void CRiMaxMin::GetMaxIndexes(int& array[]) { m_max.ToArray(array); } void CRiMaxMin::GetMinIndexes(int& array[]) { m_min.ToArray(array); } //+------------------------------------------------------------------+ //| Ändern der Größe des Ringpuffers | //+------------------------------------------------------------------+ void CRiMaxMin::OnSetMaxTotal(int max_total) { m_max.SetMaxTotal(max_total); m_min.SetMaxTotal(max_total); } //+------------------------------------------------------------------+ //| Ermitteln der Indices von Max/Min | //+------------------------------------------------------------------+ void CRiMaxMin::OnAddValue(double value) { m_max_ind--; m_min_ind--; int last = GetTotal()-1; if(m_max_ind > 0 && value >= GetValue(m_max_ind)) m_max_ind = last; if(m_min_ind > 0 && value <= GetValue(m_min_ind)) m_min_ind = last; OnCalcValue(last); } //+------------------------------------------------------------------+ //| Ermitteln der Indices von Max/Min | //+------------------------------------------------------------------+ void CRiMaxMin::OnCalcValue(int index) { int max = 0, min = 0; int offset = m_full ? 1 : 0; double value = GetValue(index); int p_ind = index-1; //Die Suche Maximums while(p_ind >= 0 && value >= GetValue(p_ind)) { int extr = m_max.GetValue(p_ind+offset); max += extr + 1; p_ind = GetTotal() - 1 - max - 1; } p_ind = GetTotal()-2; //Die Suche des Minimums while(p_ind >= 0 && value <= GetValue(p_ind)) { int extr = m_min.GetValue(p_ind+offset); min += extr + 1; p_ind = GetTotal() - 1 - min - 1; } m_max.AddValue(max); m_min.AddValue(min); if(!m_full && GetTotal() == GetMaxTotal()) m_full = true; } //+------------------------------------------------------------------+ //| Ermittel der Indices von Max/Min nach der Veränderung | //| eins Werts an einem willkürlichen Index | //+------------------------------------------------------------------+ void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value) { if(m_max_ind >= 0 && new_value >= GetValue(m_max_ind)) m_max_ind = index; if(m_min_ind >= 0 && new_value >= GetValue(m_min_ind)) m_min_ind = index; for(int i = index; i < GetTotal(); i++) OnCalcValue(i); } //+------------------------------------------------------------------+ //| Rückgabe des Index eines Maximums | //+------------------------------------------------------------------+ int CRiMaxMin::MaxIndex(int max_period = 0) { int limit = 0; if(max_period > 0 && max_period <= m_max.GetTotal()) { m_max_ind = -1; limit = m_max.GetTotal() - max_period; } if(m_max_ind >=0) return m_max_ind; int c_max = m_max.GetTotal()-1; while(c_max > limit) { int ext = m_max.GetValue(c_max); if((c_max - ext) <= limit) return c_max; c_max = c_max - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Rückgabe des Index eines Minimums | //+------------------------------------------------------------------+ int CRiMaxMin::MinIndex(int min_period = 0) { int limit = 0; if(min_period > 0 && min_period <= m_min.GetTotal()) { limit = m_min.GetTotal() - min_period; m_min_ind = -1; } if(m_min_ind >=0) return m_min_ind; int c_min = m_min.GetTotal()-1; while(c_min > limit) { int ext = m_min.GetValue(c_min); if((c_min - ext) <= limit) return c_min; c_min = c_min - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Rückgabe des Maximums | //+------------------------------------------------------------------+ double CRiMaxMin::MaxValue(int max_period = 0) { return GetValue(MaxIndex(max_period)); } //+------------------------------------------------------------------+ //| Rückgabe des Minimums | //+------------------------------------------------------------------+ double CRiMaxMin::MinValue(int min_period = 0) { return GetValue(MinIndex(min_period)); }
Der vorgestellte Algorithmus enthält noch eine Modifikation. Er speichert das aktuelle Minimum und Maximum, und, wenn sie unveränderlich bleiben, so liefert sie die Methoden MaxValue und MinValue zurück, ohne zusätzliche Berechnung.
So sieht die Abbildung der Maximums und Minimums auf dem Chart aus:
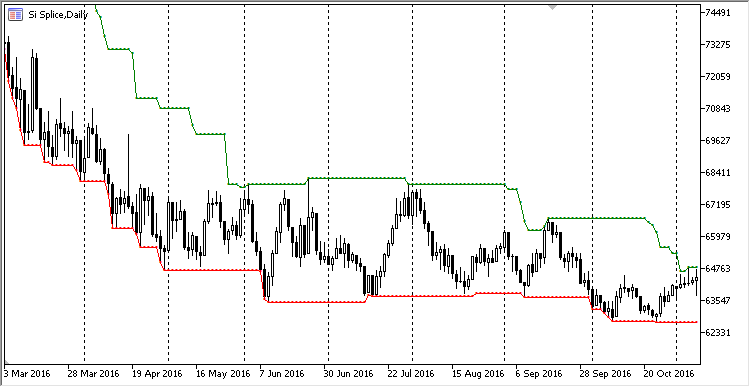
Abb. 5. Der Kanal der Maxima und Minima als Indikator
Ergänzen wir noch, dass die Klasse zur Bestimmung von Maxima und Minima erweiterte Möglichkeiten hat. Sie kann den Index des Extremums im Ringpuffer zurückliefern oder einfach seinen Wert. Auch ist sie in der Lage, ein Extremum für eine kleinere als die Periodenlänge des Ringpuffers zu berechnen, wofür es genügt, den Methoden MaxIndex/MinIndex und MaxValue/MinValue die kleinere Periodenlänge zu übergeben.
Anpassen des Ringpuffers aus der Bibliothek AlgLib
Noch ein interessantes Beispiel für die der Verwendung des Ringpuffers sind besondere mathematische Berechnungen. In der Regel werden die Algorithmen für die Berechnung verschiedenen Statistiken ohne Rücksicht auf die Verwendung eines gleitenden Fensters erstellt. Ein solcher Algorithmus ist nicht immer leicht zu verwenden. Der Ringpuffer verbessert dieses Problem. Wir werden einen Indikator schreiben, der die Hauptcharakteristiken der Gauß'schen Verteilung berechnet:
- Der Mittelwert (Mean);
- Die Standardabweichung (StdDev);
- Die Schiefe (Skewness);
- Die Wölbung (Kurtosis).
Für die Berechnung dieser Werte verwenden wir die Methode AlgLib:SampleMoments. Alles, was wir tun müssen, ist eine Klasse des Ringpuffers CRiGaussProperty zu erstellen und die Methode innerhalb des OnChangeArray Handlers zu platzieren. Der vollständige Code des Indikators, der die Klasse enthält:
//+------------------------------------------------------------------+ //| RiGauss.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiBuffDbl.mqh> #include <Math\AlgLib\AlgLib.mqh> //+------------------------------------------------------------------+ //| Berechnen der Hauptwerte der Gauß'schen Verteilung | //+------------------------------------------------------------------+ class CRiGaussProperty : public CRiBuffDbl { private: double m_mean; // Mittelwert double m_variance; // Varianz double m_skewness; // Schiefe double m_kurtosis; // Wölbung protected: virtual void OnChangeArray(void); public: double Mean(void){ return m_mean;} double StdDev(void){return MathSqrt(m_variance);} double Skewness(void){return m_skewness;} double Kurtosis(void){return m_kurtosis;} }; //+------------------------------------------------------------------+ //| Rechnen bei jeder Veränderung des Arrays | //+------------------------------------------------------------------+ void CRiGaussProperty::OnChangeArray(void) { double array[]; ToArray(array); CAlglib::SampleMoments(array, m_mean, m_variance, m_skewness, m_kurtosis); } //+-----------------------------------------------------------------+ //| Enumeration | //+-----------------------------------------------------------------+ enum ENUM_GAUSS_PROPERTY { GAUSS_MEAN, // Der Mittelwert GAUSS_STDDEV, // Die Abweichung GAUSS_SKEWNESS, // Die Asymmetrie GAUSS_KURTOSIS // Die Ausschweifung }; input int BPeriod = 13; //Period input ENUM_GAUSS_PROPERTY Property; double buff[]; CRiGaussProperty RiGauss; //+------------------------------------------------------------------+ //| Initialisierung | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); RiGauss.SetMaxTotal(BPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Berechnungen | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { RiGauss.AddValue(price[i]); buff[i] = GetGaussValue(Property); calc = true; } if(!calc) { RiGauss.ChangeValue(BPeriod-1, price[rates_total-1]); buff[rates_total-1] = GetGaussValue(Property); } return(rates_total-1); } //+----------------------------------------------------------------------+ //| Rückgabe eines der Werte der Gauß'schen Verteilung | //+----------------------------------------------------------------------+ double GetGaussValue(ENUM_GAUSS_PROPERTY property) { double value = EMPTY_VALUE; switch(Property) { case GAUSS_MEAN: value = RiGauss.Mean(); break; case GAUSS_STDDEV: value = RiGauss.StdDev(); break; case GAUSS_SKEWNESS: value = RiGauss.Skewness(); break; case GAUSS_KURTOSIS: value = RiGauss.Kurtosis(); break; } return value; }
Wie man im Code oben sieht, ist die Klasse sehr einfach. Jedoch verdeckt diese Einfachheit eine große Funktionalität. Jetzt muss nicht mehr der Funktion CAlglib:SampleMoments jedes Mal ein gleitender Array übergeben werden. Es genügt, die neuen Werte mit der Methode AddValue() hinzuzufügen. Die Abbildung zeigt den Indikator. In den Einstellungen haben wir die Berechnung der Standardabweichung ausgewählt, sie wird im Unterfenster des Charts darstellen:
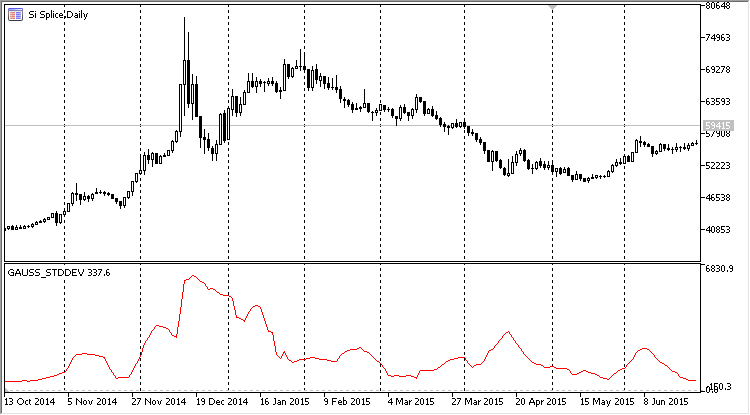
Abb. 6. Die Standardabweichung der Gauß'schen Verteilung in Form eines Indikators
Erstellen des MACD mittels einfacher Ringpuffer
Wir haben drei einfache Ringpuffer entwickelt: einen einfachen und einen exponentiellen, gleitenden Durchschnitt und den Indikator für die Maxima und Minima. Das reicht völlig, um weitere Indikatoren auf ihrer Basis zu erstellen. Zum Beispiel dem MACD Indikator. Er besteht aus zwei exponentiellen, gleitenden Mittelwerten und einer Signallinie aufgrund eines einfachen gleitenden Durchschnitts. Wir versuchen, diesen Indikator auf der Basis der vorhandenen Codes zu erstellen.
Im Beispiel des Indikators für Maxima/Minima verwendeten wir bereits zwei zusätzliche Ringpuffer in der Klasse CRiMaxMin. Wir werden das ebenso bei dem MACD machen. Unsere Klasse wird bei dem Hinzufügen eines neuen Wertes den Wert einfach in ihre zusätzlichen Puffer eintragen, und dann einfach die Differenz zwischen ihnen berechnen. Die Differenz wird dem dritten Ringpuffer zugewiesen, der damit den einfachen SMA berechnet, die Signal-Linie MACD:
//+------------------------------------------------------------------+ //| RiMACD.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiEMA.mqh" //+------------------------------------------------------------------+ //| Die Berechnung des gleitenden Mittelwerts im Ringpuffer | //+------------------------------------------------------------------+ class CRiMACD { private: CRiEMA m_slow_macd; // Der schnelle exponentielle, gleitende Durchschnitt CRiEMA m_fast_macd; // Der langsame exponentielle, gleitende Durchschnitt CRiSMA m_signal_macd; // Die Signal-Linie double m_delta; // Die Differenz zwischen dem schnellen und langsamen EMA public: double Macd(void); double Signal(void); void ChangeLast(double new_value); void SetFastPeriod(int period); void SetSlowPeriod(int period); void SetSignalPeriod(int period); void AddValue(double value); }; //+------------------------------------------------------------------+ //| Berechnen des MACD | //+------------------------------------------------------------------+ void CRiMACD::AddValue(double value) { m_slow_macd.AddValue(value); m_fast_macd.AddValue(value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.AddValue(m_delta); } //+------------------------------------------------------------------+ //| Ändern des MACD | //+------------------------------------------------------------------+ void CRiMACD::ChangeLast(double new_value) { m_slow_macd.ChangeValue(m_slow_macd.GetTotal()-1, new_value); m_fast_macd.ChangeValue(m_fast_macd.GetMaxTotal()-1, new_value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.ChangeValue(m_slow_macd.GetTotal()-1, m_delta); } //+------------------------------------------------------------------+ //| Rückgabe des Histogramms des MACD | //+------------------------------------------------------------------+ double CRiMACD::Macd(void) { return m_delta; } //+------------------------------------------------------------------+ //| Rückgabe der Signal-Linie | //+------------------------------------------------------------------+ double CRiMACD::Signal(void) { return m_signal_macd.SMA(); } //+------------------------------------------------------------------+ //| Setzen der schnellen Periodenlänge | //+------------------------------------------------------------------+ void CRiMACD::SetFastPeriod(int period) { m_slow_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Setzen der langsamen Periodenlängen | //+------------------------------------------------------------------+ void CRiMACD::SetSlowPeriod(int period) { m_fast_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Setzen der Periodenlänge der Signal-Linie | //+------------------------------------------------------------------+ void CRiMACD::SetSignalPeriod(int period) { m_signal_macd.SetMaxTotal(period); }
Beachten Sie bitte, dass die Klasse CRiMacd eine unabhängige Klasse ist, sie wird nicht von CRiBuffDbl abgeleitet. Tatsächlich verwendet die Klasse CRiMacd keine eigenen Berechnungspuffer. Stattdessen werden die einfachen Klassen der Ringpuffer über die 'include'-Direktive geladen und im 'private' Abschnitt platziert.
Die beiden wichtigsten Methoden Macd() und Signal() liefern die Werte des MACD und seiner Signallinie zurück. Der angeführte Code ist einfacher geworden, obwohl jeder Puffer seine eigene Periodenlänge hat. Die Klasse CRiMacd unterstützt nicht das Ändern willkürlicher Elemente. Stattdessen reagiert sie nur auf die Veränderung des letzten Elementes, also die Änderung der Bar mit dem Index 0.
Optisch sieht der Indikator MACD, der mit den Ringpuffern rechnet, genauso aus, wie der klassische Indikator:
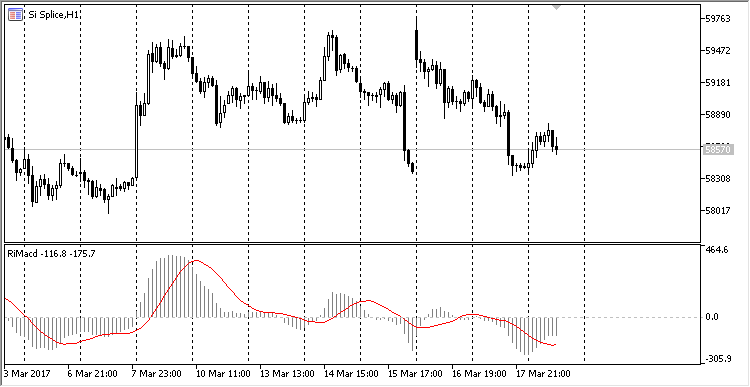
Abb. 7. Der Indikator MACD, der mit Ringpuffer rechnet.
Erstellen der Stochastic mittels einfacher Ringpuffer
Ähnlich werden wir den Indikator der Stochastic erstellen. Dieser Indikator verwendet die Suche nach Extrema und die Berechnung eines gleitenden Durchschnitts. Somit verwenden wir hier die Algorithmen, die wir früher schon beschrieben haben.
Die Stochastic verwendet drei Preis-Reihen: die Preise der Maxima ('high'), der Minima ('low') und die Schlusskurse ('close'). Die Berechnung ist einfach: Zunächst werden das Maximum und das Minimum gesucht, und dann wird das Verhältnis des Schlusskurses zur Differenz von Maximum und Minimum berechnet. Zuletzt wird der Mittelwert der Verhältnisse über die Periodenlänge N errechnet (im Indikator ist N benannt als "die Verzögerung K %"):
K% = SMA((close-min)/((max-min)*100.0%), N)
Zusätzlich wird noch ein Mittelwert der Verzögerung K% mit der Periodenlänge %D berechnet, es ist Signallinie, ähnlich der Signallinie des MACD:
Signal D% = SMA(K%, D%)
Die berechneten zwei Werte — K% und seine Signallinie D% — stellen die Stochastic dar.
Bevor wir allerdings den Code für die Stochastik mit Ringpuffern schreiben, betrachten wir erst einmal den Code der nornalen Stochastik der Datei Stochastic.mq5 aus dem Ordner Indicators\Examples:
//+------------------------------------------------------------------+ //| Stochastic Oscillator | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,k,start; //--- check for bars count if(rates_total<=InpKPeriod+InpDPeriod+InpSlowing) return(0); //--- start=InpKPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) { ExtLowesBuffer[i]=0.0; ExtHighesBuffer[i]=0.0; } } //--- calculate HighesBuffer[] and ExtHighesBuffer[] for(i=start;i<rates_total && !IsStopped();i++) { double dmin=1000000.0; double dmax=-1000000.0; for(k=i-InpKPeriod+1;k<=i;k++) { if(dmin>low[k]) dmin=low[k]; if(dmax<high[k]) dmax=high[k]; } ExtLowesBuffer[i]=dmin; ExtHighesBuffer[i]=dmax; } //--- %K start=InpKPeriod-1+InpSlowing-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtMainBuffer[i]=0.0; } //--- main cycle for(i=start;i<rates_total && !IsStopped();i++) { double sumlow=0.0; double sumhigh=0.0; for(k=(i-InpSlowing+1);k<=i;k++) { sumlow +=(close[k]-ExtLowesBuffer[k]); sumhigh+=(ExtHighesBuffer[k]-ExtLowesBuffer[k]); } if(sumhigh==0.0) ExtMainBuffer[i]=100.0; else ExtMainBuffer[i]=sumlow/sumhigh*100; } //--- signal start=InpDPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtSignalBuffer[i]=0.0; } for(i=start;i<rates_total && !IsStopped();i++) { double sum=0.0; for(k=0;k<InpDPeriod;k++) sum+=ExtMainBuffer[i-k]; ExtSignalBuffer[i]=sum/InpDPeriod; } //--- OnCalculate done. Return new prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
Dieser Code besteht aus einem Block mit 8 'for'-Schleifen, von denen 3 verschachtelt sind. Die Berechnung wird in zwei Schritten vollzogen: zuerst werden die Maxima und Minima ermittelt, und deren Werte in zwei zusätzlichen Puffern gespeichert. Die Berechnung der Maxima und Minima erfordert eine zweifache Suche: auf jeder Bar werden zusätzlich N (K%) Iterationen in der 'for'-Schleife durchgeführt.
Mit den ermittelten Maxima und Minima wird die Berechnung K% durchgeführt, wofür auch zwei Schleifen benötigtr werden. Dazu werden zusätzliche F Iterationen für mjede Bar ausgeführt, mit F als die "die Verzögerung K %".
Zum Schluss wird noch Signallinie D% berechnet, und auch mit zwei 'for'-Schleifen, welches weitere T Iterationen erfordert (mit T als die Periodenlänge D% zur Durchschnittsbildung).
Der bestehende Code ist ziemlich schnell. Das Hauptproblem hier liegt darin, dass man ohne Ringpuffer die einfachen Berechnungen in mehreren unabhängigen Schritten ausführen muss. Darunter leiden Anschaulichkeit und Einfachheit, das das Verstehen des Codes erschwert.
Um dies zu verdeutlichen, werden wir die wesentlichsten Berechnungen in der Klasse CRiStoch durchführen. Sie erledigt das Gleiche wie der Code von oben:
//+------------------------------------------------------------------+ //| Das Hinzufügen der neun Werte und die Berechnung der Stochastik | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Hinzufügen eines neuen Maximums m_min.AddValue(low); // Hinzufügen eines neuen Minimums double c = close; double max = m_max.MaxValue() // Abfrage des Maximums double min = m_min.MinValue(); // Abfrage des Minimums double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Berechnen von K% nach der Formel der Stochastik m_slowed_k.AddValue(k); // Die Glättung K% (Die Verzögerung K%) m_slowed_d.AddValue(m_slowed_k.SMA()); // Berechnen von %D, der Glättung von K% }
Diese Methode enthält keine Zwischenberechnungen. Stattdessen verwendet sie einfach die Formel der Stochastik und die vorhandenen Werte. Die Suche nach den notwendigen Werten, Maxima, Minima und dem Durchschnitt, wird von den Ringpuffern ausgeführt.
Die anderen Methoden der Klasse CRiStoch sind trivial. Es sind diese Get/Set-Methoden der Periodenlängen und weiterer Werte des Indikators. Hier ist jetzt der ganze Code von CRiStoch:
//+------------------------------------------------------------------+ //| RiStoch.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiMaxMin.mqh" //+------------------------------------------------------------------+ //| Die Klasse der Stochastik | //+------------------------------------------------------------------+ class CRiStoch { private: CRiMaxMin m_max; // Maximum CRiMaxMin m_min; // Minimum CRiSMA m_slowed_k; // Durchschnitt K% CRiSMA m_slowed_d; // Durchschnitt D% public: void ChangeLast(double new_value); void AddValue(double close, double high, double low); void AddHighValue(double value); void AddLowValue(double value); void AddCloseValue(double value); void SetPeriodK(int period); void SetPeriodD(int period); void SetSlowedPeriodK(int period); double GetStochK(void); double GetStochD(void); }; //+------------------------------------------------------------------+ //| Eintragen neuer Werte und das Berechnen der Stochastik | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Eintragen des Maximums m_min.AddValue(low); // Eintragen des Minimums double c = close; double max = m_max.MaxValue() double min = m_min.MinValue(); double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Berechnen von K% nach der Formel der Stochastik m_slowed_k.AddValue(k); // Die Glättung K% (Die Verzögerung K%) m_slowed_d.AddValue(m_slowed_k.SMA()); // Berechnen von %D, der Glättung von K% } //+------------------------------------------------------------------+ //| Setzen der schnellen Periodenlänge | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodK(int period) { m_max.SetMaxTotal(period); m_min.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Setzen der langsamen Periodenlänge | //+------------------------------------------------------------------+ void CRiStoch::SetSlowedPeriodK(int period) { m_slowed_k.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Setzen der Periodenlänge der Signal-Linie | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodD(int period) { m_slowed_d.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Abfrage von %K | //+------------------------------------------------------------------+ double CRiStoch::GetStochK(void) { return m_slowed_k.SMA(); } //+------------------------------------------------------------------+ //| Abfrage von %D | //+------------------------------------------------------------------+ double CRiStoch::GetStochD(void) { return m_slowed_d.SMA(); }
Die mit den Ringpuffer berechnete Stochastik unterscheidet sich nicht von der Standardversion. Sie können es selbst feststellen, wenn Sie beide Indikatoren auf demselben Chart starten (alle Dateien der Indikatoren und der Hilfsdateien sind im Anhang zu diesem Artikel):
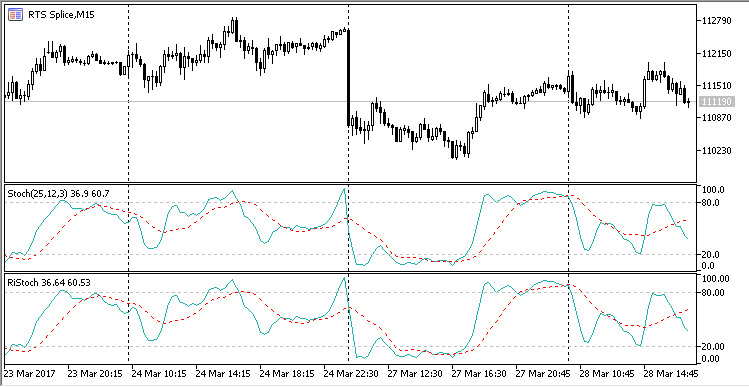
Abb. 8. Die Stochastik, MQL5-Standard und mit Ringpuffer.
Optimieren der Speicherauslastung
Die Berechnung der Indikatoren erfordert bestimmte Ressourcen. Die Arbeit mit den Systemindikatoren über 'handle' bildet da keine Ausnahme. Eigentlich ist so ein 'handle' nur ein besonderer Zeiger auf die inneren Berechnungen des Indikators und seine Datenpuffer. Ein 'handle' selbst belegt nicht viel Speicherplatz, es ist nur ein 64 Bit große Zahl. Die eigentliche Speicheranforderung wird vom MetaTrader verborgen, und, wenn ein neuer 'handle' deklariert wird, wird Speicherplatz in einem festgelegten Umfang, größer als die 64 bit, reserviert.
Außerdem erfordert auch das Kopieren der Werte für den Indikator eine bestimmte Zeit. Diese Zeit ist länger, als es für die Berechnung der Werte des Indikators innerhalb eines Experten erforderlich ist. Deshalb empfehlen Hersteller offiziell, die Berechnung des Indikators im Experten selbst auszuführen und zu verwenden. Natürlich bedeutet das nicht, dass man die Berechnung des Indikators im Code des Experten jedes Mal neu schreiben muss, und den Aufruf der Standardindikatoren verwenden soll. Es ist gar nicht schlecht, wenn in Ihrem Experten ein, zwei oder sogar fünf Indikatoren verwendet werden. Für die Arbeit halt wird etwas mehr Speicherplatz und Zeit benötigt, als wenn diese Berechnungen im inneren Code des Experten selbst aufsgeführt werden würden.
Nichtsdestoweniger könnte es Aufgaben geben, die von einer Optimierung des verwendeten Speicherplatzes und der Zeit profitieren. Gerade für solche Aufgaben würde sich der Ringpuffer anbieten. In erster Linie müssten wohl viele Indikatoren verwendet werden. Zum Beispiel geben Informationstafeln (auch Marktscanner genannt) eine ständig aktualisierte Übersicht mehrerer Symbole und Zeitrahmen und verwenden dafür eine ganze Reihe verschiedenenr Indikatoren. Hier eine Beispiel einer solchen Übersicht aus dem Marketangebot für MetaTrader 5:
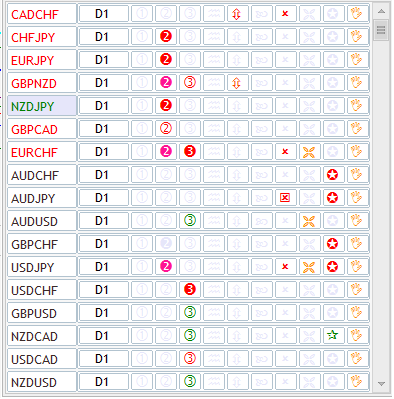
Abb. 8. Eine Übersicht mit der Verwendung einer ganzen Reihe von Indikatoren
Wir sehen hier 17 verschiedene Symbol mit jeweils 9 verschiedenen Messwerten. Jeder Wert ist das Ergebnis eines Indikators. Es ist leicht zu berechnen, dass 17 * 9 = 153 Indikatoren verwendet werden, nur um "ein paar Icons darzustellen". Für ein Analyse aller 21 Timeframes aller Symbole würden gar 3213 Indikatoren benötigt. Das würde einen riesigen Speicherverbrauch verursachen.
Um zu verstehen, wie der Speicherplatz zur Verfügung gestellt wird, schreiben wir einen Experten, der einen besonderen Belastungstest durchführt. Der Experte wird die Werte mehrerer Indikatoren berechnen. Dabei verwendet er zwei Varianten:
- Der Aufruf des Standardindikators und das Kopieren seiner Werte über dessen 'handle';
- Die Berechnung des Indikators mit dem Ringpuffer.
Im zweiten Fall werden keine Indikatoren erstellt, alle Berechnungen werden innerhalb des Experten mit Hilfe der Ringindikatoren durchgeführt. Verwendet werden der MACD und die Stochastik. Bei jedem von ihnen werden drei Varianten deklariert: eine schnelle, eine standardmäßige und eine langsame Variante. Die Indikatoren werden für vier Symbole berechnet: EURUSD, GBPUSD, USDCHF und USDJPY und jeweils 21 Zeitrahmen. Es ist einfach, die Gesamtzahl verwendeten Indikatoren zu berechnen:
Die Gesamtzahl der Indikatoren = 2 Indikatoren * 3 Parametersätze * 4 Symbole * 21 Zeitrahmen = 504 Indikatoren;
Damit in einem Experten die verschiedenen Indikatoren verwenden können, schreiben wir hilfsweise eine Containerklasse. Beim einem Zugriff geben sie den letzten Wert des Indikators zurück. Es wird je nach Typ des verwendeten Indikators unterschiedlich gerechnet. Wenn ein Standardindikator verwendet wird, wird der letzte Wert mit Hilfe der Funktion CopyBuffer und dem 'handle' des Indikators abgefragt. Falls der Ringpuffer verwendet wird, wird der Wert mit Hilfe der entsprechenden Ringindikatoren berechnet.
Der Quellcode des Container-Prototypen ist in Form einer abstrakten Klasse wie folgt realisiert:
//+------------------------------------------------------------------+ //| RiIndBase.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #property version "1.00" #include <Arrays\ArrayObj.mqh> #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Der Typ des Indikators, der erstellt wird | //+------------------------------------------------------------------+ enum ENUM_INDICATOR_TYPE { INDICATOR_SYSTEM, // Der Systemindikator INDICATOR_RIBUFF // Der Indikator des Ringpuffers }; //+------------------------------------------------------------------+ //| Der Container des Indikators | //+------------------------------------------------------------------+ class CIndBase : public CObject { protected: int m_handle; // Der 'handle' des Indikators string m_symbol; // Das Symbol des Indikators ENUM_INDICATOR_TYPE m_ind_type; // Der Typ des Indikators ENUM_TIMEFRAMES m_period; // Die Periodenlänge des Indikators CBarDetector m_bar_detect; // Der Detektor einer neuen Bar CIndBase(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type); public: string Symbol(void){return m_symbol;} ENUM_TIMEFRAMES Period(void){return m_period;} virtual double GetLastValue(int index_buffer); }; //+-----------------------------------------------------------------------------------------+ //| Der Konstruktor verlangt die Übergabe von Symbol, Zeitrahmen und Indikatortyp | //+-----------------------------------------------------------------------------------------+ CIndBase::CIndBase(string symbol,ENUM_TIMEFRAMES period,ENUM_INDICATOR_TYPE ind_type) { m_handle = INVALID_HANDLE; m_symbol = symbol; m_period = period; m_ind_type = ind_type; m_bar_detect.Symbol(symbol); m_bar_detect.Timeframe(period); } //+------------------------------------------------------------------+ //| Rückgabe des letzten Indikatorwertes | //+------------------------------------------------------------------+ double CIndBase::GetLastValue(int index_buffer) { return EMPTY_VALUE; }
Er enthält die virtuelle Methode GetLastValue(). Der Methode muss die Nummer des Indikatorpuffers überegebnwerden und sie gibt dessen letzten Wert zurück. Die Klasse verfügt auch über die grundlegenden Eigenschaften des Indikators: Symbol, Zeitrahmen und den Berechnungstyp (ENUM_INDICATOR_TYPE).
Von ihm können wir die beiden Klassen CRiInMacd und CRiStoch ableiten, die jeweils den Wert des entsprechenden Indikators berechnen und über die angepasste Methode GetLastValue() zurückgeben. Hier der erste Teile der Klasse CRiIndMacd:
//+------------------------------------------------------------------+ //| RiIndMacd.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "https://www.mql5.com" #property version "1.00" #include <RingBuffer\RiMACD.mqh> #include "RiIndBase.mqh" //+------------------------------------------------------------------+ //| Der Container des Indikators | //+------------------------------------------------------------------+ class CIndMacd : public CIndBase { private: CRiMACD m_macd; // Die Ringversion des Indikators public: CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period, int slow_period, int signal_period); virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| Wir erstellen den Indikator MACD | //+------------------------------------------------------------------+ CIndMacd::CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period,int slow_period,int signal_period) : CIndBase(symbol, period, ind_type) { if(ind_type == INDICATOR_SYSTEM) { m_handle = iMACD(m_symbol, m_period, fast_period, slow_period, signal_period, PRICE_CLOSE); if(m_handle == INVALID_HANDLE) printf("Create iMACD handle failed. Symbol: " + symbol + " Period: " + EnumToString(period)); } else if(ind_type == INDICATOR_RIBUFF) { m_macd.SetFastPeriod(fast_period); m_macd.SetSlowPeriod(slow_period); m_macd.SetSignalPeriod(signal_period); } } //+------------------------------------------------------------------+ //| Er bekommt den letzten Wert des Indikators | //+------------------------------------------------------------------+ double CIndMacd::GetLastValue(int index_buffer) { if(m_handle != INVALID_HANDLE) { double array[]; if(CopyBuffer(m_handle, index_buffer, 1, 1, array) > 0) return array[0]; return EMPTY_VALUE; } else { if(m_bar_detect.IsNewBar()) { //printf("Es wurde eine neue Bar auf der " + m_symbol + " Periode " + EnumToString(m_period)) bekommen; double close[]; CopyClose(m_symbol, m_period, 1, 1, close); m_macd.AddValue(close[0]); } switch(index_buffer) { case 0: return m_macd.Macd(); case 1: return m_macd.Signal(); } return EMPTY_VALUE; } }
Die Containerklasse für die Stochastik wurde in gleicher Weise angepasst, weshalb werden wir dessen Quellecode hier nicht anführen.
Die Berechnung der Werte der jeweiligen Indikatoren findet nur im Moment der Eröffnung einer neuen Bar statt. Es erleichtert den Test. Dazu verfügt die Basisklasse CRiIndBase über das spezielle Modul NewBarDetecter. Diese Klasse stellt die Eröffnung der neuen Bar fest und signalisiert das über die Methode IsNewBar(), die dann ein 'true' zurückgibt.
Jetzt folgt der Code des Test-Experten. Er heißt TestIndEA.mq5:
//+------------------------------------------------------------------+ //| TestIndEA.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, Vasiliy Sokolov." #property link "https://www.mql5.com" #property version "1.00" #include <Object.mqh> #include <Arrays\ArrayObj.mqh> #include "RiIndBase.mqh" #include "RiIndMacd.mqh" #include "RiIndStoch.mqh" #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Die Parameter des MACD | //+------------------------------------------------------------------+ struct CMacdParams { int slow_period; int fast_period; int signal_period; }; //+------------------------------------------------------------------+ //| Die Parameter der Stochastik | //+------------------------------------------------------------------+ struct CStochParams { int k_period; int k_slowed; int d_period; }; input ENUM_INDICATOR_TYPE IndType = INDICATOR_SYSTEM; // Der Typ des Indikators string Symbols[] = {"EURUSD", "GBPUSD", "USDCHF", "USDJPY"}; CMacdParams MacdParams[3]; CStochParams StochParams[3]; CArrayObj ArrayInd; //+------------------------------------------------------------------+ //| Initialisierung | //+------------------------------------------------------------------+ int OnInit() { MacdParams[0].fast_period = 3; MacdParams[0].slow_period = 13; MacdParams[0].signal_period = 6; MacdParams[1].fast_period = 9; MacdParams[1].slow_period = 26; MacdParams[1].signal_period = 12; MacdParams[2].fast_period = 18; MacdParams[2].slow_period = 52; MacdParams[2].signal_period = 24; StochParams[0].k_period = 6; StochParams[0].k_slowed = 3; StochParams[0].d_period = 3; StochParams[1].k_period = 12; StochParams[1].k_slowed = 5; StochParams[1].d_period = 6; StochParams[2].k_period = 24; StochParams[2].k_slowed = 7; StochParams[2].d_period = 12; // Hier werden 504 Indikatoren MACD und Stochastik erstellt for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PeriodByIndex(period), IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PeriodByIndex(period), IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } printf("Create " + (string)ArrayInd.Total() + " indicators sucessfully"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Bei einem neuen Tick | //+------------------------------------------------------------------+ void OnTick() { for(int i = 0; i < ArrayInd.Total(); i++) { CIndBase* ind = ArrayInd.At(i); double value = ind.GetLastValue(0); double value_signal = ind.GetLastValue(1); } } //+------------------------------------------------------------------+ //| Rückgabe des Zeitrahmens je nach Index | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES PeriodByIndex(int index) { switch(index) { case 0: return PERIOD_CURRENT; case 1: return PERIOD_M1; case 2: return PERIOD_M2; case 3: return PERIOD_M3; case 4: return PERIOD_M4; case 5: return PERIOD_M5; case 6: return PERIOD_M6; case 7: return PERIOD_M10; case 8: return PERIOD_M12; case 9: return PERIOD_M15; case 10: return PERIOD_M20; case 11: return PERIOD_M30; case 12: return PERIOD_H1; case 13: return PERIOD_H2; case 14: return PERIOD_H3; case 15: return PERIOD_H4; case 16: return PERIOD_H6; case 17: return PERIOD_H8; case 18: return PERIOD_H12; case 19: return PERIOD_D1; case 20: return PERIOD_W1; case 21: return PERIOD_MN1; default: return PERIOD_CURRENT; } } //+------------------------------------------------------------------+
Das Wichtigste befindet sich in der Funktion OnInit(). Hier werden Symbole, Zeitrahmen und die Parameter festgelegt. Die Parameter der Indikatoren werden in den Hilfsstrukturen CMacdParams und CStochParams gespeichert.
Die Werte selbst werden in der Funktion OnTick() bearbeitet. Von allen Indikatoren werden über die Methode GetLastalue() deren letzte Werte abgefragt. Da die Anzahl der berechneten Puffer bei beiden Indikatoren identisch ist, sind zusätzliche Tests nicht erforderlich, und die Werte beider Indikatoren können durch die für beide gültige Methode GetLastValue() erfragt werden.
Der Start des Experten zeigt Folgendes: im Modus der Berechnung mit den Standardindikatoren wurden 11,9 Gigabyte des Computer-RAMs belegt, im Modus der Berechnung der Indikatoren mit den Ringpuffer wurden nur 2,9 Gigabyte beansprucht. Die Tests wurden auf einem PC mit 16 GB RAM durchgeführt.
Wir sollten jedoch bedenken, dass der Speicher eigentlich nicht durch die Verwendung der Ringpuffer, sondern durch die Platzierung der Berechnungsmodule im EA-Code eingespart wurde. Die Platzierung der Module spart bereits viel Speicherplatz.
Den Speicherverbrauch um ein Viertel zu reduzieren ist ein sehr anständiges Ergebnis. Trotzdem werden immer noch fast 3 GB RAM benötigt. Könnte man diese Zahl noch weiter verringern? Ja, es müssten nur die Anzahl der Zeitrahmen optimiert werden. Versuchen wir, den Testcode etwas zu ändern und verwenden wir nur ein Zeitrahmen (PERIOD_M1) statt der 21. Die Anzahl der Indikatoren bleibt gleiche, auch wenn einige von ihnen dupliziert werden:
... for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PERIOD_M1, IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PERIOD_M1, IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } ...
Damit belegen die gleichen 504 Indikatoren im Modus der inneren Berechnung nur mehr 548 MB des RAMs. Genauer gesagt wird der Speicher nicht von den Indikatoren selbst verbraucht, sondern von den für die Berechnung der Indikatoren heruntergeladenen Daten. Das Terminal selbst benötigt ca. 100 MB des RAM, so dass die heruntergeladenen Daten noch weniger belegen. Damit haben wir den Speicherverbrauch weiter deutlich reduziert:
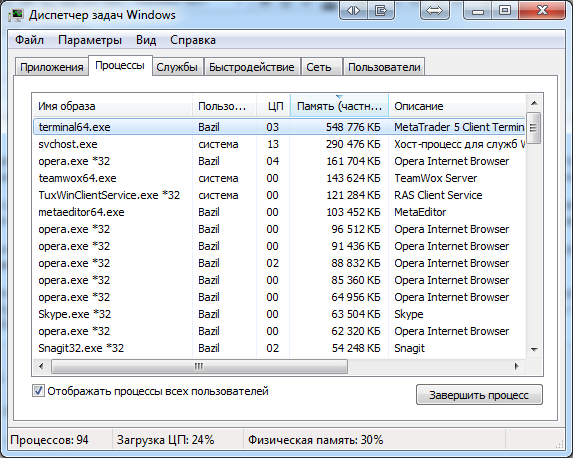
Abb. 9. Geringster Speicherverbrauch
Der Speicherverbrauch auf der Grundlage der Systemindikatoren in diesem Modus erfordert 1,9 GB RAM, was auch deutlich niedriger ist als wenn alle 21 Zeitrahmen verwendet werden würden.
Optimieren der Testszeit des Experten
MetaTrader 5 kann auf mehrere Handelsinstrumente gleichzeitig zugreifen, sowie auf einen beliebigen Zeitrahmen für jedes Instrument. Dies ermöglicht das Erstellen und Testen von Experten, die mit mehreren Symbolen gleichzeitig handeln. Der Zugriff auf das Handelsumfeld kann einige Zeit in Anspruch nehmen, insbesondere wenn wir die Daten der Indikatoren abfragen, die auf der Grundlage dieser Symbole berechnet werden. Die Zugriffszeit kann verkürzt werden, wenn alle Berechnungen innerhalb eines EAs durchgeführt werden. Lassen Sie uns dies anhand unseres vorherigen Beispiels im Strategie-Tester des MetaTrader 5 veranschaulichen. Zuerst testen wir den EA mit EURUSD M1 desa letzten Monats im Modus "Nur Eröffnungspreise". Zur Berechnung verwenden wir die Systemindikatoren. Der Test mit einem Intel Core i7870 2.9 Ghz dauerte 58 Sekunden:
2017.03.30 14:07:12.223 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:57.923.
Jetzt führen wir den gleichen Test im internen Berechnungsmodus durch:
2017.03.30 14:08:29.472 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:12.292.
Wie man sehen kann, hat sich die Rechenzeit mit nur 12 Sekunden in diesem Modus deutlich verringert.
Schlussfolgerungen und Vorschläge zur Leistungssteigerung
Wir haben die Verwendung des Speichers bei der Entwicklung von Indikatoren getestet und die Testgeschwindigkeit in zwei Betriebsmodi gemessen. Bei internen Berechnungen auf Basis von Ringpuffern ist es uns gelungen, den Speicherverbrauch zu reduzieren und die Performance mehrfach zu verbessern. Natürlich sind die vorgestellten Beispiele weitgehend künstlich. Die meisten Programmierer müssen nie mehr 500 Indikatoren gleichzeitig verwenden und auf allen möglichen Zeitrahmen testen. Ein solcher "Stresstest" hilft jedoch, die teuersten Mechanismen zu identifizieren und deren Einsatz zu minimieren. Hier sind ein paar Tipps, basierend auf den Testergebnissen:
- Setzen Sie den Berechnungsblock des Indikators in EAs. Das spart Zeit und Arbeitsspeicher beim Testen.
- Vermeiden Sie, wenn möglich, Anfragen mehrere Zeitrahmen. Verwenden Sie stattdessen einen einzigen (niedrigsten) Zeitrahmen für die Berechnungen. Wenn Sie z. B. zwei Indikatoren auf M1 und H1 berechnen müssen, M1-Daten abfragen und die in H1 umwandeln und diese Daten dann für die Berechnung eines Indikators auf H1 verwenden. Dieser Ansatz ist komplizierter, spart aber erheblich Speicherplatz.
- Nutzen Sie Ihre Rechenressourcen sparsam in Ihrer Arbeit. Die Ringpuffer sind gut dafür. Sie benötigen genau so viel Speicherplatz, wie für die Berechnung der Indikatoren benötigt wird. Außerdem können einige Berechnungsalgorithmen optimiert werden, wie z. B. die Suche nach Maxima/Minima.
- Erstellen Sie eine universelle Schnittstelle für die Arbeit mit Indikatoren und verwenden Sie sie, um ihre Werte zu erhalten. Wenn es schwierig ist, einen Indikator im internen Block zu berechnen, ruft die Schnittstelle den externe Indikator des MetaTraders auf. Wenn Sie einen internen Indikatorblock erstellen, schließen Sie ihn einfach an diese Schnittstelle an. Der EA erfährt in diesem Fall nur eine minimale Änderung.
- Bewerten Sie die Optimierungsfunktionen kritisch. Wenn Sie einen Indikator mit einem Symbol verwenden, könnte es so belassen werden wie es ist, ohne es in die interne Berechnung umzurechnen. Die Zeit, die für eine solche Konvertierung aufgewendet werden müsste, kann den Gesamtleistungsgewinn deutlich übersteigen.
Fazit
Wir haben die Entwicklung von Ringpuffern und ihre praktische Anwendung bei der Erstellung von Indikatoren beschrieben. Es ist schwierig, relevantere Anwendung für Ringpuffer zu finden als im Handel. Umso erstaunlicher ist es, dass dieser Algorithmus zur Datenkonstruktion bisher in der MQL-Community noch nicht abgedeckt ist.
Die Ringpuffer und die darauf basierenden Indikatoren sparen Speicherplatz und ermöglichen eine schnelle Berechnung. Der Hauptvorteil der Ringpuffer ist die einfache Implementierung von Indikatoren, die auf ihnen basieren, da die meisten von ihnen nach dem FIFO-Prinzip (first in - first out) arbeiten. Daher treten die Probleme in der Regel auf, wenn Indikatoren nicht in einem Ringspeicher berechnet werden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3047
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Cross-Plattform Expert Advisor: Order-Manager
Cross-Plattform Expert Advisor: Order-Manager
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Großartige Arbeit hier, vielen Dank an den Autor. Vielleicht ist der Fehler, den Sie sehen, Savio, ist hier:
int RingBuffer::iToRealInd(int iIndex)
{
if(iIndex >= iNumElements() || iIndex < 0)
return iBufferSize-1; //previous bug was caused by no -1 here
...
Ich habe das -1 in der letzten zitierten Zeile eingefügt; es war vorher nicht da und führte dazu, dass ein falscher Index zurückgegeben wurde. Beachten Sie, dass ich die Namen der Variablen/Methoden an meinen Programmierstil angepasst habe, aber die Idee ist die gleiche
Ich habe Ihre Korrektur ausprobiert, aber es wird immer noch nicht richtig aktualisiert. Es scheint etwas zu fehlen, und ich kann das Problem nicht finden, wenn ich versuche, den Ringpuffer bei der Bildung eines neuen Balkens auszuführen. Wenn der Markt läuft, werden die High/Low-Linien komplett durcheinander gebracht. Der Code funktioniert sehr gut und sehr schnell bei der Verarbeitung von alten Daten, aber mit neuen Daten ankommen während der Bildung eines neuen bar, es funktioniert einfach nicht für mich.
Wenn ich einige Anmerkungen machen darf:
1. In der Klasse void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value), in der Methode " OnChangeValue" in der Zeile
.
Bild: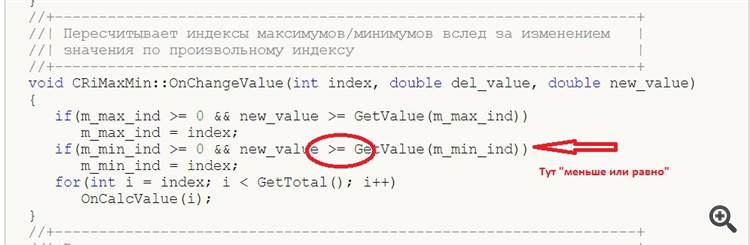
Tippfehler - Vorzeichen "kleiner oder gleich".

2. Bei der Suche nach Min- und Max-Elementen eines Arrays, wenn es genau als Ringpuffer verwendet wird (wenn neue Elemente an den Anfang des Arrays geschrieben werden), sind min und mah falsch definiert. Das Minimum ist größer als das Maximum. In einem Array. Alles funktioniert mit den Standardmethoden (ArrayMinimum und ArrayMaximum).
Bild:
Irgendwo geht die Indizierung in die Irre. Ich kann es nicht selbst beheben. Wenn es jemand beheben kann, wäre das großartig. Ich habe einen Test-Ratgeber angehängt.
Sie haben einen Fehler in ToRealInd(int index).
Es sollte lauten: