
MQL5 Cookbook - Creating a ring buffer for fast calculation of indicators in a sliding window
Contents
- Introduction
- Moving average calculation issues
- Ring buffer theory
- Working prototype
- Example of calculating a simple moving average in the ring buffer
- Example of calculating an exponential moving average in the ring buffer
- Calculating Highs/Lows in the ring buffer
- Integrating the ring buffer with the AlgLib library
- Building MACD based on the ring primitives
- Building Stochastic based on the ring primitives
- Optimizing memory usage
- Optimizing EA testing time
- Conclusions and suggestions for improving performance
- Conclusion
Introduction
Most calculations performed by traders are conducted in a sliding window. This happens due to the very nature of market data which almost always arrive in a continuous stream regardless of whether we deal with prices, bids or trading volumes. Typically, a trader needs to calculate a value for a certain period of time. For example, if we calculate a moving average, we deal with an average price value for the last N bars, where N is the moving average period. The time spent calculating the mean value should not depend on the period of this average in this case. However, it is not always easy to implement an algorithm with such a property in real conditions. From an algorithmic point of view, it is much easier to recalculate the average value completely when a new bar arrives. The ring buffer algorithm solves the efficient calculation issue providing a sliding window to the calculation block so that its internal calculations remain simple and as efficient as possible.
Moving average calculation issues
Let's consider calculating the moving average. The simple algorithm allows us to illustrate possible issues we may face when plotting it. The average value is calculated using the well-known equation:
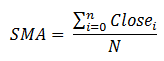
Let's implement it by writing a simple MQL5 script:
//| SMA.mq5 |
//| Copyright 2015, MetaQuotes Software Corp. |
//| http://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2015, MetaQuotes Software Corp."
#property link "http://www.mql5.com"
#property version "1.00"
input int N = 10; // Moving average period
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//---
double closes[];
if(CopyClose(Symbol(), Period(), 0, N, closes)!= N)
{
printf("Need more data");
return;
}
double sum = 0.0;
for(int i = 0; i < N; i++)
sum += closes[i];
sum /= N;
printf("SMA: " + DoubleToString(sum, Digits()));
}
//+------------------------------------------------------------------+
At first sight, all looks good. The script obtains the moving average value and displays it in the terminal window. But what should we do when working in a sliding window? The last quote changes and new bars appear constantly. The algorithm re-calculate the moving average value each time using very resource-intensive operations:
- Copying N elements to the destination array;
- Full search through the destination array in the 'for' loop.
The last operation is the most resource intensive. The period of 10 there requires 10 iterations, while the period of 500 needs 500 ones. This means the algorithm complexity directly depends on the averaging period and can be written as O(n), where O is a complexity function.
However, there is much faster algorithm for calculating the moving average in a sliding window. To implement it, we need to know the sum of all values in the previous calculation:
SMA = (Sum of all values - first value of a sliding window + new value)/Moving average period
The algorithm complexity function is an O(1) constant that does no depend on the averaging period. The performance of such an algorithm is higher, but it is more difficult to implement. Each time a new bar appears, the following steps should be performed:
- subtract the value that has been added first from the current sum and then remove that value from the series;
- add the value that has been added last to the current sum and then include that value to the series;
- divide the current sum by the averaging period and return it as a moving average.
If the last value is not added, but only updated, the algorithm becomes even more complicated:
- define the updated value and remember its current state;
- subtract the value remembered at the previous step from the current sum;
- replace the value with the new one;
- add the new value to the current sum;
- divide the current sum by the averaging period and return it as a moving average.
Another challenge is that MQL5 (similar to most other system programming languages) has built-in tools for working with basic data types (like arrays) only. The arrays without proper modification are not suitable for this role, since in most obvious cases we need to arrange a FIFO queue (First In - First Out), i.e. arrange a list where the first added element is removed when a new element appears. Arrays allow both removing and adding elements. However, these operations are rather resource-intensive since each of them re-distributes the array.
Let's turn to the ring buffer to avoid such difficulties and implement a truly efficient algorithm.
Ring buffer theory
While working the ring buffer, you are able to add and remove elements without re-distributing the array. If we assume that the number of elements in the array always remains constant (which is the case for calculations in a sliding window), adding a new element is followed by the removal of an old one. Thus, the total number of elements does not change, but their indexing changes each time a new element is added. The last element becomes the penultimate one, the second element takes the place of the first one, while the first one leaves the queue permanently.
This feature allows the ring buffer to be based on a regular array. Let's create a class based on a regular array:
{
private:
double m_array[];
};
Suppose that our buffer will consist of only three elements. In this case, the first element will be added to the array slot with the index 0, the second one will take the slot with the index 1, while the third element will occupy the slot 2. What happens if we add the fourth element? Apparently, the first element will be removed. Then, the most suitable place for the fourth element will be the place of the first one meaning its index will again be zero. How to calculate this index? Let's apply the special operation 'remainder of division'. In MQL5, this operation is denoted by a special percent symbol %. Since the numeration starts from zero, the fourth element will be the third in the queue and its placement index will be calculated using the following equation:
Here, 'total' is the total buffer size. In our example, three is divided into three without remainder. Thus, index contains a residue equal to zero. Subsequent elements will be placed according to the same rules: the number of the added element will be divided by the amount of elements in the array. The remainder of this division will be the actual index in the circular buffer. Below is a conditional calculation of indices of the first 8 elements added to the ring buffer with the dimension 3:
0 % 3 = [0] 1 % 3 = [1] 2 % 3 = [2] 3 % 3 = [0] 4 % 3 = [1] 5 % 3 = [2] 6 % 3 = [0] 7 % 3 = [1]...
Working prototype
Now, that we have a good understanding of the ring buffer, it is time to develop a working prototype. Our ring buffer is to have three basic features:
- adding a new value;
- removing the last value;
- changing the value at an arbitrary index.
The latter function is necessary for working in real time when the last bar is in the state of formation and the closing price constantly changes.
Also, our buffer has two basic properties. It contains the maximum buffer size and the current number of its elements. Most of the time, these values will match, because when the elements fill the entire buffer size, each subsequent element overwrites the oldest one. Thus, the total number of elements remains unchanged. However, during the initial filling of the buffer, the values of these properties will differ. The maximum number of elements will be a variable property. The user will be able to either increase or reduce it.
The oldest element will be removed automatically without an explicit user request. This is an intentional behavior since the manual removal of old elements complicates the calculation of auxiliary statistics.
The greatest complexity of the algorithm lies in the calculation of real indices of the internal buffer which is to store the real values. For example, if a user requests an element with index 0, the actual value the element is located in may be different. When adding the 17 th element to the ring buffer with the dimension of 10, the zero element may be located at index 8, while the last (ninth) one may be at index 7.
Let's have a look at the ring buffer header file and the contents of the main methods to see the work of the ring buffer's main operations:
//+------------------------------------------------------------------+ //| Double ring buffer | //+------------------------------------------------------------------+ class CRiBuffDbl { private: bool m_full_buff; int m_max_total; int m_head_index; protected: double m_buffer[]; //Ring buffer for direct access. Note: the indices do not match their counting number! ... int ToRealInd(int index); public: CRiBuffDbl(void); void AddValue(double value); void ChangeValue(int index, double new_value); double GetValue(int index); int GetTotal(void); int GetMaxTotal(void); void SetMaxTotal(int max_total); void ToArray(double& array[]); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CRiBuffDbl::CRiBuffDbl(void) : m_full_buff(false), m_head_index(-1), m_max_total(0) { SetMaxTotal(3); } //+------------------------------------------------------------------+ //| Set the new size of the ring buffer | //+------------------------------------------------------------------+ void CRiBuffDbl::SetMaxTotal(int max_total) { if(ArraySize(m_buffer) == max_total) return; m_max_total = ArrayResize(m_buffer, max_total); } //+------------------------------------------------------------------+ //| Get the actual ring buffer size | //+------------------------------------------------------------------+ int CRiBuffDbl::GetMaxTotal(void) { return m_max_total; } //+------------------------------------------------------------------+ //| Get the index value | //+------------------------------------------------------------------+ double CRiBuffDbl::GetValue(int index) { return m_buffer[ToRealInd(index)]; } //+------------------------------------------------------------------+ //| Get the total number of elements | //+------------------------------------------------------------------+ int CRiBuffDbl::GetTotal(void) { if(m_full_buff) return m_max_total; return m_head_index+1; } //+------------------------------------------------------------------+ //| Add a new value to the ring buffer | //+------------------------------------------------------------------+ void CRiBuffDbl::AddValue(double value) { if(++m_head_index == m_max_total) { m_head_index = 0; m_full_buff = true; } //... m_buffer[m_head_index] = value; } //+------------------------------------------------------------------+ //| Replace the previously added value with the new one | //+------------------------------------------------------------------+ void CRiBuffDbl::ChangeValue(int index, double value) { int r_index = ToRealInd(index); double prev_value = m_buffer[r_index]; m_buffer[r_index] = value; } //+------------------------------------------------------------------+ //| Convert the virtual index into a real one | //+------------------------------------------------------------------+ int CRiBuffDbl::ToRealInd(int index) { if(index >= GetTotal() || index < 0) return m_max_total; if(!m_full_buff) return index; int delta = (m_max_total-1) - m_head_index; if(index < delta) return m_max_total + (index - delta); return index - delta; }
The basis of this class is a pointer to the last added element m_head_index. When adding a new element using the AddValue method, it is increased by one. If its value starts exceeding the array size, it is reset.
The most complex function of the ring buffer is the internal ToRealInd method. It accepts a buffer index from the user's point of view and returns the actual index of the array the required element is located at.
As we can see, the ring buffer is quite simple. With the exception of the pointer arithmetic, it supports elementary actions adding a new element and providing access to an arbitrary element using GetValue(). However, this functionality is usually applied to conveniently arrange the calculation of a necessary parameter, like an ordinary moving average or High/Low search algorithm. The ring buffer allows you to calculate a set of statistical objects. These are all sorts of indicators or statistical criteria, like variance and standard deviation. Therefore, it is impossible to supply the ring buffer class with all calculation algorithms at once. In fact, we do not need that. Instead, we can apply a more flexible solution – derived classes implementing a particular indicator or statistics calculation algorithm.
To let these derived classes calculate their values conveniently, the ring buffer should be supplied with additional methods. Let's call them event methods. These are usual methods placed in the 'protected' section. All these methods can be redefined and they start with On:
//+------------------------------------------------------------------+ //| Double ring buffer | //+------------------------------------------------------------------+ class CRiBuffDbl { private: ... protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double prev_value, double new_value); virtual void OnChangeArray(void); virtual void OnSetMaxTotal(int max_total); };
Each time there are any changes in the ring buffer, a method is called to signal this. For example, if a new value appears in the buffer, the OnAddValue method is called. Its parameter contains the value to be added. If we re-define this method in a class derived from the ring buffer, the appropriate derived class calculation block is called each time a new value is added.
The ring buffer contains five events that can be monitored in a derived class (appropriate methods are specified in parentheses):
- adding a new element (OnAddValue);
- removing an old element (OnRemoveValue);
- changing an element by an arbitrary index (OnChangeValue);
- changing the entire contents of the ring buffer (OnChangeArray);
- changing the maximum number of elements in the ring buffer (OnSetMaxTotal).
A special attention should be paid to the OnChangeArray event. It is called when the indicator re-calculation requires access to the entire array of accumulated values. In this case, it is enough to re-define the method in the derived class. In the method, we need to get the entire array of values using the ToArray function and make the appropriate calculation. The example of such calculation can be found in the section devoted to the integration of the ring buffer with the AlgLib library below.
The ring buffer class is called CRiBuffDbl. As the name implies, it works with double values. Real numbers are the most common data type for computational algorithms. However, apart from real numbers, we may also need integers. Therefore, the set of classes also contains the CRiBuffInt class. On present-day PCs, fixed-point calculations are performed faster than floating-point ones. This is why it is better to use CRiBuffInt for specific integer tasks.
The approach presented here does not apply template classes that allow description and working with a universal <template T> type. This is done intentionally, since it is assumed that specific calculation algorithms are inherited directly from the circular buffer, and each algorithm of this kind works with a clearly defined data type.
Example of calculating a simple moving average in the ring buffer
We have considered the internal arrangement of classes implementing the ring buffer principle. Now, it is time to solve a few practical problems using our knowledge. Let's start with a simple task - development of a well-known Simple Moving Average indicator. This is a common moving average meaning that we need to divide a series sum by the average period. Let's repeat the calculation formula from the beginning of the article:
SMA = (Sum of all values - first value of a sliding window + new value)/Moving average period
To implement the algorithm, we need to re-define two methods in the class derived from CRiBuffDbl: OnAddValue and OnRemoveValue. The average value is to be calculated in the Sma method. Below is a code of the resulting class:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Calculate the moving average in the ring buffer | //+------------------------------------------------------------------+ class CRiSMA : public CRiBuffDbl { private: double m_sum; protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); public: CRiSMA(void); double SMA(void); }; CRiSMA::CRiSMA(void) : m_sum(0.0) { } //+------------------------------------------------------------------+ //| Increase the total sum | //+------------------------------------------------------------------+ void CRiSMA::OnAddValue(double value) { m_sum += value; } //+------------------------------------------------------------------+ //| Decrease the total sum | //+------------------------------------------------------------------+ void CRiSMA::OnRemoveValue(double value) { m_sum -= value; } //+------------------------------------------------------------------+ //| Change the total sum | //+------------------------------------------------------------------+ void CRiSMA::OnChangeValue(int index,double del_value,double new_value) { m_sum -= del_value; m_sum += new_value; } //+------------------------------------------------------------------+ //| Return the simple moving average | //+------------------------------------------------------------------+ double CRiSMA::SMA(void) { return m_sum/GetTotal(); }
Apart from the methods reacting to adding or removing an element (OnAddValue and OnRemoveValue, respectively), we needed to redefine yet another method called when changing an arbitrary element (OnChangeValue). The ring buffer supports arbitrary change of any included element, therefore such a change should be tracked. Usually, only the last element is changed (in the last bar formation mode). This case is processed by the OnChangeValue event that is to be re-defined.
Let's write a custom indicator using the ring buffer class for calculating the moving average:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_chart_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiSMA.mqh> input int MaPeriod = 13; double buff[]; CRiSMA Sma; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); Sma.SetMaxTotal(MaPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { Sma.AddValue(price[i]); buff[i] = Sma.SMA(); calc = true; } if(!calc) { Sma.ChangeValue(MaPeriod-1, price[rates_total-1]); buff[rates_total-1] = Sma.SMA(); } return(rates_total-1); } //+------------------------------------------------------------------+
At the start of the calculation, the indicator simply adds new values to the ring buffer of the moving average. You do not have to control the number of added values. All calculations and removals of obsolete elements occur automatically. If the indicator is called when changing the price of the last bar, the last moving average value should be replaced with a new one. The ChangeValue method is responsible for that.
The graphical display of the indicator is equivalent to the standard moving average:
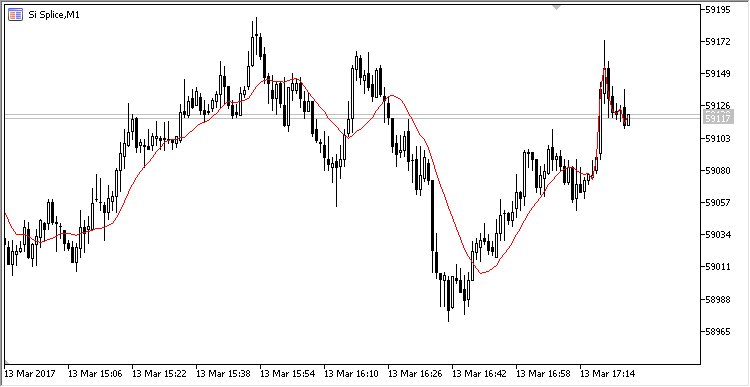
Fig. 1. The simple moving average calculated in the ring buffer
Example of calculating an exponential moving average in the ring buffer
Let's try the more complicated case – calculation of the exponential moving average. Unlike the simple average, the exponential one is not affected by removal of an old element from the value buffer, therefore we need to re-define only two methods (OnAddValue and OnChangeValue) to calculate it. Similar to the previous example, let's create the CRiEMA class derived from CRiBuffDbl and redefine the appropriate methods:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Calculate the exponential moving average in the ring buffer | //+------------------------------------------------------------------+ class CRiEMA : public CRiBuffDbl { private: double m_prev_ema; // Previous EMA value double m_last_value; // Last price value double m_smoth_factor; // Smoothing factor bool m_calc_first_v; // Flag indicating the first value calculation double CalcEma(); // Direct average calculation protected: virtual void OnAddValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiEMA(void); double EMA(void); }; //+------------------------------------------------------------------+ //| Subscribe to value adding/changing notifications | //+------------------------------------------------------------------+ CRiEMA::CRiEMA(void) : m_prev_ema(EMPTY_VALUE), m_last_value(EMPTY_VALUE), m_calc_first_v(false) { } //+------------------------------------------------------------------+ //| Calculate smoothing factor according to MetaQuotes EMA equation | //+------------------------------------------------------------------+ void CRiEMA::OnSetMaxTotal(int max_total) { m_smoth_factor = 2.0/(1.0+max_total); } //+------------------------------------------------------------------+ //| Increase the total sum | //+------------------------------------------------------------------+ void CRiEMA::OnAddValue(double value) { //Calculate the previous EMA value if(m_prev_ema != EMPTY_VALUE) m_prev_ema = CalcEma(); //Save the current price m_last_value = value; } //+------------------------------------------------------------------+ //| Correct EMA | //+------------------------------------------------------------------+ void CRiEMA::OnChangeValue(int index,double del_value,double new_value) { if(index != GetMaxTotal()-1) return; m_last_value = new_value; } //+------------------------------------------------------------------+ //| Direct EMA calculation | //+------------------------------------------------------------------+ double CRiEMA::CalcEma(void) { return m_last_value*m_smoth_factor+m_prev_ema*(1.0-m_smoth_factor); } //+------------------------------------------------------------------+ //| Get the simple moving average | //+------------------------------------------------------------------+ double CRiEMA::EMA(void) { if(m_calc_first_v) return CalcEma(); else { m_prev_ema = m_last_value; m_calc_first_v = true; } return m_prev_ema; }
The CalcEma method is responsible for calculating the moving average. It returns the sum of two products: the last known previous value multiplied by a smoothing factor plus the previous indicator value multiplied by the inverse of the smoothing factor. If the previous value of the indicator has not been calculated yet, the very first value placed in the buffer is taken for it (in our case, it is the zero bar Close price).
Let's develop an indicator similar to the one in the previous section to display calculation on the chart. It will look as follows:
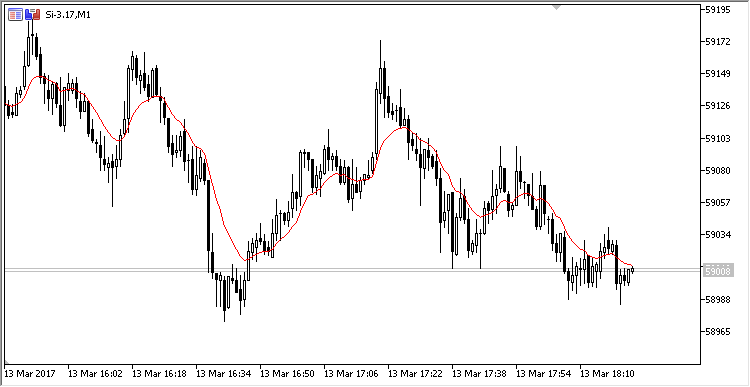
Fig. 2. The exponential moving average calculated in the ring buffer
Calculating Highs/Lows in the ring buffer
The most challenging and exciting task is calculation of Highs and Lows in a sliding window. Of course, this can be easily done by simply referring to the ArrayMaximum and ArrayMinimum standard functions. However, all advantages of calculating in a sliding window disappear in this case. If the data are added and removed from the buffer in sequence, it is possible to calculate Highs and Lows without performing a full search. Suppose that two additional values are calculated for each new value added to the buffer. The first one specifies how many previous elements are below the current element, while the second one shows how many previous elements are above the current element. The first value is used to efficiently search for a High, while the second one is applied to search for a Low.
Now, imagine that we are dealing with common price bars and we need to calculate extreme prices by their High values over a certain period. To do this, let's add a label above each bar that contains the number of previous bars with Highs below the current bar's High. The sequence of bars is displayed in the figure below:
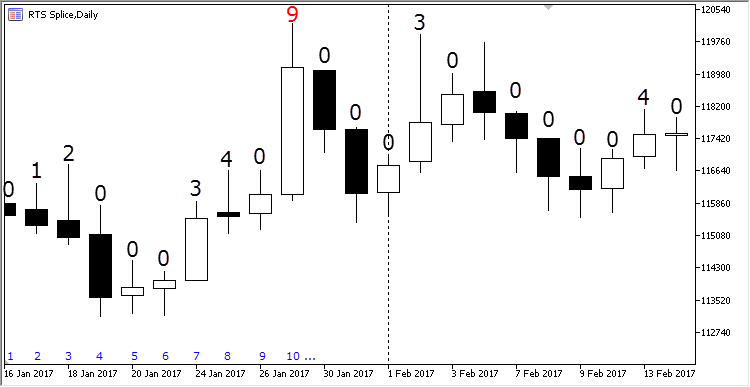
Fig. 3. Bars' extreme points hierarchy
The first bar always has a zero extreme value, since there are no previous values to check. The bar #2 is above it. Therefore, its extremum index is one. The third bar is above the previous one meaning it is above the first bar as well. Its extreme value is two. It is followed by three bars, each of which is lower than the previous one. All of them are lower than the bar #3, therefore their extreme values are zero. The seventh bar is above the previous three but below the fourth one, therefore its extremum index is three. Similarly, an extremum index is calculated for each new bar when it is added.
When all previous indices are calculated, we can easily obtain the current bar's extreme point. To do this, we should simply compare the bar's extreme point with others. We can directly access each subsequent extreme point skipping several bars in a row since we know its index thanks to the displayed numbers. The entire process is shown below:
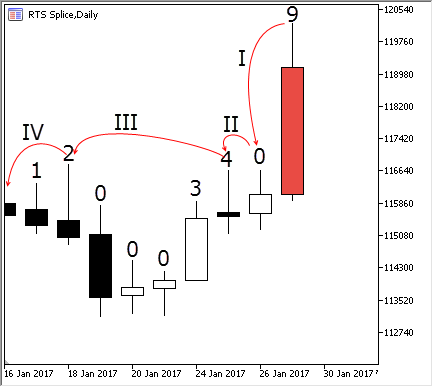
Fig. 4. looking for the current bar's extreme point
Suppose that we add a bar marked in red. This is a bar with the number 9, since the numbering starts from zero. To define its extremum index, let's compare it with the bar #8 by executing step I: the bar turns out to be higher, therefore its extreme point is equal to one. Let's compare it with the bar #7 by completing step II — it turns out to be higher as well. Since the bar #7 is above the previous four, we can immediately compare our last bar with the bar #3 by completing step III. The bar #9 is above the bar #3 and, therefore, higher than all bars at the moment. Due to to the previously calculated indices, we avoided comparison with four intermediate bars, which are certainly below the current one. This is how the fast search for extreme values works in the ring buffer. The search for Low works the same way. The only difference is the usage of the additional Lows index.
Now that the algorithm has been described, let's examine its source code. The presented class is interesting in that two ring buffers of the CRiBuffInt type are also used as auxiliary buffers. Each of them contains the High and Low indices respectively.
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiBuffInt.mqh" //+------------------------------------------------------------------+ //| Calculate the exponential moving average in the ring buffer | //+------------------------------------------------------------------+ class CRiMaxMin : public CRiBuffDbl { private: CRiBuffInt m_max; CRiBuffInt m_min; bool m_full; int m_max_ind; int m_min_ind; protected: virtual void OnAddValue(double value); virtual void OnCalcValue(int index); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiMaxMin(void); int MaxIndex(int max_period = 0); int MinIndex(int min_period = 0); double MaxValue(int max_period = 0); double MinValue(int min_period = 0); void GetMaxIndexes(int& array[]); void GetMinIndexes(int& array[]); }; CRiMaxMin::CRiMaxMin(void) { m_full = false; m_max_ind = 0; m_min_ind = 0; } void CRiMaxMin::GetMaxIndexes(int& array[]) { m_max.ToArray(array); } void CRiMaxMin::GetMinIndexes(int& array[]) { m_min.ToArray(array); } //+------------------------------------------------------------------+ //| Change the size of internal buffers according to the new size | //| of the main buffer | //+------------------------------------------------------------------+ void CRiMaxMin::OnSetMaxTotal(int max_total) { m_max.SetMaxTotal(max_total); m_min.SetMaxTotal(max_total); } //+------------------------------------------------------------------+ //| Calculate Max/Min indices | //+------------------------------------------------------------------+ void CRiMaxMin::OnAddValue(double value) { m_max_ind--; m_min_ind--; int last = GetTotal()-1; if(m_max_ind > 0 && value >= GetValue(m_max_ind)) m_max_ind = last; if(m_min_ind > 0 && value <= GetValue(m_min_ind)) m_min_ind = last; OnCalcValue(last); } //+------------------------------------------------------------------+ //| Calculate Max/Min indices | //+------------------------------------------------------------------+ void CRiMaxMin::OnCalcValue(int index) { int max = 0, min = 0; int offset = m_full ? 1 : 0; double value = GetValue(index); int p_ind = index-1; //Search for High while(p_ind >= 0 && value >= GetValue(p_ind)) { int extr = m_max.GetValue(p_ind+offset); max += extr + 1; p_ind = GetTotal() - 1 - max - 1; } p_ind = GetTotal()-2; //Search for Low while(p_ind >= 0 && value <= GetValue(p_ind)) { int extr = m_min.GetValue(p_ind+offset); min += extr + 1; p_ind = GetTotal() - 1 - min - 1; } m_max.AddValue(max); m_min.AddValue(min); if(!m_full && GetTotal() == GetMaxTotal()) m_full = true; } //+------------------------------------------------------------------+ //| Recalculate High/Low indices following the changes | //| of the value by an arbitrary index | //+------------------------------------------------------------------+ void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value) { if(m_max_ind >= 0 && new_value >= GetValue(m_max_ind)) m_max_ind = index; if(m_min_ind >= 0 && new_value >= GetValue(m_min_ind)) m_min_ind = index; for(int i = index; i < GetTotal(); i++) OnCalcValue(i); } //+------------------------------------------------------------------+ //| Get the maximum element index | //+------------------------------------------------------------------+ int CRiMaxMin::MaxIndex(int max_period = 0) { int limit = 0; if(max_period > 0 && max_period <= m_max.GetTotal()) { m_max_ind = -1; limit = m_max.GetTotal() - max_period; } if(m_max_ind >=0) return m_max_ind; int c_max = m_max.GetTotal()-1; while(c_max > limit) { int ext = m_max.GetValue(c_max); if((c_max - ext) <= limit) return c_max; c_max = c_max - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Get the minimum element index | //+------------------------------------------------------------------+ int CRiMaxMin::MinIndex(int min_period = 0) { int limit = 0; if(min_period > 0 && min_period <= m_min.GetTotal()) { limit = m_min.GetTotal() - min_period; m_min_ind = -1; } if(m_min_ind >=0) return m_min_ind; int c_min = m_min.GetTotal()-1; while(c_min > limit) { int ext = m_min.GetValue(c_min); if((c_min - ext) <= limit) return c_min; c_min = c_min - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Get the maximum element value | //+------------------------------------------------------------------+ double CRiMaxMin::MaxValue(int max_period = 0) { return GetValue(MaxIndex(max_period)); } //+------------------------------------------------------------------+ //| Get the minimum element value | //+------------------------------------------------------------------+ double CRiMaxMin::MinValue(int min_period = 0) { return GetValue(MinIndex(min_period)); }
This algorithm contains one more modification. It remembers the current Highs and Lows and if they are left unchanged, the MaxValue and MinValue methods return them bypassing the additional calculation.
Here is how the Highs and Lows look on the chart:
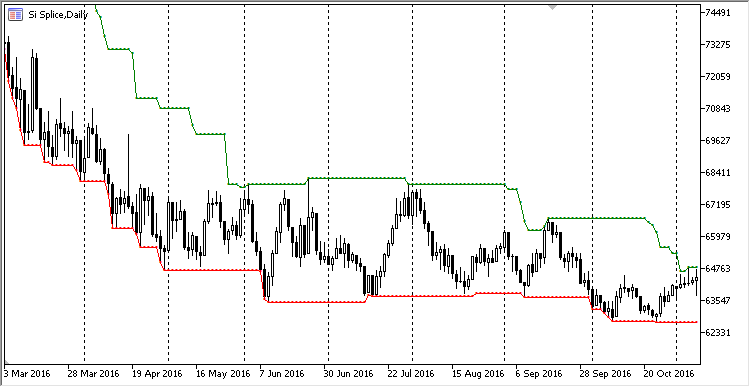
Fig. 5. The High/Low channel as an indicator
The High/Low definition class has advanced capabilities. It can return the extremum index in the ring buffer or its value only. Also, it is able to calculate the extreme value for a period less than the period of the ring buffer. To do this, specify a limiting period in the MaxIndex/MinIndex and MaxValue/MinValue methods.
Integrating the ring buffer with the AlgLib library
Another interesting example of using a ring buffer lies in the area of specialized Math calculations. Generally, statistics calculation algorithms are developed without consideration to a sliding window. This may cause inconvenience. The ring buffer solves that issue. Let's develop the indicator calculating the main Gaussian distribution parameters:
- mean value (Mean);
- standard deviation (StdDev);
- bell-shaped distribution asymmetry (Skewness);
- Kurtosis.
Let's apply the AlgLib::SampleMoments static method to calculate these characteristics. All we need to do is create the CRiGaussProperty ring buffer class and place a method inside the OnChangeArray handler. The full code of the indicator including the class:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiBuffDbl.mqh> #include <Math\AlgLib\AlgLib.mqh> //+------------------------------------------------------------------+ //| Calculate the main parameters of the Gaussian distribution | //+------------------------------------------------------------------+ class CRiGaussProperty : public CRiBuffDbl { private: double m_mean; // Mean double m_variance; // Variance double m_skewness; // Skewness double m_kurtosis; // Kurtosis protected: virtual void OnChangeArray(void); public: double Mean(void){ return m_mean;} double StdDev(void){return MathSqrt(m_variance);} double Skewness(void){return m_skewness;} double Kurtosis(void){return m_kurtosis;} }; //+------------------------------------------------------------------+ //| Calculation is performed in case of any array change | //+------------------------------------------------------------------+ void CRiGaussProperty::OnChangeArray(void) { double array[]; ToArray(array); CAlglib::SampleMoments(array, m_mean, m_variance, m_skewness, m_kurtosis); } //+------------------------------------------------------------------+ //| Gaussian distribution property type | //+------------------------------------------------------------------+ enum ENUM_GAUSS_PROPERTY { GAUSS_MEAN, // Mean GAUSS_STDDEV, // Deviation GAUSS_SKEWNESS, // Skewness GAUSS_KURTOSIS // Kurtosis }; input int BPeriod = 13; //Period input ENUM_GAUSS_PROPERTY Property; double buff[]; CRiGaussProperty RiGauss; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); RiGauss.SetMaxTotal(BPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { RiGauss.AddValue(price[i]); buff[i] = GetGaussValue(Property); calc = true; } if(!calc) { RiGauss.ChangeValue(BPeriod-1, price[rates_total-1]); buff[rates_total-1] = GetGaussValue(Property); } return(rates_total-1); } //+------------------------------------------------------------------+ //| Get the value of one of the Gaussian distribution properties | //+------------------------------------------------------------------+ double GetGaussValue(ENUM_GAUSS_PROPERTY property) { double value = EMPTY_VALUE; switch(Property) { case GAUSS_MEAN: value = RiGauss.Mean(); break; case GAUSS_STDDEV: value = RiGauss.StdDev(); break; case GAUSS_SKEWNESS: value = RiGauss.Skewness(); break; case GAUSS_KURTOSIS: value = RiGauss.Kurtosis(); break; } return value; }
As you can see from the above listing, the CRiGaussProperty class is very simple. However, this simplicity hides rich functionality. Now, you do not need to prepare a sliding array on each iteration for the CAlglib::SampleMoments function operation. Instead, simply add the new values in the AddValue method. The figure below shows the indicator operation result. Let's select the calculation of the standard deviation in the settings and plot it in the chart subwindow:
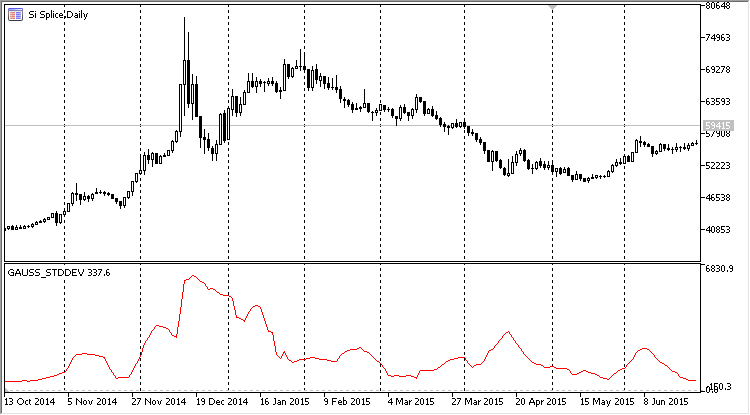
Fig. 6. Main Gaussian distribution parameters in the form of a sliding indicator
Building MACD based on the ring primitives
We have developed the three ring primitives: simple and exponential moving average, as well as the High/Low indicator. They are sufficient for building the main standard indicators based on simple calculations. For example, MACD consists of two exponential moving averages and one signal line based on a simple average. Let's try to develop the indicator using already available codes.
We have already applied two additional ring buffers within the CRiMaxMin class when dealing with the High/Low indicator. Let's do the same in case of MACD. When adding a new value, our class simply forwards it to its additional buffers and calculates a simple difference between them. The difference is forwarded to the third ring buffer and used when calculating a simple SMA. This is an MACD signal line:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiEMA.mqh" //+------------------------------------------------------------------+ //| Calculate moving average in the ring buffer | //+------------------------------------------------------------------+ class CRiMACD { private: CRiEMA m_slow_macd; // Fast exponential moving average CRiEMA m_fast_macd; // Slow exponential moving average CRiSMA m_signal_macd; // Signal line double m_delta; // Difference between fast and slow EMAs public: double Macd(void); double Signal(void); void ChangeLast(double new_value); void SetFastPeriod(int period); void SetSlowPeriod(int period); void SetSignalPeriod(int period); void AddValue(double value); }; //+------------------------------------------------------------------+ //| Re-calculate MACD | //+------------------------------------------------------------------+ void CRiMACD::AddValue(double value) { m_slow_macd.AddValue(value); m_fast_macd.AddValue(value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.AddValue(m_delta); } //+------------------------------------------------------------------+ //| Change MACD | //+------------------------------------------------------------------+ void CRiMACD::ChangeLast(double new_value) { m_slow_macd.ChangeValue(m_slow_macd.GetTotal()-1, new_value); m_fast_macd.ChangeValue(m_fast_macd.GetMaxTotal()-1, new_value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.ChangeValue(m_slow_macd.GetTotal()-1, m_delta); } //+------------------------------------------------------------------+ //| Get MACD histogram | //+------------------------------------------------------------------+ double CRiMACD::Macd(void) { return m_delta; } //+------------------------------------------------------------------+ //| Get the signal line | //+------------------------------------------------------------------+ double CRiMACD::Signal(void) { return m_signal_macd.SMA(); } //+------------------------------------------------------------------+ //| Get the fast period | //+------------------------------------------------------------------+ void CRiMACD::SetFastPeriod(int period) { m_slow_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Set the slow period | //+------------------------------------------------------------------+ void CRiMACD::SetSlowPeriod(int period) { m_fast_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Set the signal line period | //+------------------------------------------------------------------+ void CRiMACD::SetSignalPeriod(int period) { m_signal_macd.SetMaxTotal(period); }
Please note that CRiMacd is an independent class. It is not derived from CRiBuffDbl. Indeed, the CRiMacd class does not apply its own calculation buffers. Instead, ring primitive classes are placed as independent objects in the 'private' section ("inclusion" system).
The two main methods Macd() and Signal() return MACD and its signal line values. The resulting code is simple, and each buffer has the sliding period. The CRiMacd class does not track changes in the arbitrary element. Instead, it tracks changes in the last element only providing the indicator changes on a zero bar.
MACD calculated in the ring buffer visually looks the same as the standard indicator:
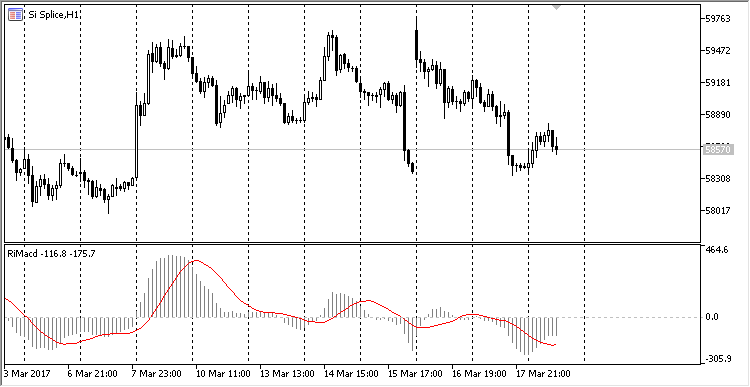
Fig. 7. MACD indicator calculated in the ring buffer
Building Stochastic based on the ring primitives
Let's plot the Stochastic indicator in a similar way. This indicator combines the search for extreme values with the moving average calculation. Thus, we use the already calculated algorithms here.
Stochastic applies the three price series: High prices (bars' High), Low prices (bars' Low) and Close prices (bars' Close). Its calculation is simple: first, the search for the High for High prices and the Low for Low prices is performed. The ratio of the current 'close' price to the High/Low range is calculated afterwards. Finally, that ratio is used to calculate the average value for N periods (the N indicator is called "K% slowing"):
K% = SMA((close-min)/((max-min)*100.0%), N)
Another average with the period of %D (the signal line similar to the MACD one) is calculated for the obtained K%:
Signal D% = SMA(K%, D%)
The two resulting values — K% and its signal D% — display the Stochastic indicator.
Before writing the code of Stochastic for the ring buffer, let's have a look at its code executed in the standard manner. To do this, we will use the ready-made example Stochastic.mq5 from the Indicators\Examples folder:
//+------------------------------------------------------------------+ //| Stochastic Oscillator | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,k,start; //--- check for bars count if(rates_total<=InpKPeriod+InpDPeriod+InpSlowing) return(0); //--- start=InpKPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) { ExtLowesBuffer[i]=0.0; ExtHighesBuffer[i]=0.0; } } //--- calculate HighesBuffer[] and ExtHighesBuffer[] for(i=start;i<rates_total && !IsStopped();i++) { double dmin=1000000.0; double dmax=-1000000.0; for(k=i-InpKPeriod+1;k<=i;k++) { if(dmin>low[k]) dmin=low[k]; if(dmax<high[k]) dmax=high[k]; } ExtLowesBuffer[i]=dmin; ExtHighesBuffer[i]=dmax; } //--- %K start=InpKPeriod-1+InpSlowing-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtMainBuffer[i]=0.0; } //--- main cycle for(i=start;i<rates_total && !IsStopped();i++) { double sumlow=0.0; double sumhigh=0.0; for(k=(i-InpSlowing+1);k<=i;k++) { sumlow +=(close[k]-ExtLowesBuffer[k]); sumhigh+=(ExtHighesBuffer[k]-ExtLowesBuffer[k]); } if(sumhigh==0.0) ExtMainBuffer[i]=100.0; else ExtMainBuffer[i]=sumlow/sumhigh*100; } //--- signal start=InpDPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtSignalBuffer[i]=0.0; } for(i=start;i<rates_total && !IsStopped();i++) { double sum=0.0; for(k=0;k<InpDPeriod;k++) sum+=ExtMainBuffer[i-k]; ExtSignalBuffer[i]=sum/InpDPeriod; } //--- OnCalculate done. Get new prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
The code is written in a single block and contains 8 'for' loops. Three of them are nested. The calculation is performed in two stages: first, Highs and Lows are calculated and their values are placed to the two additional buffers. The calculation of Highs and Lows requires a double search: additional N iterations are performed in the nested 'for' loop at each bar, where N is a K% period.
The calculation of Highs and Lows is followed by the K% calculation, during which the double loop is used again. It performs additional F iterations at each bar, where F is K% slowing period.
This is followed by the calculation of the D% signal line with the double 'for' search, where additional T iterations (T — D% smoothing period) are required for each bar.
The resulting code works fast enough. The main issue here is that without a ring buffer, simple calculations have to be performed in several independent stages, which degrades the code visibility and makes it more complex.
To illustrate this, let's have a look at the contents of the main calculation method in the CRiStoch class. It has exactly the same function as the code posted above:
//+------------------------------------------------------------------+ //| Add the new values and calculate Stochastic | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Add the new High value m_min.AddValue(low); // Add the new Low value double c = close; double max = m_max.MaxValue() // Get High double min = m_min.MinValue(); // Get Low double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Find K% using the Stochastic equation m_slowed_k.AddValue(k); // Smooth K% (K% slowing) m_slowed_d.AddValue(m_slowed_k.SMA()); // Find %D from the smoothed K% }
This method is not involved in the intermediate calculations. Instead, it simply applies the Stochastic equation to the already available values. The search for necessary values is performed by the ring primitives: Moving Average and search for Highs/Lows.
The remaining CRiStoch methods are Get/Set methods for setting the periods and the appropriate indicator values. The entire CRiStoch code is shown below:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiMaxMin.mqh" //+------------------------------------------------------------------+ //| Stochastic indicator class | //+------------------------------------------------------------------+ class CRiStoch { private: CRiMaxMin m_max; // High/Low indicator CRiMaxMin m_min; // High/Low indicator CRiSMA m_slowed_k; // K% smoothing CRiSMA m_slowed_d; // D% moving average public: void ChangeLast(double new_value); void AddValue(double close, double high, double low); void AddHighValue(double value); void AddLowValue(double value); void AddCloseValue(double value); void SetPeriodK(int period); void SetPeriodD(int period); void SetSlowedPeriodK(int period); double GetStochK(void); double GetStochD(void); }; //+------------------------------------------------------------------+ //| Adding new values and Stochastic calculation | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Add the new High value m_min.AddValue(low); // Add the new Low value double c = close; double max = m_max.MaxValue() double min = m_min.MinValue(); double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Find K% using the equation m_slowed_k.AddValue(k); // Smooth K% (K% slowing) m_slowed_d.AddValue(m_slowed_k.SMA()); // Find %D from the smoothed K% } //+------------------------------------------------------------------+ //| Set the fast period | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodK(int period) { m_max.SetMaxTotal(period); m_min.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Set the slow period | //+------------------------------------------------------------------+ void CRiStoch::SetSlowedPeriodK(int period) { m_slowed_k.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Set the signal line period | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodD(int period) { m_slowed_d.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Get the %K value | //+------------------------------------------------------------------+ double CRiStoch::GetStochK(void) { return m_slowed_k.SMA(); } //+------------------------------------------------------------------+ //| Get the %D value | //+------------------------------------------------------------------+ double CRiStoch::GetStochD(void) { return m_slowed_d.SMA(); }
The resulting Stochastic indicator is not different from its standard counterpart. You can check this by plotting the corresponding indicator together with the standard one (all the indicator and auxiliary files are attached to this article):
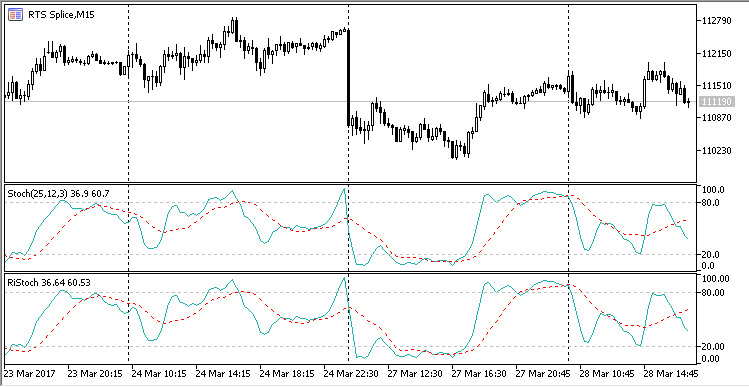
Fig. 8. Standard and ring Stochastic indicators.
Optimizing memory usage
Calculating indicators requires certain computational resources. Working with system indicators through the so-called handles is no exception. The indicator handle is a specific type of a pointer to the indicator's internal calculation block and its data buffers. The handle does not occupy too much space, since it is just a 64-bit number. The main size is hidden "behind the scenes" of MetaTrader, so when a new handle is created, a certain amount of memory larger than its size is allocated.
In addition, copying the indicator values also takes a certain amount of time. It exceeds the amount of time required to calculate the indicator values inside the EA. Therefore, the developers recommend creating an indicator calculation block directly in an EA. Of course, this does not mean you should always write the calculation of the indicator in the EA code and do not call standard indicators. Your EA may apply one, two or even five indicators. Keep in mind though that their operation will take more memory and time as compared to performing calculations directly in the EA's internal code.
However, memory and time optimization may be unavoidable in some cases. This is when ring buffers may come in handy. First, they may be useful when applying multiple indicators. For example, info panels (also called market scanners) usually provide an instantaneous picture of the market for several symbols and timeframes applying an entire set of indicators. This is how one of the panels that can be found in the MetaTrader 5 Market looks like:
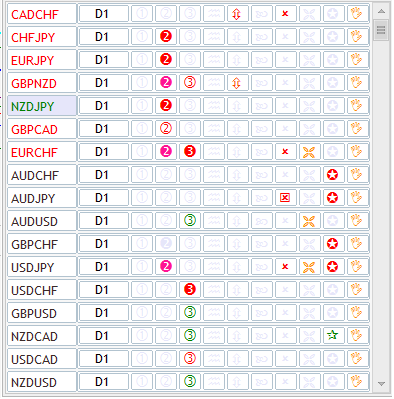
Fig. 8. The info panel applying multiple indicators
As we can see, 17 various instruments are analyzed here by 9 different parameters. Each parameter is represented by its indicator, which means that we need 17 * 9 = 153 indicators to display "just a few icons". To analyze all 21 timeframes on each symbol, we need as much as 3213 indicators. A huge amount of memory is needed to place them all.
Let's write a special load test in the form of an EA to understand how memory is allocated. It will calculate the values of multiple indicators using only two options:
- calling the standard indicator and copying its values via a resulting handle;
- calculating the indicator in the ring buffer.
In the second case, no indicators are created. All calculations are performed inside the EA using the two ring indicators – MACD and Stochastic. Each of them will have three settings: fast, standard and slow. The indicators will be calculated on four symbols: EURUSD, GBPUSD, USDCHF and USDJPY for 21 timeframes. It is easy to define the total number of calculated values:
total number of values = 2 indicators * 3 parameter sets * 4 symbols * 21 timeframes = 504;
Let's write auxiliary container classes to be able to use such different approaches within a single EA. When accessed, they will provide the last indicator value. The value will be calculated in different ways, depending on the type of indicator used. In case of a standard indicator, the last value is taken using the CopyBuffer function which is the indicator's system handle. When applying a ring buffer, the value is calculated using the corresponding ring indicators.
The source code of the container prototype in the form of an abstract class is shown below:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Arrays\ArrayObj.mqh> #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Created indicator type | //+------------------------------------------------------------------+ enum ENUM_INDICATOR_TYPE { INDICATOR_SYSTEM, // System indicator INDICATOR_RIBUFF // Ring buffer indicator }; //+------------------------------------------------------------------+ //| Indicator container | //+------------------------------------------------------------------+ class CIndBase : public CObject { protected: int m_handle; // Indicator handle string m_symbol; // Indicator calculation symbol ENUM_INDICATOR_TYPE m_ind_type; // Indicator type ENUM_TIMEFRAMES m_period; // Indicator calculation period CBarDetector m_bar_detect; // New bar detector CIndBase(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type); public: string Symbol(void){return m_symbol;} ENUM_TIMEFRAMES Period(void){return m_period;} virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| The protected constructor requires specifying the indicator's | //| symbol, timeframe and time | //+------------------------------------------------------------------+ CIndBase::CIndBase(string symbol,ENUM_TIMEFRAMES period,ENUM_INDICATOR_TYPE ind_type) { m_handle = INVALID_HANDLE; m_symbol = symbol; m_period = period; m_ind_type = ind_type; m_bar_detect.Symbol(symbol); m_bar_detect.Timeframe(period); } //+------------------------------------------------------------------+ //| Get the last indicator value | //+------------------------------------------------------------------+ double CIndBase::GetLastValue(int index_buffer) { return EMPTY_VALUE; }
It contains the GetLastValue virtual method, which accepts the indicator buffer number and returns the last indicator value for this buffer. Also, the class contains the basic indicator properties: timeframe, symbol and calculation type (ENUM_INDICATOR_TYPE).
Let's create the CRiInMacd and CRiStoch derived classes based on it. Both calculate the values of the appropriate indicators and return them via the re-defined GetLastValue method. Below is the source code of one of these classes CRiIndMacd:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <RingBuffer\RiMACD.mqh> #include "RiIndBase.mqh" //+------------------------------------------------------------------+ //| Indicator container | //+------------------------------------------------------------------+ class CIndMacd : public CIndBase { private: CRiMACD m_macd; // Indicator ring buffer public: CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period, int slow_period, int signal_period); virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| Create MACD indicator | //+------------------------------------------------------------------+ CIndMacd::CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period,int slow_period,int signal_period) : CIndBase(symbol, period, ind_type) { if(ind_type == INDICATOR_SYSTEM) { m_handle = iMACD(m_symbol, m_period, fast_period, slow_period, signal_period, PRICE_CLOSE); if(m_handle == INVALID_HANDLE) printf("Create iMACD handle failed. Symbol: " + symbol + " Period: " + EnumToString(period)); } else if(ind_type == INDICATOR_RIBUFF) { m_macd.SetFastPeriod(fast_period); m_macd.SetSlowPeriod(slow_period); m_macd.SetSignalPeriod(signal_period); } } //+------------------------------------------------------------------+ //| Get the last indicator value | //+------------------------------------------------------------------+ double CIndMacd::GetLastValue(int index_buffer) { if(m_handle != INVALID_HANDLE) { double array[]; if(CopyBuffer(m_handle, index_buffer, 1, 1, array) > 0) return array[0]; return EMPTY_VALUE; } else { if(m_bar_detect.IsNewBar()) { //printf("Received a new bar on " + m_symbol + " Period " + EnumToString(m_period)); double close[]; CopyClose(m_symbol, m_period, 1, 1, close); m_macd.AddValue(close[0]); } switch(index_buffer) { case 0: return m_macd.Macd(); case 1: return m_macd.Signal(); } return EMPTY_VALUE; } }
The container class for calculating Stochastic has the same structure, so there is no point in showing its source code here.
The indicator values are calculated only at the opening of a new bar to simplify testing. The special NewBarDetecter module is built into the CRiIndBase base class for that. This class re-defines the opening of a new bar and informs of this by returning 'true' by the IsNewBar method.
Now, let's have a look at the testing EA code. It is called TestIndEA.mq5:
//+------------------------------------------------------------------+ //| TestIndEA.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Object.mqh> #include <Arrays\ArrayObj.mqh> #include "RiIndBase.mqh" #include "RiIndMacd.mqh" #include "RiIndStoch.mqh" #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| MACD parameters | //+------------------------------------------------------------------+ struct CMacdParams { int slow_period; int fast_period; int signal_period; }; //+------------------------------------------------------------------+ //| Stoch parameters | //+------------------------------------------------------------------+ struct CStochParams { int k_period; int k_slowed; int d_period; }; input ENUM_INDICATOR_TYPE IndType = INDICATOR_SYSTEM; // Indicator type string Symbols[] = {"EURUSD", "GBPUSD", "USDCHF", "USDJPY"}; CMacdParams MacdParams[3]; CStochParams StochParams[3]; CArrayObj ArrayInd; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MacdParams[0].fast_period = 3; MacdParams[0].slow_period = 13; MacdParams[0].signal_period = 6; MacdParams[1].fast_period = 9; MacdParams[1].slow_period = 26; MacdParams[1].signal_period = 12; MacdParams[2].fast_period = 18; MacdParams[2].slow_period = 52; MacdParams[2].signal_period = 24; StochParams[0].k_period = 6; StochParams[0].k_slowed = 3; StochParams[0].d_period = 3; StochParams[1].k_period = 12; StochParams[1].k_slowed = 5; StochParams[1].d_period = 6; StochParams[2].k_period = 24; StochParams[2].k_slowed = 7; StochParams[2].d_period = 12; // 504 MACD and Stochastic indicators are created here for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PeriodByIndex(period), IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PeriodByIndex(period), IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } printf("Create " + (string)ArrayInd.Total() + " indicators sucessfully"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { for(int i = 0; i < ArrayInd.Total(); i++) { CIndBase* ind = ArrayInd.At(i); double value = ind.GetLastValue(0); double value_signal = ind.GetLastValue(1); } } //+------------------------------------------------------------------+ //| Get timeframe by its index | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES PeriodByIndex(int index) { switch(index) { case 0: return PERIOD_CURRENT; case 1: return PERIOD_M1; case 2: return PERIOD_M2; case 3: return PERIOD_M3; case 4: return PERIOD_M4; case 5: return PERIOD_M5; case 6: return PERIOD_M6; case 7: return PERIOD_M10; case 8: return PERIOD_M12; case 9: return PERIOD_M15; case 10: return PERIOD_M20; case 11: return PERIOD_M30; case 12: return PERIOD_H1; case 13: return PERIOD_H2; case 14: return PERIOD_H3; case 15: return PERIOD_H4; case 16: return PERIOD_H6; case 17: return PERIOD_H8; case 18: return PERIOD_H12; case 19: return PERIOD_D1; case 20: return PERIOD_W1; case 21: return PERIOD_MN1; default: return PERIOD_CURRENT; } } //+------------------------------------------------------------------+
The main functionality is located in the OnInit block. The sorting of symbols, timeframes and sets of indicator parameters is performed there. The sets of the indicator parameters are stored in the CMacdParams and CStochParams auxiliary structures.
The value processing block is located in the OnTick function and represents a common sorting of indicators and receiving their last values using the GetLastalue virtual method. Since both indicators have the same amount of calculation buffers, no additional checks are required. The values of both indicators can be obtained via the generalized GetLastValue method.
The EA launch shows the following: in the calculation mode based on calling the standard indicators, it took 11.9 GB of RAM, while launching in the calculation mode of indicators based on the ring primitives took 2.9 GB. Testing was performed on PC with 16 GB of RAM.
However, we should keep in mind that the memory was saved mainly not by using ring buffers, but by placing the calculation modules in the EA code. The placement of the modules already saves a lot of memory.
Reducing memory consumption four times is a very decent result. Anyway, we still have to consume almost 3 GB of RAM. Is it possible to further reduce the consumption? Yes, it is. We just need to optimize the number of timeframes. Let's try to slightly change the test code and use only one timeframe (PERIOD_M1) instead of 21 ones. The number of indicators remains the same, although some of them will be duplicated:
... for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PERIOD_M1, IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PERIOD_M1, IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } ...
In this case, the same 504 indicators take 548 MB of RAM in the internal calculation mode. More precisely, the memory is consumed by the data downloaded for the indicators' calculation rather than by the indicators themselves. The terminal itself takes about 100 MB of the total volume meaning that the amount of downloaded data is even lower. Thus, we have considerably reduced the memory consumption again:
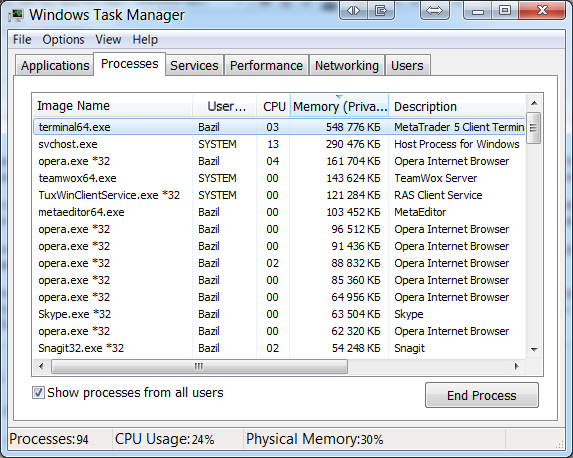
Calculation based on the system indicators in this mode requires 1.9 GB of RAM, which is also significantly lower as compared to the amount of RAM consumed when using the entire list of 21 timeframes.
Optimizing EA testing time
MetaTrader 5 is able to access multiple trading instruments simultaneously, as well as an arbitrary timeframe of each instrument. This allows creating and testing multi-experts (one EA trading on multiple symbols simultaneously). Access to the trading environment may take time, especially if we need access to the data of the indicators calculated based on these instruments. The access time can be reduced if all calculations are performed within a single EA. Let's illustrate this by testing our previous example in the MetaTrader 5 strategy tester. First, we will test the EA on EURUSD M1 for the last month in the "Open prices only" mode. We will use system indicators for calculation. The test on Intel Core i7 870 2.9 Ghz took 58 seconds:
2017.03.30 14:07:12.223 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:57.923.
Now, let's perform the same test in the internal calculations mode:
2017.03.30 14:08:29.472 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:12.292.
As can be seen, the calculation time has significantly decreased in this mode taking only 12 seconds.
Conclusions and suggestions for improving performance
We have tested the use of memory when developing indicators and measured a testing speed in two operation modes. When using internal calculations based on ring buffers, we managed to reduce the memory consumption and improve performance several times. Of course, the examples presented are largely artificial. Most programmers will never need to create 500 indicators simultaneously and test them on all possible timeframes. However, such a "stress test" helps to identify the most costly mechanisms and minimize their use. Here are a few tips based on test results:
- Place the indicator's calculation block inside EAs. This saves the time and RAM spent on testing.
- Avoid requests for receiving data on multiple timeframes if possible. Use a single (the lowest) timeframe for calculations instead. For example, if you need to calculate two indicators on M1 and H1, receive M1 data, convert it to H1 and then apply these data for calculating an indicator on H1. This approach is more complicated, but it saves memory considerably.
- Use computational resources in your work sparingly. The ring buffers are good for that. They require exactly as much memory as necessary for calculating indicators. Besides, the ring buffers allows optimizing some calculation algorithms, like searching for Highs/Lows.
- Create a universal interface for working with indicators and use it to receive their values. If it is difficult to implement the indicator calculation in the internal block, the interface calls the external MetaTrader indicator. If you create an internal indicator block, simply connect it to that interface. The EA undergoes a minimal change in that case.
- Evaluate the optimization features clearly. If you use one indicator on one symbol, it can be left as is without converting it into internal calculation. The time spent on such conversion can significantly exceed the total performance gain.
Conclusion
We have described the development of ring buffers and their practical application for constructing economic indicators. It is difficult to find more relevant application for ring buffers than in trading. It is all the more surprising that, until now, this data construction algorithm has not yet been covered in the MQL community.
The ring buffers and indicators based on them save memory and provide fast calculation. The main advantage of the ring buffers is simple implementation of indicators based on them, since most of them adhere to the FIFO (first in - first out) principle. Therefore, the issues usually arise when indicators are calculated not in a ring buffer.
All described source codes are provided below together with the codes of the indicators, as well as the simple algorithms the indicators are based on. I believe, this article will serve as a good starting point for developing a complete simple, fast and versatile library of ring indicators.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/3047
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Cross-Platform Expert Advisor: Signals
Cross-Platform Expert Advisor: Signals
 Cross-Platform Expert Advisor: Order Manager
Cross-Platform Expert Advisor: Order Manager
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Great work here, many thanks to the author. Perhaps the bug you're seeing, Savio, is here:
int RingBuffer::iToRealInd(int iIndex)
{
if(iIndex >= iNumElements() || iIndex < 0)
return iBufferSize-1; //previous bug was caused by no -1 here
...
I added the -1 on the last quoted line; it wasn't there before and would cause an improper index to be returned. Note that I changed variable/method names to my style of programming but it's the same idea
I tried your correction, but it still does not update right. It seems there is something missing and I can't find the problem when trying to run the ring buffer in the formation of a new bar. When the market is running, the High/Low lines get completly mixed up. The code works very well and very quick while processing old data, but with new data arriving during the formation of a new bar, it simply does not work for me.
If I may make some comments:
1. In the class void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value), in the method " OnChangeValue" in the line
.
Picture: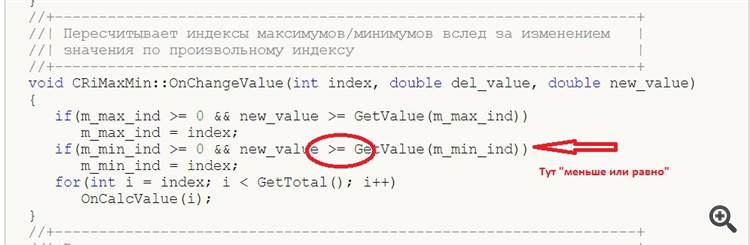
typo - sign "less than or equal to".

2.When searching for Min and Max elements of an array, if used exactly as a ring buffer (when new elements start to be written to the beginning of the array), min and mah are defined incorrectly. The minimum is greater than the maximum. In one array. Everything works using standard methods (ArrayMinimum and ArrayMaximum).
Picture:
Somewhere indexing is going astray. I can't fix it myself. If someone can fix it, it would be great. I have attached a test advisor.
You have a mistake in ToRealInd(int index).
It should be: