
R quadrado como uma estimativa da qualidade da curva de saldo da estratégia
Índice
- Introdução
- Crítica de estatísticas comuns para a avaliação do sistema de negociação
- O comportamento frequente nos testes de sistemas de negociação
- Requisitos para o critério de teste do sistema de negociação
- Regressão linear
- Correlação
- Coeficiente de determinação R²
- O teorema do arco-seno e sua contribuição para a estimação da regressão linear
- Coleta do saldo de capital da estratégia
- Cálculo do coeficiente de determinação R² usando a AlgLib
- Uso do R² na prática
- Vantagens e limitações de uso
- Conclusão
Introdução
Toda estratégia de negociação precisa de uma avaliação objetiva de sua eficácia. Uma ampla gama de parâmetros estatísticos são utilizados para isso. Muitos deles são fáceis de calcular e mostram métricas intuitivas. Outros são mais difíceis na construção e interpretação dos valores. Apesar de toda essa diversidade, há pouquíssimas métricas qualitativas para estimar um valor não trivial mas, ao mesmo tempo, óbvio - suavidade da linha de saldo do sistema de negociação. Este artigo propõe uma solução para este problema. Vamos considerar essa medida não trivial, como o coeficiente de determinação R², que calcula a estimativa qualitativa da linha do saldo mais atrativa, suave e crescente que todo trader aspira.
Obviamente, o terminal MetaTrader 5 já fornece um relatório que mostra as principais estatísticas do sistema de negociação. No entanto, os parâmetros apresentados nele nem sempre são suficientes. Felizmente, a MetaTrader 5 oferece a capacidade de escrever parâmetros de estimação personalizados, que é o que faremos. Nós não vamos construir apenas o coeficiente de determinação R², mas também tentar estimar seus valores, compará-lo com outros critérios de otimização, derivar regularidades seguidas pelas estimativas estatísticas básicas.
Crítica de estatísticas comuns para a avaliação do sistema de negociação
Cada vez que um relatório de negociação é gerado ou são testados os resultados do sistema de negociação, são apresentados vários "números mágicos", que podem ser analisados para tirar conclusões sobre a qualidade da negociação. Por exemplo, um relatório de teste típico no terminal da MetaTrader 5 aparenta ser assim:
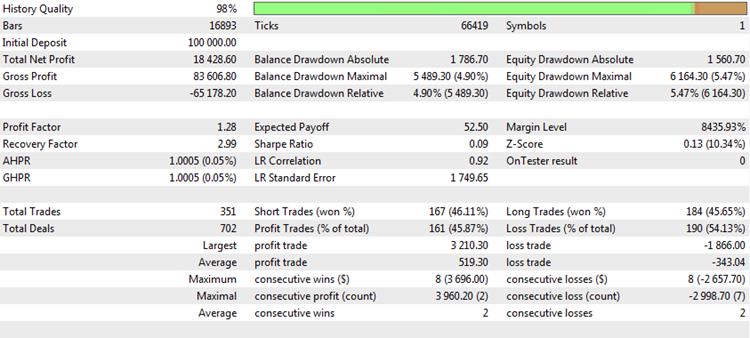
Fig. 1. Resultado do backtest de uma estratégia de negociação
Ele contém uma série de estatísticas ou métricas interessantes. Vamos analisar a mais popular delas e considerar objetivamente seus pontos fortes e fracos.
Lucro Líquido Total. A métrica mostra o montante total de capital que foi ganho ou perdido durante o período de teste ou negociação. Este é um dos parâmetros de negociação mais importantes. O principal objetivo de cada trader é maximizar o lucro. Existem várias maneiras de fazer isso, mas o resultado final é sempre um, que é o lucro líquido. O lucro líquido nem sempre depende do número de negócios e é praticamente independente de outros parâmetros, embora o contrário não seja verdadeiro. Assim, ele é invariante em relação a outras métricas, e, portanto, podem ser usadas independentemente delas. No entanto, esta medida também apresenta graves desvantagens.
Primeiro, o lucro líquido é diretamente dependente se a capitalização é usada ou não. Quando a capitalização é usada, o lucro cresce de forma não linear. Muitas vezes, há um crescimento exponencial e explosivo do saldo. Nesse caso, os números registrados como lucro líquido no final do teste geralmente alcançam valores astronômicos e não têm nada a ver com a realidade. Se um lote fixo é negociado, os incrementos do depósito são mais lineares, mas mesmo nesse caso, o lucro depende do volume selecionado. Por exemplo, se o teste, com o resultado exibido na tabela acima, foi realizado usando um lote fixo com o volume de 0.1 contrato, então o lucro obtido de $15,757 pode ser considerado um resultado notável. Se o volume do negócio fosse de 1.0 lote, o resultado do teste é mais do que modesto. É por isso que os testadores experientes preferem definir um lote fixo para 0.1 ou 0.01 no mercado Forex. Neste caso, a variação mínima no saldo é igual a um ponto do instrumento, o que torna a análise desta característica mais objetiva.
Em segundo lugar, o resultado final depende da duração do período testado ou da duração do histórico de negociação. Por exemplo, o lucro líquido especificado no quadro acima poderia ter sido de um período de 1 ano ou 5 anos. E, em cada caso, a mesma figura significa uma eficácia completamente diferente de uma estratégia.
E em terceiro lugar, o lucro bruto é fixado no momento da última data. No entanto, pode haver uma forte retração de capital nesse momento, enquanto que talvez isso não tenha estado lá há uma semana atrás. Em outras palavras, este parâmetro é profundamente dependente ponto inicial e final, que é selecionado para testar ou gerar o relatório.
Fator de lucro. Este é, sem dúvida, as estatísticas mais populares para os traders profissionais. Enquanto os novatos querem ver apenas o lucro total, os profissionais acham essencial conhecer o volume de negócios dos fundos investidos. Se a perda de uma negociação for considerada como um tipo de investimento, o fator de lucro mostra a marginalidade da negociação. Por exemplo, se apenas dois negócios forem feitos, o primeiro perdeu $1000 e o segundo ganhou $2000, o fator de lucro dessa estratégia será de $2000/1000 = 2.0. Este é um cenário muito bom. Além disso, o Fator de lucro não depende do período de tempo de teste nem do volume base do lote. É por isso que os profissionais gostam tanto dessa métrica. No entanto, ela tem suas desvantagens também.
Uma delas é que os valores do Fator de Lucro são altamente dependentes da quantidade de negócios. Se houver apenas alguns negócios, a obtenção de um fator de lucro igual a 2.0 ou mesmo 3.0 unidades é bastante possível. Por outro lado, se houver inúmeros negócios, a obtenção de um fator de lucro de 1.5 unidades seria um grande sucesso.
Retorno Esperado. É uma característica muito importante, indicando o Retorno Médio de Negociação. Se a estratégia for rentável, o Retorno Esperado é positivo; estratégias perdedoras tem um valor negativo. Se o Retorno Esperado for comparável aos custos de spread ou corretagem, a capacidade de tal estratégia ser lucrativa em uma conta real é duvidosa. Normalmente, o Retorno Esperado pode ser positivo no testador de estratégia em condições de execução ideais, e o gráfico de saldo pode ser uma linha ascendente suave. Na negociação real, no entanto, o Retorno Médio de Negociação pode resultar pior do que o resultado calculado teoricamente, devido às possíveis chamadas "requotes" ou derrapagens, o que pode ter um impacto crítico no resultado da estratégia e causar perdas reais.
Ela também tem suas desvantagens. O principal delas está relacionado à quantidade de negócios também. Se houver poucos negócios, a obtenção de um grande Retorno Esperado não é um problema. Por outro lado, com um grande número de negócios, o Retorno Esperado tende a zero. Como ele é uma métrica linear, ele não pode ser usado em estratégias que implementam os sistemas de gerenciamento de capital. Mas os traders profissionais o consideram e usam em sistemas lineares com um lote fixo, comparando-o com o número de negócios.
Número de Negócios. Este é um parâmetro importante que afeta a maioria das outras características de forma explícita ou indireta. Suponha que um sistema de negociação vença em 70% dos casos. Ao mesmo tempo, os valores absolutos de ganho e perda são iguais, sem outros resultados possíveis de um acordo na tática de negociação. Esse sistema parece ser excelente, mas o que acontece se a eficiência for avaliada apenas com base nos dois últimos negócios? Em 70% dos casos, um deles será rentável, mas a probabilidade de ambos os negócios serem rentáveis é de apenas 49%. Ou seja, o resultado total de dois negócios será zero em mais da metade dos casos. Consequentemente, na metade dos casos, as estatísticas mostrarão que a estratégia é incapaz de ganhar dinheiro. Seu fator de lucro será sempre igual a um, o Retorno Esperado e o lucro será zero, outros parâmetros também indicarão eficiência zero.
É por isso que o número de negócios deve ser suficientemente grande. Mas o que se entende por suficiência? Geralmente é aceito que qualquer amostra deve conter pelo menos 37 métricas. Este é um número mágico em estatísticas, que marca o limite inferior da representatividade de um parâmetro. Naturalmente, essa quantidade de negócios não é suficiente para avaliar um sistema de negociação. É preciso de pelo menos 10-100 negociações precisam ser feitas para que o resultado seja confiável. Além disso, isso também não é suficiente para muitos traders profissionais. Eles projetam sistemas que fazem pelo menos 500-1000 negócios e depois usam esses resultados para considerar a possibilidade de executar o sistema para negociação real.
Comportamento dos parâmetros estatísticos comuns ao testar um sistema de negociação
Os principais parâmetros nas estatísticas dos sistemas de negociação foram discutidos. Vamos ver seu desempenho na prática. Ao mesmo tempo, nos concentraremos em suas desvantagens para ver como a adição proposta na forma de estatística R² pode ajudar a resolvê-los. Para fazer isso, nós usaremos o EA CImpulse 2.0, que está descrito no artigo "Expert Advisor Universal: Indicador Cunindicator e Trabalho com Ordens Pendentes". Ele foi escolhido por sua simplicidade e por ser otimizado, ao contrário dos experts do pacote padrão da MetaTrader 5, que é extremamente importante para os propósitos deste artigo. Além disso, será necessário uma certa infraestrutura do código, que já foi escrito para o mecanismo de negociação CStrategy, portanto, não há necessidade de fazer o mesmo trabalho duas vezes. Todos os códigos-fonte para o coeficiente de determinação estão escritos de forma que sejam facilmente utilizados fora do CStrategy — por exemplo, em bibliotecas de terceiros ou experts em procedimentos.
Lucro Líquido Total. Como já mencionado, o lucro líquido (ou total) é o resultado final que o trader quer obter. Quanto maior o lucro, melhor. No entanto, a avaliação de uma estratégia baseada em seu lucro final nem sempre garante o sucesso. Consideremos os resultados da estratégia CImpulse 2.0 no par EURUSD para o período de teste de 15.01.2015 a 10.10.2017:
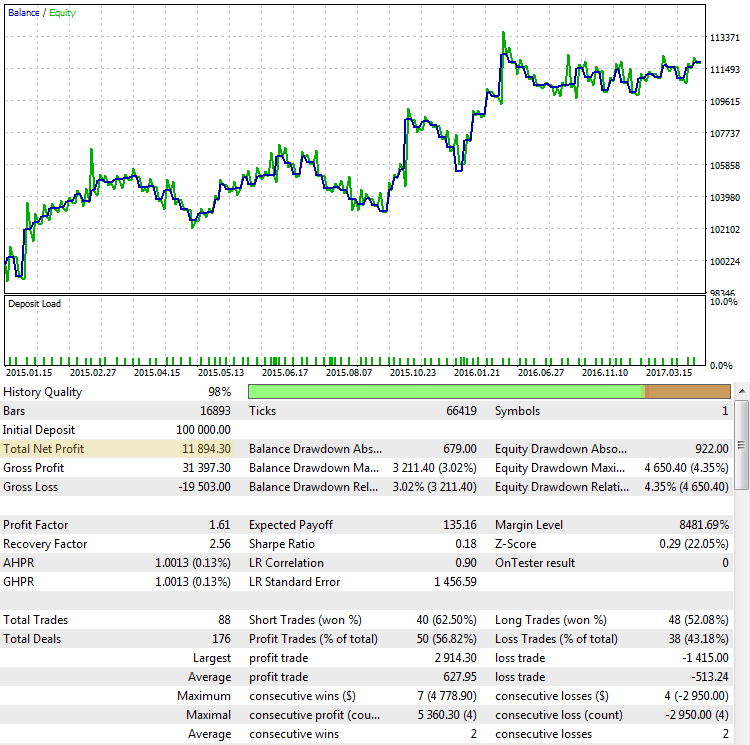
Fig. 2. A estratégia CImpulse, EURUSD, 1H, 15.01.2015 - 01.10.2017, PeriodMA: 120, StopPercent: 0.67
A estratégia é vista como um crescimento constante do lucro total nesse intervalo de testes. Ele é positivo e equivale a $11,894 pela negociação de um contrato. Este é um bom resultado. Mas vamos ver como se parece um cenário diferente, onde o lucro final é próximo do primeiro caso:
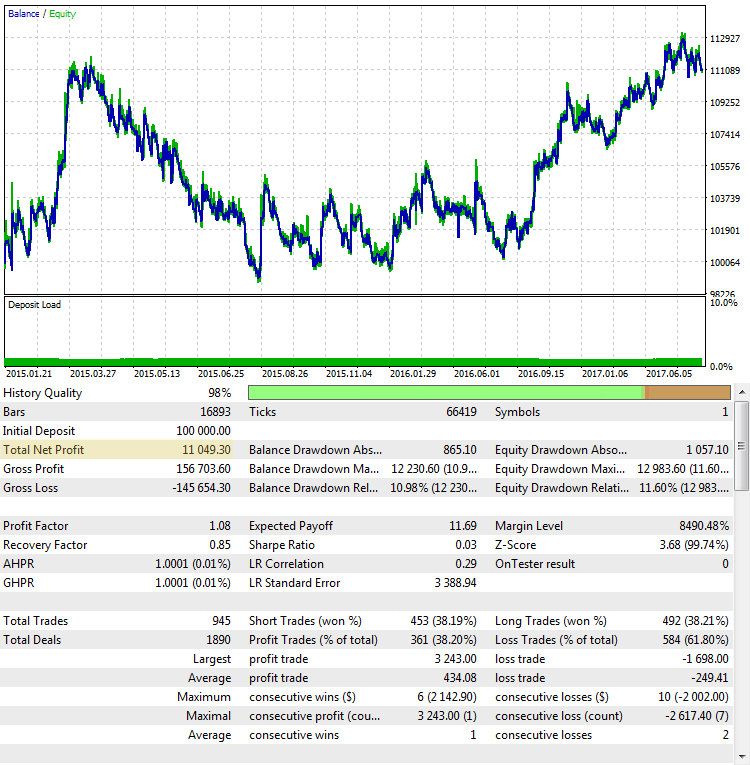
Fig. 3. A estratégia CImpulse, EURUSD, 1H, 15.01.2015 - 01.10.2017, PeriodMA: 110, StopPercent: 0.24
Apesar do lucro ser quase o mesmo em ambos os casos, eles aparentam ser sistemas de negociação completamente diferentes. O lucro final no segundo caso também parece aleatório. Se o teste tivesse terminado em meados de 2015, o lucro teria sido próximo de zero.
Aqui está outra execução mal sucedida da estratégia, com o resultado final, no entanto, também muito perto do primeiro caso:
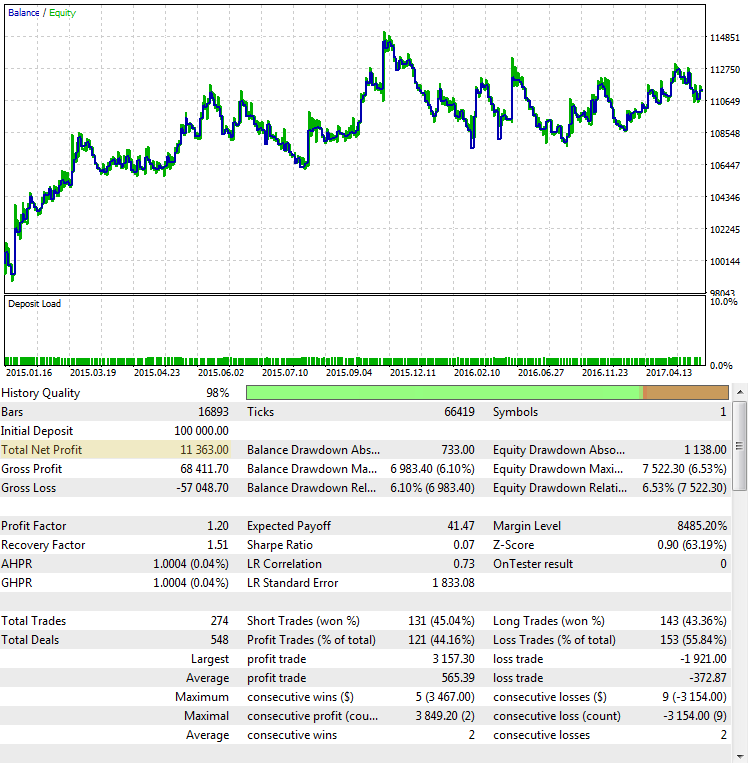
Fig. 4. CImpulse, EURUSD, 1H, 15.01.2015 - 01.10.2017, PeriodMA: 45, StopPercent: 0.44
É claro que a partir do gráfico que o lucro principal foi obtido no primeiro semestre de 2015. Ele é seguido por um período prolongado de estagnação. Tal estratégia não é uma opção viável para a negociação real.
Fator de lucro. A métrica do Fator de Lucro é muito menos dependente do resultado final. Esse valor depende de cada negócio e mostra a proporção de todo o capital ganho para todo o capital perdido. Pode-se ver que na Fig. 2, o Fator de Lucro é bem alto; na Fig. 4, é menor; e na Fig. 3, ele se aproxima do limite entre um sistema lucrativo e não lucrativo. Mas, no entanto, o Fator de Lucro não é uma característica universal que não pode ser enganada. Examinemos outros exemplos, onde as indicações do fator de lucro não são tão óbvias:
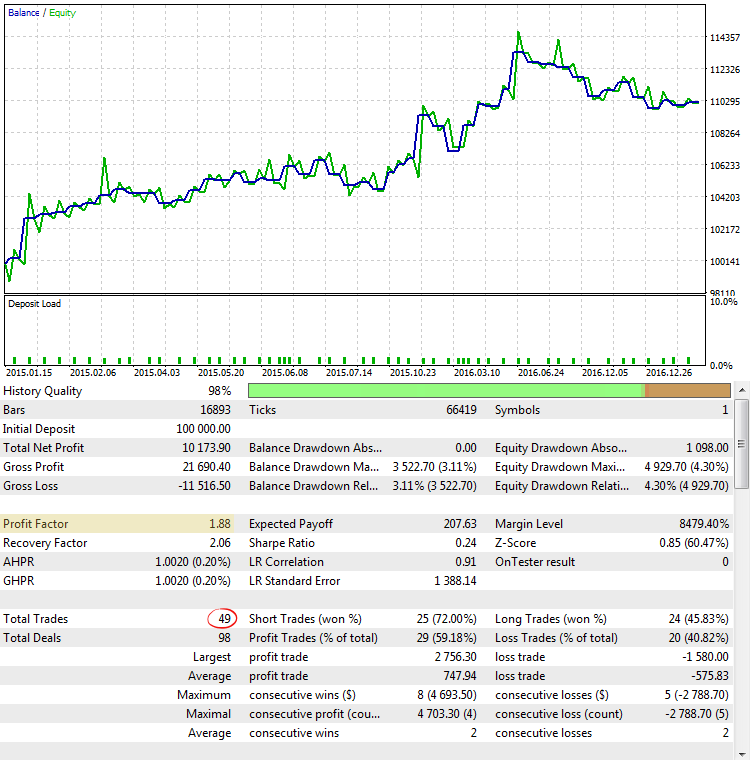
Fig. 5. CImpulse, EURUSD, 1H, 15.01.2015 - 01.10.2017, PeriodMA: 60, StopPercent: 0.82
A Fig. 5 mostra o resultado da execução do teste da estratégia com um dos maiores valores do Fator de Lucro. O gráfico do saldo parece bastante promissor, mas a estatística obtida é incorreta, já que o valor do Fator de Lucro é exagerado devido ao número muito pequeno de operações.
Vamos verificar esta afirmação de duas maneiras. O primeiro caminho: Descobrir a dependência do Fator de Lucro na quantidade de negócios. Isso é feito otimizando a estratégia CImpulse no testador de estratégia usando uma ampla gama de parâmetros:

Fig. 6. Otimização do CImpulse usando uma ampla gama de parâmetros
Armazenamento dos resultados da otimização:
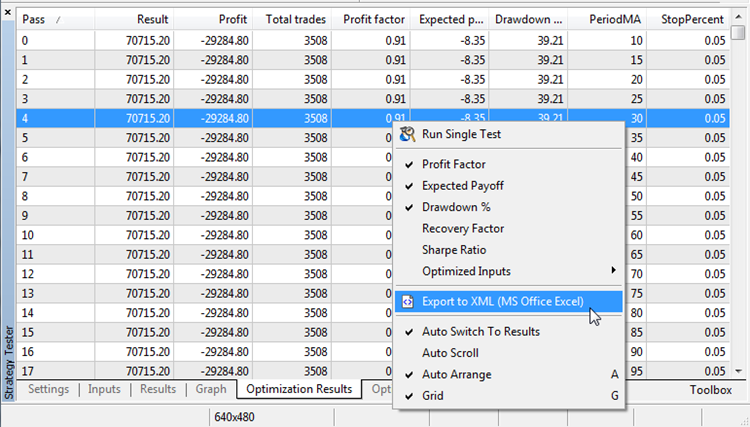
Fig. 7. Exportação dos resultados de otimização
Agora, nós podemos construir um gráfico de dependência do valor Fator de Lucro na quantidade de operações. No Excel, por exemplo, isso pode ser feito simplesmente selecionando as colunas correspondentes e pressionando o botão para traçar um gráfico de dispersão na guia Gráficos.
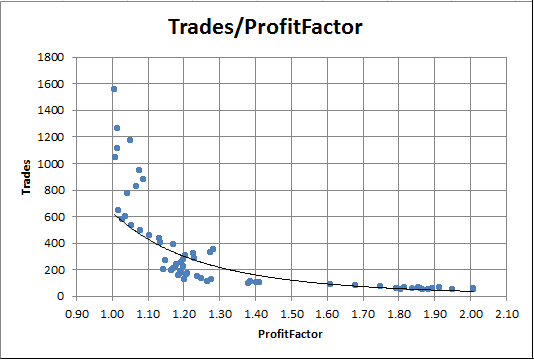
Fig. 8. Dependência do Fator de Lucro na quantidade de operações
O gráfico mostra claramente que as execuções com um alto Fator de Lucro sempre têm pouquíssimas operações. Por outro lado, com um grande número de operações, o Fator de lucro é praticamente igual a um.
O segundo caminho para determinar que os valores do Fator de Lucro neste caso dependem do número de negócios e não da qualidade da estratégia está relacionado à realização de um Out Of Sample test (Teste fora da amostra ou OOS). Por sinal, essa é uma das maneiras mais confiáveis de determinar a robustez dos resultados obtidos. A robustez é a medida da estabilidade de um método estatístico em estimativas. OOS é eficaz para testar não apenas o ProfitFactor, mas outras indicações também. Para nossos propósitos, os mesmos parâmetros serão selecionados, mas o intervalo de tempo será diferente - de 01.01.2012 a 01.01.2015:
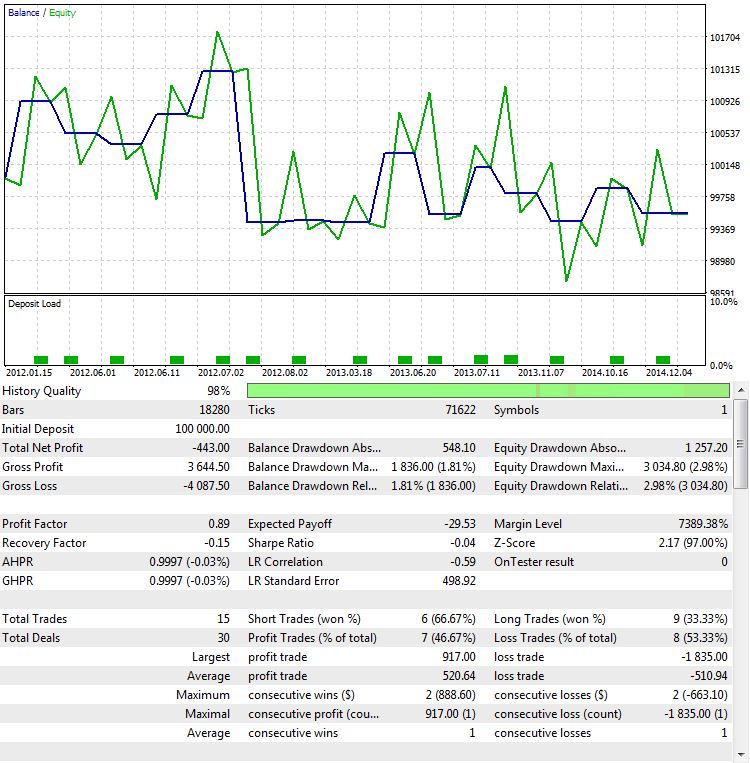
Fig. 9. Teste da estratégia fora da amostra
Como pode ser visto, o comportamento da estratégia virou de cabeça para baixo. Isso gera perda em vez de lucro. Este é um resultado lógico, já que o resultado obtido é quase sempre aleatório com um número tão pequeno de negócios. Isso significa que uma vitória aleatória em um intervalo de tempo é compensada por uma perda em outra, o que é bem ilustrado pela Fig. 9.
Retorno Esperado. Não nos deteremos muito nesse parâmetro, porque suas falhas são semelhantes ao do Fator de lucro. Aqui está o gráfico de dependência do Retorno esperado na quantidade de negócios:
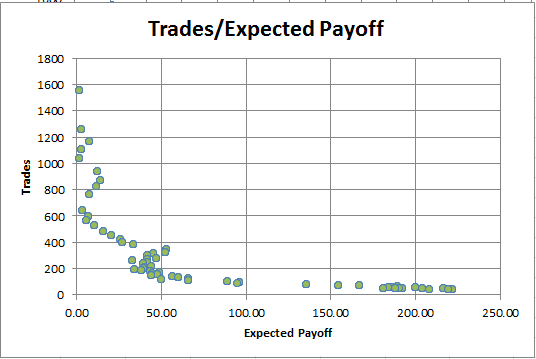
Fig. 10. Dependência do Retorno Esperado sobre o número de negócios
Pode-se ver que quanto maior for as operações realizadas, menor será o Retorno Esperado. Essa dependência é sempre observada tanto para estratégias lucrativas quanto não lucrativas. Portanto, o Retorno Esperado não pode servir como o único critério para a otimização de uma estratégia de negociação.
Requisitos para o critério de teste do sistema de negociação
Depois de considerar os principais critérios de avaliação estatística de um sistema de negociação, concluiu-se que a aplicabilidade de cada critério é limitada. Cada um deles pode ser combatido com um exemplo onde a métrica tem um bom resultado, enquanto a estratégia em si não.
Não há critérios ideais para determinar a robustez de um sistema de negociação. Mas é possível formular as propriedades que um forte critério estatístico deve ter.
- Independência da duração do período de teste. Muitos parâmetros de uma estratégia de negociação dependem de quanto tempo foi definido o período de teste. Por exemplo, quanto maior o período testado para uma estratégia rentável, maior será seu lucro final. Depende da duração e do fator de recuperação. Ele é calculado como a proporção do lucro total com o rebaixamento máximo. Uma vez que o lucro depende do período, o fator de recuperação também cresce com o aumento do período de teste. A invariância (independência) em relação ao período é necessária para comparar a eficácia de diferentes estratégias em diferentes períodos de teste;
- Independência do ponto final do teste. Por exemplo, se uma estratégia "permanece à tona" simplesmente esperando que as perdas passem, o ponto final pode ter um impacto crucial no saldo final. Se o teste for concluído no momento de tal "ultrapassagem", a perda flutuante (capital) torna-se o saldo e um rebaixamento significativo é recebido na conta. A estatística deve ser protegida de tal fraude e fornecer uma visão geral objetiva da operação do sistema de negociação.
- Simplicidade de interpretação. Todos os parâmetros do sistema de negociação são quantitativos, ou seja, cada estatística é caracterizada por uma figura específica. Essa figura deve ser intuitiva. Quanto mais simples for a interpretação do valor obtido, mais compreensível será o parâmetro. É desejável também que o parâmetro esteja dentro de certos limites, uma vez que a análise de números grandes e potencialmente infinitos é muitas vezes complicada.
- Resultados representativos com um pequeno número de negócios. Este é indiscutivelmente o requisito mais difícil entre as características de uma boa métrica. Todos os métodos estatísticos dependem do número de medidas. Quanto mais delas, mais estáveis são as estatísticas obtidas. Claro que resolver completamente este problema em uma pequena amostra é impossível. No entanto, é possível atenuar os efeitos causados pela falta de dados. Para este propósito, desenvolvamos dois tipos de função para avaliar a R²: uma implementação criará esse critério com base na quantidade de negócios disponíveis. O outro calcula o critério utilizando o lucro flutuante da estratégia (capital).
Antes de proceder diretamente à descrição do coeficiente de determinação R², vamos examinar seus componentes em detalhes. Isso ajudará a entender o propósito desse parâmetro e os princípios em que ele se baseia.
Regressão linear
Regressão linear é uma dependência linear de uma variável y de outra variável independente x, expresso pela fórmula y = ax + b. Nesta fórmula, a é o coeficiente angular, b é o coeficiente linear. Na realidade, pode haver várias variáveis independentes, e esse modelo é chamado de modelo de regressão linear múltipla. No entanto, nós vamos considerar apenas o caso mais simples.
A dependência linear pode ser visualizada na forma de um gráfico simples. Pegue o gráfico diário EURUSD a partir de 21.06.2017 até 21.09.2017. Este segmento não é selecionado por acaso: durante este período, observou-se uma tendência ascendente moderada neste par de moedas. É assim que se parece na MetaTrader:
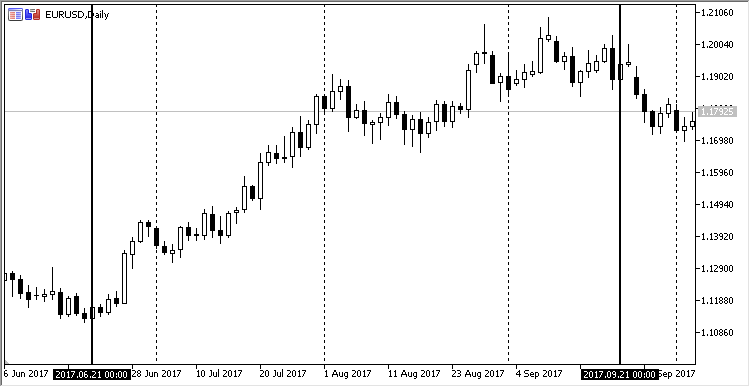
Fig. 11. Dinâmica do preço EURUSD de 21.06.2017 para 21.08.2017, período diário
Salve esses dados de preço e use-os para traçar um gráfico, por exemplo, no Excel.
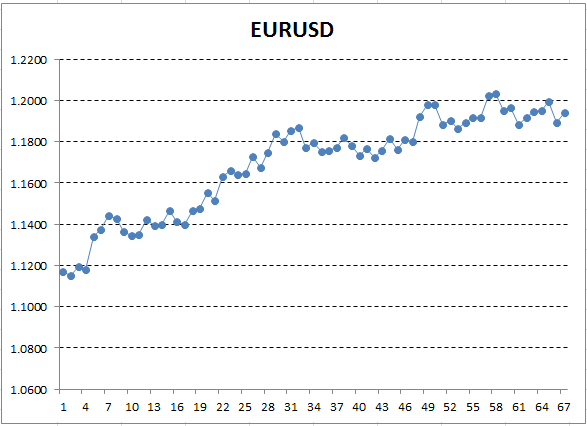
Fig. 12. Taxas EURUSD (preço de fechamento) como um gráfico no Excel
Aqui, o eixo Y corresponde ao preço, e X é o número ordinal de medição (as datas foram substituídas por números ordinais). No gráfico resultante, a tendência ascendente é visível a olho nu, mas nós precisamos obter uma interpretação quantitativa dessa tendência. A maneira mais simples é desenhar uma linha direta, o que se encaixaria com precisão na tendência examinada. Ela é chamada de regressão linear. Por exemplo, a linha pode ser desenhada assim:
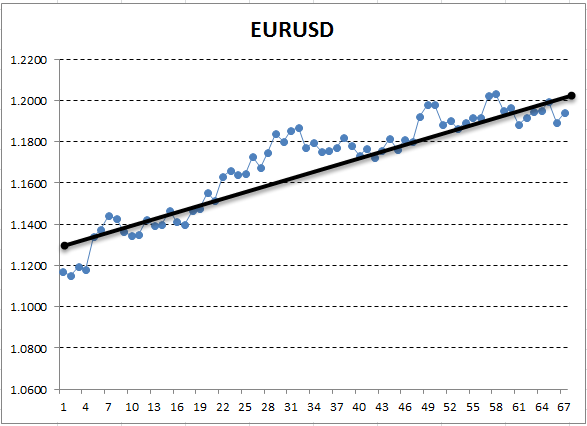
Fig. 13. Regressão linear que descreve uma tendência de alta, desenhada manualmente
Se o gráfico for bem suave, é possível desenhar essa linha, que os pontos do gráfico se desviam da distância mínima. E por outro lado, para um gráfico com grande amplitude, não é possível escolher uma linha que descreva com precisão suas mudanças. Isso se deve ao fato de que a regressão linear possui apenas dois coeficientes. Na verdade, os cursos de geometria nos ensinaram que dois pontos são suficientes para traçar uma linha. Devido a isso, não é fácil ajustar uma linha reta a um gráfico "curvo". Esta é uma propriedade valiosa que será útil mais adiante.
Mas como descobrir como desenhar uma linha reta corretamente? Os métodos matemáticos podem ser usados para calcular o coeficiente de regressão linear de forma otimizada, de tal forma que todos os pontos disponíveis tenham a soma mínima de distâncias para esta linha. Isso é explicado no gráfico a seguir. Suponha que existam 5 pontos arbitrários e duas linhas passando por eles. Das duas linhas, é necessário selecionar aquele com a menor soma de distâncias para os pontos:
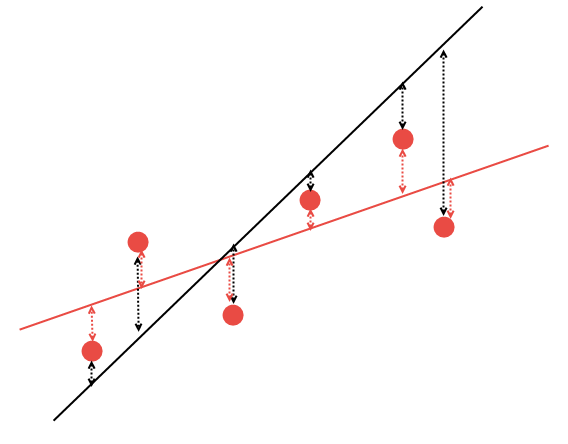
Fig. 14. Seleção da regressão linear mais adequada
É claro que, das duas variantes de regressão linear, a linha vermelha descreve os dados obtidos melhor: os pontos #2 e #6 são significativamente mais próximos da linha vermelha do que no preto. Os pontos restantes são aproximadamente equidistantes tanto da linha preta quanto do vermelho. Matematicamente, é possível calcular as coordenadas da linha que melhor descrevem essa regularidade. Nós não vamos calcular esses coeficientes manualmente, para isso, vamos usar a biblioteca matemática AlgLib.
Correlação
Uma vez que a regressão linear é calculada, é necessário calcular a correlação entre esta linha e os dados para os quais é calculado. Correlação é uma relação estatística de duas ou mais variáveis aleatórias. Nesse caso, a aleatoriedade das variáveis significa que as medidas dessas variáveis não são interdependentes. A correlação é medida de -1.0 a 1.0. Um valor próximo a zero indica que as variáveis examinadas não possuem inter-relações. O valor igual a 1.0 significa uma dependência direta, -1.0 mostra uma dependência inversa. A correlação é calculada por várias fórmulas diferentes. Aqui, será utilizado o Coeficiente de correlação de Pearson:
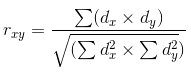
dx e dy na fórmula corresponde as variâncias calculadas as para variáveis aleatórias x e y. Variância é uma medida de variação da característica. Nos termos mais gerais, pode ser descrito como a soma dos quadrados das distâncias entre os dados e a regressão linear.
O coeficiente de correlação dos dados em sua regressão linear mostra o quão bem a linha reta descreve esses dados. Se os pontos de dados estão localizados a uma grande distância da linha, a variância é alta e a correlação é baixa e vice-versa. A correlação é muito fácil de interpretar: um valor zero significa que não há inter-relação entre a regressão e os dados; um valor próximo a um mostra uma forte dependência direta.
Os relatórios na MetaTrader possuem uma métrica estatística especial. Ela é chamada de Correlação LR, e mostra a correlação entre a curva de saldo e a regressão linear encontrada para essa curva. Se a curva de saldo for suave, a aproximação a uma linha reta será boa. Nesse caso, o coeficiente de correlação LR será próximo de 1.0, ou pelo menos acima de 0.5. Se a curva de saldo for instável, então as subidas são alternadas por quedas, e o coeficiente de correlação tende a zero.
A Correlação LR é um parâmetro interessante. Mas em estatísticas, não é costume comparar os dados e a regressão descrita diretamente através do coeficiente de correlação. O motivo para isso será discutido na próxima seção.
Coeficiente de determinação R²
O método de cálculo para o coeficiente de determinação R² é semelhante ao método de cálculo para a Correlação LR. Mas o valor final é ao quadrado. Pode levar valores de 0.0 a 1.0. Esta figura mostra a parte dos valores explicados da amostra total. A regressão linear serve como um modelo explicativo. Estritamente falando, o modelo explicativo não precisa ser uma regressão linear, outros também podem ser usados. No entanto, os valores de R² não requerem processamento adicional para uma regressão linear. Em modelos mais complexos, a aproximação é geralmente melhor e os valores de R² devem ser adicionalmente reduzidos por "penalidades" especiais para uma estimativa mais adequada.
Vejamos mais de perto o que mostra o modelo explicativo. Para fazer isso, faremos um pequeno experimento: use a linguagem de programação especializada R-Project e gere um caminho aleatório, para o qual o coeficiente requerido será calculado. Random walk (passeio aleatório) é um processo com características bastante semelhantes aos instrumentos financeiros reais. Para obter uma caminhada aleatória, é suficiente adicionar consecutivamente vários números aleatórios distribuídos de acordo com a lei normal.
O código-fonte em R com uma descrição detalhada do que está sendo feito:
x <- rnorm(1000) # Gera 1000 números aleatórios, distribuídos de acordo com a lei normal # Sua variação é igual a uma, eo valor esperado é zero rwalk <- cumsum(x) # Soma cumulativamente esses números, obtendo um gráfico do passeio aleatório clássico plot(rwalk, type="l", col="darkgreen") # Exibe os dados sob a forma de um gráfico linear rws <- lm(rwalk~c(1:1000)) # Traça o modelo linear y = a*x+b, onde x é o número de medição, e y é o valor do vetor do passeio gerado title("Line Regression of Random Walk") abline(rws) # Exibe a regressão linear resultante no gráfico
A função rnorm retorna dados diferentes a cada vez, então, se você quiser repetir esta experiência, o gráfico terá um aspecto diferente.
O resultado do código apresentado:
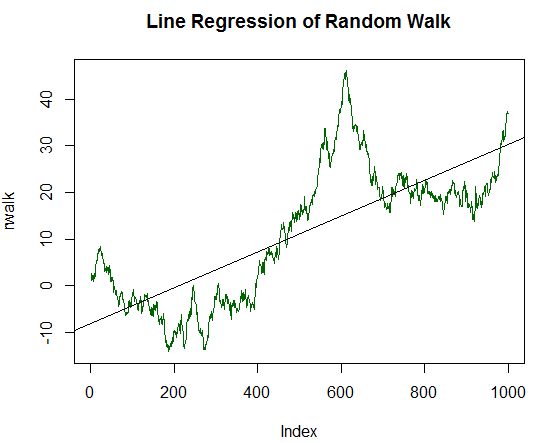
Fig. 15. Passeio aleatório e regressão linear para isso
O gráfico resultante é semelhante ao de um instrumento financeiro arbitrário. Sua regressão linear foi calculada e exibida como uma linha preta do gráfico. À primeira vista, a descrição da dinâmica do passeio aleatório é bastante medíocre. Mas nós precisamos de uma estimativa quantitativa da qualidade da regressão linear. Para este fim, é utilizado a função 'summary', que exibe as estatísticas resumidas no modelo de regressão:
summary(rws) Call: lm(formula = rwalk ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.038404 0.001013 37.92 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.5903, Adjusted R-squared: 0.5899 F-statistic: 1438 on 1 and 998 DF, p-value: < 2.2e-16
Aqui, uma figura é de maior interesse — R². Esta métrica indica um valor de 0.5903. Consequentemente, a regressão linear descreve 59.03% de todos os valores, e os 41% restantes são inexplicáveis.
Este é um indicador muito sensível que responde bem a uma linha de dados lisa e plana. Para ilustrar isso, vamos continuar com a experiência: introduzir um componente de crescimento estável para os dados aleatórios. Para fazer isso, altere o valor médio ou o valor esperado em 1/20 da variância dos dados gerados inicialmente:
x_trend1 <- x+(sd(x)/20.0) # Encontre o desvio padrão dos valores x, divida-o por 20.0 e adicione o valor obtido a cada valor de # Cada um desses valores modificados de x serão armazenados em um novo vetor de valores x_trend1 rwalk_t1 <- cumsum(x_trend1) # Soma cumulativamente esses números, obtendo um gráfico da caminhada aleatória plot(rwalk_t1, type="l", col="darkgreen") # Exibir os dados como um gráfico linear title("Line Regression of Random Walk #2") rws_t1 <- lm(rwalk_t1~c(1:1000))# Traça o modelo linear y = a*x+b, onde x é o número de medição, e y é o valor do vetor da caminhada gerada abline(rws_t1) # Exibe a regressão linear resultante no gráfico
O gráfico resultante agora está muito mais próximo de uma linha reta:
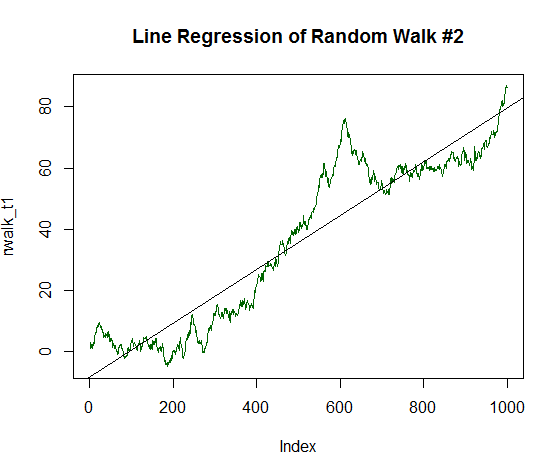
Fig. 16. O passeio aleatório com valor esperado positivo, igual a 1/20 de sua variação
As estatísticas para isso são as seguintes:
summary(rws_t1) Call: lm(formula = rwalk_t1 ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.087854 0.001013 86.75 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.8829, Adjusted R-squared: 0.8828 F-statistic: 7526 on 1 and 998 DF, p-value: < 2.2e-16
É claro que R² é significativamente maior e tem um valor de 0.8829. Mas deixe-nos ir para a milha extra e duplicar o componente de determinação do gráfico, até 1/10 do desvio padrão dos dados iniciais. O código para processar isso é semelhante ao código anterior, mas com divisão em 10.0 e não em 20.0. O novo gráfico agora é quase que completamente parecido com uma linha reta:
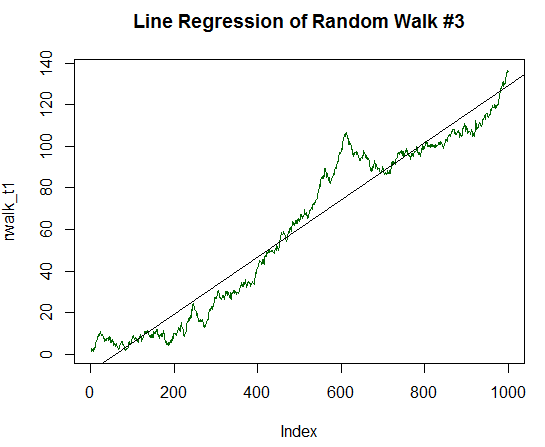
Fig. 17. Passeio aleatório com valor esperado positivo, igual a 1/10 de sua variância
Cálculo de suas estatísticas:
Call: lm(formula = rwalk_t1 ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 4 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.137303 0.001013 135.59 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.9485, Adjusted R-squared: 0.9485 F-statistic: 1.838e+04 on 1 and 998 DF, p-value: < 2.2e-16
R² tornou-se ainda maior e ascendeu para 0,9485. Este gráfico é muito parecido com a dinâmica de saldo da desejada estratégia de negociação rentável. Vamos realizar um novo ajuste novamente. Aumente o valor esperado até 1/5 do desvio padrão:
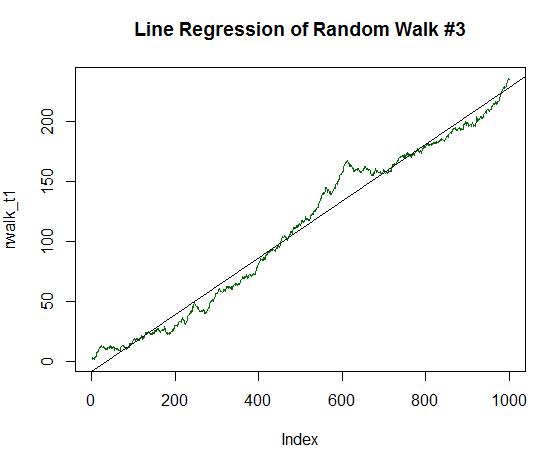
Fig. 18. Passeio aleatório com valor esperado positivo, igual a 1/5 de sua variação
Ele tem as seguintes estatísticas:
Call: lm(formula = rwalk_t1 ~ c(1:1000)) Residuals: Min 1Q Median 3Q Max -16.082 -6.888 -1.593 4.174 30.787 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -8.187185 0.585102 -13.99 <2e-16 *** c(1:1000) 0.236202 0.001013 233.25 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.244 on 998 degrees of freedom Multiple R-squared: 0.982, Adjusted R-squared: 0.982 F-statistic: 5.44e+04 on 1 and 998 DF, p-value: < 2.2e-16
É claro que R² é agora quase igual a um. O gráfico mostra claramente que os dados aleatórios na forma da linha verde quase se encontram completamente na linha reta.
O teorema do arco-seno e sua contribuição para a estimação da regressão linear
Existe uma prova matemática de que um processo aleatório eventualmente se afasta do seu ponto original. Isto foi nomeado como o primeiro e segundo teoremas do arco-seno. Eles não serão discutidos em detalhes, apenas o corolário desses teoremas será definido.
Com base neles, as tendências em processos aleatórios são bastante inevitáveis do que improváveis. Em outras palavras, existem mais tendências aleatórias em processos tais que flutuações aleatórias próximas ao ponto inicial. Esta é uma propriedade muito importante, o que contribui significativamente para a avaliação das métricas estatísticas. Isto é especialmente evidente para o coeficiente de regressão linear (Correlação LR). As tendências são melhor descritas por regressão linear que as lateralizadas. Isto é devido ao fato de que as tendências contêm mais movimentos em uma direção, que parece como uma linha suave.
Se houver mais tendências em processos aleatórios do que lateralizações, a Correlação LR também superestimará seus valores no geral. Para ver este efeito não trivial, vamos tentar gerar 10000 caminhadas aleatórias independentes com uma variância de 1.0 e valor esperado zero. Vamos calcular a correlação LR para cada gráfico desse tipo e, em seguida, traçar uma distribuição desses valores. Para esses propósitos, escreva um script de teste simples em R:
sample_r2 <- function(samples = 100, nois = 1000) { lags <- c(1:nois) r2 <- 0 # taxa de R^2 lr <- 0 # Classificação de correlação de linha for(i in 1:samples) { white_nois <- rnorm(nois) walk <- cumsum(white_nois) model <- lm(walk~lags) summary_model <- summary(model) r2[i] <- summary_model$r.squared*sign(walk[nois]) lr[i] <- (summary_model$r.squared^0.5)*sign(walk[nois]) } m <- cbind(r2, lr) }
O script calcula a Correlação LR e R². A diferença entre eles será vista mais tarde. Uma pequena adição foi feita ao script. O coeficiente de correlação resultante será multiplicado pelo sinal final do gráfico sintético. Se o resultado final for inferior a zero, a correlação será negativa; caso contrário, ela é positiva. Isso é feito para separar facilmente e rapidamente os resultados negativos dos positivos sem recorrer a outras estatísticas. É assim que a Correlação LR funciona na MetaTrader 5, o mesmo princípio será usado para R².
Então, vamos traçar a distribuição da Correlação LR para 10000 amostras independentes, cada uma das quais consiste em 1000 medidas:
ms <- sample_r2(10000, nois=1000) hist(ms[,2], breaks = 30, col="darkgreen", density = 30, main = "Distribuição da correlação LR")
O gráfico resultante indica claramente: a precisão da definição:
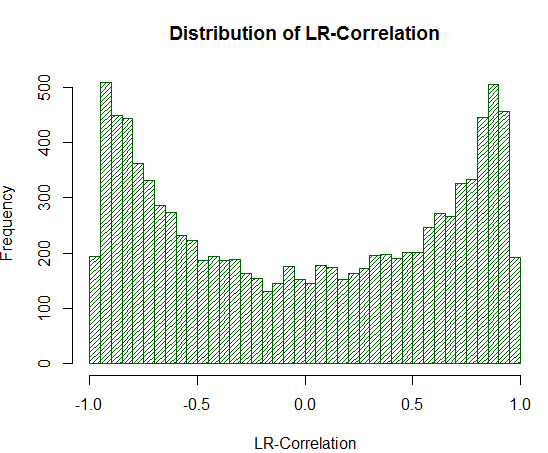
Fig. 19. Distribuição da Correlação LR para 10000 caminhadas aleatórias
Conforme visto no experimento, os valores da Correlação LR são substancialmente superestimados na faixa dos +/- 0.75 - 0.95. Isso significa que a Correlação LR muitas vezes dá falsamente uma estimativa positiva alta, na qual não deveria.
Agora, considere como R² se comporta na mesma amostra:
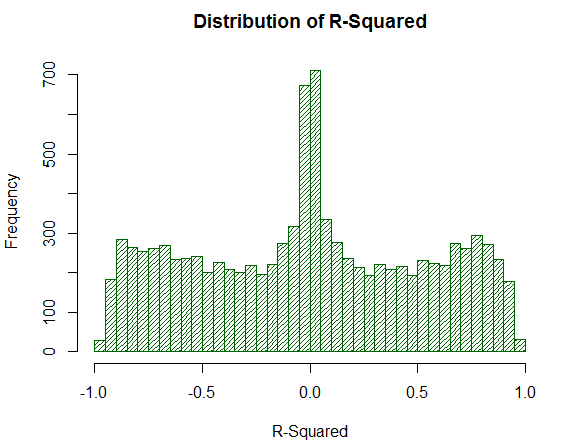
Fig. 20. Distribuição de R² para 10000 passeios aleatórios
O valor R² não é muito alto, embora sua distribuição seja uniforme. É surpreendente como uma ação matemática simples (elevando ao quadrado) anula completamente os efeitos indesejáveis da ponta da distribuição. Esta é a razão pela qual a Correlação LR não pode ser analisada diretamente — é necessário uma transformação matemática adicional. Além disso, note que R² move uma fração significativa dos saldos virtuais analisados de estratégias para um ponto próximo de zero, enquanto que a Correlação LR fornece estimativas médias estáveis. Esta é uma propriedade positiva.
Coleta do saldo de capital da estratégia
Agora que a teoria foi estudada, falta ser implementado a R² no terminal MetaTrader. Claro que nós podemos ir pelo caminho fácil e calculá-lo para as negociações no histórico. No entanto, uma melhoria adicional será introduzida. Como mencionado anteriormente, qualquer parâmetro estatístico deve ser resistente a um pequeno número de negócios. Infelizmente, o R² pode infundir o seu valor injustificadamente se houver apenas alguns negócios na conta, como qualquer outra estatística. Para evitar isso, calcule-o com base nos valores do capital — lucro flutuante. A ideia por trás disso é que, se o EA produz apenas 20 negócios por ano, é muito difícil estimar sua eficiência. É muito provável que o seu resultado seja aleatório. Mas se o equilíbrio deste EA for medido em uma periodicidade especificada (por exemplo, uma vez por hora), haverá uma quantidade razoável de pontos para traçar a estatística. Neste caso, haverá mais de 6000 medidas.
Além disso, essa medida neutraliza os sistemas que não consertam sua perda flutuante, escondendo-o. O rebaixamento do patrimônio está presente, mas não pelo saldo. Uma estatística calculada com base no saldo não avisa sobre os problemas ocorridos. No entanto, uma métrica calculada levando em consideração o lucro/perda flutuante reflete a situação objetiva na conta.
O capital da estratégia será coletado de forma não convencional. Isso ocorre porque a coleta desses valores requer dois pontos principais a serem levados em consideração:
- Frequência da coleção de estatísticas
- Determinação de eventos, recebimento que exige que o patrimônio seja verificado.
Por exemplo, um Expert Advisor funciona apenas pelo timer, no tempo gráfico H1. Ele é testado no modo "Apenas preços de abertura". Portanto, os dados para esta EA não podem ser coletados mais de uma vez por hora e a triagem desses dados pode ser realizada somente quando o evento OnTimer for gerado. A solução mais eficaz é simplesmente usar o poder do mecanismo CStrategy. O fato é que a CStrategy recolhe todos os eventos em um único manipulador de eventos e ele monitora o cronograma necessário automaticamente. Assim, a solução ótima é escrever uma estratégia de agente especial, que calcula todas as estatísticas necessárias. Ele será criado pelo gerenciador de estratégia da CManagerList. A classe só adicionará seu agente à lista de estratégias, que monitorará as alterações na conta.
O código fonte deste agente é fornecido abaixo:
//+------------------------------------------------------------------+ //| UsingTrailing.mqh | //| Copyright 2017, Vasiliy Sokolov. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, Vasiliy Sokolov." #property link "https://www.mql5.com" #include "TimeSeries.mqh" #include "Strategy.mqh" //+------------------------------------------------------------------+ //| Integrado ao portfólio de estratégias como um expert e | //| registra o capital do portfólio | //+------------------------------------------------------------------+ class CEquityListener : public CStrategy { private: //-- Frequência de gravação CTimeSeries m_equity_list; double m_prev_equity; public: CEquityListener(void); virtual void OnEvent(const MarketEvent& event); void GetEquityArray(double &array[]); }; //+------------------------------------------------------------------+ //| Definição da frequência padrão | //+------------------------------------------------------------------+ CEquityListener::CEquityListener(void) : m_prev_equity(EMPTY_VALUE) { } //+------------------------------------------------------------------+ //| Coleta o patrimônio do portfólio, monitorando todos os possíveis | //| eventos | //+------------------------------------------------------------------+ void CEquityListener::OnEvent(const MarketEvent &event) { if(!IsTrackEvents(event)) return; double equity = AccountInfoDouble(ACCOUNT_EQUITY); if(equity != m_prev_equity) { m_equity_list.Add(TimeCurrent(), equity); m_prev_equity = equity; } } //+------------------------------------------------------------------+ //| Retorna o capital como um array do tipo double | //+------------------------------------------------------------------+ void CEquityListener::GetEquityArray(double &array[]) { m_equity_list.ToDoubleArray(0, array); }
O próprio agente consiste de dois métodos: OnEvent redefinido e um método para retornar os valores do capital. Aqui, o interesse principal é sobre a classe CTimeSeries, que aparece na CStrategy pela primeira vez. É uma tabela simples, com os dados adicionados no formato: data, valor, número da coluna. Todos os valores armazenados são ordenados por horário. A data necessária é acessada através da busca binária, o que acelera substancialmente o trabalho com a coleção. O método OnEvent verifica se o evento atual é a abertura de uma nova barra e, em caso afirmativo, simplesmente armazena o novo valor do capital.
R² reage a uma situação em que não há negócios há muito tempo. Nesses momentos, os valores patrimoniais inalterados serão registrados. O gráfico de capital forma uma "escada". Para evitar isso, o método compara o valor com o valor anterior. Se os valores correspondem, a gravação é ignorada. Assim, apenas as alterações no patrimônio que se enquadram na lista.
Vamos integrar esta classe ao mecanismo CStrategy. A integração será realizada a partir de cima, no nível da CStrategyList. Este módulo é adequado para o cálculo de estatísticas personalizadas. Pode haver várias estatísticas personalizadas. Portanto, uma enumeração listando todos os tipos de estatística possíveis é introduzida:
//+------------------------------------------------------------------+ //| Determina o tipo de critério personalizado calculado após | //| a otimização. | //+------------------------------------------------------------------+ enum ENUM_CUSTOM_TYPE { CUSTOM_NONE, // O critério personalizado não é calculado CUSTOM_R2_BALANCE, // R² com base no saldo estratégico CUSTOM_R2_EQUITY, // R² com base na equidade estratégica };
A enumeração acima mostra que o critério de otimização personalizado tem três tipos: R² com base no resultado dos negócios, R² com base nos dados patrimoniais e sem cálculo de estatísticas.
Adicionado a capacidade de configurar o tipo de cálculo personalizado. Para fazer isso, forneça a classe CStrategyList com métodos adicionais SetCustomOptimaze*:
//+------------------------------------------------------------------+ //| Define R² como o critério de otimização. O coeficiente é | //| calculado para os negócios realizados. | //+------------------------------------------------------------------+ void CStrategyList::SetCustomOptimizeR2Balance(ENUM_CORR_TYPE corr_type) { m_custom_type = CUSTOM_R2_BALANCE; m_corr_type = corr_type; } //+------------------------------------------------------------------+ //| Define R² como o critério de otimização. O coeficiente é | //| calculado com base no patrimônio registrado. | //+------------------------------------------------------------------+ void CStrategyList::SetCustomOptimizeR2Equity(ENUM_CORR_TYPE corr_type) { m_custom_type = CUSTOM_R2_EQUITY; m_corr_type = corr_type; }
Cada um desses métodos define o valor de sua variável interna da ENUM_CUSTOM_TYPE para a m_custom_type e o segundo parâmetro, igual ao tipo de correlação ENUM_CORR_TYPE:
//+------------------------------------------------------------------+ //| Tipo de correlação | //+------------------------------------------------------------------+ enum ENUM_CORR_TYPE { CORR_PEARSON, // Correlação de Pearson CORR_SPEARMAN // Correlação de Spearman Rank };
Estes parâmetros adicionais devem ser mencionados separadamente. O fato é que R² não é outro senão a correlação entre o gráfico e seu modelo linear. No entanto, o próprio tipo de correlação pode diferir. Use a biblioteca matemática AlgLib. Ela suporta dois métodos para calcular a correlação: Pearson e Spearman's. A fórmula de Pearson é clássica e adequada para dados homogêneos e normalmente distribuídos. A correlação Rank-Order de Spearman é mais resistente aos picos de preços, que muitas vezes são observados no mercado. Portanto, nosso cálculo permitirá trabalhar com cada variante de cálculo de R².
Agora que todos os dados são preparados, proceda ao cálculo de R². Ele é movido para separar funções:
//+------------------------------------------------------------------+ //| Retorna a estimativa de R² com base no saldo da estratégia | //+------------------------------------------------------------------+ double CustomR2Balance(ENUM_CORR_TYPE corr_type = CORR_PEARSON); //+------------------------------------------------------------------+ //| Retorna a estimativa de R² com base na no capital da estratégia | //| Os valores do capital são passados como um array de "patrimônio" | //+------------------------------------------------------------------+ double CustomR2Equity(double& equity[], ENUM_CORR_TYPE corr_type = CORR_PEARSON);
Eles estarão localizados em um arquivo separado chamado RSquare.mqh. O cálculo é organizado sob a forma de funções, de modo que os usuários possam facilmente e rapidamente incluir esse modo de cálculo em seu projeto. Nesse caso, não há necessidade de usar o CStrategy. Por exemplo, para calcular R² em seu expert, basta redefinir a função do sistema OnTester:
double OnTester() { return CustomR2Balance(); }
Quando é necessário calcular o capital da estratégia, no entanto, os usuários que não empregam a CStrategy terão de fazê-lo sozinhos.
A última coisa que precisa ser feito no CStrategyList é definir o método OnTester:
//+------------------------------------------------------------------+ //| Adiciona o monitoramento de capital | //+------------------------------------------------------------------+ double CStrategyList::OnTester(void) { switch(m_custom_type) { case CUSTOM_NONE: return 0.0; case CUSTOM_R2_BALANCE: return CustomR2Balance(m_corr_type); case CUSTOM_R2_EQUITY: { double equity[]; m_equity_exp.GetEquityArray(equity); return CustomR2Equity(equity, m_corr_type); } } return 0.0; }
Agora considere a implementação das funções CustomR2Equity e CustomR2Balance.
Cálculo do coeficiente de determinação R² usando a AlgLib
O coeficiente de determinação R² é implementado usando a AlgLib — uma biblioteca multi-plataforma de análise numérica. Ela ajuda a calcular vários critérios estatísticos, dos simples aos mais avançados.
Aqui estão as etapas para calcular o coeficiente.
- Obtenha os valores de capital e converta-os em uma matriz M[x, y], onde x é o número de medição, y é o valor patrimonial.
- Para a matriz obtida, calcule os coeficientes a e b da equação de regressão linear.
- Gere os valores de regressão linear para cada X e coloque-os no array.
- Encontre o coeficiente de correlação da regressão linear e os valores patrimoniais usando uma das duas fórmulas de correlação.
- Calcule o R² e seu sinal.
- Retorne o valor normalizado de R² para a função de chamada.
Essas etapas são executadas pela função CustomR2Equity. Seu código-fonte é apresentado abaixo:
//+------------------------------------------------------------------+ //| Retorna a estimativa de R² com base na no capital da estratégia | //| Os valores do capital são passados como um array de "patrimônio" | //+------------------------------------------------------------------+ double CustomR2Equity(double& equity[], ENUM_CORR_TYPE corr_type = CORR_PEARSON) { int total = ArraySize(equity); if(total == 0) return 0.0; //-- Preenche a matriz: Y - valor patrimonial, X - número ordinal do valor CMatrixDouble xy(total, 2); for(int i = 0; i < total; i++) { xy[i].Set(0, i); xy[i].Set(1, equity[i]); } //-- Encontre os coeficientes a e b do modelo linear y = a*x + b; int retcode = 0; double a, b; CLinReg::LRLine(xy, total, retcode, a, b); //-- Gerar os valores de regressão linear para cada X; double estimate[]; ArrayResize(estimate, total); for(int x = 0; x < total; x++) estimate[x] = x*a+b; //-- Encontra o coeficiente de correlação dos valores com sua regressão linear double corr = 0.0; if(corr_type == CORR_PEARSON) corr = CAlglib::PearsonCorr2(equity, estimate); else corr = CAlglib::SpearmanCorr2(equity, estimate); //-- Encontra R² e seu sinal double r2 = MathPow(corr, 2.0); int sign = 1; if(equity[0] > equity[total-1]) sign = -1; r2 *= sign; //-- Retorna a estimativa de R² normalizada para dentro de centésimos return NormalizeDouble(r2,2); }
Este código se refere a três métodos estatísticos: CAlgLib::LRLine, CAlglib::PearsonCorr2 e CAlglib::SpearmanCorr2. O principal é CAlgLib::LRLine, que calcula diretamente os coeficientes de regressão linear.
Agora, deixe-nos descrever a segunda função para calcular R²: CustomR2Balance. Como o nome indica, esta função calcula o valor com base nas negociações realizadas. Todo o seu trabalho consiste em formar um array do tipo double, que contém a dinâmica do saldo, iterando sobre todos os negócios no histórico.
//+------------------------------------------------------------------+ //| Retorna a estimativa de R² com base no saldo da estratégia | //+------------------------------------------------------------------+ double CustomR2Balance(ENUM_CORR_TYPE corr_type = CORR_PEARSON) { HistorySelect(0, TimeCurrent()); double deals_equity[]; double sum_profit = 0.0; int current = 0; int total = HistoryDealsTotal(); for(int i = 0; i < total; i++) { ulong ticket = HistoryDealGetTicket(i); double profit = HistoryDealGetDouble(ticket, DEAL_PROFIT); if(profit == 0.0) continue; if(ArraySize(deals_equity) <= current) ArrayResize(deals_equity, current+16); sum_profit += profit; deals_equity[current] = sum_profit; current++; } ArrayResize(deals_equity, current); return CustomR2Equity(deals_equity, corr_type); }
Uma vez que o array é formado, ela é passada para a função CustomR2Equity mencionada anteriormente. Na verdade, a função CustomR2Equity é universal. Ele calcula o valor R² para qualquer dado contido no array equity[], seja a dinâmica do saldo ou o valor do lucro flutuante.
O último passo é uma pequena modificação no código do EA CImpulse, ou seja, a substituição do evento de sistema OnTester:
//+------------------------------------------------------------------+ //| Evento Tester | //+------------------------------------------------------------------+ double OnTester() { Manager.SetCustomOptimizeR2Balance(CORR_PEARSON); return Manager.OnTester(); }
Esta função define o tipo do parâmetro personalizado e, em seguida, retorna o seu valor.
Agora nós podemos ver o coeficiente calculado em ação. Uma vez iniciado o teste da estratégia CImpulse, o parâmetro aparecerá no relatório:
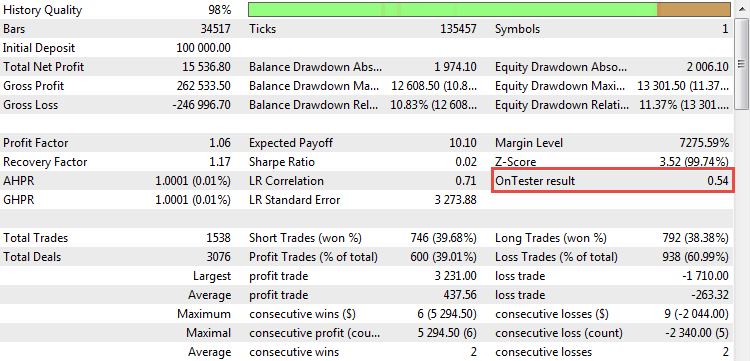
Fig. 21. O valor de R² como critério de otimização personalizado
Usando o parâmetro R² na prática
Agora que o R² foi incorporado como um critério de otimização personalizado, é hora de experimentá-lo na prática. Isso é feito pela otimização do CImpulse no período М15 do par de moeda EURUSD. Salve o resultado de otimização recebido em um arquivo do Excel e use as estatísticas obtidas para comparar várias execuções selecionadas de acordo com critérios diferentes.
A lista completa de parâmetros de otimização é fornecida abaixo:
- Símbolo: EURUSD
- Tempo gráfico: H4
- Período: 03.01.2015 - 10.10.2017
O intervalo dos parâmetros do EA está listado na tabela:
| Parâmetro | Início | Passo | Stop | Número de passos |
|---|---|---|---|---|
| PeriodMA | 15 | 5 | 200 | 38 |
| StopPercent | 0.1 | 0.05 | 1.0 | 19 |
Após a otimização, foi obtido uma nuvem de otimização, constituída por 722 variantes:
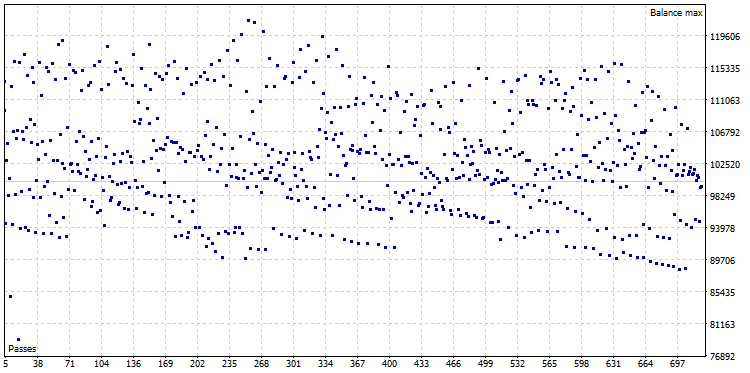
Fig. 22. Nuvem de otimização do CImpulse, símbolo - EURUSD, tempo gráfico - H1
Seleciona a execução com o lucro máximo e exibe seu gráfico de saldo:
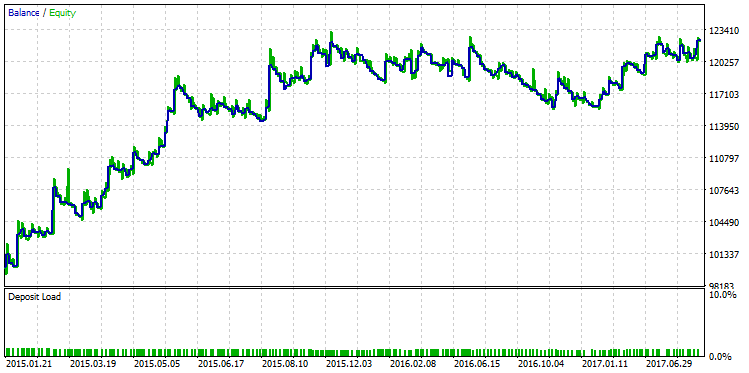
Fig. 23. Gráfico de saldo da estratégia selecionada de acordo com o critério do lucro máximo
Agora, encontre a melhor execução de acordo com o parâmetro R². Para isso, compare as execuções de otimização no arquivo XML. Se o Microsoft Excel estiver instalado no computador, o arquivo será aberto automaticamente. O trabalho envolverá a classificação e os filtros. Selecione o título da tabela e pressione o botão do mesmo nome (Home -> Sort & Filter -> Filter). Isso permite personalizar a exibição de colunas. Classifique as execuções de acordo com o critério de otimização personalizado:
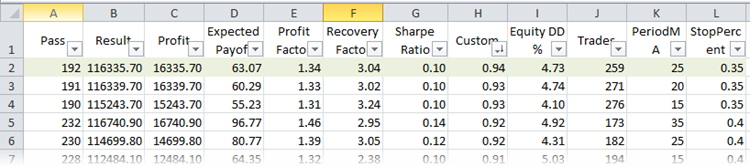
Fig. 24. A otimização é executada no Microsoft Excel, ordenada por R²
A primeira linha da tabela terá o melhor valor R² de toda a amostra. Na figura acima, está marcado em verde. Este conjunto de parâmetros no testador de estratégia fornece um gráfico de saldo que se destaca da seguinte maneira:
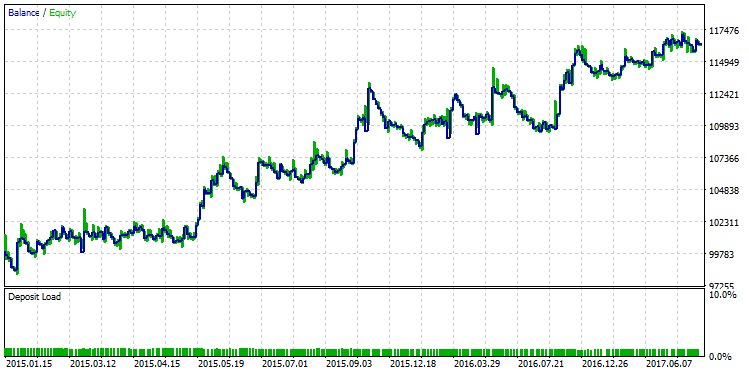
Fig. 25. Gráfico de saldo de uma estratégia selecionada de acordo com o critério do valor máximo R²
A diferença qualitativa entre esses dois gráficos de saldo é visível a olho nu. Enquanto o teste correu com o lucro máximo "quebrando" em dezembro de 2015, a outra variante com o R² máximo continuou seu crescimento estável.
Muitas vezes, R² depende do número de negócios e geralmente pode superestimar seus valores em pequenas amostras. Nesse sentido, R² correlaciona-se com o Fator de Lucro. Em certos tipos de estratégia, um alto valor do Fator de Lucro e um alto valor de R² caminham juntos. No entanto, nem sempre é esse o caso. Como ilustração, selecione um contraexemplo da amostra, demonstrando a diferença entre R² e o Fator de Lucro. A figura abaixo mostra uma estratégia executada com um dos maiores valores do fator de lucro igual a 2.98:
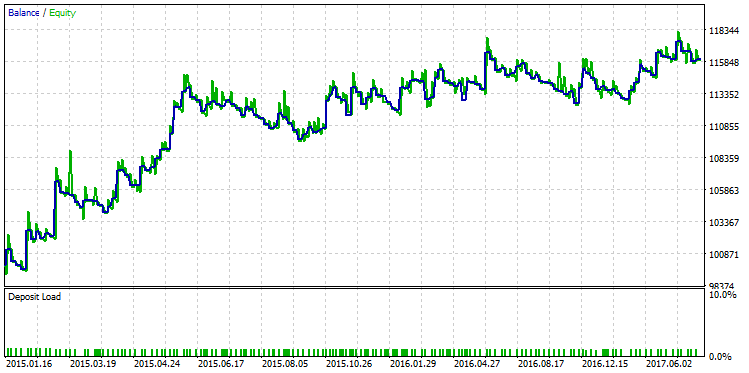
Fig. 26. Execução de teste de uma estratégia com fator de lucro igual a 2.98
O gráfico mostra que, mesmo que a estratégia mostre um crescimento estável, a qualidade da curva de saldo da estratégia ainda é menor do que a do R² máximo.
Vantagens e limitações de uso
Cada métrica estatística tem seus prós e contras. R² não é exceção a este respeito. A tabela abaixo apresenta suas falhas e soluções que podem mitigar os mesmos:
| Desvantagens | A solução |
|---|---|
| Depende do número de negócios. Sobrestima os valores com um pequeno número de negócios. | O cálculo do valor R² com base no capital da estratégia resolve parcialmente esse problema. |
| Correlaciona com as métricas existentes de eficácia da estratégia, particularmente com o Fator de Lucro e o lucro líquido da estratégia. | A correlação não é 100%. Dependendo dos recursos da estratégia, R² pode não se correlacionar com qualquer outra métrica ou correlacionar-se fracamente. |
| Para o cálculo, é necessário de cálculos matemáticos complexos. | O algoritmo é implementado usando a biblioteca AlgLib, que é delegado toda a complexidade. |
| Aplicável exclusivamente para estimativa de processos lineares ou de negociação de sistemas com um lote fixo. | Não se aplica a sistemas de negociação que utilizem um sistema de capitalização (gerenciamento de capital). |
Vamos descrever o problema de aplicar R² a sistemas não-lineares (por exemplo, uma estratégia de negociação com um lote dinâmico) com mais detalhes.
O principal objetivo de cada trader é a maximização do lucro. Uma condição necessária para isso é o uso de vários sistemas de capitalização. O sistema de capitalização é a transformação de um processo linear em um não-linear (por exemplo, em um processo exponencial). Mas essa transformação torna a maioria dos parâmetros estatísticos sem sentido. Por exemplo, o parâmetro "lucro final" não tem sentido para os sistemas capitalizados, uma vez que mesmo uma ligeira mudança no intervalo de tempo testando ou alterando um parâmetro de estratégia em um centésimo por cento pode alterar o resultado final por dezenas ou mesmo centenas de vezes.
Outros parâmetros da estratégia também perdem o seu significado, como o Fator de lucro, Retorno esperado, lucro/perda máximo, etc. Nesse sentido, R² também não é uma exceção. Criado para a estimativa linear da suavidade da curva de equilíbrio, ele torna-se impotente na avaliação de processos não-lineares. Portanto, qualquer estratégia deve ser testada em uma forma linear, e somente depois disso um sistema de capitalização deve ser adicionado à opção selecionada. É melhor avaliar os sistemas não-lineares usando métricas estatísticas especiais (por exemplo, GHPR) ou para calcular o rendimento em porcentagens anuais.
Conclusão
- Os parâmetros estatísticos padrão para avaliar os sistemas de negociação têm inconvenientes conhecidos, que devem ser levados em consideração.
- Entre as métricas padrão na MetaTrader 5, somente a Correlação LR foi projetada para estimar a suavidade da curva de saldo da estratégia. No entanto, seus valores são muitas vezes superestimados.
- R² é uma das poucas métricas que calculam a suavidade da curva de saldo e da curva de lucro flutuante da estratégia. Ao mesmo tempo, R² está livre das desvantagens da Correlação LR.
- A biblioteca matemática AlgLib é usada no cálculo de R². O cálculo em si tem muitas modificações e é descrito detalhadamente no exemplo correspondente.
- O critério de otimização personalizado pode ser incorporado em um Expert Advisor para que todos os experts possam calcular esta métrica automaticamente sem a participação deles. As instruções sobre como fazer isso são fornecidas no exemplo de integração do R² no mecanismo de negociação CStrategy.
- Um método de integração semelhante pode ser usado para calcular os dados adicionais necessários no cálculo de estatísticas personalizadas. Para R², esses dados são os dados sobre o lucro flutuante da estratégia (capital). A gravação da dinâmica de lucro flutuante é realizada pelo motor de negociação CStrategy.
- O coeficiente de determinação permite selecionar estratégias com um crescimento do saldo/capital. Nesse caso, o processo de seleção com base em outros parâmetros pode perder essas variantes.
- R² tem suas desvantagens, como qualquer outra métrica estatística, que deve ser levada em consideração ao trabalhar com esse valor.
Assim, é seguro dizer que o coeficiente de determinação R² é uma adição importante ao conjunto existente das métricas de teste da MetaTrader 5. Ele permite estimar a suavidade da curva de saldo de uma estratégia, que é um indicador não trivial por conta própria. R² é fácil de usar: seus valores estão vinculados ao intervalo de -1.0 a 1.0, sinalizando sobre uma tendência negativa no saldo da estratégia (valores próximos de -1.0), sem tendência (valores próximos de 0.0) e tendência positiva (valores tendendo a 1.0). Graças a todas essas propriedades, confiabilidade e simplicidade, o R² pode ser recomendado para uso na construção de um sistema de negociação lucrativo.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/2358
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Teste de padrões que surgem ao negociar cestas de pares de moedas Parte II
Teste de padrões que surgem ao negociar cestas de pares de moedas Parte II
 Mini-emulador do mercado ou Testador de estratégias manual
Mini-emulador do mercado ou Testador de estratégias manual
 Decompondo as entradas em indicadores
Decompondo as entradas em indicadores
 Expert Advisor Multiplataforma: As classes CExpertAdvisor e CExpertAdvisors
Expert Advisor Multiplataforma: As classes CExpertAdvisor e CExpertAdvisors
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Há muitas informações aqui explicando o raciocínio e seu código, e eu agradeço por isso. Aqui está a versão Tl;dr para aqueles de nós para quem a maior parte disso passou por cima de nossas cabeças:
1. Adicione os includes
2. E o OnTester:
É isso para implementá-lo com base no equilíbrio.
Se o seu EA usar CStrategy (como fazem os EAs assistentes), adicione os mesmos includes e você poderá alternar para o patrimônio líquido desta forma:
O que eu ainda NÃO descobri e espero que alguém possa me ajudar é o que fazer para implementar o ouvinte de patrimônio líquido em seu próprio EA que não seja baseado no CStrategy. Tudo o que o artigo diz é:
E eu não sei como fazer isso.Corrigidos os erros. O arquivo está anexado.
Obrigado, atualizei o artigo.
Deve ser muito semelhante... uma comparação está em minha longa e desorganizada lista de tarefas!
Normalize o volume: pegue o lucro e divida pelo tamanho do lote
Ou divida o saldo[0] pelo saldo[1] para obter o retorno e calcule r^2 para a curva de retorno