
Recetas MQL5 - Creando el búfer circular para calcular rápidamente los indicadores en la ventana móvil
Índice
- Introducción
- Problema del cálculo de la media móvil
- Teoría del búfer circular
- Prototipo de trabajo
- Ejemplo del cálculo de la media móvil simple en el búfer circular
- Ejemplo del cálculo de la media móvil exponencial en el búfer circular
- Cálculo de los máximos/mínimos en el búfer circular
- Integración del búfer circular con la librería AlgLib
- Construcción del MACD a base de las primitivas circulares
- Construcción del indicador Stochastic a base de las primitivas circulares
- Optimización del uso de la memoria operativa
- Optimización del tiempo de simulación del Asesor Experto
- Conclusiones y sugerencias para mejorar el rendimiento
- Conclusión
Introducción
No es un secreto que la mayoría de los cálculos que deben ser ejecutados por el trader se realizan en la ventana móvil. Ésta es la singularidad de los datos bursátiles, que van prácticamente siempre en un flujo continuo, bien la información de precios, pedidos colocados o bien volúmenes del trading. Por regla general, el trader necesita calcular algún valor para un período de tiempo determinado. Por ejemplo, si se calcula la media móvil, se tiene en cuenta el valor medio del precio para las últimas N barras, donde N significa el período de la media móvil. Es obvio que en este caso el tiempo gastado en calcular el valor medio no debe depender del período de esta media móvil. Sin embargo, no siempre en la práctica resulta fácil implementar el algoritmo con esta propiedad. Desde el punto de vista algorítmico, cuando llega una nueva barra, es mucho más fácil recalcular el valor de la media. El algoritmo del búfer circular soluciona el problema del cálculo efectivo proporcionando la ventana móvil al bloque del cómputo de tal manera que sus cálculos internos sean máximamente eficaces y simples al mismo tiempo.
Problema del cálculo de la media móvil
Vamos a analizar un ejemplo determinado: cálculo de la media móvil. Tomando de ejemplo este simple algoritmo, mostraremos con qué problemas podemos enfrentarnos durante su construcción. El valor medio se calcula de acuerdo con la fórmula bien conocida:
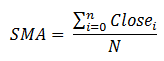
Para implementar este cálculo, escribiremos un script simple en MQL5:
//+------------------------------------------------------------------+ //| SMA.mq5 | //| Copyright 2015, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2015, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" input int N = 10; // Período de la media //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- double closes[]; if(CopyClose(Symbol(), Period(), 0, N, closes)!= N) { printf("Need more data"); return; } double sum = 0.0; for(int i = 0; i < N; i++) sum += closes[i]; sum /= N; printf("SMA: " + DoubleToString(sum, Digits())); } //+------------------------------------------------------------------+
Desde el punto de vista del propio cálculo todo está ejecutado correctamente: el resultado de trabajo de este script será el valor de la media móvil visualizado en la ventana del terminal. ¿Pero qué se puede hacer cuando trabajamos en la ventana móvil? En la práctica, el último valor de la cotización va a cambiar constantemente y van a agregarse nuevas barras. Cada vez el algoritmo va a recalcular de nuevo el valor de la media móvil incorporando dos operaciones que consumen muchísimos recursos:
- Copiado de N elementos al array receptor;
- Repaso completo del array receptor en el ciclo for.
La última acción es de mayor consumo de recursos. Para el período 10 van a ejecutarse diez iteraciones, mientras que para el período 500, ya serán quinientas. Resulta que la complejidad del algoritmo depende directamente del período de promediación y puede ser escrita como O(n), donde O es la función de la complejidad.
No obstante, hay un algoritmo mucho más rápido para calcular la media en la ventana móvil. Para eso, será suficiente saber la suma de todos los valores en el cálculo anterior:
SMA = (Suma de todos los valores - el primer valor de la ventana móvil + valor nuevo)/Período de la media
La función de complejidad de este algoritmo es la constante O(1), que no depende del período de promediación. El rendimiento de este algoritmo es mayor pero es más difícil de implimentarlo. Cada vez que se añade una barra nueva, habrá que realizar los siguientes pasos:
- de la suma actual restarle el valor que ha sido añadido primero, y luego eliminarlo de la serie;
- a la suma actual añadirle el valor que ha sido añadido el último, y luego añadirla a la serie;
- dividir la suma actual por el período de promediación y devolverla como la media móvil.
Si el último valor no se añade, sino se actualiza, el algoritmo se hace aún más complejo:
- definir el valor que se actualiza y recordar su estado final;
- de la suma actual restarle el valor que ha sido recordado en el paso anterior;
- reemplazar el valor por el nuevo;
- a la suma actual añadirle el valor nuevo;
- dividir la suma actual por el período de promediación y devolverla como la media móvil.
Una complicación adicional consiste en que MQL5, como la mayoría de los lenguajes de programación de sistema, tiene las herramientas incorporadas para trabajar sólo con los tipos de datos básicos, por ejemplo, con los arrays. No obstante, sin una modificación apropiada, los arrays no están muy indicados para este papel. Es que en el caso más evidente, es necesario organizar la cola FIFO (First In - First Out), es decir, hacer una cierta lista cuyo primer elemento añadido se elimina al ser añadido un elemento nuevo. Los arrays permiten tanto eliminar como agregar los elementos. Pero estas operaciones requieren bastantes recursos, es que durante cada una de ellas, se realiza la redistribución del array.
Para evitar semejantes complicaciones, y al mismo tiempo implementar un algoritmo realmente eficaz, nos dirigiremos al búfer circular
Teoría del búfer circular
La particularidad clave en el trabajo del búfer circular es la posibilidad de añadir y eliminar los elementos sin tener que redistribuir el array. Efectivamente, si suponemos que el número de elementos en el array siempre es una constante (los que es así para los cálculos en la ventana móvil), la adición del nuevo elemento conlleva la eliminación del elemento antiguo. De esta manera, el número total de elemento queda siendo el mismo, pero se altera su indexación cuando se añade cada elemento nuevo. El último elemento se hace penúltimo, el segundo elemento ocupa el lugar del primero, mientras que el primero se desaparece de la cola para siempre.
Gracias a esta posibilidad, el búfer circular puede ser creado a base de un array común. Crearemos la clase a base de un array común:
class CRingBuffer { private: double m_array[]; };
Supongamos que nuestro búfer va a componerse solamente de tres elementos. Entonces, el primer elemento será añadido a la celda del array con el índice 0; el segundo elemento, a la celda con el índice 1; y el tercero, a la celda con el índice 2. ¿Qué pasará si añadimos el cuarto elemento? Es evidente que al añadirlo, el primer elemento debe ser eliminado. Entonces, el lugar más apropiado para el cuarto elemento será el lugar del primero, es decir, su índice será de nueve cero. ¿Cómo se puede calcular este índice? Para eso, usaremos la operación especial 'resto de la división'. En MQL5 esta operación se denomina con un símbolo especial %. Ya que la enumeración empieza de cero, nuestro cuarto elemento será el tercero en la cola, y su índice de ubicación va a calcularse según la fórmula:
Aquí 'total' es el tamaño del búfer. En nuestro ejemplo, tres se divide por tres sin el resto. De esta manera, index va a contener el resto igual a cero. Los siguientes elementos van a ubicarse de acuerdo con las mismas reglas: el número del elemento a añadir va a dividirse por la cantidad de elementos en el array. El resto de esta división va a representar prácticamente el índice en el búfer circular. Vamos a mostrar un cálculo relativo de los índices de 8 primeros elementos que se añaden al búfer circular con dimensionalidad 3:
0 % 3 = [0] 1 % 3 = [1] 2 % 3 = [2] 3 % 3 = [0] 4 % 3 = [1] 5 % 3 = [2] 6 % 3 = [0] 7 % 3 = [1]...
Prototipo de trabajo
Hemos formado buen concepto sobre la teoría del búfer circular. Ha llegado el momento de crear el prototipo de trabajo. Nuestro búfer circular va a poseer tres capacidades principales:
- añadir el nuevo valor;
- eliminar el último valor;
- cambiar el valor por el índice arbitrario.
La última función la vamos a necesitar para el trabajo en tiempo real, cuando la última barra va a encontrarse en estado de formación y el precio de cierre va a cambiar constantemente.
Además, nuestro búfer va a tener dos propiedades principales: contener el tamaño máximo del búfer y el número actual de sus elementos. La mayor parte del tiempo, estos valores van a coincidir, es que cuando los elementos llenen la dimensión entera del búfer, cada elemento posterior va a sobrescribir el más antiguo. De esta manera, el número total de elementos va a quedarse invariable. Pero durante el llenado inicial del búfer, los valores de esta propiedades serán diferentes. El número máximo de elementos va a ser una propiedad variable. El usuario podrá aumentar o disminuirlo.
La eliminación del elemento más antiguo va a realizarse automáticamente, sin la intervención explícita del usuario. Eso ha sido hecho intencionadamente, porque en la práctica, la eliminación de los elementos antiguos complica el cálculo de las estadísticas auxiliares.
El cálculo de los índices reales del búfer interno -en el que van a contenerse los valores reales- supone la dificultad más grande en este algoritmo. Así, por ejemplo, si el usuario solicita el elemento con el índice 0, el valor real en el que se ubica este elemento puede ser diferente. Por ejemplo, al añadir el elemento 17 al búfer circular con la dimensionalidad 10 el elemento cero va a ubicarse por el índice 8, y el último, noveno, elemento, por el índice 7.
Para ver cómo funcionan las operaciones principales del búfer circular, mostraremos su archivo de cabecera y el contenido de los métodos principales:
//+------------------------------------------------------------------+ //| Búfer circular Double | //+------------------------------------------------------------------+ class CRiBuffDbl { private: bool m_full_buff; int m_max_total; int m_head_index; protected: double m_buffer[]; //Búfer circular para acceso directo. Atención: ¡Los índices no corresponden a su numero de orden! ... int ToRealInd(int index); public: CRiBuffDbl(void); void AddValue(double value); void ChangeValue(int index, double new_value); double GetValue(int index); int GetTotal(void); int GetMaxTotal(void); void SetMaxTotal(int max_total); void ToArray(double& array[]); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CRiBuffDbl::CRiBuffDbl(void) : m_full_buff(false), m_head_index(-1), m_max_total(0) { SetMaxTotal(3); } //+------------------------------------------------------------------+ //| Establece el nuevo tamaño del búfer circular | //+------------------------------------------------------------------+ void CRiBuffDbl::SetMaxTotal(int max_total) { if(ArraySize(m_buffer) == max_total) return; m_max_total = ArrayResize(m_buffer, max_total); } //+------------------------------------------------------------------+ //| Devuelve el tamaño real del búfer circular | //+------------------------------------------------------------------+ int CRiBuffDbl::GetMaxTotal(void) { return m_max_total; } //+------------------------------------------------------------------+ //| Devuelve el valor según el índice | //+------------------------------------------------------------------+ double CRiBuffDbl::GetValue(int index) { return m_buffer[ToRealInd(index)]; } //+------------------------------------------------------------------+ //| Devuelve el número total de elementos | //+------------------------------------------------------------------+ int CRiBuffDbl::GetTotal(void) { if(m_full_buff) return m_max_total; return m_head_index+1; } //+------------------------------------------------------------------+ //| Añade el valor nuevo al búfer circular | //+------------------------------------------------------------------+ void CRiBuffDbl::AddValue(double value) { if(++m_head_index == m_max_total) { m_head_index = 0; m_full_buff = true; } //... m_buffer[m_head_index] = value; } //+------------------------------------------------------------------+ //| Cambia el valor añadido antes por el nuevo | //+------------------------------------------------------------------+ void CRiBuffDbl::ChangeValue(int index, double value) { int r_index = ToRealInd(index); double prev_value = m_buffer[r_index]; m_buffer[r_index] = value; } //+------------------------------------------------------------------+ //| Transforma el índice virtual en real | //+------------------------------------------------------------------+ int CRiBuffDbl::ToRealInd(int index) { if(index >= GetTotal() || index < 0) return m_max_total; if(!m_full_buff) return index; int delta = (m_max_total-1) - m_head_index; if(index < delta) return m_max_total + (index - delta); return index - delta; }
La base de esta clase es el puntero al último elemento añadido m_head_index. Cuando se añade un elemento nuevo a través del método AddValue, él se incrementa en uno. Si su valor empieza a superar el tamaño del array, se anula.
La función más complicada del búfer circular es el método interno ToRealInd. En la entrada recibe el índice del búfer desde el punto de vista del usuario y devuelve el índice real del array, según el que se ubica el elemento necesario.
Como podemos ver, el búfer circular está organizado bastante simple: sin tomar en cuenta la aritmética direccional, soporta las acciones elementales de adición de un elemento nuevo y concede el acceso a un elemento aleatorio usando la función GetValue(). Sin embargo, esta funcionalidad en sí se utiliza habitualmente sólo para una organización más cómoda del proceso del cálculo de la característica necesaria, sea una media móvil habitual, o un algoritmo de búsqueda de máximos/mínimos. Usando el búfer circular, se puede calcular muchos objetos estadísticos. Son toda clase de indicadores o criterios estadísticos, como la dispersión y desviación estándar. Por eso, es imposible proveer la clase del búfer circular de todos los algoritmos de cálculo. Pero tampoco es necesario hacerlo. En vez de eso, se puede crear una solución más flexible: hacer las clases derivadas que implementan uno u otro algoritmo del cálculo del indicador o estadística.
Para que estas clases derivadas puedan calcular sus valores de manera cómoda, es necesario proveer el búfer circular de métodos adicionales, vamos a llamarlos métodos de eventos Son métodos comunes ubicados en la sección protected. Todos estos métodos son redefinibles y se empiezan con el prefijo On:
//+------------------------------------------------------------------+ //| Búfer circular Double | //+------------------------------------------------------------------+ class CRiBuffDbl { private: ... protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double prev_value, double new_value); virtual void OnChangeArray(void); virtual void OnSetMaxTotal(int max_total); };
Cada vez que ocurran algunos cambios en el búfer circular, se llama a algún método que indica en eso. Por ejemplo, si el búfer recibe un valor nuevo, se invocará el método OnAddValue. Su parámetro contiene el valor añadido. Si redefinimos este método en la clase derivada del búfer circular, entonces cada vez que se añada un valor nuevo, será llamado al bloque correspondiente del cálculo de la clase derivada.
El búfer circular contiene cinco eventos que pueden ser rastreados en la clase derivada (los métodos a través de los cuales se hace eso se indican entre paréntesis):
- adición de un elemento nuevo (OnAddValue);
- eliminación de un elemento antiguo (OnRemoveValue);
- cambio de un elemento según el índice arbitrario (OnChangeValue);
- cambio del contenido entero del búfer circular (OnChangeArray);
- cambio del número máximo de elementos en el búfer circular (OnSetMaxTotal).
Hay que hablas más detalladamente sobre el evento OnChangeArray. Este evento es llamado cuando el recálculo del indicador requiere el acceso al array entero de los valores acumulados. En este caso, basta con redefinir este método en la clase derivada. En el propio método -usando la función ToArray- es necesario obtener el array actual entero de valores , y usarlo para hacer el cálculo correspondiente. El ejemplo de este cálculo será mostrado más abajo, en la sección de la integración del búfer circular con la librería AlgLib.
La clase del búfer circular se llama CRiBuffDbl. Como es revelado por su nombre, trabaja con los valores tipo double. Los números reales representan el tipo de datos más común para los algoritmos computacionales. Sin embargo, aparte de los números reales, puede ser necesario trabajar con números enteros, por eso el complejo de las clases -además de la clase CRiBuffDbl- contiene la clase parecida CRiBuffInt, que trabaja con los números tipo integer. En los procesadores modernos, la aritmética de números enteros se realiza mucho más rápido que los cálculos con punto flotante. Por eso, para las tareas especializadas con números enteros es mejor usar CRiBuffInt.
En el enfoque presentado, no se utiliza la técnica de las clases de plantilla que permite describir un tipo universal <template T> y trabajar con él. Eso ha sido hecho a propósito, porque se supone que los algoritmos del cálculo se heredan directamente del búfer circular, y cada uno de estos algoritmos trabaja con un tipo de datos determinado.
Ejemplo del cálculo de la media móvil simple en el búfer circular
Hemos considerado en detalle la estructura de las clases que implementan el principio del búfer circular, y ahora ha llegado el momento para solucionar algunos problemas prácticos a través de ellas. Empezamos con lo más simple: vamos a crear el indicador bien conocido Simple Moving Average. Se trata de una media móvil común, y entonces para su cálculo será necesario dividir la suma de la serie por el período de la media. Recordemos la fórmula del cálculo expuesta al principio del artículo:
SMA = (Suma de todos los valores - el primer valor de la ventana móvil + valor nuevo)/Período de la media
Para la implementación de nuestro algoritmo habrá que redefinir dos métodos en la clase derivada de CRiBuffDbl: OnAddValue y OnRemoveValue. El valor medio va a calcularse en el método Sma. Aquí tenemos el código de la clase resultante:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Cálculo de la media móvil en el búfer circular | //+------------------------------------------------------------------+ class CRiSMA : public CRiBuffDbl { private: double m_sum; protected: virtual void OnAddValue(double value); virtual void OnRemoveValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); public: CRiSMA(void); double SMA(void); }; CRiSMA::CRiSMA(void) : m_sum(0.0) { } //+------------------------------------------------------------------+ //| Aumentamos la suma total | //+------------------------------------------------------------------+ void CRiSMA::OnAddValue(double value) { m_sum += value; } //+------------------------------------------------------------------+ //| Disminuimos la suma total | //+------------------------------------------------------------------+ void CRiSMA::OnRemoveValue(double value) { m_sum -= value; } //+------------------------------------------------------------------+ //| Cambiamos la suma total | //+------------------------------------------------------------------+ void CRiSMA::OnChangeValue(int index,double del_value,double new_value) { m_sum -= del_value; m_sum += new_value; } //+------------------------------------------------------------------+ //| Devuelve la media móvil simple | //+------------------------------------------------------------------+ double CRiSMA::SMA(void) { return m_sum/GetTotal(); }
Aparte de los métodos que reaccionan a la adición y eliminación (OnAddValue y OnRemoveValue соответственно), necesitamos redefinir un método más- el método que se invoca cuando se cambia un elemento arbitrario (OnChangeValue). El búfer circular soporta el cambio arbitrario de cualquier elemento que forma su parte, por eso hay que rastrear este cambio. Generalmente, soló el último elemento, en el modo de formación de la última barra, es objeto de la alteración. El evento OnChangeValue, que hace falta redefinir, está previsto precisamente para este caso.
Vamos a escribir el indicador personalizado que utiliza la clase del búfer circular para el cálculo de la media móvil:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_chart_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiSMA.mqh> input int MaPeriod = 13; double buff[]; CRiSMA Sma; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); Sma.SetMaxTotal(MaPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { Sma.AddValue(price[i]); buff[i] = Sma.SMA(); calc = true; } if(!calc) { Sma.ChangeValue(MaPeriod-1, price[rates_total-1]); buff[rates_total-1] = Sma.SMA(); } return(rates_total-1); } //+------------------------------------------------------------------+
Al principio del cálculo, el indicador simplemente añade nuevos valores al búfer circular de la media móvil. Además, no es necesario controlar la cantidad de valores a añadir. Todos los cálculos y la eliminación de los elementos obsoletos se realizan en modo automático. Si la llamada al indicador ocurre durante el cambio del precio de la última barra, sólo hay que reemplazar el último valor de la media móvil por uno nuevo, pues de lo que se encarga el método ChangeValue.
La visualización gráfica del indicador equivale al indicador estándar homónimo MovingAverage:
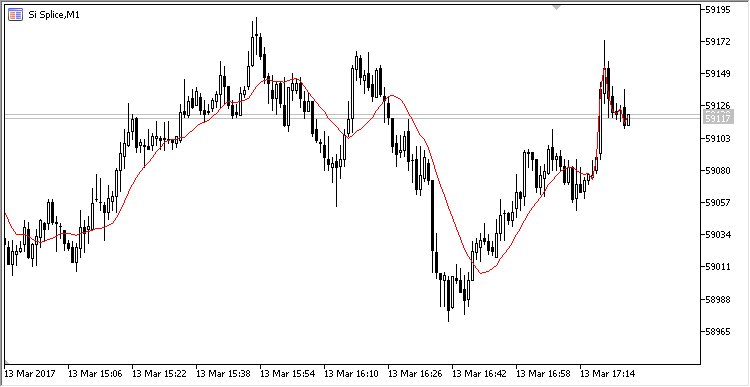
Fig. 1. Visualización de la media móvil simple calculada en el búfer circular.
Ejemplo del cálculo de la media móvil exponencial en el búfer circular
Vamos a coger un ejemplo más complicado: cálculo de la media móvil exponencial. A diferencia de la media móvil simple, la media exponencial no reacciona a la eliminación del elemento más antiguo del búfer de valores, por eso hay que redefinir solamente dos métodos para su cálculo: OnAddValue y OnChangeValue. Como en el ejemplo anterior, creamos la clase CRiEMA, heredero de CRiBuffDbl y redefinimos los métodos correspondientes:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" //+------------------------------------------------------------------+ //| Cálculo de la media móvil exponencial en el búfer circular | //+------------------------------------------------------------------+ class CRiEMA : public CRiBuffDbl { private: double m_prev_ema; // Valor anterior de EMA double m_last_value; // Último valor del precio double m_smoth_factor; // Factor del suavizado bool m_calc_first_v; // Bandera que indica en el cálculo del primer valor double CalcEma(); // Cálculo inmediato de la media protected: virtual void OnAddValue(double value); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiEMA(void); double EMA(void); }; //+----------------------------------------------------------------------------+ //| Suscribimos a las notificaciones sobre la adición y alteración del valor | //+----------------------------------------------------------------------------+ CRiEMA::CRiEMA(void) : m_prev_ema(EMPTY_VALUE), m_last_value(EMPTY_VALUE), m_calc_first_v(false) { } //+---------------------------------------------------------------------------+ //| Cálculo del factor suavizante de acuerdo con la fórmula MetaQuotes EMA | //+---------------------------------------------------------------------------+ void CRiEMA::OnSetMaxTotal(int max_total) { m_smoth_factor = 2.0/(1.0+max_total); } //+------------------------------------------------------------------+ //| Aumentamos la suma total | //+------------------------------------------------------------------+ void CRiEMA::OnAddValue(double value) { //Calculamos el valor anterior de EMA if(m_prev_ema != EMPTY_VALUE) m_prev_ema = CalcEma(); //Recordamos el precio actual m_last_value = value; } //+------------------------------------------------------------------+ //| Corregimos EMA | //+------------------------------------------------------------------+ void CRiEMA::OnChangeValue(int index,double del_value,double new_value) { if(index != GetMaxTotal()-1) return; m_last_value = new_value; } //+------------------------------------------------------------------+ //| Cálculo inmediato de EMA | //+------------------------------------------------------------------+ double CRiEMA::CalcEma(void) { return m_last_value*m_smoth_factor+m_prev_ema*(1.0-m_smoth_factor); } //+------------------------------------------------------------------+ //| Devuelve la media móvil simple | //+------------------------------------------------------------------+ double CRiEMA::EMA(void) { if(m_calc_first_v) return CalcEma(); else { m_prev_ema = m_last_value; m_calc_first_v = true; } return m_prev_ema; }
El método CalcEma se encarga del cálculo de la media móvil. En realidad, devuelve la suma de dos productos: el último valor anterior conocido multiplicado por el factor de suavizado, más el valor anterior del indicador multiplicado por la magnitud inversa al factor de suavizado. Si el valor anterior del indicador todavía no ha sido calculado, en su lugar se toma el primer valor colocado en el búfer (en nuestro caso, será el precio de cierre de la barra cero).
Para visualizar el cálculo en el gráfico, escribiremos el indicador similar al de la sección anterior. Tendrá el siguiente aspecto:
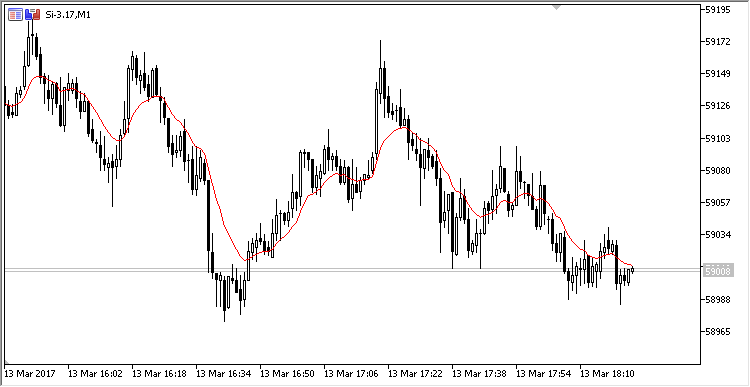
Fig. 2. Cálculo de la media móvil exponencial en el búfer circular
Cálculo de los máximos/mínimos en el búfer circular
La tarea más complicada e interesante es el cálculo de los máximos y los mínimos en la ventana móvil. Desde luego, se puede hacerlo con mucha facilidad alegando las funciones estándar ArrayMaximum y ArrayMinimum, pero todas las ventajas del cálculo en la ventana móvil desaparecen en este caso. Es que si los datos se meten y se eliminan del búfer consecutivamente, existe la posibilidad de calcular el máximo y el mínimo sin ejecutar el recorrido completo. Supongamos que para cada valor nuevo que va a caer en el búfer, van a calcularse dos valores adicionales. El primer valor va a indicar en la cantidad de elementos anteriores por debajo del elemento actual, y el segundo valor indicará la cantidad de elementos anteriores por encima del elemento actual. El primer valor va a utilizarse para la búsqueda eficaz del máximo, y el segundo, para buscar el mínimo.
Ahora imaginemos que nos vemos con unas barras comunes y precisamos calcular los extremos de los precios según sus valores High para un período determinado. Para eso, escribiremos un número encima de cada barra que sea igual a la cantidad de las barras anteriores con valores máximos inferiores al valor máximo de la barra actual. La secuencia de las barras se muestra en la siguiente imagen:
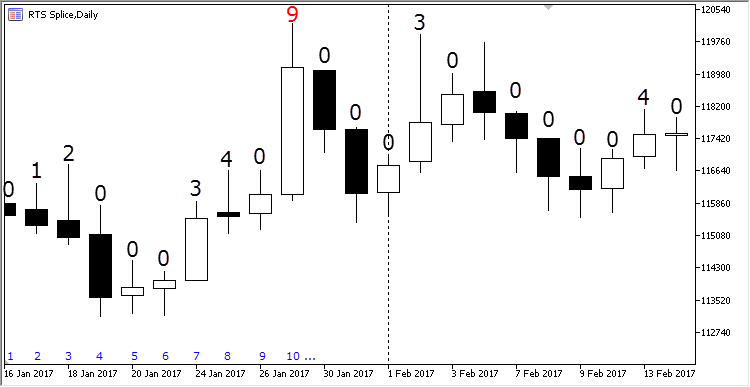
Fig. 3. Jerarquía de los extremos de las barras
La primera barra siempre tiene el extremo cero, ya que no hay ningún valor anterior para la comprobación. La barra №2 es más alta, por eso el índice de su extremo será igual a uno. La tercera barra es más alta que la anterior, con lo cual es más alta que la primera. Su número del extremo es igual a dos. Le siguen tres barras cada uno de los cuales es más bajo que el anterior. Todas ellas están por debajo de la barra № 3, por eso sus números del extremo son iguales a cero. Luego va la barra siete que es más alta que las tres anteriores pero está por debajo de la cuarta, por eso su índice del extremo será igual a tres. De la misma manera, cuando se añade cada nueva barra, se calcula su índice del extremo.
Una vez calculados todos los índices anteriores, es muy fácil calcular el extremo de la barra actual. Para eso basta con comparar el extremo de la barra con otros extremos. Se puede acceder directamente a cada extremo subsiguiente, saltando varias barras consecutivas. Es que gracias a los números colocados, sabemos su índice. Vamos a ilustrar lo dicho:
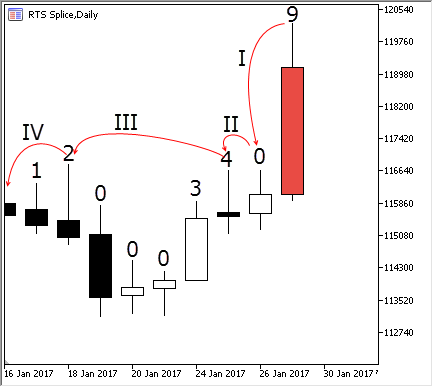
Fig. 4. Búsqueda del extremo de la barra actual
Imaginemos que estamos añadiendo la barra marcada en rojo. Es la barra con el número 9 porque la numeración va desde cero. Para determinar su índice del extremo, comparémosla con la barra №8 haciendo el paso I: ha resultado ser más alto por eso su extremo es por lo menos igual a uno. Comparémosla con la barra №7 haciendo el paso II: de nuevo es más alta que esta barra. Ya que la barra №7 está por encima de cuatro barras antecedentes, podemos comparar inmediatamente nuestra barra con la barra №3 haciendo el paso III. La barra №9 es más alta que la №3, por consiguiente, es más alta que todas las barras en este momento. Gracias a los índices calculados anteriormente, hemos evitado la comparación con cuatro barras intermedios, que son obviamente más bajos que la actual. Precisamente así funciona la búsqueda rápida de un extremo en el búfer circular. De la misma manera funciona también la búsqueda de un mínimo. La única diferencia es que se utiliza el índice adicional de los mínimos.
Ahora, cuando ya tenemos descrito el algoritmo, mostraremos su código fuente. La clase presentada posee la siguiente característica interesante: en calidad de búferes auxiliares, también se utilizan dos búferes circulares tipo CRiBuffInt. Cada uno de ellos contiene los índices de máximos y mínimos, respectivamente.
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiBuffInt.mqh" //+------------------------------------------------------------------+ //| Cálculo de la media móvil exponencial en el búfer circular | //+------------------------------------------------------------------+ class CRiMaxMin : public CRiBuffDbl { private: CRiBuffInt m_max; CRiBuffInt m_min; bool m_full; int m_max_ind; int m_min_ind; protected: virtual void OnAddValue(double value); virtual void OnCalcValue(int index); virtual void OnChangeValue(int index, double del_value, double new_value); virtual void OnSetMaxTotal(int max_total); public: CRiMaxMin(void); int MaxIndex(int max_period = 0); int MinIndex(int min_period = 0); double MaxValue(int max_period = 0); double MinValue(int min_period = 0); void GetMaxIndexes(int& array[]); void GetMinIndexes(int& array[]); }; CRiMaxMin::CRiMaxMin(void) { m_full = false; m_max_ind = 0; m_min_ind = 0; } void CRiMaxMin::GetMaxIndexes(int& array[]) { m_max.ToArray(array); } void CRiMaxMin::GetMinIndexes(int& array[]) { m_min.ToArray(array); } //+----------------------------------------------------------------------------------+ //| Cambiamos el tamaño de los búferes internos de acuerdo con el nuevo tamaño | //| del búfer principal | //+----------------------------------------------------------------------------------+ void CRiMaxMin::OnSetMaxTotal(int max_total) { m_max.SetMaxTotal(max_total); m_min.SetMaxTotal(max_total); } //+------------------------------------------------------------------+ //| Cálculo de los índices Max/Min | //+------------------------------------------------------------------+ void CRiMaxMin::OnAddValue(double value) { m_max_ind--; m_min_ind--; int last = GetTotal()-1; if(m_max_ind > 0 && value >= GetValue(m_max_ind)) m_max_ind = last; if(m_min_ind > 0 && value <= GetValue(m_min_ind)) m_min_ind = last; OnCalcValue(last); } //+------------------------------------------------------------------+ //| Cálculo de los índices Max/Min | //+------------------------------------------------------------------+ void CRiMaxMin::OnCalcValue(int index) { int max = 0, min = 0; int offset = m_full ? 1 : 0; double value = GetValue(index); int p_ind = index-1; //Búsqueda del máximo while(p_ind >= 0 && value >= GetValue(p_ind)) { int extr = m_max.GetValue(p_ind+offset); max += extr + 1; p_ind = GetTotal() - 1 - max - 1; } p_ind = GetTotal()-2; //Búsqueda del mínimo while(p_ind >= 0 && value <= GetValue(p_ind)) { int extr = m_min.GetValue(p_ind+offset); min += extr + 1; p_ind = GetTotal() - 1 - min - 1; } m_max.AddValue(max); m_min.AddValue(min); if(!m_full && GetTotal() == GetMaxTotal()) m_full = true; } //+----------------------------------------------------------------------------+ //| Recalcula los índices de los máximos/mínimos seguidamente del cambio del | //| valor por el índice arbitrario | //+----------------------------------------------------------------------------+ void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value) { if(m_max_ind >= 0 && new_value >= GetValue(m_max_ind)) m_max_ind = index; if(m_min_ind >= 0 && new_value >= GetValue(m_min_ind)) m_min_ind = index; for(int i = index; i < GetTotal(); i++) OnCalcValue(i); } //+------------------------------------------------------------------+ //| Devuelve el índice del elemento máximo | //+------------------------------------------------------------------+ int CRiMaxMin::MaxIndex(int max_period = 0) { int limit = 0; if(max_period > 0 && max_period <= m_max.GetTotal()) { m_max_ind = -1; limit = m_max.GetTotal() - max_period; } if(m_max_ind >=0) return m_max_ind; int c_max = m_max.GetTotal()-1; while(c_max > limit) { int ext = m_max.GetValue(c_max); if((c_max - ext) <= limit) return c_max; c_max = c_max - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Devuelve el índice del elemento mínimo | //+------------------------------------------------------------------+ int CRiMaxMin::MinIndex(int min_period = 0) { int limit = 0; if(min_period > 0 && min_period <= m_min.GetTotal()) { limit = m_min.GetTotal() - min_period; m_min_ind = -1; } if(m_min_ind >=0) return m_min_ind; int c_min = m_min.GetTotal()-1; while(c_min > limit) { int ext = m_min.GetValue(c_min); if((c_min - ext) <= limit) return c_min; c_min = c_min - ext - 1; } return limit; } //+------------------------------------------------------------------+ //| Devuelve el valor del elemento máximo | //+------------------------------------------------------------------+ double CRiMaxMin::MaxValue(int max_period = 0) { return GetValue(MaxIndex(max_period)); } //+------------------------------------------------------------------+ //| Devuelve el valor del elemento mínimo | //+------------------------------------------------------------------+ double CRiMaxMin::MinValue(int min_period = 0) { return GetValue(MinIndex(min_period)); }
Este algoritmo contiene una modificación más. Recuerda los mínimos y máximos actuales, y si se quedan sin alteraciones, los métodos MaxValue y MinValue los devuelven saltando el cálculo adicional.
Es la visualización de los máximos y los mínimos en el gráfico:
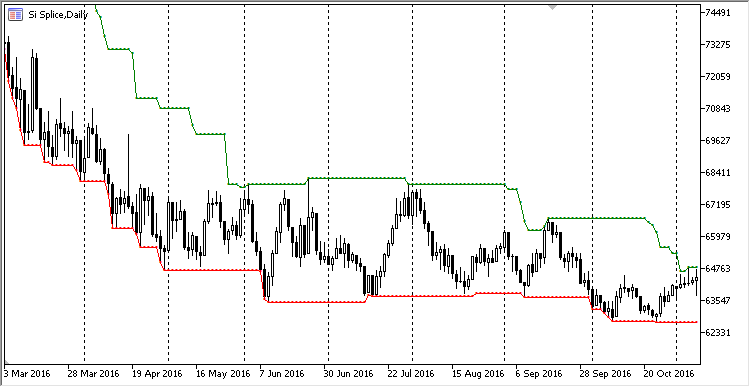
Fig. 5. Canal de los máximos/mínimos en forma del indicador
Cabe mencionar que la clase de la definición del máximo/mínimo tiene las posibilidades extendidas. Puede devolver el índice del extremo en el búfer circular, o simplemente su valor. También es capaz de calcular el extremo para un período menor que el período del búfer circular. Para eso será suficiente indicar el período límite en los métodos MaxIndex/MinIndex y MaxValue/MinValue.
Integración del búfer circular con la librería AlgLib
Otro ejemplo interesante del uso del búfer circular son los cálculos matemáticos especializados. Generalmente, los algoritmos para calcular diferentes estadísticas se crean sin tomar en cuenta el uso en la ventana móvil. No siempre es cómodo utilizar el algoritmo de este tipo. El búfer circular resuelve este problema. Vamos a escribir el indicador que calcula las características principales de la distribución de Gauss:
- valor medio (Mean);
- desviación estándar (StdDev);
- asimetría de la campana de distribución (Skewness);
- curtosis (Kurtosis).
Para calcular estas características, usaremos el método estadístico AlgLib::SampleMoments. Lo único que tendremos que hacer es crear la clase del búfer circular CRiGaussProperty y colocar el método dentro del manejador OnChangeArray. El código completo del indicador que incluye la clase:
//+------------------------------------------------------------------+ //| RiEma.mq5 | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_type1 DRAW_LINE #property indicator_color1 clrRed #include <RingBuffer\RiBuffDbl.mqh> #include <Math\AlgLib\AlgLib.mqh> //+------------------------------------------------------------------+ //| Cálculo de las características de la distribución de Gauss | //+------------------------------------------------------------------+ class CRiGaussProperty : public CRiBuffDbl { private: double m_mean; // Media double m_variance; // Desviación double m_skewness; // Asimetría double m_kurtosis; // Curtosis protected: virtual void OnChangeArray(void); public: double Mean(void){ return m_mean;} double StdDev(void){return MathSqrt(m_variance);} double Skewness(void){return m_skewness;} double Kurtosis(void){return m_kurtosis;} }; //+------------------------------------------------------------------+ //| El cálculo se realiza en caso de cualquier cambio del array | //+------------------------------------------------------------------+ void CRiGaussProperty::OnChangeArray(void) { double array[]; ToArray(array); CAlglib::SampleMoments(array, m_mean, m_variance, m_skewness, m_kurtosis); } //+------------------------------------------------------------------+ //| Tipo de la propiedad de la distribución de Gauss | //+------------------------------------------------------------------+ enum ENUM_GAUSS_PROPERTY { GAUSS_MEAN, // Media GAUSS_STDDEV, // Desviación GAUSS_SKEWNESS, // Asimetría GAUSS_KURTOSIS // Curtosis }; input int BPeriod = 13; //Period input ENUM_GAUSS_PROPERTY Property; double buff[]; CRiGaussProperty RiGauss; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0, buff, INDICATOR_DATA); RiGauss.SetMaxTotal(BPeriod); //--- return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[]) { //--- bool calc = false; for(int i = prev_calculated; i < rates_total; i++) { RiGauss.AddValue(price[i]); buff[i] = GetGaussValue(Property); calc = true; } if(!calc) { RiGauss.ChangeValue(BPeriod-1, price[rates_total-1]); buff[rates_total-1] = GetGaussValue(Property); } return(rates_total-1); } //+---------------------------------------------------------------------------+ //| Devuelve el valor de una de las propiedades de la distribución de Gauss | //+---------------------------------------------------------------------------+ double GetGaussValue(ENUM_GAUSS_PROPERTY property) { double value = EMPTY_VALUE; switch(Property) { case GAUSS_MEAN: value = RiGauss.Mean(); break; case GAUSS_STDDEV: value = RiGauss.StdDev(); break; case GAUSS_SKEWNESS: value = RiGauss.Skewness(); break; case GAUSS_KURTOSIS: value = RiGauss.Kurtosis(); break; } return value; }
Como podemos ver en el listado de arriba, la clase CRiGaussProperty ha salido elemental. No obstante, esta sencillez esconde una gran capacidad funcional. Ahora, para el trabajo de la función CAlglib::SampleMoments no hace falta preparar el array móvil durante cada iteración, será suficiente ir añadiendo nuevos valores en el método AddValue. En la imagen de abajo se muestra el resultado de trabajo de este indicador. En los ajustes, seleccionamos el cálculo de la desviación estándar y lo mostramos en la subventana del gráfico:
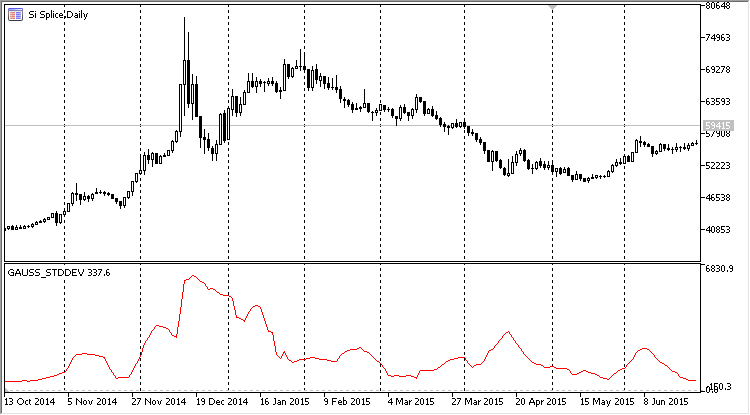
Fig. 6. Características principales de la distribución de Gauss en forma del indicador móvil
Construcción del MACD a base de las primitivas circulares
Hemos desarrollado tres primitivas circulares: las medias móviles simple y exponencial, indicador de máximos y mínimos. Es más que suficiente para construir los indicadores estándar principales, es que normalmente contienen los cálculos más simples. Por ejemplo, el indicador MACD se compone de dos medias móviles exponenciales y una línea de señal a base de la media móvil. Intentaremos construir este indicador basándose en los códigos ya existentes.
En el ejemplo con el indicador de los máximos/mínimos, ya hemos usado dos búferes circulares adicionales que integran la clase CRiMaxMin. Haremos lo mismo con el MACD. Durante la adición de un valor nuevo, nuestra clase simplemente va a traspasarlo a sus búferes adicionales, y luego calcular la diferencia simple entre ellos. La diferencia va a caer en el búfer circular que calcula la SMA basándose en ella. Ésta será la línea de señal del MACD:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiEMA.mqh" //+------------------------------------------------------------------+ //| Cálculo de la media móvil en el búfer circular | //+------------------------------------------------------------------+ class CRiMACD { private: CRiEMA m_slow_macd; // Media móvil exponencial rápida CRiEMA m_fast_macd; // Media móvil exponencial lenta CRiSMA m_signal_macd; // Línea de señal double m_delta; // Diferencia entre la EMA rápida y la lenta public: double Macd(void); double Signal(void); void ChangeLast(double new_value); void SetFastPeriod(int period); void SetSlowPeriod(int period); void SetSignalPeriod(int period); void AddValue(double value); }; //+------------------------------------------------------------------+ //| Recalcula MACD | //+------------------------------------------------------------------+ void CRiMACD::AddValue(double value) { m_slow_macd.AddValue(value); m_fast_macd.AddValue(value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.AddValue(m_delta); } //+------------------------------------------------------------------+ //| Cambia MACD | //+------------------------------------------------------------------+ void CRiMACD::ChangeLast(double new_value) { m_slow_macd.ChangeValue(m_slow_macd.GetTotal()-1, new_value); m_fast_macd.ChangeValue(m_fast_macd.GetMaxTotal()-1, new_value); m_delta = m_slow_macd.EMA() - m_fast_macd.EMA(); m_signal_macd.ChangeValue(m_slow_macd.GetTotal()-1, m_delta); } //+------------------------------------------------------------------+ //| Devuelve el histograma del MACD | //+------------------------------------------------------------------+ double CRiMACD::Macd(void) { return m_delta; } //+------------------------------------------------------------------+ //| Devuelve la línea de seññal | //+------------------------------------------------------------------+ double CRiMACD::Signal(void) { return m_signal_macd.SMA(); } //+------------------------------------------------------------------+ //| Establece el período rápido | //+------------------------------------------------------------------+ void CRiMACD::SetFastPeriod(int period) { m_slow_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Establece el período lento | //+------------------------------------------------------------------+ void CRiMACD::SetSlowPeriod(int period) { m_fast_macd.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Establece el período de la línea de señal | //+------------------------------------------------------------------+ void CRiMACD::SetSignalPeriod(int period) { m_signal_macd.SetMaxTotal(period); }
Nótese que la propia clase CRiMacd es una clase independiente, no se hereda de CRiBuffDbl. Es verdad, la clase CRiMacd no utiliza sus propios búferes de cálculo. En vez de eso, en la clase se aplica el esquema de «inclusión», cuando las clases de primitivas circulares se ubican como objetos independientes en la sección private.
Dos métodos principales Macd() y Signal() devuelven los valores del indicador MACD y de su línea de señal. El código mostrado ha salido simple, además, cada búfer tiene su período móvil. La clase CRiMacd no rastrea los cambios de un elemento arbitrario. En vez de eso, él rastrea el cambio solamente del último elemento, proporcionando el cambio del indicador en la barra cero.
El aspecto visual del indicador MACD calculado en el búfer circular es el mismo que el indicador clásico:
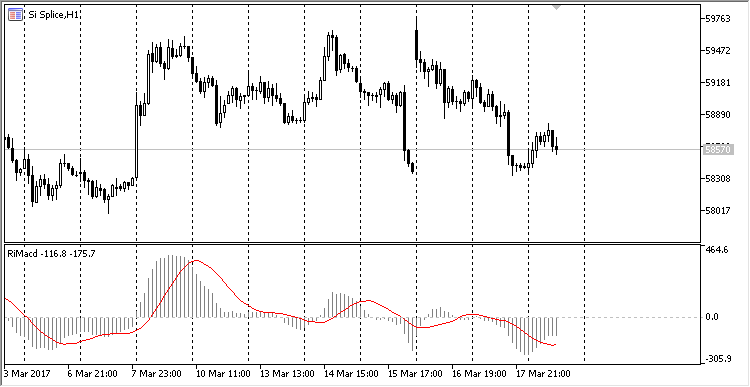
Fig. 7. Indicador MACD calculado en el búfer circular
Construcción del indicador Stochastic a base de las primitivas circulares
De la misma manera, vamos a construir el indicador Stochastic. Este indicador combina la búsqueda de los extremos y el cálculo de la media móvil. De esta manera, aquí usamos los algoritmos que ya hemos calculado antes.
Stochastic utiliza tres series de precios: precios de los máximos (barras High), precios de los mínimos (barras Low) y los precios de cierre (barras Close). Su cálculo es simple: primero, se busca el máximo para los precios High y el mínimo para los precios Low. Luego, se calcula la razón del precio actual close al diapasón entre el máximo y el mínimo. Y por fin, basándose en esta razón se calcula el valor medio para N períodos (en el indicador, N lleva el nombre "ralentización K%"):
K% = SMA((close-min)/((max-min)*100.0%), N)
Luego, para K% obtenido se calcula otra media con el período %D —es la línea de señal parecida a la línea de señal del MACD:
Signal D% = SMA(K%, D%)
Dos valores obtenidos —K% y su D% de señal— van a visualizar Stochastic.
Antes de escribir el código de Stochastic para el búfer circular, vamos a mostrar su código implementado de manera clásica. Para eso usaremos el ejemplo ya hecho de Stochastic.mq5 de la carpeta Indicators\Examples:
//+------------------------------------------------------------------+ //| Stochastic Oscillator | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,k,start; //--- check for bars count if(rates_total<=InpKPeriod+InpDPeriod+InpSlowing) return(0); //--- start=InpKPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) { ExtLowesBuffer[i]=0.0; ExtHighesBuffer[i]=0.0; } } //--- calculate HighesBuffer[] and ExtHighesBuffer[] for(i=start;i<rates_total && !IsStopped();i++) { double dmin=1000000.0; double dmax=-1000000.0; for(k=i-InpKPeriod+1;k<=i;k++) { if(dmin>low[k]) dmin=low[k]; if(dmax<high[k]) dmax=high[k]; } ExtLowesBuffer[i]=dmin; ExtHighesBuffer[i]=dmax; } //--- %K start=InpKPeriod-1+InpSlowing-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtMainBuffer[i]=0.0; } //--- main cycle for(i=start;i<rates_total && !IsStopped();i++) { double sumlow=0.0; double sumhigh=0.0; for(k=(i-InpSlowing+1);k<=i;k++) { sumlow +=(close[k]-ExtLowesBuffer[k]); sumhigh+=(ExtHighesBuffer[k]-ExtLowesBuffer[k]); } if(sumhigh==0.0) ExtMainBuffer[i]=100.0; else ExtMainBuffer[i]=sumlow/sumhigh*100; } //--- signal start=InpDPeriod-1; if(start+1<prev_calculated) start=prev_calculated-2; else { for(i=0;i<start;i++) ExtSignalBuffer[i]=0.0; } for(i=start;i<rates_total && !IsStopped();i++) { double sum=0.0; for(k=0;k<InpDPeriod;k++) sum+=ExtMainBuffer[i-k]; ExtSignalBuffer[i]=sum/InpDPeriod; } //--- OnCalculate done. Return new prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
Este código está escrito en un bloque único y contiene 8 ciclos for, tres de los cuales son incluidos. El cálculo se realiza en dos pasadas: primero, se calculan los máximos y los mínimos, los valores de los cuales se guardan en dos búferes adicionales. A su vez, el cálculo de los máximos y mínimos requiere el repaso doble: en cada barra se hacen N iteraciones adicionales en el ciclo incluido for, donde N es el período K%.
Después del cálculo de los máximos/mínimos se hace el cálculo de K%, para lo que también se usa el ciclo doble que hace las iteraciones F en cada barra, donde F es el período de ralentización K%.
Luego se calcula la línea de señal D%, también con repaso doble for, donde se requieren T iteraciones adicionales para cada barra (T — período de promediación D%).
El código obtenido trabaja bastante rápido. Aquí el problema principal es que sin el búfer circular es necesario ejecutar los cálculos simples en varios pasos independientes. Se pierde la claridad y la sencillez del entendimiento del código.
Para demostrar lo que hemos dicho antes, aquí tenemos el contenido del método principal de cálculo en la clase CRiStoch. Hace el mismo trabajo que el código ubicado más arriba:
//+------------------------------------------------------------------+ //| Adiciones de nuevos valores y el cálculo de Stochastic | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Añadimos el nuevo valor del máximo m_min.AddValue(low); // Añadimos el nuevo valor del mínimo double c = close; double max = m_max.MaxValue() // Obtenemos el máximo double min = m_min.MinValue(); // Obtenemos el mínimo double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Encontramos K% según la fórmula Stochastic m_slowed_k.AddValue(k); // Suavizamos K% (Ralentización K%) m_slowed_d.AddValue(m_slowed_k.SMA()); // Encontramos %D del K% suavizado }
Este método no se encarga de los cálculos intermedios. En vez de eso, él simplemente aplica Stochastic a los valores ya existentes. La búsqueda de los valores necesarios se delega a las primitivas circulares: media móvil, búsqueda de los máximos y mínimos.
Los demás métodos de la clase CRiStoch son triviales y representan los métodos Get/Set del establecimiento de los períodos y los valores del indicador correspondientes. Vamos a mostrar el código CRiStoch completamente:
//+------------------------------------------------------------------+ //| RingBuffer.mqh | //| Copyright 2016, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #include "RiBuffDbl.mqh" #include "RiSMA.mqh" #include "RiMaxMin.mqh" //+------------------------------------------------------------------+ //| Clase del indicador Stochastic | //+------------------------------------------------------------------+ class CRiStoch { private: CRiMaxMin m_max; // Indicador de mínimos/máximos CRiMaxMin m_min; // Indicador de mínimos/máximos CRiSMA m_slowed_k; // Promediación K% CRiSMA m_slowed_d; // Media móvil D% public: void ChangeLast(double new_value); void AddValue(double close, double high, double low); void AddHighValue(double value); void AddLowValue(double value); void AddCloseValue(double value); void SetPeriodK(int period); void SetPeriodD(int period); void SetSlowedPeriodK(int period); double GetStochK(void); double GetStochD(void); }; //+------------------------------------------------------------------+ //| Adiciones de nuevos valores y el cálculo de Stochastic | //+------------------------------------------------------------------+ void CRiStoch::AddValue(double close, double high, double low) { m_max.AddValue(high); // Añadimos el nuevo valor del máximo m_min.AddValue(low); // Añadimos el nuevo valor del mínimo double c = close; double max = m_max.MaxValue() double min = m_min.MinValue(); double delta = max - min; double k = 0.0; if(delta != 0.0) k = (c-min)/delta*100.0; // Encontramos K% según la fórmula m_slowed_k.AddValue(k); // Suavizamos K% (Ralentización K%) m_slowed_d.AddValue(m_slowed_k.SMA()); // Encontramos %D de K% suavizado } //+------------------------------------------------------------------+ //| Establece el período rápido | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodK(int period) { m_max.SetMaxTotal(period); m_min.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Establece el período lento | //+------------------------------------------------------------------+ void CRiStoch::SetSlowedPeriodK(int period) { m_slowed_k.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Establece el período de la línea de señal | //+------------------------------------------------------------------+ void CRiStoch::SetPeriodD(int period) { m_slowed_d.SetMaxTotal(period); } //+------------------------------------------------------------------+ //| Obtiene el valor %K | //+------------------------------------------------------------------+ double CRiStoch::GetStochK(void) { return m_slowed_k.SMA(); } //+------------------------------------------------------------------+ //| Obtiene el valor %D | //+------------------------------------------------------------------+ double CRiStoch::GetStochD(void) { return m_slowed_d.SMA(); }
El indicador obtenido Stochastic no se diferencia de su análogo estándar. Puede asegurarse de ello, construyendo el indicador correspondiente junto con el estándar (todos los archivos de los indicadores y los archivos auxiliares se adjuntan al artículo):
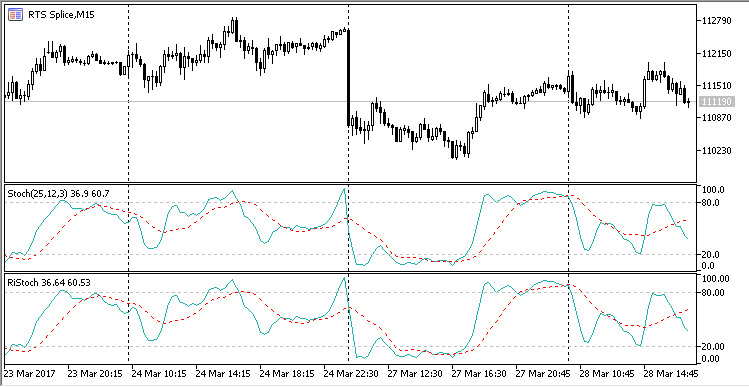
Fig. 8 Indicadores Stochastic estándar y circular.
Optimización del uso de la memoria operativa
El cálculo de los indicadores requiere determinados recursos. El trabajo con los indicadores de sistema usando así llamados «handles» no es una excepción. En realidad, el handle del indicador es un tipo especial del puntero al bloque interno de cálculo del indicador y sus búferes de datos. El hangle en sí no ocupa mucho espacio, es sólo un número de 64 bits. El tamaño principal se esconde “entre bastidores” de MetaTrader, por eso cuando se crea un handle nuevo, se asigna un tamaño de memoria determinado, mayor que el tamaño del handle.
Aparte de eso, el copiado de los valores del indicador también requiere algo de tiempo. Este intervalo es mayor de lo requerido para el cálculo de los valores del indicador dentro del propio EA. Por eso los desarrolladores recomiendan oficialmente crear un bloque de cálculo del indicador directamente en el EA y utilizarlo. Claro que eso no significa que cada vez es necesario escribir el cálculo del indicador en el código del EA y no usar la llamada a los indicadores estándar. No pasa nada si en su EA se utiliza uno, dos o incluso cinco indicadores. Lo único que para trabajar con ellos, habrá que disponer de un poco más de memoria y un poco más de tiempo de lo que habría necesario si estos cálculos fueran ejecutados directamente en el código del EA.
No obstante, hay tareas donde la optimización de la memoria utilizada y del tiempo gastado será imprescindible. El uso de los búferes circulares será más conveniente precisamente para estas tareas. En primer lugar, eso será necesario al usar varios indicadores. Por ejemplo, los paneles informativos (también llamados como scanners del mercado) normalmente, hacen un recorte de mercado momentáneo de muchos instrumentos y timeframes, usando todo el conjunto de indicadores disponibles. Por ejemplo, éste es uno de los paneles disponibles en la tienda de aplicaciones de MetaTrader 5:
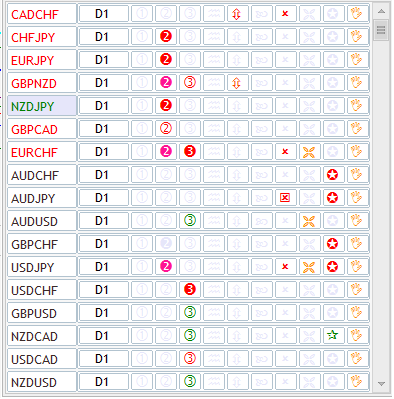
Fig. 8. Panel informativo de que utiliza varios indicadores
Vemos que aquí se analizan 17 instrumentos diferentes según 9 factores diferentes. Cada factor está representado por su indicador. No es difícil de calcular que serán necesarios 17 * 9 = 153 indicadores solamente para mostrar «apenas algunos iconos». Para analizar 21 timeframe de cada símbolo, ya serán necesarios 3 213 indicadores. Para colocarlos, necesitaremos un volumen de la memoria enorme.
Para comprender de qué manera se asigna la memoria, escribiremos una prueba especial de carga en forma de un Asesor Experto. El EA va a calcular los valores de un conjunto de indicadores usando para eso dos opciones:
- la llamada al indicador estándar y el copiado de sus valores a través del handle resultante;
- el cálculo del indicador en el búfer circular.
En el segundo caso, los indicadores no van a crearse, y todos los cálculos van a realizarse dentro del EA a través de los indicadores circulares que serán dos: MACD y Stochastic. Cada uno de ellos tendrá tres configuraciones: rápida, estándar y lenta. Los indicadores van a calcularse a base de cuatro instrumentos: EURUSD, GBPUSD, USDCHF y USDJPY para 21 timeframe. No es difícil de contar el número total de los valores calculados:
número total de los valores = 2 indicadores * 3 conjuntos de parámetros * 4 instrumentos * 21 timeframe = 504;
Para que en un EA sea posible usar los enfoque diferentes en la construcción de indicadores, escribiremos las clases contenedores auxiliares. Al llamar a ellas, van a dar el último valor del indicador. Este valor va a calcularse de maneras diferentes, dependiendo del tipo del indicador utilizado.Si se usa el indicador estándar, el último valor va a tomarse usando la función CopyBuffer del handle de sistema del indicador. En caso de usar el búfer circular, el valor va a calcularse a través de los indicadores circulares correspondientes.
Aquí tenemos el código fuente del prototipo del contenedor en forma de una clase abstracta:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Arrays\ArrayObj.mqh> #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Tipo del indicador creado | //+------------------------------------------------------------------+ enum ENUM_INDICATOR_TYPE { INDICATOR_SYSTEM, // Indicador de sistema INDICATOR_RIBUFF // Indicador del búfer circular }; //+------------------------------------------------------------------+ //| Contenedor del indicador | //+------------------------------------------------------------------+ class CIndBase : public CObject { protected: int m_handle; // Handle del indicador string m_symbol; // Símbolo para el cálculo del indicador ENUM_INDICATOR_TYPE m_ind_type; // Tipo del indicador ENUM_TIMEFRAMES m_period; // Período para el cálculo del indicador CBarDetector m_bar_detect; // Detector de la nueva barra CIndBase(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type); public: string Symbol(void){return m_symbol;} ENUM_TIMEFRAMES Period(void){return m_period;} virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------------------+ //| El constructor protegido requiere la indicación del símbolo, timeframe y tipo| //| del indicador | //+------------------------------------------------------------------------------+ CIndBase::CIndBase(string symbol,ENUM_TIMEFRAMES period,ENUM_INDICATOR_TYPE ind_type) { m_handle = INVALID_HANDLE; m_symbol = symbol; m_period = period; m_ind_type = ind_type; m_bar_detect.Symbol(symbol); m_bar_detect.Timeframe(period); } //+------------------------------------------------------------------+ //| Obtiene el último valor del indicador | //+------------------------------------------------------------------+ double CIndBase::GetLastValue(int index_buffer) { return EMPTY_VALUE; }
Contiene el método virtual GetLastValue. Este método recibe el número del búfer del indicador y devuelve el último valor del indicador para este búfer. Además, la clase contiene las propiedades básicas del indicador: su timeframe, símbolo y tipo del cálculo (ENUM_INDICATOR_TYPE).
En su base, vamos a crear dos clases derivadas: CRiInMacd y CRiStoch. Ambas van a calcular los valores de indicadores correspondientes y devolverlos a través del método redefinido GetLastValue. Mostraremos el código fuente de una de estas clases, CRiIndMacd:
//+------------------------------------------------------------------+ //| RiIndLoad.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2016, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <RingBuffer\RiMACD.mqh> #include "RiIndBase.mqh" //+------------------------------------------------------------------+ //| Contenedor del indicador | //+------------------------------------------------------------------+ class CIndMacd : public CIndBase { private: CRiMACD m_macd; // Versión circular del indicador public: CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period, int slow_period, int signal_period); virtual double GetLastValue(int index_buffer); }; //+------------------------------------------------------------------+ //| Creamos el indicador MACD | //+------------------------------------------------------------------+ CIndMacd::CIndMacd(string symbol, ENUM_TIMEFRAMES period, ENUM_INDICATOR_TYPE ind_type, int fast_period,int slow_period,int signal_period) : CIndBase(symbol, period, ind_type) { if(ind_type == INDICATOR_SYSTEM) { m_handle = iMACD(m_symbol, m_period, fast_period, slow_period, signal_period, PRICE_CLOSE); if(m_handle == INVALID_HANDLE) printf("Create iMACD handle failed. Symbol: " + symbol + " Period: " + EnumToString(period)); } else if(ind_type == INDICATOR_RIBUFF) { m_macd.SetFastPeriod(fast_period); m_macd.SetSlowPeriod(slow_period); m_macd.SetSignalPeriod(signal_period); } } //+------------------------------------------------------------------+ //| Obtiene el último valor del indicador | //+------------------------------------------------------------------+ double CIndMacd::GetLastValue(int index_buffer) { if(m_handle != INVALID_HANDLE) { double array[]; if(CopyBuffer(m_handle, index_buffer, 1, 1, array) > 0) return array[0]; return EMPTY_VALUE; } else { if(m_bar_detect.IsNewBar()) { //printf("Obtenida nueva barra en " + m_symbol + " Período " + EnumToString(m_period)); double close[]; CopyClose(m_symbol, m_period, 1, 1, close); m_macd.AddValue(close[0]); } switch(index_buffer) { case 0: return m_macd.Macd(); case 1: return m_macd.Signal(); } return EMPTY_VALUE; } }
La clase contenedor para calcular el Stochastic está organizada de la misma manera, por eso no vamos a mostrar su código fuente aquí.
El cálculo de los valores de los indicadores se realiza sólo en el momento de la apertura de una barra nueva. Eso facilita la simulación. Para eso, la clase base CRiIndBase tiene incorporado el módulo especial NewBarDetecter. Esta clase es capaz de detectar la apertura de una barra nueva y avisar sobre ello, devolviendo true a través del método IsNewBar.
Ahora mostraremos el código del EA de prueba. Se llama TestIndEA.mq5:
//+------------------------------------------------------------------+ //| TestIndEA.mq5 | //| Copyright 2017, Vasiliy Sokolov. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2017, Vasiliy Sokolov." #property link "http://www.mql5.com" #property version "1.00" #include <Object.mqh> #include <Arrays\ArrayObj.mqh> #include "RiIndBase.mqh" #include "RiIndMacd.mqh" #include "RiIndStoch.mqh" #include "NewBarDetector.mqh" //+------------------------------------------------------------------+ //| Parámetros de MACD | //+------------------------------------------------------------------+ struct CMacdParams { int slow_period; int fast_period; int signal_period; }; //+------------------------------------------------------------------+ //| Parámetros de Stoch | //+------------------------------------------------------------------+ struct CStochParams { int k_period; int k_slowed; int d_period; }; input ENUM_INDICATOR_TYPE IndType = INDICATOR_SYSTEM; // Тип индикатора string Symbols[] = {"EURUSD", "GBPUSD", "USDCHF", "USDJPY"}; CMacdParams MacdParams[3]; CStochParams StochParams[3]; CArrayObj ArrayInd; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { MacdParams[0].fast_period = 3; MacdParams[0].slow_period = 13; MacdParams[0].signal_period = 6; MacdParams[1].fast_period = 9; MacdParams[1].slow_period = 26; MacdParams[1].signal_period = 12; MacdParams[2].fast_period = 18; MacdParams[2].slow_period = 52; MacdParams[2].signal_period = 24; StochParams[0].k_period = 6; StochParams[0].k_slowed = 3; StochParams[0].d_period = 3; StochParams[1].k_period = 12; StochParams[1].k_slowed = 5; StochParams[1].d_period = 6; StochParams[2].k_period = 24; StochParams[2].k_slowed = 7; StochParams[2].d_period = 12; // Aquí se crean 504 indicadores MACD y Stochastic for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PeriodByIndex(period), IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PeriodByIndex(period), IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } printf("Create " + (string)ArrayInd.Total() + " indicators sucessfully"); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnStart() { for(int i = 0; i < ArrayInd.Total(); i++) { CIndBase* ind = ArrayInd.At(i); double value = ind.GetLastValue(0); double value_signal = ind.GetLastValue(1); } } //+------------------------------------------------------------------+ //| Devuelve el timeframe según su índice | //+------------------------------------------------------------------+ ENUM_TIMEFRAMES PeriodByIndex(int index) { switch(index) { case 0: return PERIOD_CURRENT; case 1: return PERIOD_M1; case 2: return PERIOD_M2; case 3: return PERIOD_M3; case 4: return PERIOD_M4; case 5: return PERIOD_M5; case 6: return PERIOD_M6; case 7: return PERIOD_M10; case 8: return PERIOD_M12; case 9: return PERIOD_M15; case 10: return PERIOD_M20; case 11: return PERIOD_M30; case 12: return PERIOD_H1; case 13: return PERIOD_H2; case 14: return PERIOD_H3; case 15: return PERIOD_H4; case 16: return PERIOD_H6; case 17: return PERIOD_H8; case 18: return PERIOD_H12; case 19: return PERIOD_D1; case 20: return PERIOD_W1; case 21: return PERIOD_MN1; default: return PERIOD_CURRENT; } } //+------------------------------------------------------------------+
La funcionalidad principal está implementada en el bloque OnInit. Ahí se procesan los símbolos, timeframes y conjuntos de los parámetros para los indicadores. Los conjuntos de los parámetros de los indicadores se almacenan en las estructuras auxiliares CMacdParams y CStochParams.
El bloque del procesamiento de valores se ubica en la función OnTick y representa un repaso trivial de indicadores y obtención de sus últimos valores a través del método virtual GetLastalue. Como el número de los búferes de cálculo es el mismo en ambos indicadores, no hace falta hacer comprobaciones adicionales, pudiendo obtener los valores de ambos indicadores a través del método base generalizado GetLastValue.
La ejecución del EA ha mostrado lo siguiente: en el modo del cálculo a base de las llamadas de los indicadores estándar se han requerido 11,9 GB de la RAM, mientras que la ejecución en el modo del cálculo de los indicadores a base de las primitivas circulares se han necesitado 2,9 GB. La simulación ha sido realizada en el ordenador con 16 GB de memoria operativa.
No obstante, hay que entender que la memoria ha sido ahorrada principalmente no gracias al uso de los búferes adicionales, sino debido a la colocación de los módulos de cálculo en el código del EA. El hecho de esta colocación como tal ya ahorra considerablemente la memoria.
El ahorro de la memoria en cuatro veces es un resultado más que digno. Sin embargo, igual así hemos requerido 3 GB de memoria operativa. ¿Habrá alguna manera más de reducir esta cifra? Es posible si optimizamos la cantidad de timeframes. Vamos a intentar cambiar un poco el código de prueba, y en vez de 21 timeframes, vamos a usar sólo uno — PERIOD_M1. El número de indicadores queda el mismo, sólo algunos de ellos van a duplicarse:
... for(int symbol = 0; symbol < ArraySize(Symbols); symbol++) { for(int period = 1; period <=21; period++) { for(int i = 0; i < 3; i++) { CIndMacd* macd = new CIndMacd(Symbols[symbol], PERIOD_M1, IndType, MacdParams[i].fast_period, MacdParams[i].slow_period, MacdParams[i].signal_period); CIndStoch* stoch = new CIndStoch(Symbols[symbol], PERIOD_M1, IndType, StochParams[i].k_period, StochParams[i].k_slowed, StochParams[i].d_period); ArrayInd.Add(macd); ArrayInd.Add(stoch); } } } ...
Ahora, los mismos 504 indicadores en el modo del cálculo interno ocupan ya 548 MB de la memoria operativa Si usamos las formulaciones más precisas, la memoria está ocupada no tanto por los indicadores, sino los datos que se cragan para su cálculo. Además, acerca de 100 MB del volumen total está ocupado por el propio terminal, por esa razón, los datos cargados aún son más pequeños. Hemos reducido considerablemente el consumo de la memoria.
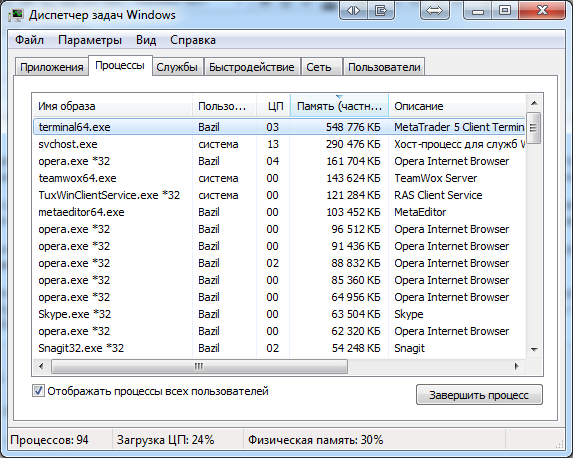
El cálculo a base de los indicadores de sistema exige en este modo 1,9 GB de memoria, lo que también es bastante menor que durante el uso de la lista entera de 21 timeframes.
Optimización del tiempo de simulación del Asesor Experto
MetaTrader 5 tiene la capacidad de dirigirse durante la prueba a varios instrumentos de trading a la vez, así como a un timeframe arbitrario de cada instrumento. Con lo cual se puede crear y probar los EAs múltiples, cuando un EA tradea en varios instrumentos. El acceso al entorno comercial puede requerir algún tiempo, sobre todo si hace falta acceder a los datos de algunos indicadores calculados a base de estos instrumentos. Es posible reducir el tiempo de acceso si todos los cálculos van a realizarse dentro de un único EA. Ilustraremos eso mediante la simulación de nuestro ejemplo anterior en el Probador de Estrategias de MetaTrader 5.Primero, probaremos el EA en EURUSD del último mes en el modo «sólo precios de apertura» en M1. Para los cálculos usaremos los indicadores de sistema. En el ordenador con el procesador Intel Core i7 870 2.9 Ghz, esta prueba fue realizada en 58 segundos:
2017.03.30 14:07:12.223 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:57.923.
Ahora, hagamos la misma prueba pero en los modos de cálculos internos:
2017.03.30 14:08:29.472 Core 1 EURUSD,M1: 114357 ticks, 28647 bars generated. Environment synchronized in 0:00:00.078. Test passed in 0:00:12.292.
Como podemos ver, el tiempo del cálculo se ha reducido considerablemente. En este modo, ha sido de 12 segundos.
Conclusiones y sugerencias para mejorar el rendimiento
Hemos probado el uso de la memoria durante la creación de los indicadores y hemos medido la velocidad de la prueba en dos modos de funcionamiento. Al usar los cálculos internos a base de los búferes circulares, hemos conseguido reducir el uso de la memoria y hemos aumentado el rendimiento en varias veces. Naturalmente, los ejemplos mostrados son artificiales en muchos aspectos. La mayoría de los desarrolladores nunca tendrá que crear 500 indicadores al mismo tiempo y probarlos en todos los tiemframes posibles. No obstante, una «prueba de estrés» semejante permite revelar también los mecanismos y reducir su uso al mínimo. Aquí tenemos algunas recomendaciones formuladas según los resultados de la prueba realizada:
- Coloque la parte de cálculo de los indicadores dentro de los EAs. Eso ahorrará tiempo y el espacio de la memoria operativa gastados en la simulación.
- En la medida de lo posible, evite los pedidos para obtener los datos de un conjunto de los timeframes. En vez de eso, para los cálculos utilice un solo timeframe (el menor). Por ejemplo, si necesita calcular dos indicadores en M1 y H1, obtenga los datos M1, conviértelos en H1 y luego envíe estos datos para el cálculo del indicador en H1. Este enfoque es más complicado, pero permitirá ahorrar considerablemente la memoria.
- Utilice el cálculo económico de indicadores en sus desarrollos. Un candidato perfecto para el cálculo económico es el búfer circular. Requieren la memoria justa para el cálculo de los indicadores. Además de eso, los búferes circulares permiten optimizar algunos algoritmos del cálculo, como por ejemplo la búsqueda de los máximos/mínimos.
- Cree una interfaz universal para el trabajo con los indicadores, y utilícela para obtener los valores. Si resulta complicado implementar el cálculo del indicador en el bloque interno, la interfaz va a llamar al indicador externo de MetaTrader. Si Usted crea el bloque interno del cálculo del indicador, simplemente conéctelo a la interfaz. En este caso, el EA será sometido a los cambios mínimos.
- Evalúe con precisión las posibilidades de la optimización. Si utiliza un solo indicador en el único instrumento, entonces se puede dejar el indicador tal como es y no pasarlo al cálculo interno. El tiempo gastado para este traspaso puede superar significativamente la ganancia final en rendimiento.
Conclusión
Hemos considerado la creación de los búferes circulares y su aplicación práctica para diseñar los indicadores económicos. Es difícil encontrar la aplicación más acuciante de los búferes circulares que en en el campo del trading. Y es aún más sorprendente que hasta ahora este algoritmo de construcción de datos todavía no ha sido enrocado en la comunidad MQL.
Los búferes circulares e indicadores creados a su base no es sólo un ahorro de la memoria y un cálculo rápido. La ventaja principal de los búferes circulares es la sencillez de la implementación de indicadores a su base. Es así porque la gran mayoría de los indicadores están organizados según el principio FIFO (el primero entra - el primero sale). Por tanto, normalmente, las dificultades surgen precisamente cuando intentan calcular los indicadores no en el búfer circular.
El anexo del artículo incluye todos los códigos fuente analizados, inclusive los códigos de propios indicadores y de los algoritmos simples en los cuales se basan. Espero que el presente material sirva de un buen punto de partida para crear una librería de los búferes circulares completamente funcional, simple, rápida y universal.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/3047
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Cómo crear documentación usando los códigos fuente MQL5
Cómo crear documentación usando los códigos fuente MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Gran trabajo aquí, muchas gracias al autor. Tal vez el error que estás viendo, Savio, está aquí:
int RingBuffer::iToRealInd(int iIndex)
{
if(iIndex >= iNumElements() || iIndex < 0)
return iBufferSize-1; //previous bug was caused by no -1 here
...
He añadido el -1 en la última línea citada; antes no estaba y provocaba que se devolviera un índice incorrecto. Ten en cuenta que he cambiado los nombres de las variables/métodos a mi estilo de programación pero es la misma idea
He probado tu corrección, pero sigue sin actualizarse bien. Parece que hay algo que falta y no puedo encontrar el problema cuando se trata de ejecutar el búfer de anillo en la formación de una nueva barra. Cuando el mercado se está ejecutando, las líneas High/Low se mezclan completamente. El código funciona muy bien y muy rápido mientras procesa datos antiguos, pero con los nuevos datos que llegan durante la formación de una nueva barra, simplemente no me funciona.
Si se me permite hacer algunos comentarios:
1. En la clase void CRiMaxMin::OnChangeValue(int index, double del_value, double new_value), en el método " OnChangeValue " en la línea
.
Imagen: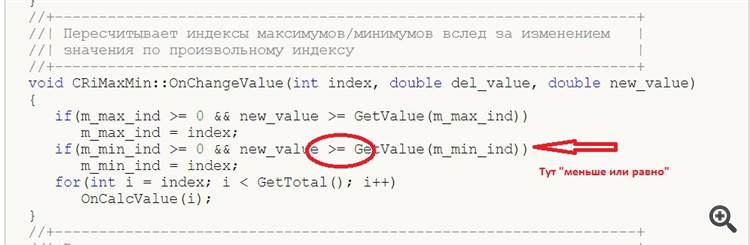
errata - signo "menor o igual que".

2.Cuando se buscan los elementos Min y Max de un array, si se utiliza exactamente como un buffer anular (cuando se empiezan a escribir nuevos elementos al principio del array), min y mah se definen incorrectamente. El mínimo es mayor que el máximo. En un array. Todo funciona usando los métodos estándar (ArrayMinimum y ArrayMaximum).
Picture:
En algún sitio la indexación va por mal camino. No puedo arreglarlo yo mismo. Si alguien puede arreglarlo, sería genial. He adjuntado un asesor de prueba.
Tienes un error en ToRealInd(int index).
Debería ser