Abordagem econométrica para análise de gráficos

Teorias sem fatos podem ser improdutivas, mas fatos sem teorias não tem sentido.

K. Boulding

Introdução

Muitas vezes eu ouço que os mercados são voláteis e não há estabilidade. E isso explica por que um sucesso comercial a longo prazo é impossível. Mas é verdade? Vamos tentar analisar esse problema cientificamente. E vamos escolher os meios econométricos de análise. Por que eles? Primeiro de tudo, a comunidade MQL ama precisão, a qual vai ser fornecida por matemática e estatística. Em segundo lugar, isso não foi descrito antes, se não estou enganado.

Deixe-me mencionar que o problema do sucesso comercial a longo prazo não pode ser resolvido dentro de um único artigo. Hoje, eu vou descrever apenas alguns métodos de diagnóstico para o modelo selecionado, que espero mostrar-se muito útil para uso futuro.

Além de que, eu vou tentar o meu melhor para descrever de forma clara algum material dessecado, incluindo fórmulas, teoremas e hipóteses. Entretanto, eu espero que o meu leitor esteja familiarizado com conceitos básicos de estatísticas, tais como: hipótese, significância estatística, estatísticas (critério estatístico), dispersão, distribuição, probabilidade, regressão, autocorrelação, etc

1. Características de uma série temporal

é evidente que o objecto de análise é uma série de preços (seus derivados), que é uma série de tempo.

Econometristas estudam série temporal do ponto de métodos de frequência (análise de espectro, análise de wavelet) e os métodos de domínio de tempo (análise de correlação cruzada, análise de autocorrelação). O leitor já foi fornecido com o artigo "Construindo análise de espectro" que descreve os métodos de freqüência. Agora eu sugiro dar uma olhada nos métodos de domínio de tempo para a análise de autocorrelação e análise de variância condicional em particular.

Modelos não-lineares descrevem o comportamento de preços de séries temporais melhor do que os lineares. é por isso que vamos nos concentrar no estudo de modelos não-lineares neste artigo.

Séries temporais de preços tem características especiais que podem ser levadas em conta apenas por alguns modelos econométricos. Primeiro de tudo, estas características incluem: "cauda gorda", clusterização de volatilidade e efeito de alavancagem.

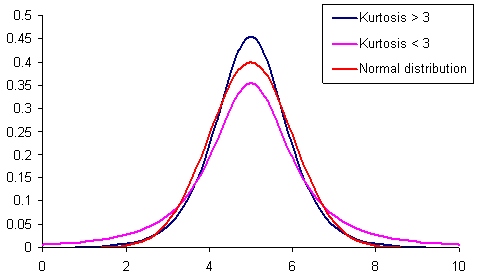
Figura 1. Distribuições com curtose diferente.

A fig. 1 mostra 3 distribuições com curtose diferente (achatamento). Distribuição, a qual o achatamento é menor do que a distribuição normal, tem as "caudas gordas" mais frequentemente do que os outros. é mostrado com a cor rosa.

Temos que mostrar a distribuição de densidade de probabilidade de um valor aleatório, a qual é utilizada para a contagem de valores da série estudada.

Por clusterização (de aglomerado - grupo, concentração) de volatilidade queremos dizer o seguinte. Um período de tempo de alta volatilidade é seguido pelo mesmo, e um período de tempo de baixa volatilidade é seguido pelo idêntico. Se os preços estavam flutuando ontem, provavelmente eles vão fazer isso hoje. Assim, existe inércia de volatilidade. A fig. 2 demonstra que a volatilidade tem uma forma de cluster.

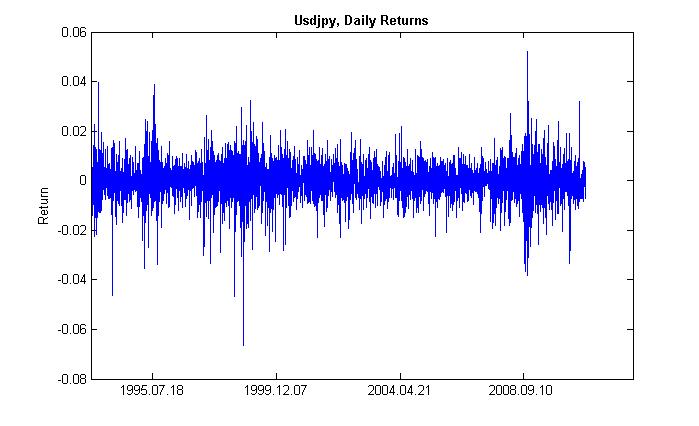
Figura 2. Volatilidade dos retornos diários de USDJPY, sua clusterização.

O efeito alavanca consiste na volatilidade de um mercado em queda ser mais elevado do que a de um mercado crescente. Fica estipulado pelo aumento do coeficiente de alavancagem, que depende da proporção de ativos emprestados e próprios quando os preços das ações caem. No entanto, este efeito se aplica ao mercado de ações, e não ao mercado de câmbio. Este efeito não será considerado mais adiante.

2. O modelo GARCH

Assim, nosso principal objetivo é a previsão da taxa de câmbio (preço) usando algum modelo. Econometristas usam modelos matemáticos que descrevem um ou outro efeito que pode ser estimado em termos de quantidade. Em palavras simples, eles adaptam a fórmula para um evento. E desta forma eles descrevem o evento.

Considerando que as séries temporais analisadas tem as propriedades mencionadas acima, um modelo ideal que considera estas propriedades será um não-linear. Um dos modelos não lineares mais universal é o modelo GARCH. Como ele pode nos ajudar? Dentro de seu corpo (função), ele vai considerar a volatilidade das séries, ou seja, a variabilidade de dispersão em diferentes períodos de observação. Econometristas chamam esse efeito com um termo obscuro - heterocedasticidade (do grego - hetero - diferente, skedasis - dispersão).

Se dermos uma olhada na fórmula em si, veremos que este modelo implica que a variabilidade atual de dispersão (σ²t) é afetada por ambas as mudanças anteriores de parâmetros (ϵ²t-i) e as estimativas anteriores de dispersão (as chamadas «notícia velha ») (σ²t-i):

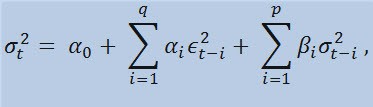
com limites

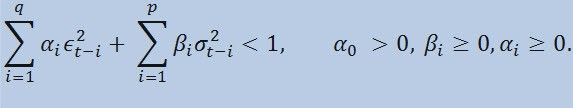
onde: ϵt - inovações não normalizadas; α0 , βi , αi , q (ordem de membros da ARCH ϵ²), p (ordem de membros da GARCH σ²) - parâmetros estimados e a ordem das modelos.

3. Indicador de retornos

Na verdade, nós não vamos estimar a própria série de preços, mas a série de retornos. O logaritmo da variação de preço (constantemente retorna cobrado) é determinado como um logaritmo natural dos retornos percentuais:

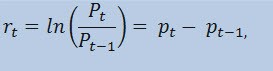
onde:

• Pt - é o valor de preço da série no tempo t;
  
• Pt-1 - é o valor de preço da série no tempo t-1;
  
• pt = ln(Pt) - é o logaritmo natural Pt.
  

Na prática, a principal razão de se trabalhar com os retornos ser preferível do que trabalhar com os preços, é porque o retorno tem melhores características estatísticas.

Então, vamos criar um indicador de retorno ReturnsIndicator.mq5, que será muito útil para nós. Aqui, eu vou referir ao artigo "Indicadores personalizados para iniciantes" que, compreensivelmente, descreve o algoritmo de criação de um indicador. é por isso que eu vou lhe mostrar apenas o código onde a fórmula mencionada é implementada. Eu acho que é muito simples e não requer explicação.

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,      // size of the array price[]
                const int prev_calculated,  // number of bars available at the previous call
                const int begin,            // index of the array price[] the reliable data starts from
                const double& price[])      // array for the calculation itself

  {
//---
   int start;
   if(prev_calculated<2) start=1;  // start filling ReturnsBuffer[] from the 1-st index, not 0.
   else start=prev_calculated-1;   // set 'start' equal to the last index in the arrays
   for(int i=start;i<rates_total;i++) {="" returnsbuffer[i]="MathLog(price[i]/price[i-1]);
     }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

A única coisa que eu quero mencionar é que a série de retornos é sempre menor do que a série primária por 1 elemento. é por isso que vamos calcular a série de retornos a partir do segundo elemento, e o primeiro será sempre igual a 0.

Assim, usando o indicador ReturnsIndicator obtivemos uma série de tempo aleatória que será utilizada para os nossos estudos.

4. Testes estatísticos

Agora é a vez dos testes estatísticos. Eles são realizados para determinar se a série temporal tem quaisquer sinais que comprovem a adequação do uso de um ou outro modelo. No nosso caso, esse modelo é o modelo GARCH.

Usando o Q-test of Ljung-Box-Pierce, verifique se as autocorrelações das séries são aleatórios ou existe uma relação. Para isso, precisamos escrever uma nova função. Aqui, por autocorrelação eu quero dizer uma correlação (ligação probabilística) entre os valores das mesmas séries temporais X (t) nos momentos de tempos t1 e t2. Se os momentos t1 e t2 são adjacentes (um segue o outro), então vamos procurar uma relação entre os membros da série e os membros das mesmas séries deslocadas por uma unidade de tempo: x1, x2, x3, ... и x1+1, x2+1, x3+1, ... Tal efeito de membros deslocados é chamado de atraso (latência, retardo). O valor do atraso pode ser qualquer número positivo.

Agora eu vou fazer observação parentética e informá-lo sobre o seguinte. Até onde eu sei, nem С++ nem MQL5 têm bibliotecas padrões que cobrem cálculos estatísticos complexos e médios. Normalmente, tais cálculos são realizados usando ferramentas especiais de estatística. Quanto a mim, é mais fácil usar ferramentas como Matlab, STATISTICA 9, etc, para resolver o problema. No entanto, eu decidi recusar a utilização de bibliotecas externas, em primeiro lugar, para demonstrar o quão poderosa a linguagem MQL5 é para cálculos, e em segundo lugar... Eu mesmo aprendi muito ao escrever o código MQL.

Agora precisamos fazer a seguinte nota. Para conduzir o teste Q, precisamos de números complexos. é por isso que eu fiz a classe Complexa. Idealmente, deve ser chamado CComplex. Bom, eu me permiti relaxar um pouco. Tenho certeza que meu leitor está preparado e eu não preciso explicar o que é um número complexo. Eu pessoalmente não gosto das funções que calculam a transformação Fourier publicada no MQL5 e MQL4; Lá, números complexos são usados de forma implícita. Além disso, há outro obstáculo - a impossibilidade de anular os operadores aritméticos em MQL5. Então eu tive que procurar por outras abordagens e evitar a notação padrão 'C'. Eu implementei a classe de número complexo da seguinte forma:

class Complex
  {
public:
   double            re,im; //re -real component of the complex number, im - imaginary
public:
   void              Complex(){};                                   //default constructor
   void              setComplex(double rE,double iM){re=rE; im=iM;}; //set method (1-st variant)
   void              setComplex(double rE){re=rE; im=0;};           //set method (2-nd variant)  
   void              ~Complex(){};                                  //destructor
   void              opEqual(const Complex &y){re=y.re;im=y.im;};   //operator=
   void              opPlus(const Complex &x,const Complex &y);      //operator+   
   void              opPlusEq(const Complex &y);                    //operator+=
   void              opMinus(const Complex &x,const Complex &y);     //operator-
   void              opMult(const Complex &x,const Complex &y);      //operator*   
   void              opMultEq(const Complex &y);                    //operator*= (1-st variant)     
   void              opMultEq(const double y);                       //operator*= (2-nd variant)    
   void              conjugate(const Complex &y);                   //conjugation of complex numbers
   double            norm();                                       //normalization 
 };

Por exemplo, a operação de soma de dois números complexos pode ser realizada utilizando o método opPlus, subtração é realizada utilizando opMinus, etc. Se você apenas escrever o código c = a + b (onde a, b, с são números complexos) então o compilador exibirá um erro. Mas ele irá aceitar a seguinte expressão: c.opPlus(a,b).

Se necessário, o usuário pode estender o conjunto de método da classe Complexa. Por exemplo, você pode adicionar um operador de divisão.

Além disso, eu preciso de funções auxiliares que processam matrizes de números complexos. é por isso que eu os implementei fora da classe Complexa, não para circular o processamento de elementos da série na mesma, mas para trabalhar diretamente com as séries passadas por uma referência. No total existem três tipos de funções:

1. getComplexArr (devolve uma série bidimensional de números reais a partir de uma série de números complexos);
2. setComplexArr (retorna uma série de números complexos a partir de uma série unidimensional de números reais);
3. setComplexArr2 (retorna uma série de números complexos a partir de uma série bidimensional de números reais).
   

Deve-se notar que estas funções retornam séries passados por uma referência. é por isso que seus corpos não contêm o operador de 'retorno'. Mas raciocinando logicamente, eu acho que podemos falar sobre o retorno apesar to tipo inválido.

A classe de números complexos e funções auxiliares é descrito no arquivo de cabeçalho Complex_class.mqh.

Então, quando conduzindo testes, vamos precisar da função de autocorrelação e da função de transformação de Fourier. Assim, precisamos criar uma classe nova, vamos chamá-la CFFT. Ela vai processar séries de números complexos para as transformações de Fourier. A classe de Fourier se parece com o seguinte:

class CFFT
  {
public:
   Complex           Input[];  //input array of complex numbers
   Complex           Output[]; //output array of complex numbers
public:
   bool              Forward(const uint N);                                   //direct Fourier transformation
   bool              InverseT(const uint N,const bool Scale=true);            //weighted reverse Fourier transformation
   bool              InverseF(const uint N,const bool Scale=false);           //non-weighted reverse Fourier transformation
   void              setCFFT(Complex &data1[],Complex &data2[],const uint N); //set method(1-st variant)
   void              setCFFT(Complex &data1[],Complex &data2[]);              //set method (2-nd variant)
protected:
   void              Rearrange(const uint N);                                 // regrouping
   void              Perform(const uint N,const bool Inverse);                // implementation of transformation
   void              Scale(const uint N);                                     // weighting
  };

Deve-se notar que todas as transformações de Fourier são realizadas com séries cujo comprimento está de acordo com a condição de 2^N (onde N é uma potência de dois). Normalmente, o comprimento da matriz não é igual a 2^N. Neste caso, o comprimento da matriz é aumentado para o valor de 2^N para 2^N >= n, onde n é o comprimento da matriz. Elementos adicionais da série são iguais a 0. Tal processamento da série é executado dentro do corpo da função autocorr usando a função auxiliar nextpow2 e a função:pow

int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two

Então, se temos uma série inicial cujo comprimento (n) é igual a 73585, então a função nextpow2 retornará o valor 17, onde 2^17 = 131072. Em outras palavras, o valor retornado é maior do que n by pow(2, ceil(log(n)/log(2))). Então vamos calcular o valor de nFFT: 2^(17+1) = 262144. Este será o comprimento da série auxiliar, cujo elementos de 73585 a 262143 serão igual a zero.

A classe de Fourier é descrita no arquivo de cabeçalho FFT_class.mqh.

Para economizar espaço, eu vou pular a descrição da implementação da classe CFFT. Os que estão interessados podem dar uma olhada no arquivo incluído em anexo. Agora vamos passar para a função de autocorrelação. 

void autocorr(double &ACF[],double &res[],int nLags)  //1-st variant of function 
/* selective autocorrelation function (ACF)  for unidimensional stochastic time series 
   ACF - output array of calculated values of the autocorrelation function;
   res - array of observation of stochastic time series;
   nLags - maximum number of lags the ACF is calculated for.
*/
  {
   Complex Data1[],Data21[], //input arrays of complex numbers
   Data2[],Data22[],         //output arrays of complex numbers
   cData[];                  //array of conjugated complex numbers           
   double rA[][2];           //auxiliary two-dimensional array of real numbers

   int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two
   ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT);    //correction of array sizes
   ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT);
   ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT);

   double rets1[];                   //an auxiliary array for observing the series
   double m=mean(res);               //arithmetical mean of the array res
   ArrayResize(rets1,nFFT);          //correction of array size
   for(int t=0;t<ArraySize(res);t++) //copy the initial array of observation 
       // to the auxiliary one with correction by average
     rets1[t]=res[t]-m;
   setComplexArr(Data1,rets1); //set input array of complex numbers   
   CFFT F,F1;                  //initialize instances of the CFFT class
   F.setCFFT(Data1,Data2);     //initialize data-members for the instance F
   F.Forward(nFFT);            //perform direct Fourier transformation
   for(int i=0;i<nFFT;i++)
     {
      Data21[i].opEqual(F.Output[i]);//assign the values of the F.Output array to the Data21 array;
      cData[i].conjugate(Data21[i]); //perform conjugation for the array Data21
      Data21[i].opMultEq(cData[i]);  //multiplication of the complex number by the one adjacent to it 
                     //results in a complex number that has only real component not equal to zero
     }
   F1.setCFFT(Data21,Data22);   //initialize data-members for the instance F1   
   F1.InverseT(nFFT);           //perform weighter reverse Fourier transformation
   getComplexArr(rA,F1.Output); //get the result in double format after
                     //weighted reverse Fourier transformation   
   for(int i=0;i<nLags+1;i++) 
     {
      ACF[i]=rA[i][0];          //in the output ACF array save the calculated values
                    //of autocorrelation function
      ACF[i]=ACF[i]/rA[0][0];   //normalization relatively to the first element
     }
  }

Assim, calculamos os valores de ACF para o número específico de atrasos. Agora podemos usar a função de autocorrelação para o teste Q. A própria função de teste se parece com o seguinte:

void lbqtest(bool &H[],double &rets[])
/* Function that implements the Q test of Ljung-Box-Pierce
   H - output array of logic values, that confirm or disprove
    the zero hypothesis on the specified lag;
   rets - array of observations of the stochastic time series;
*/
  {
   double lags[3]={10.0,15.0,20.0};       //specified lags 
   int maxLags=20;                        //maximum number of lags
   double ACF[]; ArrayResize(ACF,21);     //epmty ACF array
   double acf[]; ArrayResize(acf,20);     //alternate ACF array
   autocorr(ACF,rets,maxLags);            //calculated ACF array
   for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //remove the first element - one, fill
                                          //alternate array                            
   double alpha[3]={0.05,0.05,0.05};      //array of levels of significance of the test

/*Calculation of array of Q statistics for selected lags according to the formula:            
                  L
                |----|
                 \
       Q = T(T+2) || (rho(k)^2/(T-k)), 
                 /  
                |----| 
                  k=1
  where: T is range, L is the number of lags, rho(k) is the value of ACF at the k-th lag.
*/

   double idx[]; ArrayResize(idx,maxLags);     //auxiliary array of indexes
   int len=ArraySize(rets);                    //length of the array of observations
   int arrLags[];ArrayResize(arrLags,maxLags); //auxiliary array of lags
   double stat[]; ArrayResize(stat,maxLags);   //array of Q statistics
   double sum[]; ArrayResize(sum,maxLags);     //auxiliary array po sums
   double iACF[];ArrayResize(iACF,maxLags);    //auxiliary ACF array
   for(int i=0;i<maxLags;i++)
     {                                         //fill:
      arrLags[i]=i+1;                          //auxiliary array of lags     
      idx[i]=len-arrLags[i];                   //auxiliary array of indexes      
      iACF[i]=pow(acf[i],2)/idx[i];            //auxiliary ACF array     
     }
   cumsum(sum,iACF);                           //sum the auxiliary ACF array 
                                               //by progressive total                        
   for(int i=0;i<maxLags;i++)
      stat[i]=sum[i]*len*(len+2);              //fill the array Q statistics
   double stat1[];                             //alternate of the array of Q statistics
   ArrayResize(stat1,ArraySize(lags));
   for(int i=0;i<ArraySize(lags);i++)
      stat1[i]=stat[lags[i]-1];                //fill the alternate array of specified lags

   double pValue[ArraySize(lags)];             //array of 'p' values
   for(int i=0;i<ArraySize(lags);i++)
     {
      pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //calculation of 'p' values
      H[i]=alpha[i]>=pValue[i];                //estimation of zero hypothesis
     }
  }

<maxlags;i++) {="" <maxlags;i++) stat[i]="sum[i]*len*(len+

Assim, a nossa função executa o Q test of Ljung-Box-Pierce e retorna a série de valores lógicos para atrasos especificados. Precisamos esclarecer que o teste de Ljung-Box é então chamado teste portmanteau (teste combinado). Isso significa que alguns grupos de atrasos até um atraso especificado são verificados quanto à presença de autocorrelação. Normalmente, a autocorrelação é verificada até 10º, 15º e 20º atraso inclusivo. A conclusão sobre a presença de autocorrelação em toda a série é feita com base no último valor do elemento da série H, ou seja, do 1º ao 20º atraso.

Se o elemento da série é igual a falso, então a hipótese de zero, que indica que não há autocorrelação nos atrasos anteriores e selecionados, não é rejeitada. Em outras palavras, não existe autocorrelação quando o valor é falso. Caso contrário, o teste demonstra a presença da autocorrelação. Assim, uma alternativa para hipótese de zero é aceita quando o valor é verdadeiro.

às vezes acontece que autocorrelações não são encontrados nas séries de retornos. Neste caso, por maior segurança os quadrados dos retornos são testados. A decisão final sobre a aceitação ou rejeição da hipótese de zero é feita da mesma forma de quando se testa a série inicial de retornos. Porque devemos usar os quadrados de retornos? - Deste modo, podemos aumentar artificialmente o possível componente de autocorrelação não aleatória das séries analisadas, que é também definida dentro dos limites de valores iniciais de limites de confiança. Teoricamente você pode usar quadrados e outros domínios sobre retornos. Mas é um carregamento estatístico desnecessário que apaga o significado de testes.

No fim do corpo da função de teste Q quando o valor 'p' é calculado, a função gammp(x1/2,x2/2) apareceu. Ele permite calcular a função gama incompleta para os elementos correspondentes. Na verdade, precisamos de uma função cumulativa de χ2-distribution (chi-square-distribution). Mas é um caso particular de distribuição Gamma.

Geralmente, para provar a adequação do uso do modelo GARCH, é o suficiente obter um valor positivo de qualquer dos atrasos do teste Q. Além de que, econometristas realizam outro teste - o teste ARCH de Engle, que verifica a presença de uma heterocedasticidade. convencional. No entanto, acho que o teste Q é o suficiente por enquanto. é o mais universal.

Agora, como nós temos todas as funções necessárias para a realização do teste, precisamos pensar em apresentar os resultados obtidos na tela. Para este propósito, escrevi outra função lbqtestInfo que exibe o resultado de teste econométrico na forma de uma janela de mensagem e o diagrama de autocorrelação - diretamente no gráfico do símbolo analisado.

Vamos ver o resultado por um exemplo. Eu escolhi usdjpy como o primeiro símbolo para a análise. No início, eu abro o gráfico de linha do símbolo (por preços próximos) e carrego o indicador personalizado ReturnsIndicator para demonstrar a série de retornos. O gráfico é maximamente contraído para melhor visualizar a clusterização da volatilidade do indicador. Então eu executo o script GarchTest. Provavelmente, a resolução da sua tela é diferente da minha, então o script irá lhe perguntar sobre o tamanho desejado do diagrama em pixels. Meu padrão é 700*250.

Vários exemplos de teste são mostrados na fig. 3.

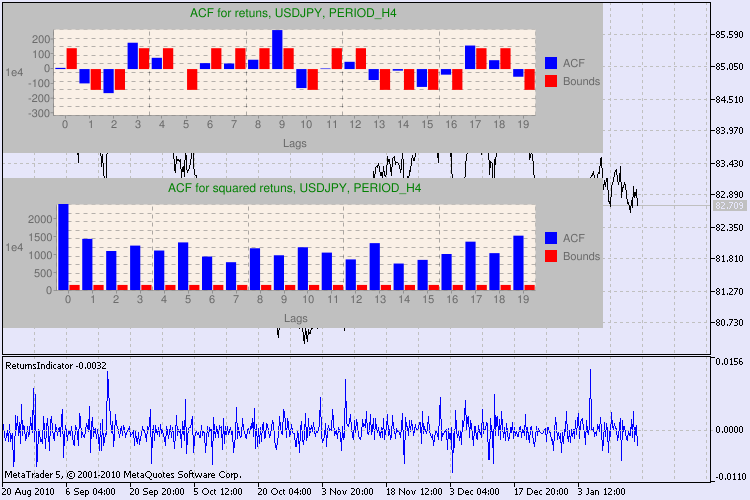
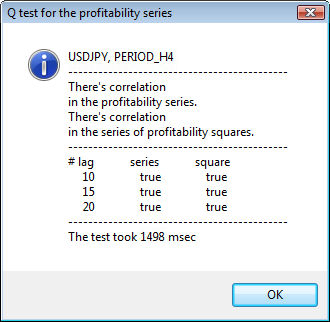
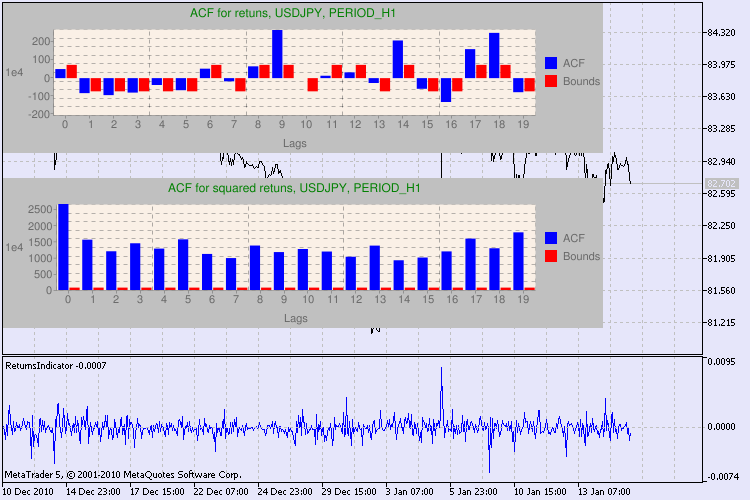
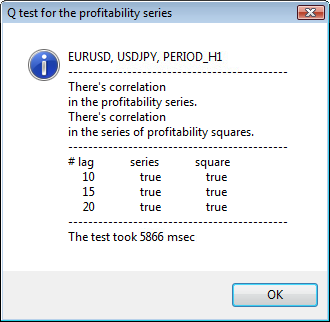
Figura 3. O resultado do teste de Q e o diagrama de autocorrelação para USDJPY para diferentes prazos..

Sim, eu procurei muito por uma variante de exibição do diagrama em um gráfico em símbolo MetaTrader 5. E eu decidi que a variante ideal é usar uma biblioteca de diagramas de desenho usando Google Chart API, que é descrito no artigo correspondente.

Como devemos interpretar essa informação? Vamos dar uma olhada. A parte superior da tabela contém o diagrama da função de autocorrelação (ACF) para a série inicial de retornos. No primeiro diagrama analisamos a série de usdjpy do prazo H4. Podemos ver que vários valores de ACF (barras azuis) excederam os limites (barras vermelhas). Em outras palavras, vemos uma pequena autocorrelação na série inicial de retornos. O diagrama abaixo é o diagrama da função autocorrelação (ACF) das séries dos quadrados dos retornos do símbolo especificado. Tudo lá está claro, uma vitória completa das barras azuis. Os diagramas H1 são analisadas da mesma maneira.

Algumas palavras sobre a descrição dos eixos do diagrama. O eixo x é claro; ele exibe os índices de atrasos. No eixo y você pode ver o valor exponencial, o valor inicial por qual o ACF é multiplicado. Assim, 1e4 significa que o valor inicial é multiplicado por 1e4 (1e4 = 10000), e 1e2 significa multiplicar por 100, etc, a multiplicação é feita para tornar o esquema mais compreensível.

A parte superior da janela de diálogo exibe um símbolo ou nome par cruzado e seu prazo. Depois deles, você pode ver duas frases que falam sobre a presença ou ausência de autocorrelação na série inicial de retorno e na série dos quadrados dos retornos. Em seguida, o 10°, 15° e 20° atraso são listados, bem como o valor de autocorrelação na série inicial e na série de quadrados. Um valor relativo de autocorrelação é apresentado aqui - um sinalizador booleano durante o teste Q que determina se há um autocorrelação à anterior e os sinalizadores especificados.

No final, se virmos que a autocorrelação existir nos sinalizadores anteriores e específicos, então o sinalizador será igual a verdadeiro, caso contrário - falso. No primeiro caso, a nossa série é um "cliente" para a aplicação do modelo GARCH não-linear, e no segundo caso, é preciso usar modelos analíticos mais simples. Um leitor atento notará que a série inicial de retorno do par USDJPY pouco se relaciona com os outros, especialmente a que tem o prazo maior. Mas a série dos quadrados dos retornos mostram autocorrelação.

O tempo gasto no teste é mostrado na parte inferior da janela.

Todo o teste foi realizado usando o script GarchTest.mq5.

Conclusões

Em meu artigo, eu descrevi como econometristas analisam séries temporais, ou para ser mais preciso, como eles começam seus estudos. Durante isso, eu tive que escrever muitas funções e código de vários tipos de dados (por exemplo, números complexos). Provavelmente, a estimativa visual de uma primeira série dá quase o mesmo resultado que a estimativa econométrica. No entanto, concordamos em utilizar apenas métodos precisos. Você sabe, um bom médico pode definir um diagnóstico sem o uso de tecnologia complexa e metodologia. Mas de qualquer forma, eles vão estudar o paciente cuidadosamente e meticulosamente.

O que obtemos da abordagem descrita no artigo? O uso de modelos GARCH permite representar a série analisada formalmente a partir do ponto de vista matemático e criar uma previsão para um determinado número de passos. Além disso ele vai nos ajudar a simular o comportamento de séries em períodos de previsão e testar qualquer Expert Advisor pronto usando as informações previstas.

Localização de arquivos:

#	Arquivo	Via
1	ReturnsIndicator.mq5	%MetaTrader%\MQL5\Indicators
2	Complex_class.mqh	%MetaTrader%\MQL5\Include
3	FFT_class.mqh	%MetaTrader%\MQL5\Include
4	GarchTest.mq5	%MetaTrader%\MQL5\Scripts

Os arquivos e descrição da biblioteca google_charts.mqh e Libraries.rar podem ser baixados do artigo mencionado anteriormente.

Literatura utilizada para o artigo:

1. Analysis of Financial Time Series, Ruey S. Tsay, 2ª Edição, 2005. - 638 pp. - 638 pp.
   
2. Applied Econometric Time Series,Walter Enders, John Wiley & Sons, 2ª Edição, 1994. - 448 pp.
   
3. Bollerslev, T., R. F. Engle, and D. B. Nelson. "Modelos ARCH ." Manual de econometria. Vol. 4, Capítulo 49, Amsterdam: Elsevier Science B.V.
4. Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3ª ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
5. Numerical Recipes in C, The Art of Scientific Computing, 2ª Edição, W.H. Press, B.P. Flannery, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 pp.
   
6. Gene H. Golub, Charles F. Van Loan. Matrix computations, 1999.
   
7. Porshnev S. V. "Computing mathematics. Series of lectures", S.Pb, 2004.