차트 분석에 대한 계량학적 접근

MetaTrader 5 — 트레이딩 | 4 8월 2021, 16:48

Denis Kirichenko

사실이 없는 이론은 황량할 수 있지만 이론이 없는 사실은 의미가 없습니다.

K. 볼딩

소개

저는 시장이 불안정하고 안정성이 없다는 말을 자주 듣습니다. 그리고 성공적인 장기 거래가 불가능한 이유를 설명합니다. 그러나 이건 사실인가요? 이 문제를 과학적으로 분석해 봅시다. 그리고 경제적 분석 수단을 선택합시다. 왜 그것들을 선택하나요? 우선 MQL 커뮤니티는 수학 및 통계를 통해 제공될 정밀도를 좋아합니다. 둘째, 제가 틀리지 않다면 이것은 이전에 설명되지 않았습니다.

성공적인 장기 거래의 문제는 한 글에서 해결할 수 없음을 언급하겠습니다. 오늘은 선택한 모델에 대한 몇 가지 진단 방법에 대해서만 설명하겠습니다. 이 방법은 향후 사용에 유용할 것입니다.

그 외에도 공식, 정리, 가설을 포함한 몇 가지 드라이한 재료를 명확하게 설명하기 위해 최선을 다할 것입니다. 그러나 저는 제 글의 독자들이 가설, 통계적 유의성, 통계(통계 기준), 분산, 분포, 확률, 회귀, 자기 상관 등과 같은 통계의 기본 개념에 익숙해지기를 기대합니다.

1. 시계열의 특징

분석의 객체가 시간 시리즈인 가격 시리즈(파생상품)라는 것은 분명합니다.

계량 경제학자는 주파수 방법(스펙트럼 분석, 웨이블릿 분석)과 시간 영역의 방법(교차 상관 분석, 자기 상관 분석)의 관점에서 시계열을 연구합니다. 독자는 주파수 방법을 설명하는 "빌딩 스펙트럼 분석" 문서를 이미 제공받았습니다. 이제 시간 영역 방법, 특히 자기 상관 분석 및 조건부 분산 분석을 살펴보는 것이 좋습니다.

비선형 모델은 선형 모델보다 가격 시계열의 동작을 더 잘 설명합니다. 그렇기 때문에 이 글에서는 비선형 모델에 대해 집중적으로 공부해 보도록 하자.

가격 시간 시리즈에는 특정 계량 경제학 모델에서만 고려할 수 있는 특별한 특성이 있습니다. 우선 이러한 특성에는 "뚱뚱한 꼬리", 변동성의 클러스터화 및 레버리지 효과가 포함됩니다.

다양한 분포의 첨도.

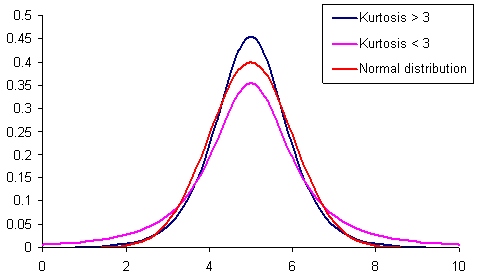
그림 1. 첨도가 다른 분포.

그림. 1은 첨도(첨두)가 다른 3개의 분포를 보여줍니다. 최고점이 정규 분포보다 낮은 분포는 다른 분포보다 "뚱뚱한 꼬리"가 더 자주 있습니다. 핑크빛으로 표현됩니다.

연구된 계열의 값을 계산하는 데 사용되는 임의 값의 확률 밀도를 표시하려면 분포가 필요합니다.

변동성의 클러스터화(클러스터 - 뭉치, 집중)는 다음을 의미합니다. 변동성이 큰 시기 뒤에는 같은 시기가 오고, 변동성이 낮은 시기 뒤에는 같은 시기가 옵니다. 가격이 어제 변동했다면 아마도 오늘 변동했을 것입니다. 따라서 변동성의 관성이 있습니다. 그림. 2는 변동성이 클러스터된 형태를 가짐을 보여줍니다.

변동성의 클러스터화.

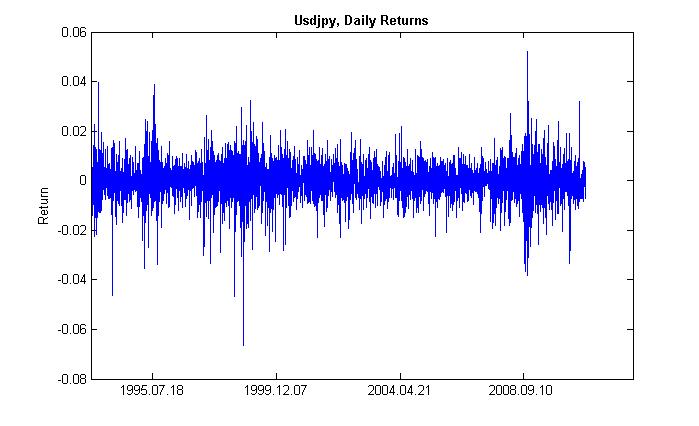
그림 2. USDJPY의 일일 수익률의 변동성, 클러스터화.

레버리지 효과는 하락 시장의 변동성이 상승 시장의 변동성보다 높다는 것입니다. 주가가 하락할 때 차입금과 자기자산의 비율에 따라 달라지는 레버리지 계수가 높아지는 것으로 규정합니다. 그러나 이 효과는 외환 시장이 아닌 주식 시장에 적용됩니다. 이 효과는 더 이상 고려되지 않습니다.

2. GARCH 모델

따라서 우리의 주요 목표는 일부 모델을 사용하여 환율(가격)을 예측하는 것입니다. 계량 경제학자는 수량으로 추정할 수 있는 하나 이상의 효과를 설명하는 수학적 모델을 사용합니다. 간단히 말해서 이벤트에 공식을 적용합니다. 그리고 이런 식으로 그들은 해당 이벤트를 설명합니다.

분석된 시계열이 위에서 언급한 속성을 가지고 있음을 고려할 때 이러한 속성을 고려한 최적의 모델은 비선형 모델이 될 것입니다. 가장 보편적인 비선형 모델 중 하나는 GARCH 모델입니다. 우리에게 어떻게 도움이 될까요? 본체(함수) 내에서 시리즈의 변동성, 즉 다양한 관찰 기간에서의 변동성 분산을 고려합니다. . 계량 경제학자는 이 효과를 이분산성이라는 난해한 용어로 부릅니다(그리스어에서 - 헤테로 - 다름, 스케다시스 - 분산< /i9>).

공식 자체를 살펴보면 이 모델이 분산의 현재 변동성(σ² t) 매개변수의 이전 변경 사항(ϵ²t-i ) 및 이전의 분산 추정치(소위 «오래된 뉴스») (σ²t -i):

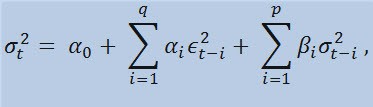
제한 있음

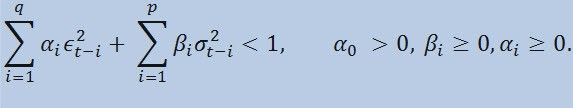
여기서: ϵt < s7>- 비정규화 혁신; < /s14></ s21>α0 , βi , αi<s28 > , q (ARCH 구성원의 순서 ϵ²) , p (GARCH 구성원의 순서 σ²) < s39>- 추정된 매개변수 및 모델의 순서.

3. 수익률 지표

사실 가격 계열 자체를 추정하는 것이 아니라 수익률의 계열을 추정하는 것입니다. 가격 변동의 로그(항상 청구되는 수익률)는 수익 비율의 자연 로그로 결정됩니다.

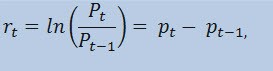
어디에:

Pt - 는 t 시점의 가격 시리즈 값입니다.
Pt-1 - 시간 t-1의 가격 시리즈 값입니다.
pt= ln(Pt) -는 자연 로그 Pt입니다.

실제로 가격으로 작업하는 것보다 수익으로 작업하는 것이 더 바람직한 주된 이유는 수익이 더 나은 통계적 특성을 가지고 있기 때문입니다.

따라서 ReturnsIndicator.mq5 반환 지표를 만들어 보겠습니다. 이는 우리에게 매우 유용합니다. 여기에서는 지표 생성 알고리즘을 이해하기 쉽게 설명하는 "초보자를 위한 맞춤 지표" 문서를 참조하겠습니다. 그래서 위의 공식이 구현된 코드만 보여드리겠습니다. 설명이 필요 없을 정도로 매우 간단합니다.

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,      // size of the array price[]
                const int prev_calculated,  // number of bars available at the previous call
                const int begin,            // index of the array price[] the reliable data starts from
                const double& price[])      // array for the calculation itself

  {
//---
   int start;
   if(prev_calculated<2) start=1;  // start filling ReturnsBuffer[] from the 1-st index, not 0.
   else start=prev_calculated-1;   // set 'start' equal to the last index in the arrays
   for(int i=start;i<rates_total;i++)
     {
      ReturnsBuffer[i]=MathLog(price[i]/price[i-1]);
     }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

제가 언급하고 싶은 유일한 것은 수익률 시리즈가 항상 기본 시리즈보다 1 요소 더 작다는 것입니다. 이것이 우리가 두 번째 요소에서 시작하는 반환 배열을 계산하는 이유이며 첫 번째 요소는 항상 0과 같습니다.

따라서 ReturnsIndicator 지표를 사용하여 연구에 사용할 임의의 시계열을 얻었습니다.

4. 통계 테스트

이제 통계 테스트의 차례입니다.< 시계열에 하나 또는 다른 모델 사용의 적합성을 증명하는 징후가 있는지 확인하기 위해 수행됩니다. 우리의 경우 이러한 모델이 GARCH 모델입니다.

Ljung-Box-Pierce의 Q-검정을 사용하여 계열의 e 자기상관이 무작위인지 또는 관계가 있는지 확인합니다. 이를 위해 새로운 함수를 작성해야 합니다. 여기서 자기상관이란 시간 t1과 t2에서 동일한 시계열 X(t)의 값 사이의 상관(확률적 연결)을 의미합니다. 모멘트 t1과 t2가 인접하면(하나가 다른 다음에 이어짐), 시리즈의 구성원과 한 시간 단위만큼 이동한 동일한 시리즈의 구성원 간의 관계를 검색합니다: x1, x2, x3, ... и x1+ 1, x2+1, x3+1, ... 이동된 구성원의 이러한 효과를 지연(지연, 지연)이라고 합니다. 지연 값은 양수일 수 있습니다.

이제 괄호 안의 말을 하고 다음에 대해서 말씀드리겠습니다. 내가 아는 한, С++나 MQL5에는 복잡하고 평균적인 통계 계산을 다루는 표준 라이브러리가 없습니다. 일반적으로 이러한 계산은 특수 통계 도구를 사용하여 수행됩니다. 저는 Matlab, STATISTICA 9 등과 같은 도구를 사용하여 문제를 해결하는 것이 더 쉽습니다. 그러나 먼저 MQL5 언어가 계산에 얼마나 강력한지 보여주기 위해 외부 라이브러리 사용을 거부하고 두 번째로... 저는 MQL 코드를 작성하면서 스스로 많은 것을 배웠습니다.

이제 우리는 다음 메모를 작성해야 합니다. Q 테스트를 수행하려면 복소수가 필요합니다. 그것이 내가 Complex 클래스를 만든 이유입니다. 이상적으로는 CComplex라고 해야 합니다. 글쎄, 저는 제 자신에게 잠시 휴식을 허용했습니다. 확실히 제 독자들은 준비가 되어 있고 복소수가 무엇인지 설명할 필요가 없을테니까요. 개인적으로 MQL5 및 MQL4에 게시된 Fourier 변환을 계산하는 함수를 좋아하지 않기에 복소수는 암시적인 방식으로 사용됩니다. 또한 MQL5에서 산술 연산자를 재정의할 수 없다는 또 다른 장애물이 있습니다. 그래서 다른 접근 방식을 찾고 표준 'C' 표기법을 피해야 했습니다. 다음과 같은 방법으로 복소수 클래스를 구현했습니다.

class Complex
  {
public:
   double            re,im; //re -real component of the complex number, im - imaginary
public:
   void              Complex(){};                                   //default constructor
   void              setComplex(double rE,double iM){re=rE; im=iM;}; //set method (1-st variant)
   void              setComplex(double rE){re=rE; im=0;};           //set method (2-nd variant)  
   void              ~Complex(){};                                  //destructor
   void              opEqual(const Complex &y){re=y.re;im=y.im;};   //operator=
   void              opPlus(const Complex &x,const Complex &y);      //operator+   
   void              opPlusEq(const Complex &y);                    //operator+=
   void              opMinus(const Complex &x,const Complex &y);     //operator-
   void              opMult(const Complex &x,const Complex &y);      //operator*   
   void              opMultEq(const Complex &y);                    //operator*= (1-st variant)     
   void              opMultEq(const double y);                       //operator*= (2-nd variant)    
   void              conjugate(const Complex &y);                   //conjugation of complex numbers
   double            norm();                                       //normalization 
 };

예를 들어, 두 개의 복소수를 더하는 연산은 opPlus 메소드를 사용하여 수행할 수 있고 빼기는 opMinus 메소드를 사용하여 수행할 수 있습니다. c = a + b 코드(여기서 a, b, с는 복소수)를 작성하면 컴파일러에서 오류를 표시합니다. 그러나 c.opPlus(a,b) 표현식을 허용합니다.

필요한 경우 사용자는 Complex 클래스의 메소드 집합을 확장할 수 있습니다. 예를 들어 나누기 연산자를 추가할 수 있습니다.

또한 복소수 배열을 처리하는 보조 함수가 필요합니다. 이것이 내가 Complex 클래스 외부에서 배열 요소의 처리를 순환하지 않고 참조에 의해 전달된 배열과 직접 작업하기 위해 구현한 이유입니다. 총 세 가지 기능이 있습니다.

getComplexArr(복소수 배열에서 실수의 2차원 배열을 반환);
setComplexArr(실수의 1차원 배열에서 복소수의 배열을 반환);
setComplexArr2(2차원 실수 배열에서 복소수 배열 반환).

이러한 함수는 참조에 의해 전달된 배열을 반환한다는 점에 유의해야 합니다. 그렇기 때문에 그들의 바디에는 '반환' 연산자가 포함되어 있지 않습니다. 그러나 논리적으로 추론하면 void 유형에도 불구하고 반환에 대해 말할 수 있다고 생각합니다.

복소수 및 보조 기능의 클래스는 헤더 파일 Complex_class.mqh에 설명되어 있습니다.

그런 다음 테스트를 수행할 때 자기상관 함수와 Fourier 변환 함수가 필요합니다. 따라서 새 클래스를 만들어야 합니다. 이름을 CFFT로 지정하겠습니다. Fourier 변환을 위해 복소수 배열을 처리합니다. Fourier 클래스는 다음과 같습니다.

class CFFT
  {
public:
   Complex           Input[];  //input array of complex numbers
   Complex           Output[]; //output array of complex numbers
public:
   bool              Forward(const uint N);                                   //direct Fourier transformation
   bool              InverseT(const uint N,const bool Scale=true);            //weighted reverse Fourier transformation
   bool              InverseF(const uint N,const bool Scale=false);           //non-weighted reverse Fourier transformation
   void              setCFFT(Complex &data1[],Complex &data2[],const uint N); //set method(1-st variant)
   void              setCFFT(Complex &data1[],Complex &data2[]);              //set method (2-nd variant)
protected:
   void              Rearrange(const uint N);                                 // regrouping
   void              Perform(const uint N,const bool Inverse);                // implementation of transformation
   void              Scale(const uint N);                                     // weighting
  };

모든 Fourier 변환은 길이가 조건 2^N(여기서 N은 2의 거듭제곱)을 준수하는 배열로 수행됩니다. 일반적으로 배열의 길이는 2^N과 같지 않습니다. 이 경우 배열의 길이는 2^N >= n에 대해 2^N 값으로 증가합니다. 여기서 n은 배열 길이입니다. 배열의 추가된 요소는 0과 같습니다. 이러한 배열 처리는 보조 기능 nextpow2 및 pow 기능을 사용하여 autocorr 기능의 본문 내에서 수행됩니다.

int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two

따라서 길이(n)가 73585인 초기 배열이 있는 경우 nextpow2 함수는 값 17을 반환합니다. 이는 2^17 = 131072인 지점에서 말이죠. 즉, 반환된 값은 pow(2, ceil(log(<s8 >n)/로그(2)))가 됩니다. 그런 다음 nFFT 값을 계산하고, 이는 2^(17+1) = 262144가 됩니다. 이는 73585에서 262143까지의 요소가 0이 되는 보조 배열의 길이가 됩니다.

Fourier 클래스는 헤더 파일 FFT_class.mqh에 설명되어 있습니다.

공간을 절약하기 위해 CFFT 클래스 구현에 대한 설명은 생략하겠습니다. 관심 있는 분들은 첨부파일에서 확인하실 수 있습니다. 이제 자기상관 함수로 넘어갑시다.

void autocorr(double &ACF[],double &res[],int nLags)  //1-st variant of function 
/* selective autocorrelation function (ACF)  for unidimensional stochastic time series 
   ACF - output array of calculated values of the autocorrelation function;
   res - array of observation of stochastic time series;
   nLags - maximum number of lags the ACF is calculated for.
*/
  {
   Complex Data1[],Data21[], //input arrays of complex numbers
   Data2[],Data22[],         //output arrays of complex numbers
   cData[];                  //array of conjugated complex numbers           
   double rA[][2];           //auxiliary two-dimensional array of real numbers

   int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two
   ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT);    //correction of array sizes
   ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT);
   ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT);

   double rets1[];                   //an auxiliary array for observing the series
   double m=mean(res);               //arithmetical mean of the array res
   ArrayResize(rets1,nFFT);          //correction of array size
   for(int t=0;t<ArraySize(res);t++) //copy the initial array of observation 
       // to the auxiliary one with correction by average
     rets1[t]=res[t]-m;
   setComplexArr(Data1,rets1); //set input array of complex numbers   
   CFFT F,F1;                  //initialize instances of the CFFT class
   F.setCFFT(Data1,Data2);     //initialize data-members for the instance F
   F.Forward(nFFT);            //perform direct Fourier transformation
   for(int i=0;i<nFFT;i++)
     {
      Data21[i].opEqual(F.Output[i]);//assign the values of the F.Output array to the Data21 array;
      cData[i].conjugate(Data21[i]); //perform conjugation for the array Data21
      Data21[i].opMultEq(cData[i]);  //multiplication of the complex number by the one adjacent to it 
                     //results in a complex number that has only real component not equal to zero
     }
   F1.setCFFT(Data21,Data22);   //initialize data-members for the instance F1   
   F1.InverseT(nFFT);           //perform weighter reverse Fourier transformation
   getComplexArr(rA,F1.Output); //get the result in double format after
                     //weighted reverse Fourier transformation   
   for(int i=0;i<nLags+1;i++) 
     {
      ACF[i]=rA[i][0];          //in the output ACF array save the calculated values
                    //of autocorrelation function
      ACF[i]=ACF[i]/rA[0][0];   //normalization relatively to the first element
     }
  }

따라서 지정된 시차 수에 대한 ACF 값을 계산했습니다. 이제 Q 테스트에 자기상관 함수를 사용할 수 있습니다. 테스트 함수 자체는 다음과 같습니다.

void lbqtest(bool &H[],double &rets[])
/* Function that implements the Q test of Ljung-Box-Pierce
   H - output array of logic values, that confirm or disprove
    the zero hypothesis on the specified lag;
   rets - array of observations of the stochastic time series;
*/
  {
   double lags[3]={10.0,15.0,20.0};       //specified lags 
   int maxLags=20;                        //maximum number of lags
   double ACF[]; ArrayResize(ACF,21);     //epmty ACF array
   double acf[]; ArrayResize(acf,20);     //alternate ACF array
   autocorr(ACF,rets,maxLags);            //calculated ACF array
   for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //remove the first element - one, fill
                                          //alternate array                            
   double alpha[3]={0.05,0.05,0.05};      //array of levels of significance of the test

/*Calculation of array of Q statistics for selected lags according to the formula:            
                  L
                |----|
                 \
       Q = T(T+2) || (rho(k)^2/(T-k)), 
                 /  
                |----| 
                  k=1
  where: T is range, L is the number of lags, rho(k) is the value of ACF at the k-th lag.
*/

   double idx[]; ArrayResize(idx,maxLags);     //auxiliary array of indexes
   int len=ArraySize(rets);                    //length of the array of observations
   int arrLags[];ArrayResize(arrLags,maxLags); //auxiliary array of lags
   double stat[]; ArrayResize(stat,maxLags);   //array of Q statistics
   double sum[]; ArrayResize(sum,maxLags);     //auxiliary array po sums
   double iACF[];ArrayResize(iACF,maxLags);    //auxiliary ACF array
   for(int i=0;i<maxLags;i++)
     {                                         //fill:
      arrLags[i]=i+1;                          //auxiliary array of lags     
      idx[i]=len-arrLags[i];                   //auxiliary array of indexes      
      iACF[i]=pow(acf[i],2)/idx[i];            //auxiliary ACF array     
     }
   cumsum(sum,iACF);                           //sum the auxiliary ACF array 
                                               //by progressive total                        
   for(int i=0;i<maxLags;i++)
      stat[i]=sum[i]*len*(len+2);              //fill the array Q statistics
   double stat1[];                             //alternate of the array of Q statistics
   ArrayResize(stat1,ArraySize(lags));
   for(int i=0;i<ArraySize(lags);i++)
      stat1[i]=stat[lags[i]-1];                //fill the alternate array of specified lags

   double pValue[ArraySize(lags)];             //array of 'p' values
   for(int i=0;i<ArraySize(lags);i++)
     {
      pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //calculation of 'p' values
      H[i]=alpha[i]>=pValue[i];                //estimation of zero hypothesis
     }
  }

따라서 우리 함수는 Ljung-Box-Pierce의 Q 테스트를 수행하고 지정된 지연에 대한 논리 값 배열을 반환합니다. Ljung-Box의 테스트를 portmanteau 테스트 (<i6 >결합 테스트). 이는 지정된 시차까지의 시차 그룹에 대해 자기상관이 있는지 확인하는 것을 의미합니다. 일반적으로 자기상관은 10번째, 15번째, 20번째 시차까지 확인합니다. 전체 시리즈에서 자기상관의 존재에 대한 결론은 H 배열 요소의 마지막 값, 즉 1차 시차부터 20차 시차까지를 기준으로 합니다.

배열의 요소가 false와 같으면 이전 및 선택된 시차에 자기상관이 없다는 0 가설은 기각되지 않습니다. 즉, 값이 거짓이면 자기상관이 없습니다. 그렇지 않으면 테스트는 자기상관의 존재를 증명합니다. 따라서 값이 true일 때 0에 대한 대체 가설이 허용됩니다.

때로는 자기상관이 일련의 수익률에서 발견되지 않는 경우가 있습니다. 이 경우 더 많은 신뢰를 얻기 위해 수익률의 제곱을 테스트합니다. 영 가설의 수용 또는 기각에 대한 최종 결정은 초기 일련의 수익을 테스트할 때와 동일한 방식으로 이루어집니다. 수익률의 제곱을 사용해야 하는 이유는 무엇입니까? - 이러한 방식으로 분석된 계열의 가능한 비랜덤 자기상관 구성요소를 인위적으로 증가시키며, 이는 신뢰할 수 있는 한계의 초기 값 범위 내에서 추가로 결정됩니다. 이론적으로 제곱 및 기타 수익률을 사용할 수 있습니다. 하지만 이는 불필요한 통계적 로딩으로 테스트의 의미를 지워버리게 됩니다.

Q 테스트 함수의 본문 끝에서 'p' 값을 계산할 때 함수 gammp(x1/2,x2/2)< /s2>이(가) 나타났습니다. 해당 요소에 대한 불완전한 감마 함수를 계산할 수 있습니다. 사실 χ2-distribution(chi-square-distribution)의 누적 함수가 필요합니다. 그러나 이는 감마 분포의 특별한 경우입니다.

일반적으로 GARCH 모델 사용의 적합성을 증명하려면 Q 검정의 시차 중 하나라도 양의 값을 얻는 것으로 충분합니다. 이에 더하여 계량 경제학자들은 또 다른 테스트인 Engle의 ARCH 테스트를 수행합니다. 이 테스트는 기존의 이분산성의 존재를 확인합니다. 하지만 제 생각에 당분간은 Q 테스트로 충분하다고 생각합니다. 가장 보편적인 것이니까요.

이제 테스트 수행에 필요한 모든 기능을 갖추었으므로 얻은 결과를 화면에 표시하는 것에 대해 생각해야 합니다. 이를 위해 계량 경제학 테스트 결과를 메시지 창 형식으로 표시하는 또 다른 함수 lbqtestInfo와 자기상관 다이어그램(분석된 차트 오른쪽)을 작성했습니다. 상징.

그 예로 결과를 봅시다. 저는 분석을 위한 첫 번째 기호로 usdjpy를 선택했습니다. 먼저 기호의 꺾은선형 차트(종가 기준)를 열고 일련의 수익을 보여주기 위해 사용자 지정 지표 ReturnsIndicator 를 로드합니다. 차트는 지표의 변동성의 클러스터화를 더 잘 표시하기 위해 최대로 축소됩니다. 그런 다음 스크립트 GarchTest를 실행합니다. 아마도 당신의 화면 해상도가 제 것과는 다를 것입니다. 스크립트는 다이어그램의 픽셀 단위원하는 크기에 대해 묻습니다. 제 기준은 700*250입니다.

테스트의 몇 가지 예가 그림 3에 나와 있습니다.

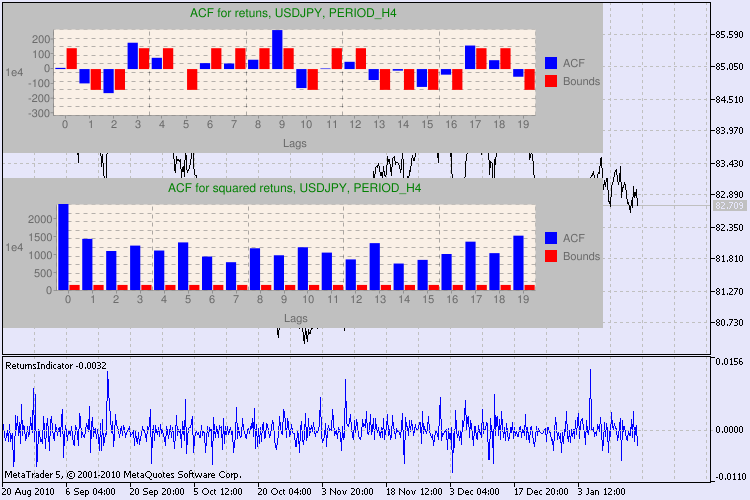
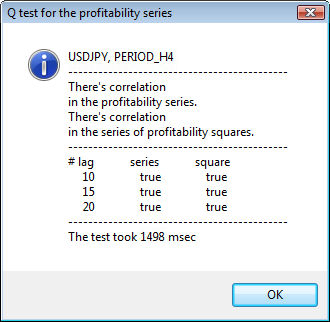
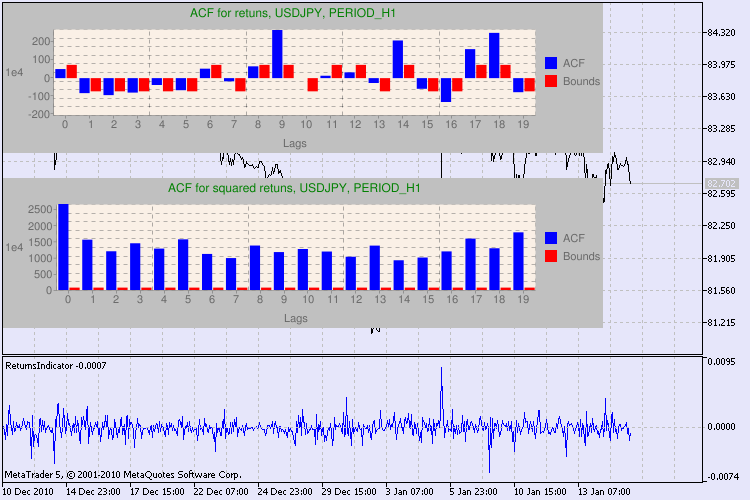
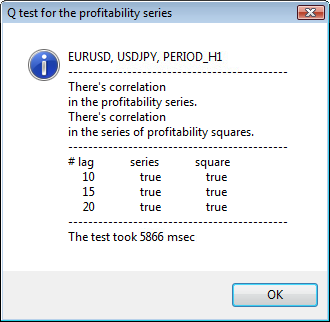
그림 3. 다양한 시간대에 대한 USDJPY에 대한 Q 테스트 및 자기 상관 다이어그램의 결과입니다.

예, MetaTrader 5에서 기호 차트에 다이어그램을 표시하는 변형을 많이 찾았습니다. 그리고 최적의 변형은 해당 문서에 설명된 Google Chart API를 사용하여 다이어그램 그리기 라이브러리를 사용하는 것이라고 결정했습니다.

이 정보를 어떻게 해석해야 합니까? 한 번 봅시다. 차트의 상단에는 초기 수익 시리즈에 대한 자기상관 함수(ACF) 다이어그램이 포함되어 있습니다. 첫 번째 다이어그램에서는 H4 기간의 usdjpy 시리즈를 분석합니다. ACF의 여러 값(파란색 바)이 한계(빨간색 바)를 초과하는 것을 볼 수 있습니다. 즉, 초기 일련의 수익에서 작은 자기상관을 보게 됩니다.. 아래 다이어그램은 지정된 기호의 반환 제곱 시리즈의 자기상관 함수(ACF)의다이어그램 입니다. 파란색 바의 완전한 승리로 모든 것이 명확합니다. H1 다이어그램도 같은 방식으로 분석됩니다.

다이어그램 축에 대한 설명에 대한 몇 마디. x 축이 명확합니다. 시차 지수를 표시합니다. y 축에서 지수 값을 볼 수 있으며, ACF의 초기 값이 곱해집니다. 따라서 1e4는 초기 값에 1e4를 곱한 값(1e4=10000)을 의미하고 1e2는 100을 곱한 값 등을 의미합니다. 이러한 곱셈은 다이어그램을 더 이해하기 쉽게 만들기 위해 수행됩니다.

대화 창의 상단에는 기호 또는 교차 쌍 이름과 해당 기간이 표시됩니다. 그 뒤에는 초기 수익률 시리즈와 수익률 제곱 시리즈에서 자기 상관의 존재 여부를 알려주는 두 문장을 볼 수 있습니다. 그런 다음 10번째, 15번째 및 20번째 지연과 초기 시리즈 및 제곱 시리즈의 자기 상관 값이 나열됩니다. 자기 상관의 상대 값이 여기에 표시됩니다. Q 테스트 중 부울 플래그는 이전 플래그와 지정된 플래그에 자기 상관이 있는지 여부를 결정합니다.

결국, 자기 상관이 이전 및 지정된 플래그에 존재한다는 것을 알면 플래그는 true와 같을 것이고 그렇지 않으면 false가 됩니다. 첫 번째 경우 우리 시리즈는 비선형 GARCH 모델을 적용하기 위한 "클라이언트"이고 두 번째 경우에는 더 간단한 분석 모델을 사용해야 합니다. 주의 깊은 독자는 USDJPY 쌍의 초기 일련의 수익률이 특히 더 큰 기간 동안 서로 약간 상관관계가 있음을 알 수 있습니다. 그러나 일련의 수익률 제곱은 자기상관을 보여줍니다.

테스트에 소요된 시간은 창 하단에 표시됩니다.

전체 테스트는 GarchTest.mq5 스크립트를 사용하여 수행되었습니다.

결론

저는 글에서 계량 경제학자가 시계열을 분석하는 방법, 더 정확하게는 연구를 시작하는 방법에 대해 설명했습니다. 그 동안 많은 함수를 작성하고 여러 유형의 데이터(예: 복소수)를 코딩해야 했습니다. 아마도 초기 시리즈의 시각적 추정은 계량 경제학 추정과 거의 동일한 결과를 제공한 것 같습니다. 그러나 우리는 정확한 방법만 사용하기로 동의했습니다. 아시잖아요. 좋은 의사는 복잡한 기술과 방법론을 사용하지 않고도 진단을 내릴 수 있다는 걸. 그러나 어쨌든 그들은 환자를 신중하고 세심하게 연구 할 것입니다.

글에 설명된 접근 방식에서 무엇을 얻을 수 있습니까?? 비선형 GARCH 모델을 사용하면 분석된 시리즈를 수학적 관점에서 공식적으로 표현하고 지정된 단계 수에 대한 예측을 생성할 수 있습니다. 또한 예측 기간에 시리즈의 동작을 시뮬레이션하고 예측 정보를 사용하여 미리 만들어진 Expert Advisor를 테스트하는 데 도움이 됩니다.

파일 위치:

#	파일	통로
1	반환 지표.mq5	%MetaTrader%\MQL5\Indicators
2	Complex_class.mqh	%MetaTrader%\MQL5\Include
3	FFT_class.mqh	%MetaTrader%\MQL5\Include
4	GarchTest.mq5	%MetaTrader%\MQL5\Scripts

라이브러리 google_charts.mqh 및 Libraries.rar에 대한 파일 및 설명은 앞서 언급한 에서 다운로드할 수 있습니다. 글.

글에 사용된 문헌:

금융 시계열 분석, Ruey S. Tsay, 2005년 제2판. - 638 pp.
Applied Econometric Time Series, Walter Enders, John Wiley & Sons, 2nd Edition, 1994. - 448 pp.
Bollerslev, T., R. F. Engle, and D. B. Nelson. "아치 모델." 계량 경제학의 핸드북. 권. 4, Chapter 49, 암스테르담: Elsevier Science B.V.
Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. 시계열 분석: 예측 및 제어. 3판. Upper Saddle River, NJ: Prentice-Hall, 1994.
C의 수치 레시피, 과학 컴퓨팅의 기술, 2판, W.H. 프레스, B.P. 플래너리, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 pp.
Gene H. Golub, Charles F. Van Loan. 행렬 계산, 1999.
Porshnev S. V. "수학 계산. 강의 시리즈", S.Pb, 2004.

MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/222

파일 첨부됨 |

ZIP파일 다운로드

autocorrelation.zip (1.02 KB)

complex_class.mqh (5.86 KB)

fft_class.mqh (6.56 KB)

returnsindicator.mq5 (2.29 KB)

garchtest.mq5 (24.67 KB)

garchtest_html.mq5 (22.81 KB)

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

토론으로 가기

MQL5 마법사: 신호 거래 모듈을 만드는 방법

이 글에서는 MQL5 마법사에 대해 생성된 클래스의 설명 형식 뿐 아니라, 가격과 이동 평균의 교차에 대한 신호 구현으로 자신만의 거래 신호 클래스를 작성하는 방법과 MQL5 마법사의 거래 전략 생성기에 포함하는 방법과 구조 뿐에 대해 설명합니다.

마이크로, 미들, 메인 추세의 지표

이 글의 목적은 James Hyerczyk의 "Pattern, Price & Time: Using Gann Theory in Trading Systems"라는 책의 몇 가지 아이디어를 기반으로 지표 및 Expert Advisor의 형태로 거래 자동화 및 분석의 가능성을 조사하는 것입니다. 완전하다고 주장하지 않고 여기서 우리는 Gann 이론의 첫 번째 부분인 모델만 조사합니다.

MQL5의 전자 테이블

이 문서에서는 1차원에 서로 다른 유형의 데이터가 포함된 동적 2차원 배열의 클래스를 설명합니다. 데이터를 테이블 형태로 저장하는 것은 서로 다른 유형의 바인딩된 정보로 배열, 저장 및 작동의 광범위한 문제를 해결하는 데 편리합니다. 테이블 작업 기능을 구현한 클래스의 소스 코드는 글에 첨부되어 있습니다.

Trading Model 기반 Multi-Expert Advisor 양성

MQL5에서 객체 지향 접근 방식을 사용하면 다중 통화/다중 시스템/다중 타임 프레임 Expert Advisors 생성이 크게 간소화됩니다. 하나의 EA가 수십 가지 거래 전략, 사용 가능한 모든 상품 및 모든 가능한 타임 프레임에서 거래한다고 상상해보십시오! 또한 EA는 테스터에서 쉽게 테스트되며 구성에 포함된 모든 전략에 대해 하나 또는 여러 개의 자금 관리 시스템이 있습니다.