Grafiklerin Analizine Ekonometrik Yaklaşım

Gerçeklere dayanmayan teoriler verimsiz olabilir ancak teorileri olmayan gerçekler anlamsızdır.

 K. Boulding

Giriş

Piyasaların oynak ve istikrarsız olduğunu sık sık duyuyorum. Ve bu başarılı bir uzun vadeli alım satımın neden imkansız olduğunu açıklıyor. Fakat bu ne kadar doğru? Bu sorunu bilimsel olarak analiz etmeye çalışalım. Ve ekonometrik analiz araçlarını seçelim. Peki neden? Her şeyden önce MQL topluluğu matematik ve istatistik tarafından sağlanacak olan kesinliği sever. İkincisi de eğer yanlışım yoksa bu daha önce anlatılmadı.

Başarılı uzun vadeli alım satım sorununun tek bir makale ile çözülemeyeceğini belirteyim. Bugün model için ileride kullanımının değerli olabileceğini umduğumuz birkaç teşhis yöntemini anlatacağım.

Buna ek olarak formüller, teoremler ve hipotezler de dâhil olmak üzere bazı belirsiz materyalleri açık bir şekilde açıklamaya çalışacağım. Bununla birlikte okuyucumun hipotez, istatistiksel anlamlılık, istatistik (istatistiksel kriter), yayılım, dağılım, olasılık, regresyon, otokorelasyon vb. gibi temel istatistik kavramlarına aşina olmasını bekliyorum.

1. Bir Zaman Serisinin Özellikleri

Analizin amacının zamanserisi olan bir fiyat serisi olduğu açıktır.

Ekonometristler zaman serilerini frekans yöntemleri (spektrum analizi, dalgacık analizi) ve zaman alanı yöntemleri (çapraz korelasyon analizi, otokorelasyon analizi) açısından inceler. Okuyucuya frekans yöntemlerini açıklayan “Spektrumu Analizini Oluşturma” makalesi zaten sunulmuştur. Şimdi zaman alanı yöntemlerine, otokorelasyon analizine ve özellikle koşullu varyans analizine bir göz atmanızı öneriyorum.

Doğrusal olmayan modeller fiyat zaman serilerinin davranışını doğrusal olanlardan daha iyi tanımlar. Bu nedenle, bu makalede doğrusal olmayan modelleri incelemeye odaklanacağız.

Fiyat zaman serileri yalnızca belirli ekonometrik modeller tarafından dikkate alınabilecek özel niteliklere sahiptir. İlk olarak bu tür nitelikler şunlardır: “ağır kuyruklu” dağılım, volatilite kümelenmesi ve kaldıraç etkisi.      

                                                                                                                

 

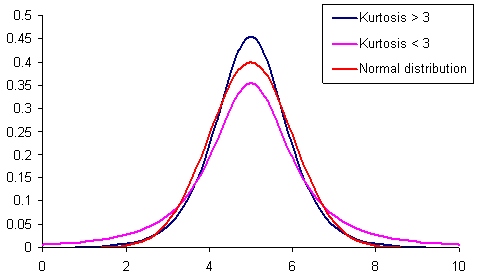
Şekil 1. Farklı basıklığa sahip dağılımlar.

Şekil 1 farklı basıklığa (dorukluluk) sahip 3 dağılım göstermektedir. Dorukluluğu normal dağılımdan daha düşük olan dağılım diğerlerinden daha çok“ağır kuyruk” niteliğine sahiptir. Pembe renk ile gösterilmiştir.

Çalışılan serinin değerlerinin sayılmasında kullanılan rastgele bir değerin olasılık yoğunluğunu göstermek için dağılıma ihtiyacımız var.

Oynaklığın kümelenmesi (küme yoğunluğu) derken aşağıdakileri kastediyoruz. Yüksek volatiliteli bir zaman periyodunun ardından aynı zaman periyodu devam eder; düşük volatiliteli bir zaman periyodunda da aynısı gerçekleşir. Fiyatlarda dün dalgalanma yaşandıysa büyük olasılıkla bugün de aynısı olacaktır. Bu nedenle volatilite durağan seyretme eğilimindedir. Şekil 2 volatilitenin kümelenmiş bir forma sahip olduğunu göstermektedir.

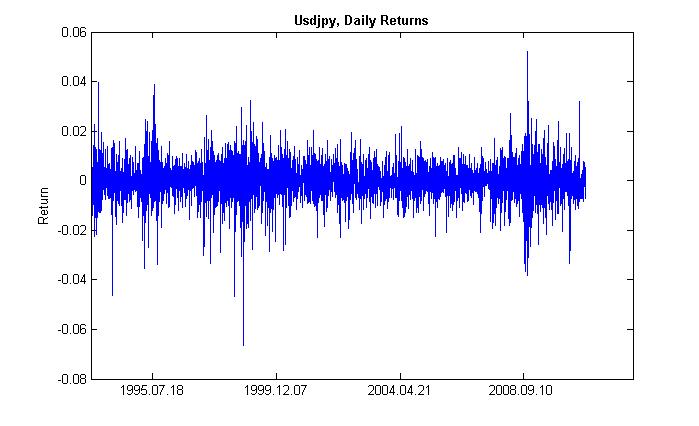
Şekil 2. USDJPY'nin günlük getirilerinin volatilitesi, kümelenmesi.

Kaldıraç etkisi, düşen bir piyasanın volatilitesinin yükselen bir piyasanınkinden daha yüksek olmasıyla oluşur. Hisse senedi fiyatları düştüğünde, ödünç alınan ve öz varlık oranına bağlı olan kaldıraç katsayısının artması öngörülür. Ancak bu etki döviz piyasası için değil borsa için geçerlidir. Bu etki üzerinde daha fazla durulmayacaktır.

2. GARCH Modeli

Bizim asıl amacımızbir model kullanarak döviz kurunu (fiyatını) tahmin etmektir. Ekonometristler nicelik açısından tahmin edilebilecek bir veya daha fazla etkiyi tanımlayan matematiksel modeller kullanırlar. Basit bir deyişle, bir formülü bir olaya uyarlarlar. Ve böylelikle bu olayı anlatırlar.

İncelenen zaman serilerinin yukarıda belirtilen özelliklere sahip olduğu göz önüne alındığında bu özellikleri ele alan optimal bir model doğrusal olmayan bir model olacaktır. En evrensel doğrusal olmayan modellerden biri GARCH modelidir. Bu bize nasıl yardımcı olabilir? İçeriği (fonksiyonu) içinde serinin volatilitesini, yani farklı gözlem dönemlerinde dağılımın değişkenliğini dikkate alacaktır. Ekonometristler bu etkiyi belirsiz bir terim olanheteroskedastisite (yunanca, hetero: farklı, skedasis: dağılım) ile adlandırırlar.

Formülün kendisine baktığımızda bu modelin, mevcut dağılım değişkenliğinin (σ ²t) hem önceki parametre değişikliklerinden (ϵ ²t-i) hem de önceki dağılım tahminlerinden (sözde «eski haber») (σ ²t-i) etkilendiğine işaret ettiğini görürüz:

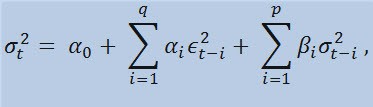
limitli

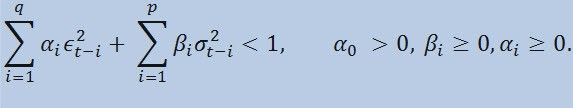
burada: ϵt : normalleştirilmemiş yeniliklerdir; α0 , βi , αi , q (ARCH üyelerinin hanesiϵ ²), p (GARCH üyelerinin hanesiσ ²)   :  tahmini parametreler ve modellerin hanesidir.

3. Getiri Göstergesi

Aslında fiyat serisinin kendisini değil getiri serisini tahmin edeceğiz. Fiyat değişiminin logaritması (sürekli olarak tahsil edilen getiriler) getiri yüzdesinin doğal logaritması olarak belirlenir:

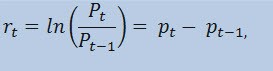
burada:

• Pt : fiyat serisinin t zamandaki değeridir;
  
• Pt-1 : fiyat serisinin t-1 zamandaki değeridir;
  
• pt = ln(Pt)  :Pt doğal logaritmasıdır.
  

Pratik olarak, getirilerle çalışmanın fiyatlarla çalışmaktan daha fazla tercih edilmesinin temel nedeni, getirilerin daha iyi istatistiksel özelliklere sahip olmasıdır.

O halde bizim için çok yararlı olacak bir ReturnsIndicator.mq5 göstergesi oluşturalım. Burada gösterge oluşturma algoritmasını anlaşılır bir şekilde açıklayan “Yeni Başlayanlar için Özel Göstergeler” makalesine atıfta bulunacağım. Bu yüzden size sadece bahsi geçen formülün uygulandığı kodu göstereceğim. Bana kalırsa bu çok basit ve açıklama gerektirmiyor.

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,      // size of the array price[]
                const int prev_calculated,  // number of bars available at the previous call
                const int begin,            // index of the array price[] the reliable data starts from
                const double& price[])      // array for the calculation itself

  {
//---
   int start;
   if(prev_calculated<2) start=1;  // start filling ReturnsBuffer[] from the 1-st index, not 0.
   else start=prev_calculated-1;   // set 'start' equal to the last index in the arrays
   for(int i=start;i<rates_total;i++)
     {
      ReturnsBuffer[i]=MathLog(price[i]/price[i-1]);
     }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Bahsetmek istediğim tek şey getiri serisinin her zaman birincil seriden 1 öge daha küçük olmasıdır. Bu yüzden ikinci ögeden başlayarak getiri dizisini hesaplayacağız ve birincisi her zaman 0'a eşit olacak.

Böylece ReturnsIndicator göstergesini kullanarak çalışmalarımızda kullanılacak rastgele bir zaman serisi elde etmiş olduk.

4. İstatistiksel Testler

Şimdiyse sıra istatistiksel testlerde. Bu testler zaman serisinin bir modeli kullanmanın uygunluğunu kanıtlayan herhangi bir işarete sahip olup olmadığını belirlemek için yapılır. Bizim durumumuzda bu model GARCH modelidir.

Q-test of Ljung-Box-Pierce kullanarak serilerin otokorelasyonlarının rastgele olup olmadığını veya aralarında bir ilişki olup olmadığını kontrol edin. Bunun için yeni bir fonksiyon yazmamız gerekiyor. Burada otokorelasyon derken aynı X(t) zaman serisinin t1 ve t2 zamanları değerleri arasında bulunan bir korelasyondan (olasılıksal bağlantı) bahsediyorum. Eğer t1 ve t2 zamanları bitişikse (biri diğerini takip ediyorsa) o zaman serinin üyeleri ile aynı serinin bir zaman birimi kaydırılmış üyeleri arasında bir ilişki ararız: x1, x2, x3, ... и x1+ 1, x2+1, x3+1, ... Taşınan üyelerin bu etkisine gecikme denir. Gecikme değeri herhangi bir pozitif sayı olabilir.

Şimdi parantez içinde bir yorumda bulunacağım ve size bundan bahsedeceğim. Bildiğim kadarıyla ne С++ ne de MQL5 karmaşık ve ortalama istatistiksel hesaplamaları kapsayan standart kütüphanelere sahip değil. Genellikle bu tür hesaplamalar özel istatistik araçları kullanılarak yapılır. Bana kalırsa sorunu çözmek için Matlab, STATISTICA 9 vb. araçları kullanmak daha kolaydır. Ancak ilk olarak MQL5 dilinin hesaplamalarda ne kadar güçlü olduğunu göstermek için harici kütüphaneleri kullanmayı reddetmeye karar verdim ve ikinci olarak da... MQL kodunu yazarken birçok şey öğrendim.

Şimdi aşağıdaki notu geçmemiz gerekiyor. Q testini yapmak için karmaşık sayılara ihtiyacımız var. Bu yüzden Complex sınıfını yaptım. İdeal olarak bu CComplex olarak adlandırılmalıdır. Pekâlâ, bir süre rahatlamama izin verdim. Eminim okuyucum hazırlıklıdır ve karmaşık sayının ne olduğunu açıklamama gerek kalmaz. Şahsen MQL5 ve MQL4'te yayınlanan Fourier dönüşümünü hesaplayan fonksiyonları sevmiyorum; karmaşık sayılar burada örtük bir şekilde kullanılır. Ayrıca başka bir engel daha mevcuttur; o da MQL5'te aritmetik operatörleri geçersiz kılmanın imkansız olması. Bu yüzden başka yaklaşımlar aramak ve standart 'C' gösterimini kullanmamak zorunda kaldım. Karmaşık sayı sınıfını şu şekilde uyguladım:

class Complex
  {
public:
   double            re,im; //re -real component of the complex number, im - imaginary
public:
   void              Complex(){};                                   //default constructor
   void              setComplex(double rE,double iM){re=rE; im=iM;}; //set method (1-st variant)
   void              setComplex(double rE){re=rE; im=0;};           //set method (2-nd variant)  
   void              ~Complex(){};                                  //destructor
   void              opEqual(const Complex &y){re=y.re;im=y.im;};   //operator=
   void              opPlus(const Complex &x,const Complex &y);      //operator+   
   void              opPlusEq(const Complex &y);                    //operator+=
   void              opMinus(const Complex &x,const Complex &y);     //operator-
   void              opMult(const Complex &x,const Complex &y);      //operator*   
   void              opMultEq(const Complex &y);                    //operator*= (1-st variant)     
   void              opMultEq(const double y);                       //operator*= (2-nd variant)    
   void              conjugate(const Complex &y);                   //conjugation of complex numbers
   double            norm();                                       //normalization 
 };

Örneğin, iki karmaşık sayının toplanması işlemi opPlus yöntemi kullanılarak çıkarma işlemi deopMinus kullanılarak gerçekleştirilir ve bu böyle gider. Sadece c = a + b kodunu yazarsanız (burada a, b, с karmaşık sayılardır) derleyici bir hata gösterecektir. Ancak şu ifadeyi kabul edecektir: c.opPlus(a,b).

Gerektiği takdirde bir kullanıcı Complex sınıfının yöntem kümesini genişletebilir. Örneğin, bir bölme operatörü ekleyebilirsiniz. 

Buna ek olarak, karmaşık sayı dizilerini işleyen yardımcı fonksiyonlara ihtiyacım var. Bu yüzden onları Complex sınıfının dışında, içindeki dizi ögelerinin işlenmesini döngüye sokmak için değil de doğrudan bir referans tarafından geçirilen dizilerle çalışmak için uyguladım. Toplamda bu tür üç fonksiyon vardır:

1. getComplexArr (bir dizi karmaşık sayı dizisinden iki boyutlu bir gerçek sayı dizisini döndürür);
2. setComplexArr (tek boyutlu bir gerçek sayı dizisinden bir dizi karmaşık sayı döndürür);
3. setComplexArr2 (iki boyutlu bir gerçek sayı dizisinden bir dizi karmaşık sayı döndürür).
   

Bu fonksiyonların bir referans tarafından geçirilen dizileri döndürdüğüne dikkat edilmelidir. Bu yüzden kodlarında “getiri” operatörü bulunmaz. Ancak geçersiz türe rağmen getiri hakkında mantıklı bir şekilde konuşabileceğimizi düşünüyorum. 

Karmaşık sayıların ve yardımcı fonksiyonların sınıfı Complex_class.mqh başlık dosyasında açıklanmıştır.

Ardından, testleri yaparken otokorelasyon fonksiyonuna ve Fourier dönüşümü fonksiyonuna ihtiyacımız olacak. Bu nedenle yeni bir sınıf oluşturmamız gerekiyor, adını CFFT koyalım. Bu sınıf Fourier dönüşümleri için karmaşık sayı dizilerini işleyecektir. Fourier sınıfı aşağıdaki gibi görünür:

class CFFT
  {
public:
   Complex           Input[];  //input array of complex numbers
   Complex           Output[]; //output array of complex numbers
public:
   bool              Forward(const uint N);                                   //direct Fourier transformation
   bool              InverseT(const uint N,const bool Scale=true);            //weighted reverse Fourier transformation
   bool              InverseF(const uint N,const bool Scale=false);           //non-weighted reverse Fourier transformation
   void              setCFFT(Complex &data1[],Complex &data2[],const uint N); //set method(1-st variant)
   void              setCFFT(Complex &data1[],Complex &data2[]);              //set method (2-nd variant)
protected:
   void              Rearrange(const uint N);                                 // regrouping
   void              Perform(const uint N,const bool Inverse);                // implementation of transformation
   void              Scale(const uint N);                                     // weighting
  };

Tüm Fourier dönüşümlerinin, uzunluğu 2^N koşuluna uyan dizilerle gerçekleştirildiğine dikkat edilmelidir (burada N, ikinin üstüdür). Genellikle dizinin uzunluğu 2^N'ye eşit değildir. Bu durumda 2^N >= n için dizinin uzunluğu 2^N değerine yükseltilir; burada n, dizi uzunluğudur. Dizinin eklenen ögeleri 0'a eşittir. Dizinin bu şekilde işlenmesi nextpow2 yardımcı fonksiyonu ve pow fonksiyonu kullanılarak autocorr fonksiyonunun içeriğinde gerçekleştirilir:

int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two

Dolayısıyla, uzunluğu (n) 73585'e eşit olan bir başlangıç dizimiz varsa nextpow2 işlevi 17 değerini döndürecektir: burada 2^17 = 131072’dir. Başka bir deyişle, döndürülen değer n çarpı pow’dan (2, ceil(log(n)/log(2))) daha büyüktür. Şimdi de nFFT'nin değerini hesaplayacağız: 2^(17+1) = 262144. Bu, 73585'ten 262143'e kadar olan ögelerin sıfıra eşit olacağı yardımcı dizinin uzunluğu olacaktır.

Fourier sınıfı FFT_class.mqh başlık dosyasında açıklanmıştır.

Yer kazanmak için CFFT sınıfının uygulanmasının açıklamasını atlayacağım. İlgilenenler ekteki dosyadan inceleyebilirler. Şimdi otokorelasyon fonksiyonuna geçelim.

void autocorr(double &ACF[],double &res[],int nLags)  //1-st variant of function 
/* selective autocorrelation function (ACF)  for unidimensional stochastic time series 
   ACF - output array of calculated values of the autocorrelation function;
   res - array of observation of stochastic time series;
   nLags - maximum number of lags the ACF is calculated for.
*/
  {
   Complex Data1[],Data21[], //input arrays of complex numbers
   Data2[],Data22[],         //output arrays of complex numbers
   cData[];                  //array of conjugated complex numbers           
   double rA[][2];           //auxiliary two-dimensional array of real numbers

   int nFFT=pow(2,nextpow2(ArraySize(res))+1);      //power rate of two
   ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT);    //correction of array sizes
   ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT);
   ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT);

   double rets1[];                   //an auxiliary array for observing the series
   double m=mean(res);               //arithmetical mean of the array res
   ArrayResize(rets1,nFFT);          //correction of array size
   for(int t=0;t<ArraySize(res);t++) //copy the initial array of observation 
       // to the auxiliary one with correction by average
     rets1[t]=res[t]-m;
   setComplexArr(Data1,rets1); //set input array of complex numbers   
   CFFT F,F1;                  //initialize instances of the CFFT class
   F.setCFFT(Data1,Data2);     //initialize data-members for the instance F
   F.Forward(nFFT);            //perform direct Fourier transformation
   for(int i=0;i<nFFT;i++)
     {
      Data21[i].opEqual(F.Output[i]);//assign the values of the F.Output array to the Data21 array;
      cData[i].conjugate(Data21[i]); //perform conjugation for the array Data21
      Data21[i].opMultEq(cData[i]);  //multiplication of the complex number by the one adjacent to it 
                     //results in a complex number that has only real component not equal to zero
     }
   F1.setCFFT(Data21,Data22);   //initialize data-members for the instance F1   
   F1.InverseT(nFFT);           //perform weighter reverse Fourier transformation
   getComplexArr(rA,F1.Output); //get the result in double format after
                     //weighted reverse Fourier transformation   
   for(int i=0;i<nLags+1;i++) 
     {
      ACF[i]=rA[i][0];          //in the output ACF array save the calculated values
                    //of autocorrelation function
      ACF[i]=ACF[i]/rA[0][0];   //normalization relatively to the first element
     }
  }

Belirtilen gecikme sayısı için ACF değerlerini hesapladık. Şimdi Q testi için otokorelasyon fonksiyonunu kullanabiliriz. Test fonksiyonunun kendisi aşağıdaki gibi görünür:

void lbqtest(bool &H[],double &rets[])
/* Function that implements the Q test of Ljung-Box-Pierce
   H - output array of logic values, that confirm or disprove
    the zero hypothesis on the specified lag;
   rets - array of observations of the stochastic time series;
*/
  {
   double lags[3]={10.0,15.0,20.0};       //specified lags 
   int maxLags=20;                        //maximum number of lags
   double ACF[]; ArrayResize(ACF,21);     //epmty ACF array
   double acf[]; ArrayResize(acf,20);     //alternate ACF array
   autocorr(ACF,rets,maxLags);            //calculated ACF array
   for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //remove the first element - one, fill
                                          //alternate array                            
   double alpha[3]={0.05,0.05,0.05};      //array of levels of significance of the test

/*Calculation of array of Q statistics for selected lags according to the formula:            
                  L
                |----|
                 \
       Q = T(T+2) || (rho(k)^2/(T-k)), 
                 /  
                |----| 
                  k=1
  where: T is range, L is the number of lags, rho(k) is the value of ACF at the k-th lag.
*/

   double idx[]; ArrayResize(idx,maxLags);     //auxiliary array of indexes
   int len=ArraySize(rets);                    //length of the array of observations
   int arrLags[];ArrayResize(arrLags,maxLags); //auxiliary array of lags
   double stat[]; ArrayResize(stat,maxLags);   //array of Q statistics
   double sum[]; ArrayResize(sum,maxLags);     //auxiliary array po sums
   double iACF[];ArrayResize(iACF,maxLags);    //auxiliary ACF array
   for(int i=0;i<maxLags;i++)
     {                                         //fill:
      arrLags[i]=i+1;                          //auxiliary array of lags     
      idx[i]=len-arrLags[i];                   //auxiliary array of indexes      
      iACF[i]=pow(acf[i],2)/idx[i];            //auxiliary ACF array     
     }
   cumsum(sum,iACF);                           //sum the auxiliary ACF array 
                                               //by progressive total                        
   for(int i=0;i<maxLags;i++)
      stat[i]=sum[i]*len*(len+2);              //fill the array Q statistics
   double stat1[];                             //alternate of the array of Q statistics
   ArrayResize(stat1,ArraySize(lags));
   for(int i=0;i<ArraySize(lags);i++)
      stat1[i]=stat[lags[i]-1];                //fill the alternate array of specified lags

   double pValue[ArraySize(lags)];             //array of 'p' values
   for(int i=0;i<ArraySize(lags);i++)
     {
      pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //calculation of 'p' values
      H[i]=alpha[i]>=pValue[i];                //estimation of zero hypothesis
     }
  }

Böylece fonksiyonumuz Ljung-Box-Pierce Q testini gerçekleştirir ve belirtilen gecikmeler için mantık değerleri dizisini döndürür. Ljung-Box testinin portmanteau testi (kombine test) olarak adlandırıldığını açıklığa kavuşturmamız gerekiyor. Bu, belirli bir gecikmeye kadar bazı gecikme gruplarının otokorelasyonun varlığı için kontrol edildiği anlamına gelir. Genellikle otokorelasyon 10’uncu, 15’inci ve 20’nci gecikmeler dâhil olacak şekilde kontrol edilir. Tüm seride otokorelasyonun varlığı hakkında bir sonuca varım H dizisinin ögesinin son değeri temelinde, yani 1'inci ila 20'nci gecikme arasında yapılır.

Dizinin ögesi false değerine eşitse önceki ve seçilen gecikmelerde otokorelasyon olmadığını belirten sıfır hipotezi reddedilmez. Başka bir deyişle, değer false olduğunda otokorelasyon olmaz. Aksi takdirde test otokorelasyonun varlığını kanıtlar. Böylece değer true olduğunda sıfır hipotezine karşılık bir alternatif kabul edilir.

Bazen bir getiri serisinde otokorelasyonlar bulunmaz. Bu durumda daha fazla güvenirlik sağlamak için getirilerin kareleri test edilir. Sıfır hipotezini kabul etme veya reddetme konusundaki nihai karar ilk getiri serisini test ederken olduğu şekilde verilir. Neden getirilerin karelerini kullanmalıyız? Bu şekilde, analiz edilen serinin daha sonra güvenilir limitlerin başlangıç değerlerinin sınırları içinde belirlenen olası rastgele olmayan otokorelasyon bileşenini yapay olarak arttırmış oluruz. Teorik olarak kareleri ve diğer getiri üstlerini kullanabilirsiniz. Ancak bu, testin anlamını ortadan kaldıran gereksiz bir istatistiksel yüklemedir.

Q test fonksiyonunun içeriğinin sonunda “p” değeri hesaplandığında gammp(x1/2,x2/2) fonksiyonu ortaya çıkmıştır. Bu, karşılık gelen ögeler için eksik gama fonksiyonunun hesaplanmasını sağlar. Aslında χ2-dağılımının (ki-kare-dağılımı) kümülatif bir fonksiyonuna ihtiyacımız var. Ancak bu, Gamma dağılımının özel bir durumudur.

Genel olarak, GARCH modelinin kullanımının uygunluğunu kanıtlamak için Q testinin herhangi bir gecikmesinin pozitif bir değerini elde etmek yeterlidir. Buna ek olarak, ekonometristler geleneksel bir değişen varyansın varlığını kontrol eden Engle'nin ARCH testi olarak bilinen başka bir test daha gerçekleştirirler . Ancak şu an için Q testinin yeterli olduğunu düşünüyorum. Bu en evrensel olanıdır. 

Şimdi testi yapmak için gerekli tüm fonksiyonlara sahip olduğumuza göre elde edilen sonuçları ekranda gösterebiliriz. Bu amaçla ekonometrik testin sonucunu bir mesaj penceresi ve otokorelasyon şeması olarak doğrudan analiz edilen sembolün grafiği üzerinde görüntüleyen lbqtestInfo fonksiyonunu yazdım.

Sonucu bir örnekle görelim. Analiz için ilk sembol olarak usdjpy'i seçtim. İlk önce sembolün çizgi grafiğini açıyorum (kapanış fiyatlarına göre) ve getiri serilerini göstermek için özel gösterge olan ReturnsIndicator'ı yüklüyorum. Grafik göstergenin volatilite kümelenmesini daha iyi göstermek için maksimum düzeyde daraltılmıştır. Sonra GarchTest komut dosyasını çalıştırıyorum. Muhtemelen ekran çözünürlüğünüz benimkinden farklıdır; bu komut dosyası size diyagramın piksel cinsinden istenen boyutunu soracaktır. Benim standardım 700*250’dir.

Şekil 3’te testin birkaç örneği verilmiştir.

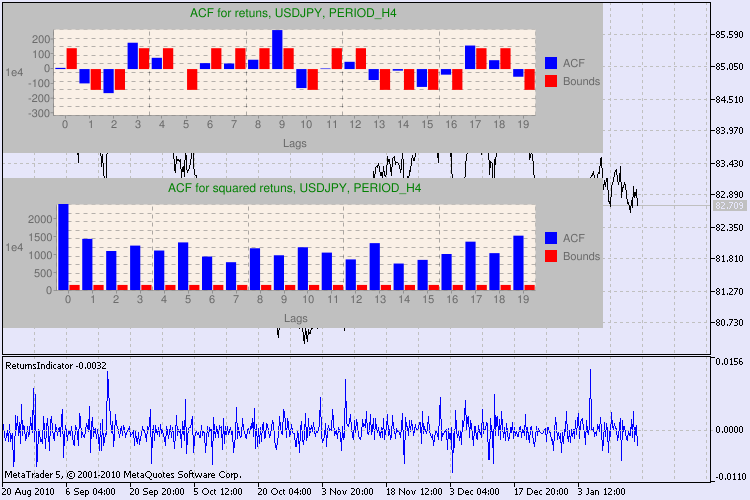
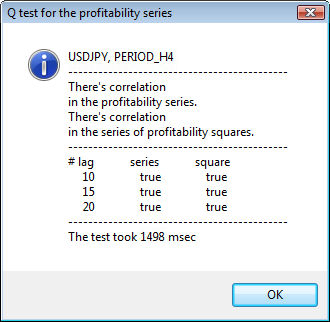
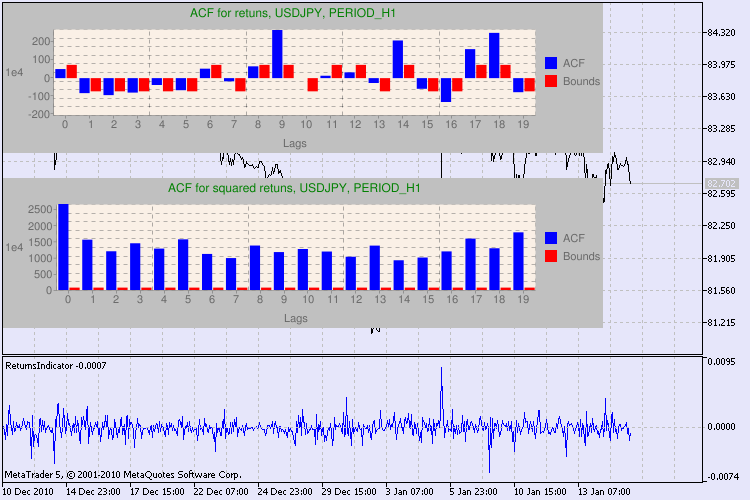
Şekil 3. Q testinin sonucu ve farklı zaman dilimlerinde USDJPY otokorelasyon diyagramı

Evet, MetaTrader 5'te diyagramı bir sembol grafiğinde görüntülemenin varyantını çok aradım. Ve en uygun varyantın ilgili makalede açıklandığı üzere Google Chart API ile bir çizim diyagramları kütüphanesi kullanmak olduğuna karar verdim.

Bu bilgiyi nasıl yorumlamalıyız? Hadi bir bakalım. Grafiğin üst kısmı ilk getiri serisi için otokorelasyon fonksiyonunun (ACF) diyagramını gösterir. İlk diyagramda H4 zaman çerçevesinin usdjpy serisini analiz ediyoruz. Birkaç ACF değerinin (mavi çubuklar) limitleri (kırmızı çubuklar) aştığını görebiliriz. Başka bir deyişle, ilk getiri serisinde küçük bir otokorelasyon görüyoruz. Aşağıdaki diyagram belirtilen sembolün kareler serisinin otokorelasyon fonksiyonunun (ACF) diyagramıdır. Her şey oldukça net, mavi çubukların kesin bir şekilde galip gelmiştir. H1 diyagramları da aynı şekilde analiz edilir.

Diyagram eksenlerinin açıklaması hakkında birkaç kelime edeyim. xeksenin anlamı açıktır; gecikme indekslerini görüntüler. yekseninde üstel değeri görebilirsiniz, ACF'nin başlangıç değeri ile çarpılır. Böylece 1e4 ilk değerin 1e4 (1e4=10000) ile çarpılması ve 1e2 de 100 ile çarpma vb. anlamına gelir. Bu bir çarpma işlemi diyagramı daha anlaşılır kılmak için yapılır. 

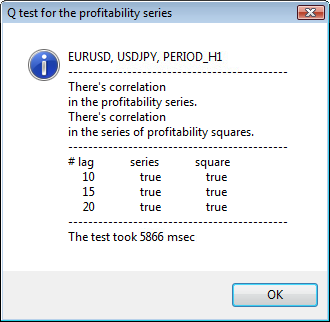
İletişim penceresinin üst kısmı bir sembol veya çapraz çift adını ve zaman dilimini görüntüler. Onlardan sonra da ilk getiri dizilerinde ve getirilerin kareler dizisinde otokorelasyonun varlığını veya yokluğunu anlatan iki cümle görebilirsiniz. Daha sonra 10’uncu, 15’inci ve 20’nci gecikmelerin yanı sıra ilk serideki ve kareler serisindeki otokorelasyon değeri listelenir. Burada göreceli bir otokorelasyon değeri görüntülenir; Q testi sırasında önceki ve belirtilen bayraklarda otokorelasyon olup olmadığını belirleyen bir boole bayrağı.

Sonuçta önceki ve belirtilen bayraklarda otokorelasyonun var olduğunu görürsek bayrak true değerine eşit olacaktır, aksi takdirde de false değerine eşit olacaktır. İlk durumda serimiz doğrusal olmayan GARCH modelini uygulamaya yönelik bir “istemci”dir ve ikinci durumda daha basit analitik modeller kullanmamız gerekir. Dikkatli bir okuyucu USDJPY çiftinin ilk getiri serisinin özellikle daha büyük bir zaman diliminden biriyle nispeten bağlantılı olduğunu fark edecektir. Ancak getirilerin kareleri serisi otokorelasyon gösterir.

Test için harcanan süre pencerenin alt kısmında gösterilmiştir.

Tüm test GarchTest.mq5 komut dosyası kullanılarak yapılmıştır.

Sonuçlar

Makalemde ekonometristlerin zaman serilerini nasıl analiz ettiklerini veya daha doğrusu çalışmalarına nasıl başladıklarını anlattım. Bu sırada birçok fonksiyon yazmak ve çeşitli veri türlerini (örneğin karmaşık sayılar) kodlamak zorunda kaldım. Muhtemelen bir ilk seri görsel tahmini ekonometrik tahminle hemen hemen aynı sonucu verecektir. Buna ek olarak, yalnızca kesin yöntemler kullanmaya karar verdik. Biliyorsunuz ki iyi bir doktor karmaşık teknoloji ve metodoloji kullanmadan teşhis koyabilir. Ama yine de hastayı dikkatle ve titizlikle muayene ederler.

Makalede açıklanan yaklaşımdan kazanımlarımız nelerdir? Doğrusal olmayan GARCH modellerinin kullanımı, analiz edilen serilerin matematiksel açıdan resmi olarak temsil edilmesine ve belirli sayıda adım için bir tahmin oluşturulmasına olanak tanır. Ayrıca bu, tahmin periyotlarında serilerin davranışını taklit etmemize ve tahmin edilen bilgileri kullanarak hazır herhangi bir Uzman Danışmanı test etmemize yardımcı olacaktır.

Dosyaların konumu:

#	Dosya	Yol:
1	ReturnsIndicator.mq5	%MetaTrader%\MQL5\Indicators
2	Complex_class.mqh	%MetaTrader%\MQL5\Include
3	FFT_class.mqh	%MetaTrader%\MQL5\Include
4	GarchTest.mq5	%MetaTrader%\MQL5\Scripts

google_charts.mqh ve Libraries.rar kütüphanesinin dosyaları ve açıklaması daha önce bahsedilen makaleden indirilebilir.

Makale için kullanılan literatür:

1. Analysis of Financial Time Series, Ruey S. Tsay, 2. Baskı, 2005. - 638 s.
   
2. Applied Econometric Time Series,Walter Enders, John Wiley & Sons, 2. Baskı, 1994. - 448 s.
   
3. Bollerslev, T., R. F. Engle ve D. B. Nelson. “ARCH Models.” Handbook of Econometrics. Vol. 4, Chapter 49, Amsterdam: Elsevier Science B.V.
4. Box, G. E. P., G. M. Jenkins ve G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
5. Numerical Recipes in C, The Art of Scientific Computing, 2. Baskı, W.H. Press, B.P. Flannery, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 s.
   
6. Gene H. Golub, Charles F. Van Loan. Matrix computations, 1999.
   
7. Porshnev S. V. “Computing mathematics. Series of lectures”, S.Pb, 2004.