Isso está fundamentalmente errado.
Em primeiro lugar, vamos falar em russo e chamar "curtose" e "insularidade" pelo termo aceito - coeficiente de curtose ou simplesmente curtose.
Em segundo lugar, "insularidade" e "caudas gordas", em geral, não estão relacionadas. Aqui está um contraexemplo - a distribuição de Laplace ( exponencial bilateral), à qual, diga-se de passagem, os gráficos da grande maioria das séries temporais financeiras obedecem. Seu excesso é igual a 3 (ou seja, seu topo é mais nítido do que o da distribuição normal), mas as caudas são grossas - elas diminuem de acordo com a lei exp(-x), ou seja, mais lentamente do que a da Gaussiana exp(-x^2).
Isso é fundamentalmente errado.
Em primeiro lugar, vamos falar em russo e chamar "curtose" e "insularidade" pelo termo aceito - coeficiente de curtose ou simplesmente curtose.
Em segundo lugar, "insularidade" e "caudas gordas", em geral, não estão relacionadas de forma alguma. Aqui está um contraexemplo - a distribuição de Laplace (exponencial bilateral), à qual, diga-se de passagem, os gráficos da grande maioria das séries temporais financeiras obedecem. Seu excesso é igual a 3 (ou seja, o topo é mais nítido do que na distribuição normal), mas as caudas são apenas grossas - elas diminuem de acordo com a lei exp(-x), ou seja, mais lentamente do que na Gaussiana exp(-x^2).
Além disso, não há um conceito de "Excesso" propriamente dito, há um conceito de "Razão de Excesso", que é uma medida para outro conceito "Excesso de Distribuição", e esse conceito é definido somente para distribuições unimodais. Assim, para usar esse coeficiente corretamente, é necessário, em primeiro lugar, determinar a função de distribuição empírica, o que não é uma tarefa trivial do ponto de vista da matemática, e, em segundo lugar, dentro da estrutura de alguns critérios probabilísticos, verificar e aceitar a hipótese de que a distribuição tem um único modo, o que nem sempre é cumprido para séries financeiras e também é uma tarefa não trivial. Sem essas etapas, o cálculo adicional é impossível, se for necessário o "Coeficiente de excesso".
P.S..
Não há nada escrito sobre o que fazer se o teste indicar que a série não é aplicável ao modelo assumido.
Nada é dito sobre por que e com base em que uma série dos chamados "rendimentos" e não outra é usada.
Na prática, o principal motivo pelo qual trabalhar com retornos de ativos é preferível a trabalhar com preços diretos de ativos é que os retornos têm propriedades estatísticas mais atraentes.
alsu:
...Vamos falar russo e chamar "curtose" e "insularidade" pelo termo aceito - coeficiente de excesso ou apenas excesso....
Gostei especialmente do fato de que alsu considera as palavras "coeficiente" e "excesso" como sendo russas...
alsu:
Em segundo lugar, a "insularidade" e as "caudas gordas" geralmente não estão relacionadas. Aqui está um contraexemplo: a distribuição de Laplace (exponencial bilateral), à qual, vale ressaltar, os gráficos da grande maioria das séries temporais financeiras obedecem. Seu excesso é igual a 3 (ou seja, o topo é mais nítido do que na distribuição normal), mas as caudas são apenas grossas - elas diminuem de acordo com a lei exp(-x), ou seja, mais lentamente do que na Gaussiana exp(-x^2).
É exatamente isso que acredito estar relacionado de modo geral.
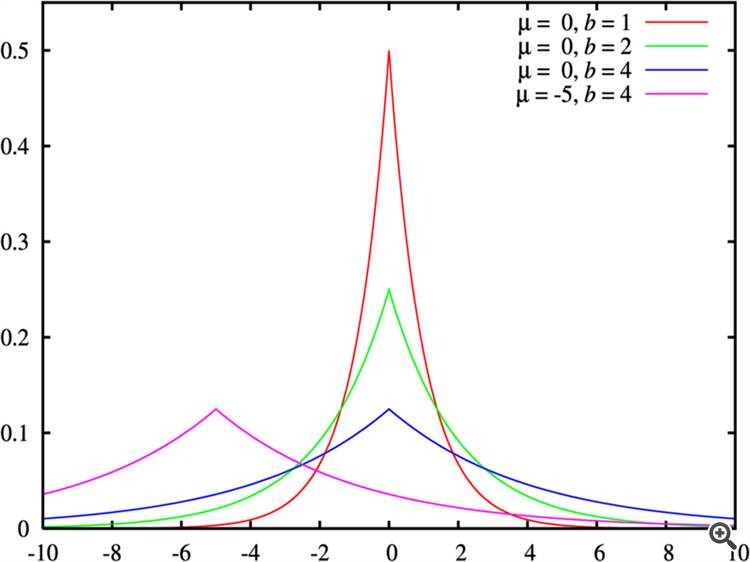
Um exemplo de "menos curtose - caudas mais grossas" é mostrado na Fig. "Distribuições de Laplace com diferentes parâmetros".
Eu apenas acrescentaria a seguinte frase ao meu artigo: "A distribuição de uma série de retornos exibe mais frequentemente um comportamento de cauda gorda do que a distribuição normal." O fenômeno das "caudas gordas" é chamado de excesso de curtose na literatura em inglês. As séries cujas distribuições têm essas caudas são chamadas de leptocúrticas, com curtose positiva (excedendo a curtose da distribuição normal).
Em seguida, sobre o coeficiente de curtose:
Adistribuição normal tem curtose zero, γ2 = 0.
Se as caudas da distribuição forem "mais leves" e o pico for mais acentuado do que a distribuição normal, então γ2 > 0.
Se as caudas da distribuição forem "mais pesadas" e o pico for mais "achatado" do que a distribuição normal, então γ2 < 0.
Eu apenas acrescentaria essa sugestão ao meu artigo:
Eu apenas acrescentaria a seguinte frase ao meu artigo: "A distribuição de uma série de retornos exibe mais frequentemente um comportamento de cauda gorda do que a distribuição normal." O fenômeno das "caudas gordas" é chamado de excesso de curtose na literatura em inglês. As séries cujas distribuições têm essas caudas são chamadas de leptocúrticas, com curtose positiva (excedendo a curtose da distribuição normal).
Em seguida, sobre o coeficiente de curtose:
Adistribuição normal tem curtose zero, γ2 = 0.
Se as caudas da distribuição forem "mais leves" e o pico for mais acentuado do que a distribuição normal, então γ2 > 0.
Se as caudas da distribuição forem "mais pesadas" e o pico for mais "achatado" do que a distribuição normal, então γ2 < 0.
Enquanto vocês estão discutindo os termos, eu já criei alguns EAs lucrativos de um dia para o outro usando as ideias deste artigo. :-)
Entretanto, seus lucros são muito pequenos, embora sejam bastante estáveis (verificados no histórico de 12 anos, os gráficos crescem lindamente). As correlações detectadas pelos métodos descritos no artigo são bastante fracas ( os coeficientes de autocorrelação da série são de cerca de 0,01, em casos excepcionais se aproximando de 0,1, dependendo de quais derivativos de preço estão correlacionados) e, ao negociar, o lucro deles é fortemente superado pelo spread. Tive de adicionar um filtro para fazer negociações somente na chegada de sinais fortes, caso contrário, a curva de lucratividade cairia quase em linha reta.
De qualquer forma, agradeço ao autor. As ideias são valiosas. Acho que os críticos não devem enfiar o nariz do autor nos abismos da teoria matemática, mas considerar o artigo como uma indicação de um amplo campo para experimentos práticos.
Enquanto vocês estão discutindo os termos, eu já criei alguns EAs lucrativos de um dia para o outro usando as ideias deste artigo. :-)
Entretanto, seus lucros são muito pequenos, embora sejam bastante estáveis (verificados no histórico de 12 anos, os gráficos crescem lindamente). As correlações detectadas pelos métodos descritos no artigo são bastante fracas (os coeficientes de autocorrelação da série são de cerca de 0,01, em casos excepcionais se aproximando de 0,1, dependendo de quais derivativos de preço estão correlacionados) e, ao negociar, o lucro deles é fortemente superado pelo spread. Tive de adicionar um filtro para fazer negociações somente na chegada de sinais fortes, caso contrário, a curva de lucratividade cairia quase em linha reta.
De qualquer forma, agradeço ao autor. As ideias são valiosas. Acho que os críticos não devem enfiar o nariz do autor nos abismos da teoria matemática, mas considerar o artigo como uma indicação de um amplo campo para experimentos práticos.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Abordagem econométrica para análise de gráficos foi publicado:
Este artigo descreve os métodos econométricos de análise, a análise de autocorrelação e a análise de variância condicional em particular. Qual é o benefício da abordagem descrita aqui? O uso de modelos GARCH permite representar a série analisada formalmente a partir do ponto de vista matemático e criar uma previsão para um determinado número de passos.
Autor: Dennis Kirichenko